Lebesgue regularity for differential difference equations with fractional damping
Corresponding Author
Carlos Lizama
Facultad de Ciencias, Departamento de Matemática y Ciencia de la Computación, Universidad de Santiago de Chile, Las Sophoras 173, Estación Central, Santiago, Chile
Correspondence
Carlos Lizama, Facultad de Ciencias, Departamento de Matemática y Ciencia de la Computación, Universidad de Santiago de Chile, Las Sophoras 173, Estación Central, Santiago, Chile.
Email: [email protected]
Search for more papers by this authorMarina Murillo-Arcila
Institut de Matemàtiques i Aplicacions de Castelló (IMAC), Universitat Jaume I, Campus del Riu Sec s/n, 12071, Castelló, Spain
Search for more papers by this authorClaudio Leal
Facultad de Ciencias, Departamento de Matemática y Ciencia de la Computación, Universidad de Santiago de Chile, Las Sophoras 173, Estación Central, Santiago, Chile
Search for more papers by this authorCorresponding Author
Carlos Lizama
Facultad de Ciencias, Departamento de Matemática y Ciencia de la Computación, Universidad de Santiago de Chile, Las Sophoras 173, Estación Central, Santiago, Chile
Correspondence
Carlos Lizama, Facultad de Ciencias, Departamento de Matemática y Ciencia de la Computación, Universidad de Santiago de Chile, Las Sophoras 173, Estación Central, Santiago, Chile.
Email: [email protected]
Search for more papers by this authorMarina Murillo-Arcila
Institut de Matemàtiques i Aplicacions de Castelló (IMAC), Universitat Jaume I, Campus del Riu Sec s/n, 12071, Castelló, Spain
Search for more papers by this authorClaudio Leal
Facultad de Ciencias, Departamento de Matemática y Ciencia de la Computación, Universidad de Santiago de Chile, Las Sophoras 173, Estación Central, Santiago, Chile
Search for more papers by this authorAbstract
We provide necessary and sufficient conditions for the existence and uniqueness of solutions belonging to the vector-valued space of sequences
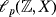for equations that can be modeled in the form
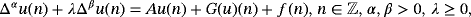
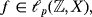A is a closed linear operator with domain D(A) defined on X, and G is a nonlinear function. The operator Δγ denotes the fractional difference operator of order γ>0 in the sense of Grünwald-Letnikov. Our class of models includes the discrete time Klein-Gordon, telegraph, and Basset equations, among other differential difference equations of interest. We prove a simple criterion that shows the existence of solutions assuming that f is small and that G is a nonlinear term.
REFERENCES
- 1Bateman H. Some simple differential difference equations and the related functions. Bull Amer Math Soc. 1943; 49: 494-512.
10.1090/S0002-9904-1943-07927-X Google Scholar
- 2Agarwal RP. Difference Equations and Inequalities. Theory, Methods, and Applications. Second edition. Monographs and Textbooks in Pure and Applied Mathematics, Vol. 228. New York: Marcel Dekker, Inc.; 2000.
- 3Elaydi S. An Introduction to Difference Equations. 3rd ed., Undergraduate Texts in Mathematics. New York: Springer-Verlag; 2005.
- 4Atanackovic TM, Pilipovic S, Zorica D. A diffusion wave equation with two fractional derivatives of different order. Phys, J A: Math Theory. 2007; 40: 5319-5333.
- 5Golmankhaneh AK, Golmankhaneh A, Baleanu D. On nonlinear fractional Klein-Gordon equation. Signal Process. 2011; 91: 446-451.
- 6Mainardi F. Fractional Calculus, Some Basic Problems in Continuum and Statistical Mechanics. International Centre for Mechanical Sciences Palazzo del Torso, Piazza Garibaldi, Udine, Italy: CISM lectures; 1997.
- 7Baleanu D, Garra R, Petras I. A fractional variational approach to the fractional Basset-type equation. Rep Math Phys. 2013; 72(1): 57-64.
- 8Beyer H, Kempfle S. Definition of physically consistent damping laws with fractional derivatives. Z Angew Math Mech. 1995; 75(8): 623-635.
- 9Abadías L, Lizama C. Almost automorphic mild solutions to fractional partial difference-differential equations. Appl Anal. 2016; 95(6): 1347-1369.
- 10Ortigueira MD, Coito FJV, Trujillo JJ. Discrete-time differential systems. Signal Process. 2015; 107: 198-217.
- 11Atici FM, Sengul S. Modeling with fractional difference equations. J Math Anal Appl. 2010; 369: 1-9.
- 12Atici FM, Eloe PW. Initial value problems in discrete fractional calculus. Proc Amer Math Soc. 2009; 137(3): 981-989.
- 13Lizama C. The Poisson distribution, abstract fractional difference equations, and stability. Proc Amer Math Soc. 2017; 145(9): 3809-3827.
- 14Dahal R, Goodrich CS. A monotonicity result for discrete fractional difference operators. Arch Math (Basel). 2014; 102(3): 293-299.
- 15Goodrich CS. Existence of a positive solution to a system of discrete fractional boundary value problems. Appl Math Comput. 2011; 217: 4740-4753.
- 16Goodrich CS. A convexity result for fractional differences. Appl Math Lett. 2014; 35: 58-62.
- 17Ferreira R. Existence and uniqueness of solution to some discrete fractional boundary value prob- lems of order less than one. J Differ Equ Appl. 2013; 19: 712-718.
- 18Holm MT. The Laplace transform in discrete fractional calculus. Comp Math Appl. 2011; 62(3): 1591-1601.
- 19Kovács B, Li B, Lubich C. A-Stable time discretizations preserve maximal parabolic regularity. SIAM J Numer Anal. 2016; 54(6):36003624.
- 20Dassios IK. Stability and robustness of singular systems of fractional nabla difference equations. Circuits Syst Signal Process. 2016; 36(1): 49-64.
- 21Dassios IK. Geometric relation between two different types of initial conditions of singular systems of fractional nabla difference equations. Math Meth Appl Sci. 2017; 40(17): 6085-6095.
- 22Dassios IK, Baleanu DI. Duality of singular linear systems of fractional nabla difference equations. Appl Math Modell. 2015; 39(14): 4180-4195.
- 23Wu GC, Baleanu D. Discrete chaos in fractional delayed logistic maps. Nonlinear Dyn. 2016; 80(4): 1697-1703.
- 24Wu GC, Baleanu D, Xie H-P. Riesz Riemann-Liouville difference on discrete domains. Chaos. 2016; 26(8): 084308, 5.
- 25Wu GC, Baleanu D, Deng ZG, Zeng SD. Lattice fractional diffusion equation in terms of a Riesz-Caputo difference. Phys A. 2015; 438: 335-339.
- 26Tarasov VE. Fractional-order difference equations for physical lattices and some applications. J Math Phys. 2015; 56(10): 1-19.
- 27Tarasov VE. Fractional Liouville equation on lattice phase-space. Phys A. 2015; 421: 330-342.
- 28Tarasova VV, Tarasov VE. Logistic map with memory from economic model. Chaos Solitons Fractals. 2017; 95: 84-91.
- 29Blunck S. Maximal regularity of discrete and continuous time evolution equations. Studia Math. 2001; 146(2): 157-176.
- 30Jin B, Li B, Zhou Z. Discrete maximal regularity of time-stepping schemes for fractional evolution equations. arXiv:1606.07587v1 [math.NA].
- 31Kemmochi T. Discrete maximal regularity for abstract Cauchy problems. Studia Math. 2016; 234(3): 241-263.
- 32Lizama C. ℓp-maximal regularity for fractional difference equations on UMD spaces. Math Nach. 2015; 288(17/18): 2079-2092.
- 33Lizama C, Murillo-Arcila M. ℓp-maximal regularity for a class of fractional difference equations on UMD spaces: the case 1<α<2. Banach. J Math Anal. 2017; 11(1): 188-206.
- 34Agarwal RP, Cuevas C, Lizama C. Regularity of Difference Equations on Banach Spaces. Cham: Springer-Verlag; 2014.
10.1007/978-3-319-06447-5 Google Scholar
- 35Denk R, Hieber M, Prüss J.
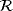-boundedness, Fourier multipliers and problems of elliptic and parabolic type. Mem Amer Math Soc. 2003; 166(788).
- 36Abadías L, Lizama C, Miana PJ, Velasco MP. Cesàro sums and algebra homomorphisms of bounded operators. Israel J Math. 2016; 216(1): 471-505.
- 37Zygmund A. Trigonometric Series. 2nd ed., Vol. I, II. New York (NY): Cambridge University Press; 1959.
- 38Lizama C, Murillo-Arcila M. Maximal regularity in lp spaces for discrete time fractional shifted equations. J Differ Equ. 2017; 263(6): 3175-3196.
