A new analysis for fractional model of regularized long-wave equation arising in ion acoustic plasma waves
Corresponding Author
Devendra Kumar
Department of Mathematics, JECRC University, Rajasthan, Jaipur-303905 India
Correspondence to: Devendra Kumar, Department of Mathematics, JECRC University, Jaipur-303905, Rajasthan, India.
E-mail: [email protected]
Search for more papers by this authorJagdev Singh
Department of Mathematics, JECRC University, Rajasthan, Jaipur-303905 India
Search for more papers by this authorDumitru Baleanu
Department of Mathematics, Faculty of Arts and Sciences, Cankaya University, Eskisehir Yolu 29. Km, Etimesgut, Yukariyurtcu Mahallesi Mimar Sinan Caddesi No: 4 06790 Turkey
Institute of Space Sciences, Magurele-Bucharest, Romania
Search for more papers by this authorCorresponding Author
Devendra Kumar
Department of Mathematics, JECRC University, Rajasthan, Jaipur-303905 India
Correspondence to: Devendra Kumar, Department of Mathematics, JECRC University, Jaipur-303905, Rajasthan, India.
E-mail: [email protected]
Search for more papers by this authorJagdev Singh
Department of Mathematics, JECRC University, Rajasthan, Jaipur-303905 India
Search for more papers by this authorDumitru Baleanu
Department of Mathematics, Faculty of Arts and Sciences, Cankaya University, Eskisehir Yolu 29. Km, Etimesgut, Yukariyurtcu Mahallesi Mimar Sinan Caddesi No: 4 06790 Turkey
Institute of Space Sciences, Magurele-Bucharest, Romania
Search for more papers by this authorAbstract
The key purpose of the present work is to constitute a numerical scheme based on q-homotopy analysis transform method to examine the fractional model of regularized long-wave equation. The regularized long-wave equation explains the shallow water waves and ion acoustic waves in plasma. The proposed technique is a mixture of q-homotopy analysis method, Laplace transform, and homotopy polynomials. The convergence analysis of the suggested scheme is verified. The scheme provides
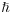and n-curves, which show that the range convergence of series solution is not a local point effects and elucidate that it is superior to homotopy analysis method and other analytical approaches. Copyright © 2017 John Wiley & Sons, Ltd.
References
- 1Peregrine DH. Calculations of the development of an undular bore. Journal of Fluid Mechanics 1966; 25: 321–330.
- 2Benjamin TB, Bona JL, Mahony JJ. Model equations for long waves in nonlinear dispersive systems. Philosophical Transactions of the Royal Society A 1972; 272: 47–78.
- 3Miller KS, Ross B. An Introduction to the Fractional Calculus and Fractional Differential Equations. Willey: New York, NY, USA, 1993.
- 4Podlubny I. Fractional Differential Equations, vol. 198. Academic Press: San Diego, Calif, USA, 1999. 340 pages.
- 5Caputo M. Elasticita e Dissipazione. Zani-Chelli: Bologna, 1969.
- 6Kilbas AA, Srivastava HM, Trujillo JJ. Theory and Applications of Fractional Differential Equations, vol. 204. Elsevier: Amsterdam, 2006. 540 pages.
10.1016/S0304-0208(06)80001-0 Google Scholar
- 7Baskonus HM, Mekkaoui T, Hammouch Z, Bulut H. Active control of a chaotic fractional order economic system. Entropy 2015; 17(8): 5771–5783.
- 8Kumar D, Singh J, Baleanu D. A hybrid computational approach for Klein–Gordon equations on Cantor sets. Nonlinear Dynamics 2017; 87: 511–517.
- 9Atangana A. On the new fractional derivative and application to nonlinear Fisher's reaction-diffusion equation. Applied Mathematics and Computation 2016; 273: 948–956.
- 10Bhrawy AH, Zaky MA, Baleanu D. New numerical approximations for space-time fractional Burgers' equations via a Legendre spectral-collocation method. Romanian Reports in Physics 2015; 67(2): 340–349.
- 11Area I, Batarfi H, Losada J, Nieto JJ, Shammakh W, Torres A. On a fractional order Ebola epidemic model. Advances in Difference Equations 2015; 278. https://doi.org/10.1186/s13662-015-0613-5.
- 12Carvalho A, Pinto CMA. A delay fractional order model for the co-infection of malaria and HIV/AIDS. International Journal of Dynamics and Control 2017; 5(1): 168–186.
10.1007/s40435-016-0224-3 Google Scholar
- 13El-Danaf TS, Ramadan MA, Alaal FEIA. The use of adomian decomposition method for solving the regularized long-wave equation. Chaos Solitions & Fractals 2005; 26: 747–757.
- 14Soltanalizadeh B, Yildirim A. Application of differential transformation method for numerical computation of regularized longwave equation. Zeitschrift für Naturforschung A 2012; 67a: 160–166.
- 15Hossieni MM, Ghaneai H, Mohyuddin ST, Usman M. Tri-prong scheme for regularized long wave equation. Journal of the Association of Arab Universities for Basic and Applied Sciences 2016; 20: 68–77.
10.1016/j.jaubas.2014.08.002 Google Scholar
- 16Aminikhah H, Sheikhani AHR, Rezazadeh H. Sub-equation method for the fractional regularized long-wave equations with conformable fractional derivatives. Scientia Iranica 2016; 23(3): 1048–1054.
10.24200/sci.2016.3873 Google Scholar
- 17Oruc O, Bulut F, Esen A. Numerical solutions of regularized long wave equation by haar wavelet method. Mediterranean Journal of Mathematics 2016; 13(5): 3235–3253.
- 18Liao SJ. Beyond Perturbation: Introduction to Homotopy Analysis Method. Chapman and Hall / CRC Press: Boca Raton, 2003.
10.1201/9780203491164 Google Scholar
- 19Liao SJ. On the homotopy analysis method for nonlinear problems. Applied Mathematics and Computation 2004; 147: 499–513.
- 20Liao SJ. An approximate solution technique not depending on small parameters: a special example. International Journal of Non-Linear Mechanics 1995; 30(3): 371–380.
- 21El-Tawil MA, Huseen SN. The q-homotopy analysis method (q-HAM). International Journal of Applied Mathematics and Mechanics 2012; 8: 51–75.
- 22El-Tawil MA, Huseen SN. On convergence of the q-homotopy analysis method. International Journal of Contemporary Mathematical Sciences 2013; 8: 481–497.
10.12988/ijcms.2013.13048 Google Scholar
- 23Khuri SA. A Laplace decomposition algorithm applied to a class of nonlinear differential equations. Journal of Applied Mathematics 2001; 1: 141–155.
10.1155/S1110757X01000183 Google Scholar
- 24Khan M, Gondal MA, Hussain I, Vanani SK. A new comparative study between homotopy analysis transform method and homotopy perturbation transform method on semi-infinite domain. Mathematical and Computer Modelling 2012; 55: 1143–1150.
- 25Kumar D, Singh J, Kumar S, Sushila, Singh BP. Numerical computation of nonlinear shock wave equation of fractional order. Ain Shams Engineering Journal 2015; 6(2): 605–611.
- 26Srivastava HM, Kumar D, Singh J. An efficient analytical technique for fractional model of vibration equation. Applied Mathematical Modelling 2017; 45: 192–204.
- 27Kumar D, Singh J, Baleanu D. A fractional model of convective radial fins with temperature-dependent thermal conductivity. Romanian Reports in Physics 2017; 69(1): Article no. 103.
- 28Kumar S, Kumar A, Argyros IK. A new analysis for the Keller–Segel model of fractional order. Numeral Algorithms 2017; 75(1): 213–228.
- 29Singh J, Kumar D, Swroop R. Numerical solution of time- and space-fractional coupled Burgers equations via homotopy algorithm. Alexandria Engineering Journal 2016; 55(2): 1753–1763.
- 30Odibat Z, Bataineh SA. An adaptation of homotopy analysis method for reliable treatment of strongly nonlinear problems: construction of homotopy polynomials. Mathematical Methods in Applied Sciences 2015; 38(5): 991–1000.
- 31Argyros IK. Convergence and Applications of Newton-type Iterations. Springer-Verlag: New York, 2008.
- 32Magrenan AA. A new tool to study real dynamics: the convergence plane. Applied Mathematics and Computation 2014; 248: 215–224.
