Infinitely many large energy solutions for superlinear Dirac equations
Jian Zhang
School of Mathematics and Statistics, Central South University, Changsha, 410083 Hunan, China
Search for more papers by this authorCorresponding Author
Xianhua Tang
School of Mathematics and Statistics, Central South University, Changsha, 410083 Hunan, China
Correspondence to: Xianhua Tang, School of Mathematics and Statistics, Central South University, Changsha, 410083 Hunan, China.
E-mail: [email protected]
Search for more papers by this authorWen Zhang
School of Mathematics and Statistics, Central South University, Changsha, 410083 Hunan, China
Search for more papers by this authorJian Zhang
School of Mathematics and Statistics, Central South University, Changsha, 410083 Hunan, China
Search for more papers by this authorCorresponding Author
Xianhua Tang
School of Mathematics and Statistics, Central South University, Changsha, 410083 Hunan, China
Correspondence to: Xianhua Tang, School of Mathematics and Statistics, Central South University, Changsha, 410083 Hunan, China.
E-mail: [email protected]
Search for more papers by this authorWen Zhang
School of Mathematics and Statistics, Central South University, Changsha, 410083 Hunan, China
Search for more papers by this authorAbstract
This paper is concerned with the nonlinear Dirac equations
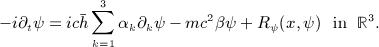
Under suitable assumptions on the nonlinearity, we establish the existence of infinitely many large energy solutions by the generalized variant fountain theorem developed recently by Batkam and Colin. Copyright © 2014 John Wiley & Sons, Ltd.
References
- 1 Thaller B. The Dirac Equation, Texts and Monographs in Physics. Springer: Berlin, 1992.
- 2 Balabane M, Cazenave T, Douady A, Merle F. Existence of excited states for a nonlinear Dirac field. Communications in Mathematical Physics 1988; 41: 153–176.
- 3 Balabane M, Cazenave T, Vazquez L. Existence of standing waves for Dirac fields with singular nonlinearities. Communications in Mathematical Physics 1990; 133: 53–74.
- 4 Cazenave T, Vazquez L. Existence of local solutins of a classical nonlinear Dirac field. Communications in Mathematical Physics 1986; 105: 35–47.
- 5 Merle F. Existence of stationary states for nonlinear Dirac equations. Journal of Different Equations 1988; 74: 50–68.
- 6 Esteban MJ. E. Séré. Stationary states of nonlinear Dirac equations: A variational approach. Communications in Mathematical Physics 1995; 171: 323–350.
- 7 Esteban MJ, Séré E. An overview on linear and nonlinear Dirac equations. Discrete and Continuous Dynamical System, Series A 2002; 8: 281–397.
- 8 Bartsch T, Ding YH. Deformation theorems on non-metrizable vector spaces and applications to critical point theory. Mathematische Nachrichten 2006; 279: 1267–1288.
- 9 Ding YH. Variational Methods for Strongly Indefinite Problems. World Scientific Press, Scientific Press: Singapore, 2008.
- 10
Kryszewski W,
Szulkin A. Generalized linking theorem with an application to semilinear Schrödinger equations. Advances in Differential Equations 1998; 3: 441–472.
10.57262/ade/1366399849 Google Scholar
- 11 Bartsch T, Ding YH. Solutions of nonlinear Dirac equations. Journal of Differential Equations 2006; 226: 210–249.
- 12 Ding YH, Ruf B. Solutions of a nonlinear Dirac equation with external fields. Archive for Rational Mechanics and Analysis 2008; 190: 57–82.
- 13 Ding YH, Wei JC. Stationary states of nonlinear Dirac equations with general potentials. Reviews in Mathematical Physics 2008; 20: 1007–1032.
- 14 Zhao FK, Ding YH. Infinitely many solutions for a class of nonlinear Dirac equations without symmetry. Nonlinear Analysis 2009; 70: 921–935.
- 15 Yang MB, Ding YH. Stationary states for nonlinear Dirac equations with superlinear nonlinearities. Topological Methods in Nonlinear Analysis 2012; 39: 175–188.
- 16 Zhang J, Qin WP, Zhao FK. Multiple solutions for a class of nonperiodic Dirac equations with vector potentials. Nonlinear Analysis 2012; 75: 5589–5600.
- 17 Zhang J, Tang XH, Zhang W. Ground state solutions for nonperiodic Dirac equation with superquadratic nonlinearity. Journal of Mathematical Physics 2013; 54: 101502.
- 18 Zhang J, Tang XH, Zhang W. On ground state solutions for superlinear Dirac equation. Acta Mathematica Scientia 2014; 34: 840–850.
- 19 Ding YH, Ruf B. Existence and concentration of semi-classical solutions for Dirac equations with critical nonlinearites. SIAM Journal on Mathematical Analysis 2012; 44: 3755–3785.
- 20 Ding YH. Semi-classical ground states concentrating on the nonlinear potential for a Dirac equation. Journal of Differential Equations 2010; 249: 1015–1034.
- 21 Ding YH, Liu XY. Semi-classical limits of ground states of a nonlinear Dirac equation. Journal of Differential Equations 2012; 252: 4962–4987.
- 22 Ding YH, Liu XY. On Semiclassical ground states of a nonlinear Dirac equation. Reviews in Mathematical Physics 2012; 24:1250029.
- 23 Ding YH, Lee C, Ruf B. On semiclassical states of a nonlinear Dirac equation. Proceedings of the Royal Society of Edinburgh Section A 2013; 143: 765–790.
- 24 Bartsch T. Infinitely many solutions of a symmetric Dirichlet problem. Nonlinear Analysis 1993; 20: 1205–1216.
- 25 Willem M. Minimax Theorems. Birkhäuser: Berlin, 1996.
- 26 Zou WM. Variant fountain theorems and their applications. Manuscripta Mathematica 2001; 104: 343–358.
- 27 Batkam CJ, Colin F. On multiple solutions of a semilinear Schrödinger equation with periodic potential. Nonlinear Analysis 2013; 84: 39–49.
- 28 Zhang J, Tang XH, Zhang W. Homoclinic orbits of nonperiodic superquadratic Hamiltonian system. Taiwan Journal of Mathematics 2013; 17: 1855–1867.
- 29 Lions PL. The concentration compactness principle in the calculus of variations. The locally compact case. Part II. Annales de l'institut Henri Poincaré (C) Analyse Non Linéaire 1984; 1: 223–283.




