Stochastic logistic equation with infinite delay

This paper perturbs the famous logistic equation with infinite delay

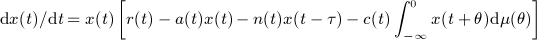
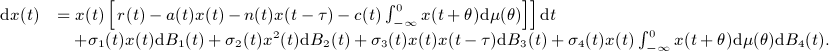
This study shows that the above stochastic system has a global positive solution with probability 1 and gives the asymptotic pathwise estimation of this solution. In addition, the superior limit of the average in time of the sample path of the solution is estimated. This work also establishes the sufficient conditions for extinction, nonpersistence in the mean, and weak persistence of the solution. The critical value between weak persistence and extinction is obtained. Then these results are extended to n-dimensional stochastic Lotka–Volterra competitive system with infinite delay. Finally, this paper provides some numerical figures to illustrate the results. The results reveal that, firstly, different types of environmental noises have different effects on the persistence and extinction of the population system; secondly, the delay has no effect on the persistence and extinction of the stochastic system.Copyright © 2012 John Wiley & Sons, Ltd.