Original Paper
Fractional integration operators of variable order: continuity and compactness properties
Mikhail Lifshits,
Werner Linde,
Mikhail Lifshits
Department of Mathematics and Mechanics, St. Petersburg State University, 198504 St. Petersburg, Russia
MAI, Linköping University, 58183 Linköping, Sweden
e-mail: [email protected]
Search for more papers by this authorCorresponding Author
Werner Linde
Friedrich-Schiller-Universität Jena, Institut für Stochastik, Ernst-Abbe-Platz 2, 07743 Jena, Germany
Corresponding author: e-mail: [email protected]Search for more papers by this authorMikhail Lifshits,
Werner Linde,
Mikhail Lifshits
Department of Mathematics and Mechanics, St. Petersburg State University, 198504 St. Petersburg, Russia
MAI, Linköping University, 58183 Linköping, Sweden
e-mail: [email protected]
Search for more papers by this authorCorresponding Author
Werner Linde
Friedrich-Schiller-Universität Jena, Institut für Stochastik, Ernst-Abbe-Platz 2, 07743 Jena, Germany
Corresponding author: e-mail: [email protected]Search for more papers by this authorAbstract
Let 
be a Lebesgue-almost everywhere positive function. We consider the Riemann-Liouville operator of variable order defined by
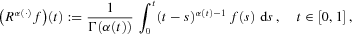
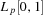to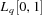 
. Our first aim is to study its continuity properties. For example, we show that 
is always bounded (continuous) in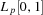 
provided that 
. Surprisingly, this becomes false for 
. In order 
to be bounded in L1[0, 1], the function 
has to satisfy some additional assumptions.
In the second, central part of this paper we investigate compactness properties of 
. We characterize functions 
for which 
is a compact operator and for certain classes of functions 
we provide order-optimal bounds for the dyadic entropy numbers 
.
References
- 1J. A. Adell and E. A. Gallardo-Gutiérrez, The norm of the Riemann-Liouville operator on
: a probabilistic approach, Bull. Lond. Math. Soc. 39, 565–574 (2007).
- 2K. F. Andersen and E. T. Sawyer, Weighted norm inequalities for the Riemann-Liouville and Weyl fractional integration operators, Trans. Am. Math. Soc. 308, 547–558 (1988).
- 3A. Ayache, S. Cohen, and J. Lévy Véhel, The covariance structure of multifractional Brownian motion, in: Proceedings of 6th IEEE International Conference on Acoustics, Speech, and Signal Processing, 3810–3813 (2000).
- 4E. S. Belinsky and W. Linde, Small ball probabilities of fractional Brownian sheets via fractional integration operators, J. Theor. Probab. 15, 589–612 (2002).
- 5E.S. Belinsky and W. Linde, Compactness properties of certain integral operators related to fractional integration, Math. Z. 252, 669–686 (2006).
- 6A. Benassi, S. Jaffard, and D. Roux, Gaussian processes and pseudodifferential elliptic operators, Rev. Mat. Iberoam. 13, 19–81 (1997).
- 7B. Carl, A. Hinrichs, and P. Rudolph, Entropy numbers of convex hulls in Banach spaces and applications, Preprint arXiv:1211.1559 (2012).
- 8B. Carl and I. Stephani, Entropy, Compactness and Approximation of Operators (Cambridge Univ. Press, Cambridge, 1990).
10.1017/CBO9780511897467 Google Scholar
- 9K. Debicki and P. Kisowski, Asymptoticsc of supremum distribution of
-locally stationary Gaussian processes, Stochastic Processes Appl. 118, 2022–2037 (2008).
- 10L. Diening et al., Lebesgue and Sobolev Spaces with Variable Exponents, Lecture Notes Math. 2017 (Springer, 2011).
- 11D. E. Edmunds and H. Triebel, Function Spaces, Entropy Numbers and Differential Operators (Cambridge Univ. Press, Cambridge, 1996).
10.1017/CBO9780511662201 Google Scholar
- 12K. J. Falconer and J. Lévy Véhel, Multifractional, multistable and other processes with prescribed local form, J. Theor. Probab. 22, 375–401 (2009).
- 13G. H. Hardy, J. E. Littlewood, and G. Polya, Inequalities (Cambridge Univ. Press, Cambridge, 1967).
- 14E. Hashorva, M. Lifshits, and O. Seleznjev, Approximation of a random process with variable smoothness, Preprint arXiv:1206.1251 (2012).
- 15L. Hedberg, On certain convolution inequalities, Proc. Am. Math. Soc. 36, 505–510 (1972).
- 16Z. Huang and B. He, Volume of unit ball in a n-dimensional normed space and its asymptotic properties, J. Shanghai Univ. 12, 107–109 (2008).
10.1007/s11741-008-0204-1 Google Scholar
- 17B. Jawerth, C. Perez, and G. Welland, The positive cone in Triebel-Lizorkin spaces and the relation among potential and maximal operators, Contemp. Math. 107, 71–91 (1990).
10.1090/conm/107/1066471 Google Scholar
- 18M. A. Krasnoselskii et al., Integral Operators in Spaces of Summable Functions (Noordhoff Intern. Publishing, Leyden, 1976).
10.1007/978-94-010-1542-4 Google Scholar
- 19Th. Kühn and W. Linde, Optimal series representation of fractional Brownian sheet, Bernoulli 8, 669–696 (2002).
- 20M. Lifshits and W. Linde, Fractional integration operators of variable order: continuity and compactness properties, Preprint arXiv: 1211.3826 (2012).
- 21W. Li and W. Linde, Approximation, metric entropy and small ball estimates for Gaussian measures, Ann. Probab. 27, 1556–1578 (1999).
- 22W. Linde, Non-determinism of linear operators and lower entropy estimates, J. Fourier Anal. Appl. 14, 568–587 (2008).
- 23E. N. Lomakina and V. D. Stepanov, Asymptotic estimates for the approximation and entropy numbers of a one-weight Riemann-Liouville operator, Mat. Tr. 9, 52–100 (2006); English translation: Sib. Adv. Math. 17, 1–36 (2007).
- 24S. G. Samko, Differentiation and integration of variable order and the spaces
in: Proceedings of Conference on Operator Theory for Complex and Hypercomplex Analysis (Mexico City, 1994), Contemp. Math. Vol. 212 (Amer. Math. Soc., Providence, RI, 1998), pp. 203–219.
- 25S. G. Samko, A. A. Kilbas, and O. I. Marichev, Fractional Integrals and Derivatives (Gordon and Breach, Amsterdam, 1993).
- 26S. G. Samko and B. Ross, Integration and differentiation to a variable fractional order, Integral Transforms and Special Functions 1, 277–300 (1993).
10.1080/10652469308819027 Google Scholar
- 27N. Samko, S. Samko, and B. Vakulov, Fractional integrals and hypersingular integrals in variable order spaces on homogeneous spaces, J. Funct. Spaces Appl. 8, 215–244 (2010).
- 28N. Samko and B. Vakulov, Spherical fractional and hypersingular integrals of variable order in generalized Hölder spaces with variable characteristic, Math. Nachr. 284, 355–369 (2011).
- 29E. M. Stein and G. Weiss, Introduction to Fourier Analysis on Euclidean Spaces (Princeton Univ. Press, Princeton, N.J., 1971).
- 30D. Surgailis, Non-homogeneous fractional integration and multifractional processes, Stoch. Proc. Appl. 116, 200–221 (2006).
