The subject is traces of Sobolev spaces with mixed Lebesgue norms on Euclidean space. Specifically, restrictions to the hyperplanes given by x₁ = 0 and x_n = 0 are applied to functions belonging to quasi-homogeneous, mixed norm Lizorkin–Triebel spaces 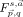equation image ; Sobolev spaces are obtained from these as special cases. Spaces admitting traces in the distribution sense are characterised up to the borderline cases; these are also covered in case x₁ = 0. For x₁ the trace spaces are proved to be mixed-norm Lizorkin–Triebel spaces with a specific sum exponent; for x_n they are similarly defined Besov spaces. The treatment includes continuous right-inverses and higher order traces. The results rely on a sequence version of Nikol'skij's inequality, Marschall's inequality for pseudodifferential operators (and Fourier multiplier assertions), as well as dyadic ball criteria. (© 2008 WILEY-VCH Verlag GmbH & Co. KGaA, Weinheim)

References

[1] H. Amann, Linear and Quasilinear Parabolic Problems. Vol. I: Abstract Linear Theory, Monographs in Mathematics Vol. 89 (Birkhäuser Boston Inc., Boston, MA, 1995).
Google Scholar
[2] R. J. Bagby, An extended inequality for the maximal function, Proc. Amer. Math. Soc. 48, 419–422 (1975).
10.1090/S0002-9939-1975-0370171-X
Web of Science® Google Scholar
[3] A. Benedek, and R. Panzone, The space L^p, with mixed norm, Duke Math. J. 28, 301–324 (1961).
10.1215/S0012-7094-61-02828-9
Web of Science® Google Scholar
[4] M. Z. Berkolaĭko, Traces of generalized spaces of differentiable functions with mixed norm, Dokl. Akad. Nauk SSSR 277, No. 2, 270–274 (1984); English translation: Soviet Math. Dokl. 30, No. 1, 60–64 (1984).
Web of Science® Google Scholar
[5] M. Z. Berkolaĭko, Theorems on traces on coordinate subspaces for some spaces of differentiable functions with anisotropic mixed norm, Dokl. Akad. Nauk SSSR 282, No. 5, 1042–1046 (1985); English translation: Soviet Math. Dokl. 31, No. 3, 540–544 (1985).
Web of Science® Google Scholar
[6] M. Z. Berkolaĭko, Traces of functions in generalized Sobolev spaces with a mixed norm on an arbitrary coordinate subspace. I, Trudy Inst. Mat. 7, No. Issled. Geom. Mat. Anal., 30–44, 199 (1987).
Google Scholar
[7] M. Z. Berkolaĭko, Traces of functions in generalized Sobolev spaces with a mixed norm on an arbitrary coordinate subspace. II, Trudy Inst. Mat. 9, No. Issled. Geom. “v tselom” i Mat. Anal., 34–41, 206 (1987).
Google Scholar
[8] O. V. Besov, V. P. Il'in, and S. M. Nikol'skij, Integral Representations of Functions and Embedding Theorems. Vol. I, translated from the Russian, edited by Mitchell H. Taibleson, Scripta Series in Mathematics (V. H. Winston & Sons, Washington, D. C., 1978).
Google Scholar
[9] O. V. Besov, V. P. Il'in, and S. M. Nikol'skij, Integral Representations of Functions and Embedding Theorems. Vol. II, translated from the Russian, edited by Mitchell H. Taibleson, Scripta Series in Mathematics (V. H. Winston & Sons, Washington, D. C., 1979).
Google Scholar
[10] O. V. Besov, V. P. Il'in, and S. M. Nikol'skij, Integralnye predstavleniya funktsii i teoremy vlozheniya, 2nd ed. (Fizmatlit “Nauka”, Moscow, 1996).
Google Scholar
[11] Ya. S. Bugrov, Function spaces with mixed norm, Izv. Akad. Nauk. SSSR Ser. Mat. 35, 1137–1158 (1971); English translation: Math USSR-Izv. 5, 1145–1167 (1971).
Google Scholar
[12] R. Denk, M. Hieber, and J. Prüss, Optimal L_p -L_q -regularity for parabolic problems with inhomogeneous boundary data, Math. Z. 257, 193–224 (2007).
10.1007/s00209-007-0120-9
Web of Science® Google Scholar
[13] W. Farkas, J. Johnsen, and W. Sickel, Traces of anisotropic Besov–Lizorkin–Triebel spaces—a complete treatment of the borderline cases, Math. Bohem. 125, 1–37 (2000).
Google Scholar
[14] L. Hedberg, and Y. Netrusov, An Axiomatic Approach to Function Spaces, Spectral Synthesis, and Luzin Approximation, Memoirs of the American Mathematical Society Vol. 188, No. 882 (Amer. Math. Soc., Providence, RI, 2007).
Google Scholar
[15] J. Johnsen, Elliptic boundary problems and the Boutet de Monvel calculus in Besov and Triebel–Lizorkin spaces, Math. Scand. 79, No. 1, 25–85 (1996).
Web of Science® Google Scholar
[16] J. Johnsen, Traces of Besov spaces revisited, Z. Anal. Anwendungen 19, No. 3, 763–779 (2000).
10.4171/ZAA/979
Web of Science® Google Scholar
[17] J. Johnsen, and W. Sickel, A direct proof of Sobolev embeddings for quasi-homogeneous Lizorkin–Triebel spaces with mixed norms, J. Funct. Spaces Appl. 5, 183–198 (2007).
10.1155/2007/714905
Web of Science® Google Scholar
[18] P. Krée, Propriétés de continuité dans L^p de certains noyaux, Boll. Un. Mat. Ital. (3) 22, 330–344 (1967).
Google Scholar
[19] P. I. Lizorkin, Multipliers of Fourier integrals and bounds of convolutions in spaces with mixed norms. Applications, Izv. Akad. Nauk SSSR Ser. Mat. 34, 225–255 (1970); English translation: Math. USSR-Izv. 4 (1970).
Google Scholar
[20] J. Marschall, Nonregular pseudo-differential operators, Z. Anal. Anwendungen 15, No. 1, 109–148 (1996).
10.4171/ZAA/691
Google Scholar
[21] Y. Meyer, and R. R. Coifman, Ondelettes et Opérateurs. III (Hermann, Paris, 1991); English version by Cambridge Univ. Press, Cambridge (1997).
Google Scholar
[22] S. M. Nikol'skij, Approximation of Functions of Several Variables and Embedding Theorems (Springer-Verlag, New York, 1975).
Google Scholar
[23] H.-J. Schmeisser, Maximal inequalities and Fourier multipliers for spaces with mixed quasinorms. Applications, Z. Anal. Anwendungen 3, 153–166 (1984).
Google Scholar
[24] H.-J. Schmeisser, and H. Triebel, Topics in Fourier Analysis and Function Spaces (Akademische Verlagsgesellschaft Geest & Portig K.-G., Leipzig, 1987). Published also by John Wiley, Chichester (1987).
Google Scholar
[25] H. Triebel, Theory of Function Spaces (Birkhäuser Verlag, Basel, 1983).
Google Scholar
[26] P. Weidemaier, Existence results in L_p -L_q spaces for second order parabolic equations with inhomogeneous Dirichlet boundary conditions, in: Progress in Partial Differential Equations Vol. 2, Pitman Research Notes Mathematics Series Vol. 384 (Longman, Harlow, 1998), pp. 189–200.
Google Scholar
[27] P. Weidemaier, Maximal regularity for parabolic equations with inhomogeneous boundary conditions in Sobolev spaces with mixed L_p -norm, Electron. Res. Announc. Amer. Math. Soc. 8, 47–51 (2002).
10.1090/S1079-6762-02-00104-X
Web of Science® Google Scholar
[28] P. Weidemaier, Lizorkin–Triebel spaces of vector-valued functions and sharp trace theory for functions in Sobolev spaces with a mixed L_p -norm in parabolic problems, Mat. Sb. 196, No. 6, 3–16 (2005).
Google Scholar
[29] M. Yamazaki, The L^p -boundedness of pseudodifferential operators with estimates of parabolic type and product type, J. Math. Soc. Japan 38, 199–225 (1986).
10.2969/jmsj/03820199
Web of Science® Google Scholar
[30] M. Yamazaki, A quasihomogeneous version of paradifferential operators. I. Boundedness on spaces of Besov type, J. Fac. Sci. Univ. Tokyo Sect. IA Math. 33, No. 1, 131–174 (1986).
Google Scholar

Citing Literature

Volume281, Issue5

May 2008

Pages 669-696

On the trace problem for Lizorkin–Triebel spaces with mixed norms

Abstract

References

Citing Literature

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On the trace problem for Lizorkin–Triebel spaces with mixed norms

Abstract

References

Citing Literature

References

Related

Information