Given a smooth projective complex curve inside a smooth projective surface, one can ask how its Hodge structure varies when the curve moves inside the surface. In this paper, we develop a general theory to study the infinitesimal version of this question in the case of ample curves. We can then apply the machinery to show that the infinitesimal variation of the Hodge structure of a general deformation of an ample curve in $\mathbb {P}^1\times \mathbb {P}^1$ is an isomorphism.

1 INTRODUCTION

Let $\pi: \mathcal {C}\rightarrow B$ be a family of (smooth projective) complex curves of genus $g$ over a smooth complex manifold $B$ , which we consider as a deformation of a fiber $C=\pi ^{-1}\left(0\right)$ over a distinguished point $0\in B$ . A tangent vector $v\in T_{B,0}$ induces a first-order infinitesimal deformation of $C$ , whose Kodaira–Spencer class we denote by $\xi _v\in H^1\left(C,T_C\right)$ . Recall that $H^1\left(C,T_C\right)$ is naturally identified with the tangent space of the moduli space (or stack) $\mathcal {M}_g$ at $\left[C\right]$ , hence we can think of elements in $H^1\left(C,T_C\right)$ as tangent directions in $\mathcal {M}_g$ .

The infinitesimal variation of the Hodge structure (IVHS) associated with the family

\pi: \mathcal {C}\rightarrow B

is given by a linear map

\begin{equation*} \theta: T_{B,0}\otimes H^0{\left(C,\Omega _C^1\right)}\rightarrow H^1{\left(C,\mathcal {O}_C\right)}, \end{equation*}

where

\begin{equation} \theta {\left(v\otimes -\right)}: H^0{\left(C,\Omega _C^1\right)}\rightarrow H^1{\left(C,\mathcal {O}_C\right)} \end{equation}

()

is given (up to non-zero scalar) by the product with the Kodaira–Spencer class

\xi _v

. The kernel of this product map consists of the holomorphic 1-forms on

C

that extend to the first-order infinitesimal neighborhood of

C\subseteq \mathcal {C}

(in the direction

v

), which can thus be considered as “infinitesimally constant” or invariant in the variation of the Hodge structure.

It is known ([6, 9]) that, for any curve $C$ , the product with a general $\xi \in H^1\left(C,T_C\right)$ induces an isomorphism $H^0\left(C,\Omega _C^1\right)\rightarrow H^1\left(C,\mathcal {O}_C\right)$ . Hence, a general deformation of $C$ has maximal variation of the Hodge structure, since the nearby fibers have no common holomorphic 1-form. We have recently used this fact to prove that, for $g\ge 4$ , the Torelli map $\mathcal {M}_g\rightarrow \mathcal {A}_g$ (as well as other natural modular maps) is infinitesimally rigid as a morphism of smooth DM-stacks [2].

The above results consider general deformations of $C$ , but in many cases it is useful to restrict the kind of deformations to those preserving certain geometric features of $C$ . In particular, it is natural to consider curves lying in a particular surface $S$ . This set-up has important applications to the study of moduli spaces of curves $\mathcal {M}_g$ in low genus, so that a general curve sits inside a given surface. For instance, the general curve of genus 3 is a smooth quartic and therefore properties of the moduli space of genus 3 curves can be given by studying them as plane curves (see, e.g., [5]). A very important example is given by curves contained in $K3$ surfaces, as a general curve of genus $g\le 9$ or equal to 11 is contained in a K3 surface, and many results about the moduli space $\mathcal {M}_g$ are proved by using related properties (see, e.g., [8, 10, 13, 14]).

The important point for our study is that, as soon as the genus grows, the general curve of genus $g$ is not expected to be sitting inside a prescribed surface. Therefore, it might very well happen that the general deformations within these restrictions no longer induce isomorphisms in (1.1). Results in this direction provide geometric information on the tangent bundle of the corresponding sublocus of the moduli space of curves $\mathcal {M}_g$ . Later in the paper, we concentrate on the case of curves in $\mathbb {P}^1\times \mathbb {P}^1$ , which is related to the study of the $k$ -gonal locus in $\mathcal {M}_g$ . Indeed, curves admitting a $g^1_k$ and a $g^1_l$ , with coprime $k,l$ , can be thought of as curves in $\mathbb {P}^1\times \mathbb {P}^1$ of bidegree $(k,l)$ .

In this paper, we address the case of deformations of an ample curve

C

inside a given fixed surface

S

. If we denote by

L=\mathcal {O}_S\left(C\right)

the associated (ample) line bundle on

S

, then we consider only (infinitesimal) embedded deformations of

C

S

within the linear system

\left|L\right|

. If

\sigma \in H^0\left(S,L\right)

is a section vanishing precisely on

C

, such deformations are given by

\begin{equation*} \mathcal {C}={\left\lbrace \sigma +\epsilon \tau =0\right\rbrace} \subseteq S\times \operatorname{Spec}{\left(\mathbb {C}{\left[\epsilon \right]}/{\left(\epsilon ^2\right)}\right)}, \end{equation*}

where

\tau \in H^0\left(S,L\right)

is another section of

L

and as usual

\epsilon

denotes the parameter of the infinitesimal deformation.

The problem is then to analyze the kernel (or the rank) of the product map $\xi _{\tau }\cdot: H^0\left(C,\Omega _C^1\right)\rightarrow H^1\left(C,\mathcal {O}_C\right)$ , where $\xi _{\tau }\in H^1\left(T_C\right)$ denotes the associated Kodaira–Spencer class.

Note that there is a natural restriction map $H^0\left(S,\Omega _S^1\right)\rightarrow H^0\left(C,\Omega _C^1\right)$ , which is injective if $C$ is ample (Proposition 2.7). The 1-forms on $C$ arising this way will be trivially preserved in any deformation of $C$ in $S$ . Hence, $\ker \left(\xi _{\tau }\cdot \right)$ will always contain a $q\left(S\right)$ -dimensional subspace (where $q\left(S\right)=h^1\left(S,\mathcal {O}_S\right)=h^0\left(S,\Omega _S^1\right)$ is the irregularity of the ambient surface).

This motivates the following definition:

Definition 1.1.Using the above notations, we say:

(1) $\tau \in H^0\left(S,L\right)$ has maximal (embedded) infinitesimal variation, if the cup-product map with $\xi _{\tau }\in H^1\left(C,T_C\right)$ has the maximal possible rank, that is,
$\begin{equation*} \operatorname{rk}{\left(\xi _{\tau }\cdot: H^0{\left(C,\Omega _C^1\right)}\rightarrow H^1{\left(C,\mathcal {O}_C\right)}\right)}=g{\left(C\right)}-q{\left(S\right)}, \end{equation*}$
(2) the curve $C\subseteq S$ has maximal (embedded) infinitesimal variation, if there is a $\tau \in H^0\left(S,L\right)$ with maximal infinitesimal variation, and
(3)
the (ample) line bundle $L$ has maximal infinitesimal variation if every smooth member $C\in \left|L\right|$ has maximal infinitesimal variation.

If only a general $C\in \left|L\right|$ has maximal infinitesimal variation, we say that $L$ has generically maximal infinitesimal variation.

Remark 1.2.The terminology “family of maximal variation” has been used since Viehweg [12] with a different meaning. For families of smooth curves, and using the language of moduli spaces, Viehweg's definition means that the map from the base of the family to $\mathcal {M}_g$ has image of dimension $\dim B$ . This is the meaning used, for example, by Dutta and Huybrechts in [3] regarding linear systems of curves in K3 surfaces. For them, a line bundle $L$ has “maximal variation” if the rational map $\left|L\right|\dashrightarrow \mathcal {M}_g$ mapping a smooth member of $\left|L\right|$ to its isomorphism class is generically of finite degree, that is, has image of dimension $\dim \left|L\right|$ . But it could still happen that all smooth curves in $\left|L\right|$ have a non-trivial common Hodge-substructure. Thus, our notion of “maximal variation” is much stronger. In order to avoid confusion, we have added the word “infinitesimal”, which should remind us that we are considering the infinitesimal variations of the Hodge structure.

The question we would like to answer is whether, on any given surface $S$ , sufficiently ample line bundles $L$ have maximal infinitesimal variation. Recall from [7] that a property holds for sufficiently ample line bundles if there is an ample line bundle $L_0$ such that the property holds for any line bundle $L$ such that $L\otimes L_0^{\vee }$ is ample (i.e. $L$ is “more ample” than $L_0$ ). With this language, our conjecture can be stated as follows:

Conjecture 1.3.Let $S$ be a projective surface. Then, any sufficiently ample line bundle $L$ has maximal infinitesimal variation.

To our best knowledge, this problem has only been recently addressed in [4], where they prove the conjecture for plane curves of degree $d\ge 3$ , that is, for all $L=\mathcal {O}_{\mathbb {P}^2}\left(d\right)$ with $d\ge 3$ (thus $L_0=\mathcal {O}_{\mathbb {P}^2}\left(2\right)$ ).

The main tool in Favale–Pirola's proof is Macaulay's theorem on the structure of the Jacobian ring of the plane curve. In this paper, we exploit and further develop Green's generalization of Jacobian ideals and rings for smooth hypersurfaces [7] to address the problem for arbitrary projective surfaces, on which some of the nice properties of Jacobian rings of plane curves no longer hold. We can then apply our machinery to prove Conjecture 1.3 for $S=\mathbb {P}^1\times \mathbb {P}^1$ .

Theorem 1.4. (Theorem 4.6)For any $d,e\ge 1$ , $L=\mathcal {O}_X\left(d,e\right)$ has maximal infinitesimal variation at every smooth $Z\in \left|L\right|$ . In other words, a general embedded deformation of any smooth ample curve $Z\subseteq \mathbb {P}^1\times \mathbb {P}^1$ has maximal infinitesimal variation.

It is natural to ask, up to which extent our proof can be extended to more general surfaces. On one hand, an important step in our proof relies on the second statement of Theorem 4.2, which can be understood as a generalization of the fact that the classical polar map of plane curves is birational onto the image. An equivalent statement for a curve

C

in a surface

S

would be that the linear subsystem of

\left|\mathcal {O}_C\left(C\right)\right|

given by the image of the natural restriction map

\begin{equation*} H^0{\left(S,T_S\right)}\rightarrow H^0{\left(C,N_{C/S}\right)}=H^0{\left(C,\mathcal {O}_C{\left(C\right)}\right)} \end{equation*}

has no base points and induces a birational map

C\rightarrow \mathbb {P}^r

(Remark 4.7). This could hold if

T_S

is positive enough, and it would be interesting to characterize for which surfaces it holds.

On the other hand, the whole strategy of the proof relies on a special property of the 1-forms $\alpha \in H^0\left(C,\Omega _C^1\right)$ not arising as restrictions from $H^0\left(S,\Omega _S^1\right)$ but lying on the kernel of a general $\xi _{\tau }$ (see Lemma 3.5), and showing that $\alpha =0$ is the only possibility (under certain appropriate hypothesis). However, this cannot be the case if $K_S$ is positive enough (see Remark 3.6), and somehow limits the applicability of our strategy to surfaces with $p_g\left(S\right)\le 1$ , such as rational, $K3$ or abelian surfaces.

In any case, some explicit computations for curves in surfaces $S\subseteq \mathbb {P}^3$ of general type (degrees 5 and 6) make us believe that Conjecture 1.3 actually holds for every surface.

The paper is structured as follows. In Section 2, we develop the general technical framework to study variations of Hodge structures of smooth hypersurfaces. More precisely, we expand the theory of generalized Jacobian ideals and rings introduced by Green in [7]. In Section 3, we focus on the case of curves on surfaces, proving the crucial Lemma 3.5 and Theorem 3.8. The latter gives a numerical condition satisfied when the curve does not have maximal infinitesimal variation. Finally, in Section 4 we study in detail the case of curves in $\mathbb {P}^1\times \mathbb {P}^1$ . We first prove that the generalized Jacobian ideals indeed coincide with the naive definition that one could make using the partial derivatives of a bihomogeneous equation. Second, we study the maps induced by the generalized Jacobian ideals in low degrees (analogous to the polar map of a curve in $\mathbb {P}^2$ ). We finally prove Theorem 4.4, which contradicts the numerical condition obtained in Theorem 3.8, and finishes the proof of Theorem 1.4.

2 GENERALIZED JACOBIAN IDEALS AND RINGS

The main technical tool to prove Theorem 1.4 will be generalized Jacobian ideals and rings, which were introduced by Green in [7], in order to prove the infinitesimal Torelli theorem for sufficiently ample smooth hypersurfaces, as well as to study the local structure of the associated period maps. We will actually need some more precise results than those developed by Green, since his main assumption is that the line bundle $L$ is sufficiently ample, which is mostly used to ensure the vanishing of enough cohomology groups. But we will actually need a better control of which cohomology groups need to vanish for the statements to hold, and also to understand up to what extent these vanishings might fail. For example, Lemma 2.12 is the first assertion in [7, Theorem 2.15], while Propositions 2.16 and 2.17 explain why and by how much the second statement of [7, Theorem 2.15] fails in some crucial cases.

For the sake of completeness, we will recall the construction of generalized Jacobian ideals. Since the constructions and first results make sense for (smooth) hypersurfaces on complex manifolds of arbitrary dimension, we start with this more general setting. Only at the end of the section we will restrict ourselves to the case of curves moving on surfaces.

2.1 The bundle $\Sigma _L$

Let $X$ be a smooth compact complex variety of dimension $n$ and $L$ a line bundle on $X$ . In this section, we summarize the properties of $\Sigma _L$ , the bundle of first-order differential operators on sections of $L$ , which is necessary to define the generalized Jacobian ideals and rings. For a more detailed explanation of $\Sigma _L$ with proofs, we refer to [11]. Note that many of the constructions and first properties are of local nature, hence are also valid for non-compact varieties. However, the statements regarding global sections or higher cohomology groups are only meaningful in the compact case.

Suppose $\left(x_1,\ldots,x_n\right)$ are coordinates on an open subset $U\subseteq X$ , and that $L_{\mid U}$ is trivialized by a nowhere-vanishing section $e\in H^0\left(U,L\right)$ , so that any other section $\sigma \in H^0\left(U,L\right)$ has the form $\sigma =fe$ for a holomorphic function $f\in \mathcal {O}_X\left(U\right)$ .

A local section

D

\Sigma _L

is then of the form

D=a_0\cdot 1+\sum _{i=1}^n a_i D_i

, where

a_0,\ldots,a_n\in \mathcal {O}_X\left(U\right)

, and

D

acts on

\sigma =fe

by differentiating the function

f

, that is,

\begin{equation} D{\left(\sigma \right)}=D{\left(fe\right)}:={\left(a_0\cdot f+\sum _{i=1}^na_i\frac{\partial f}{\partial x_i}\right)}e. \end{equation}

()

Imposing that this formula is compatible with the transition functions for

L

on the overlap of two such open subsets gives the transition functions for

\Sigma _L

The bundle

\Sigma _L

fits into a natural short exact sequence

\begin{equation} 0\longrightarrow \mathcal {O}_X\longrightarrow \Sigma _L\longrightarrow T_X\longrightarrow 0, \end{equation}

()

where the inclusion

\mathcal {O}_X\hookrightarrow \Sigma _L

is locally given by

a\mapsto a\cdot 1

(i.e., by considering holomorphic functions as differential operators of order 0 via multiplication), and the projection

\Sigma _L\rightarrow T_X

is locally given by

D_i\mapsto \frac{\partial }{\partial x_i}

Remark 2.1.The extension class of (2.2) coincides (up to non-zero scalar multiple) with the first Chern class of $L$

\begin{equation*} c_1{\left(L\right)}\in H^1{\left(X,\Omega _X^1\right)}\cong \operatorname{Ext}_{\mathcal {O}_X}^1{\left(\mathcal {O}_X,\Omega _X^1\right)}\cong \operatorname{Ext}_{\mathcal {O}_X}^1{\left(T_X,\mathcal {O}_X\right)}. \end{equation*}

2.2 The differential $d\sigma$ of a section $\sigma \in H^0\left(L\right)$ and associated bundles

Definition 2.2.Let $\sigma \in H^0\left(X,L\right)$ be a global section. The differential of $\sigma$ is the morphism of vector bundles

\begin{equation*} d\sigma: \Sigma _L\rightarrow L,\quad D\mapsto d\sigma {\left(D\right)}:=D{\left(\sigma \right)}, \end{equation*}

mapping a differential operator

D\in H^0\left(U,\Sigma _L\right)

, defined on an open subset

U\subseteq X

, to the derivative of the restriction

\sigma _{\mid U}

along

D

The kernel of $d\sigma$ is denoted by

\begin{equation*} \mathcal {E}_{\sigma }=\ker d\sigma \subseteq \Sigma _L. \end{equation*}

The following result summarizes the first properties of $d\sigma$ and $\mathcal {E}_{\sigma }$ .

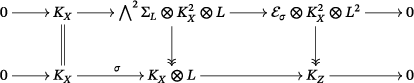
Proposition 2.3.Let $\sigma \in H^0\left(X,L\right)$ be a section of $L$ , and denote by $Z=\left\lbrace \sigma =0\right\rbrace \subseteq X$ the vanishing subvariety of $\sigma$ . Then:

(1) The cokernel of $d\sigma: \Sigma _L\rightarrow L$ is supported on the singular locus of $Z$ . In particular, $d\sigma$ is surjective if $Z$ is smooth.
(2) If $Z$ is smooth, then there is a commutative diagram with exact rows and columns
()
where $\widetilde{d\sigma }: T_X\rightarrow L_{\mid Z}$ coincides with the composition $T_X\twoheadrightarrow T_{X\mid Z}\twoheadrightarrow N_{Z/X}\cong L_{\mid Z}$ .
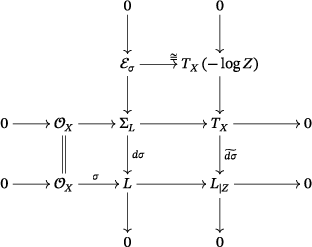(3) If $Z$ is smooth, then
$\begin{equation} \det \mathcal {E}_{\sigma }\cong K_X^{\vee }\otimes L^{\vee }. \end{equation}$ ()

Proof.

(1) Follows directly from the local description (2.1) of $d\sigma \left(D\right)=D\left(\sigma \right)$ on a trivialization of $L$ , since $Z$ is locally defined by $\left\lbrace f=0\right\rbrace$ .
(2)
Note first that $d\sigma$ acts on the subsheaf $\mathcal {O}_X\subseteq \Sigma _L$ by multiplying by $\sigma$ . There is thus a commutative diagram
()
where $\widetilde{d\sigma }: T_X\rightarrow L_{\mid Z}$ is locally given by differentiating the local equation of $\sigma$ along a local vector field $\chi$ and restricting it to $Z$ , which turns out to be well-defined, independent of the choice of a lifting of $\chi$ to $\Sigma _L$ . Writing the isomorphism $L_{\mid Z}\cong N_{Z/X}$ with the normal bundle in local coordinates gives the alternative description of $\tilde{d\sigma }$ as the composition $T_X\twoheadrightarrow T_{X\mid Z}\twoheadrightarrow N_{Z/X}\cong L_{\mid Z}$ .

With this description, it is clear that a vector field lies in $\ker \widetilde{d\sigma }$ if and only if it is tangent to $Z$ along $Z$ . That is, $\ker \widetilde{d\sigma }=T_X\left(-\log Z\right)\subseteq T_X$ , the dual of the vector bundle $\Omega _X^1\left(\log Z\right)$ of meromorphic 1-forms with at most a logarithmic pole along $Z$ .

The diagram (2.3) is obtained by completing (2.5) using the snake lemma and the surjectivity of $d\sigma$ .
(3) Since both the central row and the central column are short exact sequences of locally free sheaves, we obtain
$\begin{eqnarray*} \det \mathcal {E}_{\sigma }\cong {\left(\det \Sigma _L\right)}\otimes L^{\vee }\cong {\left(\det T_X\right)}\otimes L^{\vee }\cong K_X^{\vee }\otimes L^{\vee }.\\[-30pt] \end{eqnarray*}$
$\Box$

Using $d\sigma$ we define the following cohomology class $\delta \sigma \in H^1\left(X,\mathcal {E}_{\sigma }\otimes L^{\vee }\right)$ , which will be very useful for certain formalizations.

Definition 2.4.Let $\sigma \in H^0\left(X,L\right)$ with smooth vanishing locus. We denote by

\begin{equation*} \delta \sigma:={\left[0\rightarrow \mathcal {E}_{\sigma }\rightarrow \Sigma _L\stackrel{d\sigma }{\longrightarrow }L\rightarrow 0\right]} \in \operatorname{Ext}_{\mathcal {O}_X}^1{\left(L,\mathcal {E}_{\sigma }\right)}=H^1{\left(X,\mathcal {E}_{\sigma }\otimes L^{\vee }\right)}, \end{equation*}

the extension class of the central column of (2.5).

Note that

\delta \sigma

coincides with the image of

1\in H^0\left(X,\mathcal {O}_X\right)

, under the connecting homomorphism of the same extension tensored by

L^{\vee }

\begin{equation*} 0 \longrightarrow \mathcal {E}_{\sigma }\otimes L^{\vee }\longrightarrow \Sigma _L\otimes L^{\vee }\stackrel{d\sigma }{\longrightarrow } \mathcal {O}_X \longrightarrow 0. \end{equation*}

The Koszul komplex of

d\sigma: \Sigma _L\otimes L^{\vee }\rightarrow \mathcal {O}_X

has the form

\begin{equation*} 0\longrightarrow \bigwedge ^{n+1}\Sigma _L\otimes L^{-n-1}\longrightarrow \bigwedge ^n\Sigma _L\otimes L^{-n}\longrightarrow \cdots \longrightarrow \bigwedge ^2\Sigma _L\otimes L^{-2}\longrightarrow \Sigma _L\otimes L^{\vee }\longrightarrow \mathcal {O}_X\longrightarrow 0. \end{equation*}

Using the isomorphism

\det \Sigma _L\cong \det \mathcal {E}_{\sigma }\otimes L

at the first term, the Koszul complex can be split into short exact sequences

\begin{equation} 0\longrightarrow \bigwedge ^r\mathcal {E}_{\sigma }\otimes L^{-r}\longrightarrow \bigwedge ^r\Sigma _L\otimes L^{-r}\longrightarrow \bigwedge ^{r-1}\mathcal {E}_{\sigma }\otimes L^{-r+1}\longrightarrow 0, \end{equation}

()

for

r=1,\ldots,n

, whose extension classes all coincide with

\delta \sigma

, under the canonical identification

\operatorname{Ext}_{\mathcal {O}_X}^1\left(\bigwedge ^{r-1}\mathcal {E}_{\sigma }\otimes L^{-r+1},\bigwedge ^r\mathcal {E}_{\sigma }\otimes L^{-r}\right)\cong \operatorname{Ext}_{\mathcal {O}_X}^1\left(L,\mathcal {E}_{\sigma }\right)

2.3 Generalized Jacobian rings

Let now $M$ be another line bundle on $X$ . We still denote with $d\sigma$ the map $\Sigma _L\otimes L^{\vee }\otimes M\rightarrow M$ induced by tensoring $d\sigma$ with the identity on $M$ . Also, in order to lighten the notation, we will remove the variety $X$ from the notation of cohomology groups from now on, simply writing $H^i\left(\mathcal {F}\right)$ instead $H^i\left(X,\mathcal {F}\right)$ for any sheaf $\mathcal {F}$ on $X$ .

Definition 2.5.Due to Green [7], we define

(1) the generalized Jacobian ideal (with respect to $\sigma$ )
$\begin{equation*} J_M:=\operatorname{im}{\left(d\sigma: H^0{\left(\Sigma _L\otimes M\otimes L^{\vee }\right)}\longrightarrow H^0{\left(M\right)}\right)}\subseteq H^0{\left(M\right)} \end{equation*}$
(2) and the generalized Jacobian ring $R_M:= H^0\left(M\right)/J_M$

on degree

M

Note that $H^0\left(M\right)$ is not a ring, so neither $J_M\subseteq H^0\left(M\right)$ is an ideal nor $R_M$ is a ring. All these spaces are merely vector spaces. However, for any $M,N\in \operatorname{Pic}\left(X\right)$ , the natural multiplication maps $H^0\left(M\right)\otimes H^0\left(N\right)\rightarrow H^0\left(M\otimes N\right)$ map the subspaces $J_M\otimes H^0\left(N\right)$ and $H^0\left(M\right)\otimes J_N$ into $J_{M\otimes N}$ , and this also allows us to define a multiplication map $R_M\otimes R_N\rightarrow R_{M\otimes N}$ . Loosely speaking, although the following construction only works if $h^1\left(\mathcal {O}_X\right)=0$ , we can think of the direct sum $\bigoplus _M H^0\left(M\right)$ (over all isomorphism classes of line bundles $M$ ) as a commutative ring graded by $\operatorname{Pic}\left(X\right)$ , and then the subspace $\bigoplus _M J_M$ forms a graded ideal with quotient ring $\bigoplus _M R_M$ . The generalized Jacobian ideal $J_M$ and ring $R_M$ are just the summands of degree $M$ .

Example 2.6.For $S=\mathbb {P}^2$ (with homogeneous coordinates $\left[x_0: x_1: x_2\right]$ ) and $L=\mathcal {O}_{\mathbb {P}^2}\left(n\right)$ with $n\ne 0$ , we have $\Sigma _L\cong \mathcal {O}_{\mathbb {P}^2}\left(1\right)^{\oplus 3}$ , and the sequence (2.2) is the Euler sequence, with the first map appropriately rescaled.

For any

F\in H^0\left(\mathbb {P}^2,L\right)=\mathbb {C}\left[x_0,x_1,x_2\right]_n

, the differential

dF: \mathcal {O}_{\mathbb {P}^2}\left(1\right)^{\oplus 3}\rightarrow \mathcal {O}_{\mathbb {P}^2}\left(n\right)

is given by the partial derivatives

\left(\frac{\partial F}{\partial x_0},\frac{\partial F}{\partial x_1},\frac{\partial F}{\partial x_2}\right)

. The rescaling by

\frac{1}{n}

ensures that

dF

, restricted to

\mathcal {O}_{\mathbb {P}^2}

, coincides with the

F

, since the Euler relation gives

\begin{equation*} dF{\left(\frac{1}{n}{\left(x_0,x_1,x_2\right)}\right)}=\frac{1}{n}{\left(x_0\frac{\partial F}{\partial x_0}+x_1\frac{\partial F}{\partial x_1}+x_2\frac{\partial F}{\partial x_2}\right)}=F. \end{equation*}

The generalized Jacobian ideal in “degree” $\mathcal {O}_{\mathbb {P}^2}\left(m\right)$ is the image of

\begin{equation*} H^0{\left(\mathcal {O}_{\mathbb {P}^2}{\left(m-n+1\right)}\right)}^{\oplus 3}\stackrel{dF}{\longrightarrow } H^0{\left(\mathcal {O}_{\mathbb {P}^2}{\left(m\right)}\right)}, \end{equation*}

that is, it is generated by the partial derivatives of

F

multiplied by arbitrary polynomials of the correct degree. This means,

J_{\mathcal {O}_{\mathbb {P}^2}\left(m\right)}=\left(\frac{\partial F}{\partial x_0},\frac{\partial F}{\partial x_1},\frac{\partial F}{\partial x_2}\right)_m

is precisely the piece of degree

m

of the usual Jacobian ideal

J^F\subseteq \mathbb {C}\left[x_0,x_1,x_2\right]

, which motivates the name.

Since for any

M

and any

r=1,\ldots,n

the extension class of

\begin{equation} 0\longrightarrow \bigwedge ^r\mathcal {E}_{\sigma }\otimes L^{-r}\otimes M\longrightarrow \bigwedge ^r\Sigma _L\otimes L^{-r} \stackrel{d\sigma }{\longrightarrow } \bigwedge ^{r-1}\mathcal {E}_{\sigma }\otimes L^{-r+1}\otimes M\longrightarrow 0 \end{equation}

()

is still

\delta \sigma \in H^1\left(\mathcal {E}_{\sigma }\otimes L^{\vee }\right)

, the coboundary morphisms

\begin{equation} H^{r-1}{\left(\bigwedge ^{r-1}\mathcal {E}_{\sigma }\otimes L^{-r+1}\otimes M\right)}\longrightarrow H^r{\left(\bigwedge ^r\mathcal {E}_{\sigma }\otimes L^{-r}\otimes M\right)} \end{equation}

()

are given by cup-product with

\delta \sigma

. In particular, we have

\begin{equation*} J_M=\operatorname{im}{\left(d\sigma: H^0{\left(\Sigma _L\otimes M\otimes L^{\vee }\right)}\rightarrow H^0{\left(M\right)}\right)}=\ker {\left(\delta \sigma: H^0{\left(M\right)}\rightarrow H^1{\left(\mathcal {E}_{\sigma }\otimes L^{\vee }\otimes M\right)}\right)}, \end{equation*}

and thus, cup-product with

\delta \sigma

induces an inclusion

\begin{align} R_M=\operatorname{coker}{\left(d\sigma: H^0{\left(\Sigma _L\otimes M\otimes L^{\vee }\right)}\rightarrow H^0{\left(M\right)}\right)}\stackrel{\delta \sigma }{\cong } \ker {\left(H^1{\left(\mathcal {E}_{\sigma }\otimes L^{\vee }\otimes M\right)}\rightarrow H^1{\left(\Sigma _L\otimes L^{\vee }\otimes M\right)}\right)}\subseteq H^1{\left(\mathcal {E}_{\sigma }\otimes L^{\vee }\otimes M\right)}. \end{align}

()

Note that the last inclusion can be an equality, for example, if

H^1\left(\Sigma _L\otimes L^{\vee }\otimes M\right)=0

2.4 Jacobian in degree $K_X\otimes L$

We now focus on the generalized Jacobian ideal and ring on degree $K_X\otimes L$ , which turns out to be the piece on which the cup-product with the Kodaira–Spencer class of a general embedded deformation should become an isomorphism.

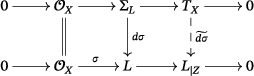
Proposition 2.7.Suppose $L$ is ample and $\sigma \in H^0\left(L\right)$ is a global section, with smooth vanishing divisor $Z:=\left\lbrace \sigma =0\right\rbrace$ . Then, the following hold:

(1) $J_{K_X\otimes L}=H^0\left(K_X\right)\cdot \sigma =\operatorname{im}\left(H^0\left(K_X\right)\stackrel{\cdot \sigma }{\rightarrow }H^0\left(K_X\otimes L\right)\right)$ .
(2) The adjunction formula induces a natural inclusion $R_{K_X\otimes L}\hookrightarrow H^0\left(K_Z\right)$ .
(3) The natural restriction morphism
$\begin{equation*} H^0{\left(\Omega _X^{n-1}\right)}\longrightarrow H^0{\left(\Omega _{X\mid Z}^{n-1}\right)}\longrightarrow H^0{\left(K_Z\right)}, \end{equation*}$
is injective, hence we can identify $H^0\left(\Omega _X^{n-1}\right)$ with its image in $H^0\left(K_Z\right)$ .
(4) Moreover, it holds $H^0\left(K_Z\right)=H^0\left(\Omega _X^{n-1}\right)\oplus R_{K_X\otimes L}$ , and in particular, $\dim R_{K_X\otimes L}=p_g\left(Z\right)-h^0\left(\Omega _X^{n-1}\right)$ .

Proof.Twisting the diagram (2.5) with $K_X$ and using the adjunction formula for $Z\subseteq X$ we obtain

()

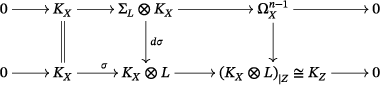where the right vertical arrow is the restriction of

\left(n-1\right)

-forms from

X

Z

(1) The connecting homomorphism $H^0\left(\Omega _X^{n-1}\right)\rightarrow H^1\left(K_X\right)$ of the long exact sequence in cohomology of the upper row is given by the cup product with the corresponding extension class, which is $c_1\left(L\right)\in H^1\left(\Omega _X^1\right)$ . Since $L$ is ample, the Lefschetz theorem implies that the connecting homomorphism is an isomorphism. Thus, there is an equality $H^0\left(K_X\right)=H^0\left(\Sigma _L\otimes K_X\right)$ and
$\begin{equation*} J_{K_X\otimes L}=\operatorname{im}{\left(d\sigma: H^0{\left(\Sigma _L\otimes K_X\right)}\longrightarrow H^0{\left(K_X\otimes L\right)}\right)}=\operatorname{im}{\left(\cdot \sigma: H^0{\left(K_X\right)}\longrightarrow H^0{\left(K_X\otimes L\right)}\right)}. \end{equation*}$
(2) Assuming (2.7) we have
$\begin{align*} R_{K_X\otimes L}=H^0{\left(K_X\otimes L\right)}/J_{K_X\otimes L}=\operatorname{coker}{\left(H^0{\left(K_X\right)}\rightarrow H^0{\left(K_X\otimes L\right)}\right)}=\ker {\left(H^0{\left(K_Z\right)}\longrightarrow H^1{\left(K_X\right)}\right)}\subseteq H^0{\left(K_Z\right)}. \end{align*}$
(3)
The first morphism $H^0\left(\Omega _X^{n-1}\right)\rightarrow H^0 \left(\Omega _{X\mid Z}^{n-1}\right)$ is injective, since its kernel is
$\begin{equation*} H^0{\left(\Omega _X^{n-1}{\left(-Z\right)}\right)}\cong H^n{\left(\Omega _X^1{\left(Z\right)}\right)}^*=0, \end{equation*}$
where the first isomorphism follows from Serre duality, and the second equality follows from the Kodaira–Nakano vanishing theorem.

The second morphism $H^0\left(\Omega _{X\mid Z}^{n-1}\right)\rightarrow H^0\left(K_Z\right)$ is also injective, since its kernel is
$\begin{equation*} H^0{\left(T_Z\otimes K_{X\mid Z}\right)}=H^0{\left(T_Z\otimes K_Z\otimes L_{\mid Z}^{\vee }\right)}\cong H^{n-1}{\left(\Omega _Z^1\otimes L_{\mid Z}\right)}^*, \end{equation*}$
which vanishes again by Kodaira–Nakano (on the hypersurface $Z$ ), because $L_{\mid Z}$ is ample.
(4) From diagram (2.10), we obtain a commutative diagram
Since the upper map is an isomorphism, we recover the injectivity of the left map and also obtain that $H^0\left(\Omega _X^{n-1}\right)\oplus \ker \nu =H^0\left(K_Z\right)$ . But $\ker \nu =R_{K_X\otimes L}$ by the proof of (2.7), and the proof is finished. $\Box$

Example 2.8.For $X=\mathbb {P}^2$ , we have $H^0\left(K_X\right)=H^0\left(\Omega _X^1\right)=0$ . Hence, for any $Z\subseteq X$ defined by a homogeneous polynomial of degree $n$ , Proposition 2.7 recovers $J_{K_X\otimes L}=J_{n-3}=0$ (since the Jacobian ideal is generated by polynomials of degree $n-1$ ) and $H^0\left(\Omega _Z^1\right)\cong R_{n-3}=\mathbb {C}\left[x_0,x_1,x_2\right]_{n-3}$ .

2.5 Jacobian in degree $L$

We have seen in Proposition 2.7 that the Jacobian ring $R_{K_X\otimes L}$ of degree $K_X\otimes L$ is a complement in $H^0\left(K_Z\right)$ of the set of top-forms on $Z$ , obtained by restricting global $\left(n-1\right)$ -forms of $X$ . This makes it a good candidate to be the “most variable” part of $H^0\left(K_Z\right)$ , under embedded deformations of $Z$ in $X$ . We now check that the Jacobian ring $R_L$ of degree $L=\mathcal {O}_X\left(Z\right)$ is a good tool to encode the (Kodaira–Spencer classes of) first-order deformations of $Z$ within the linear system $\left|L\right|$ .

The identification $\left|L\right|=\mathbb {P}\left(H^0\left(L\right)\right)$ also gives $T_{\left[Z\right]}\left|L\right|\cong H^0\left(L\right)/\left\langle \sigma \right\rangle$ , where $Z=\left\lbrace \sigma =0\right\rbrace$ . This means that every first-order deformation of $Z$ inside the linear system $\left|L\right|$ is given by $\left\lbrace \sigma +\epsilon \tau =0\right\rbrace$ , where $\tau \in H^0\left(L\right)$ is another section and $\epsilon$ is the parameter (with $\epsilon ^2=0$ ).

We now consider the following two short exact sequences of sheaves:

\begin{equation} 0 \longrightarrow \mathcal {O}_X \stackrel{\sigma }{\longrightarrow } L \longrightarrow L_{\mid Z}\cong N_{Z/X}\longrightarrow 0 \end{equation}

()

and

\begin{equation} 0 \longrightarrow T_Z \longrightarrow T_{X\mid Z}\longrightarrow N_{Z/X}\longrightarrow 0. \end{equation}

()

From (2.11), we obtain an inclusion

T_{\left[Z\right]}\left|L\right|=H^0\left(L\right)/\left\langle \sigma \right\rangle \hookrightarrow H^0\left(N_{Z/X}\right)

, which composed with the first connecting homomorphism

H^0\left(N_{Z/X}\right)\rightarrow H^1\left(T_Z\right)

of (2.12) gives a map

\begin{equation} KS: T_{{\left[Z\right]}}{\left|L\right|}\longrightarrow H^1{\left(T_Z\right)}. \end{equation}

()

This is precisely the Kodaira–Spencer map for the family of deformations of

Z

, inside the linear system

\left|L\right|

Lemma 2.9.Let $X$ be a smooth compact complex manifold, $Z\subseteq X$ a smooth hypersurface and $L=\mathcal {O}_X\left(Z\right)$ the associated line bundle. Then, the Kodaira–Spencer map (2.13) factorizes as

\begin{equation} T_{{\left[Z\right]}}{\left|L\right|}=H^0{\left(L\right)}/{\left\langle \sigma \right\rangle} \longrightarrow R_L=H^0{\left(L\right)}/J_L\longrightarrow H^1{\left(T_Z\right)} \end{equation}

()

Proof.Consider the commutative diagram

Note first that

\sigma =d\sigma \left(1\right)\in J_L

, hence the first projection

H^0\left(L\right)/\left\langle \sigma \right\rangle \rightarrow R_L

in (2.14) is well-defined and has kernel

J_L/\left\langle \sigma \right\rangle

It remains to show that $J_L/\left\langle \sigma \right\rangle \subseteq \ker \left(KS\right)$ . To this aim, recall that the map $T_X\rightarrow N_{Z/X}$ factorizes as $T_X\rightarrow T_{X\mid Z}\rightarrow N_{Z/X}$ (Proposition 2.3), and thus

\begin{align*} J_L/{\left\langle \sigma \right\rangle} &=\operatorname{im}{\left(H^0{\left(\Sigma _L\right)}\rightarrow H^0{\left(N_{Z/X}\right)}\right)}\subseteq \operatorname{im}{\left(H^0{\left(T_X\right)}\rightarrow H^0{\left(N _{Z/X}\right)}\right)}\subseteq \operatorname{im}{\left(H^0{\left(T_{X\mid Z}\right)}\rightarrow H^0{\left(N_{Z/X}\right)}\right)}\\ &=\ker {\left(H^0{\left(N_{Z/X}\right)}\stackrel{KS}{\longrightarrow }H^1{\left(T_Z\right)}\right)}. \end{align*}

\Box

Definition 2.10.By abuse of notation, we will write $KS: H^0\left(L\right)\rightarrow H^1\left(T_Z\right)$ and $KS: R_L\rightarrow H^1\left(T_Z\right)$ , for the maps induced by (2.13), and we will call all three maps indistinctly Kodaira–Spencer maps.

2.6 The top degree

We now consider a third (and last) interesting degree, that plays the role of the socle degree in the case of $\mathbb {P}^2$ .

We consider the composition of

n

connecting homomorphisms, as in (2.8) (with suitably varying

M

’s)

\begin{equation*} H^0{\left(M\right)}\longrightarrow H^n{\left(\bigwedge ^n\mathcal {E}_{\sigma }\otimes L^{-n}\otimes M\right)}=H^n{\left(\det \mathcal {E}_{\sigma }\otimes L^{-n}\otimes M\right)}, \end{equation*}

which is given by cup-product with the cup-power

\left(\delta \sigma \right)^n\in H^n\left(\bigwedge ^n\mathcal {E}_{\sigma }\otimes L^{-n}\right)

. Composing with the natural isomorphism

\begin{equation} \det \mathcal {E}_{\sigma }\otimes L^{-n}\cong \det \Sigma _L\otimes L^{-n-1}\cong K_X^{\vee }\otimes L^{-n-1}, \end{equation}

()

we then obtain a map

\begin{equation*} H^0{\left(M\right)}\stackrel{{\left(\delta \sigma \right)}^n}{\longrightarrow } H^n{\left(K_X^{\vee }\otimes L^{-n-1}\otimes M\right)}. \end{equation*}

Since the kernel of the first product with

\delta \sigma

J_M

, the above map factors through the generalized Jacobian ring as

\begin{equation*} R_M\rightarrow H^n{\left(K_X^{\vee }\otimes L^{-n-1}\otimes M\right)}. \end{equation*}

In particular, for

M=K_X^2\otimes L^{n+1}

we obtain a map

\begin{equation} \operatorname{tr}=\operatorname{tr}_{\sigma }: R_{K^2\otimes L^{n+1}}\longrightarrow H^n{\left(K_X\right)}\cong \mathbb {C}. \end{equation}

()

Definition 2.11.We call the map $\operatorname{tr}$ in (2.16) natural trace map with respect to the given section $\sigma \in H^0\left(L\right)$ .

We now investigate under which conditions the map (2.16) is an isomorphism.

Lemma 2.12.If $L$ is sufficiently ample, more precisely if $H^1\left(\Sigma _L\otimes K_X^2\otimes L^n\right)=0$ and

\begin{equation} H^{r-1}{\left(\bigwedge ^r\Sigma _L\otimes K_X^2\otimes L^{n+1-r}\right)}=H^r{\left(\bigwedge ^r\Sigma _L\otimes K_X^2\otimes L^{n+1-r}\right)}=0 \end{equation}

()

for all

r=2,\ldots,n

, then

\operatorname{tr}_{\sigma }: R_{K_X^2\otimes L^{n+1}}\rightarrow H^n\left(K_X\right)\cong \mathbb {C}

is an isomorphism.

Proof.Set $M=K_X^2\otimes L^{n+1}$ in the exact sequences (2.7), which become

\begin{equation*} 0\longrightarrow \bigwedge ^r\mathcal {E}_{\sigma }\otimes K_X^2\otimes L^{n+1-r}\longrightarrow \bigwedge ^r\Sigma _L\otimes K_X^2\otimes L^{n+1-r}\longrightarrow \bigwedge ^{r-1}\mathcal {E}_{\sigma }\otimes K_X^2\otimes L^{n+2-r}\longrightarrow 0. \end{equation*}

The condition

H^1\left(\Sigma _L\otimes K_X^2\otimes L^n\right)=0

ensures that

R_{K_X^2\otimes L^{n+1}}\stackrel{\delta \sigma }{\cong } H^1\left(\mathcal {E}_{\sigma }\otimes K_X^2\otimes L^n\right)

. The remaining conditions ensure that the connecting homomorphisms

\begin{equation*} H^{r-1}{\left(\bigwedge ^{r-1}\mathcal {E}_{\sigma }\otimes K_X^2\otimes L^{n+2-r}\right)}\stackrel{\delta \sigma }{\longrightarrow } H^r{\left(\bigwedge ^r\mathcal {E}_{\sigma }\otimes K_X^2\otimes L^{n+1-r}\right)} \end{equation*}

are isomorphisms. Thus, multiplication with

\left(\delta \sigma \right)^n

followed by the isomorphism (2.15) gives indeed an isomorphism

\begin{equation*} R_{K_X^2\otimes L^{n+1}}\cong H^n{\left(\det \mathcal {E}_{\sigma }\otimes K_X^2\otimes L\right)}\cong H^n{\left(K_X\right)}\cong \mathbb {C}. \end{equation*}

\Box

Remark 2.13.The vanishing conditions in Lemma 2.12 not only involve $L$ but also $\Sigma _L$ . We haven't deduced any ampleness of $\Sigma _L$ from the ampleness of $L$ , so it might happen that the exterior powers of $\Sigma _L$ somehow cancel the ampleness of $L$ and that the conditions (2.17) are rarely satisfied. This is, however, not the case at all, because of the first fundamental exact sequence (2.2), which gives also exact sequences

\begin{equation*} 0 \longrightarrow \bigwedge ^{r-1}T_X \longrightarrow \bigwedge ^r\Sigma _L \longrightarrow \bigwedge ^r T_X \longrightarrow 0 \end{equation*}

and thus, tensoring with

K_X^2\otimes L^{n+1-r}

, we also obtain

\begin{equation*} 0 \longrightarrow \Omega _X^{n-r+1}\otimes K_X\otimes L^{n+1-r} \longrightarrow \bigwedge ^r\Sigma _L\otimes K_X^2\otimes L^{n+1-r} \longrightarrow \Omega _X^{n-r}\otimes K_X\otimes L^{n+1-r} \longrightarrow 0. \end{equation*}

The outer terms of the above exact sequence have no higher cohomology, if

L

is sufficiently ample, and thus the vanishing conditions of Lemma 2.12 are satisfied.

Example 2.14.For $X=\mathbb {P}^2$ and $Z\subseteq \mathbb {P}^2$ defined by a polynomial of degree $n$ , Lemma 2.12 is precisely the part of and Macaulay's theorem stating that the (one-dimensional) socle of the Jacobian ring is the piece of degree $3n-6$ . Indeed, in this case we have $K_X^2\otimes L^3=\mathcal {O}_{\mathbb {P}^2}\left(3n-6\right)$ .

2.7 Natural pairings and duality maps

For any line bundle

M

, let

M^{\prime }:=K_X^2\otimes L^{n+1}\otimes M^{\vee }

denote the line bundle such that

M\otimes M^{\prime }\cong K_X^2\otimes L^{n+1}

. Combining the multiplication map with the natural trace map

\operatorname{tr}_{\sigma }: R_{K_X^2\otimes L^{n+1}}\rightarrow H^n\left(K_X\right)\cong \mathbb {C}

, we obtain a pairing

\begin{equation} R_M\otimes R_{M^{\prime }}\longrightarrow R_{K_X^2\otimes L^{n+1}}\longrightarrow \mathbb {C}, \end{equation}

()

and thus, also (mutually dual) duality maps

\begin{equation} \lambda _M: R_M\longrightarrow R_{M^{\prime }}^* \quad \text{and}\quad \lambda _{M^{\prime }}: R_{M^{\prime }}\longrightarrow R_M^*. \end{equation}

()

Remark 2.15.The main content of Macaulay's theorem for curves in $\mathbb {P}^2$ (or hypersurfaces in $\mathbb {P}^n$ ) is precisely that the pairings (2.18) are perfect.

Of course, if the natural trace is not an isomorphism, there is little hope for the pairing (2.18) to be perfect. But even if $R_{K_X^2\otimes L^{n+1}}\cong \mathbb {C}$ holds, the pairing will not be perfect in general. Thus, we cannot expect the duality maps $\lambda _M$ to be isomorphisms, but only aim for them to have maximal rank.

We now study the particular cases of duality maps that will be of most interest to us, namely when $X$ is a surface and $M=L$ or $M=K_X\otimes L$ .

Proposition 2.16.If $X$ is a surface and $L$ is an ample line bundle such that $H^1\left(\Omega _X^1\otimes L\right)=0$ , then the duality map $\lambda _{K_X\otimes L^2}$ fits into a natural exact sequence

\begin{equation*} 0 \longrightarrow H^0{\left(\mathcal {O}_X\right)}\stackrel{\cdot c_1{\left(L\right)}}{\longrightarrow } H^1{\left(\Omega _X^1\right)}\longrightarrow R_{K_X\otimes L^2} \stackrel{\lambda _{K_X\otimes L^2}}{\longrightarrow } R_{K_X\otimes L}^*\longrightarrow 0. \end{equation*}

Proof.Recall from (2.9) that $\delta \sigma$ induces the isomorphism

\begin{equation*} R_{K_X\otimes L^2} \stackrel{\cdot \delta \sigma }{\cong }\ker {\left(H^1{\left(\mathcal {E}_{\sigma }\otimes K_X\otimes L\right)}\longrightarrow H^1{\left(\Sigma _L\otimes K_X\otimes L\right)}\right)}. \end{equation*}

Twisting (2.2) with $K_X\otimes L$ , we obtain $0\rightarrow K_X\otimes L\rightarrow \Sigma _L\otimes K_X \otimes L \rightarrow \Omega _X^1\otimes L \rightarrow 0$ . Taking into account the hypothesis $H^1\left(\Omega _X^1\otimes L\right)=0$ , and that $H^1\left(K_X\otimes L\right)=0$ by Kodaira vanishing, the long exact sequence in cohomology gives

\begin{equation} H^1{\left(\Sigma _L\otimes K_K\otimes L\right)}=0,\quad \text{and thus}\quad R_{K_X\otimes L^2}\cong H^1{\left(\mathcal {E}_{\sigma }\otimes K_X\otimes L\right)}. \end{equation}

()

Again from (2.9), we have an isomorphism

\begin{equation*} R_{K_X\otimes L} \stackrel{\cdot \delta \sigma }{\cong } \ker {\left(H^1{\left(\mathcal {E}_{\sigma }\otimes K_X\right)}\longrightarrow H^1{\left(\Sigma _L\otimes K_X\right)}\right)}. \end{equation*}

Since

H^1\left(K_X\otimes L\right)=0

, because

L

is ample, we obtain an exact sequence

\begin{equation} 0\longrightarrow R_{K_X\otimes L}\longrightarrow H^1{\left(\mathcal {E}_{\sigma }\otimes K_X\right)}\longrightarrow H^1{\left(\Sigma _L\otimes K_X\right)}\longrightarrow H^1{\left(K_X\otimes L\right)}=0. \end{equation}

()

Consider finally the short exact sequence (2.2) twisted by $K_X$ :

\begin{equation*} 0\longrightarrow K_X\longrightarrow \Sigma _L\otimes K_X\longrightarrow \Omega _X^1\longrightarrow 0, \end{equation*}

whose connecting homomorphisms in cohomology are given, up to sign, by cup-product with

c_1\left(L\right)

. In particular, we have

\begin{equation*} H^0{\left(\Omega _X^1\right)}\stackrel{c_1{\left(L\right)}}{\longrightarrow } H^1{\left(K_X\right)}\stackrel{0}{\longrightarrow } H^1{\left(\Sigma _L\otimes K_X\right)}\longrightarrow H^1{\left(\Omega _X^1\right)} \stackrel{c_1{\left(L\right)}}{\longrightarrow } H^2{\left(K_X\right)} \longrightarrow 0, \end{equation*}

where the first cup-product with

c_1\left(L\right)

is an isomorphism, and the second one is surjective, because of the Lefschetz theorem. Thus, in particular, we have a short exact sequence

\begin{equation*} 0 \longrightarrow H^1{\left(\Sigma _L\otimes K_X\right)}\longrightarrow H^1{\left(\Omega _X^1\right)}\stackrel{c_1{\left(L\right)}}{\longrightarrow } H^2{\left(K_X\right)}\longrightarrow 0, \end{equation*}

which together with (2.21) gives an exact sequence

\begin{equation} 0\longrightarrow R_{K_X\otimes L}\longrightarrow H^1{\left(\mathcal {E}_{\sigma }\otimes K_K\right)}\longrightarrow H^1{\left(\Omega _X^1\right)}\stackrel{c_1{\left(L\right)}}{\longrightarrow } H^2{\left(K_X\right)} \longrightarrow 0. \end{equation}

()

The statement follows after dualizing (2.22) and using Serre duality in

H^2\left(K_X\right)^*\cong H^0\left(\mathcal {O}_X\right)

and

\begin{equation*} H^1{\left(\mathcal {E}_{\sigma }\otimes K_X\right)}^*\cong H^1{\left(\mathcal {E}_{\sigma }^{\vee }\right)}\cong H^1{\left(\mathcal {E}_{\sigma }\otimes K_X\otimes L\right)}\stackrel{(2.20)}{\cong } R_{K_X\otimes L^2}, \end{equation*}

where the isomorphism in the middle follows from

\begin{eqnarray*} \mathcal {E}_{\sigma }^{\vee }\cong \det \mathcal {E}_{\sigma }^{\vee }\otimes \mathcal {E}\cong {\left(\det \Sigma _L^{\vee }\right)}\otimes L\otimes \mathcal {E}_{\sigma }\cong K_X\otimes L\otimes \mathcal {E}_{\sigma }.\\[-30pt] \end{eqnarray*}

\Box

Proposition 2.17.Suppose that $X$ is a projective surface. If $K_X\otimes L$ is ample and $H^1\left(\Omega _X^1\otimes K_X\otimes L\right)=0$ , the duality map $\lambda _{K_X^2\otimes L^2}$ fits into a natural exact sequence

\begin{equation*} H^1{\left(L\right)}^*\stackrel{H^1{\left(d\sigma \right)}^*}{\longrightarrow } H^1{\left(\Sigma _L\right)}^*\longrightarrow R_{K_X^2\otimes L^2} \stackrel{\lambda _{K_X^2\otimes L^2}}{\longrightarrow } R_L^*\longrightarrow 0. \end{equation*}

Proof.As in the previous proof, using (2.9), we obtain

\begin{equation} R_{K_X^2\otimes L^2} \stackrel{\cdot \delta \sigma }{\cong } \ker {\left(H^1{\left(\mathcal {E}_{\sigma }\otimes K_X^2\otimes L\right)}\longrightarrow H^1{\left(\Sigma _L\otimes K_X^2\otimes L\right)}\right)}. \end{equation}

()

From (2.2),

H^1\left(\Sigma _L\otimes K_X^2\otimes L\right)

sits into the exact sequence

\begin{equation*} 0=H^1{\left(K_X^2\otimes L\right)}\longrightarrow H^1{\left(\Sigma _L\otimes K_X^2\otimes L\right)}\longrightarrow H^1{\left(T_X\otimes K_X^2\otimes L\right)}\cong H^1{\left(\Omega _X^1\otimes K_X\otimes L\right)}=0, \end{equation*}

where the first term vanishes because

K_X\otimes L

is ample, and the last term vanishes by hypothesis. Hence, also

H^1\left(\Sigma _L\otimes K_X^2\otimes L\right)=0

and (2.23) turns into an isomorphism

R_{K_X^2\otimes L^2}\stackrel{\cdot \delta \sigma }{\cong }H^1\left(\mathcal {E}_{\sigma }\otimes K_X^2\otimes L\right)

By Serre duality and the natural isomorphism $\mathcal {E}_{\sigma }^{\vee } \cong \mathcal {E}_{\sigma }\otimes K_X\otimes L$ , we also obtain

\begin{equation} R_{K_X^2\otimes L^2}\cong H^1{\left(\mathcal {E}_{\sigma }^{\vee }\otimes K_X\right)}\cong H^1{\left(\mathcal {E}_{\sigma }\right)}^*. \end{equation}

()

On the other hand, also from (2.9) we can identify $R_L\stackrel{\cdot \delta \sigma }{\cong }\ker \left(H^1\left(\mathcal {E}_{\sigma }\right)\rightarrow H^1\left(\Sigma _L\right)\right)$ , hence we have an exact sequence

\begin{equation*} 0\longrightarrow R_L\stackrel{\cdot \delta \sigma }{\longrightarrow } H^1{\left(\mathcal {E}_{\sigma }\right)}\longrightarrow H^1{\left(\Sigma _L\right)}\stackrel{H^1{\left(d\sigma \right)}}{\longrightarrow } H^1{\left(L\right)}. \end{equation*}

Dualizing it and using the natural isomorphism (2.24), we obtain the statement.

\Box

3 INFINITESIMAL VARIATION OF THE HODGE STRUCTURE OF CURVES IN SURFACES WITH GENERALIZED JACOBIAN RINGS

In this section, we show how the generalized Jacobian rings in the degrees studied above encode almost all necessary information about the IVHS of an ample smooth curve $Z$ in a surface $X$ .

In general, an (one-parameter) IVHS of a smooth curve

Z

is given by a symmetric linear map

\begin{equation*} H^0{\left(K_Z\right)}\rightarrow H^1{\left(\mathcal {O}_Z\right)}\cong H^0{\left(K_Z\right)}^*. \end{equation*}

If the IVHS comes from first-order infinitesimal deformation of

Z

, then it is given (up to non-zero scalar) by cup-product with the Kodaira–Spencer class.

Assume from now on that $X$ is a smooth projective surface and $Z\subseteq X$ is the (smooth) vanishing locus of a section $\sigma$ of an ample line bundle $L$ . This gives the whole family of generalized Jacobian rings $R_M$ for $M\in \operatorname{Pic}\left(X\right)$ , with the properties developed in the previous section.

If we consider an embedded first-order deformation given by another section $\tau \in H^0\left(L\right)$ , the associated IVHS is given by cup-product with $\xi _{\tau }:= KS\left(\tau \right)\in H^1\left(T_Z\right)$ , where $KS: H^0\left(L\right)\rightarrow H^1\left(T_Z\right)$ is as defined in Definition 2.10 (see Lemma 2.9). In particular, $\xi _{\tau }$ depends only on the class of $\tau$ in $R_L$ .

Recall also from Proposition 2.7 that

H^0\left(K_Z\right)

is naturally isomorphic to the direct sum of

R_{K_X\otimes L}

and

H^0\left(\Omega ^1_X\right)

. The latter subspace is mapped to zero by any

\xi _{\tau }

with

\left[\tau \right]\in R_L

, since it is preserved in all embedded deformations of

Z

. Thus, the IVHS

\xi _{\tau }\cdot

is completely determined by its restriction to

R_{K_X\otimes L}

. Composing this restriction with the dual of the inclusion

\nu: R_{K_X\otimes L}\hookrightarrow H^0\left(K_Z\right)

\xi _{\tau }\cdot

induces a map

\begin{equation} R_{K_X\otimes L}\stackrel{\nu }{\hookrightarrow } H^0{\left(K_Z\right)}\stackrel{\xi _{\tau }\cdot }{\longrightarrow } H^1{\left(\mathcal {O}_Z\right)}\stackrel{\nu ^*}{\twoheadrightarrow } R_{K_X\otimes L}^*. \end{equation}

()

Since both source and target spaces, as well as

\xi _{\tau }

, depend on the generalized Jacobian rings, it is natural to expect that the map is also encoded on the generalized Jacobian rings. This is actually true, as we will see in Corollary 3.4, but in order to prove it, we need the following technical result.

Proposition 3.1.Let $\tau \in H^0\left(L\right)$ with associated Kodaira–Spencer class $\xi _{\tau }\in H^1\left(T_Z\right)$ . Let also $\gamma \in H^0\left(K_X^2\otimes L^2\right)$ and consider its restriction $\gamma _{\mid Z}\in H^0\left(K_X^2\otimes L^2_{\mid Z}\right)\cong H^0\left(K_Z^2\right)$ . Then, the product

\begin{equation*} \xi _{\tau }\cdot \gamma _{\mid Z}\in H^1{\left(T_Z\otimes K_Z^2\right)}\cong H^1{\left(K_Z\right)} \end{equation*}

corresponds to

\begin{equation*} {\left(\delta \sigma \right)}^2\cdot \tau \cdot \gamma \in H^2{\left(\det {\left(\mathcal {E}_{\sigma }\otimes L^{\vee }\right)}\otimes L\otimes {\left(K_X^2\otimes L^2\right)}\right)}\cong H^2{\left(K_X\right)} \end{equation*}

under the natural connecting (iso)morphism

H^1\left(K_Z\right)\rightarrow H^2\left(K_X\right)

Proof.Consider first the commutative diagram with exact rows

where the central vertical arrow is the composition of the surjection

\Sigma _L\twoheadrightarrow T_X

and the restriction

T_X\twoheadrightarrow T_{X\mid Z}

. The first connecting homomorphisms of both rows fit in the following commutative diagram which summarizes the definition of

\xi _{\tau }

()

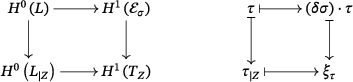Tensoring with

K_X^2\otimes L^2

gives the following diagram:

()

which induces the analogous diagram to (3.2) (in the right square we have multiplied by

\gamma

()

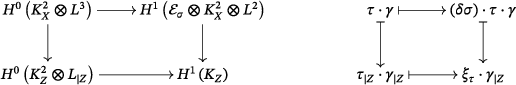Consider now (2.6) with

r=2=\operatorname{rk}\mathcal {E}_{\sigma }

and tensorize it with

K_X^2\otimes L^3

to obtain (using (2.4)):

\begin{equation*} 0 \longrightarrow \det \mathcal {E}_{\sigma }\otimes K_X^2\otimes L\cong K_X \longrightarrow \bigwedge ^2\Sigma _L\otimes K_X^2\otimes L \longrightarrow \mathcal {E}_{\sigma }\otimes K_X^2\otimes L^2\longrightarrow 0. \end{equation*}

From the projection

\Sigma _L\twoheadrightarrow T_X

we can obtain a map

\bigwedge ^2\Sigma _L\twoheadrightarrow \det T_X=K_X^{\vee }

, which tensored by

K_X^2\otimes L

fits into the following diagram:

where the rightmost morphism is the same as the left one in (3.3). We have thus commutative diagrams

()

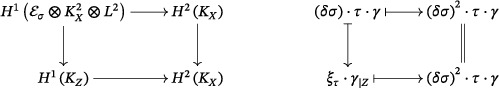The claim follows combining the lower rows in the right squares of (3.4) and (3.5).

\Box

In order to write the map (3.1) in terms of the generalized Jacobian rings, we need a bit more notation. Recall that for any $M\in \operatorname{Pic}\left(X\right)$ we have the duality map (2.19) $\lambda _M: R_M\rightarrow R_{M^{\prime }}^*$ , where $M^{\prime }=M^{\vee }\otimes K_X^2\otimes L^3$ .

Definition 3.2.For two line bundles $M,N$ on the surface $X$ and a section $\alpha \in H^0\left(N\right)$ , we define the linear map $\varphi _M\left(\alpha \right): R_M\rightarrow R_{\left(M\otimes N\right)^{\prime }}^*=R_{K_X^2\otimes L^3\otimes N^{\vee }\otimes M^{\vee }}^*$ given as the composition

\begin{equation} \varphi _M{\left(\alpha \right)}: R_M\stackrel{\cdot \alpha }{\longrightarrow } R_{M\otimes N}\stackrel{\lambda _{M\otimes N}}{\longrightarrow } R_{K_X^2\otimes L^3\otimes M^{\vee }\otimes N^{\vee }}^* \end{equation}

()

of the multiplication by

\alpha

and the duality map of

M\otimes N

Remark 3.3.It follows at once from the definition that

\begin{equation} {\left(\varphi _M{\left(\alpha \right)}\right)}^*=\varphi _{K_X^2\otimes L^3\otimes M^{\vee }\otimes N^{\vee }}{\left(\alpha \right)}. \end{equation}

()

With this last piece of notation, we can state the announced result:

Corollary 3.4.Let $\tau \in H^0\left(L\right)$ represent an embedded first-order deformation of $Z\in \left|L\right|$ with Kodaira–Spencer class $\xi _{\tau }:=KS\left(\tau \right)\in H^1\left(T_Z\right)$ . Then the cup-product with $\xi _{\tau }$ fits into the following commutative diagram:

()

In particular,

\operatorname{rk}\varphi _{K_X\otimes L}\left(\tau \right)\le \operatorname{rk}\left(\xi _{\tau }\cdot \right)

Proof.Recall from (3.6) that $\varphi _{K_X\otimes L}\left(\tau \right)$ is the composition

\begin{equation*} R_{K_X\otimes L}\stackrel{\tau \cdot }{\longrightarrow } R_{K_X\otimes L^2}\stackrel{\lambda _{K_X\otimes L^2}}{\longrightarrow } R_{K_X\otimes L}^* \end{equation*}

of the multiplication map by

\tau

and the duality map

\lambda _{K_X\otimes L^2}

. Moreover, the latter is defined by the natural pairing

R_{K_X\otimes L}\otimes R_{K_X\otimes L^2}\rightarrow R_{K_X^2\otimes L^3}\stackrel{\operatorname{tr}}{\longrightarrow } H^2\left(K_X\right)\cong \mathbb {C}

Thus, the commutativity of (3.8) is equivalent to

\begin{equation} {\left\langle \varphi _{K_X\otimes L}{\left(\tau \right)}{\left(\alpha \right)},\beta \right\rangle} ={\left\langle \nu ^*{\left(\nu {\left(\alpha \right)}\cdot \xi _{\tau }\right)},\beta \right\rangle} \end{equation}

()

for every

\alpha,\beta \in R_{K_X\otimes L}

(or even their representatives

\alpha,\beta \in H^0\left(K_X\otimes L\right)

) where with

\left\langle -,-\right\rangle

we denote the natural pairing between

R_{K_X\otimes L}

and its dual

R_{K_X\otimes L}^*

On one hand, by (2.16) and (3.6), the left-hand side of (3.9) is identified with the class

\begin{equation*} \operatorname{tr}{\left(\tau \alpha \beta \right)}={\left(\delta \sigma \right)}^2\cdot \tau \alpha \beta \in H^2{\left(K_X\right)}, \end{equation*}

which by Proposition 3.1 corresponds to

\xi _{\tau }\cdot \left(\alpha \beta \right)_{\mid Z}

, under the isomorphism

H^2\left(K_X\right)\cong H^1\left(K_Z\right)

On the other hand, the right-hand side of (3.9) corresponds to the class

\begin{equation*} \nu {\left(\alpha \right)}\cdot \xi _{\tau }\cdot \nu {\left(\beta \right)}=\xi _{\tau }\alpha _{\mid Z}\beta _{\mid Z}\in H^1{\left(K_Z\otimes T_Z\otimes K_Z\right)}=H^1{\left(K_Z\right)}. \end{equation*}

which clearly agrees with

\xi _{\tau }\cdot \left(\alpha \beta \right)_{\mid Z}

\Box

We now prove a generalization of [4, Lemma 2.4], giving a particular property of sections in the kernel of a general $\xi _{\tau }\cdot$ , which allows us to tackle the problem directly on $R_{K_X\otimes L}$ without need to consider the elements $\tau \in R_L$ .

Lemma 3.5.Let $\tau \in H^0\left(L\right)$ be such that $\varphi _{K_X\otimes L}\left(\tau \right): R_{K_X\otimes L}\rightarrow R_{K_X\otimes L}^*$ has maximal rank (among all possible $\tau \in H^0\left(L\right)$ ). Then for every $\alpha \in \ker \varphi _{K_X\otimes L}\left(\tau \right)$ it holds $\lambda _{K_X^2\otimes L^2}\left(\alpha ^2\right)=0\in R_L^*$ .

Proof.The condition $\alpha \in \ker \varphi _{K_X\otimes L}\left(\tau \right)$ means that $\lambda _{K_X\otimes L^2}\left(\tau \cdot \alpha \right)=0\in R_{K_X\otimes L}^*$ , that is,

\begin{equation} \operatorname{tr}{\left(\tau \cdot \alpha \cdot \beta \right)}=0\in H^2{\left(K_X\right)} \end{equation}

()

for every

\beta \in R_{K_X\otimes L}

Assuming this, we want to prove that $\operatorname{tr}\left(\alpha ^2\cdot w\right)=0$ for every $w\in R_L$ .

Let $w\in R_L$ be arbitrary. By semicontinuity, the rank of $\varphi _{K_X\otimes L}\left(\tau \right)$ is lower-semicontinuous, that is, the maximum is attained for $\tau$ on a dense open subset of $H^0\left(L\right)$ . In particular, there is a small neighborhood $U\subseteq \mathbb {C}$ of $0\in \mathbb {C}$ such that $\varphi _{K_X\otimes L}\left(\tau +tw\right)$ is of maximal rank for all $t\in U$ . Moreover, when $t$ varies, the kernels of $\varphi _{K_X\otimes L}\left(\tau +tw\right)$ form a (holomorphic) vector subbundle of the trivial vector bundle with fiber $R_{K_X\otimes L}$ over $U$ . Thus, $\alpha \in \ker \varphi _{K_X\otimes L}\left(\tau \right)$ can be extended to a (holomorphic) section over $U$ with $\alpha \left(t\right)\in \ker \varphi _{K_X\otimes L}\left(\tau +tw\right)\subseteq R_{K_X\otimes L}$ for every $t\in U$ and $\alpha \left(0\right)=\alpha$ . This means

\begin{equation*} \varphi _{K_X\otimes L}{\left(\tau +tw\right)}{\left(\alpha {\left(t\right)}\right)}=0\in R_{K_X\otimes L}^*\quad \forall \,t\in U, \end{equation*}

or in other words

\begin{equation} \operatorname{tr}{\left({\left(\tau +tw\right)}\cdot \alpha {\left(t\right)}\cdot \beta \right)}=0\in H^2{\left(K_X\right)}\cong \mathbb {C}\quad \forall \,t\in U,\forall \,\beta \in R_{K_X\otimes L}. \end{equation}

()

Differentiating (3.11) and evaluating at

t=0

, we obtain

\begin{equation*} \operatorname{tr}{\left(w\cdot \alpha {\left(0\right)}\cdot \beta +\tau \cdot \alpha ^{\prime }{\left(0\right)}\cdot \beta \right)}=0\quad \forall \,\beta \in R_{K_X\otimes L}. \end{equation*}

In particular, for

\beta =\alpha =\alpha \left(0\right)

we have

\begin{equation*} \operatorname{tr}{\left(w\cdot \alpha ^2\right)}=-\operatorname{tr}{\left(\tau \cdot \alpha ^{\prime }{\left(0\right)}\cdot \alpha \right)}=0, \end{equation*}

where the last equality follows from (3.10) with

\beta =\alpha ^{\prime }\left(0\right)

\Box

In view of Lemma 3.5, one way to prove that the general first-order embedded deformation of $Z$ has maximal infinitesimal variation is to prove that the only $\alpha \in R_{K_X\otimes L}$ with $\lambda _{K_X^2\otimes L^2}\left(\alpha ^2\right)=0\in R_L^*$ is $\alpha =0$ .

Remark 3.6.To prove the injectivity of $\varphi _{K_X\otimes L}\left(\tau \right)$ for a general $\tau \in R_L$ , this approach can only work if $\dim R_{K_X\otimes L}\le \dim R_L$ , which is not expected if $K_X$ is positive. Indeed, for a given $\tau \in R_L$ , the condition $\operatorname{tr}\left(\tau \cdot \alpha ^2\right)=0$ defines a quadric $Q_{\tau }\subseteq \mathbb {P}\left(R_{K_X\otimes L}\right)$ . Thus, $\lambda _{K_X^2\otimes L^2}\left(\alpha ^2\right)=0$ is equivalent to $\alpha$ lying on the intersection $Q_{\tau _1}\cap \ldots \cap Q_{\tau _m}$ for $\tau _1,\ldots,\tau _m\in R_L$ a basis. If $\dim R_L=m\le \dim \mathbb {P}\left(R_{K_X\otimes L}\right)=\dim R_{K_X\otimes L}-1$ the intersection would not be empty, hence there will be nonzero $\alpha$ ’s with $\lambda _{K_X^2\otimes L^2}\left(\alpha ^2\right)=0\in R_L^*$ .

Thus, we only expect this approach to work for curves on surfaces with somehow non-positive canonical bundle, such as del Pezzo surfaces or at most K3 or Abelian surfaces.

It will actually be more convenient to work with the representatives

\alpha \in H^0\left(K_X\otimes L\right)

(which we still denote as

\alpha

for the sake of simplicity), and thus consider the elements in the kernel of the composition

\begin{equation} \lambda: H^0{\left(K_X^2\otimes L^2\right)}\longrightarrow R_{K_X^2\otimes L^2}\stackrel{\lambda _{K_X^2\otimes L^2}}{\longrightarrow }R_L^* \end{equation}

()

Our aim is then to prove that the only

\alpha \in H^0\left(K_X\otimes L\right)

with

\lambda \left(\alpha ^2\right)=0

are those lying on

J_{K_X\otimes L}

. This leads to the following definition.

Definition 3.7.Let $D\subseteq \mathbb {P}\left(H^0\left(K_X^2\otimes L^2\right)\right)$ be defined as

\begin{equation*} D={\left\lbrace {\left[\alpha \beta \right]}\in \mathbb {P}{\left(H^0{\left(K_X^2\otimes L^2\right)}\right)}\,\mid \,\alpha,\beta \in H^0{\left(K_X\otimes L\right)}, \alpha \beta \in \ker \lambda \right\rbrace}, \end{equation*}

where from now on we use square brackets to denote the corresponding point in the projectivization of a vector space.

In other words, $D$ is the intersection of the linear subspace $\mathbb {P}\left(\ker \lambda \right)$ and the image of the Segre-multiplication map $\mathbb {P}\left(H^0\left(K_X\otimes L\right)\right)\times \mathbb {P}\left(H^0\left(K_X\otimes L\right)\right)\rightarrow \mathbb {P}\left(H^0\left(K_X^2\otimes L^2\right)\right)$ .

Theorem 3.8.Assume $L$ has not maximal infinitesimal variation at a smooth $Z\in \left|L\right|$ . Then, it holds

\begin{equation*} \dim D\ge h^0{\left(K_X\otimes L\right)}+p_g{\left(X\right)}-1. \end{equation*}

Proof.The proof follows some ideas of [4, Proposition 3.4]. Define

\begin{equation*} Y:={\left\lbrace {\left[\alpha \right]}\in \mathbb {P}{\left(H^0{\left(K_X\otimes L\right)}\right)}\,\mid \,\alpha ^2\in \ker \lambda \right\rbrace} \end{equation*}

and the following incidence variety:

\begin{equation*} W:={\left\lbrace {\left({\left[\alpha \right]},{\left[\beta \right]}\right)}\in Y\times \mathbb {P}{\left(H^0{\left(K_X\otimes L\right)}\right)}\,\mid \,\alpha \beta \in \ker \lambda \right\rbrace} . \end{equation*}

The projection onto the first factor defines a surjective morphism

\pi: W\rightarrow Y

(

\beta =\alpha

gives a preimage for any

\left[\alpha \right]\in Y

), and multiplication defines a morphism

\psi: W\rightarrow D

Note first that $\psi$ is a finite morphism: the zero locus of any element $\left[\gamma \right]\in D\subseteq \mathbb {P}\left(H^0\left(K_X^2\otimes L^2\right)\right)$ has finitely many decompositions into the sum of two effective divisors, hence in particular $\gamma$ admits finitely many decompositions (up to multiplication of one factor by $a\in \mathbb {C}^*$ ) of the form $\gamma =\alpha \beta$ with $\alpha,\beta \in H^0\left(K_X\otimes L\right)$ . Thus,

\begin{equation} \dim W\le \dim D. \end{equation}

()

We consider now the fibers of

\pi

: for

\left[\alpha \right]\in Y

, it holds

\begin{align*} \pi ^{-1}{\left({\left[\alpha \right]}\right)}&={\left\lbrace {\left[\alpha \right]}\right\rbrace} \times {\left\lbrace {\left[\beta \right]}\in \mathbb {P}{\left(H^0{\left(K_X\otimes L\right)}\right)}\,\mid \,\alpha \beta \in \ker \lambda \right\rbrace} \\ &\cong \mathbb {P}{\left(\ker {\left(H^0{\left(K_X\otimes L\right)}\stackrel{\cdot \alpha }{\longrightarrow }H^0{\left(K_X^2\otimes L^2\right)}\stackrel{\lambda }{\longrightarrow } R_L^*\right)}\right)} \end{align*}

The latter composition factorizes also as

H^0\left(K_X\otimes L\right)\twoheadrightarrow R_{K_X\otimes L}\stackrel{\varphi _{K_X\otimes L}\left(\alpha \right)}{\longrightarrow } R_L^*

, where the first map is surjective, and thus

\begin{align*} \dim \pi ^{-1}{\left({\left[\alpha \right]}\right)}&=\dim \ker {\left(H^0{\left(K_X\otimes L\right)}\twoheadrightarrow R_{K_X\otimes L}\stackrel{\varphi _{K_X\otimes L}{\left(\alpha \right)}}{\longrightarrow } R_L^*\right)}-1 \\ &=h^0{\left(K_X\otimes L\right)}-\operatorname{rk}\varphi _{K_X\otimes L}{\left(\alpha \right)}-1 \\ &\stackrel{(3.7)}{=}h^0{\left(K_X\otimes L\right)}-\operatorname{rk}\varphi _L{\left(\alpha \right)}-1 \end{align*}

Since

\pi: W\rightarrow Y

is a surjective morphism, it holds

\begin{equation} \dim W=\dim Y+\dim \pi ^{-1}{\left({\left[\alpha \right]}\right)}=\dim Y+h^0{\left(K_X\otimes L\right)}-\operatorname{rk}\varphi _L{\left(\alpha \right)}-1 \end{equation}

()

for a general

\left[\alpha \right]\in Y

It remains to find a lower bound on the dimension of $Y$ . To this aim we introduce one further incidence variety. Denote by $\lambda ^{\prime }$ the composition

\begin{equation*} \lambda ^{\prime }: H^0{\left(K_X\otimes L^2\right)}\twoheadrightarrow R_{K_X\otimes L^2}\stackrel{\lambda _{K_X\otimes L^2}}{\longrightarrow } R_{K_X\otimes L}^*, \end{equation*}

let

U\subseteq \mathbb {P}\left(H^0\left(L\right)\right)

be the dense open subset consisting of the

\left[\tau \right]

for which

\varphi _{K_X\otimes L}\left(\tau \right)

has maximal rank, and set

\begin{equation*} I:={\left\lbrace {\left({\left[\tau \right]},{\left[\alpha \right]}\right)}\in U\times \mathbb {P}{\left(H^0{\left(K_X\otimes L\right)}\right)}\,\mid \, \tau \alpha \in \ker \lambda ^{\prime }\right\rbrace}, \end{equation*}

which is equipped with two projections

\mu _1: I\rightarrow U

and

\mu _2: I\rightarrow \mathbb {P}\left(H^0\left(K_X\otimes L\right)\right)

The fiber of $\mu _1$ over a given $\left[\tau \right]\in U$ is the projectivization of the kernel of the composition

\begin{equation*} H^0{\left(K_X\otimes L\right)}\longrightarrow H^0{\left(K_X\otimes L\right)}/J_{K_X\otimes L}=R_{K_X\otimes L}\stackrel{\varphi _{K_X\otimes L}{\left(\tau \right)}}{\longrightarrow } R_{K_X\otimes L}^*, \end{equation*}

which obviously contains

J_{K_X\otimes L}=H^0\left(K_X\right)\cdot \sigma

(Proposition 2.7), with equality if and only if

\varphi _{K_X\otimes L}\left(\tau \right)

is an isomorphism. Thus,

L

has maximal infinitesimal variation at

Z\in \left|L\right|

if and only if the general fiber of

\mu _1

has dimension precisely

\dim \mathbb {P}\left(J_{K_X\otimes L}\right)=p_g\left(X\right)-1

. By assumption,

L

has not maximal infinitesimal variation, and hence

\mu _1

is surjective and its general fiber has dimension at least

p_g\left(X\right)

. Therefore, it holds

\begin{equation} \dim I\ge \dim U+p_g{\left(X\right)}=\dim \mathbb {P}{\left(H^0{\left(L\right)}\right)}+p_g{\left(X\right)}=h^0{\left(L\right)}+p_g{\left(X\right)}-1. \end{equation}

()

We now consider the projection

\mu _2

. By Lemma 3.5, for every

\left(\left[\tau \right],\left[\alpha \right]\right)\in I

it holds

\lambda \left(\alpha ^2\right)=0

, that is,

\left[\alpha \right]\in Y

and thus

\mu _2\left(I\right)\subseteq Y

. As for the fibers of

\mu _2

it holds

\begin{equation*} \mu _2^{-1}{\left({\left[\alpha \right]}\right)}\cong {\left\lbrace {\left[\tau \right]}\in U\,\mid \,\varphi _L{\left(\alpha \right)}{\left(\tau \right)}=0\in R_{K_X\otimes L}^*\right\rbrace} =U\cap \mathbb {P}{\left(\ker {\left(H^0{\left(L\right)}\twoheadrightarrow R_L\stackrel{\varphi _L{\left(\alpha \right)}}{\longrightarrow } R_{K_X\otimes L}^*\right)}\right)}. \end{equation*}

All in all we obtain

\begin{equation} \dim I=\dim \mu _2{\left(I\right)}+\dim \mu _2^{-1}{\left({\left[\alpha \right]}\right)}\le \dim Y+\dim \ker \varphi _L{\left(\alpha \right)}+\dim J_L-1 \end{equation}

()

for a general

\alpha \in \mu _2\left(I\right)

. Combining (3.15) and (3.16), we obtain

\begin{equation*} \dim Y\ge h^0{\left(L\right)}-\dim J_L-\dim \ker \varphi _L{\left(\alpha \right)}+p_g{\left(X\right)}=\operatorname{rk}\varphi _L{\left(\alpha \right)}+p_g{\left(X\right)}, \end{equation*}

which with (3.13) and (3.14) gives the wanted

\begin{eqnarray*} \dim D\ge \dim W\ge h^0{\left(K_X\otimes L\right)}+p_g{\left(X\right)}-1.\\[-30pt] \end{eqnarray*}

\Box

4 CURVES IN $\mathbb {P}^1\times \mathbb {P}^1$

We now show that for $X=\mathbb {P}^1\times \mathbb {P}^1$ and $L$ sufficiently ample (with a very explicit condition on the bidegree) we can obtain an upper-bound on $\dim D$ , contradicting the lower bound of Theorem 3.8, thus proving Theorem 1.4.

Let us then fix $X=\mathbb {P}^1\times \mathbb {P}^1$ . Recall that line bundles on $\mathbb {P}^1\times \mathbb {P}^1$ are determined by its bidegree. We denote by $\mathcal {O}_X\left(d,e\right)=\mathcal {O}_{\mathbb {P}^1}\left(d\right)\boxtimes \mathcal {O}_{\mathbb {P}^1}\left(e\right)$ . More generally, for any sheaf $\mathcal {F}$ of $\mathcal {O}_X$ -modules on $X$ we denote by $\mathcal {F}\left(d,e\right)=\mathcal {F}\otimes \mathcal {O}_X\left(d,e\right)$ .

We also denote by $\left(x_0:x_1\right)$ (resp. $\left(y_0:y_1\right)$ ) homogeneous coordinates on the first (resp. second) factor. Consider the polynomial ring $S:=\mathbb {C}\left[x_0,x_1,y_0,y_1\right]$ , bigraded so that $\deg \left(x_i\right)=\left(1,0\right)$ and $\deg \left(y_i\right)=\left(0,1\right)$ , and write $S_{d,e}$ for the summand of polynomials of bidegree $\left(d,e\right)$ , which correspond to the global sections of $\mathcal {O}_X\left(d,e\right)$ . Also, for any bihomogeneous ideal $I\subseteq S$ we denote by $I_{d,e}=I\cap S_{d,e}$ , the summand of elements of bidegree $\left(d,e\right)$ .

Let now $L=\mathcal {O}_X\left(d,e\right)$ and choose an irreducible non-zero section $F\in H^0\left(X,L\right)=S_{d,e}$ . Its zero locus $Z:=\left\lbrace F=0\right\rbrace \subseteq \mathbb {P}^1\times \mathbb {P}^1$ is a smooth curve if and only if the four partial derivatives of $F$ have no common zero, that is, $\left\lbrace \frac{\partial F}{\partial x_0}=\frac{\partial F}{\partial x_1}=\frac{\partial F}{\partial y_0}=\frac{\partial F}{\partial y_1}=0\right\rbrace =\emptyset \subseteq \mathbb {P}^1\times \mathbb {P}^1$ .

L

we can attach the bundle of first-order differential operators

\Sigma _L

, and then

F\in H^0\left(L\right)

induces the surjective morphism

dF: \Sigma _L\rightarrow L

. For any

M=\mathcal {O}_X\left(a,b\right)

we can consider the corresponding generalized Jacobian ideal

\begin{equation*} J_{a,b}:=J_M=\operatorname{im}{\left(H^0{\left(\Sigma _L\otimes L^{\vee }\otimes M\right)}=H^0{\left(\Sigma _L{\left(a-d,b-e\right)}\right)}\longrightarrow H^0{\left(M\right)}\right)}\subseteq H^0{\left(M\right)}=S_{a,b}. \end{equation*}

Lemma 4.1.The generalized Jacobian ideal coincides with the “usual” Jacobian ideal generated by the partial derivatives of $F$ , that is,

\begin{align*} J_{a,b}&={\left(\frac{\partial F}{\partial x_0},\frac{\partial F}{\partial x_1},\frac{\partial F}{\partial y_0},\frac{\partial F}{\partial y_1}\right)}_{a,b}\\ &={\left\lbrace P_0\frac{\partial F}{\partial x_0}+P_1\frac{\partial F}{\partial x_1}+Q_0\frac{\partial F}{\partial y_0}+Q_1\frac{\partial F}{\partial y_1}\,\mid \,P_0,P_1\in S_{a-d+1,b-e},Q_0,Q_1\in S_{a-d,b-e+1}\right\rbrace} . \end{align*}

In particular, the pieces of small degree are

J_{d-1,e-1}=0

\begin{equation*} J_{d-1,e}={\left\lbrace a_0\frac{\partial F}{\partial x_0}+a_1\frac{\partial F}{\partial x_1}\,\mid \,a_0,a_1\in \mathbb {C}\right\rbrace}, J_{d,e-1}={\left\lbrace b_0\frac{\partial F}{\partial y_0}+b_1\frac{\partial F}{\partial y_1}\,\mid \,b_0,b_1\in \mathbb {C}\right\rbrace}, \end{equation*}

and

J_{d,e}

is generated as a vector space by

\begin{equation*} {\left\lbrace x_0\frac{\partial F}{\partial x_0},x_1\frac{\partial F}{\partial x_0},x_0\frac{\partial F}{\partial x_1},x_1\frac{\partial F}{\partial x_1},y_0\frac{\partial F}{\partial y_0},y_1\frac{\partial F}{\partial y_0},y_0\frac{\partial F}{\partial y_1},y_1\frac{\partial F}{\partial y_1}\right\rbrace} . \end{equation*}

These generators are however not linearly independent, since the Euler relations with respect to each subset of variables give

\begin{equation} \frac{1}{d}{\left(x_0\frac{\partial F}{\partial x_0}+x_1\frac{\partial F}{\partial x_1}\right)}=F=\frac{1}{e}{\left(y_0\frac{\partial F}{\partial y_0}+y_1\frac{\partial F}{\partial y_1}\right)}. \end{equation}

()

Proof of Lemma 4.1.We first describe a trivialization of $\Sigma _L$ . For $i,j=0,1$ consider the affine open subset

\begin{equation*} \def\eqcellsep{&}\begin{array}{rcl}U_{ij}:={\left\lbrace {\left({\left[x_0:x_1\right]},{\left[y_0:y_1\right]}\right)}\,\mid \,x_iy_j\ne 0\right\rbrace} & \stackrel{\cong }{\longleftrightarrow } & \mathbb {C}^2 \\[3pt] {\left({\left[x_0:x_1\right]},{\left[y_0:y_1\right]}\right)} & \mapsto & {\left(z_{1-i},w_{1-j}\right)}:={\left(\frac{x_{1-i}}{x_i},\frac{y_{1-j}}{y_j}\right)} \end{array} \end{equation*}

U_{ij}

the line bundle

L

is trivialized by the section

e_{ij}:=x_i^dy_j^e

, and any

F\left(x_0,x_1,y_0,y_1\right)\in H^0\left(L\right)

can be uniquely written as

F=f_{ij}\left(z_{1-i},w_{1-j}\right)x_i^dy_j^e

for a polynomial

f_{ij}\in \mathbb {C}\left[z_{1-i},w_{1-j}\right]

. We can obtain

f_{ij}

explicitly, by substituting

x_i=y_j=1

x_{1-i}=z_{1-i}

and

y_{1-j}=w_{1-j}

Moreover, $\Sigma _L$ is trivialized by $\left\lbrace 1,D_z^{ij},D_w^{ij}\right\rbrace$ , where $D_z^{ij}\mapsto \frac{\partial }{\partial z_{1-i}}$ and $D_w^{ij}\mapsto \frac{\partial }{\partial w_{1-j}}$ under the natural projection $\Sigma _L\rightarrow T_{\mathbb {P}^1\times \mathbb {P}^1}$ . And the morphism $dF: \Sigma _L\rightarrow L$ is given by $dF\left(1\right)=f_{ij}e_{ij}=F$ ,

\begin{equation} dF{\left(D_z^{ij}\right)}=\frac{\partial f_{ij}}{\partial z_{1-i}}e_{ij}=\frac{\partial F}{\partial x_{1-i}}{\left(x_i=1,y_j=1\right)}x_i^ey_j^d=x_i\frac{\partial F}{\partial x_{1-i}} \end{equation}

()

and

\begin{equation*} dF{\left(D_w^{ij}\right)}=\frac{\partial f_{ij}}{\partial w_{1-j}}e_{ij}=\frac{\partial F}{\partial y_{1-j}}{\left(x_i=1,y_j=1\right)}x_i^ey_j^d=y_j\frac{\partial F}{\partial y_{1-j}}. \end{equation*}

Since the result of (4.2) is independent of

j

, we conclude that

D_z^{i0}=D_z^{i1}

U_{i0}\cap U_{i1}

, and analogously

D_w^{0j}=D_w^{1j}

U_{0j}\cap U_{1j}

. We just denote then by

D_z^i

resp.

D_w^j

the local section of

\Sigma _L

given by

D_z^{ij}

U_{ij}

resp.

D_w^{ij}

U_{ij}

In order to compare $D_z^0$ and $D_z^1$ on $U_{0j}\cap U_{1j}$ , we compare their images under $dF$ for an arbitrary $F\in H^0\left(L\right)$ , which are respectively $x_0\frac{\partial F}{\partial x_1}$ and $x_1\frac{\partial F}{\partial x_0}$ . Using the Euler relation with respect to the variables $x_0,x_1$ we obtain

\begin{equation} dF{\left(x_1^2D_z^0+x_0^2D_z^1\right)}=x_1^2x_0\frac{\partial F}{\partial x_1}+x_0^2x_1\frac{\partial F}{\partial x_0}=x_0x_1{\left(x_0\frac{\partial F}{\partial x_0}+x_1\frac{\partial F}{\partial x_1}\right)}=d\cdot x_0x_1 F =dF{\left(d\cdot x_0x_1\cdot 1\right)}. \end{equation}

()

Since this should hold for any

F\in H^0\left(L\right)

, it must hold

\begin{equation} x_1^2D_z^0+x_0^2D_z^1=d\cdot x_0x_1\cdot 1,\quad \text{i.e.}\quad D_z^1=d\cdot \frac{x_1}{x_0}\cdot 1-{\left(\frac{x_1}{x_0}\right)}^2D_z^0=d\cdot z_1\cdot 1-z_1^2D_z^0. \end{equation}

()

Analogously, we can prove

\begin{equation} D_w^1=d\cdot w_1\cdot 1-w_1^2D_w^0. \end{equation}

()

We are now ready to compute a basis of the global sections of $\Sigma _L\left(a,b\right)$ for any $a,b\in \mathbb {Z}$ .

Note first that the short exact sequence

\begin{equation} 0 \longrightarrow \mathcal {O}_X{\left(a,b\right)} \longrightarrow \Sigma _L{\left(a,b\right)}\longrightarrow T_X{\left(a,b\right)}=\mathcal {O}_X{\left(a+2,b\right)}\oplus \mathcal {O}_X{\left(a,b+2\right)}\longrightarrow 0 \end{equation}

()

gives

h^0\left(\Sigma _L\left(a,b\right)\right)=0

unless

a,b\ge -2

. Thus from now on we restrict ourselves to this case.

On $U_{ij}$ , $\Sigma _L\left(a,b\right)$ is trivialized by $1\cdot x_i^ay_j^b, D_z^i\otimes x_i^1y_j^b$ and $D_w^j\otimes x_i^ay_j^b$ , and the gluing relations are given by (4.4) and (4.5).

On $U_{ij}$ a global section of $\Sigma _L\left(a,b\right)$ is thus described as

\begin{equation*} {\left(A_{ij}\cdot 1+B_{ij}D_z^i+C_{ij}D_w^j\right)}\otimes x_i^ay_j^b \end{equation*}

for certain polynomials

A_{ij},B_{ij},C_{ij}\in \mathbb {C}\left[z_{1-j},w_{1-j}\right]

. We will now use the relations (4.4) and (4.5) to find relations between these polynomials, as well as upper bounds on their (bi)degrees.

Using (4.3) and $z_0=\frac{x_0}{x_1}=\frac{1}{z_1}$ , we obtain

\begin{equation} A_{0j}{\left(z_1,w_{1-j}\right)}\eqcellsep =\eqcellsep {\left[A_{1j}{\left(\frac{1}{z_1},w_{1-j}\right)}+d\cdot z_1B_{1j}{\left(\frac{1}{z_1},w_{1-j}\right)}\right]}z_1^a\eqbreak \end{equation}

()

\begin{equation} B_{0j}{\left(z_1,w_{1-j}\right)}\eqcellsep =\eqcellsep -B_{1j}{\left(\frac{1}{z_1},w_{1-j}\right)}z_1^{a+2}\eqbreak \end{equation}

()

\begin{equation} C_{0j}{\left(z_1,w_{1-j}\right)}\eqcellsep =\eqcellsep C_{1j}{\left(\frac{1}{z_1},w_{1-j}\right)}z_1^a. \end{equation}

()

From (4.8) and (4.9) it follows

\deg _{z_0}B_{1j}\le a+2

and

\deg _{z_0}C_{1j}\le a

By symmetry, it must also hold

\begin{align*} A_{i0}{\left(z_{1-i},w_1\right)}&={\left[A_{i1}{\left(z_{1-i},\frac{1}{w_1}\right)}+e\cdot w_1C_{i1}{\left(z_{1-i},\frac{1}{w_1}\right)}\right]}w_1^b \\ B_{i0}{\left(z_{1-i},\frac{1}{w_1}\right)}&=-B_{i1}{\left(z_{1-i},\frac{1}{w_1}\right)}w_1^{b+2} \\ C_{i0}{\left(z_{1-i},\frac{1}{w_1}\right)}&=C_{i1}{\left(z_{1-i},\frac{1}{w_1}\right)}w_1^b, \end{align*}

hence, in particular,

\deg _{w_0}B_{1j}\le b

and

\deg _{w_0}C_{1j}\le b+2

We can try with monomials $B_{11}=z_0^rw_0^s$ and $C_{11}=z_0^nw_0^m$ , where $0\le r\le a+2$ , $0\le s\le b$ , $0\le n\le a$ and $0\le m\le b+2$ , and check the possibilities for $A_{11}$ .

From (4.7) it follows that $A_{11}\left(\frac{1}{z_1},w_0\right)z_1^a+d\cdot z_1^{a+1-r}w_0^s$ must be a polynomial on $z_1$ and $w_0$ .

If $r\le a+1$ it is enough that $\deg _{z_0}A_{11}\le a$ , thus we can take any monomial $A_{11}\left(z_0,w_0\right)=z_0^tw_0^u$ with $0\le t\le a$ .
If $r=a+2$ , $A_{11}$ must contain the monomial $-d\cdot z_0^{a+1}w_0^s$ , in order to cancel the term $d\cdot z_1^{-1}w_0^s$ (and also any monomial as in the case $r\le a+1$ ).

By symmetry:

If $m\le b+1$ , $A_{11}$ can contain any monomial $z_0^tw_0^u$ with $0\le u\le b$ ,
If $m=\le b+2$ , then $A_{11}$ must contain $-e\cdot z_0^nw_0^{b+2}$ .

Altogether, we have the following basis for

H^0\left(\Sigma _L\left(a,b\right)\right)

(we give their local expressions on

U_{11}

)

(1) $z_0^tw_0^u\cdot 1\otimes x_1^ay_1^b$ with $0\le t\le a$ and $0\le u\le b$ ,
(2) $z_0^rw_0^s\cdot D_z^1\otimes x_1^ay_1^b$ with $0\le r\le a+1$ and $0\le s\le b$ ,
(3) $\left(-d\cdot z_0^{a+1}w_0^s\cdot 1+z_0^{a+2}w_0^s\cdot D_z^1\right)\otimes x_1^ay_1^b$ with $0\le s\le b$
(4) $z_0^nw_0^m\cdot D_w^1\otimes x_1^ay_1^b$ with $0\le n\le a$ and $0\le m\le b+1$ , and
(5) $\left(-e\cdot z_0^nw_0^{b+1}\cdot 1+z_0^nw_0^{b+2}\cdot D_w^1\right)\otimes x_1^ay_1^b$ with $0\le n\le a$ .

Note that if $a=-2$ or $b=-2$ there are no elements in the above list, hence also $H^0\left(\Sigma _L\left(a,b\right)\right)=0$ . This is compatible with the short exact sequence (4.6), since in this case we have $H^1\left(\mathcal {O}_X\left(a,b\right)\right)\ne 0$ , and the connecting homomorphism turns out to be an isomorphism.

In order to finish the proof, we just need to compute a set of generators of

\begin{equation*} J_{a,b}=\operatorname{im}{\left(dF: H^0{\left(\Sigma _L{\left(a-d,b-e\right)}\right)}\rightarrow H^0{\left(\mathcal {O}_X{\left(a,b\right)}\right)}\right)} \end{equation*}

by applying the differential

dF

to the elements of the above basis (replacing

a

a-d

and

b

b-d

). Since

H^0\left(\Sigma _L\left(a-d,b-e\right)\right)=0

unless

a-d,b-e\ge -1

, we can assume

a\ge d-1

and

b\ge e-1

. Recall that

dF\left(1\right)=F

dF\left(D_z^1\right)=x_1\frac{\partial F}{\partial x_0}

and

dF\left(D_w^1\right)=y_1\frac{\partial F}{\partial y_0}

, and thus

(1) $dF\left(z_0^tw_0^u\cdot 1\otimes x_1^{a-d}y_1^{b-e}\right)=\frac{x_0^t}{x_1^t}\frac{y_0^u}{y_1^u} x_1^{a-d}y_1^{b-e} F=x_0^tx_1^{a-d-t}y_0^uy_1^{b-e-u}F$ with $0\le t\le a-d$ and $0\le u\le b-e$ , that is, we obtain all possible multiples of $F$ with bidegree $\left(a,b\right)$ ;
(2)
$dF\left(z_0^rw_0^s\cdot D_z^1\otimes x_1^{a-d}y_1^{b-e}\right)=x_0^rx_1^{a-d-r+1}y_0^sy_1^{b-e-s}\frac{\partial F}{\partial x_0}$ with $0\le r\le a-d+1$ and $0\le s\le b-e$ , that is, all multiples of $\frac{\partial F}{\partial x_0}$ of bidegree $\left(a,b\right)$ ;
(3) $dF\left(\left(-d\cdot z_0^{a-d+1}w_0^s\cdot 1+z_0^{a-d+2}w_0^s\cdot D_z^1\right)\otimes x_1^{a-d}y_1^{b-e}\right)=-d\cdot x_0^{a-d+1}x_1^{-1}y_0^sy_1^{b-e-s}F+x_0^{a-d+2}x_1^{-2}y_0^sy_1^{b-e-s}x_1\frac{\partial F}{\partial x_0}=x_0^{a-d+1}x_1^{-1}y_0^sy_1^{b-e-s}\left[-d\cdot F+x_0\frac{\partial F}{\partial x_0}\right]=x_0^{a-d+1}x_1^{-1}y_0^sy_1^{b-e-s}\left[-x_1\frac{\partial F}{\partial x_1}\right]=-x_0^{a-d+1}y_0^sy_1^{b-e-s}\frac{\partial F}{\partial x_1}$ with $0\le s\le b-e$ , that is, all multiples of $x_0^{a-d+1}\frac{\partial F}{\partial x_1}$ of bidegree $\left(a,b\right)$ . The remaining multiples of $\frac{\partial F}{\partial x_1}$ of the same bidegree, admitting powers of $x_1$ , can be obtained from (4) and (4) using the Euler relation with respect to $x_0,x_1$ .
(4) $dF\left(z_0^nw_0^m\cdot D_w^1\otimes x_1^{a-d}y_1^{b-e}\right)=x_0^nx_1^{a-d-n}y_0^my_1^{b-e-m+1}\frac{\partial F}{\partial y_0}$ with $0\le n\le a-d$ and $0\le m\le b-e+1$ , and
(5) $dF\left(\left(-e\cdot z_0^nw_0^{b-e+1}\cdot 1+z_0^nw_0^{b-e+2}\cdot D_w^1\right)\otimes x_1^{a-d}y_1^{b-e}\right)=-x_0^nx_1^{a-d-n}y_1^{b-e+1}\frac{\partial F}{\partial y_1}$ with $0\le n\le a-d$ .

Thus,

J_{a,b}

contains all products of the partial derivatives of

F

and monomials (of the right bidegree), which proves the claim.

\Box

In order to find a contradiction with Theorem 3.8, we need to understand the geometry of the linear system on $Z$ induced by $J_{d,e}$ . More strictly speaking, since $F\in J_{d,e}$ , the restriction map $J_{d,e}\subseteq H^0\left(L\right)\rightarrow H^0\left(L_{\mid Z}\right)=H^0\left(\mathcal {O}_Z\left(d,e\right)\right)$ is not injective, but its image induces a linear subsystem of $\left|\mathcal {O}_Z\left(d,e\right)\right|$ that we will still denote $\left|J_{d,e\mid Z}\right|$ . It will be helpful to consider also the restrictions of $J_{d-1,e}$ and $J_{d,e-1}$ , which by degree reasons inject in $H^0\left(\mathcal {O}_Z\left(d-1,e\right)\right)$ and $H^0\left(\mathcal {O}_Z\left(d,e-1\right)\right)$ , respectively.

Theorem 4.2.Suppose $d,e\ge 2$ . Then:

(1) The base divisor of $\left|J_{d-1,e\mid Z}\right|$ coincides with the ramification divisor of the second projection $Z\hookrightarrow X=\mathbb {P}^1\times \mathbb {P}^1\stackrel{\pi _2}{\rightarrow }\mathbb {P}^1$ , and after removing the base points it induces the projection of $Z$ onto the first factor.
(2) The restricted linear system $\left|J_{d,e\mid Z}\right|$ is base point free and the induced morphism $Z\rightarrow \left|J_{d,e\mid Z}\right|^{\vee }$ is birational into its image.

Proof.

(1)
Since $\left\lbrace \frac{\partial F}{\partial x_0},\frac{\partial F}{\partial x_1}\right\rbrace$ is a basis of $J_{d-1,e}$ , the base locus of $\left|J_{d-1,e\mid Z}\right|$ consists of the points $p\in X=\mathbb {P}^1\times \mathbb {P}^1$ such that
$\begin{equation*} \frac{\partial F}{\partial x_0}{\left(p\right)}=\frac{\partial F}{\partial x_1}{\left(p\right)}=F{\left(p\right)}=0, \end{equation*}$
where the third condition $F\left(p\right)=0$ actually follows from the other two because of the Euler identity with respect to $x_0,x_1$ .

Suppose without loss of generality that $p=\left(\left[1:0\right],\left[1:0\right]\right)$ is a base point. Taking local affine coordinates $\left(z,w\right)=\left(\frac{x_1}{x_0},\frac{y_1}{y_0}\right)$ , $p$ corresponds to the origin $\left(0,0\right)$ , and the curve $Z$ is locally defined by the equation $f\left(z,w\right):=F\left(1,z,1,w\right)=0$ . Being a base point of $J_{d-1,e}$ implies in particular that $\frac{\partial f}{\partial z}\left(p\right)=\frac{\partial F}{\partial x_1}\left(p\right)=0$ . Since $Z$ is smooth, it must hold $\frac{\partial f}{\partial w}\left(p\right)\ne 0$ , and thus the tangent line to $Z$ at $p$ has equation
$\begin{equation*} 0=\frac{\partial f}{\partial z}{\left(p\right)}z+\frac{\partial f}{\partial w}{\left(p\right)}w=\frac{\partial f}{\partial w}{\left(p\right)}w, \end{equation*}$
or equivalently $w=0$ , which shows that $p$ is a ramification point of the projection onto the second factor (locally given by $\left(z,w\right)\mapsto w$ ).

One can even check that the multiplicity as a base point agrees with the multiplicity in the ramification divisor. Indeed, note first that on $Z$ we have $x_0\frac{\partial F}{\partial x_0}+x_1\frac{\partial F}{\partial x_1}\equiv 0$ , that is,
$\begin{equation*} \frac{\partial F}{\partial x_0}_{\mid Z}=-\frac{x_1}{x_0}\frac{\partial F}{\partial x_1}_{\mid Z}=-z\frac{\partial F}{\partial x_1}_{\mid Z}. \end{equation*}$
Hence, the multiplicity of $p$ as a base point of $\left|J_{d-1,e\mid Z}\right|$ coincides with the vanishing order of $\frac{\partial F}{\partial x_1}_{\mid Z}$ at $p$ . Using $z$ as a local coordinate for $Z$ around $p$ and expressing $w_{\mid Z}$ as a function $w\left(z\right)$ , we can write (locally around $p$ )
$\begin{equation*} \frac{\partial F}{\partial x_1}_{\mid Z}=\frac{\partial F}{\partial x_1}{\left(1,z,1,w{\left(z\right)}\right)}=\frac{\partial f}{\partial z}{\left(z,w{\left(z\right)}\right)}. \end{equation*}$
From $f\left(z,w\left(z\right)\right)\equiv 0$ , it follows
$\begin{equation*} \frac{\partial f}{\partial z}{\left(z,w{\left(z\right)}\right)}=-\frac{\partial f}{\partial w}{\left(z,w{\left(z\right)}\right)}w^{\prime }{\left(z\right)}. \end{equation*}$
Since $\frac{\partial f}{\partial w}\left(p\right)\ne 0$ , we have
$\begin{equation*} \operatorname{ord}_{z=0}\frac{\partial f}{\partial z}{\left(z,w{\left(z\right)}\right)}=\operatorname{ord}_{z=0}w^{\prime }{\left(z\right)}. \end{equation*}$
By the above discussion, the left-hand side is the multiplicity of $p$ in the base locus of $\left|J_{d-1,e\mid Z}\right|$ , while the right-hand side is the order of $p$ in the ramification divisor of the projection onto the second coordinate, as claimed.

The second assertion follows easily from the Euler relation with respect to $x_0,x_1$ : outside the base locus, the morphism induced by $J_{d-1,e\mid Z}$ is given for example by
$\begin{equation*} p\mapsto {\left[\frac{\partial F}{\partial x_1}{\left(p\right)}:-\frac{\partial F}{\partial x_0}{\left(p\right)}\right]}={\left[x_0{\left(p\right)}:x_1{\left(p\right)}\right]}. \end{equation*}$
(2)
The restriction $J_{d,e\mid Z}$ is generated by the restrictions of $x_i\frac{\partial F}{\partial x_j}$ and $y_i\frac{\partial F}{\partial y_j}$ (Lemma 4.1).

Suppose $p\in Z$ is a base point, so that $x_i\left(p\right)\frac{\partial F}{\partial x_j}\left(p\right)=y_i\left(p\right)\frac{\partial F}{\partial y_j}\left(p\right)=0$ for all $i,j$ .

It holds $x_i\left(p\right)\ne 0$ for at least one $i$ , so that $\frac{\partial F}{\partial x_j}\left(p\right)=0$ for both $j=0,1$ . This implies that $p$ is a ramification point for the second projection $Z\rightarrow \mathbb {P}^1$ . Considering the $y_i$ ’s one can analogously show that $p$ is also a ramification point for the first projection. This is only possible if $Z$ is not smooth at $p$ , which gives a contradiction.

It remains to show that $J_{d,e\mid Z}$ induces a birational morphism. Considering the above set of eight generators, we can describe the induced morphism $\varphi$ as
$\begin{equation*} p\mapsto {\left[\cdots: a_{ij}: \cdots: b_{ij}: \cdots \right]}:={\left[\cdots: x_i{\left(p\right)}\frac{\partial F}{\partial x_j}{\left(p\right)}: \cdots: y_i{\left(p\right)}\frac{\partial F}{\partial y_j}{\left(p\right)}: \cdots \right]}\in \mathbb {P}^7. \end{equation*}$
Note that, since the generators are not linearly independent (because of the Euler relations (4.1)), hence the image will be contained in the intersection of hyperplanes
$\begin{equation*} {\left\lbrace \frac{1}{d}{\left(a_{00}+a_{11}\right)}=\frac{1}{e}{\left(b_{00}+b_{11}\right)}=0\right\rbrace} . \end{equation*}$

Let us consider now the linear subsystem generated by the $x_i\frac{\partial F}{\partial x_j}$ , whose induced rational map $\psi _x: Z\dashrightarrow \mathbb {P}^3$ coincides with the composition of $\varphi: Z\rightarrow \mathbb {P}^7$ with the projection onto the first coordinates $\left[a_{00}: \cdots: a_{11}\right]$ . Furthermore, $\psi _x$ can be factorized as
$\begin{equation*} \psi _x: Z\dashrightarrow \mathbb {P}^1\times \mathbb {P}^1\stackrel{\Phi }{\longrightarrow } \mathbb {P}^3, \end{equation*}$
where $\Phi$ just the Segre embedding, and the first map is given by
$\begin{equation*} p\mapsto {\left({\left[x_0{\left(p\right)}:x_1{\left(p\right)}\right]},{\left[\frac{\partial F}{\partial x_0}{\left(p\right)}:\frac{\partial F}{\partial x_1}{\left(p\right)}\right]}\right)}, \end{equation*}$
that is, the first map is the product of the first projection and the morphism induced by $J_{d-1,e\mid Z }$ . By the first part of the theorem, the second factor coincides (up to an automorphism of $\mathbb {P}^1$ ) with the first projection.

Thus, with the appropriate choice of coordinates and denoting by $\Delta$ the diagonal map, we have
$\begin{equation*} \psi _x: Z\stackrel{\pi _1}{\longrightarrow } \mathbb {P}^1\stackrel{\Delta }{\longrightarrow } \mathbb {P}^1\times \mathbb {P}^1\stackrel{\Phi }{\longrightarrow }\mathbb {P}^3, \end{equation*}$
that is, from the projection of $\varphi$ onto the first four coordinates we recover the first projection of $Z\hookrightarrow \mathbb {P}^1\times \mathbb {P}^1\rightarrow \mathbb {P}^1$ .

Analogously, we can recover the second projection $\pi _2$ from the composition of $\varphi$ with the projection onto the last four coordinates $\left[b_{00}: \cdots: b_{11}\right]$ .

Altogether, we can recover the original embedding $Z\hookrightarrow \mathbb {P}^1\times \mathbb {P}^1$ from the morphism $\varphi$ induced by linear system $\left|J_{d,e\mid Z}\right|$ , which implies that $\varphi$ must be birational. $\Box$

We also need to study up to what extent the duality maps $\lambda _{K_X^2\otimes L^2}$ and $\lambda _{K_X\otimes L^2}$ fail to be isomorphisms.

Lemma 4.3.Let $L=\mathcal {O}_X\left(d,e\right)$ . Then, the following hold:

(1) If $d,e\ge 3$ , the duality map $\lambda _{K_X^2\otimes L^2}: R_{K_X^2\otimes L^2}=R_{2d-4,2e-4}\rightarrow R_L^*=R_{d,e}^*$ is an isomorphism. Thus in particular $\ker \lambda =J_{K_X^2\otimes L^2}=J_{2d-4,2e-4}$ , where $\lambda$ is as in (3.12).
(2) If $d=2$ and $e\ge 2$ , then $\lambda _{K_X^2\otimes L^2}$ is injective.
(3) If $d,e\ge 2$ , the duality map $\lambda _{K_X\otimes L^2}: R_{K_X\otimes L^2}=R_{2d-2,2e-2}\rightarrow R_{K_X\otimes L}=R_{d-2,e-2}^*$ is surjective and has one-dimensional kernel. More precisely, there is a short exact sequence
$\begin{equation*} 0 \longrightarrow H^0{\left(\mathcal {O}_X\right)}\stackrel{\cdot c_1{\left(L\right)}}{\longrightarrow } H^1{\left(\Omega _X^1\right)}\longrightarrow R_{K_X\otimes L^2} \stackrel{\lambda _{K_X\otimes L^2}}{\longrightarrow } R_{K_X\otimes L}^*\longrightarrow 0. \end{equation*}$

Proof.

(1) The assertion follows from Proposition 2.17 and $H^1\left(\Sigma _L\right)=0$ , which in turn follows from the sequence $0\rightarrow \mathcal {O}_X\rightarrow \Sigma _L\rightarrow T_X\rightarrow 0$ .
(2) In this case, we cannot apply Proposition 2.17 because $H^1\left(\Sigma _L\otimes K_X^2\otimes L\right)=H^1\left(\Sigma _L\left(-2,e-4\right)\right)\ne 0$ . Nevertheless, we can still try to follow that proof and obtain on one hand
$\begin{equation} R_{K_X^2\otimes L^2}\cong \ker {\left(H^1{\left(\mathcal {E}_F\otimes K_X^2\otimes L\right)}\rightarrow H^1{\left(\Sigma _L\otimes K_X^2\otimes L\right)}\right)}. \end{equation}$ ()
On the other hand for these degrees it still holds $H^1\left(\Sigma _L\right)=0$ , which gives
$\begin{equation} R_L\cong \ker {\left(H^1{\left(\mathcal {E}_F\right)}\rightarrow H^1{\left(\Sigma _L\right)}\right)}=H^1{\left(\mathcal {E}_F\right)}, \end{equation}$ ()
and thus $R_L^*\cong H^1\left(\mathcal {E}_F^{\vee }\otimes K_X\right)=H^1\left(\mathcal {E}_F\otimes K_X^2\otimes L\right)$ . Since both isomorphisms in (4.10) and (4.11) are given by product with the class $\delta F\in \operatorname{Ext}^1_{\mathcal {O}_X}\left(L,\mathcal {E}_F\right)$ , it turns out that $\lambda _{K_X^2\otimes L^2}$ is simply the inclusion of the kernel of $H^1\left(\mathcal {E}_F\otimes K_X^2\otimes L\right)\rightarrow H^1\left(\Sigma _L\otimes K_X^2\otimes L\right)$ into $H^1\left(\mathcal {E}_F\otimes K_X^2\otimes L\right)$ .
(3) The assertion follows directly from Proposition 2.16 and the fact that
$\begin{equation*} H^1{\left(\Omega _X^1\right)}\cong H^1{\left(\mathcal {O}_X{\left(-2,0\right)}\right)}\oplus H^1{\left(\mathcal {O}_X{\left(0,-2\right)}\right)} \cong \mathbb {C}^2. \end{equation*}$
$\Box$

We are now almost ready to prove the announced upper bound for the dimension of $D\subseteq \mathbb {P}\left(J_{2d-4,2e-4}\right)$ . To this aim, we adapt some ideas from [4] to construct a sufficiently high-dimensional linear subspace in $\mathbb {P}\left(J_{2d-4,2e-4}\right)$ disjoint from $D$ .

For a fixed

G\in J_L\subseteq S_{d,e}

with

d,e\ge 3

consider the following map:

\begin{eqnarray*} \mu _G: S_{d-4,e-4}\oplus S_{d-4,e-4} & \longrightarrow & S_{2d-4,2e-4} \\ {\left(A,B\right)} & \mapsto & AF+BG. \end{eqnarray*}

Note that, since both $F,G\in J_L$ , it holds $\operatorname{im}\mu \subseteq J_{K_X^2\otimes L^2}=J_{2d-4,2e-4}$ (for this equality we need $d,e\ge 3$ ).

Theorem 4.4.Suppose $d,e\ge 3$ . For a general $G\in J_L=J_{d,e}$ (in particular, $G\not\in \mathbb {C}F$ ) it holds:

(1) $\ker \mu _G=0$ , and
(2) $D\cap \mathbb {P}\left(\operatorname{im}\mu _G\right)=\emptyset$ .

Proof.

(1) Suppose $\mu _G\left(A,B\right)=AF+BG=0\in S_{2d-4,2e-4}=H^0\left(K_X^2\otimes L^2\right)$ . Then, the restriction to $Z=\left\lbrace F=0\right\rbrace$ is also
$\begin{equation*} B_{\mid Z}G_{\mid Z}\equiv 0\in H^0{\left({\left(K_X^2\otimes L^2\right)}_{\mid Z}\right)}. \end{equation*}$
Since $G_{\mid Z}\not\equiv 0$ (because $G$ is not a multiple of $F$ ), it must hold $B_{\mid Z}\equiv 0$ , that is, $B$ is a multiple of $F$ . But since $B\in S_{d-4,e-4}$ has smaller bidegree than $F$ , it must be $B=0$ . Thus also $FA=0\in S_{2d-4,2e-4}$ , and thus $A=0$ because the map $S_{d-4,e-4}\stackrel{\cdot F}{\longrightarrow }S_{2d-4,2e-4}$ is injective.
(2)
Consider the set
$\begin{equation*} I={\left\lbrace {\left(A,B,\alpha,\beta,G\right)}\,{\left|\, \def\eqcellsep{&}\begin{array}{l}A,B\in S_{d-4,e-4},\alpha,\beta \in H^0{\left(K_X\otimes L\right)}\setminus {\left\lbrace 0\right\rbrace} =S_{d-2,e-2}\setminus {\left\lbrace 0\right\rbrace} \\[3pt] G\in J_{d,e}\setminus {\left\langle F\right\rangle}, AF+BG=\alpha \beta \end{array} \right\rbrace} \right.} \end{equation*}$
which is a quasi-projective subvariety of $S_{d-4,e-4}\times S_{d-4,e-4}\times S_{d-2,e-2}\times S_{d-2,e-2}\times J_{d,e}$ .

By definition of $D$ , it holds
$\begin{equation*} D\cap \mathbb {P}{\left(\operatorname{im}\mu _G\right)}\ne \emptyset \end{equation*}$
if and only if $G\in \pi \left(I\right)$ , where $\pi: I\rightarrow J_{d,e}\setminus \mathbb {C}F$ denotes the projection $\left(A,B,\alpha,\beta,G\right)\mapsto G$ .

We want thus to show that $\pi$ is not dominant, for which we can replace $I$ by its (open, dense) smooth subset. Assume from now on that $\pi$ is dominant.

By Theorem 4.2, the restriction of the Jacobian $J_{d,e}$ to $Z$ induces a birational map onto a non-degenerate projective curve $C\subseteq \mathbb {P}^r$ for certain $r\le \dim J_{d,e}-2$ . The pull-backs of the hyperplane sections of $\mathbb {P}^r$ are by construction the vanishing divisors $\left(G_{\mid Z}\right)$ . Let $U$ denote the subset $\left\lbrace G\in J_{d,e}\setminus \mathbb {C}F\,\mid \,\left(G_{\mid Z}\right)\text{ is reduced}\right\rbrace$ . Given a fixed $G\in U$ with $\left(G_{\mid C}\right)=p_1+p_2+\cdots +p_n$ , the fundamental group $\pi _1\left(U,G\right)$ induces a monodromy action on $\left\lbrace p_1,\ldots,p_n\right\rbrace$ , that is, there is a group homomorphism
$\begin{equation} \rho: \pi _1{\left(U,G\right)}\rightarrow \operatorname{Sym}{\left({\left\lbrace p_1,\ldots,p_n\right\rbrace} \right)}. \end{equation}$ ()
By the uniform position theorem [1, Lemma in p. 111], the monodromy group is the full symmetric group, that is, the group homomorphism (4.14) is surjective.

Replacing $U$ by a non-empty Zariski-open subset the fundamental group does not change, hence we can assume that $U$ is contained in $\pi \left(I\right)$ (recall that we are assuming that $\pi$ is dominant). Replacing $I$ by $\pi ^{-1}\left(U\right)$ we can assume $\pi: I\rightarrow U$ is a surjective morphism of smooth (quasi-projective) varieties.

Fix $G\in U$ and set $\left(G_{\mid Z}\right)=p_1+\cdots +p_n$ , where $n=\deg \mathcal {O}_Z\left(d,e\right)=2de>2de-2d-2e=2g\left(Z\right)-2$ . By the definition of $U$ , there are $A,B,\alpha,\beta$ such that $AF+BG=\alpha \beta$ . The restriction to $Z=\left\lbrace F=0\right\rbrace$ gives then
$\begin{equation*} B_{\mid Z}G_{\mid Z}=\alpha _{\mid Z}\beta _{\mid Z}, \end{equation*}$
so $p_1+\cdots +p_n\le \left(\alpha _{\mid Z}\right)+\left(\beta _{\mid Z}\right)$ . Up to reordering the indices of the points and switching $\alpha$ and $\beta$ , we can assume $\alpha _{\mid Z}\left(p_i\right)=0$ for $i=1,\ldots,m\ge \frac{n}{2}$ , and $\alpha _{\mid Z}\left(p_i\right)\ne 0$ for $i=m+1,\ldots,n$ . Moreover since $\alpha _{\mid Z}\in H^0\left(K_Z\right)$ and thus $\deg \left(\alpha _{\mid Z}\right)=2g\left(Z\right)-2<n$ , it holds $m<n$ .

Now for every $i=1,\ldots,m$ there is a closed path $\gamma _i$ on $U$ based at $G$ whose monodromy action permutes $p_i$ and $p_{m+1}$ and leaves all other points fixed. We can lift this path to an open path on $I$ , starting on $\left(A,B,\alpha,\beta,G\right)$ , that is, we can find a continuous map
$\begin{equation*} \tilde{\gamma _i}={\left(\tilde{A},\tilde{B},\tilde{\alpha },\tilde{\beta },\tilde{G}\right)}: {\left[0,1\right]}\rightarrow I \end{equation*}$
with $\tilde{\gamma _i}\left(0\right)=\left(A,B,\alpha,\beta,G\right)$ and $\tilde{A}\left(t\right)F+\tilde{B}\left(t\right)\tilde{G}\left(t\right)=\tilde{\alpha }\left(t\right)\tilde{\beta }\left(t\right)$ for every $t\in \left[0,1\right]$ .

Set $\alpha _i:=\tilde{\alpha }\left(1\right),\beta _i:=\tilde{\beta }\left(1\right), A_i:=\tilde{A}\left(1\right)$ and $B_i:=\tilde{B}\left(1\right)$ , which satisfy $A_iF+B_iG=\alpha _i\beta _i$ . Thus restricting to $Z$ we obtain
$\begin{equation*} p_1+\cdots +p_n={\left(G_{\mid Z}\right)}\le {\left({B_iG}_{\mid Z}\right)}={\left(\alpha _{i\mid Z}\right)}+{\left(\beta _{i\mid Z}\right)}. \end{equation*}$
Moreover, it holds $\alpha _{i\mid Z}\left(p_{m+1}\right)=\alpha _{\mid Z}\left(p_i\right)=0$ and $\alpha _{i\mid Z}\left(p_j\right)=\alpha _{\mid Z}\left(p_j\right)=0$ for every $j=1,\ldots,m$ , $j\ne i$ , while $\alpha _{i\mid Z}\left(p_i\right)=\alpha _{\mid Z}\left(p_{m+1}\right)\ne 0$ .

In this way, we obtain $\alpha _0=\alpha,\alpha _1,\ldots,\alpha _m$ , whose restrictions to $Z$ are linearly independent holomorphic 1-forms, and hence $m+1\le g\left(Z\right)$ . But this is a contradiction, since
$\begin{eqnarray*} n\le 2m \le 2g{\left(Z\right)}-2<n.\\[-30pt] \end{eqnarray*}$
$\Box$

As announced, we can use the previous theorem to find an upper bound on $\dim D$ .

Corollary 4.5.If $d,e\ge 3$ it holds

\begin{align*} \dim D\le &\, de-d-e-4. \end{align*}

Proof.Let $G$ be general, so that $D\cap \mathbb {P}\left(\operatorname{im}\mu _G\right)=\emptyset \subseteq \mathbb {P}\left(J_{2d-4,2e-4}\right)$ . Then, it must hold $\dim D+\dim \mathbb {P}\left(\operatorname{im}\mu _G\right)<\dim \mathbb {P}\left(J_{2d-4,2e-4}\right)$ , and hence

\begin{align*} \dim D<\dim J_{2d-4,2e-4}-\dim \operatorname{im}\mu _G&={\left(\dim S_{2d-4,2e-4}-\dim R_{2d-4,2e-4}\right)}-2\dim S_{d-4,e-4}\\ &\stackrel{(*)}{=}{\left(2d-3\right)}{\left(2e-3\right)}-\dim R_{d,e}-2{\left(d-3\right)}{\left(e-3\right)}=2de-9-{\left(\dim S_{d,e}-\dim J_{d,e}\right)}\\ &=2de-9-{\left(d+1\right)}{\left(e+1\right)}+\dim J_{d,e}=de-d-e-10+\dim J_{d,e}\\ & \le de-d-e-10+h^0{\left(\Sigma _L\right)}=de-d-e-3. \end{align*}

Note that in

(*)

we have used

\dim R_{2d-4,2e-4}=\dim R_{d,e}

, i.e.

\dim R_{K_X^2\otimes L^2}=\dim R_L

, which follows from

d,e\ge 3

and Lemma 4.3.

\Box

We are now ready to prove the final result of the paper.

Theorem 4.6.For any $d,e\ge 1$ , $L=\mathcal {O}_X\left(d,e\right)$ has maximal infinitesimal variation at every smooth $Z\in \left|L\right|$ .

Proof.Let $Z\in \left|L\right|$ be a smooth curve defined by a polynomial $F\in H^0\left(L\right)=S_{d,e}$ . Let us consider first the cases of smaller degrees.

If $d=1$ or $e=1$ , $Z$ is a rational curve, hence the Hodge structure is trivial and there is nothing to prove.

Suppose now that $d=2$ and $e\ge 2$ . Since $H^0\left(K_X\right)=0$ , it holds $R_{K_X\otimes L}=H^0\left(K_X\otimes L\right)=S_{0,e-2}$ . Moreover, it holds $J_{K_X^2\otimes L^2}=J_{0,2e-4}=0$ because the Jacobian ideal is generated in degrees $\left(d-1,e\right)=\left(1,e\right)$ and $\left(d,e-1\right)=\left(2,e-1\right)$ . This means that $R_{K_X^2\otimes L^2}=H^0\left(K_X^2\otimes L^2\right)=S_{0,2e-4}$ .

Suppose that $\alpha \in \ker \varphi _{K_X\otimes L}\left(\tau \right)$ for a general $\tau \in H^0\left(L\right)=S_{2,e}$ , so that $\lambda _{K_X^2\otimes L^2}\left(\alpha ^2\right)=0\in R_L^*$ by Lemma 3.5. But the injectivity of $\lambda _{K_X^2\otimes L^2}$ (Lemma 4.3) implies $\alpha ^2=0\in S_{0,2e-4}$ , and thus $\alpha =0$ .

We can now consider the case $d,e\ge 3$ . If $L$ does not have maximal infinitesimal variation at $Z$ , then Theorem 3.8 implies

\begin{equation*} \dim D\ge h^0{\left(K_X\otimes L\right)}+p_g{\left(X\right)}-1=h^0{\left(\mathcal {O}_X{\left(d-2,e-2\right)}\right)}-1={\left(d-1\right)}{\left(e-1\right)}-1=de-d-e, \end{equation*}

which contradicts Corollary 4.5.

\Box

Remark 4.7.Note that a very important point in the proof of Theorem 4.4 is that the generalized Jacobian ideal in degree precisely $L$ (i.e., the image of $\widetilde{d\sigma }: H^0\left(T_X\right)\rightarrow H^0\left(L_{\mid Z}\right)$ ) induces a birational embedding of $Z$ in a projective space. This property might also hold for more general surfaces, giving some hope that this approach might work in a few more cases.

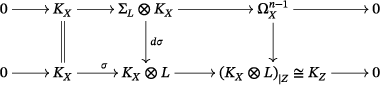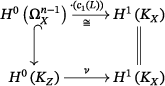
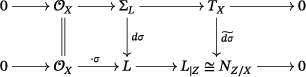
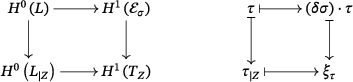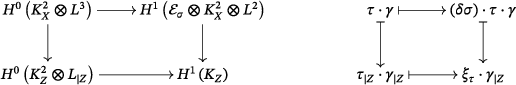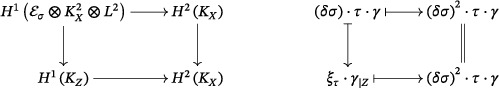ACKNOWLEDGMENTS

We are particularly grateful to Gian Pietro Pirola, for some very insightful conversations we shared during his visit at Leibniz Universität Hannover. We also thank the referees for their useful comments on the previous version of the paper. The project is partially supported by the Alexander von Humboldt Foundation.

Open access funding enabled and organized by Projekt DEAL.

CONFLICT OF INTEREST STATEMENT

The authors declare conflicts of interest.

Open Research

DATA AVAILABILITY STATEMENT

Data sharing not applicable to this paper as no datasets were generated or analyzed during this study.

REFERENCES

1E. Arbarello, M. Cornalba, P. Griffiths, and J. Harris, Geometry of algebraic curves. Vol. I, Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], vol. 267, Springer-Verlag, New York, 1985.
10.1007/978-1-4757-5323-3
Google Scholar
2G. Codogni, V. González-Alonso, and S. Torelli, Rigidity of modular morphisms via Fujita decomposition, Algebra Number Theory. 2024.
Google Scholar
3Y. Dutta and D. Huybrechts, Maximal variation of curves on $K3$ surfaces, Tunis. J. Math. 4 (2022), no. 3, 443–464.
10.2140/tunis.2022.4.443
Google Scholar
4F. F. Favale and G. P. Pirola, Infinitesimal variation functions for families of smooth varieties, Milan J. Math. 90 (2022), no. 1, 209–228.
10.1007/s00032-022-00353-2
Web of Science® Google Scholar
5M. Girard and D. R. Kohel, Classification of genus 3 curves in special strata of the moduli space, in Algorithmic number theory, vol. 4076, Lecture Notes in Comput. Sci., Springer, Berlin, 2006, pp. 346–360.
10.1007/11792086_25
Google Scholar
6V. González-Alonso and S. Torelli, Families of curves with Higgs field of arbitrarily large kernel, Bull. Lond. Math. Soc. 53 (2021), no. 2, 493–506.
10.1112/blms.12437
Web of Science® Google Scholar
7M. L. Green, The period map for hypersurface sections of high degree of an arbitrary variety, Compos. Math. 55 (1985), 135–156.
Web of Science® Google Scholar
8R. Lazarsfeld, Brill–Noether–Petri without degenerations, J. Differ. Geom. 23 (1986), 299–307.
10.4310/jdg/1214440116
Web of Science® Google Scholar
9Y. Lee and G. P. Pirola, On rational maps from the product of two general curves, Ann. Sc. Norm. Super. Pisa, Cl. Sci. (5) 16 (2016), no. 4, 1139–1152.
Google Scholar
10S. Mukai, Curves and K3 surfaces of genus eleven, in Moduli of vector bundles, Papers of the 35th Taniguchi Symposium, Sanda, Japan and a Symposium held in Kyoto, Japan, 1994, Marcel Dekker, New York, 1996, pp. 189–197.
Google Scholar
11E. Sernesi, Deformations of algebraic schemes, vol. 334, Grundlehren Math. Wiss., Springer, Berlin, 2006.
Google Scholar
12E. Viehweg, Weak positivity and the additivity of the Kodaira dimension for certain fibre spaces, Algebraic varieties and analytic varieties, Proc. Symp., Tokyo 1981, Adv. Stud. Pure Math. 1 (1983), no. 1983, 329–353.
Google Scholar
13C. Voisin, Green's generic syzygy conjecture for curves of even genus lying on a $K3$ surface, J. Eur. Math. Soc. 4 (2002), no. 4, 363–404.
10.1007/s100970200042
Google Scholar
14C. Voisin, Green's canonical syzygy conjecture for generic curves of odd genus, Compos. Math. 141 (2005), no. 5, 1163–1190.
10.1112/S0010437X05001387
Web of Science® Google Scholar

Volume298, Issue7

July 2025

Pages 2282-2308

General infinitesimal variations of the Hodge structure of ample curves in surfaces

Abstract

1 INTRODUCTION

2 GENERALIZED JACOBIAN IDEALS AND RINGS

2.1 The bundle $\Sigma _L$

2.2 The differential $d\sigma$ of a section $\sigma \in H^0\left(L\right)$ and associated bundles

2.3 Generalized Jacobian rings

2.4 Jacobian in degree $K_X\otimes L$

2.5 Jacobian in degree $L$

2.6 The top degree

2.7 Natural pairings and duality maps

3 INFINITESIMAL VARIATION OF THE HODGE STRUCTURE OF CURVES IN SURFACES WITH GENERALIZED JACOBIAN RINGS

4 CURVES IN $\mathbb {P}^1\times \mathbb {P}^1$

ACKNOWLEDGMENTS

CONFLICT OF INTEREST STATEMENT

Open Research

DATA AVAILABILITY STATEMENT

REFERENCES

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

General infinitesimal variations of the Hodge structure of ample curves in surfaces

Abstract

1 INTRODUCTION

2 GENERALIZED JACOBIAN IDEALS AND RINGS

2.1 The bundle Σ L $\Sigma _L$

2.2 The differential d σ $d\sigma$ of a section σ ∈ H 0 L $\sigma \in H^0\left(L\right)$ and associated bundles

2.3 Generalized Jacobian rings

2.4 Jacobian in degree K X ⊗ L $K_X\otimes L$

2.5 Jacobian in degree L $L$

2.6 The top degree

2.7 Natural pairings and duality maps

3 INFINITESIMAL VARIATION OF THE HODGE STRUCTURE OF CURVES IN SURFACES WITH GENERALIZED JACOBIAN RINGS

4 CURVES IN P 1 × P 1 $\mathbb {P}^1\times \mathbb {P}^1$

ACKNOWLEDGMENTS

CONFLICT OF INTEREST STATEMENT

Open Research

DATA AVAILABILITY STATEMENT

REFERENCES

References

Related

Information

2.1 The bundle $\Sigma _L$

2.2 The differential $d\sigma$ of a section $\sigma \in H^0\left(L\right)$ and associated bundles

2.4 Jacobian in degree $K_X\otimes L$

2.5 Jacobian in degree $L$

4 CURVES IN $\mathbb {P}^1\times \mathbb {P}^1$