Estimation of glomerular filtration rates after orthotopic liver transplantation: Evaluation of cystatin C–based equations†
Presented in part at the annual meeting of the American Society of Nephrology, November 8–13, 2005, Philadelphia, PA.
Abstract
Early detection of renal dysfunction in patients after orthotopic liver transplantation is important. Creatinine-based equations to estimate glomerular filtration rate (GFR) were found to be less accurate in liver transplant recipients than in their original populations. Since cystatin C (CysC) is independent from muscle mass and hepatic biosynthesis, we evaluated the diagnostic accuracy of 3 CysC-based equations (Larson, Hoek, and Filler formulae) that are based on the same CysC method as that of our center in comparison to the abbreviated creatinine-based modification of diet in renal disease (MDRD) formula in 59 liver transplant recipients. “True GFR” was measured by 99mTc-diethylene triamine pentaacetic acid (99mTc-DTPA) clearance. Neither correlation with the GFR (correlation coefficients: 0.594–0.640) nor precision (root mean square error: 15.7–18.17 mL/min/1.73 m2) differed significantly between the tested formulae. The biases of the Hoek and Larsson formulae were significantly smaller than those of the MDRD and Filler equations (−0.1 and −2.3 vs. 10.1 and 7.9 mL/min/1.73 m2, respectively; P ≤ 0.0023). Mean estimates of MDRD (61.9 ± 21.4 mL/min/1.73 m2) and Filler (61.2 ± 22.1 mL/min/1.73 m2) differed significantly from the measured GFR (52.3 ± 17.5 mL/min/1.73 m2; P < 0.005), whereas Larsson and Hoek did not (49.5 ± 20.2 and 51.4 ± 17.9 mL/min/1.73 m2, respectively). Accuracy within 30% and 50% of the true GFR was best for the Hoek (76.3% and 93.2%) formula, albeit not significantly different from MDRD (64.4% and 83.1%). Taken together, these data show the best overall performance for GFR estimates derived from the Hoek equation with respect to bias, precision, and accuracy. Liver Transpl, 2006. © 2006 AASLD.
Renal dysfunction is a common problem in patients after orthotopic liver transplantation (OLT). Early detection of impaired renal function is crucial to prevent end-stage renal disease (ESRD), which occurs in up to 10% of patients.1 Limitations of the diagnostic use of creatinine in patients with impaired liver function are well known.2 Since “gold standard” methods precisely measuring the glomerular filtration rate (GFR), such as inulin- or validated-isotope clearances, are costly and time consuming, determination of GFR remains difficult in patients with liver diseases. Several creatinine-based equations including biochemical, demographic, and anthropometric data have been extensively evaluated in liver transplant recipients. Gonwa and coworkers showed these equations to be applicable, despite poorer performance in comparison to the original population.3, 4 In cirrhotic patients5 and liver transplant recipients,6-8 cystatin C (CysC) has been applied as an alternative endogenous serum marker of GFR. Recently, CysC-based formulae were proposed to calculate GFR in patients with various kidney diseases.9-11
In this study we evaluated the diagnostic performance of 3 CysC-based formulae for GFR estimation in liver transplant recipients. The chosen equations of Filler, Larsson, and Hoek were derived from cohorts in whom the nephelometric assay (Particle-enhanced nephelometric immunoassay [PENIA], Dade Behring, Marburg, Germany) was used, the same one employed at our center. More recently Grubb and Sjöström published alternative CysC-based equations to calculate GFR.12-14 As these equations were derived from turbidimetric determinations of CysC (Particle-enhanced turbidimetric immunoassay [PETIA], Dako Cytomation, Glostrup, Denmark) they were not included in our analysis, as divergent results may be due to assay characteristics.
Abbreviations
OLT, orthotopic liver transplantation; ESRD, end-state renal disease; GFR, glomerular filtration rate; CysC, cystatin C; CV, coefficient of variation; 99mTc-DTPA, 99mTc-diethylene triamine pentaacetic acid; MDRD, modification of diet in renal disease; RMSE, root mean square error; CI, confidence interval.
PATIENTS AND METHODS
Patients
Enrolled in the study were 59 consecutive liver transplant recipients (24 female, 35 male) with a mean age of 47.6 ± 12.0 (± SD) years. The mean time after liver transplantation was 5.1 ± 3.0 years. Indications for OLT were as follows: viral hepatitis C (n = 10), viral hepatitis B (n = 12), viral hepatitis B/D (n = 3), hepatocellular carcinoma (n = 3), alcoholic liver disease (n = 9), autoimmune hepatitis (n = 3), primary biliary cirrhosis (n = 2), primary sclerosing cholangitis (n = 5), veno-occlusive disease (n = 1), Wilson's disease (n = 2), Alagille syndrome (n = 1), amyloidosis (n = 1), cystic liver disease (n = 1), Senior-Loken syndrome (n = 1), amanita phalloides intoxication (n = 1), ecstasy intoxication (n = 1), and fulminant liver failure of unknown origin (n = 3).
Immunosuppression was cyclosporine-based in 26 patients and tacrolimus-based in 33 patients. Additionally, 15 patients received prednisone and 4 patients received mycophenolate mofetil. Informed consent was achieved following the institutional guidelines as approved by the local Ethics Committee.
Parameters, Assays, and Formulae
Serum creatinine was measured with a modified Jaffé method using the Dimension Clinical Chemistry System (Dade Behring). The sensitivity of the creatinine method was 4 μmol/L. This sensitivity is defined as the concentration of 2 standard deviations above the CHEM I calibrator (Dade Behring) at 0 mmol/L creatinine (n = 20). The intra-assay coefficient of variation (CV) was 0.01 (mean, 61 μmol/L; n = 20), while the interassay CV was 0.025 (mean, 79.4 μmol/L; n = 20). Serum CysC was analyzed by fully automated, latex-enhanced immunonephelometry (N latex cystatin C on a Nephelometer II; Dade Behring). The 95% reference interval for CysC established from a representative cohort of 100 female and 100 male healthy blood donors (median age, 31 years; 2.5–97.5 percentiles, 19.0–60.5 years) was 0.475–0.820 mg/L. The sensitivity of the assay was 0.05 mg/L. The intra-assay CV for CysC was 1.9% (mean, 0.6 mg/L; n = 20), and the interassay CV was 3.6% (mean, 0.6 mg/L; n = 20).
(99mTc-DTPA) clearance was performed as single-injection technique with 2-point blood sampling according to the method of Russell et al.15 GFR was estimated using the following equations:
GFR = −4.32 + 80.35 × 1/CysC (Hoek formula10);
log(GFR) = 1.962 + [1.123 log(1/CysC)] (Filler formula9);
GFR = 77.239 × CysC−1,2623 (Larsson formula11); and (MDRD) = 186 × [serum creatinine (mg/dL)] −1.154 × [age−0.203 × [0.742 if patient is female] × [1.21 if patient is African American].16
STATISTICS
All results are given as mean ± SD unless indicated otherwise. Correlations between 99mTc-DTPA clearance and estimates of GFR were calculated by linear regression analysis (Pearson's correlation). Bias was calculated by the median difference between the true GFR (99mTc-DTPA clearance, serving as gold standard) and the estimated equation-based GFR. Pair-wise comparison of biases was performed using paired t test.
Precision of the estimates was expressed in terms of the root mean square error as described elsewhere (root mean square error (RMSE); standard deviation of the mean difference between real GFR and estimated GFR).17 The F test was used to compare different RMSEs.
The proportion of GFR estimates within 30% and 50% deviation of the true GFR served as a measure of accuracy.18 McNemar's test was used to compare the proportion of estimates within the 30% and 50% deviation. Analysis was performed using StatView (ver. 5.0 for Windows; SAS Institute, Inc., Cary, NC). Bland and Altman analysis of the GFR estimates and the true GFR was performed with Medcalc (Medcalc Software, Mariakerke, Belgium).19P values below 0.05 were considered significant.
RESULTS
The mean serum level of creatinine and CysC at the time of evaluation was 1.3 ± 0.4 mg/dL and 1.6 ± 0.5 mg/L, respectively (Fig. 1A). In 53 patients (89.8%), measured CysC levels were above the upper reference interval, whereas creatinine was elevated beyond the normal range in only 20 patients (33.9%; P < 0.01). The mean GFR (99mTc-DTPA clearance) was 52.3 ± 17.5 mL/min/1.73 m2. All formula-derived GFR estimates correlated significantly with the GFR, but correlation coefficients did not differ significantly between each other (Table 1).
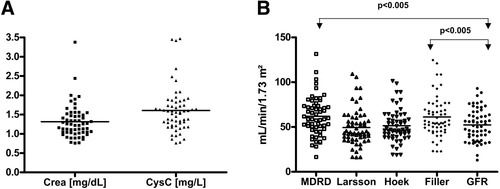
(A) Distribution of creatinine (mg/dL) and CysC (mg/L) serum levels. Each square and triangle represents the data of a single patient. Crea, creatinine. (B) Distribution of GFR measured by 99mTc-DTPA clearance in comparison to MDRD- and CysC-based estimates. Each square, dot, and triangle represents the data of a single patient.
| Correlation Coefficient | r2* | P Value | Median Difference (mL/min/1.73 m2) | Median Difference (%) | RMSE (mL/min/1.73 m2) | Accuracy Within | ||
|---|---|---|---|---|---|---|---|---|
| 30% | 50% | |||||||
| MDRD | 0.640 | 0.410 | <0.0001 | 10.1 | 19.6 | 16.9 | 64.4 | 83.1 |
| Filler | 0.601 | 0.360 | <0.0001 | 7.9 | 18.4 | 18.2 | 57.6 | 78.0 |
| Larsson | 0.594 | 0.352 | <0.0001 | −2.3 | −5.1 | 17.1 | 69.5 | 89.8 |
| Hoek | 0.606 | 0.367 | <0.0001 | −0.1 | −0.2 | 15.7 | 76.3 | 93.2 |
- * Square of correlation coefficient as a value of variability of predicted GFR account for variability of measured GFR; P value for correlation is not zero.
GFR distribution of the individual patients is shown in Figure 1B. The MDRD (61.9 ± 21.6 mL/min/1.73 m2) and Filler (61.2 ± 22.1/1.73m2) estimates differed significantly from the true GFR (52.3 ± 17.5 mL/min/1.73 m2; P < 0.005), whereas Larsson and Hoek (49.5 ± 20.2 and 51.4 ± 17.9 mL/min/1.73 m2, respectively) estimates did not.
The diagnostic precision measured as RMSE indicates a lower level of precision with higher RMSE values. Although the Hoek equation showed the highest precision, there was no significant statistical difference between the various equations (Table 1).
A small negative bias was found for the Hoek and the Larsson formula (−0.1 and −2.3 mL/min/1.73 m2, respectively), whereas a significant overestimation of the true GFR was observed in the MDRD and the Filler equation (10.1 and 7.9 mL/min/1.73 m2, respectively). The bias of the Hoek and Larsson formulae differed significantly from that of the MDRD and Filler equations (P ≤ 0.0023).
As recommended by the National Kidney Foundation, we calculated the proportion of the GFR estimates within 30% and 50% of the true GFR as a measure of accuracy. The results given in Table 1 show the highest proportion of estimates within both 30% and 50% of the measured GFR for the Hoek formula (76.3% and 93.2%, respectively). Differences between all tested equations regarding the performance within the 30% and 50% proportion of true GFR were significant (P < 0.05) only for comparison between the 50% proportions of the Hoek and the Filler equations.
Bland and Altman plots, a graphical method to demonstrate the magnitude and consistency of the differences between calculated and measured values, are presented in Figure 2A–D. This graphical technique demonstrates the span between +1.96 SD and −1.96 SD of the mean difference between the calculated and the true GFR.

Bland and Altman plots presenting (A) MDRD, (B) Larsson, (C) Hoek, and (D) Filler estimates. The Bland and Altman plots demonstrate the magnitude and consistency of the differences between calculated and measured values. The horizontal lines indicate the mean reflecting the mean difference and the span between +1.96 SD and −1.96 SD of the mean difference between the calculated and the true GFR.
The limits of agreement estimated for the Hoek equation are 30 mL/min/1.73 m2 below or 32 mL/min/1.73 m2 above the true GFR. Similarly, the Larsson equation shows a span between −37 and 31 mL/min/1.73 m2. The limits of agreement for the Filler and the MDRD equation are −27 and 45 mL/min/1.73 m2 and −24 and 43 mL/min/1.73 m2, respectively. Comparing the range between the limits of agreement, these data show a considerably higher distance between both limits for the MDRD, Larsson and Filler estimates compared to the Hoek formula estimates (66.7, 67.8, and 71.8 mL/min/1.73 m2, respectively, vs. 62.1 mL/min/1.73 m2).
Similar to the Bland and Altman plot, the widest overlap with the 95% confidence interval (CI) of the “true” GFR (95% CI: 47.6; 56.9 mL/min/1.73 m2) was seen for the Hoek formula (95% CI: 46.7; 56.1 mL/min/1.73 m2), followed by the Larsson equation (95% CI: 44.2; 54.8 mL/min/1.73 m2), whereas only a poor overlap of CIs was seen with the MDRD equation (95% CI: 56.3; 67.6 mL/min/1.73 m2) and the formula of Filler (95% CI: 55.3; 66.9 mL/min/1.73 m2).
DISCUSSION
In this cross-sectional study, we evaluated the creatinine-based MDRD formula and 3 CysC-based equations for estimation of GFR in liver transplant recipients. We demonstrate that the best overall performance for GFR estimates can be derived from the Hoek equation with respect to bias, precision, and accuracy. However, while CysC-based Hoek and Larsson equations are significantly better than the MDRD formula with respect to bias, precision and accuracy did not differ significantly.
In clinical practice, GFR is difficult to measure, and most clinicians estimate GFR from serum creatinine concentration, which has been shown to be a poor marker of GFR in patients with liver diseases.2, 20 Several creatinine-based formulae including demographic and anthropometrical parameters have been developed to estimate GFR more precisely.4, 21, 22 These equations have been evaluated in a large cohort of liver transplant recipients identifying the MDRD equations as being more precise than the Cockroft-Gault and the Nankivell formulae.3 However, the precision of the MDRD formula was much lower in the OLT cohort than in the original population.4 In liver transplant recipients, reduced muscle mass and impaired hepatic biosynthesis can contribute to false low serum creatinine levels. CysC, a cysteine protease inhibitor generated by nucleated cells, freely filtered, reabsorbed, and catabolized in the proximal tubule of the kidney, is independent from muscle mass.23, 24 Consequently, in this study we employed CysC-based formulae in comparison to the abbreviated MDRD equation to estimate GFR in a cohort of patients after OLT. The latter formula was chosen for its simplicity, its dependence on only 1 laboratory variable, and its widespread use in daily clinical practice.
In our study, the abbreviated MDRD formula overestimates true GFR. This is in agreement with recent observations in a cohort of renal transplant recipients25 but is contradictory to the findings of Gonwa, who showed an underestimation of GFR in liver transplant recipients 1 and 5 years after transplantation. Previously, the impact of the calibration of the serum creatinine assay on creatinine-based GFR estimates has been emphasized.26 As noncreatinine chromogens are known to be detected by the Jaffé method, we used a kinetic modification of the Jaffé method counteracting this possible influence.27, 28 However, this modification cannot replace a calibration of the creatinine method to that used in the original MDRD laboratory. Thus, in contrast to the original MDRD study, our results may lead to lower creatinine values and consequently to a higher estimated GFR, thereupon leading to the considerable positive bias of the MDRD formula.
By contrast, the Hoek and Larsson formulae underestimated real GFR. Low-dose corticosteroid medication, which has been supposed to increase CysC serum levels29 and consequently lead to a lower estimate in the applied formulae, was administered only in a minority of patients of our cohort (n = 15; 25%). Indeed, mean CysC serum levels in patients treated with corticosteroids were somewhat higher than in patients on a steroid-free regimen, whereas this difference lacked statistical significance (1.84 ± 0.2 vs. 1.53 ± 0.1 mg/L; P = 0.07; data not shown).
Filler formula estimates, however, overestimated the true GFR considerably, despite the fact that the gold standard clearance used in the original publication was similar to our study using a single injection technique and a multiple point blood sampling method.9 Discrepancies may be due to different patient characteristics, as the original cohort consisted of children aged 1–18 years showing hyperfiltration with a mean GFR above 100 mL/min/1.73 m2, which is roughly twice as high as that in our study. Both CysC-based formulae derived from adult populations (Hoek and Larsson) provided a significantly lower bias and tended to have a higher accuracy than the abbreviated MDRD study equation. In terms of precision, only the Hoek formula tended to be superior to the MDRD formula, albeit without statistical significance. In contrast, recently a comparison between creatinine and CysC-based equations to estimate GFR in renal transplant recipients found the formula suggested by Filler to perform best in comparison with the formulae of Hoek and Larsson.30 Despite the fact that White and coworkers used the same gold standard as we did and the mean GFR (58 ± 23 mL/min/1.73 m2) was comparable, varieties between kidney and liver transplant recipients and differences in steroid dosing between both studies (25% vs. 98% of patients) may account for the observed differences.30
Studies investigating the diagnostic accuracy of CysC and creatinine as serum markers of renal function in patients after OLT by receiver operating characteristic analyses showed significant advantages for CysC in populations with high average GFR7, 8 but failed to show superiority in cohorts with low mean GFR.6 We may therefore speculate that CysC-based formulae discriminate better in mildly impaired than in more severely impaired GFR. Thus, these CysC-based estimates may perform better in pediatric patients and patients in the early posttransplantation period than in adult long-term transplant recipients, whose renal function is diminished by, for example, accumulated calcineurin inhibitor toxicity.3, 31 However, the latter population reflects all-day practice in the outpatient department of posttransplant care.
There are limitations of our study with regard to our cohort and the methodology.
Compared to Gonwa and coworkers, we studied a small number of patients.3 The superior trend in accuracy of the Hoek and Larsson formulae in comparison to the MDRD equation might become significant in a larger patient cohort. Furthermore, the comparability of our results with data from previous studies may be limited because we studied only Caucasian patients.
A multiple point blood sampling may be the best approach to measure GFR by 99mTc-DTPA. However, several studies confirmed the accuracy of the 2-point sampling plasma method by Russel, which thus may be appropriate in an all-day clinical setting.32, 33
Moreover, as discussed before, the external validation of our study may be limited by the use of a creatinine assay that was not calibrated to the MDRD laboratory. It should be taken into account that in general, results and performances of prediction equations derived from different studies are highly affected by lack of creatinine calibration to one another and different gold-standard GFR methods.
Finally, the MDRD 6 equation may improve the performance of the 4 variable MDRD used in our study by adding blood urea nitrogen and albumin into the model. Unfortunately, albumin was not measured in our patients. However, Gonwa and coworkers evaluated both MDRD equations in their large cohort of liver transplant recipients at different time points and found no significant differences between the performance of MDRD 4 and MDRD 6.3
Taken together, in our cohort of liver transplant recipients the CysC-based Hoek and Larsson estimates of GFR showed better bias when compared to the MDRD formula but lack significant superiority regarding diagnostic accuracy and precision. Since the overall performance of these equations is at least as good or even better than that of the MDRD formula, they represent a reliable tool in the surveillance of renal function in patients after OLT. However, both the currently tested CysC-based GFR estimations and the MDRD are still unsatisfying in these patients, indicating the need to develop appropriate, disease-specific alternatives to overcome these limitations.




