Laser & Photonics Reviews
Volume 17, Issue 9 2300201
Research Article
Open Access

Transmission Efficiency Limit for Nonlocal Metalenses

Shiyu Li, 

Shiyu Li

Ming Hsieh Department of Electrical and Computer Engineering, University of Southern California, Los Angeles, California, 90089 USA

Search for more papers by this author
Chia Wei Hsu, 

Corresponding Author

Chia Wei Hsu

Ming Hsieh Department of Electrical and Computer Engineering, University of Southern California, Los Angeles, California, 90089 USA

E-mail: [email protected]

Search for more papers by this author
First published: 17 June 2023
https://doi.org/10.1002/lpor.202300201

Abstract

The rapidly advancing capabilities in nanophotonic design are enabling complex functionalities limited mainly by physical bounds. The efficiency of transmission is a major consideration, but its ultimate limit remains unknown for most systems. This study introduces a matrix formalism that puts a fundamental bound on the channel-averaged transmission efficiency of any passive multi-channel optical system based only on energy conservation and the desired functionality, independent of the interior structure and material composition. Applying this formalism to diffraction-limited nonlocal metalenses with a wide field of view shows that the transmission efficiency must decrease with the numerical aperture for the commonly adopted designs with equal entrance and output aperture diameters. It also shows that reducing the size of the entrance aperture can raise the efficiency bound. This study reveals a fundamental limit on the transmission efficiency as well as provides guidance for the design of high-efficiency multi-channel optical systems.

1 Introduction

Over the past decade, nanophotonic design and fabrication became more and more advanced. Oftentimes, what limits the device's performance is no longer fabrication constraints or the cleverness of the design, but fundamental physical bounds. Furthermore, the design process typically requires time-consuming development, simulation, and optimization. It is invaluable to know beforehand what the fundamental bounds are and how they are related to the design choices.[1] Such knowledge can significantly reduce the time spent in blind explorations and also point to better design choices that are not otherwise obvious. Of particular interest are multi-channel optical systems, such as metalenses[2-6] with a wide field of view (FOV). Their large angular diversity puts a bound on the performance and spatial footprint, such as bandwidth,[7] resolution,[8] and thickness.[9] Meanwhile, another major consideration of metalenses is the efficiency. For example, one would like the incident wave from each angle to be focused to the corresponding focal spot with unity efficiency. But is a uniformly perfect efficiency across all angles compatible with the angle dependence in the desired response? What is the highest efficiency allowed by fundamental laws?

Here, we introduce a matrix-based formalism that sets a fundamental bound on the channel-averaged transmission efficiency of any passive linear multi-channel system given its functionality. Then we apply it to diffraction-limited lenses as an example. The bound applies to any design that realizes the target functionality, so it is applicable not only to metasurfaces but also to conventional refractive and diffractive optical systems.

Metalenses are compact lenses made with metasurfaces, which show great potential for thinner and lighter imaging systems with performances comparable to or exceeding conventional lenses.[2-6] Metalenses designed from a library of unit cells have limited focusing efficiency, which can be overcome by more flexible designs.[10, 11] Inverse design,[10-18] grating averaging technique[19], and stitching separately designed sections together[20-22] are effective approaches. However, achieving high focusing efficiency at large numerical aperture (NA) remains difficult, as all such “local” metasurfaces have limited deflection efficiency at large angles.[23, 24] Since local metasurfaces have a spatial impulse response close to a delta function, they provide the same response for different incident angles, so they are also limited in their angular FOV.[9]

Nonlocal metalenses with tailored interactions between adjacent building blocks (i.e., the spatial impulse response is extended beyond a delta function) can overcome the limited angular diversity of local metalenses to enable diffraction-limited focusing over a large FOV.[9, 25, 26] Their strong nonlocality can be realized by the interaction among adjacent meta-atoms[27] or the excitation of guided resonances that travel across the device over large distances.[28, 29] Nonlocal metalenses based on doublets[30, 31] or aperture stops[32, 33] can support focusing efficiencies higher than 50% over a wide FOV, but with NA lower than 0.5. Multi-layer structures obtained from inverse design have achieved diffraction-limited focusing with NA = 0.7 over FOV = 80°, but the averaged focusing efficiency is only about 25%.[34] However, there was no guidance on the efficiency bound of these nonlocal metalenses.

From the desired response of a multi-channel optical system, we can write down its transmission matrix that relates the input to the output. Here, we rigorously bound the channel-averaged transmission efficiency using the singular values of the transmission matrix and the fact that the transmitted energy must not exceed the input energy. For commonly adopted designs with equal entrance and output apertures, we find the transmission efficiency bound of a nonlocal metalens to drop with the NA. We also find that reducing the entrance aperture size can raise the efficiency bound to close to unity.

2 Results

2.1 Nonlocality

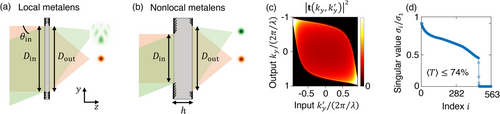
As schematically illustrated in Figure 1a, subwavelength-thick local metalenses (such as metalenses with the hyperbolic phase profile[35]) perform well only over a limited input angular range. Nonlocal metalenses can achieve diffraction-limited focusing over a much wider FOV but need a minimal thickness to provide the nonlocality.[9, 36] Since a large FOV requires an angle-dependent response (i.e., angular dispersion), a spatially localized incident wave must spread as it propagates through the metalens under space-angle Fourier transform. Thus, more angular diversity necessitates more nonlocality. As shown in Figure S1 (Supporting Information), nonlocal effects become important when the FOV is larger than a threshold. For FOV above such a threshold, a sufficient thickness is needed for light to spread and create nonlocality, so the input diameter Din and output diameter Dout can be different [Figure 1b]. The different aperture sizes provide an additional degree of freedom compared to local metalenses with subwavelength thicknesses (for which D in = D out $D_{\rm in}=D_{\rm out}$ intrinsically).

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Nonlocal metalenses and their transmission matrix. a) A local metalens with subwavelength thickness, for which the input and output apertures have the same size, i.e., D in = D out $D_{\rm in}=D_{\rm out}$ . Diffraction-limited focusing can only be achieved within a narrow range of incident angles. b) A nonlocal metalens, whose larger thickness allows nonlocal coupling, under which diffraction-limited focusing may be achieved over a wide angular range. Here, Din and Dout can be different. c,d) The squared amplitude of the transmission matrix | t ( k y , k y ′ ) | 2 $|\mathbf {t}(k_y,k_y^{\prime })|^2$ (c) and its normalized singular values σ i / σ 1 $\sigma _i /\sigma _1$ (d) for an ideal nonlocal metalens with diameter D in = D out = 300 λ $D_{\rm in}=D_{\rm out}=300\lambda$ , NA = 0.8, FOV = 140°. Here, the averaged transmission efficiency is bounded by Equation (4) as ⟨ T ⟩ ≤ 74 % $\langle T \rangle \le 74\%$ .

2.2 Transmission Matrix from the Target Response

While the formalism introduced in this work applies to different systems, for concreteness, we will consider metalenses here. Consider monochromatic, transverse magnetic waves of a 2D system invariant in the x dimension, where E = E x ( y , z ) x ̂ ${\bf E}=E_x(y,z)\hat{x}$ and H = H y ( y , z ) y ̂ + H z ( y , z ) z ̂ ${\bf H}=H_y(y,z)\hat{y}+H_z(y,z)\hat{z}$ , in s-polarization. For ideal (aberration-free) lenses under plane-wave incidence, we can obtain the transmitted phase profile on the output surface of the metalens by matching the optical path lengths between the chief ray and a marginal ray from a point r b = ( y , z = h ) $\mathbf {r}_\mathrm{b} = (y,z=h)$ on the back surface ( z = h $z=h$ ) of the metalens to the focus r f ( θ in ) = ( y = f tan θ in , z = f + h ) $\mathbf {r}_\mathrm{f}(\theta _{\rm in}) = (y=f\tan {\theta _{\rm in},z=f+h})$ for incident angle θin. This yields an incident-angle-dependent ideal phase profile on the back surface,[9, 32, 37]
ϕ out ideal ( y , z = h ; θ in ) = ψ ( θ in ) − 2 π λ f 2 + y − f tan θ in 2 $$\begin{equation} \phi _{\rm out}^{\rm ideal}(y,z=h;\theta _{\rm in}) = \psi (\theta _{\rm in})-\frac{2\pi }{\lambda }\sqrt {f^2+{\left(y-f\tan {\theta _{\rm in}} \right)}^2} \end{equation}$$ (1)
where λ is the wavelength, f and h are the focal length and lens thickness respectively, and ψ ( θ in ) $\psi (\theta _{\rm in})$ is an angle-dependent but spatially invariant global phase with no effect on the focusing quality. To perfectly focus to the focal spot r f ( θ in ) $\mathbf {r}_\mathrm{f}(\theta _\mathrm{in})$ , the field profile on the back surface of the metalens should be proportional to the conjugated field radiated from a point source at r f $\mathbf {r}_\mathrm{f}$ . Therefore,
E x ( y , z = h ; θ in ) = A ( θ in ) e i ϕ out ideal ( y , z = h ; θ in ) [ f 2 + ( y − f tan θ in ) 2 ] 1 / 4 for | y | < D out 2 0 otherwise . $$\begin{equation} E_x(y,z=h; \theta _\mathrm{in})={\begin{cases} \dfrac{A(\theta _\mathrm{in})e^{i\phi _\mathrm{out}^\mathrm{ideal}(y,z=h;\theta _\mathrm{in})}}{[f^2+(y-f\tan {\theta _\mathrm{in}})^2]^{{1}/{4}}} & \text{for } |y|&lt;\dfrac{D_\mathrm{out}}{2} \\[10pt] 0 & \text{otherwise}. \end{cases}} \end{equation}$$ (2)
here, A ( θ in ) $A(\theta _\mathrm{in})$ specifies the transmitted amplitude for incident angle θin. The factor 1 / r $1/\sqrt {r}$ comes from the decay rate of the radiated field from a point source in 2D, with r = | r b − r f | $r = |\mathbf {r}_\mathrm{b} - \mathbf {r}_\mathrm{f}|$ . Note that here we consider transmitted field across the entire back aperture of the lens to be used for focusing, for maximal utility of the lens area. An alternative telecentric configuration that uses a subset of the back aperture is considered in Section S5 (Supporting Information).
Equations (1-2) specify the target response, from which we can write down the transmission matrix. To do so, we project the incident and the transmitted wavefronts onto a finite number of channels. The incoming wavefront E x ( y ′ , z = 0 ) $E_x(y^{\prime },z=0)$ at the front surface of the system ( z = 0 $z=0$ ) can be projected onto Nin propagating plane waves with input transverse momenta k y ′ = { k y a } = ( 2 π / λ ) sin θ in $k_y^{\prime }=\lbrace k_y^a\rbrace =(2\pi /\lambda )\sin {\theta _{\rm in}}$ , yielding complex-valued amplitude α a $\alpha _a$ for the a-th plane-wave input. Each incident plane wave is truncated to the size of the input aperture, i.e., | y ′ | < D in / 2 $|y^{\prime }|&lt;D_{\rm in}/2$ . The input momentum is restricted to the FOV of interest, | k y a | < ( 2 π / λ ) sin ( FOV / 2 ) $|k_y^a|&lt;(2\pi /\lambda )\sin {(\rm FOV/2)}$ . We sample k y a $k_y^a$ within the FOV with 2 π / D in $2\pi /D_\mathrm{in}$ spacing at the Nyquist–Shannon sampling rate,[38] which is sufficient to reconstruct the incident wavefront since the wavefront is blocked beyond the entrance size Din. Doing so also makes incident channels flux-orthogonal (see Section S2, Supporting Information for more information). Similarly, the transmitted wavefront E x ( y , z = h ) $E_x(y,z=h)$ can be written as a superposition of Nout plane waves with k y = { k y b } = ( 2 π / λ ) sin θ out $k_y=\lbrace k_y^b\rbrace =(2\pi /\lambda )\sin {\theta _{\rm out}}$ truncated to | y | < D out / 2 $|y|&lt;D_{\rm out}/2$ , and the complex-valued amplitude of the b-th plane-wave output is β b $\beta _b$ , where θout is the output angle and | k y b | < 2 π / λ $|k_y^b|&lt;2\pi /\lambda$ is sampled with momentum spacing 2 π / D out $2\pi /D_{\rm out}$ at the Nyquist rate. The incoming and transmitted wavefronts are then parametrized as column vectors α = [ α 1 ; ⋯ ; α N in ] ${\bm \alpha }=[\alpha _1;\cdots ;\alpha _{N_{\rm in}}]$ and β = [ β 1 ; ⋯ ; β N out ] ${\bm \beta }=[\beta _1;\cdots ;\beta _{N_{\rm out}}]$ . For any linear optical system, the input and the output vectors are related through the transmission matrix elements t b a = t ( k y b , k y a ) $t_{ba}=\mathbf {t}(k_y^b,k_y^a)$ ,
β b = ∑ a = 1 N in t b a α a $$\begin{equation} \beta _b = \sum _{a=1}^{N_{\rm in}}t_{ba}\alpha _a \end{equation}$$ (3)
or β = t α ${\bm \beta }=\mathbf {t}{\bm \alpha }$ in matrix notation. The incident flux in z is proportional to ∑ a | α a | 2 $\sum _{a}|\alpha _a|^2$ , and the transmitted flux is proportional to ∑ b | β b | 2 $\sum _{b}|\beta _b|^2$ . The transmission efficiency for incident angle θ in a $\theta _{\rm in}^a$ is T a = ∑ b | t b a | 2 $T_a=\sum _{b}|t_{ba}|^2$ .

Fourier transforming the output field of the ideal metalens in Equation (2) from y to k y $k_y$ yields the transmission matrix t $\mathbf {t}$ ; see Section S2 (Supporting Information) for details. Such transmission matrix applies to any lens with diffraction-limited focusing over this FOV. The squared amplitude of the transmission matrix | t ( k y , k y ′ ) | 2 $|\mathbf {t}(k_y,k_y^{\prime })|^2$ for a metalens with D in = D out = 300 λ $D_{\rm in}=D_{\rm out}=300\lambda$ , NA = sin ( arctan ( D out / ( 2 f ) ) ) = 0.8 ${\rm NA} = \sin (\arctan (D_{\rm out}/(2f))) = 0.8$ and FOV = 140° is shown in Figure 1c.

For an ideal lens with no vignetting, here we choose the amplitude A ( θ in a ) $A(\theta _\mathrm{in}^a)$ in Equation (2) such that the transmission efficiency T a = ∑ b | t b a | 2 $T_a=\sum _{b}|t_{ba}|^2$ is the same for all incident angles θ in a $\theta _{\rm in}^a$ within the FOV. However, an overall amplitude prefactor of the transmission matrix that determines this T a $T_a$ is yet to be specified. Larger transmission efficiency is desired. But as shown below, setting T a = 1 $T_a = 1$ for all a will violate energy conservation because doing so leads to more transmitted flux than the incident flux for some non-plane-wave incident wavefronts, which is not allowed in a passive system. Next, we will derive a bound on the transmission efficiency for systems that yield the desired angle-dependent response while satisfying energy conservation.

The paragraphs above consider metalenses. One can similarly write down the desired transmission matrix for other multi-channel optical systems of interest.

2.3 Transmission Efficiency Bound

For any system of interest, the transmission efficiency averaged over inputs within the prescribed FOV is ⟨ T ⟩ = ∑ a T a / N in $\langle T\rangle = {\sum _{a}T_{a}}/{N_{\rm in}}$ . To obtain an upper bound on ⟨ T ⟩ $\langle T\rangle$ without specifying the overall amplitude prefactor of the transmission matrix, we consider the singular values { σ i } $\lbrace \sigma _i\rbrace$ of the transmission matrix.[39] With the singular value decomposition, the transmission matrix is factorized into orthonormal inputs and outputs as t = U Σ V † = ∑ i σ i ( u i v i † ) $\mathbf {t} = \mathbf {U}\bm {\Sigma }\mathbf {V^{\dagger }}=\sum _i \sigma _i (u_i v_i^{\dagger })$ , where each right-singular column vector v i $v_i$ is a normalized incident wavefront being a linear superposition of the input channels. The corresponding transmitted wavefront is σ i u i $\sigma _i u_i$ , with a transmission efficiency of σ i 2 $\sigma _i^2$ and with the normalized transmitted wavefront being column vector u i $u_i$ . Per min-max theorem, σ max 2 $\sigma _\mathrm{max}^2$ and σ min 2 $\sigma _\mathrm{min}^2$ are the highest-possible and lowest-possible transmission efficiency among all possible input states (singular or not). Figure 1d shows the normalized singular values of the transmission matrix in Figure 1c. Since tr( t † t $\bf t^{\dagger }t$ ) = Σ a ( t † t ) a a = ∑ b , a | t b a | 2 $\Sigma _a({\bf t^{\dagger }t})_{aa}=\sum _{b,a}|t_{ba}|^2$ equals the sum of the eigenvalues λ i = σ i 2 $\lambda _i=\sigma _i^2$ of matrix t † t $\bf t^{\dagger }t$ , we have ⟨ T ⟩ = ∑ b , a | t b a | 2 / N in = ∑ i σ i 2 / N in $ \langle T\rangle =\sum _{b,a}|t_{ba}|^2/{N_{\rm in}} = {\sum _{i} \sigma _i^2}/{N_{\rm in}}$ . The obstacle is that the overall amplitude prefactor of { σ i } $\lbrace \sigma _i \rbrace$ is not known.

Energy conservation imposes that the transmitted energy cannot exceed the input energy in a passive system, so we must have σ i 2 ≤ 1 $\sigma _i^2 \le 1$ for all i with the actual overall amplitude prefactor. One way to establish a bound on the average efficiency is to recognize that the highest possible transmission efficiency is unity, so ⟨ T ⟩ ≤ ( ∑ i σ i 2 / N in ) / σ max 2 $ \langle T\rangle \le ({\sum _{i} \sigma _i^2}/{N_{\rm in}})/\sigma _\mathrm{max}^2$ ; this expression does not depend on the overall amplitude prefactor. But since the response of a designed structure generally does not perfectly match the target response, the actual maximal singular value can also deviate from that of the target, and a bound that depends sensitively on one singular value will not be robust. To provide a robust bound that collectively depends on the system's response to all possible inputs, we quantify the effective number of high-transmission channels through an inverse participation ratio[40] as N eff = ( ∑ i = 1 σ i 2 ) 2 / ∑ i = 1 σ i 4 $N_\mathrm{eff} = (\sum _{i=1} \sigma _i^2)^2/\sum _{i=1} \sigma _i^4$ . This Neff considers all singular values and is independent of the overall prefactor of the transmission matrix. If { σ i } $\lbrace \sigma _i \rbrace$ were an array of zeros and ones, this Neff would simply count the number of ones in this array. For a perfectly transmitting system, all of the singular values are ones, and N eff = N in $N_\mathrm{eff} = N_\mathrm{in}$ . For a generic set of singular values, Neff provides an effective count of high-transmission channels. To bound the average efficiency using Neff, we recognize that ∑ i σ i 4 ≤ ∑ i σ i 2 $\sum _{i} \sigma _i^4 \le \sum _{i} \sigma _i^2$ since σ i 2 ≤ 1 $\sigma _i^2 \le 1$ , so that
⟨ T ⟩ ≡ ∑ b , a | t b a | 2 N in = N eff N in ∑ i σ i 4 ∑ i σ i 2 ≤ N eff N in $$\begin{equation} \langle T\rangle \equiv \frac{\sum _{b,a}|t_{ba}|^2}{N_{\rm in}} = \frac{N_{\rm eff}}{N_{\rm in}} \frac{\sum _{i} \sigma _i^4}{\sum _{i} \sigma _i^2} \le \frac{N_{\rm eff}}{N_{\rm in}} \end{equation}$$ (4)
In Figure 1d, ⟨ T ⟩ ≤ N eff / N in ≈ 74 $\langle T \rangle \le {N_{\rm eff}}/{N_{\rm in}} \approx 74$ %.

Given any angle-dependent response of interest, one can write down the corresponding transmission matrix (without specifying the overall amplitude prefactor), evaluate its Nin singular values { σ i } $\lbrace \sigma _i\rbrace$ and the associated Neff, and the efficiency bound follows as ⟨ T ⟩ ≤ N eff / N in $\langle T\rangle \le {N_\mathrm{eff}}/{N_\mathrm{in}}$ . Equation (4) is rigorously derived, with the only assumption being passivity, σ i 2 ≤ 1 $\sigma _i^2 \le 1$ . Therefore, this bound is fundamental and applies to any passive linear optical system for which the desired response is specified. Unlike the thickness bound of References [9, 36], Equation (4) does not rely on any empirical relation or any heuristic argument.

A bound is useful only when it is sufficiently tight. Figure S2 (Supporting Information) shows from full-wave numerical simulations[41] that Equation (4) indeed provides a reasonably tight upper bound for the averaged transmission efficiency ⟨ T ⟩ $\langle T \rangle$ , considering hyperbolic and quadratic metalenses as examples.

Figure 2a shows the transmission efficiency bound N eff / N in $N_{\rm eff}/N_{\rm in}$ as a function of NA for aberration-free nonlocal metalenses with FOV larger than the threshold shown in Figure S1 (Supporting Information). In general, both the FOV and the output diameter Dout can affect the transmission efficiency. For the metalens example considered here, Figures S3 and S4 (Supporting Information) show that they happen to have a small influence on N eff / N in $N_{\rm eff}/N_{\rm in}$ , so in Figure 2a we map out how the efficiency bound depends on the NA while averaging over FOV and Dout. We see that using equal entrance and output diameters, i.e., D in = D out $D_{\rm in}=D_{\rm out}$ , results in an efficiency bound that drops approximately as 1 − NA 2 $\sqrt {1-{\rm NA}^2}$ . This bound applies regardless of how complicated or optimized the design is, what materials are used, and how thick the device is.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Transmission efficiency bound N eff / N in $N_{\rm eff}/N_{\rm in}$ of ideal nonlocal metalenses when D in = D out $D_{\rm in}=D_{\rm out}$ and when using D in = D in th $D_{\rm in}=D_{\rm in}^{\rm th}$ from Equation (5). a) N eff / N in $N_{\rm eff}/N_{\rm in}$ averaged over FOV and output diameter Dout as a function of NA. The black line is 1 − NA 2 $\sqrt {\rm 1-NA^2}$ . b,c) The distribution of N eff / N in $N_{\rm eff}/N_{\rm in}$ among different FOV and Dout when (b) NA = 0.7 and (c) NA = 0.9.

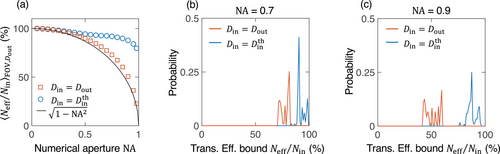
In Figure 2b,c, we show the distribution (among different FOV and output diameters) of the transmission efficiency bound with NA = 0.7 and 0.9, considering 120 combinations of different FOV and Dout for each NA. The bound is consistent with the inverse design results of Reference [34], where the achieved average absolute focusing efficiency (considering only the transmitted power within three full-widths at half-maximum around the focal peak) is 25% for a nonlocal metalens with NA = 0.7 and FOV = 80°.

In general, the transmission efficiency limit can depend on the details of the target response. In Figure S5 (Supporting Information), we show the efficiency bound for telecentric lenses where only positions within an effective output diameter D out eff = D in $D_\mathrm{out}^\mathrm{eff} = D_\mathrm{in}$ are used for focusing, which is comparable to the non-telecentric bound when the FOV is small. In Figure S6 (Supporting Information), we consider non-telecentric systems described by Equation (2) and show that the choice of the angle-dependent amplitude A ( θ in a ) $A(\theta _\mathrm{in}^a)$ has little effect on the efficiency bound.

2.4 Optimal Aperture Size

In addition to establishing a transmission efficiency limit, it would be even more useful to know what strategy one may adopt to raise such an efficiency limit. To this end, we examine the singular values of the transmission matrix. In Figure 1d where D in = D out = 300 λ $D_{\rm in}=D_{\rm out}=300\lambda$ and NA = 0.8, we see there are many zero singular values. These zero singular values lower Neff and the transmission efficiency. Removing these zero singular values (i.e., eliminating non-transmitting wavefronts) can raise the transmission efficiency bound N eff / N in $N_{\rm eff}/N_{\rm in}$ . A zero singular value corresponds to a superposition of the columns of the transmission matrix that yields a zero vector, meaning those columns are linearly dependent. Therefore, we can eliminate zero singular values by reducing the number of columns in the transmission matrix. Because the input wave vectors | k y ′ | < ( 2 π / λ ) sin ( FOV / 2 ) $|k_y^{\prime }|&lt;(2\pi /\lambda )\sin {(\rm FOV/2)}$ are sampled with momentum spacing 2 π / D in $2\pi /D_{\rm in}$ at the Nyquist rate, we expect that reducing Din can lower the number of input columns in the transmission matrix to raise the transmission efficiency bound. Figure 3 shows this strategy indeed works: reducing the input aperture size Din increases the efficiency bound N eff / N in $N_{\rm eff}/N_{\rm in}$ .

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The transmission efficiency bound N eff / N in $N_{\rm eff}/N_{\rm in}$ and the condition number κ of the ideal transmission matrix as a function of the entrance diameter Din. Black and gray vertical dotted lines indicate D in th = 185 λ $D_{\rm in}^{\rm th}=185\lambda$ and D out = 300 λ $D_{\rm out}=300\lambda$ . Lens parameters: output diameter D out = 300 λ $D_{\rm out}=300\lambda$ , NA = 0.8, FOV = 140°.

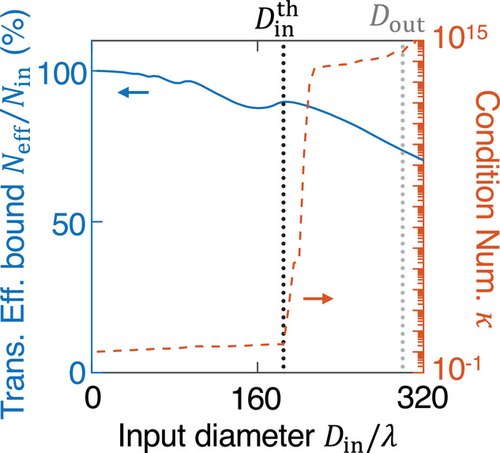
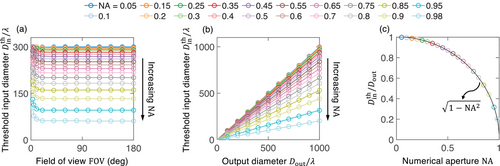
The next question is: what would be an optimal input diameter Din to use? While reducing Din raises the transmission efficiency bound, doing so also reduces the amount of light that can enter the metalens, which is not desirable. To find a balance, we examine the condition number κ, defined as the ratio between the maximal and the minimal singular values. When zero σ i $\sigma _i$ exist, the condition number κ diverges to infinity (subject to numerical precision). The right-axis of Figure 3 shows that κ abruptly shoots up by many orders of magnitude when the input diameter Din raises above a threshold that we label as D in th $D_{\rm in}^{\rm th}$ (black dotted line). When D in < D in th $D_{\rm in} &lt; D_{\rm in}^{\rm th}$ , κ is of order unity, all singular values are comparable with no zero-transmission wavefronts, so we have N eff ≈ N in ${N_{\rm eff}} \approx N_{\rm in}$ , and the transmission efficiency bound is close to unity. When D in > D in th $D_{\rm in} &gt; D_{\rm in}^{\rm th}$ , near-zero-transmission wavefronts start to appear, which results in a fast reduction of the transmission efficiency bound. Therefore, this threshold value D in th $D_{\rm in}^{\rm th}$ is an optimal input diameter to use, providing maximal entrance flux while keeping a near-unity transmission efficiency bound.

To automate the determination of D in th $D_{\rm in}^{\rm th}$ , we examine the slope ∂ κ / ∂ D in $\partial \kappa /\partial D_{\rm in}$ , which transitions from near zero to a very large number at D in th $D_{\rm in}^{\rm th}$ . Table S1 (Supporting Information) shows that different threshold values for ∂ κ / ∂ D in $\partial \kappa /\partial D_{\rm in}$ yield almost identical D in th $D_{\rm in}^{\rm th}$ and N eff / N in $N_{\rm eff}/N_{\rm in}$ . Note that the choice of the global phase ψ ( θ in ) $\psi (\theta _{\rm in})$ in Equation (1) does not influence D in th $D_{\rm in}^{\rm th}$ and the transmission efficiency bound, as shown in Figure S7 (Supporting Information).

To guide future designs, it is desirable to know how D in th $D_{\rm in}^{\rm th}$ depends on the various lens parameters. Figure 4 plots D in th $D_{\rm in}^{\rm th}$ as a function of the FOV, output diameter Dout, and NA. As described in Section 2.1, lenses with a very small FOV do not require nonlocality; for such local metalenses, we find D in th ≈ D out $D_{\rm in}^{\rm th} \approx D_{\rm out}$ as expected from the schematic in Figure 1a. As the FOV increases and nonlocality emerges, we observe in Figure 4a that D in th $D_{\rm in}^{\rm th}$ drops below Dout (as expected from the preceding discussions) and reaches a constant value that depends on NA but not on the FOV. This D in th $D_{\rm in}^{\rm th}$ for nonlocal metalenses is proportional to Dout [Figure 4b]. Figure 4a,b fix D out = 300 λ $D_{\rm out}=300\lambda$ and FOV = 140° respectively; other lens parameters share similar dependencies (Figures S8 and S9, Supporting Information). In Figure 4c, we find empirically that the NA dependence is well described by
D in th = D out 1 − NA 2 $$\begin{equation} D_{\rm in}^{\rm th} = D_{\rm out}\sqrt {1-{\rm NA}^2} \end{equation}$$ (5)
This result provides a recipe for choosing the input and output aperture sizes for nonlocal high-NA metalenses with high transmission.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Dependence of the threshold input diameter D in th $D_{\rm in}^{\rm th}$ on the lens parameters. a) D in th $D_{\rm in}^{\rm th}$ as a function of the FOV when D out = 300 λ $D_{\rm out}=300\lambda$ . b) D in th $D_{\rm in}^{\rm th}$ as a function of the output diameter Dout when FOV = 140°. Symbols are D in th $D_{\rm in}^{\rm th}$ computed from the ideal transmission matrices, and solid lines are linear fits. c) D in th / D out $D_{\rm in}^{\rm th}/D_{\rm out}$ averaged over different FOV for nonlocal metalenses as a function of NA. Black solid line is 1 − NA 2 $\sqrt {\rm 1-NA^2}$ .

To demonstrate the increased transmission efficiency bound, we also show in Figure 2a–c the transmission efficiency bound when the input aperture size Din is set to the optimal D in th $D_{\rm in}^{\rm th}$ in Equation (5). We observe a large transmission efficiency bound N eff / N in ${N_{\rm eff}}/{N_{\rm in}}$ that overcomes the 1 − NA 2 $\sqrt {1-{\rm NA}^2}$ limit when equal entrance and output apertures are used.

3 Discussion

While we use the efficiency of high-NA nonlocal metalenses as the example here, the formalism we introduce is very general and applies to any passive linear optical system. Once the target response is specified, this formalism can be used to put a bound on the channel-averaged transmission efficiency. The bound holds for any structural design and material composition, including not only metasurfaces but also volumetric nanophotonic structures and conventional optical systems.

We note that even though the transmission efficiency limit here depends only on the target functionality and not on the device thickness, this does not mean that thin and thick structures will perform similarly. Thin structures have a limited degree of nonlocality, which may not be sufficient for realizing the target angle-dependent response of interest[9]—not even with a low transmission efficiency. The efficiency bound here and the thickness bound of Reference [9] are independent constraints.

In establishing a target-driven thickness bound, Reference [9] had to use an intuition-based and empirically established relation between lateral spreading and thickness, and Reference [36] had to use a heuristic relation between channel number and thickness and the estimation of a maximal internal angle that is not clearly defined in the presence of wave scattering. In contrast, the efficiency bound here is rigorously derived with no heuristics or empirical assumption and is clearly defined.

When the input diameter is above its threshold value D in th $D_{\rm in}^{\rm th}$ , the efficiency loss may be associated with vignetting but is not necessarily so. We also note that even an ideal system with 100% transmission efficiency for all incident angles will still experience a natural falloff of the illumination flux density governed by the cos 4 θ $\cos ^4\theta$ law due to projection,[42] which is distinct from the transmission efficiency limit here.

Nonlocal metasurfaces open up a wide range of applications and tailored angle-dependent responses that are impossible for traditional local metasurfaces.[26] The efficiency bound in this work provides valuable guidance for this rapidly evolving field. For example, this work suggests that inverse-designed multi-layer wide-FOV metalenses such as in Reference [34] may benefit from expanding the size of each successive layer.

Acknowledgements

The authors thank X. Gao for helpful discussions. This work was supported by the National Science Foundation CAREER award (ECCS-2146021) and the Sony Research Award Program.

    Conflict of Interest

    The authors declare no conflict of interest.

    Data Availability Statement

    All data needed to evaluate the conclusions in this study are presented in the paper and in the supplemental document.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.