Biomechanical evaluation of total ankle arthroplasty. Part II: Influence of loading and fixation design on tibial bone–implant interaction
Abstract
Finite element (FE) models to evaluate the burden placed on the interaction between total ankle arthroplasty (TAA) implants and the bone often rely on peak axial forces. However, the loading environment of the ankle is complex, and it is unclear whether peak axial forces represent a challenging scenario for the interaction between the implant and the bone. Our goal was to determine how the loads and the design of the fixation of the tibial component of TAA impact the interaction between the implant and the bone. To this end, we developed a framework that integrated robotic cadaveric simulations to determine the ankle kinematics, musculoskeletal models to determine the ankle joint loads, and FE models to evaluate the interaction between TAA and the bone. We compared the bone–implant micromotion and the risk of bone failure of three common fixation designs for the tibial component of TAA: spikes, a stem, and a keel. We found that the most critical conditions for the interaction between the implant and the bone were dependent on the specimen and the fixation design, but always involved submaximal forces and large moments. We also found that while the fixation design influenced the distribution and the peak value of bone–implant micromotion, the amount of bone at risk of failure was specimen dependent. To account for the most critical conditions for the interaction between the implant and the bone, our results support simulating multiple specimens under complex loading profiles that include multiaxial moments and span entire activity cycles.
1 INTRODUCTION
Total ankle arthroplasty (TAA) is gaining popularity as an effective treatment for end-stage ankle osteoarthritis. Most TAA implants rely on cementless fixation by bone ingrowth and therefore require low relative micromotion between the implant and the bone in the immediate postoperative scenario. It has been shown that micromotion below 20–50 µm promotes bone ingrowth, while micromotion in excess of 150 µm promotes ingrowth of fibrous tissue instead of bone.1, 2 Micromotion is not the only consideration for long-term stable fixation. When transferring loads to the surrounding bone the implant must avoid overloading the bone, which could lead to bone failure and implant subsidence and loosening.3 To ensure both adequate micromotion and successful load transfer, TAA designs have incorporated supplemental fixation features, such as keels, stems, or spikes (Figure 1). Despite these design efforts, reported revision rates range from 5% in 2 years4 to 42% in 5 years,5 with the leading causes for failure being periprosthetic osteolysis, component loosening, and subsidence.4-6 These failure modes are thought to be related to the mechanics of the interaction between the implant and the bone.

Few studies have investigated the interplay between the design of the tibial fixation and the mechanics of the interaction between the implant and the bone. In a cadaveric study, McInnes et al.7 found that the largest micromotion occurred at the instance of the greatest applied torque and that a dual-cylinder design is better suited for resisting inversion–eversion and internal–external moments, while a short-keeled design better resists the plantarflexion–dorsiflexion moments. Sopher et al.8 utilized finite element (FE) analyses to compare the bone–implant relative micromotion of three tibial fixation designs: a central stem, dual-cylinders, and a keel. The peak value and the distribution of micromotion differed across fixation designs, with the central stem showing the largest peak micromotion and the keeled design the smallest. Similarly, the amount of bone at risk of mechanical failure was dependent on the fixation design and followed a similar trend to the implant–bone micromotion.
Although these studies provided important information about the interaction between the implant and the bone, the considered loads consisted of a purely axial load,6 or the combination of an axial load with pure moments around the anatomic axes of the foot.7 These load conditions are not representative of the complex and dynamic loading environment at the ankle during daily activities, which includes multiaxial forces and moments. In other implant systems, such as the tibial component of total knee arthroplasty, the most critical scenario for the interaction between the implant and the bone has been shown to be the result of complex combinations of submaximal loads and relatively high multiaxial moments.9-12 Thus, even though McInnes et al.7 and Sopher et al.8 showed that different fixation designs respond differently to applied loads, it remains unclear how these same fixation designs would behave under the complex loading scenarios.
To address these shortcomings in the current understanding of the biomechanics of TAA, we developed a framework that integrated robotic gait simulations of cadaveric specimens, musculoskeletal models, and FE models to evaluate the interaction between the implant and the bone. The overarching aims of our two-part study were (1) to determine the multiaxial loads at the joint during level walking following TAA and (2) to determine how the loads and the fixation design of the tibial component impact the interaction between the implant and the bone. In this second part of our two-part study, we describe how we utilized the loads determined in Part I to drive quasi-static FE simulations to evaluate the bone–implant micromotion and the risk of bone failure (i.e., with strains above yield) for three different fixation designs for the tibial component of a TAA implant: spikes, a stem, and a keel.
2 METHODS
In Part I of our study, three fresh-frozen cadaveric foot-to-mid tibia specimens (Table 1) were implanted with INFINITYTM Total Ankle Replacements (Wright Medical Technology) by an experienced board-certified orthopedic surgeon (CAD), using patient-specific PROPHECYTM guides. The cadaveric specimens were computed tomography (CT)-scanned before and after implantation on a Biograph-64 CT scanner (Siemens Healthcare), with 140 mA, 140 kVp, and 0.6 mm slice thickness.
| Specimen | Side | Age | Sex | Height (cm) | Weight (kg) | BMI (kg/m2) |
|---|---|---|---|---|---|---|
| S-1 | R | 51 | M | 185 | 104 | 30 |
| S-2 | L | 59 | M | 178 | 76 | 24 |
| S-3 | L | 61 | M | 183 | 71 | 21 |
- Abbreviation: BMI, body mass index.
To obtain the joint loads at the ankle during level walking, we utilized a framework that combines a validated robotic simulator13 with a musculoskeletal model, adapted to each specimen. A detailed description of the framework is provided in Part I. Briefly, each specimen was first experimentally tested on the robotic simulator to measure the kinematics of the individual bones of the hindfoot during level walking. The robot used an iterative control algorithm to control the forces applied to the muscle tendons and the trajectory of a force plate that represents the ground. The objective was to minimize the error in ground reaction force with respect to in vivo measurements performed on healthy human subjects during level walking. The motions of the individual bones of the hindfoot were measured by tracking retroreflective markers attached to the tibia, talus, and calcaneus with a motion capture system. The kinematics of the tibia and calcaneus, the muscle forces, and the ground reaction force were then input to specimen-specific musculoskeletal models to determine the forces and moments at the center of the ankle joint throughout a level walking cycle. These forces and moments were applied to FE models of each specimen to evaluate the interaction between the implant and the bone.
The FE models consisted of the most distal 140 mm of each implanted tibiae. To reduce the computational cost, the models did not include any of the hindfoot bones, the fibula, or the polyethylene component. We obtained the intact bone geometry and distribution of bone material properties for each specimen from the preoperative CT scans. We determined the position of the implant with respect to the intact bone for each specimen from the postoperative CT scans. To this end, we first performed a best-fit alignment between the postoperative and the preoperative CT scans based on the mid-shaft of the tibiae. We then aligned the CAD model of the implant to the component visible in the postoperative CT scan. We modeled three simplified fixation geometries commonly utilized for the tibial component: three spikes, a keel, and a central stem (Figure 1). In all cases, the implant baseplate remained unchanged. We assumed line-to-line fit between the implant and the bone for all surfaces except for the medial and lateral surfaces, where we assumed to have a gap of 0.75 mm between the resected tibia and the implant's baseplate. This gap corresponds to the thickness of the sawblade utilized during the experimental implantation. This situation represents a worst-case scenario in which the loads applied to the implant are resisted solely by the fixation geometries of the implant since no press fit exists between the implant and the bone.
The bone and implant geometries were meshed with linear tetrahedral elements in Abaqus 2017 (Dassault Systemes). The element size for the bone increased from a minimum of 0.7 mm for the edges of the fixation geometries to a maximum of 3 mm at 140 mm, the most proximal end of the tibiae. For the implants, the element size increased from 0.7 mm at the edges of the fixation geometries to a maximum of 1 mm. This resulted in between 560,446 and 917,172 elements across the nine FE models (three specimens with three fixation designs per specimen).
All materials were modeled as linear elastic and isotropic. The implant was assumed to be a homogeneous Ti6Al4V alloy (E = 114 GPa, v = 0.33). The bone was modeled as nonhomogeneous. The Hounsfield units (HUs) from the preoperative CT scans were linearly related to the bone's apparent density by assuming that the minimum HU of each bone corresponded to an apparent density of 0 g/cc, while the maximum HU corresponded to a density of 1.8 g/cc.14 We related the apparent density to elastic modulus by combining the empirical relationships from Morgan et al.15 and Snyder and Schneider.16 The combination of these equations in FE models of the proximal tibia yielded bone strains in the normal range during daily activities and strains that were close to experimental data.14, 17
The multiaxial loads and moments at the ankle joint during the stance phase of gait, obtained with the musculoskeletal model utilized in Part I of our study, were discretized in 4% increments and applied to a point located at the center of rotation of the implant (i.e., at the center of the articular surface). This specimen-specific point was kinematically coupled to all the nodes in the distal surface of the implant's baseplate (i.e., the surface that would interface with the polyethylene insert). All the nodes of the proximal end of the tibiae (i.e., 140 mm proximal to the implant's resection level) were fixed.
Simulations were done in Abaqus 2017 (Dassault Systemes). To represent the immediate postoperative scenario in which bone has not yet ingrown, we modeled frictional surface-to-surface contact between the implant and the bone with a coefficient of friction of 0.6.18 We computed the bone–implant micromotion as the difference in displacement between each pair of bone–implant closest nodes. We considered a multiaxial strain-based failure criterion for the bone,19 and we reported the amount of bone mass at the bone–implant interface that was at risk of failure as a percent of the total interfacial bone mass.
3 RESULTS
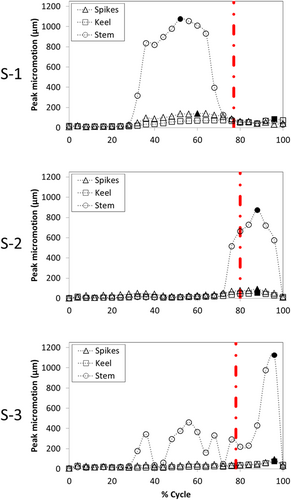
The values of the peak micromotion were similar across all three specimens, but there were large variations across fixation designs (Figure 2). For the three spikes fixation design, the maximum peak micromotion values were 140, 93, and 94 µm for specimens S-1, S-2, and S-3, respectively. For the keel fixation design, the maximum peak micromotion values were 85, 54, and 74 µm for specimens S-1, S-2, and S-3, respectively. For the stem fixation design, the maximum peak micromotion values were 1076, 874, and 1125 µm for specimens S-1, S-2, and S-3, respectively. In all cases, the keel design had the lowest maximum peak micromotion and the stem had the highest.
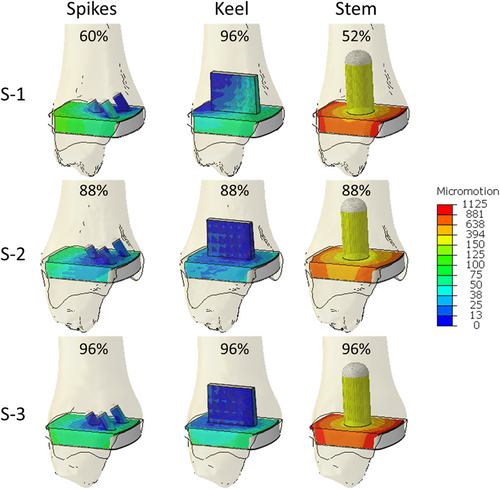
Similarly, the distribution of micromotion at the instant of the maximum peak micromotion was consistent across specimens, but important differences were found across fixation designs (Figure 3). In all cases, the micromotion was lowest around the fixation features. For the three spikes design, the peak micromotion occurred at the posterior edge of the baseplate. For the keel, the peak micromotion occurred at the anterior–medial edge of the baseplate. A concentric pattern occurred around the stem, with the peak micromotion located at the posterior edge of the baseplate.
The maximum peak micromotion for specimen S-1 occurred at 60%, 96%, and 52% of the cycle for the three spikes, keel, and stem designs, respectively (Figure 2). For specimens S-2 and S-3, the maximum peak micromotion occurred at 88% and 96% of the cycle, respectively, for all fixation designs. On the other hand, the peak compressive force occurred at a more similar point during the cycle for all three specimens (see Part 1 of the manuscript): 77%, 80%, and 78% of the cycle for specimens S-1, S-2, and S-3, respectively.
The amount of bone at risk of failure was similar across fixation designs, but large variations were found across specimens (Figure 4). For specimen S-1, the maximum amount of bone mass at risk of failure was 5.9%, 4%, and 7.2% for the three spikes, keel, and stem fixation designs, respectively. For specimen S-2, the maximum amount of bone mass at risk of failure was much lower: 0.5%, 0.1%, and 0.2% for the three spikes, keel, and stem fixation designs, respectively. For specimen S-3, the maximum amount of bone mass at risk of failure was between that found for the other two specimens: 2.9%, 0.7%, and 2.2% for the three spikes, keel, and stem fixation designs, respectively. In all cases, the keel design had the lowest amount of bone mass at risk of failure. For all specimens and fixation designs, the bone at risk of failure was concentrated on the fixation geometries, especially on the anterior–medial zones of the fixation features (Figure 5).
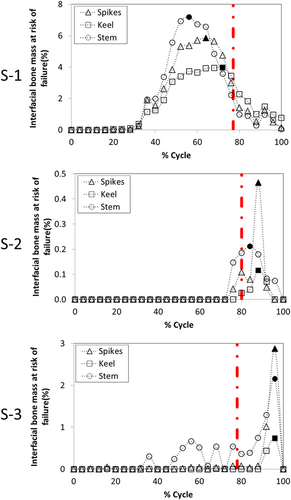
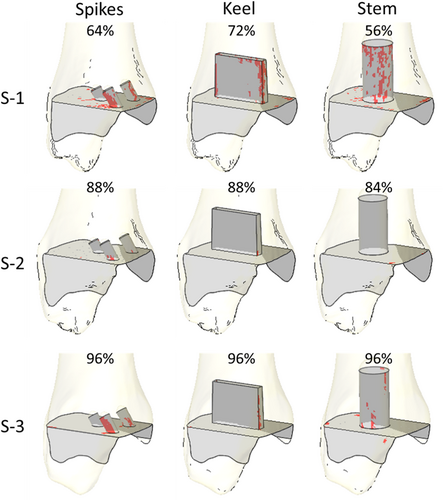
The largest amount of interfacial bone mass at risk of failure for specimen S-1 occurred at 64%, 56%, and 72% of the cycle for the three spikes, keel, and stem designs, respectively (Figure 4). For specimen S-2, the largest amount of interfacial bone mass at risk of failure occurred at 88% for the three spikes and keel designs, and at 84% for the stem design. For specimen S-3, the largest risk of bone failure was computed at 96% of the cycle for all fixation designs.
The composite micromotion was computed as the maximum micromotion that occurred at each node of the bone–implant interface during the cycle. Similarly, the composite risk of bone failure was computed as the largest risk of failure at each bone element throughout the cycle. For all specimens and fixation designs, the area with micromotion below 50 µm (the threshold for bone ingrowth) computed at the instant of the maximum peak micromotion was similar to that based on the composite micromotion (Table 2). For all specimens and fixation designs, the maximum amount of bone at risk of failure throughout the cycle was similar to the amount computed with the composite risk of bone failure (Table 2).
| Spikes | Keel | Stem | |||||
|---|---|---|---|---|---|---|---|
| Area > 50 µm (%) | Bone mass at risk of fail (%) | Area > 50 µm (%) | Bone mass at risk of fail (%) | Area > 50 µm (%) | Bone mass at risk of fail (%) | ||
| S-1 | Largest in cycle | 41.0 | 5.9 | 22.9 | 4.0 | 100.0 | 7.2 |
| Composite | 42.0 | 6.9 | 30.1 | 5.1 | 100.0 | 8.4 | |
| S-2 | Largest in cycle | 23.4 | 0.5 | 0.4 | 0.1 | 100.0 | 0.2 |
| Composite | 23.4 | 0.5 | 0.4 | 0.1 | 100.0 | 0.2 | |
| S-3 | Largest in cycle | 37.9 | 2.9 | 7.0 | 0.7 | 100.0 | 2.2 |
| Composite | 37.9 | 2.9 | 7.0 | 0.7 | 100.0 | 2.6 | |
Interestingly, if we had considered only the peak axial force during level walking as has been done by previous investigators,5, 6 the results would have been smaller peak micromotions (Table 3) and smaller amounts of bone at risk of failure (Table 4). The maximum peak micromotion values for the three spikes fixation design would have been 36, 5, and 19 µm for specimens S-1, S-2, and S-3, respectively. The maximum peak micromotion values for the keel fixation design would have been 43, 9, and 19 µm for specimens S-1, S-2, and S-3, respectively. The maximum peak micromotion values for the stem fixation design would have been 47, 11, and 25 µm for specimens S-1, S-2, and S-3, respectively. Similarly, only specimen S-1 would have had bone at risk of failure. The total amounts would have been 0.9% for three spikes and keel designs and 0.6% for the stem design.
| Spikes | Keel | Stem | ||||
|---|---|---|---|---|---|---|
| At peak axial force | Maximum during gait | At peak axial force | Maximum during gait | At peak axial force | Maximum during gait | |
| S-1 | 36 | 140 | 43 | 85 | 47 | 1076 |
| S-2 | 5 | 93 | 9 | 54 | 11 | 874 |
| S-3 | 19 | 94 | 19 | 74 | 25 | 1125 |
| Spikes | Keel | Stem | ||||
|---|---|---|---|---|---|---|
| At peak axial force | Maximum during gait | At peak axial force | Maximum during gait | At peak axial force | Maximum during gait | |
| S-1 | 0.9 | 5.9 | 0.9 | 4 | 0.6 | 7.2 |
| S-2 | 0 | 0.5 | 0 | 0.1 | 0 | 0.2 |
| S-3 | 0 | 2.9 | 0 | 0.7 | 0 | 2.2 |
4 DISCUSSION
To understand the influence of the fixation design on the burden placed on the bone–implant system during the common daily activity of level walking, we undertook an integrated approach that combined experimental testing, musculoskeletal modeling, and FE simulations. We utilized three cadaveric specimens to compare the interaction between the implant and the bone of three fixation designs: three spikes, a stem, and a keel. We evaluated the bone–implant micromotion and the risk of bone failure, as key biomechanical indicators of the success of the fixation.
We found that the fixation design played an important role in the magnitude of the maximum peak micromotion: the stem design had four to five times larger values (874–1125 µm) than the three spikes and keel designs, for which the peak micromotion was both smaller and similar to one another (~54–140 µm). Moreover, the distribution of micromotion at the instant of the maximum peak micromotion was also dependent on the fixation design: for the three spikes design, the highest micromotion was located posteriorly; for the keel, the highest micromotion was located anteriorly; and the stem design showed a concentric pattern around the stem. Such concentric pattern was a consequence of the lack of restrictions on the axial rotation for the stem design, which resulted in the high sensitivity of this fixation to internal–external moments. Conversely, the maximum amount of bone at risk of failure had greater variation across specimens than across fixation designs, although for each specimen the keel had less bone at risk of failure than the three spikes and stem designs. In this way, the amount of bone at risk of failure for specimen S-1 (range from 4% to 7.2%) was more than five times larger than for specimen S-3 (range from 0.7% to 2.9%) and more than 10 times larger than for specimen S-2 (range from 0.1% to 0.5%). In addition, the bone with the highest risk of failure was located at the fixation features for all fixation designs. These results agree with Sopher et al.,8 who found that a stem design had greater micromotion and bone at risk of failure than a keel design. Nonetheless, since we included multiaxial forces and moments, we found approximately 30 times larger values than Sopher et al.8 for the peak micromotion of the stem design. In this way, our results show that designs consisting of a single stem are at risk of high micromotion that may prevent bone ingrowth and result in the formation of fibrous tissue; therefore, they may require additional fixation features to prevent such high micromotion.
The maximum peak micromotion occurred at approximately the same instant as the largest amount of bone at risk of failure for all specimens and fixation designs except for specimen S-1 with the keel design. Thus, the instant of the highest burden placed on the bone–implant interaction differed across specimens: while for specimens S-2 and S-3 it occurred during late-stance, for specimen S-1 the highest burden occurred at mid-stance. Moreover, the highest burden for the bone–implant interaction also depended on the fixation design, especially for specimen S-1. Despite these variations, the burden on the bone–implant interface did not differ whether it was computed based on the worst-case scenario or on composite values of the entire cycle, revealing that such burden can be effectively evaluated through a single load case. Furthermore, for all specimens and fixation designs, the maximum peak micromotion and the largest amount of bone at risk of failure involved the combination of submaximal loads and relatively high moments, particularly the inversion–eversion and internal–external moments. In this way, studies of the tibial component of cementless total knee replacements have also revealed the importance of combining submaximal loads with high moments.9-12
To our knowledge, no prior study has evaluated the bone–implant micromotion and the risk of failure of total ankle replacements throughout an activity cycle. Instead, large compressive forces are often assumed to be the worst-case scenario for the interaction between the implant and the bone.8, 20 However, our results suggest that considering only the highest axial force results in an underestimation of the burden placed in the interaction between the implant and the bone compared to the combination of submaximal loads and high moments. The combination of submaximal forces with high moments has been shown to be important for predicting the worst-case scenario in other joints, like the knee.9-12 Our results show that the same is true for TAA. For example, the peak micromotion under the peak axial force alone was between 2 and 79 times smaller than the maximum peak micromotion during level walking, when the loads included multiaxial forces and moments. In this way, we obtained 30 times larger micromotion than Sopher et al.8 for the stem design. Similarly, the amount of bone at risk of failure was between 4 and 12 times smaller than the maximum amount of bone at risk of failure during level walking, when the implant was subject to multiaxial forces and moments.
We observed important interspecimen variability in terms of the magnitude and time during gait, especially for the bone at risk of failure. Such variability was the result of a complex interplay between the profile of the joint loads and the bone quality of each specimen. In this way, although specimen S-2 had the largest moments, it had also the highest average bone modulus at the interface surfaces. This specimen resulted in the lowest value of micromotion and the amount of bone at risk of failure among the three specimens. On the other hand, specimen S-1 had the lowest inversion/eversion and plantarflexion–dorsiflexion moments and similar internal/external moment to specimen S-2, but it had the lowest average bone modulus at the bone surfaces in contact with the implant. This specimen resulted in the greatest amount of bone at risk of failure and only the stem design for specimen S-2 had a larger value of the maximum peak micromotion.
This study has limitations that should be considered when interpreting the results. First, we considered a limited number of specimens. However, even this small number was enough to provide evidence of the effects of interspecimen variability. Further, studies should include more specimens to account for such variability. Second, we considered simplified fixation geometries that do not necessarily represent all the features present in commercial implants. For instance, implants with a central stem often have additional elements that prevent axial rotation of the implant. Moreover, we assumed an ideal line-to-line contact between the fixation geometries and the bones (i.e., no press fit or gaps were considered). Although implants often include additional fixation features and are often designed to achieve press fit to enhance primary stability, we made our assumptions to ensure a worst-case scenario that, by exacerbating the differences across fixation designs, helped demonstrate the effect that fixation has in resisting the loading. Third, we considered the same baseplate and articular geometry for all fixation designs. In commercial implants, different fixation types will be paired with different baseplates and articular geometries; however, our assumption allowed for isolating the comparison to the type fixation, without other design-related confounding factors. Fourth, this study lacks validation in terms of the micromotion and bone strains that were then utilized to obtain the risk of bone failure. However, the same conditions were considered for all designs; therefore, the relative comparisons among fixation designs and specimens remain valid.
In conclusion, we integrated experimental robotic testing, musculoskeletal modeling, and FE modeling to gain an understanding of the effect that the fixation design has on the interaction between the implant and the bone in TAA. Our results support considering the same loading conditions, which should be based on submaximal forces and large moments, to evaluate the most critical scenario for the interaction between the implant and the bone, irrespective of the fixation design. However, our results highlight the necessity of including multiple bones to ensure that the worst-case scenario is captured.
ACKNOWLEDGMENTS
The study reported in this publication was supported by the Clinical and Translational Science Center at Weill Cornell Medicine of the National Center for Advancing Translational Sciences under Award number TL1TR002386. The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health. The authors would also like to thank American Iron & Metal (USA) Inc. for their generous donation to our laboratory. The authors would like to thank Dr. Al Burstein for providing thoughtful review and feedback on our manuscript.
CONFLICT OF INTERESTS
The authors declare that there are no conflict of interests.
AUTHOR CONTRIBUTIONS
Fernando J. Quevedo González and Brett D. Steineman: study design, modeling, analysis and interpretation of results, and writing the manuscript. Daniel R. Sturnick: data collection and processing, and reviewing the manuscript. Jonathan T. Deland and Constantine A. Demetracopoulos: study design, interpretation of results, and reviewing the manuscript. Timothy M Wright: study design, interpretation of results, and writing the manuscript. All authors have read and approved the final submitted manuscript.




