Estimation of monkeypox spread in a nonendemic country considering contact tracing and self-reporting: A stochastic modeling study
Abstract
In May 2022, monkeypox started to spread in nonendemic countries. To investigate contact tracing and self-reporting of the primary case in the local community, a stochastic model is developed. An algorithm based on Gillespie's stochastic chemical kinetics is used to quantify the number of infections, contacts, and duration from the arrival of the primary case to the detection of the index case (or until there are no more local infections). Different scenarios were set considering the delay in contact tracing and behavior of infectors. We found that the self-reporting behavior of a primary case is the most significant factor affecting outbreak size and duration. Scenarios with a self-reporting primary case have an 86% reduction in infections (average: 5–7, in a population of 10 000) and contacts (average: 27–72) compared with scenarios with a non-self-reporting primary case (average number of infections and contacts: 27–72 and 197–537, respectively). Doubling the number of close contacts per day is less impactful compared with the self-reporting behavior of the primary case as it could only increase the number of infections by 45%. Our study emphasizes the importance of the prompt detection of the primary case.
1 INTRODUCTION
Monkeypox is a zoonotic disease caused by the monkeypox virus. Two possible means of transmission are animal-to-human and human-to-human. Animal-to-human transmission, also known as zoonotic transmission, is possible upon contact with or consumption of an infected natural host animal, such as rats, squirrels, and prairie dogs.1, 2 Human-to-human transmission can be caused by respiratory droplets or contact with lesions and bodily fluids. Contact with contaminated materials such as clothing, bedding, or eating utensils can also cause infections.3 The signs and symptoms of monkeypox are similar to smallpox but are less severe. In the current outbreak, symptoms are described as flu-like, followed by a rash starting in the genital and perianal areas, which may or may not spread to the other parts of the body.4, 5
The monkeypox virus was first reported in 1970.6 It is commonly found in Central and West Africa and occasionally identified in other countries.1 If undetected, transmission in nonendemic countries is possible, triggering outbreaks.7, 8 Since May 2022, an unprecedented outbreak of human monkeypox cases has been observed in Australia and several countries in Europe and North America.9, 10 On July 23, the World Health Organization (WHO) declared a global health emergency as the number of confirmed cases reached more than 16 000.11 As of August 11, 2022, the United States recorded the highest number of cumulative cases (10 360), followed by Spain (5482) and Germany (3025).12
- 1.
Upon the arrival of a primary case in a nonendemic country, how many infections may occur?16
- 2.
Depending on when the index case is found, how many contacts would the infector have already made?
- 3.
How long is the duration of the outbreak?
- 4.
What happens if the primary case does not self-report?
The basic reproductive number of monkeypox was estimated to be 2.13 (uncertainty bounds 1.46–2.67).17 Although it is less than the basic reproductive number of coronavirus disease of 2019 (COVID-19), monkeypox has a potential to become an epidemic.18 Hence, understanding the transmission dynamics of the disease is essential to mitigate its spread.
Numerous mathematical models have been proposed to understand the transmission dynamics of infectious diseases and evaluate the impact of different control measures.19-21 Since the COVID-19 has become a pandemic, epidemiological models have been widely used to propose strategies to control its spread.22-26 However, there are only a few works on monkeypox transmission models. Bankuru et al.27 have shown that vaccination may be able to control monkeypox transmission in a semiendemic setting (with the disease existing only on humans). Peter et al.28 suggested that isolation of infected individuals can reduce disease transmission. Bhunu et al.29 showed that increased contact between the host animal and human can lead to an increase in the number of monkeypox cases, especially in HIV-infected individuals. Han et al.30 investigated the mechanisms in the macroecology of pathogen transmission and the risk of spillover infection to humans by combining data mining with theoretical models. Tchuenche and Bauch31 emphasized the importance of empirical data aggregation about the wild animal in formulating a model. They have shown that depending on the animal-to-human contact rate, culling may have the counter-intuitive outcome of increasing the transmission of monkeypox among children. All the above-mentioned monkeypox models consider both human and animal-host compartments. However, since the disease had spread in nonendemic countries where natural animal hosts are not present, these may not be applicable in this study. Furthermore, these models focused on the long-term dynamics of the disease and not on initial countermeasures to preventing an outbreak in a community. Notably, all these models are deterministic.
To the best of our knowledge, this study is the first to use stochastic modeling to show the dynamics of monkeypox spreading in a nonendemic country. Stochastic models have been extensively used in other infectious diseases. For example, Hao et al.32 showed that multiple epidemic waves in Kansan, Japan may not be necessarily caused by infected individuals but by the stochastic nature of epidemic events. A stochastic model was formulated to investigate the impact of contact tracing in the control of infectious diseases.33 It has also been widely used in evaluating control measures for COVID-19 such as lockdown, social distancing, vaccination, contact tracing, and testing.34-38 Srivastav et al.39 compared deterministic and stochastic models and showed that for small populations, stochasticity plays a significant role. Deterministic models also do not account for fluctuations. Furthermore, transmission and recovery from infection are intrinsically stochastic processes.40 Since the focus of the study is on the effects of contact tracing and self-reporting of the primary case in the local community, we use a stochastic model to understand the dynamics of monkeypox transmission in a nonendemic setting. We focus on the early phase of the outbreak rather than the long-term view and consider essential factors such as contact tracing, which is a standard nonpharmaceutical intervention, and behavior of the primary case and infectees, whether self-reporting or not.
The rest of the article is organized as follows. Section 2 details the methodology used in this study. Section 3 presents the model simulations and hypothesis test results. Section 4 provides the discussions, limitations, and strengths of our research. Lastly, Section 5 contains the conclusions and policy implications.
2 METHODS
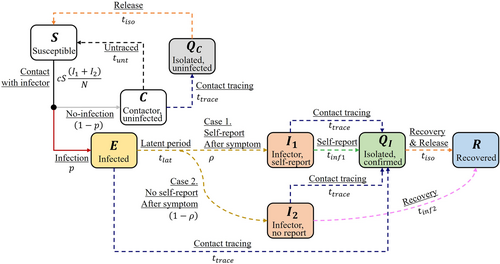
The parameters and indicate successful disease transmission reactions by and , respectively, in contrast to and . Depending on , a susceptible host who had contact with an infector can either be uninfected () or in latent stage (). Except for these four reactions, the other reactions in our model are delayed non-Markovian through the epidemiological process, which are shown in Figure 1 as dashed arrows.
The probability that an infectee will later self-report is denoted by . When an infectee in the latent stage becomes an infector ( or ), the host can spread the disease. If the infector self-reports (), then the host is isolated () and contact tracing events are generated once the case is confirmed. The duration from self-reporting of an infector to isolation is denoted by . Hosts who had contact with the confirmed host (, , , ) within contact tracing time (, 14 days, assumed) will be tracked. An infector in will stay in until the host is naturally recovered () in days, or until tracked and isolated. Note that contact tracing events are also generated if a traced host is infected (, , ). A host in can be traced and isolated () even if the host is not infected or go back to after . We assumed the isolation time is 21 days.
We assume uniform distributions for the infectious period of non-self-reporting infector, (range: 14–28 days), and contact tracing time, .44, 45 Latent period () and infectious period of self-reporting infector () are generated from log-normal distribution and aggregated from previous studies.46, 50 The average values of and are 8.5 and 2.96 days, respectively. We assume that the delay for a host with monkeypox from self-reporting to isolation () is similar to the period from symptom onset to diagnosis of a known case of COVID-19 exposure. The delays and are fixed to constant values and not generated from a distribution.
- ✓
Primary case: the person who brings the disease to a community.
- ✓
Index case: the first patient identified by health authorities with the disease.
Considering whether the primary case self-reports or not (initial condition of the simulation is or ), self-report rate of infectees in the local community (, 0.5 or 1), and delay for contact tracing (, 1–4 or 4–7 days), we set up eight scenarios, ran 100 000 simulations for each scenario, and observed the number of infections, contacts, duration of primary case arrival to index case detection (P1), and duration of primary case arrival to the end of the simulation (P2). End of the simulation means that all who were infected in the local community (except isolated) are removed, that is, . The exact stochastic simulation algorithm for systems with delays was adopted to express the delayed events. A detailed description of the algorithm, which was developed based on Gillespie's stochastic chemical kinetics, is presented by Cai.47 Figure 2 illustrates the simulation process of two different scenarios depending on whether the primary case self-reports or not. In (A), the primary case is the same as the index case and the simulation ends when all infected contacts of the primary case are isolated. In (B), contact tracing was generated later resulting to secondary infections and a longer simulation process. We simply set the population size as 10 000.
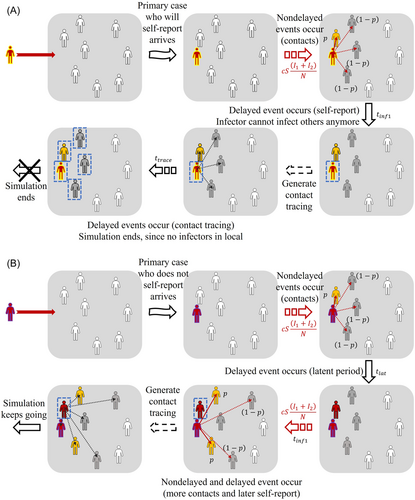
We also performed a statistical hypothesis test comparing two different scenarios to assess the significance of contact tracing time, and self-reporting of the primary case and infectees. Since it was observed that the number of infections does not follow the shape of a normal distribution, we performed the Wilcoxon signed-rank test.48 The null hypothesis is that two paired scenarios with different settings are the same, while the alternative hypothesis says that the two scenarios are different.
3 RESULTS
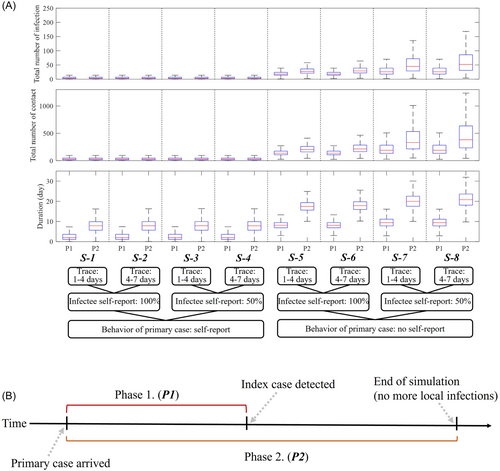
The different scenarios are labeled S-1–S-8, according to the setting of the simulation. The setting of each scenario and corresponding simulation results, illustrated as boxplots, are shown in Figure 3. Note that P1 and P2 denote the duration of the primary case arrival to index case detection and end of the simulation, respectively. Numerical results are summarized in Table 1.
| Time phase | Behavior of a primary case | Self-report rate of infected (%) | Contact tracing delay | Number of infections | Number of contacts | Duration (day) | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Median | 95% CI | Mean | Median | 95% CI | Mean | Median | 95% CI | ||||
| From primary case arrival to index case | Self-report | 100 | 1–4 day | 5 | 3 | (0–20) | 37.01 | 26 | (4–139) | 2.68 | 2 | (0.37–8.25) |
| 4–7 day | 5.01 | 3 | (0–20) | 37.05 | 26 | (4–138) | 2.69 | 2 | (0.37–8.28) | |||
| 50 | 1–4 day | 5.42 | 3 | (0–24) | 40.19 | 26 | (4–173) | 2.75 | 2 | (0.37–9.01) | ||
| 4–7 day | 5.44 | 3 | (0–24) | 40.27 | 26 | (4–175) | 2.76 | 2 | (0.36–9) | |||
| No self-report | 100 | 1–4 day | 19.67 | 18 | (8– 39) | 145.67 | 136 | (69–279) | 8.2 | 8 | (4.73–12.16) | |
| 4–7 day | 19.7 | 18 | (8– 39) | 145.96 | 136 | (69–279) | 8.21 | 8 | (4.75–12.15) | |||
| 50 | 1–4 day | 31.11 | 26 | (9– 83) | 230.26 | 191 | (77–605) | 9.58 | 9 | (5.24–14.68) | ||
| 4–7 day | 31.12 | 26 | (9– 82) | 230.33 | 192 | (77–603) | 9.58 | 9 | (5.25–14.62) | |||
| From primary case arrival to end of the simulation | Self-report | 100 | 1–4 day | 5.36 | 3 | (0–24) | 39.7 | 26 | (4–172) | 5.72 | 5 | (0.46–13.05) |
| 4–7 day | 5.56 | 3 | (0–27) | 41.14 | 26 | (4–192) | 8.53 | 8 | (0.46–17.78) | |||
| 50 | 1–4 day | 6.26 | 3 | (0–33) | 46.46 | 26 | (4–241) | 5.87 | 5 | (0.45–14.63) | ||
| 4–7 day | 7.3 | 3 | (0–46) | 54.09 | 26 | (4–331) | 8.86 | 8 | (0.46–20.97) | |||
| No self-report | 100 | 1–4 day | 26.66 | 24 | (11– 56) | 197.3 | 179 | (96–398) | 13.59 | 14 | (9.51–18.18) | |
| 4–7 day | 33.18 | 30 | (15– 67) | 245.72 | 223 | (134–481) | 19.65 | 20 | (15.88–23.98) | |||
| 50 | 1–4 day | 48.87 | 39 | (13–143) | 361.66 | 284 | (106–1051) | 15.64 | 15 | (10.15–22.07) | ||
| 4–7 day | 72.46 | 54 | (18–235) | 536.65 | 398 | (145–1734) | 22.37 | 22 | (16.52–30.12) | |||
- Abbreviation: CI, confidence interval.
We observe that if the primary case does not self-report (S-5–S-8), then the simulations are worse than in the scenarios where the primary case self-reports (S-1–S-4). The average number of infections, contacts, and duration from primary case arrival to the end of simulation for scenarios S-1–S-4 are 6.12, 45.35, and 7.25 days, respectively, which are 7.40, 7.39, and 2.46 times higher than those of scenarios S-5–S-8 (45.29, 333.33, and 17.81 days, respectively).
Considering the number of contacts per day and the probability of successful disease transmission, the expected number of infections per day is 1.72 (Number of contacts per day × probability of infection by contact). This means that in scenarios S-5–S-8, where the primary case is not the index case, the primary case would already have made dozens of secondary infections until the index case is detected, which takes (incubation period) + (duration from self-report to isolation) days. The average duration of P1 in scenarios S-1–S-4 is slightly less than 3 days since the primary case is most likely identical to the index case, while in S-5–S-8, it takes 8–10 days on average until the index case is detected.
Figure 4 shows the probability density of the total number of infections and contacts, and durations of P1 and P2 for scenarios S-1, S-4, S-5, and S-6. Scenario S-6 shows the worst outcome, with a 25% increase on the number of infections compared with S-5 as contact tracing was delayed longer. We observe skewed distributions for S-1 and S-4, suggesting that the outbreak which may result from these settings would most likely be on a small scale. The average number of infections until the end of the simulation in S-5 (26.66) is approximately four times higher than in S-1 or S-4 (5.36 or 7.3, respectively). Scenario S-4 shows a slightly higher average number of infections compared with S-1 due to the more delayed contact tracing.
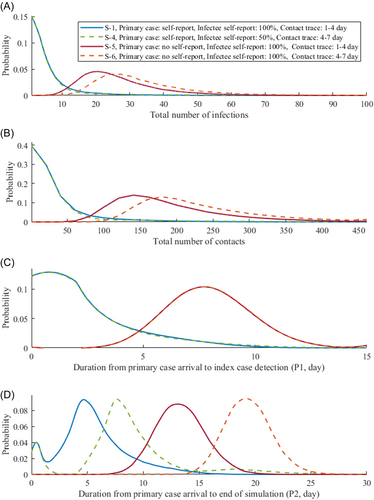
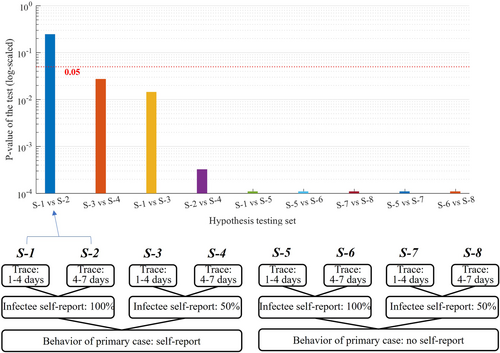
Figure 5 shows the results of the Wilcoxon signed-rank test. We observe that all the paired scenarios were significantly different, except for S-1 and S-2 (p-value: 0.25), in which all infected cases have been reported but with different values for the contact tracing delay (1–4 or 4–7 days). The p-values of the tests comparing S-3 and S-4, and S-1 and S-3 were second and third highest (0.03 and 0.01), respectively, but both are below significant level (0.05).
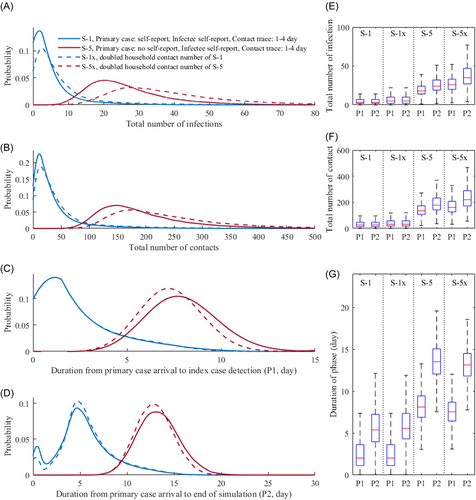
To investigate what happens if the average number of household contacts is higher, such as in a potential super-spreader event, we considered doubling the number of household contacts for scenarios S-1 and S-5. We denote these scenarios by S-1x and S-5x. The plots in Figure 6 show the simulation results. As the number of household contacts doubled from 3.20 to 6.41, the average number of contacts and probability of disease transmission through a contact increased to 15.94% and 15.87% (from 12.74% and 13.51%, respectively). The average number of infections and contacts in S-1x (S-5x), compared with S-1 (S-5), increased by 50.43% (44.96%) and 28.10% (23.35%), respectively. There were no significant changes in the durations of P1 and P2.
4 DISCUSSION
In Korea, the first monkeypox case had self-reported right after arrival.49 As a result, there were no recorded secondary infections, which would be similar to a “good” scenario (S-1–S-4) in our simulation setting. However, if the primary case was in the incubation stage and did not self-report after symptom onset, then hundreds of contacts and dozens of infections could be expected to have occurred in the local community once the index case was found. In this scenario, more efforts would have been needed to control the disease.
We observed that more cases occurred when contact tracing was delayed. The increment was small if the primary case self-reports, in which the average number of infections increased only by 11% (5.81–6.43) if contract tracing was delayed from 1–4 to 4–7 days. However, if the primary case does not self-report, then the difference is greater as the average number of infections increased by 40% (37.77–52.82). The statistical hypothesis test emphasized the importance of case finding (self-report of the primary case and secondary cases), as the result of the test showed that if all cases self-report, then the delay in contact tracing does not affect the outcome significantly.
We investigated the effects of doubling the number of household contacts per day (which can be referred to as close contact). The results illustrated in Figure 6 warn of the potential significant increase in the number of monkeypox infections when unreported initial cases have contact with more people, or if the community where the primary case belongs to has more close contacts.
This study focused on the early stage of an outbreak considering the behavior of the primary cases and infectees, and possible delay of contact tracing. This approach is more intuitive than a theoretical analysis and may guide healthcare authorities in the planning and management of possible monkeypox outbreaks in nonendemic countries. For instance, it was shown that the delay in the detection of the index case is related to the number of contacts made and knowing the scale of contact tracing efforts to be performed is crucial in managing workforce once the index case is found. In the simulations, we have used the average number of contacts per day suited for Korea, but this can easily be adapted to other countries' contact patterns. If the average household size is bigger or the number of contacts is more, then the probability of disease transmission increases.
There were limitations to our study. Contact tracing was applied to the model through a randomized sampling and not based on one's personal contacts. It is expected that using an individual-based network would realistically represent contact tracing and behavior (contact and self-report) of specific individuals. Also, we assumed that contact tracing is perfect, that is, all infectors are found if 100% coverage is in effect. The probability of successful infection after contact might be overestimated since the concept of contact from the cited literature might differ from the definition of contact used in this study.25 Finally, we did not consider sexual contact in this study due to the lack of data. These limitations can be considered in the next study.
5 CONCLUSION
In this study, the potential risk of monkeypox spread in a nonendemic country was studied using a stochastic model. We simulated outbreaks caused by a primary case that either self-reports or not and considered different coverage rates of contact tracing and self-reporting rates of infectees.
Stigma, which may result in an increase in hidden cases and negatively impact disease control, can be avoided by implementing evidence-based and rights-based approaches.13 Scientists have emphasized that knowledge about the epidemiology of the disease and awareness of its risks are important ways to prevent transmission.7, 14 Therefore, to encourage self-reporting, healthcare authorities must ensure confidentiality of confirmed cases and individuals under investigation, and access to health services. Moreover, prompt case finding and information campaigns must be conducted.
Our simulation results strongly emphasize the importance of border control to find the primary case. If the primary case self-reports, then despite having a low self-reporting rate of infectees and delayed contact tracing, the situation does not become worse compared with the scenarios where the primary case does not self-report (in Figure 3).
AUTHOR CONTRIBUTIONS
Eunok Jung acquired funding for this study. Youngsuk Ko, Jacob Lee, and Eunok Jung conceived and designed the study. Youngsuk Ko, Renier Mendoza, and Victoria May Mendoza analyzed the data and wrote the first draft. Eunok Jung, Jacob Lee, and Yubin Seo gave suggestions on improving the quality of the analysis and monitored the study progress. All authors contributed to the data collection, checking, and processing. All authors reviewed the final version of the manuscript. All authors read and approved the final manuscript.
ACKNOWLEDGMENT
This article is supported by the Korea National Research Foundation (NRF) grant funded by the Korean government (MEST) (NRF-2021M3E5E308120711). This paper is also supported by the Korea National Research Foundation (NRF) grant funded by the Korean government (MEST) (NRF-2021R1A2C100448711). We appreciate professor Jaekyoung Kim from the Korea Advanced Institute of Science & Technology for introducing Non-Markovian process during the Korean Society for Industrial and Applied Mathematics tutorial program. Thanks should also go to the Korean Society for Industrial and Applied Mathematics for organizing the tutorial program.
CONFLICT OF INTEREST
The authors declare no conflict of interest.
Open Research
DATA AVAILABILITY STATEMENT
No new data were generated or analyzed in support of this study.