Coverability of graph by three odd subgraphs

An odd graph is a graph whose vertex degrees are all odd. As introduced by Pyber in 1991, an odd edge-covering of graph 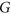is a family of odd subgraphs that cover its edges. The minimum size of such family is denoted by 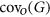. Answering a question raised by Pyber, Mátrai proved in 2006 that 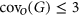for every simple graph 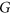. In this study, we characterize the same inequality for the class of loopless graphs by proving that, apart from four particular types of loopless graphs on three vertices, every other connected loopless graph admits an odd 3-edge-covering. Moreover, there exists such an edge-covering with at most two edges belonging to more than one subgraph and no edge to all three subgraphs. The latter part of this result implies an interesting consequence for the related notion of odd 3-edge-colorability. Our characterization presents a parity counterpart to the characterization of Matthews from 1978 concerning coverability of graph by three even subgraphs.