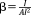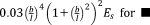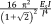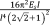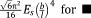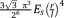Analytical relationships for prediction of the mechanical properties of additively manufactured porous biomaterials
This article was published online on 23 August 2016. An error was subsequently identified. This notice is included in the online and print versions to indicate that both have been corrected 01 September 2016.
Abstract
Recent developments in additive manufacturing techniques have motivated an increasing number of researchers to study regular porous biomaterials that are based on repeating unit cells. The physical and mechanical properties of such porous biomaterials have therefore received increasing attention during recent years. One of the areas that have revived is analytical study of the mechanical behavior of regular porous biomaterials with the aim of deriving analytical relationships that could predict the relative density and mechanical properties of porous biomaterials, given the design and dimensions of their repeating unit cells. In this article, we review the analytical relationships that have been presented in the literature for predicting the relative density, elastic modulus, Poisson's ratio, yield stress, and buckling limit of regular porous structures based on various types of unit cells. The reviewed analytical relationships are used to compare the mechanical properties of porous biomaterials based on different types of unit cells. The major areas where the analytical relationships have improved during the recent years are discussed and suggestions are made for future research directions. © 2016 Wiley Periodicals, Inc. J Biomed Mater Res Part A: 104A: 3164–3174, 2016.
INTRODUCTION
Porous biomaterials that have arbitrarily complex and precisely controlled porous microarchitectures have been the center of attention of an increasing number of scientists during the last few years. That is partly due to the emergence and maturation of several 3D printing and additive manufacturing technologies in the last few years that are capable of manufacturing arbitrarily complex microarchitectures with unprecedented accuracy. Given the fact that almost any microarchitecture is now possible to manufacture, the next natural question to ask is “how can biomaterials performance benefit from this increased flexibility in manufacturing of complex micro-architectures?” Probably one of the most important points to consider when answering this question is the fact that the physical1, biological2, and mechanical3-7 properties of porous biomaterials are functions of their microarchitecture. It may therefore be possible to obtain the optimal combination of physical, biological, and mechanical properties through rational design of the microarchitecture of porous biomaterials. To answer the aforementioned question, one may therefore need to study the shape–property relationships that describe the relationship between the microarchitecture of porous biomaterials and the various types of their properties.
Mechanical properties of regular porous biomaterials including both static8-12 and fatigue13-15 properties are shown to be strongly dependent on the microarchitecture of the porous structure including the type of repeating unit cell and its dimensions. One could therefore change both the type of unit cell and the dimensions of the unit cell to obtain the mechanical properties that optimize the performance of the biomaterial. In most cases, optimizing the performance of porous biomaterials translates to maximizing the volume and quality of the regenerated tissue. The mechanical properties of porous scaffolds play important roles in regulating their tissue regeneration performance. On one hand, the porous biomaterials should be strong enough to support the regeneration of the tissue. On the other hand, they should not be over stiff, because that would result in shielding the regenerating tissue from the mechanical load that is essential for its regeneration.
Optimal design of porous biomaterials requires tools that could be used to predict the mechanical properties resulting from any given set of design parameters. As previously mentioned, the design parameters include the type of the repeating unit cell and the dimensions of the unit cell. The dimensions of the repeating unit cell determine the properties of the porous structure such as porosity, pore size, strut diameter, and so forth. There are three approaches that could be used for predicting the mechanical properties of porous biomaterials, given the aforementioned design parameters, namely, experimental, computational, and analytical. The experimental approach is probably the most accurate approach but requires manufacturing and mechanical testing of a large number of specimens. This might be feasible for testing the final optimized design but is unfeasible for the design optimization process, where a large number of alternative designs may need to be evaluated. The computational and analytical approaches do not require manufacturing and mechanical testing of a large number of samples and, are therefore suitable for the design optimization process. The advantage of the computational approach as compared to the analytical one is the possibility to create models that better represent the actual porous biomaterials. For example, the imperfections caused by the manufacturing process could be implemented in computational models16, whereas they cannot be easily accounted for in the analytical approach. However, analytical solutions are much simpler to use, as no computational models need to be built. Moreover, it takes very little time (e.g., a fraction of a second) to calculate the mechanical properties using an analytical equation. This significantly reduced lead-time and computation times are particularly important when the mechanical properties of porous biomaterial are optimized together with the other types of their properties such as physical and biological properties. In those multiobjective optimal design problems, the mechanical properties of many thousands of alternative designs need to be evaluated by the optimization algorithm.
Given the aforementioned advantages and the ease of use of analytical equations, researchers have been developing relationships for predicting the mechanical properties of porous structures. The first of those analytical relationships appeared several decades ago, but the number of unit cells for which analytical solutions were available was limited unit recently. That was partly due to the fact that not many unit cell types could be manufactured using the conventional foam-making technologies. Given the seemingly unlimited manufacturing possibilities offered by additive manufacturing during recent years, researchers have been increasingly motivated to develop analytical relationships for many more types of repeating unit cells (Fig. 1). It is therefore a good time to review the analytical relationships that are available in the literature. In most cases, these analytical relationships predict the relative density, elastic properties, and yield stress of the porous structures given the type and dimensions of the unit cell and the mechanical properties of the parent material. In the rest of this article, we will first briefly review the porous biomaterials and their advantages. Then, we will review the analytical relationships that are available in the literature for different types of unit cells. The article concludes with a section where the applicability of the reviewed analytical relationships and limitations of the analytical approach are discussed and suggestions are made for future research.
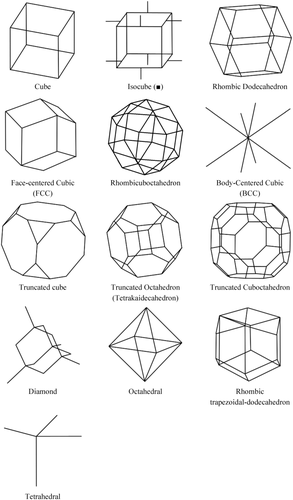
Different unit-cell types reviewed in this article.
ADDITIVELY MANUFACTURED POROUS BIOMATERIALS
Perhaps the largest difference between additive manufacturing techniques and other techniques for production of porous biomaterials is the ability to precisely control the microarchitecture of the fabricated porous biomaterials. It is within this context that the design and study of highly regular porous structures based on repeating unit cells start to make sense. Using additive manufacturing, it is possible to manufacture complex porous structures with varying unit cells, for example, to create functionally graded porous biomaterials or multiregion porous biomaterials where the microarchitecture of the porous structures changes from one region to another. It is, nevertheless, important to first study highly regular porous structures with one single repeating unit cell, because systematic study of porous biomaterials consisting of one single repeating unit cell could provide information that is at least partially applicable to more complex constructions particularly when those constructions are made from sufficiently large regions with one single-unit type of repeating unit cell. Most studies in the literature have therefore focused on porous structures that are made from one single type of repeating unit cell.
As far as porous biomaterials are concerned, most applications require open-pore structures to allow for transport of oxygen, nutrients, and waste within the biomaterial. The unit cell is often chosen to be some type of polyhedron. To make the entire porous structure from the same type of polyhedron unit cell, the polyhedron should be space-filling17, meaning that it should be possible to tessellate the three-dimensional space with that unit cell or, in simple terms, it should be possible to cover the entire three-dimensional space by repeating the unit cell in different directions. Space-filling polyhedral have been studied by mathematicians. As nicely summarized by Weisstein18 based on a number of studies19-21, space-filling convex polyhedra with regular faces are limited to five including cube, triangular prism, hexagonal prism, truncated octahedron, and gyrobifastigium. The same source puts the number of space-filling hexahedra, heptahedra, and octahedral, respectively, at 27, 34, and 49 based on the research performed by Michael Goldberg during the 1974–1980 period18. There are many more space-filling polyhedra with larger number of faces18. However, the practical importance of the space-filling polyhedra decreases as the number of faces increases. That is because additive manufacturing of porous biomaterials based on unit cells with a large number of faces becomes increasingly more challenging without necessarily yielding clear practical advantages.
Analytical relationships have been derived for estimating the mechanical properties of porous biomaterials made from a number of these space-filling polyhdera (Fig. 1). The repeating unit cells that could be used for constructing porous biomaterials are, however, not limited to these structures and many more polyhedral with less regular geometries could be used for constructing open-pore porous structures.
Even though the microarchitecture of porous biomaterials can be accurately controlled with additive manufacturing techniques, there are imperfections in what is ultimately produced. These manufacturing imperfections have been shown to significantly influence the mechanical behavior of porous biomaterials and generally result in decreased stiffness due to weak spots within which strain could localize16. This is comparable with the effects of imperfections22, 23 in limiting the deformability of other materials such as those caused by machining imperfections24. However, the microarchitecture of porous structures is almost always considered perfect when deriving analytical relationships because it is much more difficult to derive analytical relationships for imperfect porous structures.
ANALYTICAL RELATIONSHIPS
Based on the assumptions presented in the previous sections, the problem of deriving analytical relationships for estimating the mechanical properties of porous biomaterials is reduced to the study of the mechanical behavior of highly regular fully interconnected porous structures with one single repeating unit cell (Fig. 1) that is repeated in all directions and consists of struts with a uniform cross-section all over their lengths. For most relevant applications of such biomaterials, relatively large porosities and small densities are needed to ensure mass transport through these structures. The representative dimension of the cross-section (e.g., the diameter in circular cross-sections) of struts should therefore be relatively small and often much smaller than the length of struts. Under such assumptions, it is natural to use the beam theory to derive the analytical relationships. The Euler–Bernoulli and Timoshenko beam theories are the most widely used beam theories for estimation of analytical relationships applicable to porous biomaterials. Up until recent years, the vast majority of studies used the Euler–Bernoulli beam theory, which neglects the shear terms and assumes the cross-section of the beam to remain perpendicular to the bending line. The neglected terms are of limited importance for highly slender struts but become increasingly relevant as the density of the structure increases.
To derive analytical relationship for any given porous structure with infinite dimensions, one could simply study the deformations of one single-unit cell with periodic boundary conditions. In practice, the periodic boundary conditions could be interpreted as specific symmetries that impose constraints to the deformation of the various degrees of freedom of the involved beams25.
RELATIVE DENSITY
The simplest analytical relationships that could be obtained for porous structures are those aimed at estimating the relative density of the porous biomaterials given the dimensions of the unit cell (e.g., the length and diameter of struts). The volume occupied by a single-unit cell,
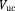 , is first calculated. Only a part of that entire volume is occupied by the struts constituting the unit cell, which is then calculated by summing up the volume of all struts of the unit cell. The total volume of the struts is then divided by the total volume of the unit cell to calculate the relative density of the porous structure. The analytical relationships presented in different studies for predicting the relative density of porous structures with various types of repeating unit cells are presented in Table 1.
, is first calculated. Only a part of that entire volume is occupied by the struts constituting the unit cell, which is then calculated by summing up the volume of all struts of the unit cell. The total volume of the struts is then divided by the total volume of the unit cell to calculate the relative density of the porous structure. The analytical relationships presented in different studies for predicting the relative density of porous structures with various types of repeating unit cells are presented in Table 1.
| Circular Cross-Section (Approximate) | Circular Cross-Section (Exact) | Other Cross-Sections | |
|---|---|---|---|
| Cube62 |
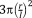 |
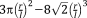 |
▲ ▪ |
| Isocube63 |
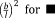 |
- | |
| Rhombicuboctahedron25 |
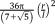 |
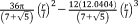 |
▲ ▪ |
| Truncated cube62 |
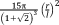 |
- |
▲ ▪ |
| Truncated cuboctahedron36 |
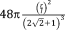 |
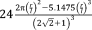 |
▲ ▪ |
| Octahedral64 |
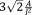 |
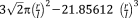 |
▲ ▪ |
| Rhombic dodecahedron26 |
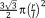 |
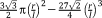 |
▲ ▪ |
| Body-centered cubic (BCC)65 |
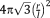 |
- | - |
| Truncated octahedron (Tetrakaidecahedron)26 |
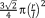 |
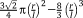 |
▲ ▪ |
| Diamond26 |
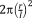 |
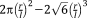 |
▲ ▪ |
The aforementioned approach suffers from one fundamental problem. The beams are not actually one-dimensional lines and occupy space in reality. At the intersection of struts, the volumes of different intersecting struts overlap, meaning that intersecting struts share part of their volume (Fig. 2). In other words, the aforementioned approach for calculating the relative density of porous structures overestimates the relative density due to multiple counting of this shared volume. The importance of this issue was not realized unit recently26, where it was shown that multiple counting could result in significant deviation of analytical solutions from numerical results and experimental observations. Those deviations were minimized when multiple counting was corrected26. When comparing the mechanical properties of the porous structures with each other, we have used both approximate (i.e., uncorrected) (Fig. 3) and exact (i.e., exact) (Fig. 4) values of relative density to demonstrate the importance of this correction in obtaining more accurate mechanical properties.
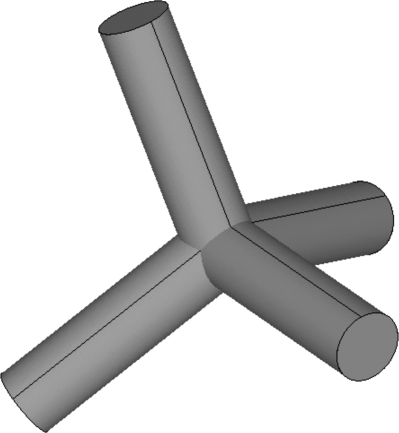
Overlapping of 4 struts at their intersection.
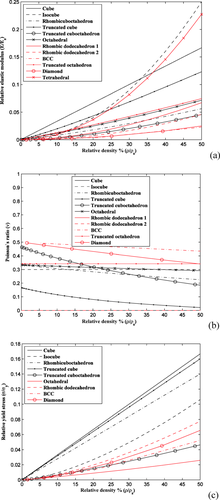
Comparison of (a) relative elastic modulus, (b) Poisson's ratio, and (c) relative yield stress of open-cell structures with different microgeometries (approximate density).
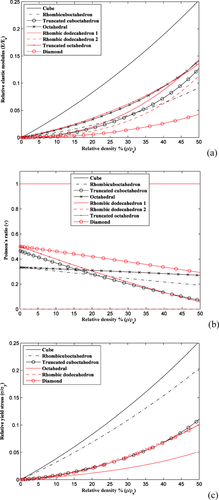
Comparison of (a) relative elastic modulus, (b) Poisson's ratio, and (c) relative yield stress of open-cell structures with different microgeometries (exact density).
ELASTIC MODULUS
The displacement of the unit cell under an applied force is used to derive the analytical relationships that describe the elastic modulus and other properties of porous structures. Depending on the type of the repeating unit cell, the porous structure may be isotropic or anisotropic. To derive the elastic modulus as well as other properties of anisotropic porous structures, loads should be separately applied in all relevant directions of anisotropy and the response of the porous structure to the applied loads should be studied separately in every direction. Different analytical relationships will then be obtained for elastic moduli in different directions. As far as porous biomaterials are concerned, compression is the most widely used mode of loading particularly when porous biomaterials are aimed for application as bone substituting biomaterials. Loading is primarily in compression in such applications.
Two primary approaches could be used for determining the response of the unit cell to an applied load. In the first approach, the governing equations of the deformation of individual beams are written while simultaneously considering all the possible loads and displacements. The advantage of this approach is that it may require relatively few steps when deriving the analytical relationships of simpler unit cells. A number of studies16, 27-32 have used the direct approach. The disadvantage of the direct approach is that it quickly becomes complex and error-prone for more complex unit cells. In the second approach, the superposition principle is used to derive the stiffness matrix of the porous structure. To apply the superposition principle, each degree of freedom of the unit cell is displaced by unity while keeping all other degrees of freedom unchanged. The loads needed for imposing such a displacement are then calculated using the equations of the applied beam theory. The relationships between that load and displacement are then used to form one column of the stiffness matrix corresponding to that particular degree of freedom. By repeating the same procedure for all the degrees of freedom of the unit cell, the entire stiffness matrix can be obtained which can then be inverted to calculate the effective mechanical properties of the porous structures as explained below. This is a very systematic approach that minimizes the risk of errors and has been used for deriving the analytical relationships of unit cells with up to 15 degrees of freedom. Table 2 presents an overview of the analytical relationships obtained in different studies for estimating the effective elastic modulus of porous structures with various types of repeating unit cells.
| Circular Cross-Section | Other Cross-Sections | Unequal Strut Lengths | |
|---|---|---|---|
| Cube62 |
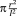 |
▲ ▪ |
Not applicable |
| Isocube63 |
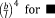 |
- | Not applicable |
| Rhombicuboctahedron25 |
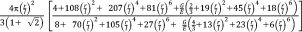 |
▲ ▪ |
Yes |
| Truncated cube62 |
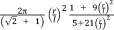 |
▲ ▪ |
Yes |
| Truncated cuboctahedron36 |
|
▲ ▪ |
Not applicable |
| Octahedral64 |
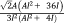 |
▲ ▪ |
Not applicable |
| Rhombic dodecahedron16, 27 |
|
- | No |
| Face-centered cubic (FCC)- rhombic dodecahedron28 |
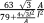 |
▲ ▪ |
No |
| Body-centered cubic (BCC)65 |
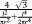 |
- | Yes |
| Truncated octahedron (Tetrakaidecahedron)29 |
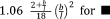 |
▲ [66] | No |
| Diamond30 |
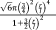 |
▲ ▪ |
Not applicable |
| Rhombic trapezoidal-dodecahedron28 |
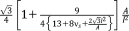 |
▲ ▪ |
No |
| Tetrahedral31, 32 |
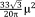 |
▲ ▪ |
No |
Comparison between the elastic moduli obtained for various types of unit cells (Table 1) shows that the elastic modulus could largely vary between porous structures based on different types of unit cells even when the relevant density is the same (Figs. 3 and 4). This highlights the importance of having access to a library of unit cells with known mechanical properties, so that the mechanical properties could be adjusted independent from other morphometric parameters of the unit cell such as porosity. In addition, it is clear that the use of exact values of apparent density (compare Figs. 3 and 4) could significantly influence the obtained mechanical properties. It is therefore important to make sure the exact values of relative density are obtained when deriving analytical relationships that describe property–density relationship of porous biomaterials. Finally, for the few structures where both Euler–Bernoulli and Timoshenko beam theories are used for deriving the analytical relationships, there is potentially large difference between both theories particularly for larger values of relevant density (Fig. 5). That is because the shear terms neglected in the Euler–Bernoulli beam theory play increasingly important role in the deformation of porous structure, as the relative density of the porous structures increases. This highlights the importance of using the Timoshenko beam theory for deriving the analytical relationships, whenever possible (Table 3).
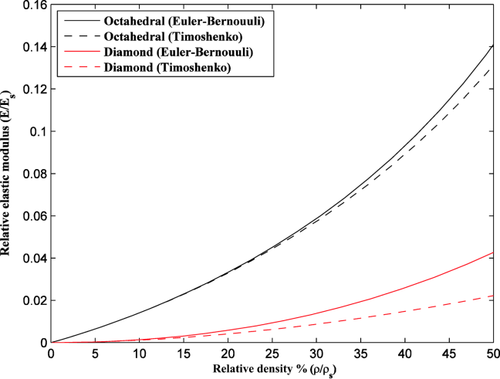
Comparison of predicted relative elastic modulus of open-cell structures by Euler–Bernoulli and Timoshenko beam theories for octahedral and diamond unit cells.
POISSON'S RATIO
Once the response of the porous structure to the applied force is determined (see the previous section), it is relatively straightforward to calculate the Poisson's ratio and other mechanical properties of the porous structure. As for the Poisson's ratio, it is sufficient to divide the lateral deformation of the porous structure by the axial deformation. Table 4 presents an overview of the analytical relationships presented in the literature for calculating the Poisson's ratio of various porous structures.
| Circular Cross-Section | Other Cross-Sections | Unequal Strut Lengths | |
|---|---|---|---|
| Cube62 | 0 |
▲ ▪ |
NA |
| Isocube63 | 0.3 for ▪ | - | NA |
| Rhombicuboctahedron25 |
 |
▲ ▪ |
Yes |
| Truncated cube62 |
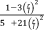 |
▲ ▪ |
Yes |
| Truncated Cuboctahedron36 |
|
▲ ▪ |
NA |
| Octahedral64 |
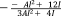 |
▲ ▪ |
NA |
| Rhombic Dodecahedron16, 27 |
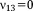 , ,
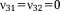 , ,
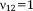 |
- | No |
| Face-centered cubic (FCC)- Rhombic dodecahedron28 |
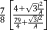 |
▲ ▪ |
No |
| Body-centered cubic (BCC)65 |
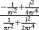 |
- | Yes |
| Truncated Octahedron (Tetrakaidecahedron)66 |
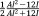 |
▲ ▪ |
NA |
| Diamond30 |
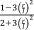 |
▲ ▪ |
NA |
| Rhombic trapezoidal-dodecahedron28 |
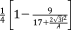 |
▲ ▪ |
No |
An important observation regarding the Poisson's ratio is that the use of correct type of beam theory could be very important for accurate description of the mechanical behavior of porous structures. Most importantly, the Euler–Bernoulli beam theory predicts negative values of the Poisson's ratio for specific ranges of relative density of certain unit cells. Materials with negative values of the Poisson's ratio called auxetic materials and have important applications in various areas of research33-35. It is therefore important to know the exact values of the Poisson's ratio of porous biomaterials. Comparison of the values of the Poisson's ratio obtained using the Euler–Bernoulli theory with those obtained using the Timoshenko theory and numerical simulations shows that neglecting the shear terms might result in inaccurate values of the Poisson's ratio and false prediction of auxetic behavior in porous structures that are actually not auxetic (see for example Fig. 18 in Ref. 25).
YIELD STRESS
A porous structure is assumed to have yielded once the maximum stress in the repeating unit cell has reached the yield stress of the bulk material from which the struts are made. Given that the stress values of the beams could be simply obtained from the analytical relationships obtained in the previous steps, the most important issue is determining which struts experiences the maximum stress. In some unit cells, this is relatively easy to determine while this is not very clear in some other unit cells. Numerical analysis is sometimes performed to determine which struts is experiencing the maximum stress36. It is, however, important to realize that there is no guarantee that the same strut experiences the maximum stress for all relevant dimensions of the unit cell and all porosity values. It is therefore essential that numerical simulations are performed for a wide range of geometrical dimensions and porosity values to ascertain the chosen struts are, indeed, the most stressed struts in all relevant conditions. The analytical relationships obtained for the yield stress are listed in Table 5.
| Circular Cross-Section | Other Cross-Sections | Unequal Strut Lengths | |
|---|---|---|---|
| Cube62 |
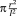 |
▲ ▪ |
NA |
| Isocube63 |
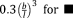 |
- | NA |
| Rhombicuboctahedron25 |
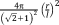 |
▲ ▪ |
Yes |
| Truncated cube62 |
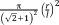 |
▲ ▪ |
Yes |
| Truncated Cuboctahedron36 | Lengthy (see appendix) |
▲ ▪ |
NA |
| Octahedral64 |
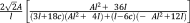 |
▲ ▪ |
NA |
|
Rhombic Dodecahedron67 |
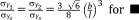 |
- | No |
| Body-centered cubic (BCC)68 |
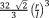 |
- | No |
| Diamond30 |
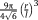 |
▲ ▪ |
NA |
BUCKLING LIMIT
Similar to the yield stress, one needs to determine which strut of the unit cell is most susceptible to buckling to calculate the buckling limit of a regular porous structure. The buckling limit of that strut can then be calculated using the Euler formula for stability analysis and applying the correct boundary conditions considering the symmetries and constrains imposed by the periodicity of the porous structure. Table 6 presents an overview of the buckling limits of the porous structures with different repeating unit cells that have been studied in the literature.
One important question regarding the failure of porous structures is whether yielding or buckling occurs first. By dividing the analytical relationships obtained for the buckling stress with those for the yield stress, one could plot the ratio of those stresses for the various types of porous structures studied in the literature (Fig. 6). According to such calculations, for all cases where analytical relationships for predicting both yield stress and buckling stress are available, the buckling stress is several times larger than the yield stress (Fig. 6). The only exceptions are extremely small relative densities for which the buckling stress may be smaller than the yield stress. These extremely small relative densities have limited biomedical applications. It can be therefore concluded that it is for most practical applications of porous biomaterials, yielding precedes buckling.
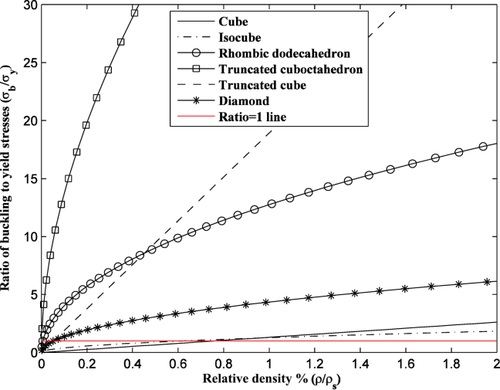
Comparison of ratio of buckling stress to yield stress of open-cell structures with different microgeometries.
DISCUSSION
The recent advances in additive manufacturing technologies have motivated renewed interest in derivation of analytical relationships that could be used to estimate the mechanical properties of regular porous structures. Because of this renewed interest, a number of developments have occurred during the last few years. First, analytical relationships are derived for a large number of unit cells that could not be easily manufactured using conventional manufacturing techniques but are now accessible thanks to additive manufacturing technologies. Second, the Timoshenko beam theory is increasingly used for derivation of the analytical relationships. Finally, it has become clear that mass multiple counting could result in significant inaccuracies that could be overcome by excluding the multiple-counted mass from the relationships used for calculating the relative density of porous structures.
Thanks to the three aforementioned developments, much more accurate estimations of the mechanical properties of a wider range of regular porous structures are now possible using analytical relationships. This has a number of practical consequences for the study and design of porous biomaterials. Comparison between regular porous structures based on different types of unit cells (Figs. 3 and 4) shows that the mechanical properties of these porous structures could widely differ depending on the type of repeating unit cell even for the same porosity values. Analytical relationships are particularly useful to understand the difference between the deformation mechanisms of all types of regular porous structures, because individual terms of the analytical relationships could be traced back to specific types of deformation of the unit cells. Moreover, the differences between the mechanical properties of porous structures that are based on different types of unit cells expand the parameter space and loosen the constraints that need to be applied when designing optimal porous biomaterials. For example, it may be desirable to keep the pore size or porosity constant throughout a multiregion porous structure to ensure proper oxygenation and nutrition of cells that invade the porous structure, either in the lab or when the porous biomaterial is implanted in the human body. At the same time, it is often desirable to optimize the distribution of the mechanical properties throughout the volume of the implant. Using porous biomaterials with various types of repeating unit cells would allow us to simultaneously satisfy both requirements.
Analytical relationships presented here could be used for fast estimation of the mechanical properties of the different zones of the multizone porous structures. Fast estimation of the mechanical properties of different zones is particularly important when the distribution of mechanical properties is optimized using iterative optimization algorithms that require many iterations. Furthermore, the optimization algorithm may have an objective function that consists of the distribution of not only mechanical properties but also mass transport properties such as permeability and diffusivity. Alleviating the computational burden of calculating the mechanical properties will leave more computational power for estimating the other physical properties that could not be calculated using analytical relationships and, thus, require more computational resources.
Despite recent advances, there are still multiple areas that require further research. First, it is desirable to take the irregularities caused by the additive manufacturing process into account when deriving the analytical relationships. This could further increase the accuracy of analytical relationships16, but is associated with increased technical difficulty because stochastic processes that simulate creation of irregularities during the additive manufacturing need to be analytically modeled. Second, analytical relationships that currently cover the elastic range of deformations need to be extended to include larger deformations that lead to failure of porous structures. Use of advanced failure prediction theories similar to the ones used for predicting the failure of engineering materials37-41 would be particularly enlightening. Third, full-field strain measurement techniques such as digital image correlation42-46 should be used to validate the predictions of the analytical relationships at the strut level and to see where do the largest differences between the analytical predictions and experimental observations originate from. Finally, more complex loading scenarios should be used in addition to simple compression to evaluate the mechanical behavior of porous biomaterials under more realistic loading conditions. More realistic loading conditions could be obtained using either large-scale musculoskeletal models47-50 or at least mass-spring-damper models51-54 that simulate the behavior of the human body during specific physical activities such as running or walking. Extending the analytical relationships in the aforementioned directions will further enhance the value of such relationships in practical applications that require rational design of porous biomaterials. Examples of such applications include bone substitution, bone tissue regeneration, and implant design.
The analytical relationships used for estimating the mechanical properties of regular porous biomaterials based on various types of repeating unit cells were reviewed in this article. Direct estimation of mechanical properties given the geometry and dimensions of the unit cell can be both replaced by and complemented by the use of computational techniques such as homogenization and (topology) optimization55-59. While homogenization techniques could be used for estimation of the mechanical properties of regular and irregular porous biomaterials, topology optimization methods could be instrumental in optimal design of the ultrastructure of porous biomaterials. A combined approach to the design of additively manufactured porous biomaterials based on combination of analytical relationships and computational techniques will be particularly welcome possibly in combination with theoretical models that could be used for simulating bone tissue fracture healing60 and adaptation61.
Even though we primarily focused on biomedical applications of regular porous structures, the analytical relationships reviewed here have many more applications in other areas of research. The recent advances in derivation of more accurate analytical relationships for an increasing number of unit cells and some of the suggested ideas for future research may therefore have much wider implications in other industries, where structural properties of porous structures are of interest including the automotive and aircraft industries.
CONCLUSIONS
Analytical relationships that have been proposed for predicting the relative density and mechanical properties of regular porous biomaterials were reviewed in this article. From the reviewed literature, it is clear that the recent years have seen a surge of interest in the mechanical properties of regular porous biomaterials largely fueled by the recent advances in additive manufacturing technologies. As a result of those recent studies, the accuracy of the available analytical relationships has improved. Using the Timoshenko beam theory for deriving the analytical relationships and correcting for the mass shared by multiple struts have been the major ways through which the accuracy of the analytical relationships has been improved. Moreover, analytical relationships have been derived for a larger number of unit cells for which no analytical relationships existed in the past. Several areas of interest for future research were also identified and discussed in the article. Widespread availability of additive manufacturing techniques, decreasing production cost, expansion of biomaterials that could be processed using additive manufacturing, and enhancement in flexibility and reliability of additive manufacturing techniques are all reasons to expect continued interest in regular porous biomaterials for years to come. It is therefore expected that more research is needed for deriving accurate and broadly applicable analytical relationships that could be used for fast and cost-effective design of (optimal) porous biomaterials.
Nomenclature
-
- r
-
- Radius of the struts, m
-
- l
-
- Length of the struts, m
-
- A
-
- Cross-sectional area of the struts, m2
-
- θ
-
- One of the main angles of rhombus faces in a rhombic dodecahedron unit cell, °
-
- b
-
- Side dimension of the strut, m
-
- c
-
- Distance between the neutral plane and the farthest portion of the beam cross-section, m
-
- μ
-
- Relative density, dimensionless
-
- κ
-
- Shear coefficient factor, dimensionless
-
- I, J
-
- Second moment of area, m4
-
- Es
-
- Elastic modulus of the bulk material, Pa
-
- E
-
- Elastic modulus of the unit cell, Pa
-
- Gs
-
- Shear modulus of the bulk material, Pa
-
- νs
-
- Poisson's ratio of the bulk material, dimensionless
-
- σY
-
- Yield stress of the porous structure, Pa
-
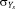
-
- Yield stress of the bulk material, Pa
-
- Subscripts 1, 2, and 3
-
- Representatives of first, second, and third main directions of unit cell, respectively
-
- Subscript s
-
- Representative of solid (bulk) material



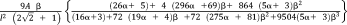 with
with
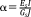 and
and
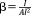
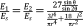
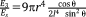 with
with
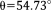
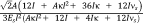
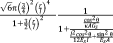
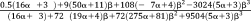 with
with
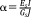 and
and