The cyclicality of R&D investment revisited
Summary
In Fabrizio and Tsolmon (Review of Economics and Statistics, 2014, 96(4), 662–675) and Barlevy (American Economic Review, 2007, 97(4), 1131–1164) it was concluded that R&D investments are procyclical. Fabrizio and Tsolmon utilized a model based on Barlevy, but it differed in some respects and allowed for more heterogeneity. However, we doubt whether their implied trends are intended. Fabrizio and Tsolmon also set missing values for R&D equal to zero, leading to unrealistic jumps in investment and its first differences. We reconcile and replicate both the Fabrizio and Tsolmon and Barlevy papers by considering extensions that encompass both models. Furthermore, we treat missing values more appropriately and consider some alternative specifications to check the robustness of the results. Procyclicality is confirmed, but we find much less heterogeneity than Fabrizio and Tsolmon did. In particular, obsolescence and patent effectiveness are no longer important but external financing is.
1 INTRODUCTION
The relation between research & development investments (R&D) and the business cycle has been studied in a large number of papers. From a theoretical point of view, Schumpeter (1939) argued that investments in innovation were countercyclical since the opportunity costs in times of a recession were lower than in an upswing. Empirical evidence on the relation between R&D and economic growth, however, suggests procyclicality. Fabrizio and Tsolmon (2014), henceforth denoted by FT, listed many references that concluded that there was a positive relation between R&D and industry output growth. From a theoretical point of view, Francois and Lloyd-Ellis (2009) reconciled Schumpeter's theory with the empirical findings by pointing out that innovation was more than only R&D and that other innovative activities might exhibit different business cycle properties. On the other hand, if we look at the empirical literature the evidence is much more heterogeneous than pointing only at procyclicality. For example, Aghion, Askenazy, Berman, Cette, and Eymard (2012) allowed for heterogeneous impacts of the business cycle and found mixed results, whereas Kraiczy, Hack, and Kellermanns (2015), for example, found no relation between R&D and the business cycle. On closer inspection, FT also found mixed effects: Although for most firms procyclical R&D investments are estimated, for some firms countercyclical R&D investments are found. Because in FT the marginal effects depend on (i) the levels of patent protection, (ii) the rate of product obsolescence, and (iii) the degree of external financing, cyclicality is heterogeneous.
There are several reasons why such ambiguous results are found. In general it can be stated that none of the studies above use the same model. Differences can be found in the definition of the dependent variable (R&D, log(R&D), yes or no R&D, etc.), differences in the covariates (none, only lags, lags and leads, firm characteristics, etc.), and functional form (linear, nonlinear). Furthermore, the character of the data (time series, cross-section, panel) and the estimation method (random effects, fixed effects, ignoring the panel character) can differ. In this investigation we will compare the methods used in two related papers to establish whether the conclusions of the papers hold in different settings. We will analyze the research of FT more deeply and compare it with Barlevy (2007). FT starts from the model used by Barlevy and allows for the effect of output growth to be different across the levels of patent protection, product obsolescence, and external financing of the industry that the firm belongs to experiences. Apart from using a different data set, FT also use a different, but related, estimation technique and use controls that are different in one important aspect: They use first-differenced explanatory variables instead of level variables in their specification. To make the analysis comparable we will estimate the model of Barlevy and extend it according to the suggestions of FT using the same data and the same estimation method. The results are in Section 2. In Section 3, we improve on the treatment of missing values of R&D expenditures, and reestimate the models to see whether the conclusions are robust. In Section 4 we discuss some related models and specifications, and Section 5 concludes.
2 THE MODELS OF FABRIZIO AND TSOLMON 2014 AND BARLEVY 2007
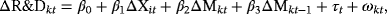 (1)
(1)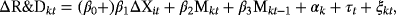 (2)
(2)Cyclicality of R&D expenditure is represented by a nonzero effect of industry output (growth): β1 ≠ 0. Procyclicality would be represented by β1 > 0 and countercyclicality by β1 < 0.
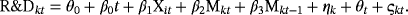 (3)
(3)First differencing this model gives Model 1 with τt = θt − θt − 1 and ωkt = ςkt − ςkt − 1. Note that first differencing takes care of the potential endogeneity due to the correlation between the firm-specific effect ηk and Xit and/or Mkt, and that ηk creates autocorrelation for sure and quite likely creates heteroskedasticity. If we compare the models in Equations 1-3, they are clearly related and Model 2 seems to be a special mix of Models 1 and 3. It allows for what is known as incidental trends (αk), whereas Model 1 does not.
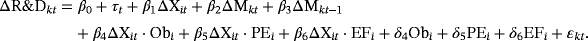 (4)
(4)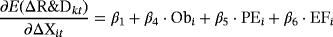
The meaning of δ4, δ5, and δ6 becomes clear if we reformulate Model 4 in level variables. As in the case of the added constant, adding the time constant variables to a first-difference specification gives rise to a trend in the level variable. In the present case, there is not only a pure time trend β0·t but also three heterogeneous incidental time trends: δ4·Obi·t , δ5·PEi·t and δ6·EFi·t. This specification can be correct, but FT do not provide theoretical or empirical arguments why adding these variables to the specification is a good idea. On top of that, the effects of these variables are only identified if no incidental trends are present. If we would actually follow the estimation method of Barlevy (2007)—that is, using a fixed-effects estimation—we would allow for firm-specific effects in Equation 1 which might potentially be correlated with the explanatory variables of Equation 1. If there is indeed correlation, then pooled OLS is not the correct estimation method to use, and a fixed-effects or first-difference estimation will not identify the constant and the parameters of Obi, PEi and EFi. Consequently, the estimation results of FT are only correct under the additional assumption of no incidental trends that Barlevy does not make.
We will now proceed with a replication of the estimation results of FT. In the next section we present estimation results of some alternative models that are less deviant from Barlevy (2007) to investigate whether the results of FT hold under less restrictive assumptions and alternative specifications.
2.1 Data
FT combine four different US data sources. 2The Compustat data provide annual information on individual firms over the period 1975–2002. This information is matched to industry-level information from the NBER Manufacturing and Productivity Data and the Carnegie Mellon survey. The Carnegie Mellon survey is a cross-section from 1994 and provides indicators of the explanatory variables' patent effectiveness and obsolescence.
The growth in R&D expenditures of a firm, measured by ΔR&Dkt, is related to the growth of the output of the industry the firm belongs to and a large number of controls: They include growth rates of cash flow, total assets, liabilities, debt, and capital stock, among others. Very similar specifications are used in Barlevy (2007) and Ouyang (2011), for example. The contribution of FT is to allow for additional heterogeneity of the effect of industrial output growth on R&D expenditures. They argue that the cyclicality of R&D investments is influenced by some characteristics of the industry: the degree of patent effectiveness, obsolescence and external financing. Patent effectiveness is measured as the average (across industry) survey response on the question of the percentage of products and process innovations for which patenting was effective in protecting the firm's competitive advantage. The obsolescence indicator is distilled from the results to the question in the Carnegie Mellon survey on the speed with which new product and process innovations are introduced in the focal industry. The external financing indicator is taken from the Compustat data by summing the annual external funds needed to finance the investments of each firm over the sample years 1975–2002 and dividing it by the firm's total capital expenditures. This is then transformed to an industry-level variable by using the median across the industry. The growth of the industry output is calculated from the NBER Manufacturing and Productivity Data by calculating the first difference in the natural logarithm of the real gross output of the industry.
2.2 Replications
We were able to reproduce the “B. R&D Estimation” panel of table 2 of FT, containing descriptive statistics, exactly. The results of the pooled OLS estimation of Equation 4 are given in Table 1, columns (1)–(3). They correspond to columns (2), (5) and (6) of table 5 of FT.
| (1) | (2) | (3) | (4) | (5) | (6) | |
|---|---|---|---|---|---|---|
| ΔOutput | 0.272*** | −0.777** | −0.747* | 0.143*** | −0.125 | −0.053 |
| (0.034) | (0.262) | (0.292) | (0.022) | (0.156) | (0.181) | |
| ΔOutput × Patent Effectiveness | −0.054 | −0.178 | −0.279 | −0.313 | ||
| (0.306) | (0.314) | (0.212) | (0.213) | |||
| Patent Effectiveness | 0.183*** | 0.101*** | 0.070*** | 0.052* | ||
| (0.023) | (0.026) | (0.018) | (0.021) | |||
| ΔOutput × Obsolescence | 0.341*** | 0.341*** | 0.114* | 0.091 | ||
| (0.079) | (0.088) | (0.048) | (0.057) | |||
| Obsolescence | 0.048*** | 0.033** | 0.029*** | 0.026*** | ||
| (0.010) | (0.010) | (0.007) | (0.008) | |||
| ΔOutput × External Financing | 0.039 | 0.044 | ||||
| (0.063) | (0.045) | |||||
| External Financing | 0.014*** | 0.001 | ||||
| (0.004) | (0.003) | |||||
| Constant | 0.038 | −0.189*** | −0.115** | −0.037** | −0.156*** | −0.142*** |
| (0.026) | (0.040) | (0.042) | (0.014) | (0.028) | (0.030) | |
| Data used | FT | FT | FT | OGGB | OGGB | OGGB |
| N (observations) | 71,264 | 71,264 | 71,264 | 40,922 | 40,922 | 40,922 |
| R2 | 0.224 | 0.225 | 0.226 | 0.122 | 0.123 | 0.123 |
| Average marginal effect output | 0.272 | 0.168 | 0.157 | 0.143 | 0.074 | 0.089 |
| % Avg. marginal effect < 0 | 0.0 | 8.1 | 14.9 | 0.0 | 5.0 | 12.0 |
- Note. Robust standard errors, clustered by firm in parentheses. *p < 0.05, **p < 0.01, ***p < 0.001. Additional controls as in FT, i.e. first differenced, including year fixed effects.
The results presented in these columns are not an exact reproduction of the results presented in table 5 of FT but the estimated coefficients are very similar both in size and significance. 2All conclusions drawn by FT remain valid. In most cases R&D expenditures are procyclical, depending on patent effectiveness, obsolescence, and the external financing within the industry. As noted before, the inclusion of these variables introduces heterogeneity and for some firms this will result in a negative marginal effect, indicating countercyclicality. The average marginal effects indicate that for most model specifications and most firms R&D expenditures are procyclical. Patent effectiveness and external financing do not appear to have an effect via growth in output but do have a positive significant effect themselves. Note that, if anything, patent effectiveness has a negative indirect effect in combination with output growth. This is in line with the procyclicality of R&D investments, as argued by FT. Also confirming the hypothesis of procyclicality of R&D expenditures, obsolescence has both a direct positive impact and an indirect effect via output growth. The average marginal effect of output growth is about 16% (Table 1, column 3), when allowing for interaction effects.
We now turn to the estimation of the model of Barlevy (2007) on the data of FT. The specification of the model is given in Equation 2 and the model is estimated using a fixed-effects estimator. The results can be found in Table 2, columns (1)–(4). In the fixed-effects estimation the significance of output growth is lost if the control variables are added to the specification. Barlevy found strongly significant positive results pointing at procyclicality of the growth in R&D expenditures. We find no relation to the business cycle if we control for the same firm characteristics. Although the data come partly from the same source (Compustat), there are differences in the data: Here we use about twice the number of observations, the time period considered is slightly different, and a different number of industries are being examined. However, the definitions of the variables are the same. It should be noted that the Barlevy estimation results are highly varying with the model specification: His estimates of the effect of output growth on growth in real R&D, where the data used vary across industry codes, included number of observations and the way output is measured, and ranged from 0.21 to 0.92.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
| ΔOutput | 0.241*** | 0.230*** | −0.026 | 0.019 | 0.357*** | 0.263*** | 0.133*** | 0.101** |
| (0.044) | (0.055) | (0.042) | (0.050) | (0.027) | (0.034) | (0.028) | (0.033) | |
| Data used | FT | FT | FT | FT | OGGB | OGGB | OGGB | OGGB |
| Year fixed effects | No | Yes | No | Yes | No | Yes | No | Yes |
| Balance sheet controls | No | No | Yes | Yes | No | No | Yes | Yes |
| N (observations) | 85,604 | 85,604 | 75,807 | 75,807 | 52,870 | 52,870 | 44,144 | 44,144 |
| R2 (overall) | 0.003 | 0.000 | 0.237 | 0.236 | 0.007 | 0.004 | 0.114 | 0.111 |
- Note. Robust standard errors, clustered by firm in parentheses. *p < 0.05, **p < 0.01, ***p < 0.001. Balance sheet controls in levels as in Barlevy (2007).
As previously concluded, the estimations of FT are based on stronger assumptions than those of Barlevy. Before estimating both specifications using the same estimation technique and investigating some alternative models, we will first correct an important mistake in the preparation of the data.
3 TREATING MISSING OBSERVATIONS DIFFERENTLY
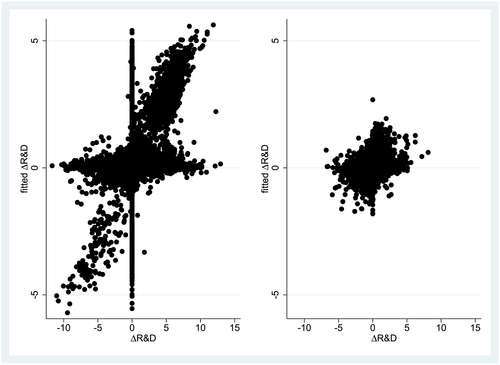
A simple diagnostic scatter graph of the dependent variable and the fitted values reveals an interesting problem. The scatter plots in Figure 1 display the dependent variable in the regressions in Table 1 (x-axis) and the fitted values from the regression of Model 1 (y-axis). In the left figure, on both the y- and x-axis there is an unusual concentration of points. Closer inspection of the files supplied by FT in the data archive of the Review of Economics and Statistics reveals that missing observations on R&D expenditures and some other variables are replaced by zeros. This results in a large number of zero R&D observations (38.2% of the 71,264 observations) and this explains the concentration of points on the y-axis. Another consequence of putting the log R&D expenditures to zero are extreme positive and negative changes in the R&D growth rates: If for a certain firm R&D is not observed in a certain year and it is observed in the next year, the growth rate is calculated to be huge if R&D is set to zero. The other way around generates very negative growth rates. 2We corrected the data by leaving the missing observations untouched, and this resulted in 40,922 remaining observations that are plotted in the right-hand scatter in Figure 1. Although the growth rates are still quite large in absolute value in some cases, the problem appears to have been solved to a large extent. We will use this restricted data set in the remaining part of this paper and indicate it by OGGB in Tables 2 and 3.
| (1) | (2) | (3) | (4) | |
|---|---|---|---|---|
| R&D | ΔR&D | ΔR&D | ΔR&D | |
| Output | 0.055 | |||
| (0.148) | ||||
| Output × Patent Effectiveness | 0.066 | |||
| (0.234) | ||||
| Output × Obsolescence | −0.005 | |||
| (0.053) | ||||
| Output×External Financing | 0.105*** | |||
| (0.029) | ||||
| ΔOutput | −0.069 | −0.098 | −0.159 | |
| (0.160) | (0.299) | (0.279) | ||
| ΔOutput×Patent Effectiveness | 0.004 | −0.068 | −0.112 | |
| (0.199) | (0.279) | (0.262) | ||
| ΔOutput × Obsolescence | 0.076 | 0.074 | 0.102 | |
| (0.049) | (0.090) | (0.083) | ||
| ΔOutput × External Financing | 0.142*** | 0.038 | 0.042 | |
| (0.032) | (0.053) | (0.051) | ||
| Constant | −2.452*** | −0.118*** | −0.526*** | −0.025 |
| (0.356) | (0.023) | (0.068) | (0.015) | |
| Estimation method | FE | OLS | FE | FE |
| Type of controls | Level | Level | Level | Δ |
| N (observations) | 45,061 | 44,144 | 44,144 | 40,922 |
| R2 | 0.451 | 0.124 | 0.092 | 0.088 |
| Average marginal effect output | 0.135 | 0.238 | 0.107 | 0.103 |
| % Avg. marginal effect < 0 | 4.8 | 2.5 | 1.2 | 3.5 |
- Note. Robust standard errors, clustered by firm in parentheses. *p < 0.05, **p < 0.01,∗∗∗p<0.001.
Columns (4)–(6) in Table 1 and columns (5)–(8) in Table 2 contain the same estimations as in the earlier columns but using the corrected data. If we only look at the estimated signs of the coefficients in Table 1, by and large the conclusions with respect to the FT specification do not change. The estimated coefficients are usually closer to zero and the significance appears to have reduced somewhat despite the calculated standard errors being smaller. We also find smaller R2s. The significance of obsolescence and patent effectiveness remains. If we concentrate on the full model as displayed in column (6), actually only obsolescence and patent effectiveness themselves have a significant impact. However, the significance of the interaction terms is lost. Note that none of the variables related to output growth are significant. For most firms there is procyclicality of the R&D expenditures, and this is stronger if the corrected data are used and if we judge this by the number of firms with procyclical R&D. However, the average marginal effect of output growth has reduced to 9%. Table 2, columns (5)–(8) display larger and more significant results than Table 2, columns (1)–(4). As in Barlevy (2007), the estimates of the effect of output growth while controlling for balance sheet variables are now strongly significant.
4 RECONCILIATION AND ALTERNATIVE SPECIFICATIONS
- • FT use additional controls relating to patent effectiveness, obsolescence and external financing. This is the key contribution of FT: They allow for heterogeneous effects of output growth.
- • Both models relate the growth of R&D to the growth in output but use different estimation methods. FT apply OLS, and the resulting estimates are in fact a result of a first-difference estimation on R&D. 2By first differencing they remove the firm-specific effect and according to FT (their footnote 4) also autocorrelation and heteroskedasticity. Barlevy estimates using a fixed-effects estimation. Consequently he allows for second-order fixed effects or incidental trends.
- • FT use first-differenced balance sheet controls in the growth in R&D equation, whereas Barlevy uses level controls.
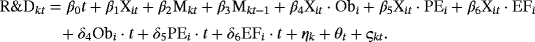 (5)
(5)As such, this model can make perfect sense, but in their discussion of R&D investments, indeed as a level variable, the growth in R&D investment is only introduced when discussing their empirical model. FT do not discuss time trends in general and time trends related to patent effectiveness, obsolescence and external financing in particular. If we review the results in Table 1, we can conclude that there is in general a negative trend in R&D expenditures but that this negative trend is less negative or even positive for firms with relatively high degrees of patent effectiveness, obsolescence and/or external financing.
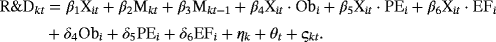 (6)
(6)The difference from Equation 5 is that we deleted all variables related to the trend. We estimate this model using the fixed-effects estimator. Due to using this estimator the effects of the time-constant explanatory variables cannot be estimated. 6The relevant estimation results are presented in Table 3, column (1). Note that the estimations now are performed on 45,061 observations. The conclusions we can draw from the estimation results in Table 3, column (1) are quite different from the conclusions from Table 1, column (6). The effect of industry output growth remains insignificant, although the sign has changed. The effect of patent effectiveness and obsolescence on the impact of industry output growth has also changed: Using a fixed-effect estimation reverses the sign and maintains insignificance. The signs are now contrary to the theoretical predictions of FT. This can signal two things: Either the model estimated is not the correct model and the model estimated by FT represents reality better, or there is a tendency in the direction of acyclical R&D expenditures for firms in industries with higher patent effectiveness and with lower levels of obsolescence. Finally, the effect of external financing remains positive but has become strongly significant. With respect to heterogeneity we can conclude from the average marginal effects of output growth on R&D expenditures that the procyclicality of R&D is even stronger in this alternative model: Procyclicality is found for 95.2% of the firms whereas it was 88% in Table 1.
We now turn to using the same controls as Barlevy (2007). Instead of controls specified as first differences, Barlevy uses level variables. The results, using pooled OLS as FT do, are presented in Table 3, column (2). The results are far from significant, apart from the interaction term relating to external financing. The effect of obsolescence in combination with output growth is again corresponding to the theoretical expectations of FT, although far from significant. The average marginal effect of output growth for this model is quite large (almost 24%), and the number of firms with countercyclical R&D is very small (2.5%).
If we now estimate the same model using a fixed-effects estimation, which is the estimation method used by Barlevy (2007), except that three interactions are used as additional regressors, we obtain Table 3, column (3). All significance of the reported coefficients is lost and incidental trends appear to be nonexistent. Note that the R2 is in line with the previous results, so any significance derives from the control variables.
The same conclusion follows if we estimate the model of FT, see Table 1, and therefore use controls in differences, but not applying pooled OLS but the fixed-effects estimator. The results are in Table 3, column (4). As explained before, the effects of the time-constant explanatory variables cannot be estimated.
Due to the lack of significance, we conclude that it is not necessary to allow for second-order fixed effects as suggested by Barlevy (2007). If we concentrate only on the signs of the estimated coefficients, the conclusions are very similar to those following from Table 1. There is almost a one-to-one correspondence of the signs (14 out of 16 cases). However, as noted, almost all significance is lost. With respect to heterogeneity, only the external financing cross term is significant but this is precisely the variable that is not emphasized in FT. In fact, it is hardly discussed by them apart from entries in regression tables.
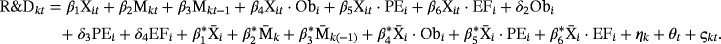
Our conclusion is that if the same explanatory variables and appropriate estimation methods are used, the heterogeneity of cyclicality of R&D investment found by FT is reduced considerably. Heterogeneity appears to be dependent especially on the external financing of the firm. Just like FT, we do find procyclicality for the vast majority of firms.
Finally, we conduct two robustness checks as suggested by one of the referees. Barlevy (2007) and Fabrizio and Tsolmon (2014) both relate R&D to industry output. Although this reduces firm-specific idiosyncrasies, using firm-specific output appears to be the more direct measure and this is more in line with the hypotheses of Schumpeter (1939). In Table 4, columns (1)–(4), we therefore present estimates of the same specifications as in Table 3 but replacing industry output by firm output. The estimation results are very similar: The vast majority of firms appear to display procyclical R&D investments and there is heterogeneity but mainly with respect to external financing. Compared to Table 3, the sign of this variable has changed, indicating that depending more on external financing tends to make R&D expenditures less procyclical.
| (1) | (2) | (3) | (4) | (5) | (6) | (7) | (8) | |
|---|---|---|---|---|---|---|---|---|
| R&D | ΔR&D | ΔR&D | ΔR&D | R&D | ΔR&D | ΔR&D | ΔR&D | |
| Output | 0.007 | 0.062 | ||||||
| (0.112) | (0.139) | |||||||
| Output × Patent Effectiveness | 0.048 | 0.080 | ||||||
| (0.093) | (0.114) | |||||||
| Output × Obsolescence | 0.008 | 0.010 | ||||||
| (0.035) | (0.041) | |||||||
| Output × External Financing | −0.021** | −0.022* | ||||||
| (0.008) | (0.009) | |||||||
| ΔOutput | 0.033 | 0.042 | 0.053 | 0.079 | 0.082 | 0.023 | ||
| (0.091) | (0.108) | (0.128) | (0.049) | (0.052) | (0.045) | |||
| ΔOutput × Patent Effectiveness | −0.207** | −0.086 | 0.002 | −0.078 | −0.043 | −0.020 | ||
| (0.077) | (0.089) | (0.109) | (0.041) | (0.041) | (0.037) | |||
| ΔOutput × Obsolescence | 0.051 | 0.036 | 0.024 | 0.008 | 0.001 | 0.008 | ||
| (0.030) | (0.036) | (0.043) | (0.016) | (0.017) | (0.015) | |||
| ΔOutput × External Financing | −0.007 | −0.018* | −0.029** | −0.009** | −0.012*** | −0.009** | ||
| (0.006) | (0.007) | (0.009) | (0.003) | (0.003) | (0.003) | |||
| Constant | −1.093*** | −0.102*** | −0.518*** | −0.029* | −1.142*** | −0.061*** | −0.288*** | 0.004 |
| (0.157) | (0.021) | (0.061) | (0.014) | (0.190) | (0.010) | (0.030) | (0.006) | |
| Sample | Full | Full | Full | Full | Restricted | Restricted | Restricted | Restricted |
| Estimation method | FE | OLS | FE | FE | FE | OLS | FE | FE |
| Type of controls | Level | Level | Level | Δ | Level | Level | Level | Δ |
| N (observations) | 52891 | 51690 | 51690 | 45840 | 36678 | 36678 | 36678 | 37589 |
| R2 | 0.433 | 0.135 | 0.099 | 0.094 | 0.504 | 0.080 | 0.061 | 0.081 |
| Average marginal effect output | 0.036 | 0.084 | 0.096 | 0.103 | 0.112 | 0.061 | 0.058 | 0.030 |
| % Avg. marginal effect < 0 | 8.2 | 0.2 | 0.0 | 7.8 | 0.0 | 0.0 | 7.5 | 7.4 |
- Note. Robust standard errors, clustered by firm in parentheses. *p < 0.05, **p < 0.01, ***p < 0.001. Full: full OGGB sample, no restrictions on growth R&D. Restricted: restricted OGGB sample, abs(growth R&D) ≤ 50%.
From Table 2 of FT it is clear that the growth in R&D attains some unrealistically high values in absolute sense: the minimum of the growth rate is −1,169% and the maximum 1,294%. As discussed, these large growth rates are partly due to replacing missing observations on R&D by zeros and adding 1 to the logarithm. Apart from our doubt regarding whether these figures can be correct, there is also another problem. The difference of the year-to-year log of R&D only measures the growth rate for relatively small changes. To investigate this we restrict the sample to R&D growth rates of 50% or less (in absolute values). 8This reduces the number of observations from about 45,000 to about 37,000. The estimation results, again for the same specification as in Table 3, are in columns (5)–(8) of Table 4. The overall conclusions do not change: More than 90% of the firms display procyclical R&D expenditures and there is heterogeneity again, but only due to external financing.
5 CONCLUSION
In this paper we replicated Fabrizio and Tsolmon (2014) and Barlevy (2007). The results of FT were retrieved almost precisely whereas significance was lost in the Barlevy specification. Significance of the Barlevy estimates was restored after having corrected the data, whereas the overall conclusion of FT remained the same after this correction. If we use suitable (fixed-effects) estimation methods, no significance was found for the key factors of Fabrizio and Tsolmon obsolescence and patent effectiveness. Heterogeneity of the cyclicality of R&D expenditures remained due to the external financing interaction term. These conclusions were corroborated when we generalized to firm-specific output growth instead of industry-specific output growth and when we restricted the sample to more realistic growth numbers of R&D.
Finally, our replication confirms the procyclicality of R&D expenditures as found by Barlevy (2007) and the heterogeneity of the procyclicality as found by Fabrizio and Tsolmon (2014), although the heterogeneity estimated by econometrically sound specification and estimation methods is quite different in nature.
ACKNOWLEDGEMENTS
We are grateful to two referees for their useful remarks.
REFERENCES
- 1 A referee suggested testing for unit roots. After selecting all firms with at least 10 years of consecutive data, we have applied a Fisher-type panel unit root test using STATA's xtunit root fisher …, dfuller trend lags() statement. Based on Choi's (2001) Z test, which is the least restrictive test available according to Baltagi (2013, chapter 12), the null hypothesis that all panels contain unit roots is rejected at the 5% significance level for all variables except the control variable log of firm's total assets. If we use the demean option of the test, also for this variable the null of nonstationarity is rejected.
- 2 The data are taken from the Review of Economics and Statistics replication database.
- 2 In their table 5, FT have the entry Output× …(3 times), but this should read ΔOutput × ….
- 2 FT calculate growth rates by calculating the year-to-year differences in
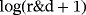 . This is an inappropriate method if changes are large.
. This is an inappropriate method if changes are large. - 2 We will disregard the difference between a fixed-effects estimation and the first-difference estimation. As discussed in Baltagi (2013) both estimation methods yield consistent estimates under the same assumptions, but the fixed-effects estimator is more efficient.
- 3 A constant is present in the model of FT on page 666; the three time invariant variables are not, although they are presented in table 5 on page 672.
- 4 The authors do not actually mention the potential existence of firm-specific effects in footnote 4 as a reason for using first differences. However, note that the autocorrelation and heteroskedasticity experienced by FT might be due to these firm-specific effects.
- 5 :We added Ob, PE and EF as well; although not discussed in the theoretical part of FT, they are included in their estimations.
- 6 This deviates from estimation in first differences employed by FT. However, the fixed-effects estimator is more efficient and more observations are actually used in the estimation. Note also that the first-difference estimator does not make it possible to identify time-constant effects. The differences in the estimation results, however, are marginal. Another advantage of the fixed-effects estimator is that it is a more natural approach if the data contain gaps in time as in the present case.
- 7 No mention of this more general result can be found in Baltagi (2013), for example. In sociology and biology, for example, adding the time averages of the time-varying explanatory variables is quite common (see, e.g., Allison, 2009; Neuhaus & Kalbfleisch, 1998; Phillips, 2006).
- 8 A proof of these claims is available on request.
- 8 We also estimated with a cutoff of 25% and 100% but the conclusions remain the same.




