Steady-state modeling and macroeconomic forecasting quality
Summary
Vector autoregressions (VARs) with informative steady-state priors are standard forecasting tools in empirical macroeconomics. This study proposes (i) an adaptive hierarchical normal-gamma prior on steady states, (ii) a time-varying steady-state specification which accounts for structural breaks in the unconditional mean, and (iii) a generalization of steady-state VARs with fat-tailed and heteroskedastic error terms. Empirical analysis, based on a real-time dataset of 14 macroeconomic variables, shows that, overall, the hierarchical steady-state specifications materially improve out-of-sample forecasting for forecasting horizons longer than 1 year, while the time-varying specifications generate superior forecasts for variables with significant changes in their unconditional mean.
1 INTRODUCTION
Bayesian vector autoregressions (BVARs) are standard tools in macroeconomic forecasting and policy analysis among both academics and practitioners such as central banks. 1A key element in BVARs is the use of informative priors which shrink the dynamic coefficients towards a specific representation of the data and deal with the over-parametrization problem. The amount of prior shrinkage is of crucial importance to improve forecast accuracy, especially in large-scale applications (see, e.g., Giannone, Lenza, & Primiceri, 2015; Koop, 2017; and references therein).
Although there is a plethora of available priors in the BVAR literature, these are typically noninformative with respect to the deterministic component of the model, which regulates the steady state or the trend of the process in stationary and nonstationary variables, respectively. 2The quality of long-horizon forecasts is of decisive economic importance and depends, to a large extent, on whether we discipline the deterministic component of VARs using appropriate prior specifications. 3Only a handful of studies have moved towards this direction, with the seminal contribution of Villani (2009) being the first to propose a steady-state VAR parametrization which enables the incorporation of steady-state prior beliefs in a VAR model. Since policymakers have usually strong prior beliefs on the steady-state of an economy, these can be used to enhance economic forecasting. 4 In the same vein, Giannone, Lenza, and Primiceri (2018) use the insights of economic theory to elicit a prior for the long-run behavior of stationary and nonstationary variables correcting for the deterministic overfitting of VARs. 5, 6For both approaches, the literature documents substantial macroeconomic forecasting improvements especially at longer-term horizons (Beechey Österholm, 2008, 2010; Clark, 2011; Louzis, 2016b; Wright, 2013). 7
This paper concentrates on steady-state VARs and aims to examine, among other things, whether the informativeness of steady-state priors plays a significant role in forecasting quality, as is the case for the dynamic coefficients discussed above. The amount of shrinkage of steady-state prior has received relatively little attention and it is typically chosen in an ad hoc way, under the general rule of a sufficiently informative prior. The only exception is Wright (2013), who chooses the steady-state prior informativeness on the basis of a forecasting exercise over a presample. Obviously, a steady-state VAR with uninformative priors is of no use, while a very tight prior may lead to biased steady-state estimates when the mean of the steady-state prior distribution is misspecified due to the limited or no prior information regarding the long-run expectations of an economy. 8
A hierarchical steady-state prior framework may overcome some of the shortcomings of the typical Normal prior approach, since the prior tightness is determined by combining both prior beliefs and information from the data. In general, Bayesian hierarchical modeling treats the hyperparameters—that is, the coefficients used to parametrize the prior—as additional parameters with their own priors, leading to a more objective Bayesian analysis (Giannone et al., 2015; Korobilis, 2013). In a steady-state VAR framework this implies that we treat the variances of the steady-state prior distribution as parameters to be estimated by the data. As mentioned above, such an approach requires choosing a prior for the hyperparameters (the hyperprior), which may be crucial in terms of inference and forecasting.
In particular, this paper proposes the hierarchical normal-gamma (NG) prior of Grifin and Brown (2010, 2017) for steady states, which has recently been used to shrink dynamic VAR coefficients (Huber & Feldkircher, 2017; Korobilis & Pettenuzzo, 2017) The NG prior is a conditionally Normal prior with scaling parameters following a gamma density and belongs to the family of flexible global–local shrinkage priors (Polson & Scott, 2010). This means that all steady states shrink toward their prior means according to a global variance component, while idiosyncratic or local variance components control for the tail behavior of the marginal prior. Thus, in contrast to the Normal or Student t priors, the NG has the advantageous property of being, at the same time, highly informative, imposing heavy shrinkage on the steady-state coefficients, and capable of utilizing the information available in the data if the likelihood strongly suggests different prior mean locations. 9
Although the NG steady-state prior adds flexibility to the standard steady-state VAR, potentially resulting in better inference and forecasting, it cannot capture possible structural breaks in the unconditional mean of a VAR process (see, e.g., Chan & Koop, 2014). Clark (2011) and Wright (2013) implicitly account for structural breaks in the steady states through the use of long-term macroeconomic expectations in the setting of the steady-state prior. In contrast to the previous studies, we propose a time-varying steady-state VAR specification which explicitly accounts for structural breaks in steady states and we also show how to apply hierarchical shrinkage on time-varying steady states via the NG prior. 10Recent empirical evidence indicates that time-varying parameter VAR (TVP-VAR) models that take into account the structural breaks in the dynamic coefficients generate superior forecasts compared to constant parameter models (see, e.g., D'Agostino, Gambetti, & Giannone, 2013; Koop & Korobilis, 2013; Koop, Korobilis, & Pettenuzzo, 2017). Here, we focus only on steady-states comparing the forecasting ability of the time-varying steady-state model against the standard (hierarchical) steady-state VARs discussed above. The key point for estimation of the time-varying steady-state VAR model is to rewrite the model as a standard TVP-VAR and then use the Gibbs sampling algorithm developed by Primiceri (2005).
In line with the literature, we also generalize the proposed hierarchical and time-varying steady-state VAR specifications to account for fat-tailed and heteroskedastic innovations. In particular, we augment the models with common stochastic volatility (CSV) and student t innovations based on the methods developed by Carriero, Clark, and Marcellino (2016a) and Chan (2018), which exploit the Kronecker structure of the likelihood in order to speed up computations. In the same vein, we also employ the equation-by-equation estimation method of Carriero, Clark, and Marcellino (2016b) to estimate the proposed models with asymmetric priors for the dynamic coefficients and standard stochastic volatility structure as in Primiceri (2005).
To sum up, we contribute to the BVAR literature by extending the standard steady-state VAR in three directions. First, we propose an adaptive hierarchical NG prior for the steady states as opposed to the Normal prior typically used. Second, we specify a time-varying steady-state VAR model to allow for more flexibility in the unconditional mean of the process, aiming to capture possible structural changes in the steady state. Finally, the proposed specifications are extended to incorporate fat tails and time-varying volatility. We estimate the alternative specifications using Gibbs and Metropolis-within-Gibbs algorithms based on the derived posterior distributions, and we examine whether they can materially improve the out-of-sample forecasting ability compared to standard benchmarks using a real-time data set of 14 variables from the US economy.
A Monte Carlo simulation evaluation reveals that the hierarchical prior approach can produce accurate steady-state estimates even when the prior steady-state mean is well misspecified, possibly leading to significant forecasting gains. Indeed, the empirical findings suggest that the more flexible NG steady-state VARs produce, on average, better point and density forecasts for forecasting horizons longer than 1 year. On the other hand, the time-varying steady-state specifications provide better forecasts for variables with significant structural changes in their unconditional mean. In line with the literature, models with stochastic volatility and/or Student t innovations tend to outperform their counterparts with constant volatility and Gaussian errors.
The rest of the paper is organized as follows. Section 2 discusses the hierarchical and time-varying extensions of the steady-state VAR. Section 3 presents the models with stochastic volatility and fat tails. In Section 4 we discuss the Bayesian estimation of the models and in Section 5 we perform the Monte Carlo simulations. In Section 6 we present the competing models, the specification of the priors, the in-sample estimation results, and the out-of-sample forecasting analysis. Finally, Section 7 summarizes and concludes this paper.
2 EXTENSIONS TO VARS WITH INFORMATIVE STEADY-STATE PRIORS
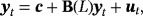 (1)
(1)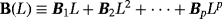 with
with
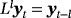 are n × n matrices of dynamic regression coefficients, and ut are exogenous shocks distributed as i.i.d.
are n × n matrices of dynamic regression coefficients, and ut are exogenous shocks distributed as i.i.d.
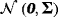 , where
, where
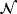 is the Normal distribution.
is the Normal distribution.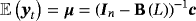 . Obviously, the steady state is a nonlinear expression of the VAR coefficients, making it hard for the econometrician to encapsulate his prior opinions with respect to μ. To circumvent this problem, Villani (2009) proposes a mean-adjusted or steady-state representation of the VAR model:
. Obviously, the steady state is a nonlinear expression of the VAR coefficients, making it hard for the econometrician to encapsulate his prior opinions with respect to μ. To circumvent this problem, Villani (2009) proposes a mean-adjusted or steady-state representation of the VAR model:
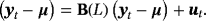 (2)
(2)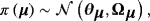 (3)
(3)2.1 An adaptive hierarchical steady-state prior
Prior elicitation with respect to Equation 3 means that the researcher has to choose each of the elements of θμ, θμ,j, and then decide with regard to the prior informativeness by setting the diagonal elements of Ωμ, ωμ,j,j = 1,…,n. According to the literature, the steady-state prior distribution should be reasonably informative, translating to reasonably small values for
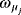 , to reap the benefits of the mean-adjusted VAR model in terms of forecasting performance and avoid convergence problems of the MCMC algorithm (Villani, 2005, 2009).
, to reap the benefits of the mean-adjusted VAR model in terms of forecasting performance and avoid convergence problems of the MCMC algorithm (Villani, 2005, 2009).
In general, prior tightness for each of the n variables in the VAR model depends on the uncertainty of the researcher regarding the selected level of the steady-state prior mean. For variables with much a priori information available—for example, long-term survey forecasts—a researcher may feel much more comfortable with a very tight prior—that is, very small ωμ,j. Otherwise, in cases where it is difficult to formulate a prior opinion on the unconditional mean and as a result the steady-state prior mean differs largely from its true value, then a very informative prior may lead to inaccurate steady-state inference. Therefore, we seek for a prior distribution adaptive enough to place a lot of mass on θμ,js but at the same time have heavy tails to let the data speak.
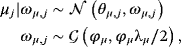 (4)
(4)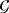 is the gamma distribution and ϕμ and λμ are hyperparameters, with their own hyperprior distributions playing an important role in adaptive shrinkage.
is the gamma distribution and ϕμ and λμ are hyperparameters, with their own hyperprior distributions playing an important role in adaptive shrinkage.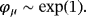 (5)
(5)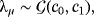 (6)
(6)2.2 Time-varying steady states
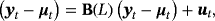 (7)
(7)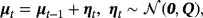 (8)
(8)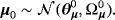 (9)
(9)We can also extend the TVSS-VAR to adopt the NG prior on the initial conditions and thus combining the hierarchical shrinkage towards economic information with the time variation of the steady states. The full details of such a model are provided in Appendix B.
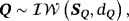 (10)
(10)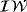 is the inverse Wishart distribution with scale matrix, SQ and degrees of freedom dQ. The prior on Q plays an important role in empirical applications since it governs the degree of time variation of μt. Usually the literature prefers a tight prior to avoid implausible behavior in terms of the time evolution of the time-varying parameter and optimize the forecasting performance of the model (see, e.g., D'Agostino et al., 2013).
13
is the inverse Wishart distribution with scale matrix, SQ and degrees of freedom dQ. The prior on Q plays an important role in empirical applications since it governs the degree of time variation of μt. Usually the literature prefers a tight prior to avoid implausible behavior in terms of the time evolution of the time-varying parameter and optimize the forecasting performance of the model (see, e.g., D'Agostino et al., 2013).
133 GENERALIZING STEADY-STATE VARS: FAT TAILS AND STOCHASTIC VOLATILITY
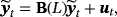 (11)
(11)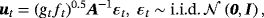 (12)
(12)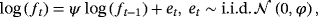 (13)
(13)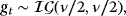 (14)
(14)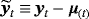 is the vector of the mean-adjusted variables and μ(t) is the unconditional mean possibly specified using one of the techniques proposed in Section 2. A is a lower diagonal matrix with ones on its main diagonal; ft is a time-varying scalar with its law of motion being defined in Equation 13 as an AR(1) process with autoregressive parameter ψ and error variance ϕ. Finally, each gt is assumed to follow independently an inverse-gamma (
is the vector of the mean-adjusted variables and μ(t) is the unconditional mean possibly specified using one of the techniques proposed in Section 2. A is a lower diagonal matrix with ones on its main diagonal; ft is a time-varying scalar with its law of motion being defined in Equation 13 as an AR(1) process with autoregressive parameter ψ and error variance ϕ. Finally, each gt is assumed to follow independently an inverse-gamma (
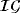 ) distribution implying that ut is marginally distributed as a multivariate t distribution with zero mean, time-varying error covariance matrix Σt = ftΣ, with
) distribution implying that ut is marginally distributed as a multivariate t distribution with zero mean, time-varying error covariance matrix Σt = ftΣ, with
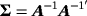 , and ν degrees of freedom (Chan, 2018; Geweke, 1993).
, and ν degrees of freedom (Chan, 2018; Geweke, 1993).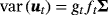 . This product structure reduces substantially the computational burden of estimation, especially when n is large, but it involves a Kronecker structure of the likelihood. This means that we have to use appropriate conjugate priors to get posteriors which reserve the same (Kronecker) structure. Therefore, we use the natural conjugate normal-inverse Wishart (N-IW) prior for the VAR coefficients and the covariance matrix Σ, which is defined as (Giannone et al., 2015)
. This product structure reduces substantially the computational burden of estimation, especially when n is large, but it involves a Kronecker structure of the likelihood. This means that we have to use appropriate conjugate priors to get posteriors which reserve the same (Kronecker) structure. Therefore, we use the natural conjugate normal-inverse Wishart (N-IW) prior for the VAR coefficients and the covariance matrix Σ, which is defined as (Giannone et al., 2015)
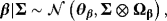 (15)
(15)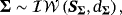 (16)
(16)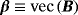 , with
, with
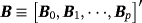 . We also assume that ψ and ϕ are a priori distributed as
. We also assume that ψ and ϕ are a priori distributed as
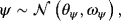 (17)
(17)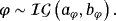 (18)
(18)3.1 Asymmetric priors and stochastic volatility
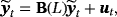 (19)
(19)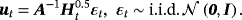 (20)
(20)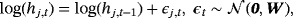 (21)
(21)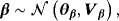 (22)
(22)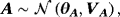 (23)
(23)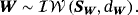 (24)
(24)Obviously, the prior on VAR coefficients in Equation 22 is not conditional on the variance of the VAR coefficients, meaning that we can introduce asymmetry in the prior across equations as in the traditional Minnesota prior of Litterman (1986).
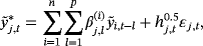 (25)
(25)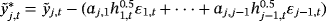 ,
,
 . Given that we have estimated all previous j − 1 equations, the terms on the left-hand side of Equation 25 can be replaced with their estimations and the model can be estimated equation by equation, alleviating substantially the computational burden (for more details see Carriero et al., 2016b).
. Given that we have estimated all previous j − 1 equations, the terms on the left-hand side of Equation 25 can be replaced with their estimations and the model can be estimated equation by equation, alleviating substantially the computational burden (for more details see Carriero et al., 2016b).4 BAYESIAN ESTIMATION
We estimate the alternative proposed specifications using MCMC methods and particularly the Gibbs sampler, where the parameters are drawn iteratively from the full conditional posterior distributions. Generally, conditional on the steady-state coefficients, μ(t), the VAR models for the mean-adjusted series,
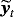 , outlined in Sections 2 and 3, can be estimated using the Gibbs samplers proposed in related studies (see, e.g., Carriero et al., 2016a, 2016b; Chan, 2018; Villani, 2009) with minor modifications, since they do not include a constant term (see the Technical Appendix for more details). In this section, we concentrate on these steps of the Gibbs sampler that draw from the conditional posteriors of the parameters related to the NG steady-state prior and the time-varying steady-state specification.
, outlined in Sections 2 and 3, can be estimated using the Gibbs samplers proposed in related studies (see, e.g., Carriero et al., 2016a, 2016b; Chan, 2018; Villani, 2009) with minor modifications, since they do not include a constant term (see the Technical Appendix for more details). In this section, we concentrate on these steps of the Gibbs sampler that draw from the conditional posteriors of the parameters related to the NG steady-state prior and the time-varying steady-state specification.
4.1 Posterior distributions related to the NG steady-state prior
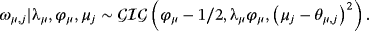 (26)
(26)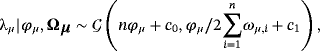 (27)
(27)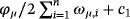 , respectively. The conditional posterior distribution of ϕμ has no closed form and, thus, we rely on a random-walk Metropolis–Hastings (RWMS) step. Particularly, the proposed values for ϕμ are given by
, respectively. The conditional posterior distribution of ϕμ has no closed form and, thus, we rely on a random-walk Metropolis–Hastings (RWMS) step. Particularly, the proposed values for ϕμ are given by
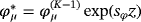 , where
, where
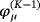 is the last accepted draw, sϕ is a scaling factor, and z is a standard normal random variable. The proposed value,
is the last accepted draw, sϕ is a scaling factor, and z is a standard normal random variable. The proposed value,
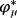 , is accepted with probability
, is accepted with probability
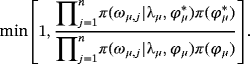 (28)
(28)The scaling factor sϕ is calibrated to achieve an acceptance rate of approximately 30%. As soon as we have the posterior draws for ωμ,js we form the diagonal matrix Ωμ and we draw μ as in Villani (2009).
4.2 Estimation of the time-varying steady-state parameters
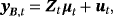 (29)
(29)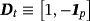 ,
,
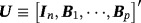 , and 1p is a 1 × p vector of ones (a proof of this result is provided in Louzis, 2016a). Equations 29 and 8 form the observation and transition equations respectively, and conditional on all other parameters we can use standard Bayesian techniques for TVP-VARs to estimate the series of μt (see, e.g., (Primiceri, 2005). In particular, assuming a prior on initial conditions as in Equation 9, we draw μt ∀t from its conditional posterior distribution using the Carter and Kohn (1994) (CK) algorithm. Next, conditional on the dth draw,
, and 1p is a 1 × p vector of ones (a proof of this result is provided in Louzis, 2016a). Equations 29 and 8 form the observation and transition equations respectively, and conditional on all other parameters we can use standard Bayesian techniques for TVP-VARs to estimate the series of μt (see, e.g., (Primiceri, 2005). In particular, assuming a prior on initial conditions as in Equation 9, we draw μt ∀t from its conditional posterior distribution using the Carter and Kohn (1994) (CK) algorithm. Next, conditional on the dth draw,
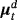 , we calculate the demeaned variables
, we calculate the demeaned variables
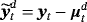 , and then we can apply standard Bayesian estimation for the rest of the parameters.
, and then we can apply standard Bayesian estimation for the rest of the parameters.5 MONTE CARLO SIMULATIONS
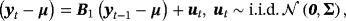 (30)
(30)
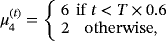
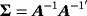 . This is a four-variable stationary steady-state VAR model with one lag which is used to generate 100 samples of length T = 140. Next, we use each of the 100 samples to estimate four alternative models. First, we estimate two standard SS-VAR models with steady-state prior covariance matrices Ωμ=kIn and k being equal to 0.2 and 2 representing a tight prior and a less informative prior around the mean, respectively. We also estimate a hierarchical steady-state VAR (HSS-VAR) with NG steady-state prior presented in Section 2.1 and a TVSS-VAR presented in Section 2.2. The details for the prior specification of the dynamic coefficients and the error covariance matrix are presented in detail in Supporting Information Appendix D. Here, we concentrate solely on the steady-state prior and we set the prior mean equal to θμ=[1,2,3,4]′. Obviously, we choose the prior means for the 2nd, 3rd, and 4th variables to differ from the true values considered in the DGP in order to evaluate the estimation performance of the proposed extensions under conditions of prior misspecification. In particular, the level of the prior mean for the 2nd (3rd) variable is well below (above) the level of the steady state implied by the true DGP, while for the 4th variable we choose the average level of the two regimes.
. This is a four-variable stationary steady-state VAR model with one lag which is used to generate 100 samples of length T = 140. Next, we use each of the 100 samples to estimate four alternative models. First, we estimate two standard SS-VAR models with steady-state prior covariance matrices Ωμ=kIn and k being equal to 0.2 and 2 representing a tight prior and a less informative prior around the mean, respectively. We also estimate a hierarchical steady-state VAR (HSS-VAR) with NG steady-state prior presented in Section 2.1 and a TVSS-VAR presented in Section 2.2. The details for the prior specification of the dynamic coefficients and the error covariance matrix are presented in detail in Supporting Information Appendix D. Here, we concentrate solely on the steady-state prior and we set the prior mean equal to θμ=[1,2,3,4]′. Obviously, we choose the prior means for the 2nd, 3rd, and 4th variables to differ from the true values considered in the DGP in order to evaluate the estimation performance of the proposed extensions under conditions of prior misspecification. In particular, the level of the prior mean for the 2nd (3rd) variable is well below (above) the level of the steady state implied by the true DGP, while for the 4th variable we choose the average level of the two regimes.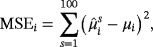 (31)
(31)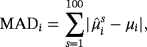 (32)
(32)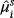 is the mean of the steady-state posterior distribution for the ith variable and the sth artificial sample.
is the mean of the steady-state posterior distribution for the ith variable and the sth artificial sample.The Monte Carlo simulation results presented in Table 1 suggest that the HSS-VAR model is the overall best-performing model across evaluation metrics followed closely by the TVSS-VAR model. Nonetheless, the most interesting part of the results is the performance of the standard SS-VAR model, which reveals the trade-off mechanism as regards the steady-state prior informativeness. Using highly informative steady-state priors we enhance the performance of the model, given that the level of the steady-state prior mean is correctly specified, as expected. Otherwise, when the prior mean differs from the true steady-state level, a less informative prior gives better overall results, but, at the same time, reduces the estimation accuracy of the steady-state coefficients with prior means equal to the true steady-state values. Our hierarchical prior approach manages to account for this kind of trade-off mechanism by automatically inferring the optimal steady-state prior informativeness. Given that the researcher has no a priori knowledge of whether he misspecifies the prior level of the steady states or not, our approach has very important implications for the applied researcher since it diminishes the need for tedious and time-consuming robustness checks as regards the steady-state prior covariance matrix.
| MSE | MAD | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Model | Avg. | μ1 | μ2 | μ3 | μ4 | Avg. | μ1 | μ2 | μ3 | μ4 |
| SS-VAR (0.2) | 3.084 | 0.009 | 3.762 | 8.511 | 0.077 | 1.292 | 0.076 | 1.939 | 2.917 | 0.276 |
| SS-VAR(2) | 0.047 | 0.032 | 0.045 | 0.048 | 0.058 | 0.171 | 0.145 | 0.167 | 0.169 | 0.190 |
| HSS-VAR | 0.032 | 0.024 | 0.043 | 0.048 | 0.021 | 0.138 | 0.122 | 0.162 | 0.174 | 0.127 |
| TVSS-VAR | 0.045 | 0.037 | 0.062 | 0.041 | 0.043 | 0.171 | 0.150 | 0.204 | 0.170 | 0.160 |
- Note. Bold entries indicate the best-performing model.
6 EMPIRICAL ANALYSIS
6.1 Competing models
The main scope of the paper is to investigate whether the proposed steady-state VAR extensions improve the forecasting ability of the VAR models relative to the standard benchmarks. Therefore, except for the stationary steady-state VAR specifications using variables in growth rates, we also consider VAR models with variables in log levels, a typical approach in macroeconomic forecasting literature (see, e.g., Carriero, Clark, & Marcellino, 2015; Giannone et al., 2015). A list of competing models, along with a short description of the alternative specifications and their priors, is presented in Table 2.
| Model | Description | Summary of priors |
|---|---|---|
| Benchmark | Bayesian VAR (BVAR) with variables in | Natural conjugate N-IW prior with shrinkage |
| growth rates (see Table 3) | parameter ϑ = 0.2 | |
| L | Standard BVAR with variables in log levels | |
| (see Table 3) and i.i.d. Gaussian | ||
| innovations. | (a) Natural conjugate N-IW prior with shrinkage | |
| L-t | BVAR in log levels with t innovations | parameter ϑ = 0.2; (b) sum-of-coefficients and |
| L-CSV-t | BVAR in log levels with common stochastic | dummy-of-initial-observations priors with both |
| volatility (CSV) and t innovations | shrinkage hyperparameters being set equal to 1 | |
| SS | Standard steady-state BVAR with variables | |
| in growth rates and i.i.d. Gaussian | ||
| innovations | ||
| SS-t | Steady-state BVAR with t innovations | (a) Natural conjugate N-IW prior; (b) normal |
| SS-CSV-t | Steady-state BVAR with CSV and t | prior for the steady-state parameters |
| innovations | ||
| SS-SV | Steady-state BVAR with stochastic volatility | (a) Asymmetric Minnesota prior; (b) normal prior |
| for the steady-state parameters | ||
| HSS | Hierarchical steady-state BVAR with variables | |
| in growth rates and i.i.d. Gaussian | ||
| innovations | ||
| HSS-t | Hierarchical steady-state BVAR with t | (a) Natural conjugate N-IW prior; (b) |
| innovations | hierarchical NG prior for the steady-state | |
| HSS-CSV-t | Hierarchical steady-state BVAR with CSV | parameters |
| and t innovations | ||
| HSS-SV | Hierarchical steady-state BVAR with | (a) Asymmetric Minnesota prior; (b) hierarchical |
| stochastic volatility | NG prior for the steady-state parameters | |
| TVSS | Time-varying steady-state BVAR with- | |
| variables in growth rates and i.i.d. Gaus | ||
| sian innovations | ||
| TVSS-t | Time-varying steady-state BVAR with t | (a) Natural conjugate N-IW prior; (b) normal |
| innovations | prior for the initial conditions of the steady-state | |
| TVSS-CSV-t | Time-varying steady-state BVAR with | process |
| CSV and t innovations | ||
| TVSS-SV | Time-varying steady-state BVAR with | (a) Asymmetric Minnesota prior; (b) normal prior |
| stochastic volatility | for the initial conditions of the steady-state | |
| process |
The benchmark model is a standard BVAR model in growth rates with a natural conjugate N-IW prior (see Equations 15 and 16). The VAR models using variables in levels (L) are also enriched with the routinely used sum-of-coefficients and dummy-initial-observation priors (Doan, Litterman, & Sims, 1984; Sims, 1993). The former, also known as no-cointegration prior, is imposed on the sum of coefficients of the model lags and assumes that each variable has a separate stochastic trend, as opposed to common stochastic trends implied by cointegration. The use of the sum-of-coefficients is standard in macroeconomic forecasting since it improves the predicting ability of the models by correcting for the deterministic overfitting in VARs. 14On the other hand, the sum-of-coefficients prior cancels out cointegration in the limit (when the prior is too tight), which is an undesirable property for models using variables in levels. The dummy initial observation, also known as single-unit-root prior, alleviates this shortcoming and assumes that no-change forecast provides a good description of the dynamics of the model. Thus, depending on the tightness, the prior either forces the variables towards the unconditional mean of the model, suggesting stationarity, or assumes that there is an unspecified number of unit roots without drift; both extremes are consistent with cointegration. For consistency and comparability reasons we also augment the VARs in levels with fat tails (suffix “-t”) and common stochastic volatility combined with fat tails (suffix “-CSV-t”), as described in Section 3.
All three categories of steady-state models—that is, the standard steady-state model (SS), the hierarchical steady-state model with the NG prior (HSS), and the time-varying steady-state model (TVSS)—are combined with fat tails and common stochastic volatility for the error terms. For the steady-state models we also consider the original asymmetric Minnesota prior for the dynamic VAR coefficients combined with stochastic volatility (suffix “-SV”) and estimated as described in Section 3.1.
Generally, the aforementioned choice of competing models allows us (i) to investigate the forecasting performance of the HSS and TVSS models relative to standard benchmarks in the literature—that is, the SS and L models—revealing the value added of the proposed steady-state specifications in terms of forecasting, and (ii) to examine whether fat tails and stochastic volatility improve the forecasting ability across alternative specifications with informative steady states—that is, L, SS, HSS and TVSS—thus providing additional support to the use of large-scale VAR models with nonconstant volatility and non-Gaussian innovations.
6.2 Data
We examine the estimation and forecasting properties of the proposed specifications using a large dataset of 14 macroeconomic time series from the US economy. Table 3 presents the details on the data set along with the transformations of the variables for the stationary and nonstationary models and the corresponding sources.
| Transformation | |||
|---|---|---|---|
| Variable | Steady-state VARs | VARs in log levels | Source |
| Real GDP |
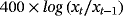 |
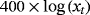 |
RTDSM |
| Consumption |
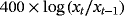 |
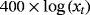 |
RTDSM |
| Business fixed inv. (BFI) |
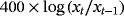 |
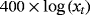 |
RTDSM |
| Resind. inv. |
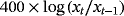 |
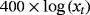 |
RTDSM |
| Ind. prod. |
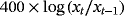 |
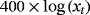 |
RTDSM |
| Cap. util. | None | None | RTDSM |
| Employment |
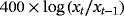 |
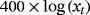 |
RTDSM |
| Hours |
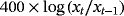 |
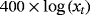 |
RTDSM |
| Unempl. rate | None | None | RTDSM |
| GDP deflator |
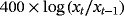 |
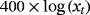 |
RTDSM |
| PCE deflator |
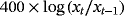 |
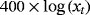 |
RTDSM |
| Fed funds rate | None | None | FRED |
| Term spread | None | None | FRED |
| Real stock prices |
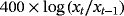 |
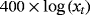 |
FRED |
- Notes.
- 1. “Term spread” is the difference between the 10-year treasury bond yield and the fed funds rate.
- 2. “Real stock prices” is the S&P 500 stock index deflated with the GDP deflator.
- 3. “RTDSM” is the Real Time Data Set for Macroeconomists database of the Federal Reserve Bank of Philadelphia; “FRED” is the Federal Reserve Economic Data maintained by the Federal Reserve Bank of St. Louis.
In brief, the dataset includes quarterly variables from the real sector of the economy, such as the real gross domestic product (GDP), consumption, investments, employment, capacity utilization, industrial production, etc.; prices (GDP and consumption deflators); and monetary and financial variables (i.e., the short-term interest rate, the term spread, and a stock index). All variables are expressed in annualized log differences or log levels except for those already expressed in annualized percentages, such as the unemployment rate, capacity utilization, or the interest rate. For variables available only at the monthly frequency we take the average value within the quarter.
More specifically, we rely on the real-time dataset for macroeconomists (RTDSM) obtained form the website of the Federal Reserve Bank of Philadelphia, and we use exactly the same 14 variables as in Carriero et al. (2016a), employing real-time vintages from 1965:Q1 to 2016:Q2. The quarterly values of the variables in each vintage reflect the information available at the middle of each quarter, while the t vintage contains data until t − 1 (Croushore & Stark, 2001). For instance, the available observations in the 1985:Q1 real-time vintage run through 1984:Q4. Following the literature, for the variables with immaterial or no revisions, such as the unemployment rate or the financial variables, we depart from the real-time approach and we use the last available vintage: 2016:Q2 in this paper. 11
6.3 Specification of the priors
In this section we concentrate on the specification of the priors with respect to the steady-state and time-varying steady-state parameters. For the prior elicitation of the rest of the parameters we follow closely the contributions of Carriero et al. (2016a, 2016b) and Chan (2018); full details are provided in Supporting Information Appendix D.
As regards the prior mean on the steady-state coefficients, θμ, we follow the recent literature and set the steady-state prior mean across all steady-state specifications—that is, SS, HSS, TVSS—according to the second column of Table 4 (see, e.g., Clark, 2011; Jarocinski & Smets, 2008; Österholm, 2012).
| θμ,j (%) |
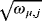 (%) (%) |
|
|---|---|---|
| GDP | 3 | 0.5 |
| Cons. | 3 | 0.7 |
| BFI | 3 | 1.5 |
| Resind. inv. | 3 | 1.5 |
| IP | 3 | 0.7 |
| Cap. util. | 80 | 0.7 |
| Empl. | 3 | 0.5 |
| Hours | 3 | 0.5 |
| UR | 6 | 1 |
| GDP def. | 2 | 0.5 |
| PCE def. | 2 | 0.5 |
| FFR | 5 | 0.7 |
| Spread | 1 | 1 |
| S&P 500 | 0 | 2 |
For the standard SS models we also have to elicit the diagonal elements of the prior covariance matrix, Ωμ. A typical but somewhat restrictive strategy in larger VAR models is to suppose a common prior variance across all variables (see, e.g., (Wright, 2013). To add more flexibility to the SS models we choose to specify a different prior standard deviation for each variable, presented in the third column of Table 4.
The hyperparameters related to the NG steady-state prior employed by the HSS models are specified in Section 2.1, while for the TVSS we also set the prior mean,
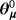 and covariance matrix,
and covariance matrix,
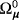 , of the initial conditions according to Table 4. For the degrees of freedom, dQ, and the scale matrix, SQ, in Equation 10, we follow a standard approach in the literature (see, e.g., (Primiceri, 2005) and we use a training sample for prior elicitation. In particular, we set dQ = T∗ and SQ=kQ·T∗·ΓQ, where T∗ = 40 is the number of observations in the training sample and ΓQ is a diagonal matrix the main diagonal of which contains the sample variance of the variables estimated over the presample. The hyperparameter kQ controls for the degree of time variation of the steady states and should be sensibly specified to avoid implausible behavior, hence we set kQ = 0.005.
, of the initial conditions according to Table 4. For the degrees of freedom, dQ, and the scale matrix, SQ, in Equation 10, we follow a standard approach in the literature (see, e.g., (Primiceri, 2005) and we use a training sample for prior elicitation. In particular, we set dQ = T∗ and SQ=kQ·T∗·ΓQ, where T∗ = 40 is the number of observations in the training sample and ΓQ is a diagonal matrix the main diagonal of which contains the sample variance of the variables estimated over the presample. The hyperparameter kQ controls for the degree of time variation of the steady states and should be sensibly specified to avoid implausible behavior, hence we set kQ = 0.005.
6.4 In-sample estimation and MCMC convergence
In general, throughout this paper, we estimate all constant volatility models using 6,000 draws after discarding the first 5,000 draws used for initial convergence (burn-in period). The estimation of all models encompassing stochastic volatility is also based on 1,000 retained draws, but now they are obtained from a total of 10,000 draws with 5,000 draws of burn-in period and a thinning of 5; that is, we keep one every five draws. The lag length for all models using variables in growth rates is set equal to 4 (p = 4), while for those using variables in log levels we use 5 lags (p = 5).
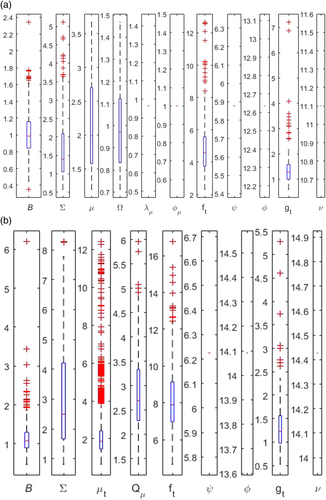
First, we evaluate the convergence of the proposed MCMC algorithms by implementing the inefficiency factors (IFs) metric of Primiceri (2005) . We present IF results for the most flexible models (i.e., HSS-CSV-t and TVSS-CSV-t) using the last vintage data of the US economy. More specifically, Figure 1 presents the box-plots of the inefficiency factors corresponding to the posterior draws of the parameters. Box-plots summarize visually the distribution of the inefficiency factors, with the middle line in the box being the median of the distribution, while the upper and lower lines are the 75 and 25 percentiles respectively. The tails in each box-plot are the maximum and minimum. The empirical evidence reveals that all maximum values are well below the threshold value of 20 (see Primiceri, 2005), meaning that the convergence of the Gibbs sampler is more than satisfactory and the proposed sampler can produce posterior draws that are not highly correlated.
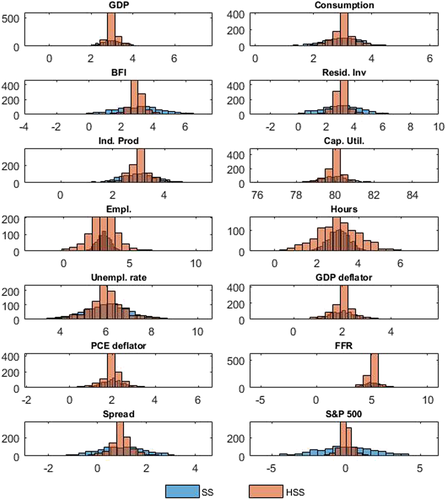
Next, we present in Figure 2 the steady-state prior distribution implied by the standard SS and hierarchical HSS models. 12For the SS model we simulate from a normal distribution with first and second moments given in Table 4, while for the HSS model we simulate from the marginal distribution of the steady-state parameters using a normal distribution with first moments given in Table 4 and second moments using the posterior estimates of ωμ,js. The histograms in Figure 2 reveal a typical shape of the NG prior, placing most of its mass around the predetermined mean values but at the same time allowing for fatter tails compared to an informative normal prior, thus giving the model enough space to draw information from the likelihood.
In Figures 3-6 we also present the posterior median of the steady-state parameter for four selected variables routinely examined in similar forecasting applications—that is, the real GDP growth rate, the unemployment rate, the GDP deflator, and the federal funds rate (FFR)—using the SS-CSV-t, HSS-CSV-t, and TVSS-CSV-t models. 13The steady-state estimates produced by the SS and HSS models (dotted and dashed lines, respectively) are very close to each other for the GDP and the FFR, while the HSS model produces lower estimates for the remaining two variables. More specifically, the SS model estimates the steady-state level for the unemployment rate (GDP deflator) at 5.36% (2.49%) as opposed to 5.12% (2.22%) of the HSS model. The intriguing point here is to examine whether these differences in estimates between the alternative methods have a significant effect on forecasting accuracy.
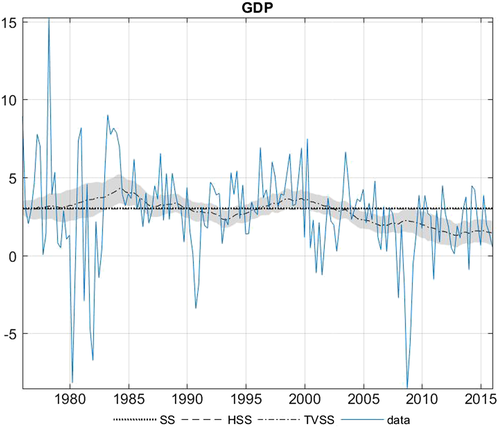
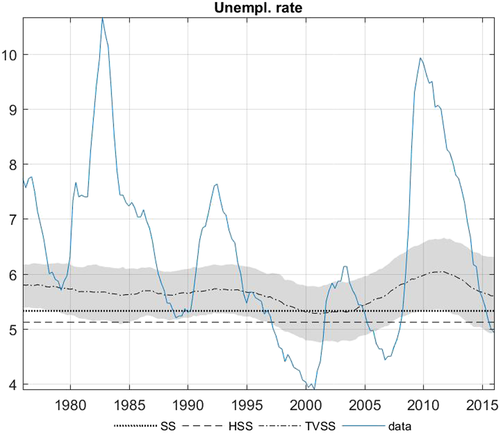

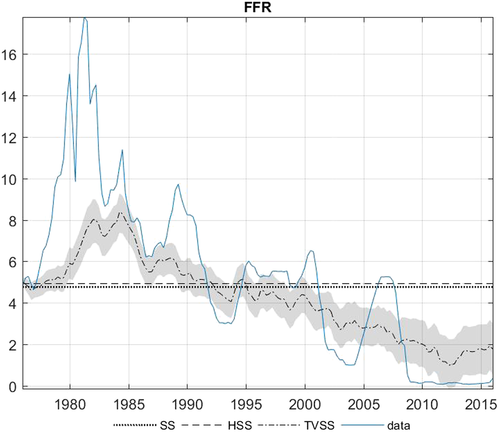
Estimation results regarding the TVSS model are, overall, in line with the stylized facts for the US economy. Particularly, the steady-state estimates for the GDP deflator and especially for the FFR have both an upward trend during the 1970s and the Great Inflation period and they de-escalate in the 1980s during the Great Moderation period. This empirical evidence aligns also with Chan and Koop (2014), who find a structural break on the steady state of inflation and the interest rates during the 1970s. Another interesting point is that during the Great recession (2007–2009) the steady-state level for all variables fall well below (above for the unemployment rate) the constant steady-state level (see the dashed and dotted straight lines). Finally, excluding GDP, all other variables seem to recover towards the end of the sample, probably pointing at a lower growth rate regime for the US economy.
6.5 Forecasting analysis and evaluation
We evaluate the alternative VAR specifications listed in Table 2 in terms of out-of-sample point and density forecasting. The out-of-sample evaluation period is from 1985:Q1 to 2015:Q4 and requires real-time data vintages from 1985:Q1 to 2016:Q2. Moreover, we follow the standard practice in the literature and we choose the second available estimate of the real-time variables as the observed value in the forecasting evaluation (see, e.g., the discussion in ; Clark, 2011; Carriero et al., 2016a and references therein). Following Chan (2018), we proceed with a recursive estimation of all models generating h-step-ahead iterated forecasts with h = 1, 2, 5, 9 and 13, which correspond to current quarter nowcasts, 1-quarter-ahead forecasts, 1-, 2-, and 3-year-ahead forecasts, due to reporting lags.
 (33)
(33) denotes the observed value, while
denotes the observed value, while
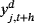 and
and
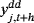 are independent random draws from the posterior predictive density. We follow Panagiotelis and Smith (2008) and we compute Equation 33 using the posterior draws from the MCMC output, where
are independent random draws from the posterior predictive density. We follow Panagiotelis and Smith (2008) and we compute Equation 33 using the posterior draws from the MCMC output, where
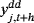 is obtained by independently resampling
is obtained by independently resampling
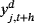 from the posterior predictive density without replacement. It is also worth noting that the aforementioned definition of the CRPS metric implies that the lower the values of the CRPS, the more accurate the predictive density is.
from the posterior predictive density without replacement. It is also worth noting that the aforementioned definition of the CRPS metric implies that the lower the values of the CRPS, the more accurate the predictive density is.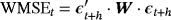 (34)
(34)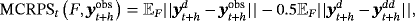 (35)
(35)Following the standard practice in the related literature, we present the results concerning both point and density metrics in relation to the benchmark VAR model. Thus we facilitate comparisons between the models and the benchmark, but also among the various competing models, since values of the relative metrics below one indicate that the corresponding model outperforms the benchmark and vice versa.
We also provide a rough gauge of whether the improvement in the forecasting accuracy relative to the benchmark is significant. To that end, we employ the Diebold and Mariano (1995) t-statistic for equal MSE and CRPS, both compared against normal critical values (see also ; Amisano & Giacomini, 2007). Following the literature, we choose the Diebold and Mariano (1995) test because it is considered a conservative test for nesting models in finite samples, in a sense that its size tends to be below the nominal size (Clark & McCracken, 2011, 2015). Therefore, we consider one-sided tests (we reject the null in favor of the benchmark and not the alternative model in favor of the benchmark), because most of the models can be viewed as nesting the benchmark (see, e.g., Carriero et al., 2016a). In addition, t-statistics are robust to serial correlation using a rectangular kernel with h − 1 lags for the variances, which are also adjusted according to Harvey, Leybourne, and Newbold (1997) in order to alleviate size distortions related to small samples.
6.6 Forecasting results
This section discusses the forecasting results generated by the various competing models using the real-time dataset for the US economy. Table 5 presents the overall point and density forecasting results using the WMSE and MCRPS metrics, respectively. Regarding the point forecasts the picture is clear cut. All models outperform the benchmark across all horizons, and the more flexible HSS-CSV-t model ranks first for horizons that are equal to or greater than 1 year—that is, for h = 5, 9, and 13, while the L-CSV-t model ranks first for current and next-quarter forecasts (h = 1 and 2). A closer look at panel A of Table 5 also reveals that the HSS-CSV-t outperforms the standard SS-type models across almost all horizons, with forecasting gains ranging between 0.3% for h = 2 to 3.6% for h = 13, highlighting the importance of the NG steady-state priors in forecasting applications. The TVSS type models are usually the second-best-performing class of models across all horizons and generally produce better short-term forecasts (h = 1 and 2) compared to the HSS-type models. 16Finally, in line with Carriero et al. (2016a, 2016b) and Chan (2018), among others, we find that, overall, the models that incorporate stochastic volatility and/or fat tails produce better forecasts compared to the models with constant volatility and Gaussian errors.
| Model | h = 1 | h = 2 | h = 5 | h = 9 | h = 13 |
|---|---|---|---|---|---|
| Panel A: WMSE | |||||
| L | 0.922*** | 0.906*** | 0.886** | 0.860* | 0.894 |
| L-t | 0.878*** | 0.847*** | 0.883** | 0.874* | 0.880 |
| L-CSV-t | 0.876*** | 0.844*** | 0.885** | 0.884* | 0.916 |
| SS | 0.971** | 0.968* | 0.930* | 0.902* | 0.868* |
| SS-t | 0.907*** | 0.904*** | 0.899** | 0.877* | 0.845* |
| SS-CSV-t | 0.899*** | 0.891*** | 0.887** | 0.860** | 0.825* |
| SS-SV | 0.908*** | 0.890** | 0.935* | 0.941* | 0.957* |
| HSS | 0.976* | 0.965* | 0.904** | 0.861* | 0.832* |
| HSS-t | 0.918*** | 0.904** | 0.888** | 0.838** | 0.808* |
| HSS-CSV-t | 0.901*** | 0.887*** | 0.870** | 0.820** | 0.789** |
| HSS-SV | 0.912*** | 0.902** | 0.958 | 0.965 | 0.989 |
| TVSS | 0.952*** | 0.950** | 0.922** | 0.884* | 0.843* |
| TVSS-t | 0.889*** | 0.878*** | 0.894** | 0.860** | 0.822** |
| TVSS-CSV-t | 0.892*** | 0.869*** | 0.874** | 0.847** | 0.812** |
| TVSS-SV | 0.879*** | 0.863*** | 0.879*** | 0.858** | 0.837** |
| Panel B: MCRPS | |||||
| L | 0.972** | 1.008 | 1.019 | 1.020 | 1.033 |
| L-t | 0.928*** | 0.970* | 1.000 | 1.033 | 1.053 |
| L-CSV-t | 0.927*** | 0.960** | 0.996 | 1.029 | 1.059 |
| SS | 1.013 | 1.006 | 0.987 | 0.967 | 0.945 |
| SS-t | 0.971* | 0.981 | 0.974 | 0.962 | 0.955 |
| SS-CSV-t | 0.964** | 0.973 | 0.981 | 0.970 | 0.954 |
| SS-SV | 0.972* | 0.976 | 1.019 | 1.051 | 1.070 |
| HSS | 1.018 | 1.012 | 0.987 | 0.959 | 0.944 |
| HSS-t | 0.979 | 0.985 | 0.981 | 0.953 | 0.943 |
| HSS-CSV-t | 0.969* | 0.977 | 0.987 | 0.963 | 0.952 |
| HSS-SV | 0.991 | 1.000 | 1.041 | 1.081 | 1.103 |
| TVSS | 0.985** | 0.988 | 1.013 | 1.010 | 1.029 |
| TVSS-t | 0.949*** | 0.959** | 0.995 | 1.002 | 1.028 |
| TVSS-CSV-t | 0.939*** | 0.943*** | 0.983 | 0.987 | 1.017 |
| TVSS-SV | 0.939*** | 0.944*** | 0.991 | 1.017 | 1.046 |
- Notes.
- 1. The table presents the ratios of the weighted mean squared errors (WMSEs) and the multivariate continuous ranked probability scores (MCRPSs) relative to the WMSEs and MCRPSs of the benchmark VAR model. Values below one indicate that the model outperforms the benchmark and vice versa. Bold entries indicate the best-performing model.
- 2. A short description of the competing models is provided in Table 2.
- 3. We provide a rough gauge that the gains in accuracy are statistically different from zero using the Diebold and Mariano (1995) t-statistics, computed with a serial-robust variance, using a rectangular kernel, h − 1 lags, and the small-sample adjustment of Harvey et al. (1997). Asterisks denote that the ratios are significantly below one at *10%, **5%, and ***1% significance level.
- 4. The out-of-sample evaluation period runs from 1985:Q1 to 2015:Q4 and all models in growth rates (log levels) are estimated recursively using four lags (five lags) . All variables are expressed as annualized percentages.
Turning to panel B of Table 5 and the joint density forecasting results, we see that the overall picture is slightly different compared to the point forecasting results presented in panel A. Now, only two classes of models outrank the benchmark across all forecasting horizons: the HSS- and SS-type models augmented with stochastic volatility and/or fat tails—that is, HSS-t, HSS-CSV-t, SS-t, and SS-CSV-t. Generally, the HSS-type models are again the best-performing models for h ≥ 9, with the HSS-t model ranking first for forecasting horizons of 2 and 3 years, while the L-CSV-t, TVSS-CSV-t, and SS-t models outrank their counterparts for h = 1, 2 and 5, respectively. The stochastic volatility and/or the t-distributed error terms improve materially the forecasting performance across models especially for shorter-term forecasting horizons, a result that is also supported by the empirical findings of Carriero et al. (2016a). In general, the empirical evidence presented so far suggests that for forecasting horizons exceeding 1 year steady-state priors play a crucial role in terms of density forecasting, while for nowcasts and shorter-terms horizons fat tails and stochastic volatility of either kind are the key factors that improve forecasting accuracy.
In Tables 6-9 we also provide point and density forecasting results for the real GDP, the unemployment rate, the GDP deflator, and the Fed Funds rate (the results for the rest of the variables are provided in the Supporting Information because of space considerations). Starting from GDP, it is evident that the HSS-type models augmented with stochastic volatility and/or t distributed innovations are usually the best-performing models for h ≥ 5 across evaluation metrics. In general, the results for GDP growth, but also for consumption, business fixed investment, residential investment, the spread and partially for hours and the S&P 500 are, on average, in line with the multivariate results presented in Table 5, with the HSS class prevailing over its rivals for longer-term forecasts. 12
| Model | h = 1 | h = 2 | h = 5 | h = 9 | h = 13 |
|---|---|---|---|---|---|
| Panel A: RMSE | |||||
| L | 0.957** | 0.955* | 0.967 | 0.978 | 0.971 |
| L-t | 0.922*** | 0.931* | 0.968 | 0.962 | 0.976 |
| L-CSV-t | 0.921*** | 0.914** | 0.967 | 0.962 | 0.979 |
| SS | 0.991 | 0.987 | 0.979 | 1.004 | 1.015 |
| SS-t | 0.934*** | 0.944** | 0.951* | 0.960 | 0.970 |
| SS-CSV-t | 0.951*** | 0.925** | 0.931* | 0.952 | 0.969 |
| SS-SV | 1.006 | 0.942 | 0.942 | 0.949 | 1.000 |
| HSS | 0.993 | 0.987 | 0.968* | 0.979 | 0.988 |
| HSS-t | 0.935*** | 0.940** | 0.954* | 0.940* | 0.957 |
| HSS-CSV-t | 0.947*** | 0.915*** | 0.933* | 0.936 | 0.958 |
| HSS-SV | 0.995 | 0.944* | 0.936* | 0.942 | 0.997 |
| TVSS | 1.044 | 1.058 | 1.039 | 1.026 | 1.016 |
| TVSS-t | 1.001 | 1.008 | 1.029 | 0.999 | 0.996 |
| TVSS-CSV-t | 1.010 | 0.988 | 1.004 | 0.985 | 0.995 |
| TVSS-SV | 1.022 | 0.986 | 1.019 | 0.985 | 0.995 |
| Panel B: CRPS | |||||
| L | 0.946*** | 1.059 | 1.054 | 1.078 | 1.092 |
| L-t | 0.890*** | 0.999 | 1.034 | 1.026 | 1.062 |
| L-CSV-t | 0.887*** | 0.986 | 1.015 | 1.022 | 1.073 |
| SS | 0.985** | 0.990 | 0.974 | 0.995 | 1.004 |
| SS-t | 0.923*** | 0.940*** | 0.944** | 0.940* | 0.958 |
| SS-CSV-t | 0.931*** | 0.923*** | 0.924** | 0.935* | 0.959 |
| SS-SV | 0.944** | 0.901*** | 0.898** | 0.926 | 0.963 |
| HSS | 0.986* | 0.981* | 0.968* | 0.970* | 0.975 |
| HSS-t | 0.928*** | 0.936*** | 0.946** | 0.917** | 0.948 |
| HSS-CSV-t | 0.932*** | 0.912*** | 0.919** | 0.920* | 0.950 |
| HSS-SV | 0.928*** | 0.904*** | 0.887** | 0.918* | 0.960 |
| TVSS | 1.026 | 1.042 | 1.027 | 1.024 | 1.015 |
| TVSS-t | 0.978 | 0.998 | 1.019 | 0.986 | 0.991 |
| TVSS-CSV-t | 0.979 | 0.968* | 0.986 | 0.975 | 0.987 |
| TVSS-SV | 0.960* | 0.938** | 0.965 | 0.955 | 0.959** |
- Notes.
- 1. The table presents the ratios of the average root mean squared errors (RMSEs) and the continuous ranked probability scores (CRPSs) relative to the RMSEs and CRPSs of the benchmark VAR model. Values below one indicate that the model outperforms the benchmark and vice versa. Bold entries indicate the best-performing model.
- 2. A short description of the competing models is provided in Table 2.
- 3. We provide a rough gauge that the gains in accuracy are statistically different from zero using the Diebold and Mariano (1995) t-statistics, computed with a serial-robust variance, using a rectangular kernel, h − 1 lags, and the small-sample adjustment of Harvey et al. (1997). Asterisks denote that the ratios are significantly below one at *10%, **5%, and ***1% significance level.
- 4. The out-of-sample evaluation period runs from 1985:Q1 to 2015:Q4 and all models in growth rates (log level) are estimated recursively using four lags (five lags). All variables are expressed as annualized percentages.
| Model | h = 1 | h = 2 | h = 5 | h = 9 | h = 13 |
|---|---|---|---|---|---|
| Panel A: RMSE | |||||
| L | 0.943* | 0.925* | 0.929 | 0.953 | 0.972 |
| L-t | 0.955* | 0.917* | 0.937 | 0.989 | 1.019 |
| L-CSV-t | 0.940** | 0.904** | 0.913 | 0.978 | 1.018 |
| SS | 1.027 | 1.044 | 1.049 | 1.032 | 1.007 |
| SS-t | 1.019 | 1.021 | 1.028 | 1.038 | 1.007 |
| SS-CSV-t | 1.009 | 1.009 | 1.004 | 1.018 | 0.991 |
| SS-SV | 0.971 | 0.935 | 0.951 | 0.978 | 0.970 |
| HSS | 1.007 | 1.014 | 1.019 | 1.015 | 0.991 |
| HSS-t | 1.003 | 0.997 | 1.011 | 1.026 | 0.996 |
| HSS-CSV-t | 0.995 | 0.984 | 0.982 | 1.003 | 0.979 |
| HSS-SV | 0.971 | 0.929* | 0.942 | 0.968 | 0.967 |
| TVSS | 1.025 | 1.047 | 1.060 | 1.052 | 1.000 |
| TVSS-t | 1.030 | 1.030 | 1.050 | 1.060 | 1.011 |
| TVSS-CSV-t | 1.023 | 1.020 | 1.025 | 1.044 | 1.001 |
| TVSS-SV | 1.008 | 0.992 | 1.018 | 1.046 | 1.006 |
| Panel B: CRPS | |||||
| L | 0.948** | 0.928** | 0.922 | 0.942 | 0.961 |
| L-t | 0.913*** | 0.912** | 0.938 | 0.990 | 1.013 |
| L-CSV-t | 0.905*** | 0.899** | 0.906 | 0.969 | 1.013 |
| SS | 1.019 | 1.076 | 1.129 | 1.098 | 1.047 |
| SS-t | 0.991 | 1.054 | 1.116 | 1.115 | 1.050 |
| SS-CSV-t | 0.987 | 1.044 | 1.075 | 1.080 | 1.024 |
| SS-SV | 0.963* | 0.959 | 0.977 | 1.000 | 0.981 |
| HSS | 1.000 | 1.023 | 1.069 | 1.056 | 1.008 |
| HSS-t | 0.978 | 1.012 | 1.072 | 1.071 | 1.015 |
| HSS-CSV-t | 0.961** | 1.001 | 1.019 | 1.027 | 0.985 |
| HSS-SV | 0.954** | 0.949* | 0.957 | 0.978 | 0.971 |
| TVSS | 1.040 | 1.067 | 1.095 | 1.087 | 1.012 |
| TVSS-t | 1.001 | 1.035 | 1.086 | 1.109 | 1.039 |
| TVSS-CSV-t | 0.988 | 1.026 | 1.065 | 1.091 | 1.025 |
| TVSS-SV | 0.986 | 1.002 | 1.051 | 1.101 | 1.044 |
- Notes.
- 1. The table presents the ratios of the average root mean squared errors (RMSEs) and the continuous ranked probability scores (CRPSs) relative to the RMSEs and CRPSs of the benchmark VAR model. Values below one indicate that the model outperforms the benchmark and vice versa. Bold entries indicate the best-performing model.
- 2. A short description of the competing models is provided in Table 2.
- 3. We provide a rough gauge that the gains in accuracy are statistically different from zero using the Diebold and Mariano (1995) t-statistics, computed with a serial-robust variance, using a rectangular kernel, h − 1 lags, and the small-sample adjustment of Harvey et al. (1997). Asterisks denote that the ratios are significantly below one at *10%, **5%, and ***1% significance level.
- 4. The out-of-sample evaluation period runs from 1985:Q1 to 2015:Q4 and all models in growth rates (log level) are estimated recursively using four lags (five lags). All variables are expressed in annualized percentages.
| Model | h = 1 | h = 2 | h = 5 | h = 9 | h = 13 |
|---|---|---|---|---|---|
| Panel A: RMSE | |||||
| L | 0.902** | 0.837*** | 0.671*** | 0.635** | 0.715* |
| L-t | 0.881*** | 0.794*** | 0.630*** | 0.576** | 0.614* |
| L-CSV-t | 0.875*** | 0.799*** | 0.638*** | 0.601** | 0.657* |
| SS | 0.930* | 0.859** | 0.736** | 0.677** | 0.632* |
| SS-t | 0.916** | 0.840** | 0.696** | 0.651** | 0.623* |
| SS-CSV-t | 0.906** | 0.828*** | 0.670** | 0.628** | 0.595* |
| SS-SV | 0.948** | 0.945** | 0.891** | 0.874** | 0.870* |
| HSS | 0.921** | 0.859** | 0.729** | 0.675** | 0.644* |
| HSS-t | 0.926** | 0.847** | 0.710** | 0.658** | 0.627* |
| HSS-CSV-t | 0.903** | 0.832*** | 0.670** | 0.611** | 0.579* |
| HSS-SV | 0.965** | 0.982 | 0.962* | 0.957 | 0.957 |
| TVSS | 0.908** | 0.831** | 0.703** | 0.655** | 0.602* |
| TVSS-t | 0.887** | 0.806*** | 0.666** | 0.608** | 0.549** |
| TVSS-CSV-t | 0.885** | 0.804*** | 0.651*** | 0.597** | 0.540** |
| TVSS-SV | 0.893** | 0.820*** | 0.658** | 0.621** | 0.587** |
| Panel B: CRPS | |||||
| L | 0.914*** | 0.879** | 0.687*** | 0.594** | 0.632* |
| L-t | 0.907*** | 0.858*** | 0.651*** | 0.579** | 0.617* |
| L-CSV-t | 0.895*** | 0.850*** | 0.657*** | 0.574** | 0.617* |
| SS | 0.944* | 0.881** | 0.735** | 0.645** | 0.596* |
| SS-t | 0.927** | 0.860*** | 0.696** | 0.626** | 0.591* |
| SS-CSV-t | 0.918** | 0.849*** | 0.674*** | 0.601** | 0.563* |
| SS-SV | 0.966* | 0.948** | 0.879** | 0.859** | 0.854* |
| HSS | 0.934** | 0.879** | 0.727** | 0.646** | 0.608* |
| HSS-t | 0.943** | 0.872** | 0.708** | 0.636** | 0.597* |
| HSS-CSV-t | 0.916** | 0.849*** | 0.670*** | 0.590** | 0.550* |
| HSS-SV | 0.975* | 0.979 | 0.944* | 0.945 | 0.954 |
| TVSS | 0.929** | 0.847*** | 0.693*** | 0.620** | 0.565* |
| TVSS-t | 0.918** | 0.836*** | 0.656*** | 0.577** | 0.517* |
| TVSS-CSV-t | 0.909** | 0.831*** | 0.644*** | 0.570** | 0.508** |
| TVSS-SV | 0.930* | 0.853*** | 0.656*** | 0.598** | 0.556** |
- Notes.
- 1. The table presents the ratios of the average root mean squared errors (RMSEs) and the continuous ranked probability scores (CRPSs) relative to the RMSEs and CRPSs of the benchmark VAR model. Values below one indicate that the model outperforms the benchmark and vice versa. Bold entries indicate the best-performing model.
- 2. A short description of the competing models is provided in Table 2.
- 3. We provide a rough gauge that the gains in accuracy are statistically different from zero using the Diebold and Mariano (1995) t-statistics, computed with a serial-robust variance, using a rectangular kernel, h − 1 lags, and the small-sample adjustment of Harvey et al. (1997). Asterisks denote that the ratios are significantly below one at *10%, **5%, and ***1% significance level.
- 4. The out-of-sample evaluation period runs from 1985:Q1 to 2015:Q4 and all models in growth rates (log level) are estimated recursively using four lags (five lags). All variables are expressed as annualized percentages.
| Model | h = 1 | h = 2 | h = 5 | h = 9 | h = 13 |
|---|---|---|---|---|---|
| Panel A: RMSE | |||||
| L | 0.850*** | 0.988 | 0.968 | 0.923 | 0.916 |
| L-t | 0.733*** | 0.852*** | 0.923 | 0.937 | 0.941 |
| L-CSV-t | 0.726*** | 0.846*** | 0.903 | 0.925 | 0.965 |
| SS | 1.014 | 0.988 | 0.930** | 0.840** | 0.768* |
| SS-t | 0.962** | 0.950** | 0.908** | 0.848** | 0.807* |
| SS-CSV-t | 0.945*** | 0.950* | 0.904** | 0.842** | 0.804* |
| SS-SV | 0.752*** | 0.848** | 0.987 | 1.023 | 1.018 |
| HSS | 1.016 | 0.998 | 0.930** | 0.863* | 0.814* |
| HSS-t | 0.959 | 0.958* | 0.915** | 0.871** | 0.839 |
| HSS-CSV-t | 0.923*** | 0.934** | 0.901** | 0.856** | 0.827* |
| HSS-SV | 0.746*** | 0.843*** | 0.977 | 1.018 | 1.015 |
| TVSS | 0.934 | 0.918 | 0.881** | 0.814* | 0.714* |
| TVSS-t | 0.881** | 0.886** | 0.865** | 0.815** | 0.726* |
| TVSS-CSV-t | 0.866*** | 0.876** | 0.867** | 0.816** | 0.727* |
| TVSS-SV | 0.746*** | 0.809*** | 0.861*** | 0.842** | 0.800** |
| Panel B: CRPS | |||||
| L | 0.905*** | 0.984 | 0.933 | 0.855 | 0.778 |
| L-t | 0.734*** | 0.810*** | 0.874 | 0.858 | 0.827 |
| L-CSV-t | 0.711*** | 0.799*** | 0.862* | 0.849 | 0.824 |
| SS | 0.997 | 0.974* | 0.917** | 0.835** | 0.752* |
| SS-t | 0.898*** | 0.911*** | 0.901** | 0.853** | 0.799* |
| SS-CSV-t | 0.847*** | 0.894*** | 0.895** | 0.844** | 0.798* |
| SS-SV | 0.648*** | 0.788*** | 1.018 | 1.052 | 1.039 |
| HSS | 1.006 | 0.990 | 0.912** | 0.855** | 0.793* |
| HSS-t | 0.908*** | 0.918** | 0.908** | 0.877** | 0.833 |
| HSS-CSV-t | 0.843*** | 0.889*** | 0.892** | 0.853** | 0.823 |
| HSS-SV | 0.649*** | 0.782*** | 1.006 | 1.047 | 1.043 |
| TVSS | 0.912*** | 0.904** | 0.873** | 0.813** | 0.693** |
| TVSS-t | 0.810*** | 0.835*** | 0.858** | 0.823** | 0.713** |
| TVSS-CSV-t | 0.772*** | 0.811*** | 0.856** | 0.822** | 0.712** |
| TVSS-SV | 0.662*** | 0.751*** | 0.856*** | 0.833** | 0.781** |
- Notes.
- 1. The table presents the ratios of the average root mean squared errors (RMSEs) and the continuous ranked probability scores (CRPSs) relative to the RMSEs and CRPSs of the benchmark VAR model. Values below one indicate that the model outperforms the benchmark and vice versa. Bold entries indicate the best-performing model.
- 2. A short description of the competing models is provided in Table 2.
- 3. We provide a rough gauge that the gains in accuracy are statistically different from zero using the Diebold and Mariano (1995) t-statistics, computed with a serial-robust variance, using a rectangular kernel, h − 1 lags, and the small-sample adjustment of Harvey et al. (1997). Asterisks denote that the ratios are significantly below one at *10%, **5%, and ***1% significance level.
- 4. The out-of-sample evaluation period runs from 1985:Q1 to 2015:Q4 and all models in growth rates (log level) are estimated recursively using four lags (five lags). All variables are expressed as annualized percentages.
By contrast, for the nominal variables GDP deflator and FFR, the TVSS-type models are typically the best performers across all forecasting horizons (with the exception of the point forecasts for the GDP deflator). This also holds true for some of the real variables of the model such as industrial production, capacity utilization, and employment, and partly for residential investment (for h = 1, 2, and 5), where the TVSS models usually rank among the best models and never forecast poorly. To shed more light on this interesting empirical finding we should go back to the figures presenting the steady-state estimates (see Figures 3-6 in Section 6.4 and Supporting Information Figures F.2–F.11). A more detailed look at the relevant figures reveals that the time-varying steady-state estimates for the above-mentioned variables share a common characteristic: They fall consistently well below the constant steady-state estimates after 2000, probably capturing a structural break on the unconditional mean of these variables. See, for instance, the steady-state estimates for the capacity utilization, which after 2000 fluctuates around 76% as opposed to 80% estimated by the constant steady-state models; or the steady-state of FFR, which declines constantly after 2000 and stabilizes slightly below 2% after 2012. This evidence underlines the empirical relevance of the proposed time-varying specification in cases where the unconditional mean of the variable has undergone a significant structural change.
Finally, the results for the unemployment rate presented in Table 7 reveal that generally steady-state models do not consistently outperform the benchmark except for the HSS-SV model, which outranks the benchmark across all horizons. The models in log levels typically rank first, with the exception of the 3 years forecasting horizon, where the HSS-SV model beats its counterparts.
For robustness we also present results concerning an out-of-sample period ending in 2007:Q4 and excluding the global financial crisis. The joint forecasting results are presented in Table 10 and are qualitatively similar to those for the full out-of-sample period. The only exception is for the short-term point forecasts, where now the TVSS-SV model ranks first. The results for each variable separately for the normal out-of-sample period 1985:Q1–2007:Q4 are presented in the Supporting Information.
| Model | h = 1 | h = 2 | h = 5 | h = 9 | h = 13 |
|---|---|---|---|---|---|
| Panel A: WMSE | |||||
| L | 0.938*** | 0.936** | 0.914** | 0.900 | 0.972 |
| L-t | 0.890*** | 0.885*** | 0.891** | 0.903 | 0.928 |
| L-CSV-t | 0.887*** | 0.877*** | 0.892** | 0.916 | 0.990 |
| SS | 0.952** | 0.943** | 0.880** | 0.830* | 0.765* |
| SS-t | 0.896*** | 0.894*** | 0.849** | 0.815* | 0.756* |
| SS-CSV-t | 0.889*** | 0.882*** | 0.833** | 0.806** | 0.745* |
| SS-SV | 0.910*** | 0.903*** | 0.891** | 0.931* | 0.927** |
| HSS | 0.956** | 0.936** | 0.834** | 0.751** | 0.695** |
| HSS-t | 0.908*** | 0.885*** | 0.821** | 0.744** | 0.685** |
| HSS-CSV-t | 0.883*** | 0.870*** | 0.800*** | 0.729** | 0.675** |
| HSS-SV | 0.915*** | 0.909*** | 0.915* | 0.967 | 0.993 |
| TVSS | 0.925*** | 0.920*** | 0.859** | 0.786** | 0.731** |
| TVSS-t | 0.873*** | 0.866*** | 0.838*** | 0.784** | 0.728** |
| TVSS-CSV-t | 0.884*** | 0.866*** | 0.834*** | 0.771** | 0.715** |
| TVSS-SV | 0.868*** | 0.856*** | 0.810*** | 0.771** | 0.718** |
| Panel B: MCRPS | |||||
| L | 0.970** | 1.018 | 1.027 | 1.035 | 1.058 |
| L-t | 0.922*** | 0.978 | 1.006 | 1.043 | 1.068 |
| L-CSV-t | 0.918*** | 0.964** | 1.003 | 1.040 | 1.081 |
| SS | 1.011 | 0.999 | 0.972 | 0.941 | 0.912* |
| SS-t | 0.971* | 0.979 | 0.971 | 0.942 | 0.914* |
| SS-CSV-t | 0.959** | 0.972 | 0.972 | 0.948 | 0.912* |
| SS-SV | 0.964** | 0.973 | 1.012 | 1.040 | 1.055 |
| HSS | 1.018 | 1.010 | 0.975 | 0.934 | 0.912* |
| HSS-t | 0.980 | 0.985 | 0.976 | 0.932 | 0.898* |
| HSS-CSV-t | 0.962* | 0.976 | 0.984 | 0.940 | 0.911* |
| HSS-SV | 0.985 | 0.995 | 1.033 | 1.085 | 1.108 |
| TVSS | 0.974*** | 0.978** | 1.002 | 0.961* | 0.951* |
| TVSS-t | 0.935*** | 0.948*** | 0.982 | 0.957* | 0.947* |
| TVSS-CSV-t | 0.919*** | 0.935*** | 0.973* | 0.942** | 0.940* |
| TVSS-SV | 0.926*** | 0.936*** | 0.972* | 0.965* | 0.963* |
- Notes.
- 1. The table presents the ratios of the weighted mean squared errors (WMSEs) and the multivariate continuous ranked probability scores (MCRPSs) relative to the WMSEs and MCRPSs of the benchmark VAR model. Values below one indicate that the model outperforms the benchmark and vice versa. Bold entries indicate the best-performing model.
- 2. A short description of the competing models is provided in Table 2.
- 3. We provide a rough gauge that the gains in accuracy are statistically different from zero using the Diebold and Mariano (1995) t-statistics, computed with a serial-robust variance, using a rectangular kernel, h − 1 lags, and the small-sample adjustment of Harvey et al. (1997). Asterisks denote that the ratios are significantly below one at *10%, **5%, and ***1 % significance level, respectively.
- 4. The out-of-sample evaluation period runs from 1985:Q1 to 2007:Q4 and all models in growth rates (log level) are estimated recursively using four lags (five lags). All variables are expressed as annualized percentages.
Overall, we provide empirical evidence that VAR models with NG steady-state priors can materially improve forecasting quality upon standard steady-state models or models using variables in log levels for forecasting horizons greater than 1 year. The models using a time-varying steady-state specification produce superior forecasts across all forecasting horizons in the case of structural changes in the unconditional mean of the process. Finally, the performance of the proposed models is further improved when we account for the stochastic volatility and/or fat tails of the error terms.
7 CONCLUSIONS
Empirical evidence in the literature suggests that informative steady-state priors play a crucial role in macroeconomic forecasting and improve considerably the long-term forecasting behavior of the VAR models. The main scope of this article is to examine whether alternative specifications and extensions of the standard steady-state VARs can improve macroeconomic forecasting against established benchmarks. Specifically, we first use the insights of hierarchical modeling and we propose the adaptive hierarchical NG prior for the steady-state parameters (i.e., a purely Bayesian approach) for determining the steady-state prior informativeness. Next, we propose a time-varying steady-state specification aiming to capture structural changes in the unconditional mean of the process. Lastly, the proposed steady-state specifications are generalized by taking into account the stochastic volatility and the fat tails of the error terms. The proposed models are estimated using the Gibbs and Metropolis-within-Gibbs algorithms based on the derived conditional posterior distributions.
The evidence presented in this paper, based on a large real-time dataset of 14 variables from the US economy, clearly demonstrates that, overall, the NG steady-state prior models outperform the steady-state and other benchmark VARs in terms of out-of-sample point and density forecasting for horizons that usually exceed 1 year. On the other hand, time-varying steady-state models typically produce more accurate forecasts for those variables, for example for the interest rate or the capacity utilization, characterized by significant structural changes in the their unconditional means. The incorporation of stochastic volatility and fat tails for the innovations of the model also plays a crucial role especially in short-term macroeconomic forecasting quality, as expected. The good forecasting performance of the proposed models in conjunction with the appealing properties and the flexibility of the hierarchical and time-varying modeling methods suggest that our approaches might be seen as a useful device for macroeconomic forecasting.
ACKNOWLEDGMENTS
The author gratefully acknowledges Heather Gibson, Dimitris Korobilis, the Editor Fabio Canova, and three anonymous reviewers for their constructive and insightful comments and suggestions, which considerably improved the quality of the article. The views expressed in this article do not necessarily represent the Bank of Greece.
APPENDIX A: HIERARCHICAL STEADY-STATE VEC MODEL
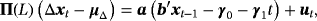 (A.1)
(A.1)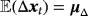 , while the mean of the long-run equilibrium is
, while the mean of the long-run equilibrium is
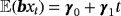 .
.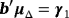 and
and
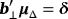 , where b⊥ is an n × (n − k) matrix orthogonal to b and δ is a (n − k)-dimensional vector of unrestricted parameters—Villani (2005) proposes the following priors on a,
, where b⊥ is an n × (n − k) matrix orthogonal to b and δ is a (n − k)-dimensional vector of unrestricted parameters—Villani (2005) proposes the following priors on a,
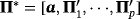 and
and
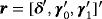 :
:
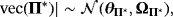 (A.2)
(A.2)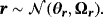 (A.3)
(A.3)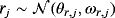 (A.4)
(A.4)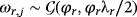 (A.5)
(A.5)The properties of the NG prior discussed in Section 2.1 also hold for the SS-VEC model, with hyperparameter λr controlling for the overall tightness of the prior and ϕr for the excess kurtosis.
Villani (2005) proposes a Gibbs sampler to draw iteratively from the full conditional posteriors of Π∗ and r given that b is known (see also (Villani, 2009), for an alternative approach).
-12 In the case of the NG prior and assuming that ϕr∼exp(1) and
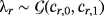 , the Gibbs sampler is completed with the following steps:
, the Gibbs sampler is completed with the following steps:
 (A.6)
(A.6)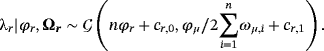 (A.7)
(A.7)Finally, ϕr is updated using a random-walk Metropolis step analogous to the one applied for the stationary HSS-VAR.
APPENDIX B: HIERARCHICAL SHRINKAGE AND TIME VARIATION IN STEADY STATES
B.1 The model
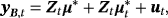 (B.1)
(B.1)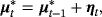 (B.2)
(B.2)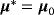 ,
,
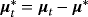 and the initial condition for
and the initial condition for
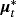 is a Dirac delta function concentrated at zero; that is,
is a Dirac delta function concentrated at zero; that is,
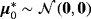 . This parametrization allows us to separate out the initial condition, μ0, by decomposing the model into a constant parameter (
. This parametrization allows us to separate out the initial condition, μ0, by decomposing the model into a constant parameter (
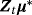 ) and a time-varying (
) and a time-varying (
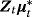 ) parameter part. Thus, concentrating on the initial condition, we specify a NG prior as follows:
) parameter part. Thus, concentrating on the initial condition, we specify a NG prior as follows:
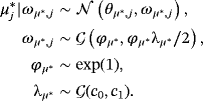 (B.3)
(B.3)In terms of estimation, conditional on
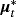 we have a standard HSS model and we can use Step 6.I of the Gibbs algorithm presented in the Technical Appendix C.2 to draw from the posterior distribution of μ∗. The only difference is that now we use
we have a standard HSS model and we can use Step 6.I of the Gibbs algorithm presented in the Technical Appendix C.2 to draw from the posterior distribution of μ∗. The only difference is that now we use
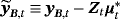 instead of yB,t. Next, conditional on μ∗, we use Step 6.II to draw from the posterior of
instead of yB,t. Next, conditional on μ∗, we use Step 6.II to draw from the posterior of
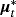 using again
using again
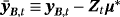 instead of yB,t and zero mean and variance initial conditions. Finally, we obtain draws of μt by using the identity
instead of yB,t and zero mean and variance initial conditions. Finally, we obtain draws of μt by using the identity
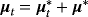 .
.
B.2 Forecasting results
Table B1 presents the forecasting results for the hierarchical TVSS-VAR model against the standard TVSS-VAR model presented in Section 2.2 across all variables and forecasting horizons. The first row of each panel (panels A and B) shows the overall point and density forecasting performance of the model using the multivariate evaluation metrics. Overall, the results clearly indicate that the two models have similar forecasting performance, with the hierarchical TVSS model being only marginally better. However, this outcome does not affect the overall picture of the forecasting analysis presented in Section 6.6.
| Models | h = 1 | h = 2 | h = 5 | h = 9 | h = 13 |
|---|---|---|---|---|---|
| Panel A: (W)MSE | |||||
| Overall (WMSE) | 1.001 | 0.997 | 0.994 | 0.991 | 0.992 |
| Real GDP | 1.001 | 0.992 | 1.011 | 1.004 | 0.988 |
| Consumption | 0.996 | 1.006 | 0.999 | 0.994 | 0.991 |
| Business fixed inv. (BFI) | 0.998 | 0.990** | 0.990* | 1.004 | 1.007 |
| Resind. inv. | 1.012 | 1.012 | 0.998 | 0.984* | 0.990 |
| Ind. prod. | 0.992* | 0.991* | 1.001 | 0.994* | 0.989* |
| Cap. util. | 0.994 | 0.991 | 0.993 | 1.008 | 1.023 |
| Employment | 1.001 | 0.995 | 1.004 | 1.004 | 0.986 |
| Hours | 1.000 | 0.993 | 1.008 | 1.003 | 0.983* |
| Unempl. rate | 1.001 | 0.994 | 0.992 | 0.999 | 1.007 |
| GDP deflator | 1.009 | 1.020 | 0.985 | 0.970 | 0.969 |
| PCE deflator | 0.994 | 0.995 | 0.987 | 0.968 | 0.958 |
| Fed funds rate | 1.010 | 1.006 | 0.988 | 0.986 | 1.006 |
| Term spread | 1.008 | 1.004 | 0.994 | 0.974 | 0.981 |
| Real stock prices | 1.001 | 1.000 | 0.991** | 1.003 | 1.002 |
| Panel B: (M)CRPS | |||||
| Overall (MCRPS) | 1.001 | 1.001 | 0.991** | 0.995 | 0.999 |
| Real GDP | 1.004 | 0.995 | 1.013 | 1.001 | 0.991 |
| Consumption | 0.995 | 1.013 | 1.005 | 0.998 | 0.999 |
| Business fixed inv. (BFI) | 0.997 | 0.993 | 0.984* | 1.008 | 1.009 |
| Resind. inv. | 1.011 | 1.005 | 1.001 | 0.989 | 0.991 |
| Ind. prod. | 0.994 | 0.993 | 0.999 | 0.993 | 0.995 |
| Cap. util. | 0.993 | 0.996 | 0.991 | 1.009 | 1.033 |
| Employment | 1.003 | 0.995 | 1.008 | 1.009 | 0.986 |
| Hours | 1.006 | 0.994 | 1.013 | 1.005 | 0.988 |
| Unempl. rate | 0.994 | 0.988 | 0.985 | 0.997 | 1.010 |
| GDP deflator | 1.012 | 1.018 | 0.981 | 0.982 | 0.973 |
| PCE deflator | 0.997 | 0.999 | 0.982 | 0.972 | 0.961 |
| Fed funds rate | 1.000 | 1.005 | 0.987 | 0.987 | 1.009 |
| Term spread | 1.005 | 1.003 | 0.995 | 0.971 | 0.977 |
| Real stock prices | 1.004 | 1.000 | 0.988** | 1.006 | 1.003 |
- Notes.
- 1. The table presents the ratios of the (weighted) mean squared errors ((W)MSEs) and the (multivariate) continuous ranked probability scores ((M)CRPSs) produced by the hierarchical TVSS-VAR model relative to the (W)MSFEs and (M)CRPSs of the benchmark TVSS-VAR model. Values below one indicate that the hierarchical TVSS-VAR outperforms the benchmark and vice versa.
- 2. We provide a rough gauge that the gains in accuracy are statistically different from zero using the Diebold and Mariano (1995) t-statistics, computed with a serial-robust variance, using a rectangular kernel, h − 1 lags, and the small-sample adjustment of Harvey et al. (1997). Asterisks denote that the ratios are significantly below one at *10%, **5%, and ***1% significance level.
- 3. The out-of-sample evaluation period runs from 1985:Q1 to 2015:Q4 and the models are estimated recursively using four lags. All variables are expressed as annualized percentages.
APPENDIX C: TECHNICAL APPENDIX
C.1 Derivations of conditional posterior distributions related to the NG steady-state prior
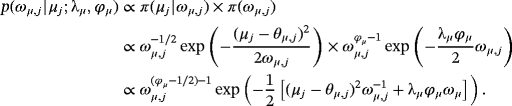 (C.1)
(C.1)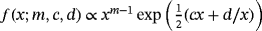 . Analogously, the conditional posterior distribution of λμ in Equation 27 is derived as follows:
. Analogously, the conditional posterior distribution of λμ in Equation 27 is derived as follows:
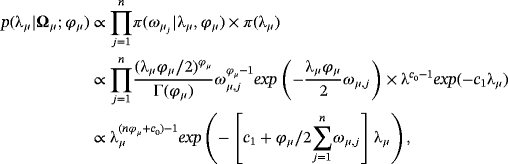 (C.2)
(C.2)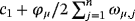 , respectively. The conditional posterior distribution of hyperparameter ϕμ is given by
, respectively. The conditional posterior distribution of hyperparameter ϕμ is given by
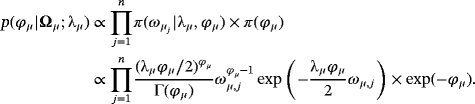 (C.3)
(C.3)C.2 Gibbs sampler for steady-state VARs with common stochastic volatility and t errors
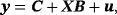 (C.4)
(C.4)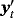 , C is a T × n matrix with tth row c′,
, C is a T × n matrix with tth row c′,
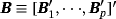 , X is a T × np matrix with its tth row being
, X is a T × np matrix with its tth row being
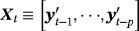 , and u is the T × n matrix of the residuals. Equivalently, a mean-adjusted VAR can be written as
, and u is the T × n matrix of the residuals. Equivalently, a mean-adjusted VAR can be written as
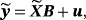 (C.5)
(C.5)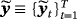 ,
,
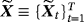 ,
,
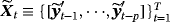 and
and
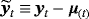 .
.For estimation of the VAR models with common stochastic volatility and student t errors we extent the MCMC algorithm of Carriero et al. (2016a) and Chan (2018) to accommodate the proposed steady-state specifications. Specifically, we follow Del Negro and Primiceri (2015), who implement the multi-move algorithm of Kim, Shephard, and Chib (1998) (KSC hereafter) to estimate the unobserved components of stochastic volatility and Chan (2018) to estimate the parameters related to the t errors specification. -15
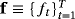 ,
,
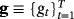 , and
, and
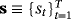 , where st is a 1 × n vector with each element selecting the component of the normal mixture approximation (for more details see also Supporting Information Appendix E). Next, we describe the essential steps of the Gibbs sampler, where we draw each parameter block sequentially from the corresponding full conditional posterior:
, where st is a 1 × n vector with each element selecting the component of the normal mixture approximation (for more details see also Supporting Information Appendix E). Next, we describe the essential steps of the Gibbs sampler, where we draw each parameter block sequentially from the corresponding full conditional posterior:
- Step 1. Draw f|B,Σ,μ(t),ψ,ϕ,s,g,y using the KSC approximation, the Kalman filter, and the simulation smoother of Carter and Kohn (1994) (see also Supporting Information Appendix E).
- Step 2. Draw B|Σ,μ(t),f,g,y from
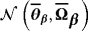 , where
, where
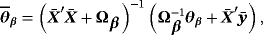 (C.6)with
(C.6)with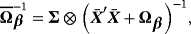 (C.7)
(C.7)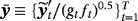 and
and
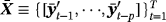 being the rescaled data matrices
being the rescaled data matrices
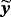 and
and
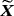 , respectively.
, respectively. - Step 3. Draw Σ|B,μ(t),f,g,y from
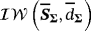 , where
, where
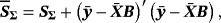 (C.8)
(C.8)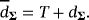 (C.9)
(C.9) - Step 4. Draw ψ|B,Σ,μ(t),ϕ,f,g,y from
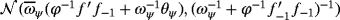 , where f and f−1 are T × 1 vectors defined as
, where f and f−1 are T × 1 vectors defined as
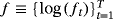 and
and
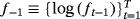 , respectively.
, respectively. - Step 5. Draw ϕ|B,Σ,μ(t),ψ,f,g,y from
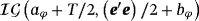 where e is a T × 1 vector collecting et, t = 1,…,T.
where e is a T × 1 vector collecting et, t = 1,…,T. -
Step 6. Draw steady-state coefficients μ(t) using
I. An NG prior
-
Draw μ|Ωμ,B,Σ,f,g,y from
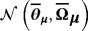 , where
, where
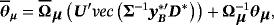 (C.10)where
(C.10)where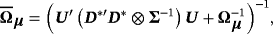 (C.11)
(C.11)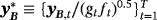 , yB,t = yt − XtB,
, yB,t = yt − XtB,
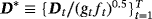 ,
,
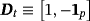 with 1ξ being a 1 × ξ vector of ones and
with 1ξ being a 1 × ξ vector of ones and
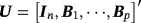 .
. - Draw ωμ,j, j = 1,…,n, λμ and ϕμ as described in Equations 26-27 and 28 in the main text, respectively.
II. A time-varying steady state specification
- Draw μt|μ0,B,Σ,f,g,y using the Carter and Kohn (1994) (CK) algorithm and the state-space representation of the model in Equations 29 and 8 in the main text. In particular, we have
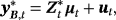 (C.12)where
(C.12)where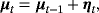 (C.13)
(C.13)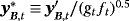 and
and
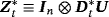 with
with
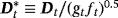 are the rescaled data matrices defined in Section 4.2. Given the initial conditions we apply the Kalman filter and the CK smoother (for more details see (Louzis, 2016a).
are the rescaled data matrices defined in Section 4.2. Given the initial conditions we apply the Kalman filter and the CK smoother (for more details see (Louzis, 2016a). - Draw Q|μt,B,Σ,f,g,y from
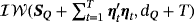 .
.
-
- Step 7. Draw gt|μ(t),B,Σ,f,ν,y, ∀t, conditional on other parameters from
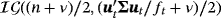 .
. - Step 8. Draw ν conditional on other parameters and data using an independence-chain Metropolis–Hastings step as proposed in Chan (2018). -14
- Step 9. Draw s|,Σ,μ,ψ,ϕ,f,y as described in more detail in Supporting Information Appendix E.
The HSS and TVSS models with constant volatility and Gaussian errors are estimated by setting ft = 1 and gt = 1 ∀t, while for the HSS-t and TVSS-t models we set ft = 1 ∀t. For both cases we omit the respective Gibbs steps.
Open Research
OPEN RESEARCH BADGES

This article has earned an Open Data Badge for making publicly available the digitally-shareable data necessary to reproduce the reported results. The data is available at [http://qed.econ.queensu.ca/jae/2019-v34.2/louzis/].
REFERENCES
- 1 See, for example, Koop and Korobilis (2010) and Karlsson (2013) for excellent BVAR reviews, and Dieppe, Legrand, and van Roye (2016) for the Bayesian estimation, analysis and regression (BEAR) MATLAB toolbox developed by the European Central Bank.
- 2 The steady state is the unconditional mean of the process and both terms are used interchangeably in this paper.
- 3 For instance, the accuracy of impulse response functions computed as the difference between unconditional and conditional forecasts depends largely on the accuracy of (long-term) economic forecasts.
- 4 For example, central banks have strong prior beliefs about the long-run inflation when they operate in an inflation targeting environment. Moreover, long-term survey forecasts may serve as sources of long-run expectations and used to inform the steady-state prior distribution (Clark, 2011; Wright, 2013).
- 5 Deterministic overfitting is the tendency of the estimated VARs to attribute a large portion of the low-frequency behavior of the variables to the deterministic component of the model.
- 6 Jarocinski and Smets (2008) also show how to employ economic theory to specify steady-state priors.
- 7 Steady-state VARs also serve as forecasting benchmarks for the theoretical grounded DSGE models with well-defined steady states (see also Adolfson, Andersson, Lindé, Villani, & Vredin, 2007; Adolfson, Lindé, & Villani, 2007).
- 8 Uninformative steady-state priors may also lead to convergence issues of the Markov chain Monte Carlo (MCMC) estimation (Villani, 2009).
- 9 Assuming an inverse gamma distribution for the steady-state prior variances we get a Student t prior distribution for the steady states (Geweke, 1993). Introducing a steady-state prior distribution with fatter tails may have beneficial effects when we are relatively uncertain about the prior mean giving more space to data information, but may result in poorer inference when we have much stronger prior beliefs regarding the true unobserved steady-state level.
- 10 See Louzis (2016a) for an early discussion on time-varying steady-state VAR models.
- 11 Generally, priors on μ, B and Σ are assumed to be mutually independent.
- 12 For the sake of completeness, we discuss a potential extension of the steady-state vector error correction (VEC) model using the NG prior in Appendix A. An empirical analysis of the proposed model is beyond the scope of this paper and we leave it to future research.
- 13 We have also experimented with the hierarchical approach of Chib and Greenberg (1995), where μt depends on a small number of factors, but there were almost no gains in terms of computational time. Possibly, a factor structure on the dynamics of μt will have beneficial computational effects on larger-scale models. We leave the investigation of a factor structure on steady-states to future research.
- 14 As noted in Carriero et al. (2016b), the common stochastic volatility imposes a factor structure on volatilities assuming no idiosyncratic components for the conditional volatilities and a proportional order of magnitude of the movements in volatility across variables. Moreover, under the natural conjugate prior each equation has the same explanatory variables, and the prior covariance of the coefficients in any two equations is restricted to be proportional to one another (Koop & Korobilis, 2010).
- 14 The sum-of-coefficients corresponds to a mechanistic approach of the prior for the long run proposed by Giannone et al. (2018). See also this contribution for a thorough discussion on the deterministic overfitting in VARs.
- 11 The nonrevised financial variables were download from the St. Louis FRED database.
- 12 See Supporting Information Table F.1 for the histograms of the posterior distributions of the two alternative approaches.
- 13 The corresponding figures for the remaining variables can be found in the Supporting Information.
- 14 The CRPS metric is also widely used in applications to macroeconomic forecasting (see, e.g., Clark & Ravazzolo, 2015; Groen, Paap, & Ravazzolo, 2013; Ravazzolo & Vahey, 2014).
- 15 The log score is the logarithm of the predictive density evaluated at the observed value
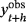 .
. - 16 As shown in Table B1 (Appendix B), the forecasting ability of a hierarchical TVSS-VAR with an NG prior on initial conditions is almost identical to the standard TVSS-VAR model. Therefore, the main conclusions of the paper are case insensitive and we choose to present the forecasting results using only the standard TVSS specifications to avoid the extra computational burden of the hierarchical specification.
- 12 See also Supporting Information Tables G.1–G.10.
- -12 The mathematical formulas of the conditional posterior distributions are not given here owing to time and space considerations. The interested reader is refereed to Proposition 3.1 and Appendix B of Villani (2005).
- -15 The Gibbs sampler of Del Negro and Primiceri (2015) is actually the original algorithm of Primiceri (2005) with different ordering of the various Gibbs steps but with the individual steps remaining unchanged.
- -14 For more details see Chan and Hsiao (2014). The MATLAB code for this step is available online at J. Chan's website: http://joshuachan.org



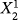 distribution
distribution
