Fertility decisions and the norm of intergenerational support to aging parents
Abstract
This paper examines the impact of the social norm of intergenerational support to aging parents on fertility decisions in developing economies. The traditional expectation of receiving support from adult children in old age has historically been a significant factor in the decision to have children, especially in developing countries. The study develops a life cycle model that endogenizes fertility choices and incorporates the expectation of transfers from children based on the filial responsibility norm. We utilize household survey data from Indonesia to estimate earnings profiles and uncertainties over the life cycle, and to estimate the transfers from adult children to parents to indicate the current strength of the norm in 2000s. We conducted counterfactual experiments to explore the impact of the filial responsibility norm on fertility and found that a weakening of the norm could account for a significant proportion of the decline in the total fertility rate.
1 INTRODUCTION
This paper examines the impact of the social norm of intergenerational support on fertility decisions among parents in developing economies. The traditional expectation of receiving support from adult children in old age has historically been a significant factor in the decision to have children, particularly in East Asian and developing countries. However, recent research suggests a weakening of this norm, with important implications for demographic and economic outcomes.1
Unlike developed economies with well-established pension and social security systems, the financial incentive for having children to ensure support in old age is often more salient in developing countries where social security is underdeveloped, and many individuals have low-paying and insecure jobs, making it challenging to accumulate sufficient assets for a comfortable old age. For example, İmrohoroğlu and Zhao (2018a) mentioned that family support for the elderly is an important factor to consider when studying the social security reform in China. Pei and Cong (2020) suggested that family support for the elderly is still important in rural China although it is weaker in urban areas. Cai et al. (2006) found private transfers from children as an important insurance for the elderly when the pension coverage is low.
To explore the relationship between the social norm of intergenerational support and fertility decisions, we construct a life cycle model that endogenizes fertility choices and incorporates the expectation of intergenerational transfers from children based on the filial responsibility norm. In the model, individuals would like to have children not only because children bring happiness (utility), but also because they anticipate a financial return from having children. We use Indonesia as an illustrative example to conduct our quantitative exploration. We also employ household survey data from Indonesia to estimate earnings profiles and uncertainties and ensure that our model accurately captures the financial considerations of individuals throughout their life cycle. Specifically, we use data from the Indonesia Family Life Survey (IFLS) conducted between 2000 and 2014, which is a comprehensive socioeconomic survey that provides detailed information on a wide range of economic outcomes and behaviors of Indonesian households.
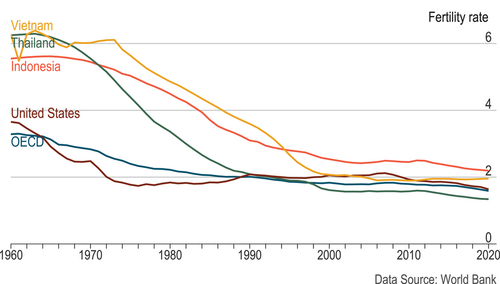
To gauge the strength of the filial responsibility norm in Indonesia, we estimate the transfers from adult children to their elderly parents based on the IFLS data. Our findings suggest that although over 70% of elderly parents (age 60+) in Indonesia receive transfers from their adult children, the average net transfer is relatively low, accounting for only 3% of the average earnings of young adults. This result points to a relatively weak norm of old-age support, which seems consistent with the declining fertility rate in Indonesia over time. In fact, the total fertility rate (TFR) in Indonesia has decreased from above 5 in the 1960s to below 2.5 in the 2000s (see Figure 1).2
In addition to directly estimating the above mentioned model parameters from data, we estimated the other parameters by minimizing the distance between data and model moments, such as the average fertility rate and fertility differentials across income groups.
Using our calibrated benchmark model for the Indonesian economy in the 2000s, we conducted counterfactual experiments to explore the impact of the filial responsibility norm on fertility decisions in response to financial incentives for parents. Our findings suggest that a stronger norm of intergenerational support to aging parents, at a level of 10% of average earnings, would result in an increase in the TFR by 0.6 from the current level. Specifically, if this norm was in place in the 1960s, it could have explained up to about 25% of the fertility decline observed in Indonesia from the 1960s to the 2000s. In addition, we also find that if an economic slowdown is expected, the fertility would be further reduced. Moreover, the impact of the social norm on fertility is significant across wealth categories, especially when parents expect their children's income to be significantly higher than their own. Low-income households are more affected by the norm in case of zero income growth due to higher returns from children relative to their own savings. However, in economies with persistent growth (e.g., Indonesia), the norm provides financial incentives even for wealthy parents.
The literature analyzing fertility choice and its impact on demographic change began with Becker (1960), which introduced the concept of the quantity-quality tradeoff concerning children. Subsequent research, including studies by Barro and Becker (1989), Becker et al. (1990), Galor and Weil (1996), Zhang (1997), Doepke (2004), Doepke and Zilibotti (2005), and Liao (2011), aimed to associate fertility and demographic shifts with economic growth based on this quantity-quality tradeoff mechanism. Furthering the scope of these studies, Jones et al. (2008) delved into alternative theories such as the opportunity cost of time and the quantity-quality tradeoff, discussing their ability to explain the relationship between fertility and income. Complementing these works, this paper emphasizes the exploration of the role in family transfers from children under the lens of the filial responsibility norm.
Moreover, studies examining family transfers in developed countries tend to focus on transfers from parents to children. Altonji et al. (1992, 1997), for instance, employed the Panel Study of Income Dynamics (PSID) to test whether the observed family transfers from parents to children are consistent with the standard altruism model. Their findings reject the hypothesis that the transfers are motivated by altruism. Greenwood et al. (2003), also developed a model of parents' fertility decisions and human capital investments in their children to evaluate the child tax credit policy.
However, as mentioned earlier, the financial incentive for having children to ensure support in old age is often more valued in developing countries. In contrast to the aforementioned studies, which focus on caring/altruism from parents toward children, some macroeconomic studies have considered old-age support from children as the incentive for parental fertility decisions. Boldrin and Jones (2002), for example, developed a three-period overlapping-generations model with endogenous decisions on fertility and support to old-age parents to explain the fertility transition in historical data. Zhao (2011) extended the framework in Boldrin and Jones (2002) to study the effects of social security on fertility and earnings distribution through the channel of differential fertility change across income groups, illustrating that the fertility channel could be quantitatively important in accounting for the distributional effect of social security. Boldrin et al. (2015) further compared two types of models with endogenous fertility: the Barro and Becker (1989) type model, where rearing children is due to parental altruism, and the Boldrin and Jones (2002) type model, where rearing children is due to children's filial support in old age. They found that the latter can better account for the negative relationship between old-age pension and fertility observed from Europe/US data.
In addition to the endogenous fertility literature, İmrohoroğlu and Zhao (2018a) also showed that it is important to consider family support from children to the elderly when studying social security issues in developing economies. İmrohoroğlu and Zhao (2018b) studied the saving rate dynamics in China and found that transfers from children to parents provide additional insurance value against parents' old-age risks, suggesting that the saving rate would have been significantly lower if the one-child policy had not been implemented.
In this study, we consider both incentives shaping parental fertility decisions: the altruistic valuation of children and the expectation of support in old age. Drawing upon the life-cycle framework developed by Daruich and Kozlowski (2020), originally crafted to explore transfers from parents to children in support of educational attainment within developed countries, this study focuses on the filial support for elderly parents in developing economies and uses the model to investigate the fertility dynamics given the trend of changes in intergenerational transfers.
One limitation of our paper is that we assume the norm is exogenously given, without specifying any evolution of the norm in the model. In future research, it would be interesting to explore the dynamics of the norm and its interactions with other institutional changes, such as social security development. In addition, the model developed in the paper is a partial equilibrium life-cycle model because the earnings age profile, earnings shocks and the interest rate are all estimated from the data. The general equilibrium effect is not captured in this model. Overall, our findings highlight the importance of considering the role of intergenerational transfers and social norms in shaping fertility decisions and demographic outcomes in developing economies.
The rest of the paper is organized as follows: Section 2 presents the model, Section 3 details the data sources, estimation techniques, and parameter selection, Section 4 provides a quantitative analysis of the role of the norm of old-age support from children, and Section 5 concludes.
2 MODEL
The model economy is populated with ex-ante identical individuals, who become heterogeneous ex-post due to income shocks over the life cycle, differentiated choices of fertility and uncertainty of transfers. As is typical in the literature, we assume asexual reproduction, meaning that we model only a generic parent and abstract from marriage. Similarly, we do not differentiate between genders and abstract from gender differences in our model.
2.1 Time line of the life cycle
The model time is discretized, and each period corresponds to a single year. We denote the age of the agent as , where represents the age at which individuals begin to work and make economic decisions. The probability of survival from age to is denoted as , and it is strictly less than 1 after age . The terminal age in our model is .
Labor supply is assumed to be inelastic, and each individual faces idiosyncratic earnings shocks, including both persistent and transitory shocks, as well as uncertainty regarding survival. Individuals make decisions regarding consumption and savings after the realization of shocks in each period. At age , individuals make fertility decisions and choose the number of children they will have. We simplify this decision by assuming that it is a one-time decision and denote the number of children as the discrete variable . Parents derive utility from having children, but raising children comes with both monetary and time costs. From age , individuals receive transfers from their children.
2.1.1 Filial norm and intergenerational transfers
We incorporate the concept of the filial norm in the model, whereby adult individuals follow a social norm of transferring a proportion of their earnings to their parents for years. Specifically, we assume that individuals transfer a proportion of their earnings to their parents, and they expect their own children to follow the same norm and transfer a similar proportion when they become adults. The parameter captures the strength of the filial norm, with a smaller value of indicating a weaker norm.
2.2 Individual's problem
2.2.1 Fertility stage
2.2.2 Parenting stage
2.2.3 Old age
3 DATA, ESTIMATION/CALIBRATION AND THE BENCHMARK MODEL
In this paper, we use Indonesia as an example to characterize a large developing economy. We utilize a household level data set in Indonesia that provides rich information to quantify our benchmark model.
3.1 Data and measurement
To perform a precise quantitative analysis, this study utilizes data from the Indonesia Family Life Survey (IFLS) spanning the years 2000 to 2014, with a 7-year interval between waves. The IFLS is a comprehensive socioeconomic survey that offers extensive data on a wide range of behaviors and outcomes of Indonesian households. This data includes information on demography, employment, labor force participation, education, health, income, expenditure, housing, fixed assets and durable goods, involvement in poverty alleviation programs, general economic conditions, agricultural production, local infrastructure and transportation, and social problems. These surveys enable the construction of panel data that is well-suited for the purpose of our estimation.4
3.1.1 Family transfers
From IFLS data in the period 2014, we focus on adult child at aged 25 and over and construct a sample consisting of pairs of child-parent. The information on transfer flow between children and parents is based on those following questions:
During the last year, did you receive any money transfer from your children? About how much were those transfers?
and During the last year, did you send any transfer to your children? About how much were those transfers?
These questions specifically inquire about support from children, which is advantageous compared to other surveys that do not specify the relationship or purpose of the transfers. We collected data on both upstream and downstream transfers for respondents and their non-coresiding children. Figure 2 shows that more than 70% of old parents received positive transfers from children.

3.2 Parameter estimation and calibration
The model parameters are determined through a two-stage process. During the first stage, we estimate/choose the parameters that can be identified outside of the model, such as earnings age profiles, earnings shocks, and the strength of the norm of old-age support from children (measured by net transfer to income ratios), either from data or by adopting values from previous studies. In the second stage, we calibrate the remaining parameters to match targeted moments.
3.2.1 First-stage estimation/parameterization
Earnings
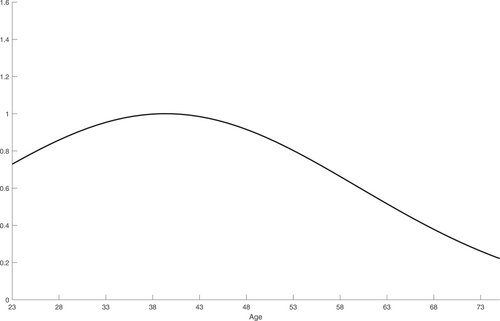
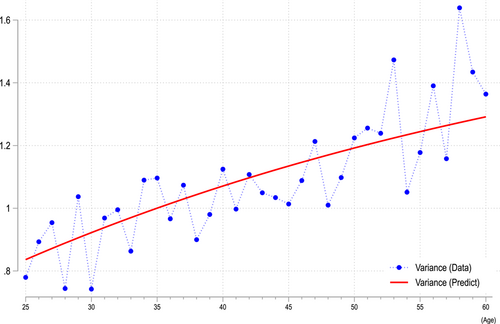
Figure 3 displays the predicted earnings age profile from the estimation, which shows a hump-shaped pattern as observed in the literature. We normalize earnings at age 40 to one. Regarding shocks, our estimation results suggest values of , , , and . While the persistence and variances of persistent and fixed shocks are close to those observed in the United States (Storesletten et al., 2004), the variance of the transitory shock in Indonesia is higher. Figure 4 displays the predicted variance of earnings by age, which exhibits an increasing pattern with age.
Strength of the old-age support norm
We calculate the average net transfers to parents from individuals aged 25 and above using data from the IFLS 2014 and use the fraction of average earnings to represent the current strength of the norm of supporting aging parents (i.e., in the model). We find that is relatively low, at , which is close to that estimated for China in Curtis et al. (2015).
Other parameters
Survival rates are identified from the life tables of the World Health Organization. The interest rate is based on the average real interest rate in the 2000s, which was 6%, and thus the annual time discount factor is set to 0.94. We follow Daruich and Kozlowski (2020) and set the value of intertemporal elasticity at 0.5, which is commonly used in the literature studying fertility choices with OLG models, for example, Greenwood et al. (2003) and Roys and Seshadri (2017). Manuelli and Seshadri (2009) have estimated this parameter and also obtained roughly this value. In addition, we assume parents expect an increase in children's earnings . Because one period is 30 years in the model, where is the average annual growth rate. We utilized the average real GDP per capita growth rate in Indonesia from 1980 to 2010, obtained from the World Bank, to approximate as our benchmark scenario. The annual average growth rate () during this period is 3.4%. Table 1 summarizes the parameters in the benchmark model.
| Description | Value | Source/targeted moment | |
|---|---|---|---|
| Parameters identified outside of the model | |||
| 1) Earnings age profile | see text | Estimated (IFLS) | |
| 2) Earnings shocks | see text | Estimated (IFLS) | |
| Strength of norm | 0.03 | Estimated (IFLS) | |
| Survival rates | see text | Estimated (WHO) | |
| (, ) | Interest rate/discount factor (annual) | (0.06, 0.94) | World Bank |
| Relative risk aversion | 0.5 | Daruich and Kozlowski (2020) | |
| Real GDP growth rate (annual) | 0.034 | 1980–2010, World Bank | |
| Parameters calibrated in the model | |||
| Utility parameter | 0.49 | Match average TFR and | |
| () | Child rearing cost | (0.17, 0.68, 0.81) | Fertility rates by wealth level |
3.2.2 Second-stage calibration
We calibrate four parameters, including the utility parameter and child-rearing cost parameters, to match the average TFR and fertility by wealth groups as reported in the 2002–2003 Indonesia Demographic and Health Survey (IDHS). We adopt the functional form of child-rearing cost with taking into account parents' income and number of children from Daruich and Kozlowski (2020): for . is to capture the basic cost of having a child as a fraction of income, while captures the curvature of parents' time opportunity cost based on income levels. Additionally, accounts for the marginal cost of having more than one child. By minimizing the distance between the model and data moments, we obtain values of , , , and . Our calibrated parameters for the cost function are close to those found in Daruich and Kozlowski (2020), except for , which reflects lower child-raising costs in developing countries.
3.3 Benchmark model
Table 2 displays the fertility rates across different wealth groups in both the benchmark model and the data. The model accurately captures the average TFR and the declining fertility trend with increasing wealth level. However, the model overpredicts the fertility differential between the top and bottom wealth groups.
| Targeted moments | Data | Model |
|---|---|---|
| Average fertility | 2.6 | 2.6 |
| By wealth group | ||
| Bottom 40% | 2.9 | 3.2 |
| Middle 20% | 2.6 | 2.8 |
| Top 40% | 2.3 | 1.8 |
- Note: Data moments are calculated from the 2002–2003 Indonesia Demographic and Health Survey (IDHS).
Given that in the benchmark model, earnings and income uncertainties over the life cycle as well as net transfers from children have been carefully estimated from the household-level data, we ensure that the model accurately reflects individuals' financial considerations throughout their life cycle. The costs and benefits of having children are calibrated to match the average TFR in Indonesia in the 2000s. Consequently, we have a plausible platform for conducting counterfactual experiments to investigate the impact of the norm of supporting aging parents on fertility decisions.
4 QUANTITATIVE ANALYSIS—ROLE OF THE FILIAL NORM OF SUPPORTING AGING PARENTS
We perform several counterfactual experiments by varying the strength of the norm () in the benchmark model. A larger value of indicates a stronger norm of support from children to aging parents (as children transfer proportion of their average earnings to their parents). In the benchmark, is relatively small, indicating a weak norm in the 2000s. Since direct data on family transfers in the 1960s, when the fertility rate was high, is unavailable, we consider several scenarios with different values of for the experiments.
Table 3 presents the results with at 5% and 10%, in addition to the benchmark (), under an annual income growth rate scenario of . Our findings suggest that a stronger norm of old-age support increases fertility. Specifically, the TFR would increase from 2.6 in the benchmark to 3.2 if increases to 10%.
| (Benchmark) | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Income growth rate, | |||||||||
| Strength of norm () | 3% | 5% | 10% | 3% | 5% | 10% | 3% | 5% | 10% |
| Average TFR | 2.6 | 2.9 | 3.2 | 2.9 | 3.4 | 4.2 | 2.2 | 2.3 | 2.6 |
| TFR by wealth | |||||||||
| Bottom 40% | 3.2 | 3.8 | 4.0 | 3.8 | 4.0 | 4.6 | 2.8 | 2.9 | 3.2 |
| Middle 20% | 2.8 | 3.0 | 3.8 | 3.0 | 3.9 | 4.8 | 2.1 | 2.2 | 2.9 |
| Top 40% | 1.8 | 1.9 | 2.2 | 2.0 | 2.5 | 3.5 | 1.7 | 1.8 | 1.9 |
Furthermore, we observe that the impact of the social norm change on fertility is significant across wealth when parents expect their children's income to be significantly higher than their own (i.e., in the benchmark, implying an average income of children in the next 30 years to be 2.7 times that of parents'). For instance, increasing to 10% leads to a rise in the fertility rate from 3.2 to 4.0 for those in the bottom 40% of the wealth distribution, while those in the top 40% also experience an increase from 1.8 to 2.2.
Given that income growth may vary considerably across countries and over time, we conduct additional experiments with alternative income growth rates , in addition to the benchmark setting of . Table 3 presents two additional scenarios: one with a higher growth case () and another with a zero growth case ().
In the case where parents expect a higher income growth (e.g., ), even if the filial norm remains unchanged, the average fertility rate would increase from 2.6 in the benchmark to 2.9 (see the 4th column of Table 3). Conversely, if parents expect the economy to stop growing (e.g., ), the fertility rate would decrease to 2.2 even with the filial norm remaining the same (see the 7th column, the 3% case under in Table 3).
One noteworthy finding is that the fertility decisions of poor households are more strongly affected by the norm than those of rich households in the case of zero income growth. This stronger impact on low-income parents can be attributed to the higher returns from children compared to their own savings, as they have lower opportunity costs of rearing children. In contrast, high-income parents face higher opportunity costs associated with having children, and the return on future transfers from children may not necessarily exceed the return on savings. Consequently, the channel of old-age support is more valuable for poorer households.
However, in economies experiencing persistent growth, such as Indonesia, the filial norm with a significant increase in children's income brings nontrivial financial incentives even for wealthy parents.
Our quantitative analysis suggests that a stronger norm of intergenerational support to aging parents, at a level of 10% of average earnings, would increase the TFR by 0.6 from the benchmark level (representing the 2000s). Specifically, if this norm had been in place in the 1960s, it could have explained about 25% of the observed fertility decline in Indonesia from the 1960s to the 2000s. Furthermore, our experiments also show that with higher income growth, the impact of the norm on fertility decisions will be more pronounced. If parents expect an economic slowdown, they would further reduce the number of children.
5 CONCLUSION
This paper examines the impact of the social norm of intergenerational support on fertility decisions in developing economies, using Indonesia as an illustrative example. The study constructs a life cycle model that endogenizes fertility choices and incorporates the expectation of intergenerational transfers from children based on the filial responsibility norm. Using the Indonesia Family Life Survey data, we estimate earnings profiles and uncertainties and ensure that the benchmark model accurately captures the financial considerations of individuals throughout their life cycle. We also estimate transfers from adult children to elderly parents and find that the strength of the norm of old-age support is relatively weak in Indonesia in the 2000s. With the costs and benefits of having children calibrated to match the average fertility in Indonesia in the 2000s, we have a plausible platform for conducting counterfactual experiments. The results show that a stronger norm of intergenerational support to aging parents would result in an increase in the TFR. If a more stringent norm, which required children to transfer 10% of their income to support their aging parents, had been in place in the 1960s, the decline in social norm could have accounted for approximately 25% of the decline in fertility that was observed in Indonesia between the 1960s and the 2000s. Furthermore, our experiments also show that with higher income growth, the impact of the norm on fertility decisions will be more pronounced. It implies that an economic slowdown may also lead to a decline in fertility. The study suggests the importance of considering the role of intergenerational transfers in shaping fertility decisions and demographic outcomes in developing economies.
ACKNOWLEDGMENTS
Minchung Hsu expresses gratitude for the financial support received from JSPS Kakenhi Grant Numbers (B)17H02537 and (C)21K01439, as well as from the Nomura Foundation and GRIPS Policy Research Center during the period of conducting this project. Thu Trang Le expresses gratitude for the financial support received from the 2022-23 Sustainable Development Goals Research Grant, Business School, University of New South Wales during the period of conducting this project.
CONFLICT OF INTEREST STATEMENT
The authors declare no conflict of interest.
ETHICS STATEMENT
This study exclusively involves theoretical analysis and utilizes publicly available data. No primary data collection was conducted, and the study does not involve any interaction with human or animal subjects.
APPENDIX A:
A.1 Data for earnings estimation
We use data from the Indonesia Family Life Survey (IFLS) in the last three waves, covering the years 2000, 2007, and 2014, with a 7-year gap.5 These surveys collect rich socioeconomic information on a wide range of behaviors and outcomes for the Indonesian population, such as demography, employment, labor force participation, education, health, income, expenditure, housing, fixed assets, and durable goods, involvement in poverty alleviation programs, general economic conditions, agricultural production, local infrastructure and transportation, and social problems. They allow us to construct panel data for our analysis.
To estimate earnings empirically, we apply some restrictions to the output sampling. First, we focus on individual earnings and follow the common practice in the literature of restricting the working age range from 25 to 60 years.
Second, we only consider male workers. This exclusion is necessary because women's labor force participation in Indonesia is significantly lower than men's. For historical and cultural reasons, a large proportion of women do not have continuous full-time work, and the statistics on their income appear to be too volatile to be reliable.
Third, although researchers in developed countries often exclude farmers and self-employed individuals from their samples, we keep those occupations because they are prevalent in Indonesia and occupy a large share of the informal sector. However, since income is the essential variable for our investigation, we exclude “no-income” categories, including people with no job or who report themselves as “unpaid family workers.”
Finally, to improve the accuracy of the estimation, we drop all observations with missing key variables, including education, age, and working sectors, from the constructed sample.
The rich information in the IFLS data and the high number of observations allow us to apply these restrictions feasibly and ensure that the remaining data sampling is adequate for our empirical analysis.
A.2 Measurement of earnings
The construction of the earnings variable for formal and informal workers is different. In IFLS, the annual earnings of each individual are constructed as the total salary (including bonuses) from their main job and any extra job they may have, as well as the net profit from their farm or nonfarm business if they are self-employed. Since self-employed individuals only report the net profit from their business or household business, it is technically difficult to distinguish between labor earnings and capital earnings.
The currency unit in IFLS is the Indonesian Rupiah. When pooling data from different survey years, we use the Consumer Price Index (CPI) obtained from the IMF website to construct real annual earnings.
REFERENCES
- 1 Ogawa and Retherford (1993) found that norms of filial care for elderly parents were fairly constant from 1963 until 1986 in Japan, but significantly weakened in 1990.
- 2 Data in Figure 1 is from the World Bank, measuring the total fertility rates (TFR) for selected countries from 1960 to 2020. We follow the definition of TFR from the World Bank: The number of children that would be born to a woman if she were to live to the end of her childbearing years and bear children in accordance with age-specific fertility rates currently observed.
- 3 This is a simplification given our focus is on the number of children, not the timing of having children.
- 4 The IFLS data and accompanying documentation are accessible online at http://www.rand.org/labor/FLS/IFLS.html, and for additional details, please refer to the User's Guide for the Indonesia Family Life Survey, Wave 5, page 1.
- 5 IFLS data and documentation are available online at http://www.rand.org/labor/FLS/IFLS.html. For more details, see the User's Guide for the Indonesia Family Life Survey, Wave 5, p. 1.




