International Studies of Economics
Early View
RESEARCH ARTICLE
Open Access

Coordination Effect of Oligopolists' Multimarket Contact

Zuo Yu, 

Zuo Yu

Center for Industrial and Business Organization, Dongbei University of Finance and Economics, Liaoning, China

Contribution: Conceptualization, Project administration, Supervision

Search for more papers by this author
Tianyu Luo, 

Corresponding Author

Tianyu Luo

Center for Industrial and Business Organization, Dongbei University of Finance and Economics, Liaoning, China

Correspondence: Tianyu Luo ([email protected])

Contribution: Methodology, Writing - original draft

Search for more papers by this author
First published: 10 January 2025
https://doi.org/10.1002/ise3.107

Tianyu Luo contributed equally to this work.

ABSTRACT

In this article, we examine the coordination effect of oligopolists' multimarket contact with asymmetric cost. We extend a model of infinitely repeated multimarket contact games with “symmetric advantage” in the seminal paper of Bernheim and Whinston (The RAND Journal of Economics 1990; 21(1): 1–26). We consider Stackelberg and Cournot competition as the stage game while Bernheim and Whinston consider Bertrand competition. Different from Bernheim and Whinston, we show that collusive sustainability under multimarket contact is the same to single-market if the stage games are Stackelberg competition. Our research has policy implications for the antimonopoly review of the merger and detecting cartels.

1 Introduction

Multimarket contact refers to the competitive relationships between two or more enterprises in two or more markets. This is not limited to product markets but to geographic markets.

In many industries, oligopolists competed in multi-market. In semiconductors, Intel competed with AMD in the CPU (X86) market and FPGA market after 2020; Samsung, SK-Hynix, and Micron competed in the DRAM market and NAND market. In agriculture, Monsanto, Dupont, Dow, and Syngenta have competed in the Amercian corn seed market and Amercian soybean seed; Monsanto has competed with Dow in the Amercian upland cotton seed market. In the soybean seed market, Monsanto, Dow, and Syngenta already competed in Brazil and the United States; Monsanto and Syngenta already competed in Argentina, Paraguay, and Uruguay; Monsanto and Dupont competed in South Africa. Monsanto, Dupont, Dow, and Syngenta also are worldwide pesticide oligopolist.

Industrial empirical works reveal a significant positive correlation between increases in the extent of firms' multimarket contact and price or profit. Such as airline (Kim 1993; Gimeno and Woo 1999; Ciliberto and Williams 2014; Zhou 2017), bank (Pilloff 1999; Feinberg 2003; Hannan 2006; Coccorese and Pellecchia 2013; Molnar, Violi, and Zhou 2013), telephone (Parker and Röller 1997; Busse 2000), hospital (Schmitt 2018), health insurance (Lin and McCarthy 2023), and audit (Dekeyser et al. 2021). But Igami and Sugaya (2022) present an empirical result that firms do not collude in a manner to the multimarket-contact-collusion even though firms have contacts in several markets.

For theoretical analyses, there is still no consensus on the issue. Edwards (1955) first raised the idea that multimarket contact facilitates collusion. Multimarket contact means multimarket punishment, it is likely to sustain collusion, known as “mutual forbearance.” Bernheim and Whinston (1990) first formal theoretical analysis of the “mutual forbearance hypothesis.” They identify multimarket contact also means return from multimarket deviation which is greater than from single-market deviation. Multimarket contact breaks up collusion.

1.1 Related Literature and Contribution

Our paper contributes to the theoretical literature with multimarket contact and collusion. Some scholars support the view that multimarket contact facilitates collusion. Bernheim and Whinston (1990) identify multimarket contact facilitates collusion in certain circumstances, typically implying asymmetries between firms or markets. Spagnolo (1999) shows that if the firms' payoffs are strictly concave in their profits, then multimarket contact always relaxes the incentive compatibility constraints. Chen and Ross (2007) study the effects on prices and welfare of multimarket contact when firms serve multiple markets from a single facility with rising marginal costs. They analyze a sequential game and show that multimarket contact reduces the returns for deviating from any collusive agreement. The theoretical contribution of their study to emphasis is that the market has linked. Matsushima (2001) studied an imperfect monitoring model with multimarket contact and showed that imperfect monitoring expands the risk of incorrectly identifying deviation. They show that the risk decreases by the Law of Large Numbers if the extent of this market contact is large. Kobayashi and Ohta (2012) also investigate collusion in multimarket contact under imperfect monitoring. They argue that multimarket contact gives firms more information on a rival's behavior and makes punishment more severe than single-market competition. Wen and Zheng (2024) consider models of linked enforcement in the presence of imperfect observation and show that a spillover effect arises from linking enforcement across games to facilitate cooperation when at least one of the games has imperfect observation.

Some scholars support the contrary view. Arie, Markovich, and Varela (2017) study a model of a two-stage dynamic where quantity is constrained by capacity. They show that multi-market firms can avoid competition by exiting the market that contacts a competitor if sunk costs can freely transfer from markets one by one. This leads to increasing the competitors' returns for deviating from the collusive agreement of the contacted market. Sugaya and Wolitzky (2018) find that—under some assumptions—transparency hinders collusion when the cartel's objective is to segment the market according to the home-market principle.

In contrast to these articles, the present article focuses on a sequential game. Chen and Ross (2007) are much more related to this paper. Contrary to Chen and Ross (2007), we assume that firms sequential-move. This is a key part of our contribution since we are interested in the collusion sustainability of multimarket firms under a sequential game. Mouraviev and Rey (2011) explore the role of price or quantity leadership in facilitating collusion. They show that the issue of collusion in a sequential game differs from a simultaneous game. They also collected many cartel cases which has been price leadership in the European Commission. Similar views also have been verified on theoretical and empirical (Rotemberg and Saloner 1990; Kovenock and Widdows 1998; Ishibashi 2008; Lewis 2012; Andreoli-Versbach and Franck 2015; Marshall, Marx, and Raiff 2008). In the international Vitamin market and Chinese liquor market, leader–follower collusion and multimarket contact coexist.

Our paper is also related to extensive work on multimarket contact with asymmetric cost. The typical approach in modeling multimarket contact with collusion in a duopoly setting is to adopt symmetric cost assumptions. Bernheim and Whinston (1990) is another article related to this paper. They analyze the relation of multimarket contact and collusion under the assumption of asymmetric cost and simultaneous game. As mentioned above, this work has mainly focused on how multimarket contact affects collusion sustainability in a sequential game. Our results differ from Bernheim and Whinston (1990). We found a substitute mechanism of “mutual forbearance” when firms' costs are asymmetric.

Our results have policy implications for the antimonopoly review of the merger. A merger may diminish competition by enabling or encouraging post-merger coordinated interaction among firms in the relevant market that harms customers. Multimarket contact has been documented in some merger cases. In the AB InBev/SABMiller case, for example, InBev competed with Heineken and Carlsberg in several EEA markets after the merger, which implemented and adapted to the collusive price leadership model in these markets both as price leaders and price followers. The Decision of the European Commission states:

Multi-market contacts therefore mutually reinforce the incentives to coordinate between price leaders and followers across markets and enhance the stability of price coordination in national markets.

Our results also have policy implications for detecting cartels, especially international cartels. First, the globalization of business means cartel activity is increasingly international in scope. The cartels that were convicted by both the EC and the DOJ and that correspond to 22% of all of the cartels that were convicted by the EC between 1998 and 2020 (Marvão and Spagnolo 2023). Our research can explain why some international cartels can be formed even though face some hindering factor, which contributes to enriching the structural screen tools. Second, leadership–follower collusion has been documented in many cartel cases. Some cartel cases are related to multimarket contact. In the Vitamins cartel, for example, Roche and BASF designated a company that would lead a price increase and commonly competed in the 10 Vitamin products market (for details, see Appendix A.3).

Our analysis proceeds as follows. Section 2 sets out the basic model and discusses the assumed rationality. Section 3 analyzes the equilibrium of non-coordinate, collusion and deviation under sequential and simultaneous games. Section 4 compares collusive sustainability between single-market and multimarket contact under sequential games and simultaneous games. Section 5 concludes. All proofs are relegated to the appendix.

2 The Model

2.1 Assumptions

Our model essentially introduces the “symmetric advantage” market structure in Bernheim and Whinston (1990) into the Stackelberg and Cournot competition. Consider two duopoly Markets A and B with homogeneity demands, and two Firms 1 and 2 compete in these markets with heterogeneity costs. We define the demand function and cost function by
P k = a − Q k , k = A , B ${P}_{k}=a-{Q}_{k},k=A,B$
and
T C 1 A = T C 2 B = c q 1 A = c q 2 B T C 1 B = T C 2 A = c ¯ q 1 B = c ¯ q 2 A , c < c ¯ < a $\left\{\begin{array}{c}T{C}_{1A}=T{C}_{2B}=c{q}_{1A}=c{q}_{2B}\\ T{C}_{1B}=T{C}_{2A}=\bar{c}{q}_{1B}=\bar{c}{q}_{2A}\end{array}\right\},c\lt \bar{c}\lt a$

In Section 3, we first consider a model of infinitely repeated Stackelberg competition between Firms 1 and 2 in Markets A and B. The low-cost firm chooses quantity first in each market, and the high-cost firm subsequently. Then, we consider a model of infinitely repeated Cournot competition between Firms 1 and 2 in Markets A and B. Firms choose quantity simultaneously whether the cost is high or low. Finally, based on the setup, we characterize and compare the incentive compatibility constraint with and without multimarket contact for each of these models in Section 4.

Before the start of the game, the firms decide whether or not to form a cartel. Collusion for maximizing joint profit needs a rule under cost asymmetry. We adopt “side-payment” as the rule, which requires the high-cost firm to cease to produce and share the joint profit. If the firms could coordinate their decisions and share profits, they would jointly obtain the monopoly profit:
π 1 A m = π 2 B m = λ Π m , π 2 A m = π 1 B m = ( 1 − λ ) Π m ${\pi }_{1A}^{m}={\pi }_{2B}^{m}=\lambda {{\rm{\Pi }}}^{m},{\pi }_{2A}^{m}={\pi }_{1B}^{m}=(1-\lambda ){{\rm{\Pi }}}^{m}$
where λ ∈ [ 0 , 1 ] $\lambda \in [0,1]$ , denotes the share of the low-cost firm. The maximized joint profit Π m ${{\rm{\Pi }}}^{m}$ consistent in each market for symmetric market demand and cost difference.
If they choose to collude in Market A, Firm 1 will produce its monopoly output and Firm 2 will produce 0 to maximize the joint profit. They also decide how to share the monopoly profit. The value of λ $\lambda $ must be met following condition, i.e., firms only participate in collusion when monopoly profit is larger than competition profit for each firm within a period:
π 1 k m ≥ π 1 k c π 2 k m ≥ π 2 k c , k = A , B $\left\{\begin{array}{c}{\pi }_{1k}^{m}\ge {\pi }_{1k}^{c}\\ {\pi }_{2k}^{m}\ge {\pi }_{2k}^{c}\end{array}\right\},k=A,B$
which boils down to:
π 1 A c Π m ≤ λ ≤ 1 − π 2 A c Π m π 2 B c Π m ≤ λ ≤ 1 − π 1 B c Π m $\left\{\begin{array}{c}\displaystyle \frac{{\pi }_{1A}^{c}}{{{\rm{\Pi }}}^{m}}\le \lambda \le 1-\displaystyle \frac{{\pi }_{2A}^{c}}{{{\rm{\Pi }}}^{m}}\\ \displaystyle \frac{{\pi }_{2B}^{c}}{{{\rm{\Pi }}}^{m}}\le \lambda \le 1-\displaystyle \frac{{\pi }_{1B}^{c}}{{{\rm{\Pi }}}^{m}}\end{array}\right\}$

Any collusive agreement is not self-enforcing when the share is outside of this range.

As the game begins, there is one period that consists of two stages. In Stage 1, these firms choose their output quantities sequentially or simultaneously in each market. In Stage 2, the low-cost firm in each market decides whether to transfer profit to the high-cost firm. Figure 1 shows the time structure of the game under the Stackelberg competition.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Time line.

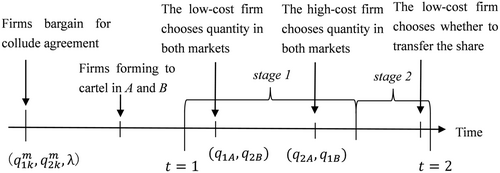
Firms recognize that any deviation will be met with punishment in both markets. Thus, if a firm decides to deviate, it will do so in both markets. It is the same as Bernheim and Whinston (1990). For Market A, Firm 1 can choose not to pay the transfer if Firm 2 deviates in the first stage. Firm 1 has no incentive to deviate during the first stage but has an incentive to not pay the transfer in the second stage. On the other hand, Firm 2 has no action at all in the second stage, and Firm 1 has incentive to not pay in the second stage.

Firms always have deviation incentives if the return from deviation is larger than collusion. To sustain collusion in any market on a given quantity-share vector Q m = ( q 1 m , q 2 m , λ ) ${Q}^{m}=({q}_{1}^{m},{q}_{2}^{m},\lambda )$ , where denotes the quantity that maximizes the joint profit, the best strategies are then of the grim-trigger type, where both firms stick to the collusion equilibrium as long as their rival does, and otherwise revert to the non-coordinate equilibrium. In the spirit of Friedman (1971), firms would sustain the formed collusion if:
π 1 k d + δ 1 1 − δ 1 π 1 k c ≤ 1 1 − δ 1 π 1 k m π 2 k d + δ 2 1 − δ 2 π 2 k c ≤ 1 1 − δ 2 π 2 k m , k = A , B $\left\{\begin{array}{c}{\pi }_{1k}^{d}+\displaystyle \frac{{\delta }_{1}}{1-{\delta }_{1}}{\pi }_{1k}^{c}\le \displaystyle \frac{1}{1-{\delta }_{1}}{\pi }_{1k}^{m}\\ {\pi }_{2k}^{d}+\displaystyle \frac{{\delta }_{2}}{1-{\delta }_{2}}{\pi }_{2k}^{c}\le \displaystyle \frac{1}{1-{\delta }_{2}}{\pi }_{2k}^{m}\end{array}\right\},k=A,B$
which boils down to:
δ 1 ≥ π 1 k d − π 1 k m π 1 k d − π 1 k c δ 2 ≥ π 2 k d − π 2 k m π 2 k d − π 2 k c , k = A , B $\left\{\begin{array}{c}{\delta }_{1}\ge \displaystyle \frac{{\pi }_{1k}^{d}-{\pi }_{1k}^{m}}{{\pi }_{1k}^{d}-{\pi }_{1k}^{c}}\\ {\delta }_{2}\ge \displaystyle \frac{{\pi }_{2k}^{d}-{\pi }_{2k}^{m}}{{\pi }_{2k}^{d}-{\pi }_{2k}^{c}}\end{array}\right\},k=A,B$
where π i k d ${\pi }_{ik}^{d}$ denotes the return from deviation within a period, and δ i ∈ ( 0 , 1 ) ${\delta }_{i}\in (0,1)$ denotes the discount factor. Note that collusion is self-enforcing only when δ ≥ m a x { δ 1 , δ 2 } $\delta \ge max\{{\delta }_{1},{\delta }_{2}\}$ . We use the threshold value of δ $\delta $ to measure the sustainability of collusion.

2.2 Discussion

Here, we discuss our modeling assumptions and how they map to the literature.

2.2.1 Symmetric Advantage

We consider the “symmetric advantage” market structure defined by Bernheim and Whinston (1990). For cost asymmetry firms multimarket contact, Bernheim and Whinston (1990) also consider the “absolute advantage” market structure, in which a firm maintains a cost advantage in two markets. We mainly focus on the “symmetric advantage” market structure. The reasons are as follows: (1) Our results are different from Bernheim and Whinston (1990) under the “symmetric advantage” market structure. Under the “absolute advantage” market structure, the results from our model are the same as Bernheim and Whinston (1990). Specifically, comparing incentive compatibility constraints between single market and multimarket contact under the “absolute advantage” market structure and not allowing discriminatory pricing between the markets A and B, it is the same as the “irrelevance result” of Bernheim and Whinston (1990) which incentive compatibility constraint are proportional expansive; (2) Antitrust authority pays attention to the “symmetric advantage” market structure. We found that the “symmetric advantage” market structure is widely extended in cartel and merger cases (for cases details, see Appendices A.4, A.5, and A.6).

2.2.2 Quantity Leadership

We consider a Stackelberg model to examine the coordination effect of oligopolists' multimarket contact with asymmetric cost. Mouraviev and Rey (2011) show that price leadership can enhance the profitability of collusion, the less efficient firm must act as the leader when firms face asymmetric costs. They also show that if the leader reduces its output then the follower should increase its quantity to sustain collusion when facing quantity leadership. Intuitively, the more efficient firm is more likely to be the leader. It doesn't matter whether that strategy is price or quantity but complementarity or substitution. So we consider the strategic substitution model in the case of asymmetric cost.

2.2.3 Side-Payment

We suppose “side-payment” is the collusion rule in the case of asymmetric cost. Schmalensee (1987) introduces four technologies when firm cost is asymmetric. Only “side-payment” can maximize joint profit. While such rules may not be legal, they can nevertheless be disguised in a technological transfer agreement (Lin 1996). Miklos-Thal (2011) collected some cartel cases that use illegal payments, e.g., Florida bid rigging and worldwide lysine cartel. We also found such a rule used in some Chinese cartel cases, e.g., Chongqing bottled LPG cartel.

We also assume that a − c > 3 ( c ¯ − c ) $a-c\gt 3(\bar{c}-c)$ for the high-cost follower has positive profit in non-coordinate equilibrium, otherwise, they would exit the market.

3 Analysis

3.1 Sequential Game

To analyze collusion in only one market, we consider the following strategies:

3.1.1 Non-Coordinate

The payoff to a firm i = 1 , 2 $i=1,2$ sequential decides quantity ( q 1 A c , q 2 A c ) $({q}_{1A}^{c},{q}_{2A}^{c})$ in Market A for its profit maximization is
π 1 A c = ( P − c ) q 1 A c = a − q 1 A c − q 2 A c − c q 1 A c π 2 A c = ( P − c ¯ ) q 2 A c = a − q 1 A c − q 2 A c − c ¯ q 2 A c $\left\{\begin{array}{c}{\pi }_{1A}^{c}=(P-c){q}_{1A}^{c}=\left(a-{q}_{1A}^{c}-{q}_{2A}^{c}-c\right){q}_{1A}^{c}\\ {\pi }_{2A}^{c}=(P-\bar{c}){q}_{2A}^{c}=\left(a-{q}_{1A}^{c}-{q}_{2A}^{c}-\bar{c}\right){q}_{2A}^{c}\end{array}\right\}$
Because Firm 1 first decides the quantity strategy, we adopt a backward method to solve the problem. Hence, the problem is
max q 2 A c ≥ 0 π 2 A c q 1 A c * , q 2 A c $\mathop{\max }\limits_{{q}_{2A}^{c}\ge 0}{\pi }_{2A}^{c}\left({{q}_{1A}^{c}}^{* },{q}_{2A}^{c}\right)$
where q 1 A c * ${{q}_{1A}^{c}}^{* }$ is the best-reply function of the Firm 1.
First, consider Firm 2 strategies, the solution to the FOC of Firm 2 gives the best-reply function of Firm 1 to the decision of rivals' quantity. Next, we calculate the FOC of Firm 1 and obtain Firm 1 equilibrium quantity. Finally, we contact the best-reply function of Firm 2 and Firm 1 equilibrium quantity. We obtain the non-coordinate equilibrium:
q 1 A c = a − 2 c + c ¯ 2 , q 2 A c = a − 3 c ¯ + 2 c 4 ${q}_{1A}^{c}=\frac{a-2c+\bar{c}}{2},{q}_{2A}^{c}=\frac{a-3\bar{c}+2c}{4}$
hence, the equilibrium profit is
π 1 A c = ( a − 2 c + c ¯ ) 2 8 , π 2 A c = ( a − 3 c ¯ + 2 c ) 2 16 ${\pi }_{1A}^{c}=\frac{{(a-2c+\bar{c})}^{2}}{8},{\pi }_{2A}^{c}=\frac{{(a-3\bar{c}+2c)}^{2}}{16}$

3.1.2 Collusion

As explained after the assumption of “side-payment,” the payoff of firm i = 1 , 2 $i=1,2$ sequential decides strategic ( q 1 A m , q 2 A m , λ ) $({q}_{1A}^{m},{q}_{2A}^{m},\lambda )$ in Market A for joint profit maximization is equal to monopoly profit. We obtain the collusion equilibrium:
q 1 A m = a − c 2 , q 2 A m = 0 ${q}_{1A}^{m}=\frac{a-c}{2},{q}_{2A}^{m}=0$
hence, the equilibrium profit is
π 1 A m = λ ( a − c ) 2 4 , π 2 A m = ( 1 − λ ) ( a − c ) 2 4 ${\pi }_{1A}^{m}=\lambda \frac{{(a-c)}^{2}}{4},{\pi }_{2A}^{m}=(1-\lambda )\frac{{(a-c)}^{2}}{4}$

3.1.3 Deviation

Firm 1 could obtain the whole joint profit if the low-cost firm deviated. Firm 2 could choose the quantity in Market A to maximize its profit when Firm 1 follows the collusion equilibrium:
max q 2 A d ≥ 0 ( P − c ¯ ) q 2 A d = a − q 1 A m − q 2 A d − c ¯ q 2 A d $\mathop{\max }\limits_{{q}_{2A}^{d}\ge 0}(P-\bar{c}){q}_{2A}^{d}=\left(a-{q}_{1A}^{m}-{q}_{2A}^{d}-\bar{c}\right){q}_{2A}^{d}$
Solve the FOC of Firm 2, we obtain
q 2 A d = a − 2 c ¯ + c 4 ${q}_{2A}^{d}=\frac{a-2\bar{c}+c}{4}$
and
π 2 A d = ( a − 2 c ¯ + c ) 2 16 ${\pi }_{2A}^{d}=\frac{{(a-2\bar{c}+c)}^{2}}{16}$
where Firm 1 ceases to pay the return to Firm 2 for “side-payment.”
Consider the condition now that Firms 1 and 2 form and sustain collusion in Market A. First, we analyze the incentive of collusion. Firms would form collusion only if they satisfy the following conditions:
π 1 A m ≥ π 1 A c π 2 A m ≥ π 2 A c $\left\{\begin{array}{c}{\pi }_{1A}^{m}\ge {\pi }_{1A}^{c}\\ {\pi }_{2A}^{m}\ge {\pi }_{2A}^{c}\end{array}\right\}$
which boils down to:
λ ≥ λ ̲ = ( a + c ¯ − 2 c ) 2 2 ( a − c ) 2 ( 1 ) λ ≤ λ ¯ = 1 − ( a − 3 c ¯ + 2 c ) 2 4 ( a − c ) 2 ( 2 ) $\left\{\begin{array}{lr}\lambda \ge \underline{\lambda }=\displaystyle \frac{{(a+\bar{c}-2c)}^{2}}{2{(a-c)}^{2}} & (1)\\ \lambda \le \bar{\lambda }=1-\displaystyle \frac{{(a-3\bar{c}+2c)}^{2}}{4{(a-c)}^{2}} & (2)\end{array}\right.$
which can be satisfied simultaneously because of π 1 A m + π 2 A m ≥ π 1 A c + π 2 A c ${\pi }_{1A}^{m}\,+{\pi }_{2A}^{m}\ge {\pi }_{1A}^{c}+{\pi }_{2A}^{c}$ .
Second, we analyze the sustainability of collusion. Firms would sustain collusion only if satisfies the following conditions:
π 1 A d + δ 1 1 − δ 1 π 1 A c ≤ 1 1 − δ 1 π 1 A m π 2 A d + δ 2 1 − δ 2 π 2 A c ≤ 1 1 − δ 2 π 2 A m $\left\{\begin{array}{c}{\pi }_{1A}^{d}+\displaystyle \frac{{\delta }_{1}}{1-{\delta }_{1}}{\pi }_{1A}^{c}\le \displaystyle \frac{1}{1-{\delta }_{1}}{\pi }_{1A}^{m}\\ {\pi }_{2A}^{d}+\displaystyle \frac{{\delta }_{2}}{1-{\delta }_{2}}{\pi }_{2A}^{c}\le \displaystyle \frac{1}{1-{\delta }_{2}}{\pi }_{2A}^{m}\end{array}\right\}$
which boils down to:
δ 1 ≥ δ 1 ( λ ) = ( 1 − λ ) 2 ( a − c ) 2 2 ( a − c ) 2 − ( a + c ¯ − 2 c ) 2 ( 3 ) δ 2 ≥ δ 2 ( λ ) = ( a − 2 c ¯ + c ) 2 ( a − 2 c ¯ + c ) 2 − ( a − 3 c ¯ + 2 c ) 2 − ( 1 − λ ) 4 ( a − c ) 2 ( a − 2 c ¯ + c ) 2 − ( a − 3 c ¯ + 2 c ) 2 ( 4 ) $\left\{\begin{array}{lr}{\delta }_{1}\ge {\delta }_{1}(\lambda )=(1-\lambda )\displaystyle \frac{2{(a-c)}^{2}}{2{(a-c)}^{2}-{(a+\bar{c}-2c)}^{2}} & (3)\\ {\delta }_{2}\ge {\delta }_{2}(\lambda )=\displaystyle \frac{{(a-2\bar{c}+c)}^{2}}{{(a-2\bar{c}+c)}^{2}-{(a-3\bar{c}+2c)}^{2}}-(1-\lambda )\displaystyle \frac{4{(a-c)}^{2}}{{(a-2\bar{c}+c)}^{2}-{(a-3\bar{c}+2c)}^{2}} & (4)\end{array}\right.$

From the incentive compatibility constraints (inequalities (3) and (4)), we can derive the thresholds of discount factors to sustain collusion via trigger strategy given λ ∈ [ λ ̲ , λ ¯ ] $\lambda \in [\underline{\lambda },\bar{\lambda }]$ . We denote the threshold δ i ( λ ) ${\delta }_{i}(\lambda )$ for i ∈ 1 , 2 $i\in 1,2$ . Note that collusion is self-enforcing only when δ ≥ m a x { δ 1 ( λ ) , δ 2 ( λ ) } $\delta \ge max\{{\delta }_{1}(\lambda ),{\delta }_{2}(\lambda )\}$ .

We characterize δ i ( λ ) ${\delta }_{i}(\lambda )$ and derive the lower bound of discount factors that minimizes m a x { δ 1 ( λ ) , δ 2 ( λ ) } $max\{{\delta }_{1}(\lambda ),{\delta }_{2}(\lambda )\}$ through the choice of λ ∈ [ λ ̲ , λ ¯ ] $\lambda \in [\underline{\lambda },\bar{\lambda }]$ . We can derive δ 1 ( λ ̲ ) = 1 ${\delta }_{1}(\underline{\lambda })=1$ and δ 2 ( λ ¯ ) = 1 ${\delta }_{2}(\bar{\lambda })=1$ . Further, we obtain δ 1 ( λ ) > 0 , δ 1 ′ ( λ ) < 0 ${\delta }_{1}(\lambda )\gt 0,{\delta }_{1}^{^{\prime} }(\lambda )\lt 0$ and δ 2 ′ ( λ ) > 0 ${\delta }_{2}^{^{\prime} }(\lambda )\gt 0$ for any λ ∈ [ λ ̲ , λ ¯ ] $\lambda \in [\underline{\lambda },\bar{\lambda }]$ . From these properties, there exists a self-enforcing share λ * ${\lambda }^{* }$ such that δ 1 ( λ * ) = δ 2 ( λ * ) ${\delta }_{1}({\lambda }^{* })={\delta }_{2}({\lambda }^{* })$ :
λ * = 1 − ( a − 2 c ¯ + c ) 2 [ 2 ( a − c ) 2 − ( a + c ¯ − 2 c ) 2 ] 2 ( a − c ) 2 [ 4 ( a − c ) 2 − 2 ( a + c ¯ − 2 c ) 2 + ( a − 2 c ¯ + c ) 2 − ( a − 3 c ¯ + 2 c ) 2 ] ${\lambda }^{* }=1-\frac{{(a-2\bar{c}+c)}^{2}[2{(a-c)}^{2}-{(a+\bar{c}-2c)}^{2}]}{2{(a-c)}^{2}[4{(a-c)}^{2}-2{(a+\bar{c}-2c)}^{2}+{(a-2\bar{c}+c)}^{2}-{(a-3\bar{c}+2c)}^{2}]}$ ()
Then, we obtain the lower bound of discount factors as δ 1 ( λ * ) = δ 2 ( λ * ) ${\delta }_{1}({\lambda }^{* })={\delta }_{2}({\lambda }^{* })$ :
δ 1 ( λ * ) = δ 2 ( λ * ) = ( a − 2 c ¯ + c ) 2 4 ( a − c ) 2 − 2 ( a + c ¯ − 2 c ) 2 + ( a − 2 c ¯ + c ) 2 − ( a − 3 c ¯ + 2 c ) 2 ${\delta }_{1}({\lambda }^{* })={\delta }_{2}({\lambda }^{* })=\frac{{(a-2\bar{c}+c)}^{2}}{4{(a-c)}^{2}-2{(a+\bar{c}-2c)}^{2}+{(a-2\bar{c}+c)}^{2}-{(a-3\bar{c}+2c)}^{2}}$ ()
Finally, taking together the results, we have obtained so far, we have proof of the condition that Firms 1 and 2 form and sustain collusion in Market A is
δ ≥ δ s i n g l e = ( a − 2 c ¯ + c ) 2 4 ( a − c ) 2 − 2 ( a + c ¯ − 2 c ) 2 + ( a − 2 c ¯ + c ) 2 − ( a − 3 c ¯ + 2 c ) 2 $\delta \ge {\delta }^{single}=\frac{{(a-2\bar{c}+c)}^{2}}{4{(a-c)}^{2}-2{(a+\bar{c}-2c)}^{2}+{(a-2\bar{c}+c)}^{2}-{(a-3\bar{c}+2c)}^{2}}$ ()
We then consider multimarket contact. After basic assumptions, the equilibrium has no difference in both markets A and B, we then have the following result:
π 1 A c = π 2 B c = ( a + c ¯ − 2 c ) 2 8 , π 2 A c = π 1 B c = ( a − 3 c ¯ + 2 c ) 2 16 π 1 A m = π 2 B m = λ ( a − c ) 2 4 , π 2 A m = π 1 B m = ( 1 − λ ) ( a − c ) 2 4 π 1 A d = π 2 B d = ( a − c ) 2 4 , π 2 A d = π 1 B d = ( a − 2 c ¯ + c ) 2 16 $\left\{\begin{array}{c}\begin{array}{ll} & {\pi }_{1A}^{c}={\pi }_{2B}^{c}=\displaystyle \frac{{(a+\bar{c}-2c)}^{2}}{8},{\pi }_{2A}^{c}={\pi }_{1B}^{c}=\displaystyle \frac{{(a-3\bar{c}+2c)}^{2}}{16}\\ & {\pi }_{1A}^{m}={\pi }_{2B}^{m}=\lambda \displaystyle \frac{{(a-c)}^{2}}{4},{\pi }_{2A}^{m}={\pi }_{1B}^{m}=(1-\lambda )\displaystyle \frac{{(a-c)}^{2}}{4}\\ & {\pi }_{1A}^{d}={\pi }_{2B}^{d}=\displaystyle \frac{{(a-c)}^{2}}{4},{\pi }_{2A}^{d}={\pi }_{1B}^{d}=\displaystyle \frac{{(a-2\bar{c}+c)}^{2}}{16}\end{array}\end{array}\right\}$
We can observe that any firm has the incentive of collusion and deviation because of:
∑ k = A , B π i k c ≤ ∑ k = A , B π i k m ≤ ∑ k = A , B π i k d , i = 1 , 2 $\sum _{k=A,B}{\pi }_{ik}^{c}\,\le \sum _{k=A,B}{\pi }_{ik}^{m}\le \sum _{k=A,B}{\pi }_{ik}^{d},i=1,2$
( q 1 A m , q 2 A m , λ ) $({q}_{1A}^{m},{q}_{2A}^{m},\lambda )$ are formable and sustainable as an equilibrium if and only if, for i = 1 , 2 $i=1,2$ ,
∑ k = A , B π i k d + δ 1 − δ ∑ k = A , B π i k c ≤ 1 1 − δ ∑ k = A , B π i k m $\sum _{k=A,B}{\pi }_{ik}^{d}+\frac{\delta }{1-\delta }\sum _{k=A,B}{\pi }_{ik}^{c}\le \frac{1}{1-\delta }\sum _{k=A,B}{\pi }_{ik}^{m}$
which we rewrite as:
( a − c ) 2 4 + ( a − 2 c ¯ + c ) 2 16 + δ 1 − δ ( a + c ¯ − 2 c ) 2 8 + ( a − 3 c ¯ + 2 c ) 2 16 ≤ 1 1 − δ ( a − c ) 2 4 $\frac{{(a-c)}^{2}}{4}+\frac{{(a-2\bar{c}+c)}^{2}}{16}+\frac{\delta }{1-\delta }\left[\frac{{(a+\bar{c}-2c)}^{2}}{8}+\frac{{(a-3\bar{c}+2c)}^{2}}{16}\right]\le \frac{1}{1-\delta }\frac{{(a-c)}^{2}}{4}$
Summing the inequality over i = 1 , 2 $i=1,2$ , we see that this requires that
δ ≥ δ m u l t i = ( a − 2 c ¯ + c ) 2 4 ( a − c ) 2 − 2 ( a + c ¯ − 2 c ) 2 + ( a − 2 c ¯ + c ) 2 − ( a − 3 c ¯ + 2 c ) 2 $\delta \ge {\delta }^{multi}=\frac{{(a-2\bar{c}+c)}^{2}}{4{(a-c)}^{2}-2{(a+\bar{c}-2c)}^{2}+{(a-2\bar{c}+c)}^{2}-{(a-3\bar{c}+2c)}^{2}}$ ()

3.2 Simultaneous Game

So far, we have assumed firm sequential-move and asymmetry cost. This is because this article aims to characterize the coordination effect of oligopolists' multimarket contact in sequential-move by model. However, in the punishment phase, the inefficient firm may not remain the follower because of its profit maximization, and the rational firms expect this fact. Analyzing the simultaneous-move model is necessary for identifying the effect of first-mover advantage affect collusion sustainability under multimarket contact. Therefore, it is worthwhile to discuss an extension of the analysis to the case in which firm simultaneous move is allowed.

Bernheim and Whinston (1990) discussed the relationship of multimarket contact and collusion with asymmetric cost and simultaneous games. They showed that multimarket contact facilitates collusion by relaxing incentive compatibility constraints but ignores individual rationality constraints. Bernheim and Whinston (1990) set the Bertrand model which ensures that non-coordinate equilibrium profit (equal to zero) is always less than coordinate equilibrium profit as the basic assumption so that firms always participate in collusion. In other words, firms always have collusion incentives. Further, we can analyze the mechanism that increases collusion incentive in a simultaneous game by the Cournot model. Our basic assumptions are in line with Bernheim and Whinston (1990) except strategic type. Also, we can associate with Section 3.1 by doing so. Our analytic frame is the same as in Section 3.1.

To analyze collusion in only one market, we consider the following strategies:

3.2.1 Non-Coordinate

The payoff to a firm i = 1 , 2 $i=1,2$ simultaneous decides quantity ( q 1 A c , q 2 A c ) $({q}_{1A}^{c},{q}_{2A}^{c})$ in Market A for its profit maximization is
π 1 A c = ( P − c ) q 1 A c = a − q 1 A c − q 2 A c − c q 1 A c π 2 A c = ( P − c ¯ ) q 2 A c = a − q 1 A c − q 2 A c − c ¯ q 2 A c $\left\{\begin{array}{c}{\pi }_{1A}^{c}=(P-c){q}_{1A}^{c}=\left(a-{q}_{1A}^{c}-{q}_{2A}^{c}-c\right){q}_{1A}^{c}\\ {\pi }_{2A}^{c}=(P-\bar{c}){q}_{2A}^{c}=\left(a-{q}_{1A}^{c}-{q}_{2A}^{c}-\bar{c}\right){q}_{2A}^{c}\end{array}\right\}$
hence, the problem is
max q i A c ≥ 0 π i A c , i = 1 , 2 $\mathop{\max }\limits_{{q}_{iA}^{c}\ge 0}{\pi }_{iA}^{c},i=1,2$
We solve the FOC of Firms 1 and 2, respectively, and contact the best-reply function of Firm 1 and Firm 2 equilibrium quantity. We obtain the non-coordinate equilibrium:
q 1 A c = a − 2 c + c ¯ 3 , q 2 A c = a − 2 c ¯ + c 3 ${q}_{1A}^{c}=\frac{a-2c+\bar{c}}{3},{q}_{2A}^{c}=\frac{a-2\bar{c}+c}{3}$
hence, the equilibrium profit is
π 1 A c = ( a − 2 c + c ¯ ) 2 9 , π 2 A c = ( a − 2 c ¯ + c ) 2 9 ${\pi }_{1A}^{c}=\frac{{(a-2c+\bar{c})}^{2}}{9},{\pi }_{2A}^{c}=\frac{{(a-2\bar{c}+c)}^{2}}{9}$

3.2.2 Collusion

Nothing different from Section 3.1.

3.2.3 Deviation

Nothing different from Section 3.1.

Consider the condition now that Firms 1 and 2 form and sustain collusion in Market A. Firms would form collusion only if they satisfy the following conditions:
π 1 A m ≥ π 1 A c π 2 A m ≥ π 2 A c $\left\{\begin{array}{c}{\pi }_{1A}^{m}\ge {\pi }_{1A}^{c}\\ {\pi }_{2A}^{m}\ge {\pi }_{2A}^{c}\end{array}\right\}$
which can be satisfied simultaneously because of π 1 A m + π 2 A m ≥ π 1 A c + π 2 A c ${\pi }_{1A}^{m}+{\pi }_{2A}^{m}\ge {\pi }_{1A}^{c}+{\pi }_{2A}^{c}$ .
Firms 1 or 2 would deviate from the collusion equilibrium only if satisfies the following conditions:
π 1 A d ≥ π 1 A m , o r π 2 A d ≥ π 2 A m $\left\{\begin{array}{l}{\pi }_{1A}^{d}\ge {\pi }_{1A}^{m},or\\ {\pi }_{2A}^{d}\ge {\pi }_{2A}^{m}\end{array}\right\}$
which boils down to:
λ ≤ 1 , o r 1 − λ ≤ ( a − 2 c ¯ + c ) 2 4 ( a − c ) 2 $\left\{\begin{array}{l}\lambda \le 1,or\\ 1-\lambda \le \displaystyle \frac{{(a-2\bar{c}+c)}^{2}}{4{(a-c)}^{2}}\end{array}\right\}$
Therefore, Firm 1 always has the incentive of deviation. Furthermore, we investigate Firm 2 incentive of collusion and deviation jointly, we show
1 − λ ≥ 4 ( a − 2 c ¯ + c ) 2 9 ( a − c ) 2 1 − λ ≤ ( a − 2 c ¯ + c ) 2 4 ( a − c ) 2 $\left\{\begin{array}{c}1-\lambda \ge \displaystyle \frac{4{(a-2\bar{c}+c)}^{2}}{9{(a-c)}^{2}}\\ 1-\lambda \le \displaystyle \frac{{(a-2\bar{c}+c)}^{2}}{4{(a-c)}^{2}}\end{array}\right\}$
which cannot be satisfied simultaneously. Therefore, the high-cost firm (Firm 2) never deviates from the collusion equilibrium if would participates in collusion.
So that ( q 1 A m , q 2 A m , λ ) $({q}_{1A}^{m},{q}_{2A}^{m},\lambda )$ is an equilibrium only if the following incentive compatibility constraint holds:
π 1 A m ≥ π 1 A c π 2 A m ≥ π 2 A c π 1 A d + δ 1 − δ π 1 A c ≤ 1 1 − δ π 1 A m $\left\{\begin{array}{l}{\pi }_{1A}^{m}\ge {\pi }_{1A}^{c}\\ {\pi }_{2A}^{m}\ge {\pi }_{2A}^{c}\\ {\pi }_{1A}^{d}+\displaystyle \frac{\delta }{1-\delta }{\pi }_{1A}^{c}\le \displaystyle \frac{1}{1-\delta }{\pi }_{1A}^{m}\end{array}\right\}$
which we rewrite as:
λ ≥ 4 ( a + c ¯ − 2 c ) 2 9 ( a − c ) 2 ( 9 ) 1 − λ ≥ 4 ( a − 2 c ¯ + c ) 2 9 ( a − c ) 2 ( 10 ) λ ≥ 1 − δ 9 ( a − c ) 2 − 4 ( a + c ¯ − 2 c ) 2 9 ( a − c ) 2 ( 11 ) $\left\{\begin{array}{lr}\lambda \ge \displaystyle \frac{4{(a+\bar{c}-2c)}^{2}}{9{(a-c)}^{2}} & (9)\\ 1-\lambda \ge \displaystyle \frac{4{(a-2\bar{c}+c)}^{2}}{9{(a-c)}^{2}} & (10)\\ \lambda \ge 1-\delta \left[\displaystyle \frac{9{(a-c)}^{2}-4{(a+\bar{c}-2c)}^{2}}{9{(a-c)}^{2}}\right] & (11)\end{array}\right.$

Lemma 1.The low-cost firm (Firm 1) would participate in collusion if the collusion is sustainable.

Proof.See Appendix A.1.

In Lemma 1 below, we need not care about the Inequality (9). Combine with Inequalities (10) and (11) to get the condition that Firms 1 and 2 form and sustain collusion in Market A is
δ ≥ δ s i n g l e = 4 ( a − 2 c ¯ + c ) 2 9 ( a − c ) 2 − 4 ( a + c ¯ − 2 c ) 2 $\delta \ge {\delta }^{single}=\frac{4{(a-2\bar{c}+c)}^{2}}{9{(a-c)}^{2}-4{(a+\bar{c}-2c)}^{2}}$ ()
Consider multimarket contact, the equilibrium has no difference in both markets A and B, we then have the following result:
π 1 A c = π 2 B c = ( a + c ¯ − 2 c ) 2 9 , π 2 A c = π 1 B c = ( a − 2 c ¯ + c ) 2 9 π 1 A m = π 2 B m = λ ( a − c ) 2 4 , π 2 A m = π 1 B m = ( 1 − λ ) ( a − c ) 2 4 π 1 A d = π 2 B d = ( a − c ) 2 4 , π 2 A d = π 1 B d = ( a − 2 c ¯ + c ) 2 16 $\left\{\begin{array}{c}\begin{array}{ll} & {\pi }_{1A}^{c}={\pi }_{2B}^{c}=\displaystyle \frac{{(a+\bar{c}-2c)}^{2}}{9},{\pi }_{2A}^{c}={\pi }_{1B}^{c}=\displaystyle \frac{{(a-2\bar{c}+c)}^{2}}{9}\\ & {\pi }_{1A}^{m}={\pi }_{2B}^{m}=\lambda \displaystyle \frac{{(a-c)}^{2}}{4},{\pi }_{2A}^{m}={\pi }_{1B}^{m}=(1-\lambda )\displaystyle \frac{{(a-c)}^{2}}{4}\\ & {\pi }_{1A}^{d}={\pi }_{2B}^{d}=\displaystyle \frac{{(a-c)}^{2}}{4},{\pi }_{2A}^{d}={\pi }_{1B}^{d}=\displaystyle \frac{{(a-2\bar{c}+c)}^{2}}{16}\end{array}\end{array}\right\}$
We can observe that any firm has the incentive of collusion and deviation because of
∑ k = A , B π i k c ≤ ∑ k = A , B π i k m ≤ ∑ k = A , B π i k d , i = 1 , 2 $\sum _{k=A,B}{\pi }_{ik}^{c}\,\le \sum _{k=A,B}{\pi }_{ik}^{m}\le \sum _{k=A,B}{\pi }_{ik}^{d},i=1,2$
( q 1 A m , q 2 A m , λ ) $({q}_{1A}^{m},{q}_{2A}^{m},\lambda )$ are formable and sustainable as an equilibrium if and only if, for i = 1 , 2 $i=1,2$ ,
∑ k = A , B π i k d + δ 1 − δ ∑ k = A , B π i k c ≤ 1 1 − δ ∑ k = A , B π i k m $\sum _{k=A,B}{\pi }_{ik}^{d}+\frac{\delta }{1-\delta }\sum _{k=A,B}{\pi }_{ik}^{c}\le \frac{1}{1-\delta }\sum _{k=A,B}{\pi }_{ik}^{m}$
which we rewrite as
( a − c ) 2 4 + ( a − 2 c ¯ + c ) 2 16 + δ 1 − δ ( a + c ¯ − 2 c ) 2 9 + ( a − 2 c ¯ + c ) 2 9 ≤ 1 1 − δ ( a − c ) 2 4 $\frac{{(a-c)}^{2}}{4}+\frac{{(a-2\bar{c}+c)}^{2}}{16}+\frac{\delta }{1-\delta }\left[\frac{{(a+\bar{c}-2c)}^{2}}{9}+\frac{{(a-2\bar{c}+c)}^{2}}{9}\right]\le \frac{1}{1-\delta }\frac{{(a-c)}^{2}}{4}$
Summing the inequality over i = 1 , 2 $i=1,2$ , we see that this requires that
δ ≥ δ m u l t i = 9 ( a − 2 c ¯ + c ) 2 36 ( a − c ) 2 − 16 ( a + c ¯ − 2 c ) 2 − 7 ( a − 2 c ¯ + c ) 2 $\delta \ge {\delta }^{multi}=\frac{9{(a-2\bar{c}+c)}^{2}}{36{(a-c)}^{2}-16{(a+\bar{c}-2c)}^{2}-7{(a-2\bar{c}+c)}^{2}}$ ()

4 Results

We, respectively, compared δ s i n g l e ${\delta }^{single}$ and δ m u l t i ${\delta }^{multi}$ under the Stackelberg competition and Cournot competition. We show δ s i n g l e = δ m u l t i ${\delta }^{single}={\delta }^{multi}$ under Stackelberg competition, which implies multimarket contact did not increase the sustainability of collusion compared to single-market, while δ s i n g l e > δ m u l t i ${\delta }^{single}\gt {\delta }^{multi}$ under Cournot competition. We can get Proposition 1 and Proposition 2.

Proposition 1.Multimarket contact can not facilitate collusion by relaxing incentive compatibility constraints when firms face Stackelberg competition in the “symmetric advantage” market structure.

Proposition 2.Multimarket contact facilitates collusion by relaxing incentive compatibility constraints when firms face Cournot competition in the “symmetric advantage” market structure.

Proof.For calculation detail see Appendix A.1.

Proposition 1 is our main conclusion that differs from Bernheim and Whinston (1990). Proposition 2 could be immediate from Bernheim and Whinston (1990). Therefore, we analyze the reason why “mutual forbearance” mechanism ineffective under Stackelberg competition.

In general, low-cost firms are more difficult to discipline (Ivaldi et al. 2007). We consider the incentive compatibility constraint of the low-cost firm. First, we compare δ s i n g l e ${\delta }^{single}$ under Stackelberg competition and Cournot competition to identify the effect of first-mover advantage affect collusion sustainability under a single market. We found that δ s i n g l e ${\delta }^{single}$ under Stackelberg competition is less than under Cournot competition which means the first-mover advantage relaxes the incentive compatibility constraint. There are two opposite effects to affect collusion sustainability. The low-cost firm (Firm 1) has the first-mover advantage to increase its profits under non-coordinate equilibrium and thus decrease the cost of deviation. But it also can increase their profits under collusion equilibrium by relaxing individual rationality constraints and covering the effect of hindering collusion. For simplicity, consider Stackelberg competition and Cournot competition when firms cost homogeneous, i.e., c ¯ = c $\bar{c}=c$ , the joint profit Π m ${{\rm{\Pi }}}^{m}$ averagely share when firms face Cournot competition, but Firm 1 could allocate more share when firms face Stackelberg competition, i.e., 1 2 ≤ λ ≤ 3 4 $\frac{1}{2}\le \lambda \le \frac{3}{4}$ . Based on our setup, the joint profit Π m ${{\rm{\Pi }}}^{m}$ maximized by the “side-payment” rule, and thus maximizing aggravates the effect of facilitating collusion. In other words, the low-cost firm as a leader would be maximizing the high-cost firms' enforcement power that punishes deviation and thus maximizing relaxed the low-cost firms' incentives to deviate. We obtained that the low-cost firm that has the first-mover advantage could facilitate collusion in a single market. For the calculation detail see Appendix A.2.

Bernheim and Whinston (1990) introduced that multimarker contact facilitates collusion by linking the punishment across markets, the firms can potentially transfer slack enforcement power from one market to another market and sustain collusion in both markets. In our model, Firm 2 as the follower in Market A can transfer slack enforcement power from Market B to Market A and thus increase the enforcement power to punish if Firm 1 deviated. But as previously mentioned, Firm 2 as the leader in Market B has the first-mover advantage and thus maximizes relaxed incentives to deviate. The enforcement power transferred from Market B would be minimized. Therefore, the difference in incentive-compatible constraint conditions between single-market and multimarket contact would be minimized.

To sum up, low-cost firms hinder collusion in general when cost asymmetry. The low-cost firm as the leader can allowed to allocate more shares and thus induce discipline. The mechanism is effective in single-market, which is the substitute mechanism of “mutual forbearance.” The discount factor threshold for some collusion is thus the same under multimarket contact as under single-market.

Further, our result can obtain a potential implication that the effect of the “mutual forbearance” mechanism has a cap under certain cases. Some mechanisms that facilitate collusion under a single market may be equivalent to the “mutual forbearance” mechanism. The cost of coordinating many markets is so large that collusive members decide to sustain collusion in each market one by one. Our model can explain the curious phenomena presented by Igami and Sugaya (2022).

5 Conclusions

We analyze the coordination effect of oligopolists' multimarket contact. We study a two-stage game between two players, the low-cost and the high-cost, under two symmetrical markets when the players decide on strategy sequential and simultaneous. The ineffective firm can benefit from ceasing production. We analyze the effect that multimarket contact has on collusion sustainability.

We have shown that, compared to single-market, multimarket contact facilitates collusion due to increasing the intensity or scope of punishment. However, the mechanisms are ineffective when firms move sequentially.

In the case of firms that can move sequentially, we find that firms can reach a shared policy that balances the low-cost firm's incentive of collusion and deviation. So that is equivalent to the “mutual forbearance” mechanism. From this point of view, multimarket contact didn't facilitate collusion. It's similar to the “irrelevance result” of Bernheim and Whinston (1990).

Author Contributions

Zuo Yu: conceptualization, project administration, supervision. Tianyu Luo: methodology, writing–original draft.

Acknowledgments

The authors sincerely thank the Associate Editor, Quan Wen, and all anonymous referees for their valuable comments and suggestions on our work. We also appreciate Haokai Ning for his encouragement. Any errors are our own.

    Ethics Statement

    The authors have nothing to report.

    Conflicts of Interest

    The authors declare no conflicts of interest.

    Endnotes

  1. 1 See the Concentration in Seed Markets: Potential Effects and Policy Responses, OECD (2018).
  2. 2 Vitamins cartel proved that vitamins oligopolists' multimarket contact.
  3. 3 Kweichow Moutai Company Limited and Sichuan Yibin Wuliangye Group Limited et al. have competed in every Chinese province (Liu and Wu 2016).
  4. 4 ABF/GBI BUSINESS is another merger case which relate to multimarket contact and collusive price leadership. Case detail can see the Commission Decision Case No COMP/M.4980 at paragraph 353 – 357 $353\mbox{--}357$ .
  5. 5 See the Commission Decision Case No. COMP/M.7881 at paragraph 89.
  6. 6 See the Commission Decision COMP/E-1/37.512 – Vitamins (OJ 2003L 6, p. 1) at paragraph 203.
  7. 7 Five companies reached an agreement that only the Xinglong company active in the market and other suspended businesses. The Xinglong company only acquires 24% profits and transfers the remaining profit average to each suspended company. The case details see https://www.samr.gov.cn/jzxts/tzgg/xzcf/art/2021/art_f0e40b4455ec40f0b79cbd49ab8eec7e.html.
  8. 8 The vitamin cartels did not seem to employ such punishment schemes, nor did the breakup of a cartel trigger punishment in other markets, even when the same members (and the cheating firms) were involved.

    9. Appendix A: Calculation Detail and Cases' Detail

    A.1 Proofs for Lemma 1 and Proposition 2

    Proof of Lemma 1.We start by showing that Inequality (9) must be satisfied if Inequality (11) is satisfied. Because the discount factor δ $\delta $ is bounded, we have the following result:

    1 − δ 9 ( a − c ) 2 − 4 ( a + c ¯ − 2 c ) 2 9 ( a − c ) 2 > 4 ( a + c ¯ − 2 c ) 2 9 ( a − c ) 2 $1-\delta \left[\frac{9{(a-c)}^{2}-4{(a+\bar{c}-2c)}^{2}}{9{(a-c)}^{2}}\right]\gt \frac{4{(a+\bar{c}-2c)}^{2}}{9{(a-c)}^{2}}$

    Consequently, the low-cost firm (Firm 1) would participate in collusion if the collusion is sustainable. □ $\square $

    Proof of Proposition 2.Recall that the critical discount factor in the presence of single-market and multi-market under simultaneous game is

    δ s i n g l e = 4 ( a − 2 c ¯ + c ) 2 9 ( a − c ) 2 − 4 ( a + c ¯ − 2 c ) 2 ${\delta }^{single}=\frac{4{(a-2\bar{c}+c)}^{2}}{9{(a-c)}^{2}-4{(a+\bar{c}-2c)}^{2}}$
    and
    δ m u l t i = 9 ( a − 2 c ¯ + c ) 2 36 ( a − c ) 2 − 16 ( a + c ¯ − 2 c ) 2 − 7 ( a − 2 c ¯ + c ) 2 ${\delta }^{multi}=\frac{9{(a-2\bar{c}+c)}^{2}}{36{(a-c)}^{2}-16{(a+\bar{c}-2c)}^{2}-7{(a-2\bar{c}+c)}^{2}}$

    We need to compare the two critical discount factors. First, we rewrite the expression of the critical discount factor by reducing of fraction to a common numerator:

    δ s i n g l e = 36 ( a − 2 c ¯ + c ) 2 81 ( a − c ) 2 − 36 ( a + c ¯ − 2 c ) 2 δ m u l t i = 36 ( a − 2 c ¯ + c ) 2 144 ( a − c ) 2 − 64 ( a + c ¯ − 2 c ) 2 − 28 ( a − 2 c ¯ + c ) 2 $\left\{\begin{array}{l}{\delta }^{single}=\displaystyle \frac{36{(a-2\bar{c}+c)}^{2}}{81{(a-c)}^{2}-36{(a+\bar{c}-2c)}^{2}}\\ {\delta }^{multi}=\displaystyle \frac{36{(a-2\bar{c}+c)}^{2}}{144{(a-c)}^{2}-64{(a+\bar{c}-2c)}^{2}-28{(a-2\bar{c}+c)}^{2}}\end{array}\right\}$

    Second, we can directly compare the two critical discount factors by comparing their denominator. Consider the assume of a − c > 3 ( c ¯ − c ) $a-c\gt 3(\bar{c}-c)$ , we show

    9 ( a − c ) 2 − 4 ( a + c ¯ − 2 c ) 2 − 4 ( a − 2 c ¯ + c ) 2 = [ ( a − c ) + 10 ( c ¯ − c ) ] [ ( a − c ) − 2 ( c ¯ − c ) ] > 0 $9{(a-c)}^{2}-4{(a+\bar{c}-2c)}^{2}-4{(a-2\bar{c}+c)}^{2}=[(a-c)+10(\bar{c}-c)][(a-c)-2(\bar{c}-c)]\gt 0$
    hence, δ s i n g l e > δ m u l t i ${\delta }^{single}\gt {\delta }^{multi}$ .

    A.2 Stackelberg Competition and Cournot Competition Under Single-Market

    Recall that the δ s i n g l e ${\delta }^{single}$ under Stackelberg competition and Cournot competition is
    δ S t a c k e l b e r g s i n g l e = ( a − 2 c ¯ + c ) 2 4 ( a − c ) 2 − 2 ( a + c ¯ − 2 c ) 2 + ( a − 2 c ¯ + c ) 2 − ( a − 3 c ¯ + 2 c ) 2 ${\delta }_{Stackelberg}^{single}=\frac{{(a-2\bar{c}+c)}^{2}}{4{(a-c)}^{2}-2{(a+\bar{c}-2c)}^{2}+{(a-2\bar{c}+c)}^{2}-{(a-3\bar{c}+2c)}^{2}}$
    and
    δ C o u r n o t s i n g l e = 4 ( a − 2 c ¯ + c ) 2 9 ( a − c ) 2 − 4 ( a + c ¯ − 2 c ) 2 ${\delta }_{Cournot}^{single}=\frac{4{(a-2\bar{c}+c)}^{2}}{9{(a-c)}^{2}-4{(a+\bar{c}-2c)}^{2}}$
    We need to compare the two critical discount factors. First, we rewrite the expression of the critical discount factor by reducing the fraction to a common numerator:
    δ S t a c k e l b e r g s i n g l e = 4 ( a − 2 c ¯ + c ) 2 16 ( a − c ) 2 − 8 ( a + c ¯ − 2 c ) 2 + 4 ( a − 2 c ¯ + c ) 2 − 4 ( a − 3 c ¯ + 2 c ) 2 δ C o u r n o t s i n g l e = 4 ( a − 2 c ¯ + c ) 2 9 ( a − c ) 2 − 4 ( a + c ¯ − 2 c ) 2 $\left\{\begin{array}{l}{\delta }_{Stackelberg}^{single}=\displaystyle \frac{4{(a-2\bar{c}+c)}^{2}}{16{(a-c)}^{2}-8{(a+\bar{c}-2c)}^{2}+4{(a-2\bar{c}+c)}^{2}-4{(a-3\bar{c}+2c)}^{2}}\\ {\delta }_{Cournot}^{single}=\displaystyle \frac{4{(a-2\bar{c}+c)}^{2}}{9{(a-c)}^{2}-4{(a+\bar{c}-2c)}^{2}}\end{array}\right\}$
    Second, we can directly compare the two critical discount factors by comparing their denominator. Consider the assume of a − c > 3 ( c ¯ − c ) $a-c\gt 3(\bar{c}-c)$ , we show:
    7 ( a − c ) 2 − 4 ( a + c ¯ − 2 c ) 2 + 4 ( a − 2 c ¯ + c ) 2 − 4 ( a − 3 c ¯ + 2 c ) 2 = 3 [ ( a − c ) 2 − 8 ( c ¯ − c ) 2 ] > 0 $7{(a-c)}^{2}-4{(a+\bar{c}-2c)}^{2}+4{(a-2\bar{c}+c)}^{2}-4{(a-3\bar{c}+2c)}^{2}=3[{(a-c)}^{2}-8{(\bar{c}-c)}^{2}]\gt 0$
    hence, δ C o u r n o t s i n g l e > δ S t a c k e l b e r g s i n g l e ${\delta }_{Cournot}^{single}\gt {\delta }_{Stackelberg}^{single}$ .

    A.3 Summary of Vitamin Cartel − Market Segment (%)

    Vitamin A E B5 B6 B1 Folic-acid B2 C H β $\beta $ -carotene Carotinoids D3
    Participants
    Roche 40–50 35–45 30–40 45 53 65 47 40 45 70–80 70–80 40
    BASF 30–40 20–30 15–25 11 29 6 4 20–30 20–30 15
    Add: Roche + BASF 70–90 55–75 45–65 45 64 65 76 46 49 90–100 90–100 55
    Takeda 9 24 26 12 24
    Rhône-Poulenc (Aventis) 20–30 10–20 9
    Daiichi 25–35 10
    Merck 8 7
    Sumitomo 23
    Sumika 4
    Eisai 5–15
    Kongo 5
    Tanabe 16
    Lonza 5
    Solvay Pharm 32
    Total 96 96 86 64 88 100 88 78 100 100 100 96
    Duration from: 1989.9 1991.1 H: 1991.10
    β $\beta $ -carotene: 1992.9
    Carotinoids: 1993.5
    D3: 1994.1
    Duration to: 1999.2 1994.6 B2: 1995.9 H: 1994.4
    C: 1995.8 β $\beta $ -carotene: 1998.12
    Carotinoids: 1998.12
    D3: 1998.6
    • Note: The number in the table is the worldwide market share. The duration is not necessarily the same for all participants.
    • Source: The Commission Decision COMP/E-1/37.512 – Vitamins (OJ 2003L 6, p. 1).

    A.4 Summary of Tax Control Disk and Financial Control Disk Cartel (Changsha City, China) – Market Segment (%)

    Relevant Geography Market YuHua District; TianXin District; YueLu District; FuRong District; KaiFu District; GaoXin District;
    Participants WangCheng District; WangCheng County LiuYang District; ChangSha County
    Hunan Baiwang Golden Fu Technology Co. Ltd. 34 (B) 72 (B)
    1 (A) 97 (A)
    Hunan Aerospace Information Co. Ltd. 66 (B) 28 (B)
    99 (A) 3 (A)

    A.5 Beer Market Shares in the Partial EEA Countries (2014) (%)

    Relevant Geography Market Hungary Poland Romania Czech France Netherlands Belgium Italy United Kingdom Slovakia
    Parties
    AB InBev 5–10 0–5 0–5 0–5 10–20 20–30 50–60 (L) 10–20 10–20 0–5
    SAB 20–30 30–40 (L) 30–40 (L) 40–50 (L) 0–5 10–20 0–5 10–20 0–5 30–40
    Add: AB InBev + SAB (After merger) 30–40 (L) 30–40 (L) 30–40 (L) 40–50 (L) 20–25 30–40 50–60 (L) 20–30 20–30 30–40
    Heineken 30–40 20–30 30–40 10–20 20–30 40–50 (L) 5–10 20–30 (L) 20–30 (L) 30–40 (L)
    Carlsberg 0–5 10–20 5–10 0–5 30–40 (L) 0–5 0–5 5–10 10–20 0–5
    • Note: Market share calculated according to sales volume. (L) Mean to the firm is leader in the market.
    • Source: Case No. COMP/M.7881 – AB INBEV/SABMILLER.

    A.6 ×86 CPUs and FPGA Market Shares (2020) (%)

    Relevant Product Market ×86 CPUs FPGA
    Parties
    Intel 90–100 30–40
    AMD 5–10
    Xilinx 50–60
    Add: AMD+Xilinx (After merger) 5–10 50–60
    • Note: The numbers in the table is the worldwide market share. Market share is calculated according to sales.
    • Source: Case M.10097 – AMD/XILINX.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.