Enhanced Cherenkov radiation in twisted hyperbolic Van der Waals crystals
Abstract
Cherenkov radiation in artificial structures experiencing strong radiation enhancements promises important applications in free-electron quantum emitters, broadband light sources, miniaturized particle detectors, etc. However, the momentum matching condition between swift electrons and emitted photons generally restricts the radiation enhancement to a particular momentum. Efficient Cherenkov radiation over a wide range of momenta is highly demanded for many applications but still remains a challenging task. To this end, we explored the interaction between swift electrons and twisted hyperbolic Van der Waals crystals and observed enhanced Cherenkov radiation at the flatband resonance frequency. We show that, at the photonic magic angle of the twisted crystals, the electron momentum, once matching with that of the flatband photon, gives rise to a maximum energy loss (corresponding to the surface phonon generation), one-order of magnitude higher than that in conventional hyperbolic materials. Such a significant enhancement is attributed to the excitation of flatband surface phonon polaritons over a broad momentum range. Our findings provide a feasible route for highly directional free-electron radiation and radiation shaping.
1 INTRODUCTION
Cherenkov radiation refers to a directional photon emission from a swiftly charged particle. To enable Cherenkov radiation, the swift charged particles should fulfill the Cherenkov phase-matching condition, that is, .1 Here, and ω correspond to the wave vector and frequency of emitted photonic modes, respectively; accounts for the particle velocity. Particularly, in a homogenous, dispersionless and isotropic medium, this Cherenkov phase-matching condition could be simplified as cosθc = 1/(nβ),2 where θc is the angle between the photon emission direction and particle trajectory, n is the refractive index of the medium, β = ve/c is the normalized velocity, and c is the light speed in vacuum. Such a unique relation is widely applied to detect particle masses by measuring the Cherenkov angles at a given particle momentum,3 leading to the famous discovery of elementary particles such as anti-proton and J-particle.4, 5
The Cherenkov phase-matching condition also indicates the flexibility to engineer the behaviors of Cherenkov radiation by controlling the material and structural dispersions.6, 7 For example, double negative metamaterials, whose refractive indices are negative, have been proposed to reverse the direction of Cherenkov radiation.8-10 Swift electrons can emit surface Dyakonov–Cherenkov radiation only at a particular particle trajectory, owing to the narrow angular existing domain of Dyakonov surface waves.11 By exploiting the high-wave vector (high-k) modes in plasmonic structures, one can largely reduce the velocity threshold of Cherenkov radiation and enhance the photon emission rate at a given frequency.12-15 Recent advances further demonstrate the broadband enhancement of Cherenkov radiation by interacting free electrons with the dispersionless surface plasmons.16 These novel effects broaden the applications of Cherenkov radiation in the miniaturized particle detectors,3, 17, 18 novel X-ray/terahertz light sources,19-24 molecular imaging,25 and radiation therapy,26 among others.
Despite great effort made to enhance Cherenkov radiation, free electrons generally emit the photonic modes with a particular wave vector at a particular frequency. Here, θp refers to the angle between the particle trajectory and the wave vector of emitted photonic modes, and θp = θc only in homogeneous isotropic media. This constraint limits the maximum achievable emission rate of swift electrons. To break this limit, the Cherenkov phase-matching condition has to be satisfied in a wide range of θp, and hence . A recent experimental work has demonstrated a feasible solution to enhance free-electron radiation in a finite range of by exploiting the flatband Bloch modes in all-dielectric photonic crystals.27 However, the mode indices of the Bloch modes in all-dielectric photonic crystals are close to the unity. This not only makes the existing domain of flatband modes relatively narrow in the momentum space, but also necessitates an electron velocity comparable to the light speed in vacuum. Thus, a novel scheme to enhance Cherenkov radiation in a broad range of wave vectors is highly desired for constructing, for example, high-performance free electron light sources on a chip.
To this end, we propose flatband surface phonon polaritons to enhance Cherenkov radiation in a broad range of wave vectors. Flatband surface phonon polaritons widely exist in the twisted hyperbolic Van der Waals crystals.28-31 As the photonic analog of moire superlattice in condensed matter physics,32, 33 the twisted hyperbolic Van der Waals crystals can enable flatband surface phonon polaritons with the flat isofrequency contour at a relatively large twisted angle (i.e., the photonic magic angle29). Remarkably, such surface modes are featured with large mode indices (generally over 100). Thus, flatband surface phonon polaritons open up a new opportunity to enhance Cherenkov radiation in a broad range of wave vectors with low-energy electrons. Here, we investigate the interaction between swift electrons and the twisted hyperbolic Van der Waals crystal α-MoO3 that supports flatband surface phonon polaritons. With a suitable selection of electron velocity, Cherenkov radiation is mediated by flatband surface phonon polaritons. Our studies show that the wave vector linewidth of photon emission from swift electrons is enhanced by nearly 20 times at the photonic magic angle, as that compared to the conventional ones. As such, the maximum achievable photon number of Cherenkov radiation is one-order of magnitude higher than that in an individual α-MoO3 slab. Furthermore, the particle velocity that leads to the maximum achievable photon number could be readily controlled by tuning the gap width of the twisted α-MoO3 slabs. Our work not only facilitates the realization of free-electron light sources on the chip but also could find applications in particle detection.
2 RESULTS
Without loss of generality, we consider a twisted hyperbolic Van der Waals material composed of two stacked α-MoO3 slabs. The permittivity of α-MoO3 is adopted from the recent work34 (as detailed in Supporting Information S1: Section S1). The thickness of each α-MoO3 slab is denoted as h, and the gap width between two α-MoO3 slabs is denoted as g. The twisted angle of the top- (bottom-) layer α-MoO3 slab with respect to x-axis is ϕ/2 (−ϕ/2). As such, the twisted angle between two α-MoO3 slabs is ϕ. A free electron (with the current density of ) is moving along x-axis at the velocity of ve, where q0 is the elementary charge.35 For conceptual demonstration, the free electron is traveling in the gap of the twisted hyperbolic material.
We first demonstrate that the twisted angle of α-MoO3 slabs can strongly influence Cherenkov radiation. To illustrate this, we plot in Figure 1B,C, the photon number as a function of the wave vectors ky = q/sinθp in different twisted angles, when the wavenumber is fixed at ν = 900 cm−1. Here, refers to the in-plane wavevector of photon polaritons. As shown in Figure 1B, the free electron can emit photons with a broad range of wave vectors (with the normalized linewidth up to 21.3) when the twisted angle equals to the photonic magic angle, that is, ϕ = ϕmagic = 44.07°. In sharp contrast, the free electron only emits photons with a narrow range of wave vectors (with the normalized linewidth of 1.2), if ϕ ≠ ϕmagic (Figure 1C). Here, the photonic magic angle ϕmagic is known as the one that can enable the open-to-close topological transition of the isofrequency contour of surface phonon polaritons, accompanied with the variation in the number of anti-crossing points (the anti-crossing point is defined as the crossing point of isofrequency contours when the constituent materials are uncoupled).28 The magic angle is theoretically calculated by ϕ = 2φ,28, 29 with φ to be the open angle of the isofrequency contour of an individual α-MoO3 slab (see black solid line in the inset of Figure 2C). Specifically, at υ = 900 cm−1, the magic angle is ϕmagic = 44.07° where open-to-close topological transition emerges: if ϕ = 20° < ϕmagic at υ = 900 cm−1, the isofrequency contour is an open hyperbola with 2 anti-crossing points; if ϕ = 60° > ϕmagic at υ = 900 cm−1, the isofrequency contour becomes an open hyperbola with 4 anti-crossing points (see the inset of Figure 2C).
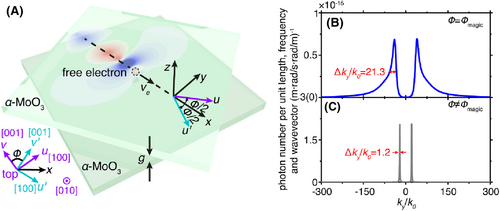
Schematic of Cherenkov radiation in twisted hyperbolic Van der Waals crystals. (A) Structural setup. Two α-MoO3 slabs are stacked in the z-direction. The u-axis and v-axis are oriented in the [100] and [001] directions for the top-layer α-MoO3 slab, respectively; The u'-axis and v'-axis are oriented in the [100] and [001] directions for the bottom-layer α-MoO3 slab, respectively. The twisted angle of the top- (bottom-) layer α-MoO3 slab with respect to x-axis is ϕ/2 (−ϕ/2). As such, the twisted angle between two α-MoO3 slabs is ϕ. A free electron with the velocity of ve propagates inside the gap of twisted α-MoO3 slabs along x-axis. (B) Photon number spectrum at the magic angle ϕ = ϕmagic. (C) Photon number spectrum at the conventional angle ϕ ≠ ϕmagic. In (B, C), ky corresponds to the tangential wave vector of photons emitted by the free electron. Without particular statement, other parameter setups here and below are: the inverse of the normalized velocity of free electron is 1/β = 10.78; the thickness of each α-MoO3 slab is h = 100 nm; the gap width between two α-MoO3 slabs is g = 5 nm; the wavenumber is υ = 900 cm−1; the magic angle is ϕmagic = 44.07° at υ = 900 cm−1. Moreover, the optical parameters of each α-MoO3 are provided in Supporting Information S1: Section S1.
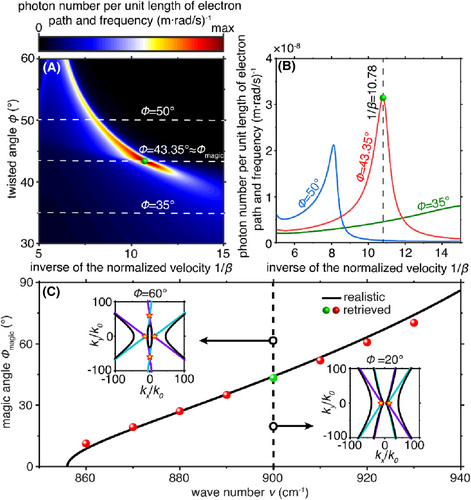
Enhancing Cherenkov radiation by flatband surface photon polaritons. (A) Photon number as a function of twisted angle and inverse of the normalized velocity, defined as 1/β = c/ve. (B) Photon number as a function of the inverse of the normalized velocity. The twisted angles are ϕ = 35°, ϕ = 43.35°, and ϕ = 50°, respectively. (C) Comparison of retrieved and realistic magic angles. The realistic magic angle corresponds to the one that enables the open-to-close topological transition of the isofrequency contour of surface phonon polaritons (see the isofrequency contours before and after the topological transition at υ = 900 cm−1 in the inset of [C]). The retrieved magic angle corresponds to the one allowing the maximum photon number in (A). In each inset, the blue and purple curves correspond to the isofrequency contours of uncoupled surface phonon polaritons, and the black curve corresponds to the isofrequecy contour of coupled surface phonon polaritons.
The broad wave vector spectrum at the photonic magic angle largely enhances the Cherenkov radiation. To demonstrate this, we plot in Figure 2A the photon number as a function of twisted angle and inverse of the normalized velocity, where the inverse of the normalized velocity is related to the realistic electron velocity by 1/β = c/ve, when υ = 900 cm−1. Obviously, the photon number reaches a maximum value, that is, 3.1 × 10−8 (m · rad/s)−1, only when ϕ = 43.35° and 1/β = 10.78 (see Figure 2A). Such a large photon number implies the total energy of Cherenkov radiation per electron up to 5.73 × 10−22 J, if the electron interaction length is 1 μm and the frequency range of interest is [890 920] cm−1 (seeing calculation details in Supporting Information S1: Section S3). By contrast, the maximum photon numbers are 0.8 × 10−8 and 2.1 × 10−8 (m · rad/s)−1, when the twisted angles are ϕ = 35° and ϕ = 50°, respectively (see Figure 2B). The twisted angles that enable the maximum photon number are highly close to the photonic magic angles in theory, indicating that the broad wave vector spectrum at the photonic magic angle plays a key role in enhancing Cherenkov radiation (see Figure 2C).
To further explain the reason for the emergence of the broad wave vector spectrum, we analyze the field patterns of free-electron radiation in the twisted α-MoO3 slabs. Figure 3A–C shows the field pattern of Cherenkov radiation, when we vary the twisted angle ϕ from 35°, 43.35° to 50° and the inverse of the normalized velocity is fixed at 1/β = 10.78. When ϕ = 35o, the isofrequency contour of surface photon polaritons is hyperbolic. As such, a free electron with 1/β = 10.78 only emits two photonic modes satisfying (see Fourier spectrum of Cherenkov radiation in Figure 3D). When ϕ = 43.35o, the isofrequency contour becomes nearly flat. In this case, modes with a broad range of wave vectors, that is, from ky = 40k0 to ky = 60k0 satisfy the Cherenkov phase-matching conditions. Thus, these modes are efficiently excited by free electrons (see Fourier spectrum of Cherenkov radiation in Figure 3E). With a further increase in the twisted angle, for example, ϕ = 50°, no surface mode is excited by the free electron (see Fourier spectrum of Cherenkov radiation in Figure 3F).
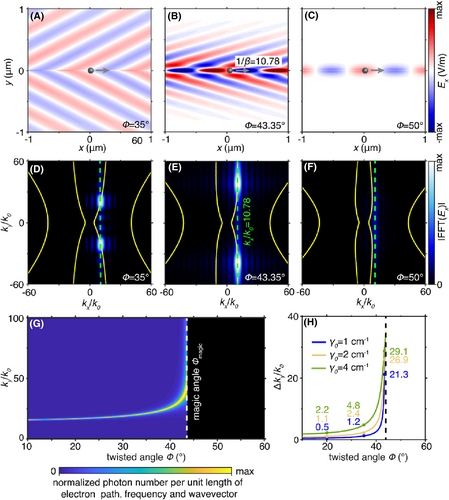
Field patterns and its Fourier spectrum of Cherenkov radiation mediated by flatband and hyperbolic surface phonon polaritons. (A–C) Field patterns of Cherenkov radiation mediated by surface phonon polaritons. The twisted angles of α-MoO3 slabs are ϕ = 35°, ϕ = 43.35°, and ϕ = 50°, respectively. (D–F) Fourier spectrum of field patterns in (A–C). The yellow solid curves correspond to the theoretical isofrequency contours of surface photon polaritons. (G) The normalized photon number emitted by free electrons at kx/k0 = 10.78 as a function of twisted angle. (H) The linewidth of ky as a function of twisted angle at kx/k0 = 10.78. The loss rates are γ = 1 cm−1, γ = 2 cm−1, and γ = 4 cm−1, respectively.
To quantitively demonstrate the influence of the twisted angle on the wave vector spectrum, we plot the photon number as a function of ky and ϕ in Figure 3G. We extract linewidth Δky of Cherenkov radiation from the Figure 3G. The twisted angle is varied from 20° to 43.35°, the linewidth Δky is broadened by 13 times (if the material loss rate is γ = 4 cm−1, which is the typical value for α-MoO3). Such an enhancement rate can even reach 43 when the material loss rate is reduced from 4 to 1 cm−1 (Figure 3H).
Finally, we investigate the influence of the gap width g on the behaviors of Cherenkov radiation mediated by flatband surface phonon polaritons. Figure 4 plots the photon number as a function of normalized velocity and gap width of α-MoO3 slabs, where the twisted angle is fixed at the photonic magic angle. As the gap width increases, the electron velocity that enables the maximum photon number increases (Figure 4A). To be specific, the normalized electron velocities βpeak for the maximum achievable photon number are 0.075, 0.093, and 0.106, respectively, when the gap widths are 2, 5, and 10 nm, respectively (Figure 4B). This is because the gap width determines the mode confinement of the flatband surface photon-polaritons. As the gap width decreases, the coupling strength of the photon-polariton mode in each flake becomes stronger, introducing larger dispersion line splitting in momentum space and thus pushing the kx (of the mode closest to the origin) larger. That is, to excite such flatband surface photon-polaritons with a larger kx, a smaller electron velocity is required. Such an effect may inspire novel particle detectors based on enhanced Cherenkov radiation in twisted hyperbolic Van der Waals crystals.
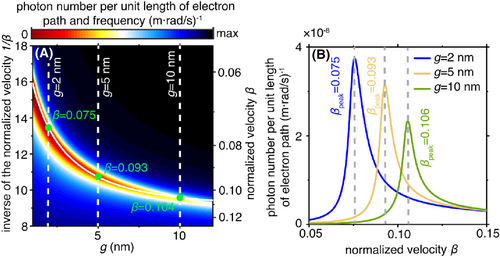
Influence of the gap width on the behaviors of Cherenkov radiation mediated by flatband surface phonon polaritons. (A) Photon number as a function of gap width and inverse of the normalized velocity. (B) Photon number as a function of normalized velocity. The gap widths are g = 2 nm, g = 5 nm, and g = 10 nm, respectively. In (A), the white-solid curve corresponds to the theoretical value of normalized velocity to excite flatband surface phonon polaritons at different gap widths of twisted α-MoO3 slabs. In (B), the βpeak corresponds to the normalized velocity that enables the maximum photon number.
3 DISCUSSIONS
To conclude, we report on Cherenkov radiation mediated by flatband surface phonon polaritons, in twisted hyperbolic Van der Waals crystals at the photonic magic angle. This revealed that Cherenkov radiation comprises of photons with a broad range of wave vectors at the working frequency. Such behavior largely enhances the emission rate of free electrons in passive media, leading to the maximum electron energy loss at the working frequency. By altering the twisted angle between two hyperbolic materials, the flatband resonance frequency could be flexibly tuned from the terahertz to mid-infrared frequency range. Through on-chip integration of hyperbolic Van der Waals crystals with gradually varied twisted angles (see configurations and discussions in Supporting Information S1: Section S6), the revealed mechanism is promising for realizing bright and tunable free-electron light sources, that operate in the terahertz and mid-infrared frequency ranges. On the other hand, since the excitation of enhanced Cherenkov radiation highly relies on the twisted angle, this technique offers a potential solution to measure the photonic magic angle in twisted photonic structures. This technique demonstrates superior efficiency over the existing optical and electron microscopy methods for measuring twist angles, owing to its non-scanning and non-invasive nature. Moreover, as the excitation of enhanced Cherenkov radiation is also highly sensitive to the particle velocity, this system may open a new door for particle selection. We remark that this mechanism could be extended to multilayered twisted photonic systems, opening up an opportunity to enhance Cherenkov radiation in 3D scenarios.36 Finally, we highlight that these findings are general as it can apply to other polaritonic systems and a broad range of hyperbolic materials,37, 38 including hyperbolic metasurface,28 hexagonal boron nitride,39 vanadium pentoxide,40 dichalcogenide tungsten diselenide,41 black phosphorus42 or their hybrids.43
AUTHOR CONTRIBUTION
Hao Hu initiated the project. Yu Luo supervised the project. Hao Hu performed the analytical calculations and numerical simulations. All authors contributed to the analysis and discussion of the results. Hao Hu and Yu Luo wrote the paper. All authors have read and approved the final version of the manuscript.
ACKNOWLEDGMENTS
This work is sponsored in part by Distinguished Professor Fund of Jiangsu Province (grant no. 1004-YQR23064, 1004-YQR24010); Selected Chinese Government Talent-recruitment Programs of Nanjing (grant no. 1004-YQR23122); Startup Grant of Nanjing University of Aeronautics and Astronautics (grant no. 1004-YQR23031); National Natural Science Fund for Excellent Young Scientists Fund Program (Overseas) of China; National Natural Science Foundation of China (grant no. 62175212); Zhejiang Provincial Natural Science Fund Key Project (grant no. LZ23F050003); the Fundamental Research Funds for the Central Universities (grant no. 226-2024-00022, NS2024022).
CONFLICT OF INTEREST STATEMENT
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Open Research
DATA AVAILABILITY STATEMENT
Data will be made available on request.




