Financial liberalization, exchange-rate regime, and banking crisis likelihood
Abstract
This paper provides empirical evidence of the impact that financial liberalization plays, within various exchange rate regimes, on the likelihood of systemic banking crisis. Using a sample of 50 banking crisis episodes over the period of 1985–2005, I investigate the impact of financial liberalization and exchange-rate regime on the likelihood of systemic banking crisis. When interacted with an overall financial liberalization measure, exchange-rate regime was significant and positive under a flexible regime. Other empirical results show that when interacted with financial liberalization dimensions, exchange-rate regime variables produced significant results under intermediate and flexible exchange-rate regimes.
1 INTRODUCTION
Numerous papers have analysed the effectiveness of financial liberalization programs as a means of promoting financial and economic growth. Some researchers have found that nations benefit from financial liberalization (Baier et al., 2012; Beck et al., 2013; Klein & Olivei, 2008; Quinn & Toyoda, 2008; Shehzad & De Haan, 2009). On the contrary, several studies have found financial liberalization to be a major factor in the occurrence of banking crises or the weakening of economic growth (Demirgüç-Kunt & Detragiache, 2001; Noy, 2004), whereas others have found mixed results on financial crisis likelihood from liberalization policies (Joyce, 2011).
To shed light on this issue, this paper examines 50 banking crisis episodes from 71 least-developed, emerging, and advanced economies over the period of 1985–2005 to measure the roles of financial liberalization and exchange-rate regime play on the likelihood of systemic banking crisis occurrence. I also utilize the financial liberalization data to breakdown the financial liberalization data into dimensions to test each of their impact on the likelihood of banking crisis onset. I also employ banking crisis, financial liberalization, and exchange-rate regime data to create an interaction term between financial liberalization and exchange-rate regime in order to test the impact of financial liberalization, conditional upon exchange-rate regime, on the probability of banking crisis occurrence.
My empirical results indicate that the choice of exchange-rate regime, ceteris paribus, has an insignificant effect on the likelihood of banking crisis. These results hold when I run the exchange-rate regime variable with the aggregated financial liberalization variable as well as in individual regressions with the dimensions of financial liberalization. However, I find that when interacted with financial liberalization, exchange-rate regime becomes a statistically significant indicator of banking crisis likelihood under flexible exchange-rate regimes. When interacted with particular financial liberalization dimensions, intermediate and flexible exchange-rate regimes produce statistically significant results. However, when interacted with financial liberalization (in whole or with various liberalization dimensions), fixed exchange-rate regimes do not produce statistically significant results in the total sample or any of the subsamples.
This paper contributes to the existing literature on the role that financial liberalization and exchange-rate regimes play in the occurrence of banking crises. First of all, I not only test the significance of financial liberalization as a whole on the likelihood of banking crisis but also break down financial liberalization into its seven dimensions and test each dimension on the likelihood of crisis occurrence. Second, by providing analysts and policymakers with an introduction to the interaction of financial liberalization and exchange-rate regime and their composite effect on the likelihood of systemic banking crisis, the results may assist policymakers in making decisions that avert potential toxic combinations between liberalization dimensions and a particular exchange-rate regime.
The remainder of the paper is organized as follows. Section 2 reviews the literature. Section 3 describes the data, defines the variables, and presents the models used in the study. Section 4 presents the empirical results. Section 5 concludes.
2 REVIEW OF THE LITERATURE
2.1 Financial liberalization and banking crisis
Over the last several decades, numerous developed and developing nations have moved towards liberalization of their financial and banking systems.
1Countries have eliminated interest rate ceilings, lowered reserve-ratio requirements, reduced government interference in credit allocation decisions, and privatized many banks and insurance companies. Also, some countries have actively promoted the development of local stock markets and encouraged entry of foreign financial intermediaries. These liberalization measures have shown increased economic growth in empirical studies (see Bekaert, Harvey, & Lundblad, 2005; Klein & Olivei, 2008; Quinn & Toyoda, 2008; Ranciere, Tornell, & Westermann, 2006).
The favourable view of financial liberalization is somewhat clouded by the sharp increase in financial problems experienced by both advanced and emerging countries throughout the 1980s and 1990s. Banking industries around the world were hit by a number of problems, some of which erupted into systemic crises. These crises underscore the view that the benefits of financial liberalization must be weighed against the costs of financial fragility. A number of researchers find that financial liberalization has a significant effect on the likelihood of banking crises (for example, see Demirgüç-Kunt & Detragiache, 1998; Noy, 2004; and Allen et al., 2012).2 Shehzad and De Haan (2009) suggest that although liberalization reduces the likelihood of systemic banking crises, conditional on quality banking supervision, they find evidence that the likelihood of “borderline crises” increases after financial liberalization. A recent study by Angkinand, Sawangngoenyuang, and Wihlborg (2010) argues that banking crises are most likely to occur after an “intermediate degree” of financial liberalization. They find an “inverted U-shaped relationship” (similar to that in deposit insurance schemes) between financial liberalization and the probability of crises.
2.2 Exchange rate regime and banking crisis
Unlike the work on the linkages between financial liberalization and banking crisis, the research done on the connection between exchange-rate regime and banking crisis remains scant, with most work concentrated on the relationship between exchange-rate regime and currency crisis or twin crisis3 (currency and banking crisis). In some early empirical investigations on the link between exchange-rate regimes and banking crises, Eichengreen and Arteta (2002) found no compelling link between exchange-rate regimes and crisis. Domac and Peria (2003) examine a large sample of developed and developing countries over the period of 1980–1997 and find that after controlling for an array of macroeconomic and financial variables, a “proper exchange-rate regime is dependent upon circumstances of particular countries and time.” They also contend that banking crises are less likely under fixed exchange-rate regimes. However, once a crisis occurs, they find its costs are higher under fixed regimes relative to other regimes.
Recent studies on the topic of exchange-rate regimes and banking crises rely on updated data sets of exchange-rate classifications that distinguish regimes into more than two classifications. Bubula and Otker-Robe (2003) use the Internal Monetary Fund (IMF) de facto exchange-rate regimes from 1990 to 2001 to analyse the crisis proneness of various regimes. They find that pegged regimes, as a whole, have been characterized by a higher likelihood of currency crises than floating regimes and that intermediate regimes have been more crisis prone than both hard pegs and other floating regimes—a view consistent with the “two corners” viewpoint of exchange-rate regimes.
A study by Reinhart and Rogoff (2004) relies on the Reinhart and Rogoff exchange regime classification and finds no support for the two-corners view: a hypothesis that economies tend to move to the polar extremes of free floats or rigid pegs over time. Angkinand, Chiu, and Willett (2009) support the unstable-middle hypothesis, which holds that soft pegs appear to be the most crisis-prone exchange-rate regime; however, they do not agree with the two corners hypothesis. Lastly, Angkinand and Willett (2011) find that it is not necessary to move all the way to corner regimes in order to reduce the effect of exchange-rate regimes on the probability of banking crises.
3 DATA AND METHODOLOGY
I retrieve the annual banking crisis data from 43 countries over the period of 1985–2005. The sample includes 71 countries; however, only 43 incurred a banking crisis over the sample period. Several countries (Argentina, Bolivia, Brazil, Cameroon, Costa Rica, and Kenya) suffered more than one banking crisis episode throughout the sample period (see the Appendix for a list of banking crisis episodes by country). The primary sources for the data are statistical reports from the IMF's International Financial Statistics (IFS), the World Bank's world development indicators, and publicly available data sets from Abiad, Detragiache, and Tressel (2010) and Laeven and Valencia (2008, 2012). I obtain financial liberalization data from Abiad et al.'s (2010) database.
3.1 Banking crisis data and definition
In the most comprehensive and quantitative definition of banking crises, Laeven and Valencia (2008) define a systemic banking crisis and also identify cases of borderline banking crises.4 They define a banking crisis as systemic if two conditions are met: (1) There exist “significant signs of financial distress in the banking system” (as indicated by significant bank runs, losses in the banking system, and bank liquidations); and (2) there exist “significant banking policy intervention measures in response to significant losses in the banking system.” Laeven and Valencia (2008) consider the first year that both conditions are met to be the onset of the banking crisis. To measure significant policy intervention, Laeven and Valencia state that at least three out of the following six intervention measures must have been used: (1) extensive liquidity support (5% of deposits and liabilities to non-residents), (2) bank restructuring costs (at least 3% of GDP), (3) significant bank nationalizations, (4) significant guarantees put in place, (5) significant asset purchases (at least 5% of GDP), and (6) deposit freezes and bank holidays.
Data on financial liberalization comes from Abiad et al. (2010), who distinguish seven dimensions (or dimensions) for which the financial sector has been liberalized. Each financial liberalization dimension is measured on a scale from 0 to 3, where 0, 1, 2, and 3 represent fully repressed, partially repressed, largely liberalized, and fully liberalized, respectively, giving a range of 0–21. The first dimension refers to credit controls and reserve requirements and focuses on the existence of credit ceilings or floors and reserve requirements. The second dimension consists of interest rate controls and examines whether they are administered by the government and if the controls contain floors, ceilings, or bands.
The third dimension examines entry barriers. The fourth dimension covers state ownership in the banking sector or the percentage of the assets in the banking sector that are controlled by state-owned banks. The fifth dimension refers to capital account restrictions. The sixth dimension covers prudential regulations and supervision5 of the banking sector. The seventh dimension refers to securities market policy and focuses on the auctioning of government securities, degree of openness to foreign investors, and capital market development. In the empirical section, I regress the financial liberalization variable as a whole, as well as each dimension individually, on the likelihood of crisis occurrence.
My other variable of interest is exchange-rate regime. Exchange rate regime is an exchange rate regime dummy variable that consists of three categories: fixed, intermediate, and floating regimes. I retrieve the data from Reinhart and Rogoff's (2004) exchange-rate regime database, which can be downloaded in the updated form. In the baseline model, I run the regressions with the whole exchange-rate regime variable. In the interaction models, I break down the dummy into three dimensions; fixed, intermediate, and flexible. The fixed dummy includes pre-announced pegs, de facto pegs, and pre-announced horizontal bands that are narrower than or equal to +/−2%. The intermediate dummy includes pre-announced and de facto crawling pegs as well as pre-announced and de facto crawling and moving bands. The flexible dummy includes freely and managed floating regimes.
I add another explanatory variable, currency crisis, to test its effect on the likelihood of banking crisis. The dummy variable, currency crisis, takes a value of one if country i experienced a currency crisis in year t and 0 otherwise. Currency crisis is a standard type of currency crisis dummy based on Glick and Hutchinson (2000), who construct an indicator of currency crises based on significant changes in an index of “currency pressure,” defined as the weighted average of real exchange-rate changes and international reserve losses. The addition of this explanatory variable may help clear the debate on whether currency crises impact the likelihood of banking crises.
Finally, to avert identification of spurious correlations due to omitted variable bias, I include several financial and economic controls that are consistent with those of other empirical banking crisis papers. Credit growth is based on private credit data taken from the IFS. I operationalize credit growth as the annual change in the natural log of real credit (the natural log of real credit in year t minus the natural log of real credit in year t−1). Following Beck et al. (2000) and Mendoza and Terrones (2008), real credit is the average of two continuous end-of-year values of nominal credit, deflated by the end-of-year consumer price index.6 Private credit is defined as the amount of claims held by both banks and non-bank financial intermediaries to the nonfinancial private sector. The remaining control variables are as follows: GDP growth rate, inflation, and real interest rate.
3.2 Model specifications
To test the relationship between financial liberalization and banking crisis, conditional upon exchange-rate regime classification, I estimate the likelihoods with a random-effects probit model. I chose a random-effects probit model over a fixed-effects logit model because the financial liberalization and exchange-rate regime variables may show some patterns of persistence over time for a specific country. Thus, relying on probit models with fixed effects might result in some estimation bias. Further, the random-effects estimator proposed in this study, which allows the use of data from noncrisis nations as well as crisis nations, provides superior performance compared with the fixed-effects models, which rely on data solely from crisis-hit nations.
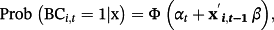
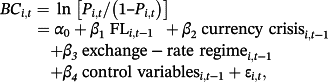 (1)
(1)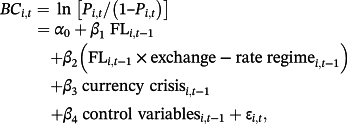 (2a)
(2a)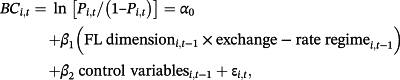 (2b)
(2b)In the second Equation 2a, I add an interaction term: (FL × exchange-rate regime). I run exchange-rate regimes with financial liberalization to test the effect of exchange-rate regimes, in the presence of financial liberalization, on the likelihood of banking crises. In this model, exchange-rate regime represents fixed exchange-rate regimes, intermediate exchange-rate regimes, and flexible exchange-rate regimes. In Equation 2b, I break down the interaction term and run the model with each of the seven financial liberalization dimensions interacted with the target exchange-rate regime.
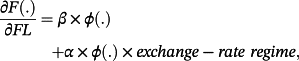 (3)
(3)4 EMPIRICAL RESULTS
I first report the effects of total financial liberalization and its breakdown into dimensions on systemic banking crises with equation 1 in Section 4.1. Section 4.2 and 4.3 reports the results of financial liberalization and financial liberalization dimensions interacted with exchange-rate regimes on the likelihood of banking crisis.
4.1 Effect of financial liberalization on banking crisis
In Table 1, I break down the financial liberalization variable into its seven dimensions and run the model for the full sample of countries. The negative and significant results of the seven financial liberalization dimensions in columns 1–7 indicate that each contributes to a decrease in the likelihood of a banking crisis onset at various magnitudes, with banking supervision and privatization having the strongest impact. More effective banking supervision, such as on-site and off-site audits, provides a way to discipline banks and prevent excessive credit growth, as the information gained by bank supervisors enables them to more effectively enforce measures on imprudent banks (Delis & Staikouras, 2011).
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| Credit controls(t–1) | −0.138b (0.070) | ||||||
| Currency crisis(t–1) | 0.231 (0.345) | 0.225 (0.342) | 0.651a (0.390) | 0.174 (0.349) | 0.247 (0.347) | 0.249 (0.354) | 0.224 (0.365) |
| Exchange rate regime(t–1) | −0.006 (0.118) | −0.008 (0.121) | 0.124 (0.152) | 0.038 (0.115) | −0.001 (0.119) | −0.027 (0.123) | −0.007 (0.126) |
| Credit growth(t–1) | 1.017c (0.384) | 0.982b (0.383) | 0.765 (0.562) | 0.991c (0.372) | 0.879b (0.404) | 1.095c (0.396) | 0.936b (0.396) |
| GDP(t–1) | −0.079a (0.044) | −0.086b (0.043) | −0.085 (0.061) | −0.062 (0.044) | −0.089b (0.043) | −0.018 (0.044) | −0.071 (0.044) |
| Inflation(t–1) | −0.011 (0.248) | −0.004 (0.244) | −0.568 (0.447) | 0.048 (0.241) | 0.005 (0.213) | −0.075 (0.239) | −0.009 (0.218) |
| Real interest rate(t–1) | 0.009b (0.004) | 0.009b (0.004) | 0.009b (0.005) | 0.011c (0.004) | 0.009b (0.004) | 0.008c (0.003) | 0.00b (0.003) |
| Securities market policy(t–1) | −0.116a (0.064) | ||||||
| Capital account restrictions( t–1) | −0.449b (0.213) | ||||||
| Interest rate controls(t–1) | −0.142b (0.065) | ||||||
| Entry barriers(t–1) | −0.295c (0.068) | ||||||
| Banking supervision(t–1) | −0.341c (0.091) | ||||||
| Privatization(t–1) | −0.151c (0.058) | ||||||
| Observations | 1,158 | 1,158 | 1,158 | 1,158 | 1,158 | 1,158 | 1,158 |
| Prob > chi2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
- This table presents the baseline regression results of equation 1, with the financial liberalization variable broken into dimensions. The dependent variable, banking crisis, is equal to 1 if country i experienced a banking crisis in year t and 0 otherwise. Regressions are estimated using the probit model with robust and clustered standard errors, and a, b, and c denote statistical significance at 10, 5, and 1%, respectively. Marginal effects are reported. Z statistics are in parentheses.
The entry barriers dimension resembles findings with the literature, as researchers have shown that when concentration in the banking sector intensifies, inefficient banks fail due to charging higher interest rates to risk-seeking firms (Boyd and De Nicolo, 2003). For control variables, credit growth had a negative and significant impact on banking crisis likelihood in all columns except column 3. This finding suggests that capital account restrictions, a financial liberalization dimension, help mitigate the effects of excessive credit growth.
The major contribution of my paper lies in the effects of financial liberalization, conditional on exchange-rate regime, on the likelihood of banking crisis. First, I create an interaction term of exchange-rate regime × financial liberalization and run equation 2a with the same independent variables as in equation 1. In Table 2, I run the model with the interaction term between the financial liberalization variable and each of the exchange-rate regime variables. When these two variables interact, the impact of one variable's effect on the likelihood of banking crisis depends on the other. I report the results from fixed exchange-rate regimes, intermediate exchange-rate regimes, and flexible exchange-rate regimes in columns 1–3, respectively. In column 1, the financial liberalization variable remains a negative and significant indicator; however, when interacted with the fixed-regime variable, the results were insignificant. The results indicate that changes in the level of financial liberalization are not associated with an increase in the likelihood of systemic banking crisis under the rigidity of a fixed exchange-rate regime. Column 2 reports the results of the model with the intermediate exchange-rate regime interacted with financial liberalization. The results of the interaction between intermediate regimes and financial liberalization failed to yield a significant result.
| 1 | 2 | 3 | |
|---|---|---|---|
| Fixed | Intermediate | Flexible | |
| Financial liberalization(t–1) | −0.054c (0.013) | −0.046c (0.015) | −0.059c (0.013) |
| Fixed regime × financial liberation(t–1) | 0.000 (0.018) | ||
| Intermediate regime × financial liberation(t–1) | −0.013 (0.011) | ||
| Flexible regime × financial liberation(t–1) | 0.040b (0.017) | ||
| Currency crisis(t–1) | 0.207 (0.359) | 0.171 (0.368) | 0.166 (0.370) |
| Exchange-rate regime(t–1) | 0.009 (0.169) | 0.035 (0.105) | −0.203 (0.139) |
| Credit growth(t–1) | 1.183c (0.389) | 1.231c (0.389) | 1.249c (0.386) |
| GDP(t–1) | −0.007 (0.050) | −0.002 (0.052) | −0.005 (0.052) |
| Inflation(t–1) | −0.089 (0.278) | −0.11 (0.282) | −0.035 (0.252) |
| Real interest rate(t–1) | 0.010c (0.004) | 0.010c (0.003) | 0.010c (0.003) |
| Sample size | 1,158 | 1,158 | 1,158 |
| Prob > chi2 | 0.000 | 0.000 | 0.000 |
- This table presents the baseline regression results of equation 2a with the interaction term of fixed exchange-rate regime × financial liberalization. The dependent variable, banking crisis, is equal to 1 if country i experienced a banking crisis in year t and 0 otherwise. Regressions are estimated using the probit model with robust and clustered standard errors, and a, b, and c denote statistical significance at 10, 5, and 1%, respectively. Marginal effects are reported. Z statistics are in parentheses.
Column 3 reports the results of equation 2a, wherein I interact the flexible regime variable with the financial liberalization variable. The results of the interaction between flexible regimes and financial liberalization starkly contrast with those of intermediate and fixed regimes. The interaction variable between flexible regimes and financial liberalization was significant and positive for the sample, implying that financial liberalization, in the presence of a flexible exchange rate, leads to a higher likelihood of banking crisis occurrence. However, the results, at this stage, do not confirm which dimensions of the financial liberalization variable provide a significant effect in the prediction of banking crisis onset.
In this section, I break down the financial liberalization variable into its dimensions and create an interaction term with the financial liberalization dimensions and the exchange-rate regime variable. When these two variables interact, the impact of the financial liberalization dimension on the likelihood of banking crisis depends on the presence of a certain exchange rate regime. Thus, I attempt to determine if certain liberalization dimensions, in the presence of a particular exchange-rate regime, statistically increase or decrease the likelihood of banking crisis occurrence. I have to iterate here that in the event of insignificance, policymakers can gain preliminary insight into interactions that may not “definitively” lead to toxic consequences.
Table 3 presents the results of equation 2b with the interaction terms between the financial liberalization dimensions and the fixed exchange-rate regime variable. The results from this table also show that all interaction terms played an insignificant role in explaining the likelihood of banking crisis. One of the advantages of a fixed exchange-rate regime lies in the ability of an exporting country to keep its exchange rate low, allowing a competitive advantage in selling goods abroad. These sales play a role in preventing declines in GDP, a key determinant in the banking crisis definition. The GDP variable was significant in all regressions, as was the real interest rate and the credit growth variable.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| Credit controls × fixed(t–1) | −0.002 (0.072) | ||||||
| Credit growth(t–1) | 0.980a (0.542) | 0.993a (0.544) | 0.563 (0.742) | 1.007a (0.543) | 1.002a (0.544) | 1.041a (0.551) | 1.039a (0.550) |
| GDP(t–1) | −0.080b (0.038) | −0.080b (0.038) | −0.097b (0.048) | −0.076b (0.038) | −0.080b (0.038) | −0.063a (0.037) | −0.074a (0.038) |
| Inflation(t–1) | 0.33a (0.185) | 0.334a (0.184) | 0.115 (0.247) | 0.320a (0.184) | 0.334a (0.184) | 0.295 (0.185) | 0.311a (0.185) |
| Real interest rate(t–1) | 0.012c (0.004) | 0.012c (0.004) | 0.011a (0.007) | 0.012c (0.004) | 0.012c (0.004) | 0.012c (0.004) | 0.012c (0.004) |
| Securities market policy × fixed(t–1) | 0.004 (0.070) | ||||||
| Capital restriction × fixed(t–1) | −0.109 (0.238) | ||||||
| Interest rate controls × fixed(t–1) | −0.031 (0.084) | ||||||
| Entry barriers × fixed(t–1) | 0.005 (0.071) | ||||||
| Bank supervision × fixed(t–1) | −0.204 (0.129) | ||||||
| Privatization × fixed(t–1) | −0.074 (0.075) | ||||||
| Sample size | 1,158 | 1,158 | 1,158 | 1,158 | 1,158 | 1,158 | 1,158 |
| Prob > chi2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
- This table presents the regression results of equation 2b with the interaction term of financial liberalization dimension × fixed exchange-rate regime. The dependent variable, banking crisis, is equal to 1 if country i experienced a banking crisis in year t and 0 otherwise. Regressions are estimated using the probit model with robust and clustered standard errors, and a, b, and c denote statistical significance at 10, 5, and 1%, respectively. Marginal effects are reported. Z statistics are in parentheses.
Next, I report the empirical results in Table 4 of equation 2b with the intermediate exchange-rate regime interacted with each financial liberalization dimension. In columns 1–7, each of the interaction terms between the intermediate exchange-rate regime and the financial liberalization dimension is statistically (negative) significant. These results identify the aspects of financial liberalization within a particular regime that provide the significant effect in the onset of banking crisis. For example, in column 2 of Table 4, the interaction between capital account restrictions and the intermediate exchange-rate regime variable was negatively significant.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| Credit controls × intermediate(t–1) | −0.138b (0.056) | ||||||
| Credit growth(t–1) | 1.127b (0.550) | 1.140b (0.550) | 0.638 (0.733) | 1.070a (0.548) | 1.037a (0.548) | 1.009a (0.548) | 1.025a (0.543) |
| GDP(t–1) | −0.072a (0.038) | −0.073a (0.038) | −0.085a (0.047) | −0.070a (0.037) | −0.072a (0.038) | −0.062a (0.037) | −0.065a (0.038) |
| Inflation(t–1) | 0.293 (0.190) | 0.294 (0.190) | 0.067 (0.251) | 0.317a (0.191) | 0.307 (0.190) | 0.305 (0.193) | 0.31 (0.193) |
| Real interest rate(t–1) | 0.013c (0.004) | 0.013c (0.004) | 0.012a (0.006) | 0.013c (0.004) | 0.013c (0.004) | 0.013c (0.004) | 0.013c (0.004) |
| Securities market policy × intermediate(t–1) | −0.136b (0.056) | ||||||
| Capital restriction × intermediate(t–1) | −0.398a (0.192) | ||||||
| Interest rate controls × intermediate(t–1) | −0.081a (0.048) | ||||||
| Entry barriers × intermediate(t–1) | −0.105b (0.053) | ||||||
| Bank supervision × intermediate(t–1) | −0.218b (0.099) | ||||||
| Privatization × intermediate(t–1) | −0.167b (0.074) | ||||||
| Sample size | 1,165 | 1,165 | 1,165 | 1,165 | 1,165 | 1,165 | 1,165 |
| Prob > chi2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
- This table presents the regression results of equation 2b with the interaction term of financial liberalization dimension × intermediate exchange-rate regime. The dependent variable, banking crisis, is equal to1 if country i experienced a banking crisis in year t and 0 otherwise. Regressions are estimated using the probit model with robust and clustered standard errors, and a, b, and c denote statistical significance at 10, 5, and 1%, respectively. Marginal effects are reported. Z statistics are in parentheses.
Unlike the rigidities that monetary authorities of a fixed exchange-rate regime possess, financial authorities in an intermediate regime do not have to accumulate reserves to maintain a peg, thus averting price increases and potential inflationary problems. Another finding of this interaction lies in the sign of the interaction terms. All of the interaction terms between financial liberalization dimensions and intermediate exchange-rate regimes in columns 1–7 report significant and negative signs, indicating that within intermediate exchange-rate regimes, financial authorities can take policy measures to mitigate the occurrence of systemic banking crisis.
Table 5 reports the empirical results of equation 2b, wherein I interact the flexible regime variable with each of the financial liberalization dimensions. The results of Table 5 show a different picture of the interaction between financial liberalization and exchange-rate regime. The interaction variable between flexible regimes and financial liberalization dimensions returned positively significant results for the credit controls, securities market policy, capital account restrictions, entry barriers, and privatization dimensions.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
|---|---|---|---|---|---|---|---|
| Credit controls × flexible(t–1) | 0.181b (0.075) | ||||||
| Credit growth(t–1) | 1.153b (0.558) | 1.157b (0.558) | 0.778 (0.740) | 1.075a (0.555) | 1.239b (0.567) | 1.039a (0.552) | 1.044a (0.552) |
| GDP(t–1) | −0.099b (0.041) | −0.099b (0.041) | −0.122b (0.053) | −0.091b (0.041) | −0.088b (0.039) | −0.082b (0.040) | −0.089b (0.039) |
| Inflation(t–1) | 0.241 (0.175) | 0.244 (0.173) | −0.103 (0.341) | 0.232 (0.191) | 0.278 (0.199) | 0.335a (0.186) | 0.326 (0.199) |
| Real interest rate(t–1) | 0.011c (0.004) | 0.011c (0.004) | 0.008 (0.006) | 0.012c (0.004) | 0.012c (0.004) | 0.013c (0.004) | 0.013c (0.004) |
| Securities market policy × intermediate(t–1) | 0.183b (0.076) | ||||||
| Capital restriction × intermediate(t–1) | 0.569c (0.209) | ||||||
| Interest rate controls × intermediate(t–1) | 0.109 (0.070) | ||||||
| Entry barriers × intermediate(t–1) | 0.141b (0.068) | ||||||
| Bank supervision × intermediate(t–1) | 0.065 (0.088) | ||||||
| Privatization × intermediate(t–1) | 0.130a (0.070) | ||||||
| Sample size | 1,165 | 1,165 | 1,165 | 1,165 | 1,165 | 1,165 | 1,165 |
| Prob > chi2 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 | 0.000 |
- This table presents the regression results of equation 2b with the interaction term of financial liberalization dimension × intermediate exchange-rate regime. The dependent variable, banking crisis, is equal to 1 if country i experienced a banking crisis in year t and 0 otherwise. Regressions are estimated using the probit model with robust and clustered standard errors, and a, b, and c denote statistical significance at 10, 5, and 1%, respectively. Marginal effects are reported. Z statistics are in parentheses.
These results suggest the importance of regime choice when implementing financial liberalization measures. Although a flexible exchange-rate regime allows monetary authorities with more flexibility to pursue independent monetary policy decisions, when interacted with financial liberalization methods, it leads to an increase in the likelihood of banking crisis. This finding stresses the importance of an alternative anchor, such as a sound banking system or developed banking system regulations, to combat volatilities in the exchange rate, which may preclude a banking crisis. Further, within a flexible regime, monetary authorities need to resist temptations to overuse expansionary policies, such as interest rate cuts, which may induce inflation or cause imbalances in the current account.
5 CONCLUSION
This study investigates the impact of financial liberalization, within a particular exchange-rate regime, on the likelihood of systemic banking crisis. I find that under certain financial liberalization dimensions, exchange-rate regime plays a significant role in explaining banking crisis likelihood. I find financial liberalization, as a whole and under its specific dimensions, to be a significant determinant of the likelihood of banking crisis onset. Also, I find that exchange-rate regimes do not, across the board, appear to be a likely candidate for a main determinant of banking crisis; however, in regards to the determinants of banking crises in emerging market and developing economies, the exchange-rate regime classification deserves further investigation.
My empirical results point out that the interaction variable between financial liberalization components and exchange-rate regime was significant within intermediate (negative significance) and flexible exchange-rate regimes (positive significance), indicating certain combinations may work better to decrease the likelihood of banking crisis. However, further research in this area needs to be done. Exchange-rate regimes may change capriciously, and de facto regimes do not necessarily match de jure regimes.7 As a result, one cannot thoroughly conclude the role exchange-rate regimes play on the likelihood of financial crisis by investigating a wide panel data set. For example, further research needs to be conducted at the regional, economic (advanced, emerging, and least developed), or country level to obtain more robust results on the interaction between financial liberalization and currency regimes. Furthermore, my initial breakdown of exchange-rate regimes into three categories as follows: fixed, intermediate, and flexible may not entirely capture the wide range of rigidity (or lack thereof) that might exist in any one category. Subsequent research should expand the variable into six or even 12 categories and apply the model to the regional and or income level in order to represent the disparity that exists between “currency board arrangements” and “freely floating (or falling)” exchange-rate regimes.
ENDNOTES
- 1 The study of financial liberalization began with the seminal work of McKinnon (1973) and Shaw (1973), who examined nations' attempts to steer away from “financial repression.” According to McKinnon (1973) and Shaw (1973), financial repression, which forces financial institutions to pay low and often negative real interest rates, reduces private savings and the resources available to finance capital budgeting projects. Through financial liberalization, however, developing nations can stimulate domestic savings with higher rates and reduce dependence on foreign capital.
- 2 See Komulainen and Lukkarila (2003) for an explanation of financial liberalization, capital flows, and crises.
- 3 See Glick and Hutchinson (2000); Hutchinson and Noy (2005).
- 4 I use the most widely cited data set on banking crises; however, not all authors agree with existing metrics of financial crises dating. See Bordo and Meissner (2016) for a review.
- 5 Abiad et al. (2010) assert that the prudential regulation of banks and supervision of the banking sector dimension differs from the others in terms scoring. A higher score in this dimension translates into “greater” regulation. In the first part of my empirical analysis, I will regress each of the dimensions individually to determine its significance on the likelihood of banking crisis.
- 6 I use the following equation: real credit = ½ ×
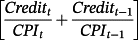
- 7 There has been progress on the distinction between de facto and de jure exchange-srate regime selection, as well as on the differences of opinion on this score. See Ilzetzki, Reinhart, and Rogoff (2017) for an up-to-date chronology.
APPENDIX A
LIST OF BANKING CRISIS EPISODES
| Country | Banking crisis onset year(s) | Country | Banking crisis onset year(s) | Country | Banking crisis onset year(s) |
|---|---|---|---|---|---|
| Albania | 1994 | Estonia | 1992 | Paraguay | 1995 |
| Argentina | 1989, 1995, 2001 | Finland | 1991 | Philippines | 1997 |
| Bangladesh | 1987 | Hungary | 1991 | Poland | 1992 |
| Bolivia | 1986, 1994 | India | 1993 | Russia | 1998 |
| Brazil | 1990, 1994 | Indonesia | 1997 | Senegal | 1988 |
| Bulgaria | 1996 | Jamaica | 1996 | Sri Lanka | 1989 |
| Burkina Faso | 1990 | Japan | 1997 | Sweden | 1991 |
| Cameroon | 1987, 1995 | Jordan | 1989 | Tanzania | 1987 |
| China | 1998 | Kenya | 1985, 1992 | Thailand | 1997 |
| Colombia | 1998 | South Korea | 1997 | Uganda | 1994 |
| Costa Rica | 1987, 1994 | Malaysia | 1997 | United States | 1988 |
| Cote d'Ivoire | 1988 | Mexico | 1994 | Uruguay | 2002 |
| Dominican Republic | 2003 | Nepal | 1988 | Venezuela | 1994 |
| Ecuador | 1998 | Nigeria | 1991 | ||
| El Salvador | 1989 | Norway | 1991 |




