Correlating disease-related mutations to their effect on protein stability: A large-scale analysis of the human proteome†
Communicated by Mauno Vihinen
Abstract
Single residue mutations in proteins are known to affect protein stability and function. As a consequence, they can be disease associated. Available computational methods starting from protein sequence/structure can predict whether a mutated residue is or not disease associated and whether it is promoting instability of the protein-folded structure. However, the relationship among stability changes in proteins and their involvement in human diseases still needs to be fully exploited. Here, we try to rationalize in a nutshell the complexity of the question by generalizing over information already stored in public databases. For each single aminoacid polymorphysm (SAP) type, we derive the probability of being disease-related (Pd) and compute from thermodynamic data three indexes indicating the probability of decreasing (P−), increasing (P+), and perturbing the protein structure stability (Pp). Statistically validated analysis of the different P/Pd correlations indicate that Pd best correlates with Pp. Pp/Pd correlation values are as high as 0.49, and increase up to 0.67 when data variability is taken into consideration. This is indicative of a medium/good correlation among Pd and Pp and corroborates the assumption that protein stability changes can also be disease associated at the proteome level. Hum Mutat 32:1161–1170, 2011. ©2011 Wiley-Liss, Inc.
Introduction
Recent technological advancement is largely contributing to the rapid increase of personal human genome sequencing, to the study of genetic variation and its role in determining health and disease [Ashley et al., 2010]. Most traits of the human phenotype depend on the combination of various genetic factors together with environmental influences, and in the postgenomic era, a major challenge is the understanding of the relationship among genetic and phenotype variations [Ormond et al., 2010]. Among genetic variations, single nucleotide polymorphism (SNP) refers to a genetic change in which a nucleotide is replaced. When this occurs in a coding exon, an amino acid change may occur in the corresponding protein (single aminoacid polymorphism, SAP). Although less than 1% of all SNPs result in an amino acid variation at the protein level, SAP is the type of mutation mostly related to human diseases [Yip et al., 2008]. Several databases are currently recording information on human variation, both at the gene and at the protein level, also in relation to clinical association studies [McKusick, 1998; Forbes et al., 2010; Yip et al., 2008]. In this respect, the Human Variome Project aims at collecting, curating, and distributing all the human genetic variations affecting health [Kohonen-Corish et al., 2010].
Several available computational tools estimate with various scoring efficiencies whether a mutation is or is not disease related starting from the protein sequence and/or structure [for review, see Tavtiagian et al., 2008; see also Calabrese et al., 2009, and references therein; Adzhubei et al., 2010 and reference therein]. However, the risk assessment of common variants is still unclear and comprehensive correlation studies among SNP detection and their effect on protein structure and function are needed [Ormond et al., 2010].
For decades, the problem of protein stability has been investigated in relation to the effect of amino acid substitution in the chain both theoretically and experimentally [Bross et al., 1999; Ferrer-Costa et al., 2002; Steward et al., 2003; Wang and Moult, 2001; Yue et al., 2005; for more recent reviews, see Dill et al., 2008; Fersht, 2008; Scheraga et al., 2007]. Chemically induced mutations at the gene level promote the expression of mutated proteins whose Gibbs free energy change of unfolding with respect to that of wild type can be experimentally detected. A database of mutational thermodynamic data in proteins is available and regularly updated [Kumar et al., 2006]. This information has been routinely used to train/test predictors specifically suited to compute whether a mutation is or is not causing a change of protein stability starting from the sequence and/or the protein structure [for a recent review and benchmark of the different methods see Khan and Vihinen, 2010].
The problem of how protein misfolding is promoting certain types of insoluble fibrillar aggregates, at the basis of several amyloid disorders, has been documented in vitro and a list of putative residue mutations causing protein aggregates is available [Chiti and Dobson, 2009; Naiki and Nagai, 2009; Uversky, 2008]. Other human diseases have been proposed to be related to protein misfolding [see Thusberg and Vihinen, 2009; Groenendyk et al., 2010 and references therein]. Hampering stability of several proteins causes perturbation/loss of function and this is routinely indicated as the major consequence of pathogenic missense mutations [Khan and Vihinen, 2010]. Severe disease phenotypes have been associated to mutations decreasing [Lindberg et al., 2005; Randles et al., 2006; Wang and Moult, 2001] and also increasing protein stability [Ling et al., 2010; Seidle et al., 2005; Worth et al., 2011 and references therein]. However, the number of validating experiments is still negligible as compared to the proteome size.
The question then poses as to which extent SAPs affecting protein folding have or do not have medical consequences in a proteome-wide scale. Before attempting any computational modeling within a framework of structural systems biology, it is therefore urgent to determine to which extent residue mutations that are disease related affect also protein stability. Overall, our goal aims at complementing the amino acid mutational spectrum of human diseases with the corresponding effect on protein stability by generalizing over information stored in specialized databases.
For this, we collect SAPs in relation to their involvement in diseases (and neutral cases) and with measured effects on the Gibbs free energy of unfolding between a wild-type protein and its mutant (ΔΔG). SAP features are generalized by computing probability indexes that characterize the correspondent SAP type. By this, each SAP type is associated to probability indexes indicating to which extent it may be associate to disease (Pd) and promote increase, decrease, and perturbation of protein structure stability (P+, P−, Pp). Statistical correlation analysis indicates that Pd best correlates at a moderate/good level with Pp, the probability index of protein structure perturbation, corroborating the view that mutations altering protein stability may be also disease related. Pd and Pp values well correlate with other frequently adopted substitution scoring matrixes, respectively, and with experimental data. This indicates that Pd and Pp well encode also protein chemico-physical, evolutionary features and specific trends of large collection of thermodynamic and phenotype-genetic data.
Overall, our data indicate that at a proteome scale SAP types can be increasingly harmful at increasing damaging of protein stability, in line with previous observations done on a much more restricted set of proteins. They also corroborate the notion that disease-associated mutation types can decrease or increase protein stability. Finally, since Pd/Pp correlation is not perfect, our analysis indicates that protein stability perturbation, although important, is not the only molecular mechanism that can be related to mutation pathogenicity.
Materials and Methods
Databases
SAPs and Maladies
In this study, we consider the mutation data sets listed in Table 1. Our data set of neutral mutations comprises all the missense mutations that were retained from dbSNP (11/09/2010:RELEASE: NCBI dbSNP Build 132, http://www.ncbi.nlm.nih.gov/projects/SNP/), provided that the minor allele frequency is >5% in each and all (12) populations. SAP-UniProtKB was downloaded from the disease mutation set of UniProtKB: release 2010_04/23 March 2010 (http://www.uniprot.org/docs/humsavar) [Yip et al., 2008]. Only residue mutations derived from SNP nonrelated to somatic cancer and with reference in OMIM (http://www.ncbi.nlm.nih.gov/omim) were retained. From this, a reduced SAP final set (SAP-Final) comprising the 141 SAP mutation types for which thermodynamic data are available in ProTherm was generated and it includes 9,896 disease-related and 7,274 neutral SAPs annotated in 5,305 protein sequences.
| SAPsa | ||||
|---|---|---|---|---|
| SAP-data base | Disease related | °Neutral | Total | Proteinsa |
| dbSNP | 7,417 | 7,417 | 4,781 | |
| UniProt | 10,322 | - | 10,322 | 837 |
| SAP − UniProt + dbSNP (150) | 10,322 | 7,417 | 17,739 | 5,380 |
| SAP-Final (141) | 9,896 | 7,274 | 17,170 | 5,305 |
- Disease-related SAPs (Single Aminoacid Polymorphisms) of nonmembrane proteins are derived from UniProtKB (release 2010_04/23 March 2010) considering only mutations with reference in OMIM and excluding those related to somatic cancer. The set of neutral mutations comprises all the missense mutations that were retained from dbSNP (11/09/2010 RELEASE, Build 132, http://www.ncbi.nlm.nih.gov/projects/SNP/), provided that the minor allele frequency is >5% in each and all (12) populations. The SAP-Final dataset is obtained by merging both UniProt and dbSNP mutations (SAP −UniProt + dbSNP) and by excluding from the 150 SAP types (corresponding to missense Single Nucleotide Polymorphisms) those for which thermodynamic data are not available in ProTherm. By this SAP-Final comprises 141 SAP types.
- aFigures are given as numbers of SAPs and proteins, respectively.
In Figure 1, the residue composition (percentage frequency in the set) of our protein database (bars in grey color) is compared to that of the human proteome (bars in pale blue color) indicating a very similar composition in spite of the lower number of proteins (5,305 and 77,748 chains, respectively). The frequency of total, disease-related and neutral SAPs in our sets (bars in yellow [total], red [disease-related], and green [neutral]) is compared to the expected frequency of SAPs given the human genome (and computed as detailed below) (violet bars). This indicates that our SAP data are indeed representative of the expected mutation rate in the human genome. Differences as in the case of Argine (R) are direct consequences of high mutability of the 5′-CpG dinucleotides in the corresponding codons and were noticed before [Vitkup et al., 2003].
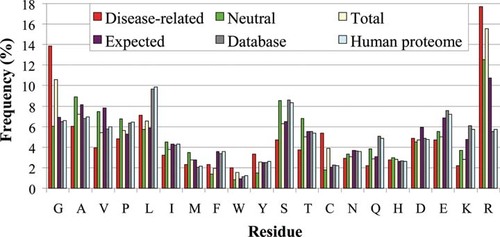
Frequency of protein residues in the databases. Frequency of residues in disease-related, neutral, and total SAP mutation subsets of SAP −UniProt + dbSNP database (Table 1) and in the corresponding total proteins (Database). The frequency of residues in the human proteome (from EnsEMBL ver 5, based on the build of Genome Reference Consortium 37, with a total of 34,369,508 residues, and 77,748 sequences) and that of the expected mutations rate as computed from the human genome are also shown. Residues are grouped as follows: apolar (GAVPLIM), aromatic (FWY), polar (STCNQH), charged (DEKR), with residues in the same group listed at increasing order of size.
The frequency of mutation is different for the different residue types and different from the frequency of a given residue type in the database set. For most of the residues, the frequency of occurrence in the neutral mutation set is similar to that of the expected one. In the disease mutation set, Glycine (G) and Cysteine (C) have frequency of occurrence two fold higher than in that of neutral cases. Only 24 mutations in 19 proteins are labeled as active site (ACT_SITE) in UniProtKB. About 89% of the whole protein set contains 1–3 mutations per protein.
Thermodynamic Data
Thermodynamic data were derived from ProTherm, release 31 March, 2010, a database for proteins and mutants collecting some 10,341 experiments corresponding to 4,044 mutations in 212 proteins (http://gibk26.bse.kyutech.ac.jp/jouhou/protherm/protherm.html) [Kumar et al., 2006]. In ProTherm, mutation data corresponding to 141 SAP types are presently available. Excluding two membrane proteins, we downloaded data of 3,089 experiments corresponding to 141 SAP types in 129 proteins, from different organisms, including Homo sapiens. The distribution of the different experimental values of the unfolding Gibbs free energy change (ΔΔG) detected upon protein single mutations is shown in Figure 2. Most of the data (63% of the values, corresponding to black bars) lies within the |ΔΔG|≤1 kcal/mol interval (average ΔΔG = −0.79 kcal/mol). In ProTherm, the average experimental uncertainty on thermodynamic data of mutations endowed with more than one experiment is in the range of 1 kcal/mol. For this reason, we classify a SAP as neutral when its associated |ΔΔG| value is ≤1 kcal/mol, increasing protein stability when ΔΔG is >1kcal/mol, decreasing protein stability when ΔΔG is < −1kcal/mol and perturbing to include either case. With this definition, a perturbing mutation is characterized by |ΔΔG|>1kcal/mol and it can be either increasing or decreasing the corresponding protein stability. For each SAP, a corresponding ΔΔG value was determined from all the experimental data as follows: (1) when the same mutation in the same protein was present in the database with different ΔΔG values, we adopted a majority rule provided that the values were in the same ΔΔG region (perturbing or neutral) in Figure 2; (2) otherwise, the average ΔΔG value was computed.
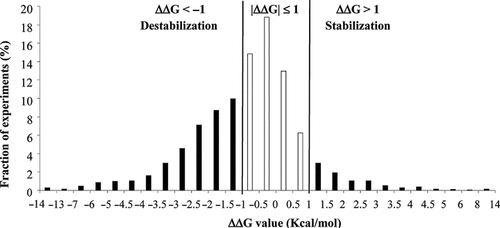
Distribution of ΔΔG values corresponding to 141 SAP types found in ProTherm. Each bar represents the fraction of experiments (total is 3,089) with ΔΔG values in the corresponding range. Residue mutations corresponding to ΔΔG < −1 kcal/mol and ΔΔG >1 kcal/mol are labeled as destabilizing and increasing the stabilization of the protein structure, respectively. Residue mutations are labeled as perturbing the protein stability when |ΔΔG|> 1 kcal/mol (see text for details). ProTherm is at http://gibk26.bse.kyutech.ac.jp/jouhou/Protherm/protherm.html.
The 129 reference proteins whose mutations contribute to the thermodynamic data cover all the SCOP major structural classes, inclusive of different folds, super families, and families. This indicates that prototypes of the majority of structural protein domains are contributing to the thermodynamic data set. Proteins are from different organism sources: 55% from Eukaryotes, including Homo sapiens (26%); the remaining 45% is mostly from Prokaryotes. Some 40% of the mutated residues in the ProTherm data set can be classified “buried” (not exposed to solvent). When required, the relative solvent accessibility of a specific side chain was evaluated from the corresponding protein structure (downloaded from the Protein Data Bank, http://www.pdb.org/) with the program Define Secondary Structure of Proteins (DSSP) [Kabsch and Sander, 1983].
Computing the Frequency of Expected SAP Types
The base-line distribution of SAPs is computed by considering the frequency of occurrence of the four nucleotides and of the 64 codons in the human genome as reported in the Codon Usage database (http://www.kazusa.or.jp/codon/). For each codon, all the nine possible single-nucleotide mutations are generated. The probability of each mutation is estimated according to a matrix that reports the mutation rates of each nucleotide depending on the all 16 possible 5′ and 3′ neighborhoods [Hess et al., 1994]. SAP frequency distribution is computed as the sum of the probabilities of all the corresponding SNPs.
Definition of Probability Indexes
When computing indexes for each SAP type, we add a pseudocount to all the classes in order to regularize the estimation and to prevent over fitting when a small number of examples are available [Durbin et al., 1998]. This smoothing scheme assumes an a priori equi-probability of the classes and it corrects for possible flaws due to underrepresented data [Durbin et al., 1998]. In a set of observed data, especially with low-probability events and/or small data sets, the number of occurrences can be under- or overrepresented. In this case, it is possible to eliminate the bias by adding “pseudocounts.” The simplest approach is to add one to each observed number of events. This is sometimes called Laplace's rule of succession [Laplace, 1814]. More generally, the pseudocounts should be set in proportion to the prior estimate of the event probabilities. However, when there is no reason to prefer unbalanced prior estimates as in our cases (disease/neutral; perturbing/nonperturbing; destabilising/nondestabilising; increasing stability/nonincreasing stability), the pseudo counts must be added using the principle of indifference or maximum entropy (all entries have equal prior probabilities) [Jaynes, 1957].
The Disease Index Pd
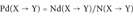 (1)
(1)The Probability Indexes of Protein Incorrect Folding P+, P−, and Pp
For each SAP type (X → Y), we compute three probability indexes as follows:
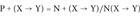 (2)
(2)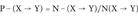 (3)
(3)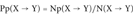 (4)
(4)Computing Standard Errors
An estimate of the reliability of the probability values Pd (X → Y), P+ (X → Y), P–(X → Y), and Pp(X → Y) was obtained by computing their Standard Errors (SEPs). A bootstrapping procedure was applied as follows. One thousand resamples were generated by means of a random extraction with replacement from the different original data sets (SAP-Uniprot + dbSNP and thermodynamic data). The size of each resample is set to 90% of the complete dataset and the value of each index for each sample is computed. The standard deviation (σ) across the 1,000 resamples is then the standard error [Moore and McCabe, 2004].
Computing the Regression Line and the Weighted Residuals
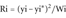 (5)
(5)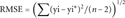 (6)
(6)Computing Correlation and its Statistical Significance
We checked the normality of the data sets with the Jarque–Brera Lagrange Multiplier test (LM) [Jarque and Bera, 1987] and its significance from tables listing values for LM statistics computed with a Monte Carlo simulation [Wuertz and Katzgraber, 2009].
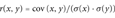 (7)
(7)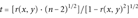 (8)
(8) (9)
(9)In order to have correlation coefficients less sensitive to nonnormal distributions and nonlinear dependence, correlation was also estimated with the Spearman's rank correlation coefficient (that assumes that the variables under consideration were measured on at least an ordinal [rank order] scale) [Hill and Lewicki, 2007]. Significance tests were performed accordingly and as previously described [Myers and Well, 2003].
Results
The Disease Index
We compute the disease index as the probability that a given SAP type in our data set is associated to disease (Equation 1). SAPs are considered nondamaging in our database provided that they correspond to missense SNPs derived from dbSNP with the constraints described before. Disease related variants are collected from UniprotKB provided that they have a reference in OMIM (for details, see SAPs and maladies). SAPs are then classified as disease related and neutral and the probability index for a given SAP type to be disease related is computed (Equation 1).
The disease index values for each SAP type are listed in Figure 3 with the correspondent number of cases and of proteins (among round brackets). All the 150 possible SAP types expected considering the genetic code variability (missense SNPs) are present in the set and the index ranges from the lowest value of 0.14 (L → I) up to the highest value of 0.92 (W → C). The average Pd value is 0.58 and the average standard error (ASE) is 0.05. Stars label the nine Pd indexes without SAP type counterparts in the set of thermodynamic data (see below). Given its definition, a Pd value of 0.5 can be considered a natural threshold to classify mutation types as endowed with low/medium and high probability of being disease associated. A total of 52 SAP types (35% of the total) have a Pd value < 0.5. A total of 26 SAP types (17%) have Pd values ranging from ≥ 0.5 to < 0.6. The remaining 72 (48%) are endowed with Pds ≥0.6.
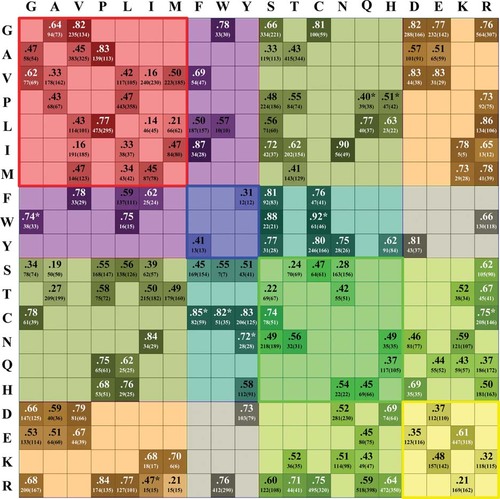
The Disease Index values (Pd) for each SAP type. The darker is the color, the higher the Pd value. Wild-type residues are shown on the left and target residues at the top. For each mutation type, the corresponding number of mutations and, between round brackets, the number of proteins in which mutations are annotated, are shown. Pd is computed for the 150 SAP types due to SNPs; when for a given SAP type no thermodynamic data are available in ProTherm, the corresponding Pd is marked with *. Residues are grouped as in Figure 1. Squares comprising mutations within the same residue group are colored in red, blue, green, and yellow, respectively. All the other off-diagonal squares comprising mutations included in different groups are shown as a combination of the four colors.
The Effect of Disease Related SAP Types on Protein Stability
Considering the available thermodynamic data, we can compute for each SAP type three indexes indicating (1) the probability of increasing the Gibbs free energy change upon mutation (P+); (2) the probability of decreasing the Gibbs free energy change upon mutation (P−), and (3) the probability of perturbing the Gibbs free energy change upon mutation (or perturbing index, Pp) (Equations 2–4). For lack of thermodynamic data, all the indexes can be computed only for 141 of the 150 SAP types (missing SAP types for which thermodynamic data are not available are P → Q, P → H, W → G, W → C, C → F, C → W, C → R, N → Y, R → I).
Given our problem, all the relevant features of a SAP type are now encoded in its Pd and the various P+, P−, and Pp values. A correlation analysis can be computed to determine to which extent the disease probability is related to the probability of affecting the protein stability. Results are shown in Table 2, where Pearson (r) and Spearman (Corrs) correlation coefficients are reported with the correspondent p-values (pr and ps, respectively). An estimation of the correlation accounting for standard errors of the data (disattenuation) is also included (r*, Equation 9).
| Indexa | R | Pr | r* | Corrs | Ps |
|---|---|---|---|---|---|
| P+ | 0.45 | 2 × 10−8 | 0.65 | 0.48 | 10−9 |
| P− | 0.35 | 3 × 10−5 | 0.48 | 0.32 | 10−4 |
| Pp | 0.49 | 8 × 10−10 | 0.67 | 0.50 | 4 × 10−10 |
- aPd(the SAP disease index) is correlated with three different probability indexes, computed for each SAP type from thermodynamic data (see Materials and Methods): P+, the probability index of increasing protein structure stabilization upon residue type mutation (Equation 2); P−, the probability index of protein structure destabilization upon residue type mutation (Equation 3); Pp, the probability index of perturbing the protein structure stability upon residue type mutation (Equation 4); r, Pearson correlation coefficient (Equation 9); Pr , significance of r (p-value) (Equation 10); r* (Equation 11) , correlation when standard errors of the data are taken into account (disattenuation); Corrs, Spearman correlation coefficient and its correspondent p-value (Ps) (see Materials and Methods).
Pd significantly correlates (although with different values) with all the thermodynamic indexes. Pd correlates with P− and also with P+. Evidently, the highest significant correlation value is obtained among Pd and Pp (Table 2) indicating that both destabilizing and stabilizing residue mutations in proteins are relevant in promoting diseases. When correlation values are corrected for standard errors, correlation increases. The strength of the correlation (r2, the coefficient of determination) is about 25% and this indicates that 25% of the Pd value of a given SAP type directly accounts for the Pp value (and vice versa). The strength of the correlation doubles when standard errors of the data are considered (r*2). All together, our results indicate that the correlation is moderate/good. Correlation is also independent of nonnormal distributions and nonlinear dependence as indicated by comparing the Pearson and Spearman coefficients. p-values are very low highlighting in all cases the significance of the correlation.
Correlation among Pp and Pd values for each SAP type (141 SAP types) is linear. In Figure 4, all the data are plotted with the correspondent standard error as evaluated with bootstrapping.
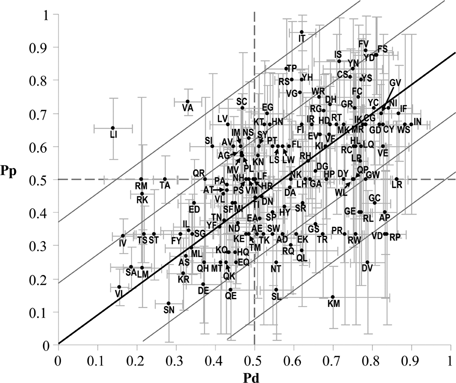
The correlation among Pd and Pp is linear. The correlation among the disease (Pd) and the perturbing (Pp) indexes is computed over 141 SAP mutation types. The regression line (Pp = 0.88Pd) is computed with a BLMS regression (see Materials and Methods). Pearson correlation (r) and the corresponding p-value are 0.49 and 8 × 10−10, respectively (Table 2). Lines parallel to the fitting one are drawn at y distance equal to one/two fold the root mean square of the residuals (RMSE = 0.18).
When residuals (the differences between Pp(X → Y) and the corresponding fitting value on the fitting line BLMS(X → Y)), weighted with respect to the variances of the SAP type X → Y on both axes, are plotted as a function of Pd, most of the SAP types (98%) have a weighted residual that clusters within two standard deviations from the average residual values for both sets of values (with the exception of L → I, I → T, and V → A) (Supp. Fig. S1).
The Perturbing Index Pp
The Pp values for each SAP type along with the number of mutations in the ProTherm database and the number of proteins where the mutational effect was detected (among round brackets) are shown in Figure 5. Pp values range from a minimum value of 0.13 (for S → N) to a maximum value of 0.94 (for I → T). The average Pp value is 0.51 with an ASE of 0.16. The Pp values for each mutation type are indicative of the expected thermodynamic effect at the protein level considering the thermodynamic data stored in the database. By definition, the perturbing index gives the probability that a certain mutation type is associated to some effect on the protein stability (see Equation 4). Considering a Pp value of 0.5 as a natural discriminative threshold for qualifying the extent of perturbation probability, 43% (61 SAP types) is characterized by Pp values < 0.5. Some 23% of SAP types have Pp values ≥ 0.5 and ≤ 0.6 and 34% is perturbing protein stability with Pp > 0.6.
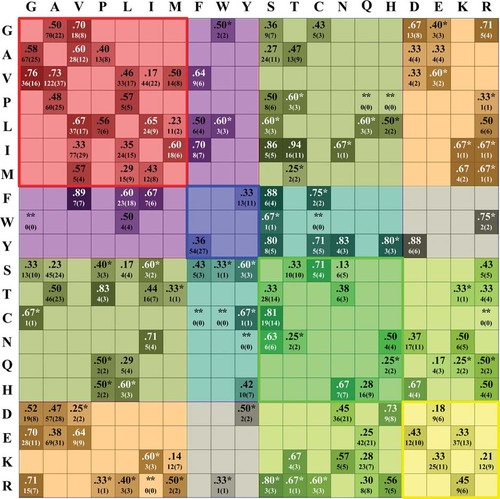
Values of the Perturbation Probability Index (Pp) for each SAP type. The darker is the color, the higher the Pp value. Wild-type residues are shown on the left, target residues at the top. For each mutation type, the corresponding number of mutations reported in ProTherm and, among round brackets, the number of proteins in which mutations were tested are shown (*labels Pp computed from less than four mutations, 10% of the total). Pp is not computed (**) for a mutation type when data are not available in ProTherm. Pp values are computed according to Equation 4. Residues are grouped as in Figure 1. Colors are as in Figure 3.
Comparison of Pd and Pp Values with Other Scoring Substitution Matrices and Experimental Data
The problem of how a SAP type affects the protein stability has been addressed before and many scoring matrices for amino acid substitution are available (94 are presently listed in the AA index ver.9.1, http://www.genome.jp/aaindex/AAindex/list_of_matrices) [Kawashima et al., 2008]. In line with general observations on biochemical evaluation of protein stability [see for a recent review Thomas et al., 2010 and references therein], our computed Pp values corroborate the view that the effect of the corresponding mutation type on protein stability correlates to some extent both with the conservation of polarity (or apolarity) and of the steric effect of the substituted residue. In order to confirm that our Pp index is a general estimator of the mutation effect on protein stability, we correlate its values with a set of different matrices computed under different assumptions (Table 3). Pp values are correlated with symmetrical and asymmetrical substitution matrices. Correlation values are lower with symmetric than with asymmetric matrices. In all the cases, correlation is significant as indicated by the corresponding p-values.
| Scoring matrixes | Pp | Pd |
|---|---|---|
| Symmetric | ||
| Similarity of pairs of amino acids [McLachlan, 1971] | −0.52 | −0.67 |
| Chemical distance [Grantham, 1974]a | 0.42 | 0.64 |
| BLOSUM62 [Henikoff and Henikoff, 1992] | −0.57 | −0.76 |
| Structure-based amino acid scoring table [Johnson and Overington, 1993] | −0.55 | −0.70 |
| SM obtained by maximum likelihood estimation (VTML160) [Mueller et al., 2002] | −0.52 | −0.73 |
| SM computed from the Dirichlet Mixture Model [Crooks and Brenner, 2005] | −0.52 | −0.70 |
| Asymmetric | ||
| Environment-specific amino acid SM for accessible residues [Overington et al., 1992] | −0.67 | −0.68 |
| Context-dependent optimal SM for exposed residues [Koshi and Goldstein, 1995] | −0.61 | −0.72 |
| Context-dependent optimal SM for buried residues [Koshi and Goldstein, 1995] | −0.49 | −0.67 |
| Context-dependent optimal SM for all residues [Koshi and Goldstein, 1995] | −0.58 | −0.73 |
| Exchangeability of amino acids in proteins [Yampolsky and Stoltzfus, 2005] | −0.55 | −0.62 |
| Experimental datab | ||
| SAP-Final | 0.53 | - |
| ProTherm ΔΔG values | - | 0.61 |
- Correlation among Pp and Pd values and the corresponding SAP mutation values of the different scoring matrixes is computed according to Equation 9 by taking into account the average standard errors of the data (PpASE = 0.16; σ(Pp) = 0.19; PdASE = 0.05; σ(Pd) = 0.18) and considering without error the corresponding scores of the different substitution matrices. The corresponding p-values (Equation 8) range from 10−7 to 10−19 for Pp and from 10−17 to 10−29 for Pd, respectively.
- aCorrelation values are positive since the Grantham matrix lists distances among mutations [Grantham 1974].
- bPp and Pd values are correlated to the original data of disease associated and neutral mutations (SAP-Final, Table 1) and ProTherm ΔΔG values, respectively.
Historical matrices, such as the McLachlan's and the Grantham's ones, are derived from amino acid physico-chemical properties, being the latter based on a mean chemical distance for each amino acid pair of three basic properties, such as overall chain composition, polarity, and molecular volume [Grantham, 1974; McLachlan, 1971]. For this reason, and only in this case, we observe a positive correlation value; in all other cases, correlation is negative indicating that the higher the Pp value, the lower is the probability of observing the targeted substitution as scored under different assumptions.
In line with previous observations, the conservation of the physico-chemical properties is not the only important variable when considering mutation effects on protein stability. The relevance of polar solvent exposure and of the protein structure was also described. We observe that when matrices based on properties directly derived from protein structures, such as the extent of amino acid exchangeability, and from the weight of the genetic code redundance [Crooks and Brenner, 2005; Johnson and Overington, 1993; Müller et al., 2002], the correlation of the Pp index with the corresponding matrices increases with respect to that based on physico-chemical properties and chemical distances (Table 3). Furthermore, a good correlation is also observed when the weight of evolution is taken into account (BLOSUM 62).
Interestingly enough and again in line with what previously discussed, residue substitution may also be asymmetrical in relation to its effect on protein stability. Pp correlation values increase when asymmetric substitution matrices are considered [Overington et al., 1992; Koshi and Golstein 1995; Yampolsky and Stoltzfus, 2005] and the best correlation is obtained with the environment-specific substitution matrix for accessible residues [Overington et al., 1992]. Indeed some 32 SAP types (23% of the total) corresponding to 16 mutation pairs have a Pp difference (|P(X → Y) − P(Y → X)|) >0.3, sufficient to include one of the two mutation types below or above the 0.5 perturbing threshold value (Fig. 5). Considering Pp values and residue substitution types, changing steric effect when a given side chain is mutated from small to large is on average more perturbing than changing its polarity.
All together, our results support the notion that the perturbing Pp index, as derived from thermodynamic data, is indicative of the effect that a SAP type can have on protein stability and that its value correlates with other scoring values accounting for physico-chemical properties, such as solvent exposure, structure conservation, environment specificity, and also conservation through evolution.
In Table 3, Pd values are also correlated with the most popular substitution matrices. Correlation is high both for symmetric and asymmetric substitution scoring values. The highest correlation value is obtained with the BLOSUM62 substitution matrix, indicating that the more a SAP type is allowed through evolution the less it is associated to disease.
We also correlate Pp and Pd with the phenotype-genetic data contained in SAP-Final and with the ProTherm derived ΔΔG values, respectively. These last correlation values indicate that correlation holds also when the two inferred indexes are correlated with the original experimental data of disease associated and neutral mutations and thermodynamic data, respectively, and well compare with their direct correlation value (0.49, Table 2).
Summing up, and from the results in Table 3, we can conclude that both Pd and Pp are indeed casting for the different SAP types different physico-chemical, structural, compositional, evolutionary features, and general trends of experimental data.
Discussion
SAP annotation is an issue in many deep sequencing experiments aiming at clinical association studies. Here, we test the hypothesis that SAPs due to SNPs and disease associated are also perturbing to some extent protein stability. The problem is addressed separately in the pertinent literature. Methods are available for computing whether a residue mutation is disease associated [Tavtigian et al., 2008] and for predicting whether a residue mutation can affect the protein stability [Khan and Vihinen, 2010].
The question of how to relate disease associated protein variations with their effect on stability is still open, considering that direct association studies in cells are hampered by the difficulty of assessing in vivo to which extent a mutated protein is expressed and how its interaction with other proteins is eventually modified in protein networks involved in biological processes.
Our present effort focuses on the generation of probability indexes casting the different SAP type features derived from the available databases of thermodynamic data and disease association studies. For each SAP type, we generate a set of probability indexes encoding the probability of being disease related and the probability of increasing, decreasing, and perturbing the protein stability, respectively. These indexes generalize over the specific property at hand as derived from databases. Probability indexes are computed over a large number of mutations for all the mutation types both in relation to mutational data and also to thermodynamic data. Each index is endowed with a standard error to allow for data variability. Computing probabilities allows us to abstract from each specific context (protein structure, sequence, and environment) and to cast features into numerical values.
A first result of our analysis is that each SAP type can be endowed with probability values of being disease related (Pd) and of promoting increasing (P+), decreasing (P−), or perturbation (P+) of protein stability. We show that Pd significantly correlates with all the thermodynamic indexes. However, the highest correlation value is found when Pd is correlated with the perturbing index Pp. This is so, considering that Pd correlated with P− and even better with P+ corroborating the notion that also stabilizing mutations can be harmful. Our cumulative index Pp is therefore casting for each SAP and by definition (Equation 4) both possibilities of affecting protein stability.
The correlation among Pd and Pp is linear. This is obtained with a robust procedure that takes standard errors on both indices into account [Del Rio et al., 2001]. Statistical validation indicates that the correlation value is medium/good. Therefore, the assumption that a mutation type promoting protein stability perturbation is also disease associated cannot be rejected (with a strength [r2] of about 25% that nearly doubles if data variability is taken into account). When disattenuation is evaluated [Spearman, 1904/1987] and errors are taken into account, results indicate that data are compatible with an increased correlation coefficient value (from 0.49 to 0.67, Table 2).
Our analysis supports the notion that incorrect folding is likely to be one of the possible molecular mechanisms of the whole diseasome [Goh et al., 2007]. In the majority of diseases, the molecular basis of the phenotype is not yet fully characterized. From our Pp/Pd medium/good correlation value, we can conclude that although important protein stability is not the only source of disease. Showing that Pp and Pd correlate allow us to include protein stability effects due to mutations as a possible molecular mechanism of disease also at the proteome scale. This notion had been documented before in small sets of proteins separately for increasing or decreasing the protein stability. After this analysis, the concept of protein stability perturbation as a possible molecular mechanism of disease-related mutation effects can be extended at the proteome level. All the possible disease molecular sources due to missense mutations, including protein truncation and loss/gain of function, modification of protein solubility, modification of biological processes, such as posttranslational processes, signaling, translocation to cell compartments, and modification of interaction networks, are not considered in our analysis and can probably justify why correlation is not perfect.
Also, as our error estimates indicate, probabilistic indices and their correlation are enough tolerant to increase in database volumes likely to occur in the near future due to the great shift of interest in SNP detection. Two major outliers are detected: V → A and I → T (Supp. Fig. S1). For these mutation types, the Pp values (0.73 and 0.94) are much higher than that expected considering the Pd-associated values (0.26 and 0.38 for V → A and I → T, respectively) that indicate a moderate tendency to be disease related. In ProTherm, mutational data (122 V → A mutations in 37 proteins, and 16 I → T mutations in 11 proteins, respectively) are derived from proteins whose structure is known with atomic resolution. In both cases, about 90% of the mutations are located in the protein core region (buried, see Material and Methods: Thermodynamic data) and rather perturbing as indicated by the Pp values. This sampling is different from average in our data where only 40% of the mutations are buried and it can bias the association with low Pd values.
We compare the Pd and Pp values with other substitution scoring matrixes encoding different properties as derived upon chemical mutation from the protein universe and find that the two indexes significantly correlates both with symmetrical and asymmetrical substitution matrices. This indicates that properties emerging from residue composition and their accessibility as well as from residue conservation through evolution are also encoded in our indexes (correlation with the only exception of the chemical distance substitution matrix [Grantham, 1974] is negative meaning that the higher the Pd and Pp values the lower the corresponding SAP type value in the specific substitution matrix). Also, we show that the inferred indexes correlate with the phenotype-genetic and thermodynamic data to an extent that is similar to their direct correlation value. This confirms that the two indexes cast the general trend of the counterpart experimental data, respectively.
In our effort of confining in a nut shell all the available information on mutation types, we provide a feature annotation table of SAP types. This table should be regarded as a useful baseline summing up the characteristics of a specific SAP type in relation to the present data bases, useful in selecting mutations for more detailed SAP annotation (Table 1S).
Acknowledgements
We thank MIUR for the PNR 2003 project (FIRB art.8) termed LIBI-Laboratorio Internazionale di BioInformatica delivered to R.C. S.T. received support from the University of Bologna (2008–2010) and a Residential fellowship by the Institute of Advanced Studies through a “Brains-in” project (2009–2010).




