Enhancement of teaching outcome through neural prediction of the students' knowledge state
Funding information: National Natural Science Foundation of China, Grant/Award Numbers: 31622030, 31411130158; Fundamental Research Funds for the Central Universities, Grant/Award Numbers: 2017EYT32, 2017XTCX04; Open Research Fund of the State Key Laboratory of Cognitive Neuroscience and Learning, Grant/Award Numbers: CNLYB1605, CNLZD1604
Abstract
The neural mechanism for the dyadic process of teaching is poorly understood. Although theories about teaching have proposed that before any teaching takes place, the teacher will predict the knowledge state of the student(s) to enhance the teaching outcome, this theoretical Prediction-Transmission hypothesis has not been tested with any neuroimaging studies. Using functional near-infrared spectroscopy-based hyperscanning, this study measured brain activities of the teacher–student pairs simultaneously. Results showed that better teaching outcome was associated with higher time-lagged interpersonal neural synchronization (INS) between right temporal-parietal junction (TPJ) of the teacher and anterior superior temporal cortex (aSTC) of the student, when the teacher's brain activity preceded that of the student. Moreover, time course analyses suggested that such INS could mark the quality of the teaching outcome at an early stage of the teaching process. These results provided key neural evidence for the Prediction-Transmission hypothesis about teaching, and suggested that the INS plays an important role in the successful teaching.
1 INTRODUCTION
Theories about teaching suggest that teaching must involve joint mental activities between the teacher and her/his student(s) (Kline, 2015; Nurmi & Kiuru, 2015; Palincsar, 1998; Ryan & Deci, 2000). In particular, before any teaching takes place, the teacher will predict the knowledge state of the student(s), that is, to figure out their Zone of Proximal Development (i.e., ZPD, Vygotsky, 1978), which will help the teacher formulate an appropriate representation of the knowledge to be transmitted to the student(s). This process of transmitting knowledge from the teacher to the student is known as the Prediction-Transmission hypothesis (Figure 1a). Although this hypothesis is widely accepted, it has not been directly tested with neural evidence.
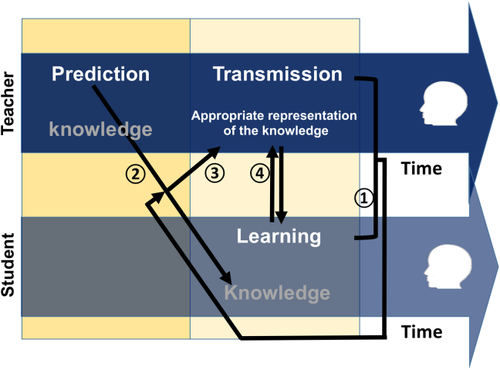
A hypothesized mechanistic model based on teaching theories. Specifically, teaching should start with high-quality communications between the teacher and the student ①. Before the knowledge is actually taught ④, the teacher will predict the student's knowledge state ② (Vygotsky, 1978), whereby to formulate an appropriate representation of the knowledge that can be transmitted to the student ③. When these processes proceed successfully, knowledge will be transmitted from the teacher to the student. Otherwise, the transmission will fail [Color figure can be viewed at wileyonlinelibrary.com]
Several previous studies have examined the neural mechanism of some aspects of teaching that may be of relevance to the Prediction-Transmission hypothesis. For example, Dikker et al. (2017) recently found that the neural synchronization between pairs of students could reflect the level of the students' social engagement in a classroom. This study, however, did not examine the teacher–student relationship. Two studies specifically examined the teaching process using functional near-infrared spectroscopy (fNIRS)-based hyperscanning (Holper et al., 2013; Takeuchi, Mori, Suzukamo, & Izumi, 2017), and found significant correlations between the averaged brain activities of the teacher and those of the students who acquired the knowledge taught to them, but not between the brain activities of the teacher and the students who did not acquire the knowledge. However, neither study tested the Prediction-Transmission hypothesis as described above. Finally, one study on speaker-listener's neural coupling found that the listener's brain activity was coupled with the speaker's brain activity with a time lag, which suggested that the listener was involved in a prediction process to help him/her to understand the subsequent speech information (Stephens, Silbert, & Hasson, 2010). Unlike a conversation involving the interlocutors who play a comparable role, however, teaching involves an asymmetry of the knowledge states of the teacher and the student(s), with the teacher knowing much more than the students do. Consequently, the teacher is in a position to know what to teach, how much to teach, and how to teach, etc., whereas the student(s) would not know the content of the material to be taught and how the teacher would teach them. In this context, it seems logical that the teacher would involve the Prediction-Transmission process, whereas the student(s) would not be able to effectively predict what the teacher would do. This conjecture has yet to be tested. Furthermore, it remains unclear whether such prediction by the teacher would enhance the teaching outcome, that is, better knowledge transmission from the teacher to the student(s).
Another unresolved issue in teaching is whether different teaching styles are associated different teaching outcomes. For example, while some studies showed that students benefited more from lecturing than interactive teaching when the learning materials are abstract (Hein et al., 2012; Wetzel, Potter, & O'Toole, 1982), other studies did not find this difference (Aitkin, Bennett, & Hesketh, 1981; Coop & Brown, 1970). Moreover, video teaching was reported to be just as efficient as teaching in the traditional face-to-face style (Tallent-Runnels et al., 2006). As far as we know, no neuroimaging studies have examined the potential neural differences between teaching styles.
This study addressed the above issues by employing the fNIRS-based hyperscanning approach because fNIRS has clear advantages over other techniques such as fMRI and EEG in terms of portability, high tolerance of movement artifacts, and measurements of local hemodynamic effect. In terms of brain areas of interest to this study, previous studies have clearly implicated the prefrontal cortex (PFC) in teacher–student interactions (Holper et al., 2013; Takeuchi et al., 2017); the temporal-parietal junction (TPJ) in the processing of others' mental state (i.e., mentalizing and interpersonal prediction) (Carter, Bowling, Reeck, & Huettel, 2012; Dobbins, Long, Dedrick, & Clemons, 1990), memory retrieval (Bzdok et al., 2013), and asymmetrical social interactions (i.e., leader-follower) (Jiang et al., 2015); and the superior temporal cortex in the representation of semantic knowledge needed for teaching (Correia et al., 2014; Pobric, Lambon Ralph, & Zahn, 2016). Focusing on these three brain areas, this study aimed (a) to identify the interpersonal neural synchronization (INS) that would be associated with teachers' prediction process and (b) to determine any potential modulating effect of teaching style on the prediction process.
2 MATERIALS AND METHODS
2.1 Participants
Four healthy adults (2 females, mean age = 25 ± 2.4 years) were recruited from a postgraduate teacher training program at Beijing Normal University and assigned as teachers. All teachers had received teacher training for 6 or 7 years (4 years of undergraduate and 2 or 3 years of graduate training). In addition, 60 healthy undergraduate students were recruited from universities in Beijing through advertisements (30 females, mean age = 23 ± 2.3 years). The 60 students were pseudorandomly (equal numbers of males and females for each group) split into 3 groups for the 3 teaching styles (to be described in the next section). The 20 students in each group were randomly assigned to the 4 teachers. Each teacher taught 5 students in the one-on-one format for each teaching style. All participants were right-handed (Oldfield, 1971) and had normal or corrected-to-normal vision. The average age of the students did not differ significantly by teaching style (F(2, 57) = 0.01, p = .99).
Written informed consent was received from all subjects. The study protocol was approved by the Institutional Review Board of the State Key Laboratory of Cognitive Neuroscience and Learning, Beijing Normal University.
2.2 Experimental tasks and materials
To assess teaching outcome, we asked the “teachers” to teach the “students” about numerical reasoning, that is, looking for the hidden rule about numerical relationship among a given sequence of numbers. We selected numerical reasoning tasks as the content for teaching because they are novel to most young adults and yet can be taught within 10–20 min. This content was selected from a national standard guidebook [Chinese Civil Servants Administrative Professional Knowledge Level Tests (CCSAPAT), 2014] that aims to measure and improve various abilities including numerical reasoning in young adults (18–40 years old). Numerical reasoning involves finding hidden relations among a given number sequence. For instance, the number sequence of “2, 4, _, 8, 10, 12” follows the rule that all numbers are even numbers that differ by the constant of 2, so “6” is the correct answer. CCSAPAT has proven to have good validity and reliability (Wu, 2013). The students in our sample had not been exposed to CCSAPAT.
Eight training examples were selected from CCSAPAT's training section, each of which represented a specific approach to numerical reasoning. These approaches have proven to be fast and efficient in finding the hidden rules under various conditions. For instance, if a number sequence was composed of fractions, for example,
,
,
,
,
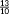, _, one should consider the numerator and denominator separately. The numerators (after converting the fractions into a sequence of increasing magnitude) have a difference of 3 (1, 4, 7, 10, 13), while the denominators have a difference of 2 (2, 4, 6, 8, 10). Thus, the missing next number should be
=
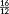. The specific approach was described in a teaching script.
All teaching was in the format of one teacher to one student (Figure 2a). Each of the 4 teachers taught the same content to 3 groups of individual students in 3 different styles, that is, lecturing, interactive, and video. Prior to the experiment, all teachers were trained for teaching the contents. First, all teachers were given the 8 examples and the teaching script for each teach style. For the lecturing style, the teacher explained to the student the steps for solving each example. The teacher did not ask questions and the student was not allowed to ask questions, either. For the interactive style, the teacher first presented an example on a computer screen, and the student read and thought about the problem for about 20 s. Next, the teacher would guide the student to solve the problem according to the approach described in the script, in a Q&A approach. For the video style, the videos were recorded when the teacher simulated the lecturing style alone (her/his fNIRS data were collected at this time). Then, the students learnt by watching the video alone while being scanned with fNIRS.
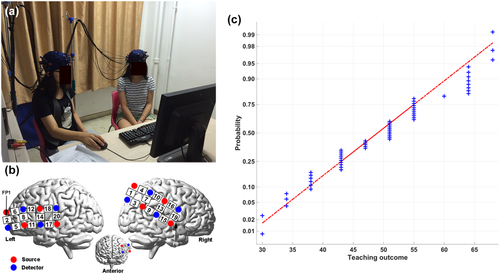
Experimental setup and teaching outcome. (a) Experimental paradigm. Teacher–student pairs were seated in a room side-by-side in front of a computer, similar to a typical tutoring setting. They went through the three teaching styles, the order of which was counterbalanced across teacher–student pairs. (b) fNIRS data acquisition. Customized optode sets covered the frontal, temporal, and parietal cortices. Measured channels are marked by numbers. The position was confirmed by MRI of one typical participant (normalized to the MNI coordinate space). (c) Distribution of teaching outcome. Each point represents the difference between post- and pre-test scores. The scores have been converted into T scores [Color figure can be viewed at wileyonlinelibrary.com]
All teachers were required to prepare teaching at home for 2 days. They practiced with each other in the lab until they were satisfied with their own teaching performance in both lecturing and interactive teaching styles. Then they demonstrated teaching to the experimenter in a one-on-one format until their performance met the approval of the experimenter.
2.3 Experimental procedures
Data collection started with a 10-min resting-state session, which served as a baseline. During this session, the participants were required to keep still with their eyes closed, relax their mind, and remain as motionless as possible (Jiang et al., 2012).
The teaching session immediately followed the resting-state session. For lecturing and interactive styles, the teacher and the student sat side-by-side in front of a table in a silent room (Figure 2a). For the video style, only the student sat in front of a table with a computer screen on the table. The length of the teaching periods was flexible and up to the teacher and the student. They lasted 13–26 min. The whole experimental procedures were video recorded.
2.4 Behavioral tests
Students' knowledge of numerical reasoning was tested immediately before the onset of resting-state session and after the end of the teaching session. A total of 30 4-choice items were selected from CCSAPAT's test bank. To create equivalent pre- and post-tests, additional 8 participants not involved in this experiment were recruited to take the 30-item test and their scores (% correct) were used to index the difficulty levels of the 30 items. Three items with potentially confusing expressions (based on subjects' feedback) were deleted. Seven items with highest (>70%) and lowest levels of accuracy (<30%) were also deleted for their lack of contribution to the variance and to avoid the ceiling and flooring effects. The remaining 20 items were randomly split into two halves, one for the pretest and the other for the post-test. The difficulty levels of the pre- and post-tests did not differ based on the 8 pilot testing participants' scores [t(18) = 0.974, p = .343]. For the actual experiment, the participants had 20 min to finish each of the tests. All students finished the test within this time limit.
2.5 fNIRS data acquisition
The imaging data were collected from the teacher and the student simultaneously during teaching using an ETG-4000 optical topography system (Hitachi, Japan). Four sets of the customized optode probes were used in each pair. Each set had 4 emitters and 4 detectors that consisted of 10 measurement channels (30 mm optode separation). For each participant, the probe sets covered the bilateral frontal, temporal, and parietal cortices. The probe set on the left hemisphere was more anterior, whereas that on the right was more posterior, to better cover the left frontal cortex and right temporal-parietal cortex. CH2 was placed at FP1 on the left hemisphere, and CH19 was placed at F8 on the right hemisphere, according to the international 10–20 system (Figure 2b). The probe sets were checked and adjusted to ensure consistency within the teacher–student pair and across pairs.
To confirm the anatomical position of each optode, MRI was obtained from one typical participant with a high-resolution T1-weighted magnetization-prepared rapid gradient echo sequence (TR= 2,530 ms; TE = 3.30 ms; flip angle = 7°; slice thickness = 1.3 mm; in-plane resolution = 1.3
1.0 m2; number of interleaved sagittal slices = 128). SPM8 (Statistical Parametric Mapping, Wellcome Department of Cognitive Neurology, London, UK) was used to normalize the MRI to the standard MNI coordinate space with a modulated normalization method (Ashburner & Friston, 2005). According to the Automated Anatomical Labeling template (Tzourio-Mazoyer et al., 2002), the anatomical positions below the optode were identified. This information was used to provide neurofunctional explanations of the significant teaching outcome or the teaching style effects (see below) based on the CH combinations' roughly corresponding brain areas.
The absorption of near-infrared light at two wavelengths (695 and 830 nm) was measured with a sampling rate of 10 Hz. Based on the modified Beer–Lambert Law, changes of the oxy-hemoglobin (HbO) and deoxy-hemoglobin (HbR) concentrations were obtained by measuring the absorption changes of fNIRS light after its transmission through the tissue. Previous studies have shown that HbO is a sensitive indicator of the change in regional cerebral blood flow (Hoshi, 2007). Thus, this study focused on the HbO concentrations only.
2.6 Data analyses
2.6.1 Behavioral teaching outcome
The percentage of correctly answered testing items was calculated and used as the test score. To test the effect of teaching and teaching style (lecturing, interactive, and video), a repeated measures ANOVA was conducted on the test score, with the time of test (pre- vs post-test) and teaching style as the independent variables. For subsequent analyses, teaching outcome was indexed by the difference between post- and pre-test scores after they were transformed into T scores.
2.6.2 fNIRS data analysis
Individual-level analysis
fNIRS data collected during the resting-state and teaching sessions were analyzed. Data from the first and last 10 s were deleted during the preprocessing to obtain data within the period of steady state. During preprocessing, no filtering or detrending procedures were applied (Cui, Bryant, & Reiss, 2012). These procedures were conducted on the coherence value as described below. In addition, we also did not perform any artifact corrections at the single-subject level, as wavelet transform coherence (WTC) normalizes the amplitude of the signal according to each time window and thus is not vulnerable to the transient spikes induced by movements (Nozawa, Sasaki, Sakaki, Yokoyama, & Kawashima, 2016).
Next, a Matlab package was used to perform WTC (Grinsted, Moore, & Jevrejeva, 2004) to assess the cross-correlation between the two fNIRS time series generated by each pair of the participants as a function of frequency and time (Torrence & Compo, 1998). For example, for a specific teacher–student pair, two time-series of HbO were obtained, one from CH1 of the teacher and the other from CH2 of the student. The two time-series had the same length of the teaching period because the teacher and student interacted with each other. Then, WTC was applied to these two time-series to find regions in the time frequency space where the two time-series co-varied. This generated a 2-D matrix of the coherence value. In the matrix, each line corresponded to a specific frequency point, while each column corresponded to a specific time point. For more thorough information about wavelet coherence, please see Grinsted et al. (2004) and Chang and Glover (2010). Because there were 20 measurement channels for each participant, 400 pairs of time-series were generated for each pair of the participants, and WTC was thus conducted 400 times. Next, the coherence values were time-averaged across the whole teaching period, and converted into Fisher z-values. These procedures were conducted for each of the three teaching styles as well as the resting state. According to previous studies (Cui et al., 2012; Jiang et al., 2012), the coherence value increases during the task session compared to the resting-state session. Thus, the coherence value from the resting-state was subtracted from that of the teaching period, resulting in an index of INS increase. At this stage, no specific frequency ranges were selected.
Group-level analysis
To identify the INS increases that were specifically associated with the teaching outcome and teaching style, the following steps were performed. First, to identify the frequency ranges that were specifically associated with the teaching outcome or teaching style, one-way ANCOVA was conducted on the time-averaged coherence value of each CH combination (400 in total) along the full frequency range (0.01–0.7 Hz). For that analysis, the teaching style (a categorical variable) was an independent variable and the teaching outcome (a continuous variable) was a covariate. Following previous studies (Barrett, Barman, Boitano, & Brooks, 2015; Guijt, Sluiter, & Frings-Dresen, 2007; Tong, Lindsey, & Frederick, 2011), data above 0.7 Hz were not included to avoid aliasing of higher frequency physiological noise such as cardiac activity (∼0.8–2.5 Hz); data below 0.01 Hz were also not used to remove very low frequency fluctuations; and finally, data within the frequency range of respiratory activity (∼0.15–0.3 Hz) were not considered, either. The ANCOVA results were thresholded at p < .0005. No further correction for multiple comparisons was applied because this analysis was only used to identify the pattern along the frequency range rather than to obtain the final results. For the teaching outcome analysis, only two frequencies (i.e., 0.6Hz and 0.03 Hz) had CH combinations whose p value survived the thresholding (Supporting Information, Figure S1). Then, the frequencies that were around these two frequencies and meanwhile whose p values were <0.05 were selected, resulting in two frequency ranges, that is, 0.5–0.7 Hz and 0.02–0.03 Hz. The same procedures were applied to the analysis of teaching style, and two frequency ranges were selected, that is, 0.3–0.4 Hz and 0.06–0.07 Hz. Second, the coherence values within these two frequency ranges were averaged separately. One-way ANCOVA was conducted again, on the time-averaged and frequency-averaged data. Results were corrected with the false discovery rate (FDR) method for all CHs at p < .05 level. As a general approach to the multiple comparisons problem, an FDR threshold is determined from the observed p value distribution, and hence is adaptive to the amount of signal in the data. The procedure used here is an extension (Genovese, Lazar, & Nichols, 2002; Nichols & Hayasaka, 2003) of SPM8 (Statistical Parametric Mapping, Wellcome Department of Cognitive Neurology, London, UK) that implemented the Benjamini–Hochberg method (Benjamini, Krieger, & Yekutieli, 2006; Benjamini & Yekutieli, 2001). The overall procedures are summarized in Supporting Information, Figure S2.
In addition, to examine whether and when the teacher predicted the student's knowledge state (per the Prediction-Transmission hypothesis), we added various time-lags to the computation of INS increases (Liu et al., 2017; Stephens et al., 2010). Specifically, the time course of the teacher's brain activity was shifted forward or backward relative to that of the student's brain activity by 2–14 s (step = 2 s) and the INS increases were recomputed and statistically tested. Results were corrected with the FDR method for all CHs across all time-lags at p < .05 level.
To identify the earliest time-point whose INS increase was associated with teaching outcome and/or teaching style, the one-way ANCOVA described above was rerun with the following five steps. First, for the particular CH combination that showed significant results either for teaching outcome or teaching style, its 2-D matrix of coherence values was obtained for each of the teaching styles and the resting state. Second, the coherence values were averaged within the selected frequency range(s), generating a 1-D frequency-averaged time-series of coherence values. Third, for each teacher–student pair, the time-series of coherence values during teaching was temporally resampled into the same length as that during the resting state. The resampling procedure kept the regional features (in time) but only changed the length of the time-series. Thus, the temporal dynamics of the teaching process was still retained. Fourth, the INS increase was obtained by subtracting the INS of resting state from that of different teaching styles. Finally, one-way ANCOVA with the teaching style as the independent variable and teaching outcome as a covariate was conducted on the INS increase at each time point along the time-series, resulting in two time-series of p values, one for the teaching outcome, the other for the teaching style. The p values were corrected by FDR method across the time points (p < .05) for the teaching outcome and teaching style respectively. Based on the time-series of the p values, the earliest time point whose INS increase reached significance was identified.
2.7 Linking teaching behaviors with the INS
To link the pattern of teaching behaviors with the INS with time-lags, additional two participants were recruited to code the teaching behaviors frame-by-frame based on the video of teaching with the interactive style. Only the interactive teaching style was analyzed because (a) there were no explicit interaction behaviors in the other two teaching styles and (b) the INS increase with a time-lag at TPJ-aSTC was correlated with teaching outcome regardless of the teaching style. Three teacher–student pairs were removed due to video-recording failure. The two coders identified the time point where the teacher just started to ask a question and where the student just started to answer the question within each of the 8 examples. The intraclass correlation (ICC) was conducted across all the time points in each teacher–student pair to assess the intercoder reliability. The coefficient was high (mean of Cronbach's Alpha = 0.902, SD = 0.082). Then, the two coders discussed the coding results in order to reach a consensus. During this process, one additional teacher–student pair was removed because the two coders could not reach an agreement about the coding of one specific example (number 6). We also calculated the percentage of correct answers of the student for each teacher-student pair. Pairs whose percentage of correct answers was below 50% were not included in the following analyses (3 pairs) because for these pairs, the teachers' prediction was likely to be unsuccessful. Thus, there were 13 teacher-student pairs left. Next, the time-durations for asking and answering questions were averaged across the 8 examples and then across all teacher–student pairs by calculating the median (here median was used because there was large variance across examples and pairs). Finally, to test the relationship between asking and answering questions with INS, INS at time points immediately before the teacher asked questions and before the student answered questions were averaged and compared to INS at other time points.
3 RESULTS
3.1 Behavioral results
To demonstrate the effectiveness of teaching, test scores were transformed into T scores (mean = 50, SD = 10). Repeated measures ANOVA on test scores (time of test vs teaching style) showed a significant main effect of time of test (F(1, 57) = 502.981, p < .001), with post-test scores being significantly higher than pretest scores. Teaching style did not have a significant effect (F(2, 57) = 0.499, p = .61), nor did the interaction between teaching style and time of test (F(1, 57) = 0.58, p = .563). For subsequent analyses, the teaching outcome was indexed by the change score (pre-test scores were subtracted from post-test scores). The distribution of the teaching outcome in all teacher-student pairs is shown in Figure 2c, which indicates a wide distribution.
3.2 Confirmation of the INS between the teacher and the student when their brain activities were temporally aligned
To identify the INS increases that were associated with teaching outcome and/or teaching style, we conducted one-way ANCOVA with the teaching style (a categorical variable of three teaching styles) as the independent variable and the teaching outcome (a continuous variable) as a covariate. Results were corrected with the false discovery rate (FDR) method for all CHs at p < .05 level. Teaching outcome was a significant positive covariate of INS between teachers' anterior superior temporal cortex (aSTC, CH17) and students' TPJ (CH3, F(1, 56) = 19.297, p < .001) at the frequency band of 0.5–0.7 Hz (Figure 3a–e). There were no significant results of the teaching outcome for other CHs and other frequency bands (p > .05, FDR corrected).
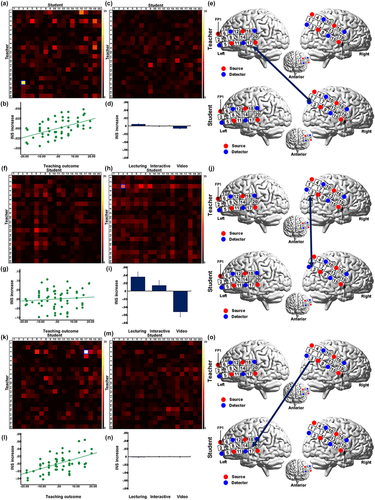
ANCOVA results. (a–e) Results without time-lags at the frequency band of 0.5–0.7 Hz. (f–j) Results without time-lags at the frequency band of 0.06–0.07 Hz. (k–o) Results when the teacher's brain activity preceded that of the student by 10 s at the frequency band of 0.5–0.7 Hz. (a), (f), and (k) F-maps for teaching outcome. (c), (h), and (m) F-maps for teaching style. The blue rectangle highlights the significant result. The numbers represent CHs. (b), (g), and (l) Partial correlation plot between the INS increase and teaching outcome. (d), (i), and (n) Pairwise comparison across the three teaching styles. The error bars indicate standard errors. (e), (j), and (o) Thresholded results that are showed on the brain [Color figure can be viewed at wileyonlinelibrary.com]
In terms of the effect of the teaching style, there was a significant INS increase at right TPJ-TPJ (CH3, teacher-student) at the frequency band of 0.06–0.07 Hz (F(2, 56) = 12.472, p < .001) (Figure 3f–j). Pairwise comparison (p < .05, Šidák correction) indicated that INS increase was significantly lower for the video style than for the other two styles (both at p < .001). There was no significant difference between the lecturing and interactive teaching styles (p = .505). It is worth noting that the effect of teaching style was not significant for the teaching outcome-related CH combination of aSTC-TPJ mentioned above (F(2, 56) = 2.844, p = .067).
As the length of the teaching periods varied across the teacher–student pairs, it might have affected teaching outcome and the INS increase. To exclude this possibility, a Pearson correlation was conducted between the teaching outcome and the length of the teaching period. No significant correlation was found (r = −.011, p = .933). Next, we repeated the one-way ANCOVA by adding the length of the teaching period as an additional covariate. Results showed that teaching outcome was still a significant positive covariate of INS at aSTC-TPJ (CH17-3) (F(1, 55) = 17.548, p < .001). There was no significant effect either for the teaching style (F(2, 55) = 2.273, p = .075) or for the length of the teaching period (F(1, 55) = 0.112, p = .74).
3.3 INS between the teacher and the student when the teacher's brain activity was shifted forward or backward
The time-lag results showed that teaching outcome was a significant positive covariate of the INS increase at TPJ-aSTC (i.e., CH3–17, from the teacher to the student) at 0.5–0.7 Hz when the teacher's brain activity preceded that of the student by 10 s (F(1, 56) = 24.889, p < .001) (Figures 3k–o and 4). No significant effect was found for the teaching style at this time-lag (F(2, 56) = 0.287, p = .752) or other time-lags (p > .05, FDR corrected). Also, when the length of the teaching period was added as an additional covariate, there was still a significant positive relationship between the INS increase at TPJ-aSTC and the teaching outcome (F(1, 55) = 23.655, p < .001). There was no significant effect either for the teaching style (F(2, 55) = .168, p = .846) or for the length of the teaching period (F(1, 55) = 0, p = .999). No significant results were found when the student's brain activity preceded that of the teacher at any time-lags, at any CH combinations (p > .05, FDR corrected).
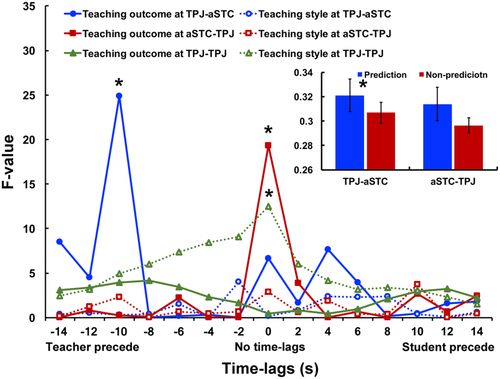
A summary of the INS increase pattern. The stars indicate significance at p < .05 level with FDR correction for all CH combinations across all time-lags. No further statistical tests were conducted on the specific CH combinations. The bar plot shows the relationship between the INS increase and teaching behavioral pattern. The error bars indicate standard errors. Note that prediction and non-prediction indicate the averaged INS across time points immediately before asking and answering questions and across other time points respectively. The star indicates a significance at p < .05 level [Color figure can be viewed at wileyonlinelibrary.com]
3.4 Linking the teaching behaviors with INS
The average duration for the teachers to ask a question was 7 s (SD = 5), and the average duration for the students to answer a question was 11 s (SD = 7). Thus, there was one round of an alternation between asking and answering questions within about 18 s. The teacher was more likely to make prediction about what the students' answer might be and what to ask next. This hypothesis would predict higher INS at time points immediately before the teacher asked the question and immediately before the student answered the question (i.e., before Q&A) than at other time points.
To test this hypothesis, the INS at time points before Q&A were averaged and compared to INS at other time points. Results showed higher INS at time points before Q&A than at other time points [t(12) = 2.004, p = .034, one-tailed]. Similar tests were conducted on the INS increase at aSTC-TPJ, which was suggested to be associated with actual teaching rather than prediction. No significant result was found [t(12) = 1.593, p = .069, one-tailed]. These results confirmed the earlier hypothesis that the teacher might make predictions immediately before she/he asked a question and the students answered the question.
3.5 How early could the INS increase mark eventual teaching outcome?
To identify the earliest time-point whose INS increase at aSTC-TPJ (which was associated with teaching outcome as reported above) would predict the eventual teaching outcome, ANCOVA as described above was conducted for each time point along the time course. Results showed that by the time of 486 s after the start of teaching, the INS increase at aSTC-TPJ became a significant correlate of the teaching outcome, suggesting that about eight min into the teaching period, the INS increase could mark successful knowledge transmission (Figure 5a). No significant effect of the teaching style was found at any time points for the aSTC-TPJ CH combination (p > .05, FDR corrected). Meanwhile, the teaching style-related INS increase at TPJ-TPJ as reported reached significance after about 76 s of teaching (Figure 5b). Again, no significant results for the teaching outcome were found at the TPJ-TPJ CH combination at any time points (p > .05, FDR corrected).
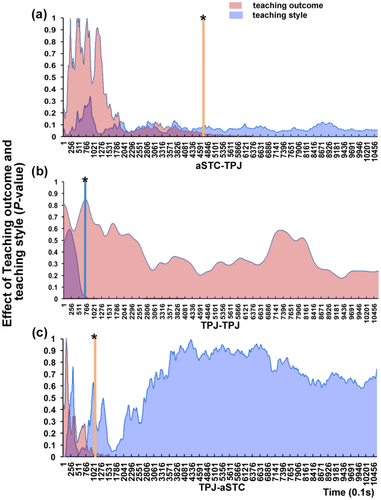
The temporal dynamics of the relationship between the INS increase and teaching outcome and style. (a) and (b) Patterns when there was no time-lags. (c) Pattern when the teacher's brain activity preceded that of the student by 10 s. The stars indicate significance at p < .05 level with FDR correction for all CH combinations across all time-lags. No further statistical tests were conducted on the specific CH combinations. The vertical line for each panel indicates the earliest time point that the effect reached significance. The red and blue colors represent the results of teaching outcome and teaching style, respectively [Color figure can be viewed at wileyonlinelibrary.com]
The same time-point-by-time-point analyses were also conducted after time lags were added to the data. For the INS increase at TPJ-aSTC, which was associated with the teaching outcome when the teacher's brain activity preceded that of the student by 10 s, we found that it reached significance around 102 s after the onset of teaching (Figure 5c). No significant effect was found for the teaching style at TPJ-aSTC CH combination at any time points for any time lags (p > 0.05, FDR corrected).
4 DISCUSSION
INS has been hypothesized to be associated with teaching, but there has been little direct evidence based on simultaneous recordings of the neural activities of the teachers and the students. Using fNIRS-based hyperscanning, this study measured brain activities from the teachers and the students simultaneously, identified the INS increase associated with a prediction process that was positively associated with teaching outcome regardless of the teaching style.
First, we identified a significant INS increase that was positively associated with teaching outcome between left aSTC of the teacher and right TPJ of the student when the brain activities of the teacher and student were temporally aligned. This finding was consistent with previous evidence that INS could be a neural marker for social interactions in the educational settings (Dikker et al., 2017), but this study expanded from student-to-student relationship (Dikker et al., 2017) to teacher-to-student relationship. The present finding also confirmed that successful knowledge transmission was related to correlations of the teacher's and the student's brain activities (Holper et al., 2013; Takeuchi et al., 2017) using a novel method, that is, examining the temporal dynamic covariation of brain activities of the teacher and the student along the teaching process in a large sample of participants (N = 60 pairs). Previous evidence has shown that while left aSTC is the modality-invariant representational hub within the semantic system (Correia et al., 2014; Pobric et al., 2016), right TPJ is exclusively involved in high-level mentalizing (Carter et al., 2012; Dobbins et al., 1990) and memory retrieval (Bzdok et al., 2013). Thus, the current findings suggested that INS at aSTC-TPJ might reflect a knowledge-related joint mental activity between the teacher and the student, whereby knowledge was transmitted from the teacher to the student.
Second, when the brain activity of the teacher at right TPJ preceded that of the student at left aSTC by 10 s, a significant INS increase was associated with the teaching outcome but not teaching style. According to the theory of language communication (Pickering & Garrod, 2007), prediction plays an important role in both speech production and comprehension. Both behavioral (for a review, see Pickering & Garrod, 2007) and neural evidence (Liu et al., 2017; Stephens et al., 2010) supports this theory. Consistent with this proposition, we found that the teacher's brain activity was associated with subsequent brain activity of the student. Moreover, we found that the INS increase occurred specifically at TPJ-aSTC, which is generally considered to be a key area for theory of mind (ToM) or mentalizing (Carter et al., 2012). Thus, the INS increase with a time-lag at TPJ-aSTC should reflect the function of TPJ in predicting the mental state of the student. More specifically, the length of the time-lag (10 s) roughly corresponded to the amount of time the teacher used to ask a question as well as the amount of time of the student used to answer a question. The INS was also significantly higher immediately before the teacher asked a question and the student answered a question than at other time points. Therefore, it was more likely that the teacher made predictions about what the student's answer would be and what to ask next. In sum, it seems that the teacher might make a prediction about the knowledge state of the student prior to actual knowledge transmission, and then proceed to formulate an appropriate representation of the knowledge that can be transmitted to the student (Figure 6).
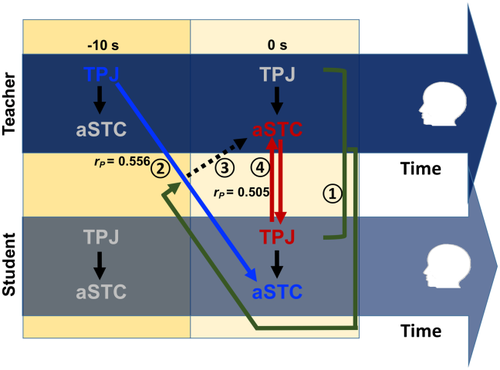
A proposed neural mechanistic model based on the present findings. The establishment of high-quality communication takes about 1 min ①. Before the knowledge is actually taught (about 10 s before), the teacher will predict the students' knowledge state ②, whereby to formulate an appropriate representation of the knowledge that can be transmitted to the student ③. When the knowledge is actually taught, there will be a joint mental activity between aSTC of the teacher and TPJ of the student ④. The numbers indicate partial correlations with teaching outcomes [Color figure can be viewed at wileyonlinelibrary.com]
We did not find a similar result of INS increase when the student's brain activity preceded that of the teacher. One possibility was that we had two teaching styles that involved only one-way information flow from the teacher to the student, that is, lecturing and video teaching. Previous evidence has shown that in such a one-way communication context, the speaker's brain activity preceded that of the listener at TPJ but not vice versa (Stephens et al., 2010). Even in the interactive teaching style, the teacher still played a dominant role. Previous evidence has shown that in a communication context that occurs within a dominant relationship, the leader's brain activity was always temporally ahead of that of the followers (Jiang et al., 2015; Konvalinka et al., 2014). Thus, it seems that the teacher's prediction played a dominant role in this study. However, our findings could not exclude the possibility that with other teaching styles not included in our study, there is student's prediction about the teacher's mental state as well.
Third, teaching style was associated with the INS increase at TPJ-TPJ at a lower frequency band. In this study, INS that differed among the three teaching styles was expected to reflect the neural correlates for various levels of general communications such as visual inputs, turn-takings, and even mutual comprehension (Jiang et al., 2012; Osaka et al., 2015; Stephens et al., 2010). Previous fMRI evidence showed that in a strictly controlled unidirectional communication context (i.e., between a speaker and a listener), INS occurred at widely distributed brain areas including PFC, IFC, TPJ, and so on (Stephens et al., 2010). When the communication occurred bi-directionally in a more naturalistic context, INS was found at left IFC and TPJ (Jiang et al., 2015; Jiang et al., 2012; Osaka et al., 2015). Only TPJ was identified when there was a dominant (leader-follower) rather than an egalitarian relationship between communicators. The present results confirmed this postulation in another type of dominant social relationship, that is, teacher–student pairs, suggesting that INS at TPJ might be a neural marker for the dominant social relationship. A new finding of this study was that the INS increase was significantly lower in the video-teaching style compared to the lecturing and interactive styles despite their similar teaching outcomes. In the video style, the teacher and the student did not interact directly with each other, which might have led to the decoupling of their brain activities at TPJ.
In this study, it seems that different frequency ranges were associated with different brain functions. This finding should not be directly compared with results about frequency ranges from EEG studies because fNIRS signal differs from EEG signal in different aspects of the underlying neuronal activity. In previous fNIRS-based hyperscanning study, the INS at a lower frequency range [such as 0.01–0.1 (Jiang et al., 2012) or 0.02–0.2 (Jiang et al., 2015)] was found to be closely associated with the turn-taking behaviors in free verbal conversations. The INS at this frequency range is also closely associated with the function of frontal cortex and TPJ (Balardin et al., 2017; Balconi & Vanutelli, 2017; Jiang et al., 2012, 2015; Pan, Cheng, Zhang, Li, & Hu, 2017; Tang et al., 2016; Zhang, Liu, Pelowski, Jia, & Yu, 2017a; Zhang, Liu, Pelowski, & Yu, 2017b). The INS at right TPJ is found to be specifically associated with a frequency range of 0.06–0.08 Hz (Tang et al., 2016). Therefore, previous evidence is consistent with the present finding on TPJ-TPJ at 0.06–0.07 Hz during teaching.
However, spectral analysis of the INS indicates that the INS is not limited to the frequency range that directly corresponds to communicating behavior (Nozawa et al., 2016). The frequency range of 0.43–0.57 Hz also has an enhancement of the INS in a conversation condition as compared to the control condition (Nozawa et al., 2016). This frequency range roughly corresponds to the present findings on TPJ-aSTC at 0.5–0.7 Hz. This frequency range has already excluded the potential influence of physiological activity such as cardiac (∼0.8–2.5 Hz) or respiratory (∼0.15–0.3 Hz) activity. Moreover, even though there are still some residuals of the physiological influence on the INS at this frequency range, evidence has shown that this influence will enhance the INS in a non-interactional context (e.g., resting state) rather than in the interactional context (Nozawa et al., 2016). Moreover, the influence of physiological activity tends to be spatially more global and homogeneous than the neural signals (Kohno et al., 2007; Zhang, Brooks, Franceschini, & Boas, 2005). Thus, the local enhancement of the INS at 0.5–0.7 Hz is more likely to have a neural origin. This is also consistent with recent fMRI evidence indicating the neural relevance and functional contribution of higher frequency fluctuations in BOLD signals (up to 0.8 Hz) (Chen & Glover, 2015; Gohel & Biswal, 2015). Recent fMRI evidence has suggested that while low-frequency BOLD signal may reflect the general excitability (Raichle, 2011) and spatially overlapped neural networks (Smith et al., 2012), high-frequency BOLD signal may be confined to focal functions and offer a more direct and precise characterization of cognitive processes (Chen & Glover, 2015). Moreover, the temporal regions can be reliably detected with the high-frequency BOLD signal around 0.5–0.8 Hz (Gohel & Biswal, 2015). This is also consistent with the present findings that the INS at TPJ-aSTC occurred at 0.5–0.7 Hz, suggesting that the INS at this frequency range might be related to the function of TPJ-aSTC in predicting the student's semantic representations. However, as little evidence exists about the functional significance of the high frequency in the hemodynamic signal, we would refrain from drawing further conclusions. Further studies are definitely required to clarify this issue.
Finally, this study demonstrated that INS could mark knowledge transmission at a specific stage of teaching. Previous evidence indicates that INS reached significance at a very early stage when the roles of communicators were assigned a priori or emerged in the task (Jiang et al., 2015; Konvalinka et al., 2014). However, a study on teacher–student interactions found that the brain activities of teachers and students correlated at a later stage of teaching (Holper et al., 2013). In this study, the onset time of the INS increase at TPJ-TPJ appeared very early (about 1 min after the onset of teaching), which was consistent with previous findings on general communications (Jiang et al., 2015; Konvalinka et al., 2014); the onset time of the INS increase at TPJ-aSTC and aSTC-TPJ appeared late (about 2 and 8 min, respectively), which was consistent with previous findings on teaching (Holper et al., 2013). These results suggested that different types of INS might mark different aspects of teacher–student interactions, and the INS increase between TPJ and aSTC could specifically mark the quality of teaching outcome.
Together, the present findings suggest a neural mechanistic model of Prediction-Transmission for successful teaching (Figure 6). That is, a good communication between the teacher and the student should be established at the beginning of the teaching process, which might be a prerequisite for teaching (see ① of Figure 6). With a good communication, the teacher will be able to predict the students' knowledge state (see ② of Figure 6), whereby to formulate the appropriate representation of knowledge (see ③ of Figure 6). When teaching actually happens, knowledge is transmitted from the teacher to the student (see ④ of Figure 6). Finally, when knowledge is transmitted, the students' knowledge state will change accordingly, and the above processes will be repeated again. Initially, the teacher's prediction might not be successful. However, after some practice (e.g., <2 min), the prediction is improved (i.e., the INS increased significantly). Then, knowledge can be successfully transmitted from the teacher to the student (about 8 min into the process in this study).
ACKNOWLEDGMENTS
This work was supported by National Natural Science Foundation of China (31622030 and 31411130158), the Fundamental Research Funds for the Central Universities (2017EYT32 and 2017XTCX04), and the Open Research Fund of the State Key Laboratory of Cognitive Neuroscience and Learning (CNLYB1605 and CNLZD1604). The authors declare no competing financial interests.
