Relationship between structural and functional connectivity change across the adult lifespan: A longitudinal investigation
This research was carried out in whole or in part at the Athinoula A. Martinos Center for Biomedical Imaging at the Massachusetts General Hospital, using resources provided by the Center for Functional Neuroimaging Technologies, P41EB015896, a P41 Biotechnology Resource Grant supported by the National Institute of Biomedical Imaging and Bioengineering (NIBIB), National Institutes of Health. This work also involved the use of instrumentation supported by the NIH Shared Instrumentation Grant Program and/or High-End Instrumentation Grant Program; specifically, grant number(s) S10RR023401, S10RR019307, S10RR019254, S10RR023043.
Abstract
Extensive efforts are devoted to understand the functional (FC) and structural connections (SC) of the brain. FC is usually measured by functional magnetic resonance imaging (fMRI), and conceptualized as degree of synchronicity in brain activity between different regions. SC is typically indexed by measures of white matter (WM) properties, for example, by diffusion weighted imaging (DWI). FC and SC are intrinsically related, in that coordination of activity across regions ultimately depends on fast and efficient transfer of information made possible by structural connections. Convergence between FC and SC has been shown for specific networks, especially the default mode network (DMN). However, it is not known to what degree FC is constrained by major WM tracts and whether FC and SC change together over time. Here, 120 participants (20–85 years) were tested at two time points, separated by 3.3 years. Resting-state fMRI was used to measure FC, and DWI to measure WM microstructure as an index of SC. TRACULA, part of FreeSurfer, was used for automated tractography of 18 major WM tracts. Cortical regions with tight structural couplings defined by tractography were only weakly related at the functional level. Certain regions of the DMN showed a modest relationship between change in FC and SC, but for the most part, the two measures changed independently. The main conclusions are that anatomical alignment of SC and FC seems restricted to specific networks and tracts, and that changes in SC and FC are not necessarily strongly correlated. Hum Brain Mapp 38:561–573, 2017. © 2016 Wiley Periodicals, Inc.
INTRODUCTION
Understanding the brain by mapping its functional and structural connections has sparked enormous interest. Functional (FC) and structural connectivity (SC) are closely related at a conceptual level, with FC being intrinsically dependent on SC for fast and efficient transfer of information. However, it is not known to what degree FC is constrained by or related to characteristics of the major white matter (WM) tracts of the brain, that is, their microstructural properties as measured by diffusion weighted imaging (DWI), and whether FC and the microstructural properties of SC change together over time. The aim of the present study was to use longitudinal data to test this in an adult lifespan sample where participants were scanned twice, separated by 3.3 years. Here, FC is measured by functional magnetic resonance imaging (fMRI), and indexed as degree of synchronicity in brain activity between different regions when the participant is not performing any specific task in the scanner (resting-state fMRI). Resting-state functional connectivity then reflects spontaneously occurring synchronization of brain activity between distant brain areas in the absence of an externally presented task, and is typically interpreted as indexing degree of communication between these areas. SC is used to refer to diffusion characteristics of major WM tracts identified by automated tractography, not to the actual existence or absence of fiber tracts.
Several lines of evidence support a relationship between FC and SC, for example, by convergence between FC and SC of the default mode network (DMN) [Greicius et al., 2009; Horn et al., 2014; Zhu et al., 2014], and demonstrations that both FC and properties of SC differ between groups of, for example, schizophrenic patients vs. controls [Skudlarski et al., 2010; Zhou et al., 2008] and between younger and older adults [Fling et al., 2012]. Still, the relationship is complex, and regions with few or no direct structural connections can show high FC, indicating presence of indirect connections [Damoiseaux and Greicius, 2009; Honey et al., 2009]. This means that tight connections can exist also between regions not connected by major WM tracts, possibly through smaller connections not easily captured by tractography or through common connections with a third region. Nevertheless, changes in microstructural properties of major WM tracts are proposed to be a major causal factor for FC changes in aging [Ferreira and Busatto, 2013], supported by cross-sectional FC-SC correlations where higher FC are related to higher FA or lower MD or RD [Andrews-Hanna et al., 2007; Chen et al., 2009; Davis et al., 2012; Lowe et al., 2008; Teipel et al., 2010; van den Heuvel et al., 2008; Wang et al., 2009]. However, striking differences in reported age-trajectories for microstructural WM tract properties and FC indicate that the relationship is unlikely to be simple. While age has a profound effect on WM microstructure, with negative age-relationship for fractional anisotropy (FA—degree of anisotropy of diffusion of water molecules) and positive for axial (AD—longitudinal, parallel or principal diffusion), radial (RD—transverse diffusion, mean of the two minor axes of diffusion) and mean (MD—mean diffusion across all three axes) diffusivity [Bennett and Madden, 2014; Lockhart and DeCarli, 2014; Salat et al., 2005a, 2005b; Sexton et al., 2014; Westlye et al., 2010c], both positive and negative correlations between age and FC have been reported [Antonenko and Floel, 2014; Ferreira and Busatto, 2013]. Different age-trajectories for FC and WM microstructure may not be surprising, since FC and SC usually are measured from tissue classes with different macrostructural age-trajectories, that is, gray vs. white matter [Walhovd et al., 2005, 2011]. Other lines of evidence indicating a complex relationship between SC and FC are reports of higher FC associated with lower WM integrity [Hawellek et al., 2011] and that major WM tracts are conduits for smaller bundles that connect disparate functional entities [Lehman et al., 2011]. Here, high FC has been interpreted as reflecting less-differentiated patterns of neural activity, reduced cognitive efficiency, or anatomical disconnectivity leading to loss of functional diversity among brain networks. For instance, lack of differentiation has been proposed as a possible result of loss of flexibility in the brain's functional interactions, so that stronger apparent functional connectivity could result from degradation of structural connections due to specific regions more frequently participating in prevalent patterns of global activity seen, for example, in DMN [Hawellek et al., 2011].
Further, several cross-sectional developmental studies either did not observe strong relationships between microstructural WM properties and FC, or found that the relationships could change during development [Gordon et al., 2011; Uddin et al., 2011]. For instance, one study of the default mode network (DMN) found that FC in children aged 7 to 9 years could reach adult-like levels despite weak SC [Supekar et al., 2010].
To examine the relationship between FC and microstructural properties of major WM tracts at an individual level, we measured FC and WM diffusion characteristics at two time points separated by 3.3 years on average in 120 participants, and tested whether they (a) related similarly to age, and (b) to what extent change in one connectivity measure was related to change in the other. We hypothesized partly different age-relationships for SC vs. FC, with negative (FA) and positive (MD, RD, AD) relationships for SC, accelerating in the last part of the age-range, and a negative but weaker relationship for FC. Such changes may be related to myelin disruption or loss, axonal injury or other processes, but the exact neurobiological underpinnings still are controversial [see Sexton et al., 2014], for a more thorough review, see [Bennett and Madden, 2014]. Longitudinally, we hypothesized that changes in SC and FC would be moderately related, especially within the DMN. As these diffusion metrics are regarded as related to the integrity of the WM tracts, changes in them would entail that changes can also be expected in FC.
MATERIALS AND METHODS
Sample
The longitudinal sample was drawn from the ongoing project Cognition and Plasticity through the Lifespan at the Center for Lifespan Changes in Brain and Cognition (LCBC), Department of Psychology, University of Oslo [Storsve et al., 2014; Walhovd et al., 2014; Westlye et al., 2010a, 2010b]. All procedures were approved by the Regional Ethical Committee of Southern Norway, and written consent was obtained from all participants. For the first wave of data collection, participants were recruited through newspaper ads. Recruitment for the second wave was by written invitation to the original participants. At both time points, participants were screened with a health interview. Participants were required to be right handed, fluent Norwegian speakers, and have normal or corrected to normal vision and normal hearing. At both time points, exclusion criteria were history of injury or disease known to affect central nervous system (CNS) function, including neurological or psychiatric illness or serious head trauma, being under psychiatric treatment, use of psychoactive drugs known to affect CNS functioning, and MRI contraindications. Moreover, participants were required to score ≥26 on the Mini Mental State Examination (MMSE) [Folstein et al., 1975], have a Beck Depression Inventory (BDI) [Beck and Steer, 1987] score ≤16, and obtain a normal IQ or above (IQ ≥ 85) on the Wechsler Abbreviated Scale of Intelligence (WASI) [Wechsler, 1999]. At both time points scans were evaluated by a neuroradiologist and were required to be deemed free of significant injuries or conditions. At follow-up, an additional set of inclusion criteria was employed: MMSE change from time point one to time point two < 10%; California Verbal Learning Test II – Alternative Version (CVLT II) [Delis et al., 2000] immediate delay and long delay T-score > 30; CVLT II immediate delay and long delay change from time point one to time point two < 60%.
Two hundred and eighty-one participants completed time point 1 (Tp1) assessment. For the follow-up study, 42 opted out, 18 could not be located, 3 did not participate due to health reasons (the nature of these were not disclosed), and 3 had MRI contraindications, yielding a total of 66 dropouts (35 females, mean (SD) age = 47.3 (20.0) years). Detailed dropout characteristics are published elsewhere [Storsve et al., 2014]. Of the 215 participants that completed MRI and neuropsychological testing at both time points, 8 failed to meet one or more of the additional inclusion criteria for the follow-up study described above, 4 did not have adequately processed diffusion MRI data, and 2 were outliers (4 or more tracts showing change values >6 SD from mean). This resulted in a follow-up sample of 201 participants (118 females) aged 20–84 years at Tp1, see [Storsve et al., 2014; Walhovd et al., 2014]. Age-effects on the DTI measures in these participants have previously been published [Sexton et al., 2014]. Of these, resting-state fMRI was not acquired for the first 81, yielding a sample of 120 with quality checked functional MRI data and 117 with quality checked segmented diffusion imaging data for both time points. The resting-state Functional Connectivity (rsFC) data in relation to aging has been described in a previous publication. Due to previous reports showing different rsFC change-patterns in younger and middle-aged vs. older participants [Fjell et al., 2015, 2016b], for some analyses, the sample was split in two age-groups. Sample descriptives are provided in Table 1, with information about sex distribution across 10 year age bins provided in Supplemental Table 1.
| Young & middle-aged | Older adults | Sig | |
|---|---|---|---|
| N | 64 | 56 | |
| Age | 32.9 (23–52) | 71.6 (63–86) | a |
| Sex (females/males) | 40/24 | 29/27 | |
| Education | 15.9 (12–23) | 16.5 (8–26) | |
| IQ | 119 (101–133) | 120 (90–146) | |
| MMSE | 29.6 (27–30) | 29.0 (26–30) | a |
| Follow-up interval | 3.4 (2.7–4.0) | 3.1 (2.8–3.8) | a |
- Age, IQ, and MMSE values from Tp2, education from Tp1. Mean (range) values are provided.
- a P < 0.05.
MRI Acquisition and Analysis
Imaging data was collected using a 12-channel head coil on a 1.5 T Siemens Avanto scanner (Siemens Medical Solutions; Erlagen, Germany) at Rikshospitalet, Oslo University Hospital. The same scanner and sequences were used at both time-points. The pulse sequences used had the following parameters:
For structural segmentation: The pulse sequence used for morphometric analyses included two repetitions of a 160 slices sagittal T1-weighted magnetization prepared rapid gradient echo (MPRAGE) sequences with the following parameters: repetition time(TR)/echo time(TE)/time to inversion(TI)/flip angle(FA)= 2,400 ms/3.61 ms/1,000 ms/8°, matrix = 192 × 192, field of view (FOV) = 240, voxel size = 1.25 × 1.25 × 1.20 mm, scan time 4 min 42 s.
For structural connectivity: Diffusion-weighted MRI (dMRI) was performed using a single-shot twice-refocused spin-echo echo planar imaging pulse sequence optimized to minimize eddy current-induced distortions (Reese et al., 2003) (primary slice direction, axial; phase encoding direction, columns; repetition time, 8,200 ms; echo time, 82 ms; voxel size, 2.0 mm isotropic; number of slices, 64; FOV, 256; matric size, 128 × 128 × 64; b value, 700 s/mm2; number of diffusion encoding gradients directions, 30; number of b = 0 images, 10; number of acquisitions, 2). Acquisition time was 11 min 21 s.
For functional connectivity: The resting-state BOLD sequence included 28 transversally oriented slices (no gap), measured using a BOLD-sensitive T2*-weighted EPI sequence (TR = 3,000 ms, TE = 70 ms, FA = 90°, voxel size = 3.44 × 3.44 × 4 mm, FOV = 220, descending acquisition, GRAPPA acceleration factor = 2), producing 100 volumes and lasting for ∼5 min. Three dummy volumes were collected at the start to avoid T1 saturation effects. Since the baseline data were acquired some time ago, a 1.5 T scanner and a BOLD scan consisting of 100 volumes was used. To assess the comparability of the results with data from the now more commonly used 3 T scanners and longer scanning sequences, 44 young participants were scanned both on the 1.5 T scanner with 100 volumes, and on a 3 T scanner with 150 volumes on the same day. Previously reported validation analyses [Fjell et al., 2016a] demonstrated excellent convergence between network structure detected across 1.5 and 3 T scanners and 100 vs. 150 volumes
Surface reconstruction and subcortical labeling were performed at the Neuroimaging Analysis Laboratory, Research Group for Lifespan Changes in Brain and Cognition, Department of Psychology, University of Oslo. Morphometry analyses were performed by use of FreeSurfer v. 5.1 (http://surfer.nmr.mgh.harvard.edu/) [Dale et al., 1999; Fischl and Dale, 2000; Fischl et al., 1999, 2002], please see a detailed account elsewhere [Storsve et al., 2014; Walhovd et al., 2014]. All volumes were inspected for accuracy and minor manual edits were performed when needed by a trained operator on the baseline images, usually restricted to removal of nonbrain tissue included within the cortical boundary. For dMRI analyses, TRActs Constrained by UnderLying Anatomy (TRACULA), part of FreeSurfer v.5.3 was used to delineate major WM tracts of interest [Yendiki et al., 2011]. This is a novel algorithm for automated global probabilistic tractography that estimates the posterior probability of each pathway given the dMRI data. The posterior probability is decomposed into a data likelihood term, which uses the “ball-and-stick” model of diffusion [Behrens et al., 2007], and a pathway prior term, which incorporates prior anatomical knowledge on the pathways from a set of training subjects. The segmentation labels required by TRACULA were obtained by processing the T1-weighted images of the study subjects with the automated cortical parcellation and subcortical segmentation tools in FreeSurfer [Fischl et al., 2002, 2004a,b]. We used the longitudinal version of TRACULA, which computes the joint posterior probability of each pathway given the dMRI data and anatomical segmentations of both time points at once. This has been shown to improve both test-retest reliability and sensitivity to longitudinal WM changes, when compared to reconstructing the pathways at each time point independently [Yendiki et al., 2016]. All pathways reconstructed by TRACULA were included in the analyses, that is, in each hemisphere the anterior thalamic radiation (ATR), the cingulum angular bundle (CAB), cingulum–cingulate gyrus bundle (CCG), the corticospinal tract (CST), the inferior longitudinal fasciculus (ILFT), superior longitudinal fasciculus-temporal part (SLFT) and parietal part (SLFP) and the uncinate fasciculus (UNC), in addition to the two commissural tracts forceps major (Fmaj) and minor (Fmin). Tracts and tract endings, averaged over all participants in the study, are illustrated in Figure 1 [Fjell et al., 2016b]. For some participants, specific tracts were not reliably identified by Tracula (TRActs Constrained by UnderLying Anatomy), that is, CST (8 missing), Fmaj (6 missing), ATR right (1 missing), SLFP right (2 missing), SLFT right (1 missing), and UNC right (1 missing).
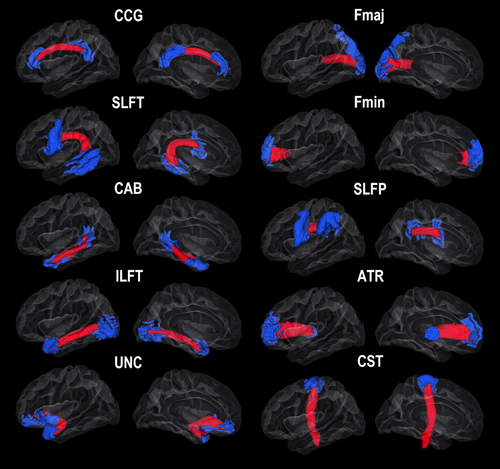
Tracts of interest and corresponding surface seed regions. Reconstructed mean pathways and endpoints in the left hemisphere. For abbreviations, please see the main text.
Resting-state functional imaging data was preprocessed following Center for Lifespan Changes in Brain and Cognition's custom analysis stream. Images were motion corrected, slice timing corrected, and smoothed (5 mm FWHM) in volume space using FSL's FMRI Expert Analysis Tool (FEAT; http://fsl.fmrib.ox.ac.uk/fsl/fslwiki). Then, FSL's Multivariate Exploratory Linear Optimized Decomposition into Independent Components (MELODIC) was used in combination with FMRIB's ICA-based Xnoiseifier (FIX) to auto-classify independent components into signal components (brain activity) and noise components (e.g., motion, nonneuronal physiology, scanner artefacts) and remove these noise components from the 4D fMRI data [Salimi-Khorshidi et al., 2014]. The FIX classifier was not trained on the actual data, but the standard classifier was used. To ensure that this did not bias the data, we compared the performance of the standard classifier with a classifier trained on actual data using a dataset of our own, consisting of 32 adults between 18 and 80 years. Using the classifier trained on the data, performance was 94.7% for signal components detected as signal and 82.6% for noise components detected as noise. In comparison, the standard classifier performed at 91.6% and 74.3%, respectively. Further cleaning of data was also performed. FreeSurfer-defined individually estimated anatomical masks of cerebral white matter (WM) and cerebrospinal fluid/lateral ventricles (CSF) were resampled to each individual's functional space. All anatomical voxels that “constituted” a functional voxel had to be labeled as WM or CSF for that functional voxel to be considered a functional representation of noncortical tissue. Average time series were then extracted from (FIX-cleaned) functional WM- and CSF-voxels, and were regressed out of the FIX-cleaned 4D volume together with a set of 24 motion parameters estimated during preprocessing (rigid body, their temporal derivatives, and the squares of all 12 resulting regressors). The WM and CSF confound regressors were extracted from FIX-cleaned data, and thus have the FIX cleanup applied. Following recent recommendations about noise removal from resting-state data [Hallquist et al., 2013] we band-pass filtered the data (0.009–0.08 Hz) after regression of the confound variables representing signal from WM- and CSF-voxels and the motion parameters.
Individually estimated TRACULA tract endings were converted to FreeSurfer's average surface space and averaged to produce seed points for calculation of rsFC between tract endings. The tracts and endpoints were thresholded at 10% before registering to FreeSurfer's standard template cortical surface (fsaverage) and summed. The endpoints were projected to the surface by sampling 4 mm on each side of the surface and smoothed by FWHM of 2 mm. The labels were expanded into underlying GM, and the top 25% of the summed vertices and voxels are displayed in Figure 1.
This group-representative set of seeds were resampled into each participant's surface space. All conversions of seeds from FreeSurfers' fsaverage surface space to individual surface space was performed using nonlinear surface-based registration parameters automatically calculated during FreeSurfer's recon-all stream. The resulting individualized tract endings were converted into functional volume space using a projection factor of 0.5 from the estimated white/gray matter boundary (i.e., half way into the cortical sheet). rsFC between tract endings was calculated as the average correlation between all preprocessed voxel time series in two seeds, each correlation being variance-stabilized using the Fisher z-transformation [Silver and Dunlap, 1987].
To calculate rsFC within established cortical functional networks, we took advantage of Yeo and colleagues' (2011) cortical parcellation estimated by intrinsic functional connectivity from 1,000 participants and made available in FreeSurfer's average surface space (http://surfer.nmr.mgh.harvard.edu/fswiki/CorticalParcellation_Yeo2011). The parcellation scheme consists of 17 networks in each hemisphere as well as values representing the estimated confidence of each surface vertex belonging to its assigned network. Spheres (six dilations around center vertex; 127 vertices) were drawn on the average surface around each network's highest confidence vertex (vertices if a network consisted of several disconnected segments), resampled into individual subject space, and correlated following similar routines as for the tract ending analyses. This resulted in rsFC estimates for each of the 17 networks (mean across hemispheres) for each participant.
Statistical Analyses
For all analyses where relevant, age at time point 1, head motion at both time points during BOLD and dMRI scanning and interval between scans were included as covariates of no interest. First, to delineate the relationship between each connectivity measure and age, mean FA, MD, RD, DA, and FC across all tracts, were computed. Generalized Additive Mixed Models (GAMM), implemented in R (www.r-project.org) using the package “mgcv” [Wood, 2006], were used to map the age-trajectories of each measure based on longitudinal and cross-sectional observations, run through the PING data portal [Bartsch et al., 2014]. A smoothing term for age was compared to linear age models, and the
Akaike Information Criterion (AIC) [Akaike, 1974] and the Bayesian Information Criterion (BIC) were used to guide model selection and help guard against over-fitting. GAMM takes advantage of both cross-sectional and longitudinal information, and by use of the smoothing term for age, is able to model any trajectory—linear or nonlinear—of any form. An important point is that there are no explicit assumptions about the shape of the relationships that are modeled, with nonparametric fits with relaxed assumptions on the actual relationship between age and the connectivity variable.
Next, mean FC between tract ending regions were averaged across time points (within-tract FC), and compared to FC between each tract ending region and all other tract ending regions (between-tract FC) by paired-samples t-tests. Mean values across time points were used in these analyses to increase reliability compared to using a single time point for the analyses.
Further, longitudinal changes in connectivity (FC and SC measures) were quantified as the difference between time points. To test the relationship between tract-wise changes in structural and functional connectivity, within-tract FC change was correlated with tract-wise changes in diffusion parameters (FA, MD, RD, AD). This was done for each of the tracts (8 in each hemisphere and two commissural). We chose this procedure instead of the Generalized Additive Mixed Models (GAMM) approach for these analyses to ensure that the results were caused by purely longitudinal change and not being influenced by cross-sectional effects. Correlations were also run between diffusion change and between tract FC change to allow testing specificity of connectivity relationships.
In addition to calculating FC from seed regions based on structurally defined tracts, we also used the opposite approach of quantifying FC in pre-established and well-validated functional networks of high FC [Yeo et al., 2011]. Change across time points was calculated for all networks, and correlated with dMRI change as described above.
Results were corrected for multiple comparisons by Bonferroni corrections. Since the Bonferroni correction is too conservative when outcome variables are mutually correlated, a corrected alpha is required. The corrected α-threshold was adjusted as a function of the correlations between the dependent variables (http://www.quantitativeskills.com/sisa/calculations/bonfer.htm) [Perneger, 1998; Sankoh et al., 1997], using the triangular matrix (without the diagonal) of the correlations between the outcome variables, sum the correlations and divide the result by the number of correlations used.
RESULTS
Relationships to Age
First, the summary measures of cross-sectional FA, MD, RD, DA, and FC, calculated as the mean value of all tracts, were mapped to age by GAMM. Using a linear model, all connectivity measures were significantly related to age (FA t = −6.39, P < 0.0001; MD t = 7.01, P < 0.0001; RD t = 7.47, P < 0.0001; AD t = 4.06, P < 0.0001; FC t = −3.32, P < 0.002). To test for nonlinearity, we replaced the linear term by a smoothing term for age. The fit lines in Figures 2 and 3 indicated an accelerated increase in MD, RD, and AD with age, and a tendency for accelerated reduction of FA among the oldest. FC appeared mostly linearly related to age. For MD, RD and AD, the smooth term yielded clearly lower AIC and BIC values (> 19 points), indicating that a nonlinear age-function best described the data. For FA and FC, the AIC and BIC values did not indicate that the nonlinear term yielded a better fit to the data.
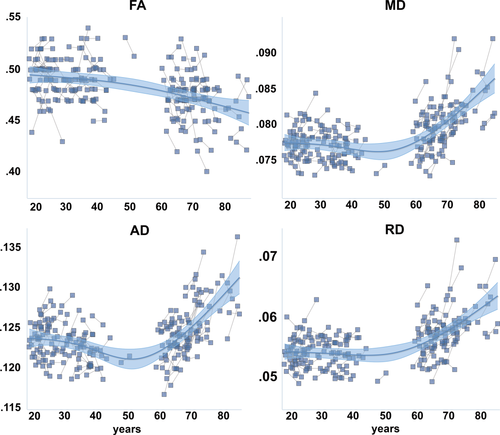
Age-trajectories for structural connectivity. Generalized Additive Mixed Models with a smooth term for age were used to delineate the relationship between the global diffusion tensor imaging measures and age, taking advantage of both the cross-sectional and the longitudinal observations. The shaded area around the fit line represents 95% confidence interval of the mean.
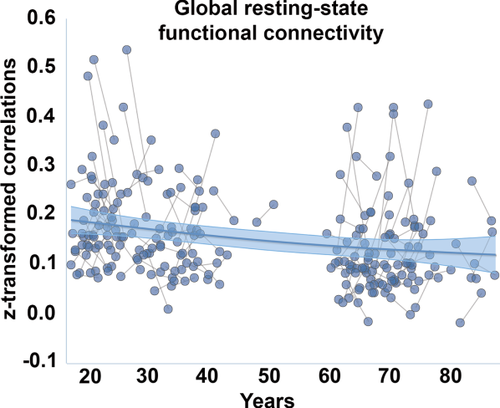
Age-trajectories for functional connectivity. Generalized additive mixed model with a smooth term for age was used to delineate the relationship between the global resting-state functional connectivity (FC) measure and age, taking advantage of both the cross-sectional and the longitudinal observations. The shaded area around the fit line represents 95% confidence interval of the mean.
Convergence of Overall Structural-Functional Connectivity Structure
FC between regions representing the ends of each tract was calculated (within tract), and compared with FC between each tract ending region and all other tract ending regions (between tract). FC was averaged across time-points and hemispheres. The results are shown in Table 2. Of 10 tracts, higher FC was seen for within vs. between tract for five tracts (CCG, Fmaj, Fmin, SLFP, SLFT), while higher between-tract FC was seen for the other five tracts (ATR, CAB, CST, ILF, UNC). The correlations between FC within vs. between tracts were high, with a median r of 0.91–0.94.
| Within-tract rsFC | Between-tract rsFC | |||||
|---|---|---|---|---|---|---|
| Tract | Mean | SD | Mean | SD | P | r |
| Anterior thalamic radiation | 0.09 | 0.08 | 0.11 | 0.07 | a | 0.86 |
| Cingulum angular bundle | 0.08 | 0.06 | 0.11 | 0.07 | a | 0.87 |
| Cingulum–cingulum gyrus | 0.27 | 0.13 | 0.18 | 0.10 | a | 0.95 |
| Corticospinal tract | 0.09 | 0.07 | 0.13 | 0.08 | a | 0.88 |
| Forceps major | 0.31 | 0.16 | 0.17 | 0.09 | a | 0.90 |
| Forceps minor | 0.22 | 0.11 | 0.15 | 0.09 | a | 0.94 |
| Inferior long fasciculus | 0.13 | 0.09 | 0.14 | 0.08 | a | 0.94 |
| Superior long fasciculus, parietal | 0.23 | 0.14 | 0.16 | 0.10 | a | 0.98 |
| Superior long fasciculus. temporal | 0.15 | 0.10 | 0.14 | 0.09 | a | 0.97 |
| Uncinate | 0.09 | 0.06 | 0.10 | 0.06 | a | 0.91 |
- a Mean rsFC (z transformed correlations) different for within vs. between tracts (P < 0.05).
- r: Correlation between rsFC “within” vs. “between” tracts, that is, the rsFC between the endpoints of a given tract (“within”) vs. the endpoints of all other tracts (“between”).
Relationship Between Tract-Wise Changes in Structural and Functional Connectivity
For each of the tracts (eight in each hemisphere and two commissural), FC changes within and between tracts were correlated with tract-wise changes in diffusion parameters (FA, MD, RD, AD), controlling for age, motion at both time points and interval between scans. 10 correlations at P < 0.05 uncorrected, ranging between 0.19 and 0.24 were found, but none of these survived Bonferroni corrections for number of comparisons.
Relationship Between Network-Wise Changes in Structural and Functional Connectivity
In the tract-based analyses, DTI-based tractography was used as basis for selecting FC ROI seeds. We also chose the opposite approach by measuring FC in 17 pre-established networks [Yeo et al., 2011]. For all networks, significantly higher within than between FC was observed (all Ps < 10 × 10−17), validating the established networks from an independent sample [Yeo et al., 2011] in the present data (Table 3). As can be seen, FC was much higher when a network-approach was used compared to a tract approach. This further underscores the finding that high FC is not given for regions connected by high degree of SC.
| Within-network FC (z) | Between-network FC (z) | |||||
|---|---|---|---|---|---|---|
| Network | Mean | SD | Mean | SD | P | r |
| NW 1 | 0.88 | 0.37 | 0.36 | 0.19 | a | 0.61 |
| NW 2 | 1.11 | 0.41 | 0.45 | 0.20 | a | 0.75 |
| NW 3 | 0.72 | 0.38 | 0.42 | 0.22 | a | 0.81 |
| NW 5 | 0.84 | 0.30 | 0.40 | 0.20 | a | 0.62 |
| NW 6 | 0.56 | 0.24 | 0.38 | 0.19 | a | 0.89 |
| NW 7 | 0.66 | 0.26 | 0.39 | 0.21 | a | 0.90 |
| NW 8 | 0.52 | 0.23 | 0.36 | 0.19 | a | 0.91 |
| NW 9 | 0.31 | 0.27 | 0.24 | 0.17 | a | 0.70 |
| NW 11 | 0.78 | 0.25 | 0.38 | 0.18 | a | 0.74 |
| NW 12 | 0.53 | 0.23 | 0.36 | 0.19 | a | 0.92 |
| NW 13 | 0.57 | 0.23 | 0.35 | 0.19 | a | 0.88 |
| NW 14 | 0.60 | 0.34 | 0.39 | 0.21 | a | 0.76 |
| NW 15 | 0.76 | 0.23 | 0.40 | 0.18 | a | 0.78 |
| NW 16 | 0.73 | 0.21 | 0.38 | 0.18 | a | 0.84 |
| NW 17 | 0.61 | 0.22 | 0.35 | 0.19 | a | 0.81 |
- The cerebral cortex was parcellated according to a 17 networks scheme [Yeo et al., 2011], and FC was calculated within and between networks. Two networks (NW 4 and NW 10) exists in lefts hemisphere only, and was omitted from the analyses.
- a Mean rsFC different for within vs. between networks (P < 0.05).
- r: Correlation between rsFC “within” vs. “between” networks.
FC change across time points and hemispheres was calculated for all networks, and correlated with SC change for each tract, controlling for age, motion at both time points and interval between scans. The total number of tests performed was 17 networks × 18 tracts × 4 diffusion measures, adding up to 1,224 tests. However, the intercorrelations between FC change across tracts (r ≈ 0.4), SC change across tracts (r ≈ 0.3) and FA/MD/RD/AD across tracts (r ≈ 0.6) indicate that the Bonferroni correction threshold should be adjusted. With an approximated median correlation of 0.45 between dependent variables, this would yield an adjusted Bonferroni correction level of P < 0.001. According to this threshold, the correlations between Network 11 and MD (r = 0.35) and RD (r = 0.32) change in left CCG survived corrections (Fig. 4).
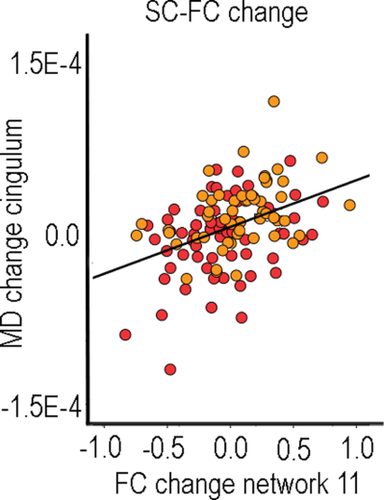
Relationship between longitudinal structural and functional connectivity change. Scatterplot of the relationship between change in MD (Tp2 – Tp1) in the left cingulate-cingulate gyrus and change in FC in Network 11 (precuneus and isthmus of the cingulate) (Tp2 – Tp1). Red circles indicate young and middle-aged participants (23–52 years) and yellow circles indicate older participants (63–86 years). The line is fitted to the total sample.
DISCUSSION
The results confirm the hypothesis that structural connectivity and microstructural properties of major WM tracts relate differently to age. Further, within-tract FC was low, and in general not higher than between-tract FC, indicating loose constraints on FC from microstructural properties of WM tracts. Direct tests of the relationship between change in WM microstructure and FC measures confirmed that they were weakly related at best. However, calculation of FC in predefined networks based on FC alone yielded two significant FC-SC change relationships in the DMN, in line with some previous cross-sectional investigations [Greicius et al., 2009; Horn et al., 2014]. The direction of the relationships—increased FC with increased MD and RD—was not expected.
Relationships to Age
The age-trajectories for WM microstructure and FC were not very similar. Reduced FA and increased MD, RD, and AD with higher age, accelerating in the last part of the age-span for MD, RD, and AD, are established in previous literature [Bennett and Madden, 2014; Lockhart and DeCarli, 2014; Salat et al., 2005a, 2005b; Westlye et al., 2010c ], including a previous report on a sample overlapping the present where a voxel-based approach was used [Sexton et al., 2014]. These curves fit reasonably well with trajectories for WM volume [Fjell et al., 2013; Walhovd et al., 2005, 2011] and cortical myelin content [Grydeland et al., 2013]. Thus, different measures of WM properties seem to share some commonalities in their age-relationships. In contrast, convergence has not been reached regarding the age-trajectories of FC. Both reduced and increased FC with age have been reported [Andrews-Hanna et al., 2007; Antonenko and Floel, 2014; Ferreira and Busatto, 2013; Geerligs et al., 2014; Mowinckel et al., 2012; Sala-Llonch et al., 2014], often within the same study, indicating network-specific effects. We found a moderate negative effect of age on FC across tracts, with a basically linear trend. This fits with a previous report [Fjell et al., 2015] from the same sample where age-effects were tested across the 17 established functional networks defined by Yeo et al. [Yeo et al., 2011]. In that study, the direction of age-effects did not vary across networks, indicating that the summary measure used in the present article is valid for testing age-effects.
Discrepancies in age-trajectories between FC and WM microstructure could stem from the two measures being derived from different tissue classes affected differently by age. In contrast to the inverse U-shaped age-relationships of WM, aging-studies of different GM properties, such as thickness, volume, area, and curvature, all show negative and often rather linear relationships with age [Fjell et al., 2014; Grydeland et al., 2013; Hogstrom et al., 2013; Salat et al., 2004; Storsve et al., 2014]. The age-trajectories of these different WM vs. GM measures could transfer over to SC vs. FC. One problem with this explanation is that FC-relationships often are reported to be independent of structural GM properties [Damoiseaux et al., 2008; Mowinckel et al., 2012; Onoda et al., 2012]. Regardless of the neurobiological foundation, FC and SC related differently to age, indicating that they are at least partly independent measures.
Convergence of Overall Structural-Functional Connectivity Structure
In a benchmark study, Greicius et al. defined DMN based on FC data, and then performed DTI-based tractography from the identified nodes [Greicius et al., 2009]. The results showed good correspondence between FC and SC. Recently, Horn et al. used a voxel-based anatomically unconstrained approach. They found weak relationships between FC and SC, except in regions associated with the DMN [Horn et al., 2014]. The convergence of SC and FC is not straightforward, with regions of few or no direct structural connections in some cases still showing high FC, which could mean that FC in these cases is not mediated by direct structural connections [Damoiseaux and Greicius, 2009; Honey et al., 2009]. Lehman et al. used macaques to show that major WM tracts are conduits for many smaller sub-bundles that connect different end regions [Lehman et al., 2011]. For instance, the uncinate not only connects the ventral prefrontal cortex (vPFC) and the temporal lobe but also different vPFC regions and indirectly the ventral and dorsal PFC by merging with other WM bundles. Thus, when we segment and measure the major WM pathways, these include axons from different regions of the cortex supporting widely different cognitive functions. We did not observe consistently higher FC for within-tract compared to between-tract regions, indicating that the level of detail in the projected cortical regions may be too course to disentangle specific functional and structural subentities. For some tracts, like ATR and CST, the low FC is likely also caused by one tract ending being situated in subcortical regions. On the positive side, the four instances of FC exceeding z = 0.2 were found within-tract (CCG, Fmaj, Fmin, and SLFP), with lower FC (z < 0.2) for all other tracts. Thus, there was some convergence between SC and FC on the level of cortical anatomy, but the generally low FC indicated that SC only very weakly constrained FC. This is in line with a recent cross-species study finding poor correspondence in connectivity from four different imaging modalities [Reid et al., 2015]. In some respects, it can be argued that SC has a clearer biological basis in the brain than FC, as structural connections can be observed with the naked eye based on MR images or autopsy samples. In contrast, FC represents a statistical property inferred from covariance between brain regions that may not be directly connected at all.
Relationship Between Changes in WM Tract Microstructure and Functional Connectivity
There is a paucity of previous reports of FC-SC-change relationships, but several previous cross-sectional studies have reported positive FC-SC correlations [Andrews-Hanna et al., 2007; Chen et al., 2009; Davis et al., 2012; Lowe et al., 2008; Teipel et al., 2010; van den Heuvel et al., 2008; Wang et al., 2009]. However, there are also reports of higher FC being associated with lower WM integrity [Fling et al., 2012; Hawellek et al., 2011]. We calculated FC change using the two different seed-based approaches, either defined by dMRI-based tractography or based on a well-validated network parcellation approach by use of FC data only [Yeo et al., 2011]. Using the tract approach, FC and WM microstructural property changes were weakly related. Selecting seed regions based on major WM tract endings yielded low FC, possibly causing less reliable change measures. Thus, we also used a network approach, yielding significantly higher within- than between-network FC. Now several correlations satisfied the uncorrected exploration threshold of P < 0.01, and two also survived corrections: MD and RD change in CCG and FC change in Network 11 (isthmus cingulate-precuneus). This is likely due to these structures' critical involvement in the DMN [Greicius et al., 2009; Horn et al., 2014]. However, FC changes in other typical DMN regions did not correlate with SC changes in relevant tracts.
Contrary to our expectations, increases in RD and MD were related to relative increase in FC, although similar findings have occasionally been reported in cross-sectional studies [Fling et al., 2012; Hawellek et al., 2011]. Increased FC in risk groups, such as Alzheimer disease patients, has been reported [Adamczuk et al., in press; Agosta et al., 2012; Lim et al., 2014], often interpreted as a compensatory response to negative brain events. One speculation is thus that relative increase of isthmus cingulate-precuneus FC is a response to reduced integrity of the CCG. If so, we would expect a mixture of relationships in opposite directions in different networks. Contrary to this, most correlations were in the same direction, that is, positive FC–MD/RD and negative FC—FA. A compensation account would need compelling evidence, and may not be relevant for the present findings.
Highest FC-WM tract-change correspondence was found when based on FC-derived, not tract-derived, seed regions. This may be related to high FC sometimes being found between regions with little or no direct structural connections [Damoiseaux and Greicius, 2009; Honey et al., 2009]. Also, as discussed above, the large tract endings are likely encapsulating several functionally distinct cortical regions projecting through the same major tracts. Thus, FC is not constrained by dMRI tractography to a degree that ensures high FC between regions that connects through the same major WM tract (Fig. 1).
Limitations
The test–retest reliability of resting-state FC is not always high, with test–retest reliability ranging from low to high [Braun et al., 2012; Ferreira and Busatto, 2013; Meindl et al., 2010; Shehzad et al., 2009]. Thus, in the FC change—WM microstructure change analyses, some of the variance will be related to lack of reliability, which will naturally lower the correlations observed. We do not know whether the used 3.5 year interval is sufficient to enable the real changes in brain connectivity to exceed the noise due to less than perfect test-retest reliability, although at least for WM microstructure, this should be sufficient [Sexton et al., 2014]. The issue of test-retest reliability will naturally apply in some extent to any study of FC change-relationships, and should ideally be tested in each study to allow estimation of the impact of this source of error. Related, an ex vivo primate study showed limited anatomical accuracy for tractography methods, also potentially lowering the FC-WM microstructure relationships [Thomas et al., 2014]. Further, the low sampling density in the age-range 50–60 years is not ideal in an adult life-span perspective. Also, since we only had two time points, only linear change could be measures. However, it is possible that nonlinear relationships between FC and WM microstructure exist, which would not be captured by the current analyses. Finally, we used two different approaches to test convergence between FC and SC: calculations of FC between WM tract endings, and correlations between WM microstructure changes and changes in FC based on the established Yeo et al. parcellation scheme [Yeo et al., 2011]. However a third option was not attempted—to do structural tractography using the regions from the Yeo parcellation as seed points. This could potentially have yielded better correspondence between FC and WM microstructural changes.
CONCLUSION
Regions with tight structural couplings, as indexed by dMRI tractography, were generally weakly related in terms of FC as measured by rs-fMRI. The longitudinal analyses showed that the relationship between WM microstructure and FC change was strongest for regions of the DMN, and weakest when the FC measures were constrained by SC measures. Anatomical alignment of structural and functional connectivity measures seemed restricted to specific networks and tracts, and convergence at the aggregate level of anatomical organization did not entail that changes in WM microstructure and FC necessarily were correlated. It is possible that relationships between WM tract properties and FC are stronger in other populations, but the present results indicate weak relationships in healthy participants across the adult life-span.
CONFLICT OF INTEREST
The authors declare no competing financial interests.