Fact learning in complex arithmetic and figural-spatial tasks: The role of the angular gyrus and its relation to mathematical competence
Abstract
Neuroimaging studies have revealed a strong link between mental calculation and the angular gyrus (AG) which has been interpreted to reflect arithmetic fact retrieval. Moreover, a stronger AG activation in individuals with higher mathematical competence has been reported. The present fMRI study investigates the specificity of the AG for arithmetic fact learning and the interplay between training and mathematical competence on brain activation. Adults of lower and higher mathematical competence underwent a five-day training on sets of complex multiplication and figural-spatial problems. In the following fMRI test session, trained and untrained problems were presented. Similar training effects were observed in both problem types, consisting of AG activation increases bilaterally and wide-spread activation decreases in frontal and parietal regions. This finding indicates that the AG is not specifically involved in the learning of arithmetic facts. Competence-related differences in the AG only emerged in untrained but not in trained multiplication problems. The relation between AG activation and mathematical competence in arithmetic problem solving therefore seems to be due to differences in arithmetic fact retrieval which can be attenuated through training. Hum Brain Mapp 2009. © 2009 Wiley-Liss, Inc.
INTRODUCTION
Successful learning of arithmetic skills is an essential step in the development of mathematical competence and consists in the acquisition of knowledge about arithmetic facts, calculation algorithms, and mathematical key concepts. Numerous behavioural studies have investigated this long-term learning process and revealed age and competence-related changes in the involved cognitive processes and problem solving strategies. For instance, it has been repeatedly shown that preschool children solve arithmetic problems predominantly by applying effortful and slow procedural strategies such as counting, whereas older children and adults more strongly rely on effortless and fast retrieval of arithmetic facts (such as the multiplication tables) from memory [Ashcraft,1982; Bisanz et al.,2005; Campbell and Xue,2001; Siegler,1988]. How this process of arithmetic skill acquisition is reflected in the brain has only recently moved into the focus of neuroimaging research [e.g., Delazer et al.,2005; Ischebeck et al.,2007; Rivera et al.,2005; Delazer et al.,2003] and is still a developing field with many open questions remaining [cf. Ansari,2008]. The aim of the present study is to provide further insights into the cerebral correlates of arithmetic fact learning and into the relationship between brain activation patterns and individual differences in the level of mathematical competence.
The first brain imaging study on arithmetic problem solving was conducted by Roland and Friberg [1985] who used single photon emission tomography to measure regional changes in cerebral blood flow. They had participants perform an arithmetic task (subtraction), as well as a verbal, and a spatial task and observed widespread fronto-parietal blood flow increases in all three tasks compared with rest. In comparing the three cognitive tasks, areas of exclusive activation emerged which were located in the angular gyrus bilaterally during subtraction, in the right mid-temporal cortex during the verbal task, and in inferior temporal, superior parietal, and occipital cortices while working on the spatial task. On the basis of neuropsychological studies showing that lesions in the angular gyrus are often accompanied by arithmetic deficits [e.g., Gerstmann,1940; Henschen,1919], the authors concluded that the blood flow increase in the angular gyri “was due to the retrieval of the memory for subtraction and integers that, at least partly, must have been located here” (p. 1241).
Subsequent fMRI studies have corroborated Roland and Friberg's finding of a strong link between the angular gyrus and mental calculation and have also shed some light on the functional significance of this brain area for mental arithmetic [Cowell et al.,2000; Dehaene et al.,1999; Delazer et al.,2003,2005; Ischebeck et al.,2007; Lee,2000; Menon et al.,2000a,b; Prabhakaran et al.,2001; Stanescu-Cosson et al.,2000; Venkatraman et al.,2006; Zago and Tzourio-Mazoyer,2002]. An influential study in this context was conducted by Dehaene et al. [1999]. They required participants to solve simple addition tasks in an exact (indicate correct solution) or an approximate condition (indicate which of two numbers is closer to the solution) and found that bilateral parietal regions around the intraparietal sulcus (IPS) showed greater activation for approximate calculation, whereas the left inferior frontal cortex and the angular gyrus were more strongly engaged in the exact condition. They concluded that approximate arithmetic relies on quantity representations located in visuo-spatial regions of the parietal cortex, bilaterally [but see also Venkatraman et al.,2005]. Exact arithmetic, in contrast, would involve the retrieval of arithmetic facts, stored as strings of words (e.g., “three times nine is twenty-seven”) in verbal long-term memory, and would thus depend on language-specific representations in the left hemisphere [see also Dehaene,2001; Dehaene et al.,2003].
Further support for a link between the angular gyrus and arithmetic fact retrieval from verbal long term memory comes from studies comparing different arithmetic operations. Behavioural studies have provided converging evidence that multiplication problems are much more likely to be solved by fact retrieval (from the rote-learned multiplication tables) than subtraction problems [Campbell and Xue,2001]. In line with this, Lee [2000] presented participants with single-digit multiplication and subtraction problems and observed larger activation in the IPS bilaterally during subtraction but stronger involvement of the left angular and supramarginal gyri during multiplication [see also Fehr et al.,2007]. Likewise, greater activation within the angular gyrus was observed for addition problems with small operands than for problems with larger operands [Stanescu-Cosson et al.,2000]. As the solutions to simple addition problems are more likely to be retrieved from memory than the results to complex addition problems, this finding is also compatible with the supposition of an involvement of the angular gyrus in arithmetic fact retrieval.
Neuropsychological studies have generally corroborated the assumption of a specific role of the angular gyrus for arithmetic fact retrieval in multiplication [for reviews, see Dehaene et al.,2003; Domahs and Delazer,2005]. As an example, Lee [2000] described a patient with a lesion in the left parieto-temporal junction (involving the angular gyrus) who showed relatively preserved subtraction performance, but severely impaired multiplication performance. Van Harskamp et al. [2002], however, report on a patient with lesions in the left supramarginal and angular gyri who displayed no impairments in multiplication fact retrieval [see also Van Harskamp et al.,2005].
A different approach in elucidating the neural correlates underlying arithmetic fact retrieval was pursued in fMRI studies on the effects of arithmetic training. Delazer et al. [2003] trained adults on a set of 18 complex two-digit times one-digit multiplication problems over 5 days until they achieved high accuracy. In the subsequent fMRI session, participants were presented with trained and untrained multiplication problems. Contrasts between trained and untrained problems revealed higher activation in frontal cortices and in the lPS for the untrained problems; the trained set, in contrast, showed stronger activation than the untrained set in the left angular gyrus. This finding of activation shifts from fronto-parietal areas, especially the IPS, to the angular gyrus indicated that training induced a transition from quantity-based processing to automatic fact retrieval [for similar results, see Ischebeck et al.,2007]. Importantly, the training effect in the angular gyrus also depended on the type of training and type of operation being trained. Delazer et al. [2005] compared learning by drill with learning by new calculation algorithms (strategy learning) and observed that problems learned by drill elicited higher activation in the angular gyrus whereas problems learned by strategy were associated with higher activation in frontal regions and in the precuneus. Ischebeck et al. [2006] compared the training effects for multiplication (two-digit times one-digit) and subtraction (two-digit minus two-digit) problems and found an activation increase within the left angular gyrus only for trained multiplication problems but not for trained subtraction problems even though the training-related performance increases were comparable for both operations.
Recent results suggest that angular gyrus activation is also related to individual differences in mathematical competence as assessed by means of psychometric tests of intelligence structure. Grabner et al. [2007] compared two groups of healthy male adults who only differed in mathematical competence but not in verbal and figural-spatial abilities. In the fMRI test session, participants had to solve simple (one-digit times one-digit) and complex (two-digit times one-digit) multiplication problems. Activation contrasts between both competence groups revealed that the individuals with higher mathematical competence displayed stronger activation of the left angular gyrus in both conditions, simple and complex multiplication problems. In addition, angular gyrus activation was found to be correlated with the individual level of mathematical competence, even after controlling for experimental task performance (i.e., accuracy and response times in both, simple and complex multiplication problems). This finding was interpreted to reflect a stronger reliance on automatic, language-mediated processes, including fact retrieval, in mathematically more competent individuals.
In the present investigation, we combined the fact training procedure employed in previous fMRI studies [Delazer et al.,2003,2005; Ischebeck et al.,2006] with the individual differences approach in Grabner et al. [2007] to address two research objectives: First, it is investigated whether training-related activation increases in the angular gyrus are specific to arithmetic learning or whether they can also be observed in other, nonarithmetic tasks. Previous studies have shown that training-related activation increases within the left angular gyrus were more pronounced when the arithmetic operation being trained or the type of training emphasized arithmetic fact retrieval. However, they have not yet compared activation changes induced by arithmetic training with the training of a nonarithmetic cognitive task. Consequently, it is still unclear whether training-related activation increases in the angular gyrus specifically reflect the acquisition of (presumably verbally stored) arithmetic facts or whether they also emerge in a nonarithmetic and nonverbal task which would indicate the involvement of the angular gyrus in more general processes of (fact) learning. It has recently been proposed, for instance, that the angular gyrus might be engaged in general mapping processes, such as the mapping between a symbol and a referent or between a problem and its solution, independent of the problem domain [Ansari,2008]. Because the angular gyrus is a cross-modal integration area involved in language [e.g., Callan et al.,2005; Joubert et al.,2004] and in figural-spatial mnemonic processes [e.g., Roland and Gulyas,1995], it might support mappings even across different cognitive domains. To investigate the specificity of the angular gyrus for arithmetic fact retrieval, we trained participants for five consecutive days on two types of problems and presented them with trained and untrained problems of both tasks in the subsequent fMRI test session. For the arithmetic domain, 10 complex multiplication problems (two-digit times one-digit problems with two digit-solutions) similar to those used by Delazer et al. [2003] and Ischebeck et al. [2006,2007] were selected. For the nonarithmetic domain, 10 complex figural-spatial problems of comparable task difficulty were chosen. Participants were presented with drawings of three-dimensional objects and had to determine the number of object faces as quickly as possible. This task strongly relies on spatial visualization abilities and is included in psychometric test scales assessing figural-spatial abilities [cf. Carroll,1993; Horn,1962,1983]. Trained problems of both tasks can be expected to be solved by retrieval of the solutions from memory whereas untrained problems require mental multiplication or spatial visualization. If the angular gyrus displays stronger activation for trained as compared with untrained problems only in the multiplication task, the present data can be regarded as evidence of the specificity of this brain region for arithmetic fact learning. If, on the other hand, training-related activation increases in the angular gyrus emerge in both tasks, this specificity can be questioned.
The second objective of the present study was to investigate the interplay of training and individual differences in mathematical competence on angular gyrus activation. As outlined above, we have recently found that mathematically more competent individuals display stronger activation of the angular gyrus than their less competent peers during solving (untrained) multiplication problems [Grabner et al.,2007]. The functional significance of this activation difference, however, remained elusive. Given the strong training effects in this brain area it is particularly unclear whether the angular gyrus is a key region of mathematical competence displaying stable activation differences between more and less competent individuals or whether these activation differences diminish after a short training period. Whether and how training alters the angular gyrus activation of more and less competent individuals also provides insights into the origins of the competence-related activation differences. If these differences diminish after fact training, it would suggest that the more competent individuals more strongly relied on processes of fact retrieval in novel or untrained multiplication problems. The solutions to the trained multiplication problems, in contrast, should be similarly available in both groups after the training. However, if more competent individuals show stronger angular gyrus activation also in the trained problems, the competence-related activation difference cannot be traced back to differences in mere fact retrieval. For the present study, participants of higher and lower mathematical competence underwent the 5-day training of complex multiplication and figural-spatial problems. In administering both problem types we could not only investigate the stability of the competence-related activation differences in the multiplication task but also whether mathematical competence is related to angular gyrus activation in the figural-spatial task.
MATERIALS AND METHODS
Participants
A sample of 28 healthy male adults between 22 and 33 years (M = 26.86, SD = 3.16) was selected from a pool of 140 adults (German speaking, enrolled at the University; 100 males) who were previously (in a separate test session) screened with respect to their intelligence structure by means of the Berlin Intelligence Structure Test [BIS-T-Jäger et al.,1997]. The selection of participants was guided by the aim to achieve two groups who only differ in mathematical competence but not in other intellectual abilities. To this end, we employed the same procedure as in Grabner et al. [2007]: From all male adults of average verbal and figural-spatial intelligence (i.e., within ±1 SD of the standard mean IQ of 100), two groups of participants were selected that differed with regard to mathematical-numerical IQ but had similar verbal and figural-spatial IQ. The descriptive statistics of the two competence groups is presented in Table I. Two-sample t-tests revealed that the group of higher mathematical competence (higher math group; n = 14) displayed significantly higher mathematical-numerical intelligence than the group of lower mathematical competence (lower math group, n = 14), t(21.75) = −9.63, P < 0.001, but did neither differ significantly in verbal, t(26) = −0.90, P = 0.38, and figural-spatial IQ, t(26) = −1.32, P = 0.20, nor in age, t(26) = −0.83, P = 0.41. All participants were healthy, right-handed, and had normal or corrected-to-normal vision. The movement of participants in the MRI scanner did not exceed 3.5 mm in translation and 3.5° in rotation direction. All participants gave written informed consent and were paid for their participation. The study was approved by the local ethics committee (Medical University of Graz, Austria).
| Lower mathematical competence | Higher mathematical competence | |||||||
|---|---|---|---|---|---|---|---|---|
| Min | M | SD | Max | Min | M | SD | Max | |
| Age in years | 22.00 | 26.36 | 3.15 | 33.00 | 23.00 | 27.36 | 3.20 | 33.00 |
| Intelligence structurea | ||||||||
| Mathematical-numerical intelligence | 80.50 | 88.26 | 4.84 | 95.50 | 102.10 | 111.85 | 7.79 | 125.50 |
| Verbal intelligence | 92.80 | 103.19 | 5.07 | 112.60 | 92.50 | 105.10 | 6.16 | 114.70 |
| Figural-spatial intelligence | 88.90 | 99.38 | 6.75 | 110.20 | 93.40 | 103.02 | 7.77 | 115.00 |
- a IQ scale (M = 100, SD = 15).
Materials
In total, 20 multiplication and 20 figural-spatial problems were administered (see Fig. 1). The multiplication problems were taken from the study by Ischebeck et al. [2006]. They consisted of two-digit (range, 12–19, excluding 15) times, one-digit (range, 3–8) problems with two-digit solutions (between 42 and 98, excluding solutions divisible by 5). The figural-spatial problems were developed after a figural-spatial subscale of a well-established German intelligence test [Leistungs-Prüf-System; LPS Horn,1962,1983]. In each problem, a drawing of a three-dimensional geometric object is presented, and the participant is required to determine the number of faces as fast and accurately as possible. Each face is defined by salient angles and can be plane, concave, or convex. As an example, a cube consists of six faces whereas a sphere has no salient angles and, consequently, only one face. The rationale for selecting this type of figural-spatial problems was threefold: First, these problems require spatial visualization and have turned out to be a good measure of figural-spatial abilities [cf. Carroll,1993; Horn,1962,1983]. Second, in contrast to most other figural-spatial problems, the solution is a number. Consequently, multiplication and figural-spatial problems only differ in their cognitive demands (numerical vs. figural) but not in the response format (numerical). Third, it could be assumed that the solutions to these problems can be learned very similarly to the results of multiplications (arithmetic facts). Forty figural-spatial problems were created and evaluated in a pilot study with 16 participants. From this set, 20 problems were selected so that they were of similar task difficulty (in terms of solution rates and response latencies) as the multiplication problems. The solutions to these problems (i.e., number of faces) ranged between 3 and 10. In both tasks, half of the problems were included in the training sessions, resulting in 10 trained multiplication and 10 trained figural-spatial problems. The trained problems and the remaining 10 untrained problems of each task were matched with respect to task difficulty.
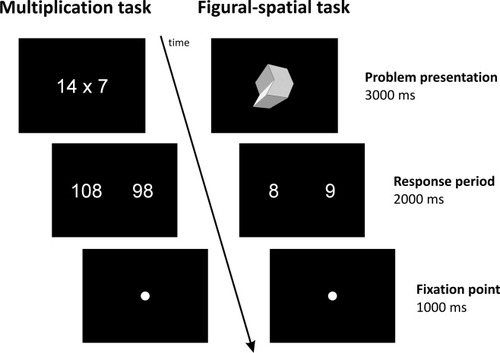
Paradigm design of the multiplication and figural-spatial task. After the problem presentation, the participant had to select the correct solution by left or right-hand button press. In these example items, the correct solutions are 98 to the multiplication problem and eight (i.e., the number of faces of the object) to the figural-spatial problem.
Training Procedure
All participants underwent a five-day training of 10 multiplication and 10 figural-spatial problems. Each training session comprised two runs: one run with multiplication and one run with figural-spatial problems. Similar to Ischebeck et al. [2006], the 10 trained problems were presented in random order in blocks with the number of blocks per run (i.e., the number of repetitions of the 10 trained problems) increasing across the five training sessions, i.e., 9, 12, 15, 18, and 21, for the first to the fifth session, respectively. The order of the runs (tasks) in each training session was counterbalanced. The overall training time (for both runs) per day was about 20 min in the first session and about 35 min in the fifth session. Participants performed the training on five consecutive days preceding the day of the fMRI test session.
All problems were presented (once at a time) as white characters (multiplication problems) or white-and-gray objects (figural-spatial problems) on a black screen and participants were required to solve the problems as fast and as accurately as possible. Responses were given using the number computer keypad. After the response was confirmed (with the ENTER key), a positive or negative feedback (including the correct solution) was provided. To increase training motivation and training progress, feedback on the number of correctly solved problems and the average response latency was presented after every 10 problems. Participants were also instructed to increase their speed and accuracy. Because not all participants were familiar with the number keypad, a typing training, in which random two-digit numbers had to be entered as fast as possible, preceded each of the five training sessions. In addition to the training sessions, before the first and after the last training session, a pre- and post-test (without feedback) were conducted in which the trained multiplication and figural-spatial problems were presented intermixed in random order.
fMRI Design and Procedure
There were four experimental conditions given by the two tasks (multiplication vs. figural-spatial task) and the two training conditions (untrained vs. trained problems). One experimental condition comprised 10 different problems which were repeated three times to obtain 30 trials per condition (i.e., in total 120 trials). As depicted in Figure 1, each trial started with the problem presentation for 3,000 ms, which was followed by the presentation of the correct result (solution) and a distractor. Both numbers were presented next to each other horizontally on the screen for 2,000 ms. Participants had to indicate the position of the solution by pressing the left-hand button for the left number and the right-hand button for the right number on the screen using their index fingers. In half of the problems, the solution was presented on the left, in the other half on the right side of the screen. In the subsequent intertrial interval, a fixation point was presented for 1,000 ms. Distractors in the multiplication task were either operand related (solution plus or minus the smaller operand) or numbers with incorrect decade digit [plus or minus 1; for the rationale, see Delazer et al.,2003; Ischebeck et al.,2006]. In the figural-spatial task, distractors consisted of the solution plus or minus 1 or 2. Thus, in both tasks, distractors could not be rejected with the help of short-cut strategies such as approximation, checking the unit-digit in multiplication or checking the parity of the geometrical objects in the figural-spatial task.
The four experimental conditions (each with 10 problems repeated three times) were presented in a block design with five trials (problems) per block, resulting in six blocks per condition. The 24 blocks were divided into six runs in which one block of every experimental condition was presented. The order of the four blocks in each run was counterbalanced so that experimental conditions that were contrasted in the fMRI analysis were equally often temporally adjacent to each other. As an example, trained multiplication problems followed untrained multiplication problems equally often as trained figural-spatial problems followed untrained figural-spatial problems. Each run started with the number of the run presented on the screen for 5 s and the presentation of a fixation point for 30 s. Between the blocks and also at the end of each run fixation periods of 25 s were included. The total experimental time was about 25 min. Before MR imaging was performed, tasks and response mode were demonstrated. Instructions stressed speed and accuracy.
MRI Acquisition
Imaging was performed on a 3.0 T Tim Trio system (Siemens Medical Systems, Erlangen, Germany) using an eight channel head coil. To minimize head movement, subjects' heads were stabilized with foam cushions. Functional images were obtained with a single shot gradient echo EPI sequence sensitive to blood oxygen level-dependent (BOLD) contrast (TR = 2,800 ms, TE = 30 ms, FA = 90°, matrix size = 64 × 64, slice thickness = 3 mm, spatial resolution = 3 × 3 mm). Thirty-six transverse slices with 0.75 mm gap were acquired in descending order parallel to the AC-PC line. In each session, 514 functional volumes were obtained. The first two volumes were discarded to allow for signal stabilization. Structural images were obtained using a T1-weighted 3D MPRAGE sequence (TR = 1,900 ms, TE = 2.2 ms) which provided 1 × 1 × 1 mm isotropic resolution.
Stimulus presentation was accomplished with the Eloquence system (Invivo Corporation, Orlando, FL), containing an LCD display with full XGA solution, visible for the participant through a mirror mounted above the head coil. The paradigm was presented using the software package Presentation (Neurobehavioral Systems, Albany, CA). For responding, two response boxes were placed in the participants' left and right hand, respectively. Responses were given with the index finger of the right or left hand on a scanner-compatible response recording device which forms part of the Eloquence system.
Analysis of fMRI Data
FMRI data analysis was performed using SPM5 (Wellcome Department of Imaging Neuroscience, London, U.K.). The functional data of each participant were motion-corrected, spatially normalized into the standard MNI space (Montreal Neurological Institute) using the original voxel size of 3 × 3 × 3 mm, and smoothed using a Gaussian kernel of 8-mm FWHM. The statistical analysis was conducted on the basis of the general linear model as implemented in SPM. Model time courses for each experimental condition block and the fixation periods were generated on the basis of the hemodynamic response function as given by SPM5. The time interval during the presentation of the task information at the beginning of each run and the six motion parameters were entered into the model as regressors of no interest. A high-pass filter with a cut-off frequency of 1/512 Hz was employed to remove low frequency drifts. No global normalization was used. The analysis for the entire group was performed by computing linear t-contrasts for each subject individually which were then entered into a random effects model. Significant activation differences between experimental conditions were identified using a threshold of P < 0.05 corrected for multiple comparisons by means of the FWE (family wise error) procedure. Only activation clusters exceeding a spatial extent threshold of 20 voxels are reported.
Based on results from previous studies (see introduction) we conducted region-of-interest (ROI) analyses for the left and right angular gyrus. For these analyses, the contrast estimates for the contrasts between experimental condition and fixation period were used. Similar to Grabner et al. [2007], the two ROIs were defined anatomically on the basis of the Anatomical Automatic Labeling (AAL) atlas [Tzourio-Mazoyer et al.,2002]. Contrast estimates were averaged over all voxels of the ROI for each participant. These values were then entered into an analysis of variance (ANOVA) with the factors Task, Training, Math competence, and Hemisphere (left vs. right angular gyrus).
Analysis of the Behavioural Data
For the behavioural training data (response latencies and solution rates) ANOVAs for repeated measurements were calculated with the factors Task (multiplication vs. figural-spatial task), Time (pre-test, 5 training sessions, post-test), and Math competence (lower vs. higher). Because of technical problems, training logfiles were lost for three participants. These participants were discarded from the analysis of the behavioural training data, resulting in a sample of 25 (12 lower and 13 higher math) for the analysis of the behavioural training effects. For all other data, the entire sample of 28 participants (14 lower and 14 higher math) was analyzed.
Experimental task performance (solution rates) in the fMRI test session was analyzed using ANOVAs with the factors Task, Math competence, and Training (untrained vs. trained problems). During functional MR imaging response latencies were also recorded, but not analyzed, because problems were presented for 3 s before the presentation of two response alternatives. The response latencies measured from the onset of the response alternatives might therefore no longer reflect the duration of problem solving. Only correctly answered trials were considered.
Solution rates of the behavioural training data and the experimental task performance were transformed using the 2arcsin√p transformation [Bishop et al.,1975] to achieve approximate variance equality before they were entered into the ANOVAs. For the sake of clarity, always the untransformed solution rates are reported in the descriptive statistics and in Figure 2. In all ANOVAs, in case of violations of the sphericity assumption degrees of freedom were corrected by means of the Greenhouse Geisser procedure. If applicable, uncorrected df values, together with the corrected p value and the Greenhouse Geisser epsilon (ε) are reported. Post-hoc comparisons were performed using Student's t-tests with Bonferroni corrected alpha levels for multiple comparisons.
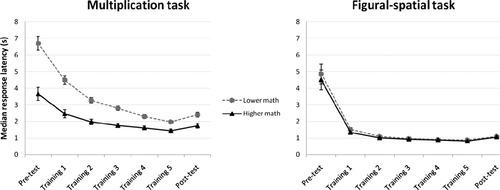
Behavioural training effects on response latencies in the multiplication (left) and figural-spatial task (right) for both math competence groups. Error bars indicate ±1 SE of the mean. N = 25 (n = 12 lower, n = 13 higher math competence).
RESULTS
Behavioural Results: Training
As expected, training significantly improved the performance of the participants in both tasks.
In the analysis of the solution rates, accuracy increased from pre-test over training to post-test (92.00, 93.60, 94.60, 96.30, 96.90, 97.20, and 98.40%; main effect of time: F(6,138) = 16.65, P < 0.001, ϵ = 0.41). Solution rates were also generally higher for the figural-spatial than the multiplication task (96.60 vs. 94.50%; main effect of task: F(1,23) = 19.54, P < 0.001). No other effect or interaction was significant.
In the analysis of the response latencies, also a strong performance improvement was observed. As depicted in Figure 2, response latencies decreased across the measurement time points (main effect of time: F(6,138) = 134.22, P < 0.001, ϵ = 0.20). The training effect was moderated by task and math competence. Greater training-related response latency decreases were observed in the figural-spatial than in the multiplication task, especially from pre-test to the first training session (Time × Task: F(6,138) = 9.12, P < 0.01, ϵ = 0.23). Math competence influenced response latencies and the training effect only in the multiplication task. At all time points, participants with higher math competence outperformed less competent participants in multiplication (all ps < 0.05) whereas both groups always displayed similar performance levels in the figural-spatial task (Task × Math competence: F(1,23) = 36.50, P < 0.001). Moreover, in the multiplication task, the training-related decrease in response latencies was greater in the lower as compared with the group with higher math competence (Time × Task × Math competence: F(6,138) = 5.61, P < 0.05, ϵ = 0.23). The interaction of Time X Math competence also reached significance (F(6,138) = 5.56, P < 0.05, ϵ = 0.20). In addition, the analysis revealed longer response latencies for the multiplication than for the figural-spatial task (main effect of Task: F(1,23) = 140.18, P < 0.001) and for the lower than the higher math competence group (main effect of Math competence: F(1,23) = 26.33, P < 0.001).
The response latency data indicate that math competence influenced only the performance in the multiplication task but not in the figural-spatial task. To investigate whether the figural-spatial task draws specifically on figural-spatial abilities, correlation analyses were performed, between participants' numerical and figural-spatial IQ scores and response latencies in pre- and post-test, as well as the performance improvement (calculated as pre-test minus post-test response latency divided by the average response latency). The results are presented in Table II. Significant correlations were observed between mathematical-numerical IQ and performance in the multiplication task, as well as between the figural-spatial IQ and performance in the figural-spatial task. This result is particularly noteworthy as the variance in figural-spatial IQ is much smaller than the variance in the mathematical-numerical IQ.
| Multiplication task | Figural-spatial task | |||||
|---|---|---|---|---|---|---|
| Pre-test | Improvement | Post-test | Pre-test | Improvement | Post-test | |
| Mathematical-numerical intelligence | −0.70** | −0.39* | −0.57** | −0.16 | −0.24 | −0.26 |
| Figural-spatial intelligence | −0.22 | −0.33 | −0.01 | −0.41* | −0.55** | −0.10 |
- * P < 0.05.
- ** P < 0.01.
Behavioural Results: Task Performance in the Scanner
Clear training effects were also observed during fMRI measurement. We observed higher solution rates for the trained compared with the untrained problems (main effect of Training: F(1,26) = 30.08, P < 0.001). In addition, the solution rate in the multiplication task was generally lower than in the figural-spatial task (94.35 vs. 97.14%; main effect of Task: F(1,26) = 9.86, P < 0.01). The higher math group again outperformed the lower math group (main effect of Math competence: F(1,26) = 7.70, P = 0.01), but only in the multiplication task (97.14 vs. 91.55%; figural-spatial task: 97.02 vs. 97.26%; Task × Math competence: F(1,26) = 13.25, P < 0.01) and only in the untrained problems (95.71 vs. 90.60%; trained problems: 98.45 vs. 98.21%; Training × Math competence: F(1,26) = 6.21, P < 0.05).
fMRI Results
Similarities and Differences Between Experimental Tasks
Before reporting on training effects in the brain activation data, we will first analyze similarities and differences between both tasks. This analysis should reveal whether, as the behavioural data suggests, the multiplication and figural-spatial task indeed draw on different neurocognitive resources which is a prerequisite for the interpretation of the training effects in both tasks. To investigate similarities, conjunction analyses were conducted for both tasks against baseline separately for the untrained and the trained condition. To investigate differences, contrasts between both tasks were calculated, separately for the untrained and trained condition. The results of these analyses are presented in Table III and Figure 3.
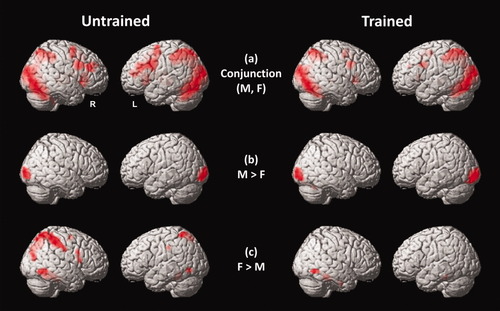
Similarities and differences between the multiplication (M) and figural-spatial task (F) in untrained (left) and trained (right) condition. (a) Conjunction analysis of both tasks. (b) Multiplication minus figural-spatial task. (c) Figural-spatial task minus multiplication. Activation clusters (voxelwise P < 0.05 family wise error corrected) are depicted on the standard single-subject volume-rendered brain implemented in SPM5 (sagittal views). [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
| Brain area | x | y | z | k | t |
|---|---|---|---|---|---|
| Untrained | |||||
| Conjunction (Multiplication, Figural-spatial) | |||||
| R lingual G, L inf parietal Ga, L cerebelluma, L mid occipital Ga, R angular Ga | 12 | −81 | −3 | 8364 | 15.81 |
| L precentral G, R SMAa | −42 | 3 | 30 | 2245 | 12.95 |
| R thalamus, R putamen | 24 | −27 | 0 | 337 | 11.42 |
| R inf frontal G, R insula | 48 | 9 | 30 | 830 | 10.66 |
| R precentral G, R sup frontal G | 39 | −3 | 48 | 195 | 8.01 |
| Multiplication > Figural-spatial | |||||
| R calcarine C | 21 | −93 | −3 | 217 | 12.01 |
| L mid occipital G, L calcarine C, L inf occipital G | −24 | −96 | 3 | 300 | 11.22 |
| Figural-spatial > Multiplication | |||||
| R sup parietal G, R inf parietal G, R SMG | 24 | −69 | 54 | 975 | 13.10 |
| R fusiform G. R inf temporal G | 30 | −39 | −15 | 364 | 13.07 |
| L cerebellum | −27 | −42 | −21 | 86 | 9.40 |
| L sup parietal G, L precuneus | −21 | −57 | 63 | 182 | 9.03 |
| R sup frontal G | 27 | −3 | 60 | 41 | 8.57 |
| R precentral G | 57 | 9 | 30 | 77 | 8.50 |
| L inf temporal G | −57 | −66 | −6 | 30 | 7.36 |
| L SMG | −57 | −24 | 39 | 21 | 7.15 |
| Trained | |||||
| Conjunction (Multiplication, Figural-spatial) | |||||
| R lingual, R inf parietal Ga, L sup parietal Ga | 12 | −81 | −3 | 5981 | 16.31 |
| R thalamus | 24 | −27 | 0 | 43 | 10.32 |
| R SMA | 6 | 9 | 51 | 270 | 9.46 |
| L thalamus | −21 | −30 | 0 | 45 | 8.71 |
| L precentral G | −42 | 3 | 30 | 115 | 8.65 |
| R precentral G | 48 | 6 | 30 | 127 | 8.47 |
| L mid frontal G | −27 | −6 | 54 | 69 | 8.40 |
| R insula | 39 | 18 | 0 | 115 | 7.46 |
| R putamen | 21 | 3 | 9 | 31 | 6.63 |
| R precentral G | 33 | −6 | 54 | 71 | 6.49 |
| L insula | −33 | 18 | 9 | 40 | 6.47 |
| Multiplication > Figural-spatial | |||||
| L calcarine C, L inf and mid occipital G | −15 | −93 | −6 | 458 | 13.61 |
| R mid occipital G, R inf occipital G, R lingual G | 24 | −96 | 6 | 362 | 11.02 |
| R cerebellum | 30 | −63 | −27 | 24 | 7.23 |
| Figural-spatial > Multiplication | |||||
| R fusiform G | 30 | −39 | −21 | 93 | 9.58 |
| R inf temporal G | 54 | −63 | −9 | 42 | 7.49 |
| R fusiform G | 33 | −9 | −36 | 26 | 7.40 |
| L fusiform G | −24 | −39 | −18 | 32 | 7.37 |
- Coordinates are reported in MNI space as given by SPM5 and correspond only approximately to Talairach and Tournoux space [Talairach and Tournoux1988]. Anatomical labels are based on the AAL (automated anatomical labeling) atlas [Tzourio-Mazoyer et al.2002]. The first label represents the location of the peak activation, additional labels denote submaxima if located in a different brain region.
- a In large activation clusters (k > 1000 voxel), submaxima are denoted if separable as significant clusters at a higher threshold (t > 10) with an extent threshold of at least 20 voxels.
- Abbreviations: L, left hemisphere; R, right hemisphere; G, Gyrus; C, cortex; inf, inferior; sup, superior, mid, middle; SMA, supplementary motor region.
In the case of the untrained problems, both tasks engage a widespread network of frontal, parietal, and occipital regions, including the inferior and superior parietal regions around the intraparietal sulcus (IPS), bilaterally, as well as the right angular gyrus. In the frontal lobe, activation was observed in the precentral gyri bilaterally, extending to inferior and middle frontal regions, the insulae, and supplementary motor areas. Further activations were observed in the basal ganglia, the right thalamus and the putamen.
Despite the large activation overlap of both tasks, several task differences emerged in the contrast analyses for the untrained problems. The figural-spatial tasks more strongly engaged right-hemispheric brain areas, including inferior and superior parietal areas, inferior temporal regions including the fusiform gyrus, and the superior frontal and precentral cortices. Parietal activation in the left hemisphere was mainly restricted to the superior parietal cortex. Smaller activation clusters in the left hemisphere were also observed in the inferior temporal gyrus, supramarginal gyrus, precuneus and cerebellum. The contrast untrained multiplication minus untrained figural-spatial problems yielded significant activation clusters in (inferior and middle) occipital cortices, bilaterally.
Because the brain activation patterns in the trained problems not only reflect task effects but also training effects, they should generally be interpreted with caution. The conjunction analysis revealed a similar network of activated areas as in the case of the untrained problems (see Table III and Fig. 3a). There seem to be less pronounced activation differences for trained items between both tasks suggesting that training diminished activation differences between the two tasks (see Fig. 3b).
Training Effects
Training effects were assessed by comparing trained and untrained problems within each task. These results are presented in Table IV and Figure 4.
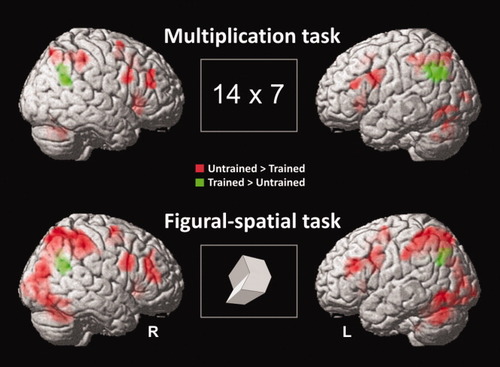
Training effects in the multiplication (upper row) and figural-spatial task (lower row). Activation clusters from the contrast untrained minus trained are depicted in red colour; activation clusters from the contrast trained minus untrained in green colour. All effects at voxelwise P < 0.05 family wise error corrected. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
| Brain area | x | y | z | k | t |
|---|---|---|---|---|---|
| Multiplication task | |||||
| Untrained > Trained | |||||
| L SMA | −6 | 12 | 48 | 165 | 11.22 |
| L inf frontal G | −45 | 6 | 27 | 207 | 10.44 |
| L insula | −27 | 24 | 3 | 89 | 10.39 |
| L cerebellum, R cerebellum | −6 | −75 | −30 | 249 | 9.43 |
| Pons, L thalamus | 9 | −21 | −18 | 74 | 9.33 |
| R sup parietal G, R SMG, R inf parietal G | 27 | −69 | 54 | 219 | 9.14 |
| L cerebellum | −27 | −57 | −36 | 30 | 8.96 |
| L sup parietal G, L inf parietal G | −27 | −57 | 48 | 292 | 8.90 |
| R insula | 30 | 24 | 3 | 139 | 8.78 |
| R inf frontal G | 51 | 9 | 27 | 94 | 8.60 |
| R mid frontal G | 45 | 33 | 21 | 80 | 7.87 |
| L cerebellum | −36 | −69 | −27 | 32 | 7.28 |
| L inf temporal G | −54 | −60 | −12 | 62 | 7.28 |
| L mid occipital G | −21 | −87 | 12 | 32 | 7.23 |
| R sup frontal G | 30 | 3 | 63 | 47 | 7.09 |
| Trained > Untrained | |||||
| L angular G | −60 | −48 | 39 | 126 | 8.31 |
| R angular G | 57 | −57 | 24 | 75 | 7.89 |
| L mid cingulum | −3 | −42 | 36 | 36 | 6.91 |
| Figural-spatial task | |||||
| Untrained > Trained | |||||
| R SMG, R sup parietal Ga, L sup parietal Ga, L inf parietal Ga | 42 | −36 | 42 | 4100 | 15.02 |
| L inf frontal G, L precentral G | −51 | 30 | 27 | 319 | 12.57 |
| R precentral G | 51 | 6 | 27 | 168 | 10.37 |
| L SMA | −9 | 12 | 48 | 72 | 8.91 |
| R inf frontal G | 48 | 33 | 30 | 189 | 8.70 |
| R sup frontal G | 24 | −3 | 54 | 137 | 8.70 |
| R insula | 30 | 21 | 3 | 84 | 8.45 |
| L mid frontal G, L precentral G | −27 | 0 | 57 | 109 | 8.18 |
| L insula | −27 | 21 | 6 | 41 | 7.38 |
| Trained > Untrained | |||||
| R angular G | 54 | −57 | 24 | 99 | 8.69 |
| L angular G | −54 | −66 | 33 | 64 | 7.21 |
| L precuneus | −3 | −63 | 24 | 129 | 7.20 |
- Coordinates are reported in MNI space as given by SPM5 and correspond only approximately to Talairach and Tournoux space [Talairach and Tournoux1988]. Anatomical labels are based on the AAL (automated anatomical labelling) atlas [Tzourio-Mazoyer et al.2002]. The first label represents the location of the peak activation, additional labels denote submaxima if located in a different brain region.
- a In large activation clusters (k > 1000 voxel), submaxima are denoted if separable as significant clusters at a higher threshold (t > 10) with an extent threshold of at least 20 voxels.
- Abbreviations: L, left hemisphere; R, right hemisphere; G, Gyrus; C, cortex; inf, inferior; sup, superior, mid, middle; SMA, supplementary motor region; SMG, supramarginal gyrus.
In both tasks, solving untrained as compared with trained problems was accompanied by stronger fronto-parietal activation in inferior and superior parietal regions around the IPS, the inferior frontal cortices and insulae, bilaterally. Further activation clusters common to both tasks emerged in the left SMA and right superior frontal gyrus. The contrast untrained minus trained multiplication problems additionally revealed significant activation clusters in the cerebellum, bilaterally, in left inferior temporal and middle occipital regions, in the right middle frontal gyrus, and in the left thalamus. The contrast untrained minus trained figural-spatial problems yielded further activation clusters in the left precentral and middle frontal gyri.
When trained problems were compared with untrained problems, relative increases in brain activation were observed in both tasks. In the multiplication task, trained problems more strongly activated the left angular gyrus, but also the right angular gyrus and the left middle cingulum (see Table IV and Fig. 4). In the figural-spatial task, a similar result pattern was observed. The contrast trained minus untrained problems yielded activation clusters in the angular gyri, bilaterally, followed by a cluster in the left precuneus. The results also suggest slight hemispheric differences in the training-related increases between both tasks. Although the peak activation in this contrast for the multiplication task was observed within the left angular gyrus, in the figural-spatial task it was observed in the right angular gyrus (see Table IV).
To examine activation differences due to mathematical competence, we also conducted whole-brain analyses of activation differences between both groups of mathematical competence. However, this analysis did not yield effects surviving significance thresholds corrected for multiple comparisons. As both, training and mathematical competence were found to modulate angular gyrus activation, we conducted an ROI analysis for the left and right angular gyri to evaluate the interplay of training-related and competence-related effects in more detail.
ROI Analysis
The results of the ROI analysis are presented in Figure 5. Math competence influenced activation within the two ROIs very specifically, which is reflected in the significant four-way interaction of Hemisphere, Task, Training, and Math competence (F(1,26) = 6.30, P < 0.05), and the lower-order interactions of Hemisphere × Task × Math competence (F(1,26) = 4.74, P < 0.05), Math competence × Task (F(1,26) = 10.17, P < 0.01), and Math competence × Training (F(1,26) = 9.14, P < 0.01). First, in the left angular gyrus, both math competence groups differ only in the untrained multiplication condition (P < 0.05 corrected) with the higher math competence group showing relatively more activation than the lower competence group. In the trained problems, both groups show a similar level of angular gyrus activation. No activation difference between groups emerged in the figural-spatial task and right angular gyrus. Second, the lower math group shows stronger training-related activation increases than the higher math group and this is particularly pronounced in the left angular gyrus and the multiplication task. The left angular gyrus training effect of both groups is almost perfectly the same in the figural-spatial task. Third, the weaker training effect in the right angular gyrus also slightly differs between the groups but, in contrast to the left angular gyrus, this holds true for both tasks.
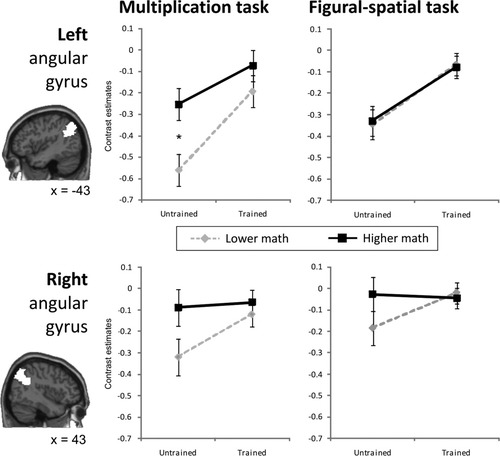
Results of ROI analysis in the left (upper row) and right (lower row) angular gyrus. *Post-hoc comparison significant at P < 0.05 Bonferroni corrected.
Further significant activation differences were observed with regard to hemisphere (main effect of Hemisphere: F(1,26) = 11.91, P < 0.01; Hemisphere × Training: F(1,26) = 27.01, P < 0.001), task (main effect of Task: F(1,26) = 10.18, P < 0.01), and training condition (main effect of Training: F(1,26) = 58.56, P < 0.001). It should be noted, that the ROI analysis revealed mostly negative contrast estimates, suggesting that the angular gyri were less activated during the tasks than during baseline (fixation). Therefore, the activation differences observed here can only be interpreted as relative rather than absolute differences.
To investigate the relation between activation and ability beyond the competence group dichotomy, correlation analyses of the two ability scores (math and figural-spatial abilities) with angular gyrus activation and the training-induced activation changes (trained minus untrained) were performed. Similar to the group analysis results, mathematical competence only correlated significantly with left angular gyrus activation for untrained multiplication problems (see Table V). This correlation even remained significant after controlling for solution rate in the untrained multiplication problems (partial r = 0.47, P < 0.05). In the trained multiplication problems, in contrast, the correlation was comparably low and nonsignificant. The difference between both correlation coefficients turned out to be significant (z = 1.89, P < 0.05 one-tailed). Likewise, the correlation for the untrained multiplication task differed significantly from the correlations for both figural-spatial task conditions in the left angular gyrus (trained: z = 3.05; untrained: z = 2.25; ps < 0.05). This suggests that mathematical competence modulates activation in the left angular gyrus only in untrained multiplication problems but neither in trained multiplication nor in any of the figural-spatial problems. Furthermore, the training-related activation increase was negatively correlated with math competence in the left angular gyrus only in the multiplication task (r = −0.40, p < 0.05; figural-spatial task: r = −0.13, P = 0.52) but in the right angular gyrus in both tasks (both rs = −0.38, ps < 0.05). None of the correlations with figural-spatial abilities reached significance (all rs between −0.10 and 0.13).
| Mathematical- numerical intelligence | Figural-spatial intelligence | |
|---|---|---|
| Left angular gyrus | ||
| Trained multiplication task | 0.26 | 0.29 |
| Untrained multiplication task | 0.51** | 0.16 |
| Trained figural-spatial task | −0.01 | 0.12 |
| Untrained figural-spatial task | 0.11 | 0.18 |
| Right angular gyrus | ||
| Trained multiplication task | 0.17 | 0.00 |
| Untrained multiplication | 0.32 | −0.06 |
| Trained figural-spatial task | −0.04 | −0.07 |
| Untrained figural-spatial task | 0.26 | −0.06 |
- ** P < 0.01.
DISCUSSION
In the present fMRI study, participants of lower and higher mathematical competence underwent a five-day training on sets of complex multiplication and figural-spatial problems to investigate (a) the specificity of training-related increases in the angular gyrus for arithmetic fact learning and (b) the interplay between training and individual competence differences on angular gyrus activation.
One the whole, training effects in both tasks were similar rather than different. In the behavioural data clear training effects were observed. The solution rates increased over the training period and reached almost perfect accuracy after the training in both tasks. Likewise, the response latencies strongly decreased from about 5 s in the pre-test to about 2 s in the multiplication problems and about 1 s in the figural-spatial problems in the post-test. The observed training effects in the multiplication problems are highly similar to those reported in previous studies [Delazer et al.,2003; Ischebeck et al.,2006] and suggest that the participants had acquired the complex multiplication facts successfully during training. The same holds true for the figural-spatial task which even displayed a much steeper learning curve (see Fig. 2).
In the brain activation data, training effects for both tasks were also similar rather than different. The results for the multiplication problems generally replicate those of previous training studies using multiplication problems [Delazer et al.,2003; Ischebeck et al.,2006]. Untrained (vs. trained) multiplication problems elicited higher activation in frontal and parietal regions including the inferior frontal cortex and the IPS; trained (vs. untrained) problems, in contrast, showed higher activation in the angular gyrus. The stronger fronto-parietal activation for untrained problems has been interpreted to show quantity-based processing in the IPS [Dehaene et al.,2003] as well as attentional and working memory resources in the frontal cortex [Collette and Van der Linden,2002; Smith and Jonides,1999]. The activation increase within the angular gyrus for trained problem was interpreted to reflect automatic retrieval of the acquired arithmetic facts from verbal long term memory [Delazer et al.,2003; Ischebeck et al.,2006]. In the figural-spatial task also strong training-related activation differences were observed, that overlapped considerably with the network of brain areas for multiplication. The contrast untrained minus trained figural-spatial problems yielded bilateral fronto-parietal activation, extending to the occipital and inferior temporal cortex. Similar to multiplication, the contrast of trained minus untrained figural-spatial problems yielded an activation increase within the angular gyri, bilaterally.
The finding of highly similar training effects of both tasks in the angular gyrus suggests that training-related increases in this brain region are not specific for the learning of arithmetic facts and supports the notion that the angular gyrus may be involved in more general processes in learning. Considering the overall dissimilarity of the two tasks with regard to the required neuro-cognitive processes it is conceivable that the angular gyrus supports learning across different domains. Interestingly, the angular gyrus is not considered to be a critical region in encoding or retrieval of declarative memory [cf. Gabrieli,1998; Habib et al.,2000; Simons and Spiers,2003] nor does it emerge regularly in neuroimaging studies involving practice and learning [for reviews, cf. Chein and Schneider,2005; Kelly and Garavan,2005]. Therefore, it may be assumed that the angular gyrus is not generally involved in learning but may support a specific type of (fact) learning. It has recently been suggested that the angular gyrus subserves the mapping between a symbol and its referent [Ansari,2008]. This can include the mapping between a numeral and its quantity, or between a solution and a problem. Extensive training of problem-solution pairs (e.g., arithmetic facts such as “3 × 3 = 9”) may finally result in an automatic activation and/or retrieval of the solution upon recognition of the problem. Evidence in favour of this assumption comes from several language studies demonstrating that the angular gyrus is also involved in the mapping between phonological and orthographic units at both, the letter and word level, and in their integration with semantic representations [Booth et al.,2002; Callan et al.,2005; Joubert et al.,2004; Meyler et al.,2007]. Callan et al. [2005], for instance, showed that the acquisition of new orthographic-phonological mappings results in increasing angular gyrus activation. They trained Japanese participants on a set of previously unknown Korean or Thai phonograms and found training-related activation increases in the left angular gyrus while processing the newly acquired phonograms. A PET study by Roland and Gulyas [1995] suggests that the angular gyrus may also support mappings for more complex figural-spatial problems. They compared brain activation patterns during storing, retrieving and recognizing complex geometrical patterns and observed that the angular gyrus is one of four areas that are specifically activated in retrieval and recognition. The association of the angular gyrus with symbol-referent mapping can be reconciled with the findings from previous neuroimaging studies on numerical information processing [for a review, cf. Dehaene et al.,2003]. Exact calculation problems, over-learnt arithmetic problems with small operands, and multiplication problems might be automatically mapped with the solution stored in long-term memory. The angular gyrus might support the retrieval of this stored information or the mapping process itself. In contrast, problems that can only or more easily be solved by quantity manipulation might recruit the core quantity system assumed to reside in the IPS rather than the angular gyrus. After this argument, the present results indicate that both tasks required a mapping between a problem and its solution. Our finding of an increase in activation within the angular gyrus in both tasks would also be compatible with the view that this region mediates the mapping across different domains. In the multiplication task, both, problem and solution were numerical, whereas in the figural-spatial task a figural-spatial problem had to be associated with a numerical solution.
Given the largely task-independent training effects in the angular gyrus, it might be argued that the observed activation differences between trained and untrained problems simply reflect differences in task difficulty that are not related to changes in cognitive processing. To preclude this alternative interpretation, we have performed additional random-effects analyses for trained minus untrained problems in both tasks with the performance improvement as covariate (see also Table II). These analyses revealed the same activation clusters in both tasks as the analysis without this covariate, suggesting that the observed training-related differences cannot be attributed to differences in task difficulty.
Despite strong similarities of both tasks in performance and brain activation, behavioural and fMRI data suggest that they also engaged partly different cognitive resources and cortical networks. The correlation analyses of task performance during the training revealed clearly distinct relationships of mathematical-numerical intelligence with multiplication performance and of figural-spatial intelligence with the performance in the figural-spatial task. Moreover, in contrast to a gradual training-related decrease of response latencies in the multiplication problems, the figural-spatial task displayed a steeper learning curve (see Fig. 2). This indicates that the solutions to the figural-spatial problems had been successfully acquired already after the first training session whereas it took the participants longer to acquire the solutions to the multiplication problems.
The contrasts of brain activation between the multiplication and figural-spatial task revealed that solving untrained figural-spatial problems compared with solving untrained multiplication problems was accompanied by stronger activation in several right-hemispheric brain regions that are associated with visuo-spatial processing. The superior parietal cortex, in particular in the right hemisphere [Vogel et al.,2003], has been found to be consistently activated in a wide variety of visuo-spatial tasks involving two-dimensional or three-dimensional stimuli [Cohen et al.,1996; Jordan et al.,2001; Kosslyn et al.,1998; Suchan et al.,2006; Trojano et al.,2004; Zacks,2008]. Another large activation cluster was found in the right inferior temporal cortex including the fusiform gyrus. This brain region is considered as the final stage of the ventral visual processing pathway and is assumed to be involved in object discrimination [e.g., Faillenot et al.,1999; Schacter et al.,1995], as well as in the storage and processing of complex visual objects in working memory [cf. Ranganath,2006]. Further activations were observed in the right superior frontal and precentral gyri probably reflecting attentional processes and motor imagery in visuo-spatial tasks [Baddeley,2003; Zacks,2008]. The reverse contrast (untrained multiplication minus untrained figural-spatial problems) only yielded significant activation clusters in inferior and middle occipital cortices, bilaterally, but not a stronger activation in parietal regions associated with calculation (such as areas around the IPS and angular gyrus). This result is in line with the results from previous imaging studies showing similar activation within the IPS for numerical and visuo-spatial tasks [Cohen-Kadosh et al.,2005; Simon et al.,2002]. The activation of occipital areas likely reflects higher visual processing demands in the multiplication task than in the figural-spatial task, as more digits have to be discriminated and processed when the response alternatives were presented (see Fig. 1). This has also been observed in other experiments involving calculation [Kucian et al.,2006; Pesenti et al.,2000]. When brain activation patterns were compared for the trained problems, similar, but somewhat reduced, differences were observed between both tasks. Although it is possible that this reduction is due to the generally lower demand on processing resources in the case of the trained problems, it is also conceivable that the trained problems were similarly processed by retrieving the numerical solution after recognizing the problem.
Task differences also emerged in the training-related activation increases. Although trained (as compared with untrained) problems elicited stronger angular gyrus activation in both tasks, two additional and slightly different activation clusters emerged. Similar to Delazer et al. [2003], trained multiplication problems elicited stronger activation in the left cingulum. Even though this brain region was repeatedly found to be involved in mental calculation, it is regarded to reflect working memory and episodic memory processes rather than processes specific to arithmetic problem solving [Delazer et al.,2003]. In the figural-spatial task, training-related activation increases were also found in the left precuneus. The precuneus is thought to support visuo-spatial imagery and also memory retrieval [for a review, cf. Cavanna and Trimble,2006] which fits nicely into the view that the solutions to the figural-spatial problems were also retrieved from memory. Besides these additional areas, both tasks differ in the hemisphere of angular gyrus peak activation. The training-related activation increase peaked in the left angular gyrus in the multiplication task but in the right angular gyrus in the figural-spatial task. However, this hemispheric difference did not emerge in the average level of activation for the anatomically defined angular gyrus in the ROI analysis.
The second objective of the present study was to investigate the interplay between individual differences in mathematical competence and training on the activation in the angular gyrus. In the behavioural data, math competence modulated performance only in the multiplication task. The more competent participants outperformed their less competent counterparts during the entire training (Fig. 2, Table II) and in the untrained multiplication problems in the fMRI test session.
In the brain activation data, the higher math group displayed a stronger (relative) activation in the left angular gyrus than the lower math group for the untrained multiplication problems, replicating the results of Grabner et al. [2007]. In the ROI analyses of the angular gyrus, a significant positive correlation was observed between math competence and overall activation within the left angular gyrus, even after controlling for individual differences in task performance. However, no significant correlation or group difference was observed for the trained multiplication problems. This finding shows that the competence-related activation differences in the left angular gyrus can be attenuated through acquiring a high level of expertise or knowledge in a small set of problems. This agrees with results from other studies investigating neurophysiological correlates of intelligence and expertise in different domains [Grabner et al.,2003,2006]. In the study by Grabner et al. [2003], for instance, intelligence-related activation differences were only observed for novel problems but not for problems in which the participants possessed a high level of expertise.
Interestingly, the attenuation of competence-related activation differences in the left angular gyrus due to training results from larger activation increases in the participants with lower math competence (see Fig. 5). Through training, they achieved the same (relatively higher) level of activation as their more competent peers. Similar activation changes have been reported after intervention programs to improve reading performance. There is a large body of evidence that individuals with reading disabilities display lower or absent activity in the left temporo-parietal cortex (including the angular gyrus) during phonological processing [for a review, cf. Temple,2002]. Behavioural training protocols (e.g., focusing on phonological processing) resulted in activation increases in this brain region which was interpreted to reflect a growing normalization of brain function [Eden et al.,2004; Temple, et al.,2003]. In the present study, we compared adults with relatively lower and higher mathematical competence and observed convergent activation of both groups after a five-day arithmetic fact training. This suggests that the differential left angular gyrus activation in novel [Grabner et al.,2007] or untrained multiplication problems is due to a differential reliance on or automaticity of arithmetic fact retrieval.
In line with the behavioural data, mathematical competence did not impact on angular gyrus activation during figural-spatial task performance. In the left angular gyrus, the groups neither differed in untrained and trained figural-spatial problems nor in the training-related activation increase. In the right angular gyrus the training-related activation increase was moderated by mathematical competence in both tasks, though more weakly. These ROI results complement those from the whole-brain training contrasts by suggesting a certain degree of hemispheric specificity of the angular gyrus for arithmetic problem solving and mathematical competence. Both, the left and the right angular gyrus displayed training-related activation increases in the multiplication and the figural-spatial task. However, only the left angular gyrus displayed (a) a significant competence-related activation difference in the untrained multiplication problems, and (b) a strong dissociation between the multiplication and figural-spatial task with regard to the impact of mathematical competence on brain activity and training-related activation increases. Thus, it might be speculated that both angular gyri support general fact learning processes such as symbol-referent mapping but that their functions may differ slightly between the hemispheres. Future studies comparing fact training in different domains are needed to provide further insights into the functional significance of left vs. right angular gyrus.
The ROI analyses revealed that the angular gyrus was less activated during the experimental tasks than during the fixation period. Such relative deactivations have also been observed in previous studies on mental calculation [Dehaene et al.,1996; Grabner et al.,2007; Ischebeck et al.,2006; Rickard et al.,2000; Venkatraman et al.,2006; Zago et al.,2001]. Training-related increases in activation were actually decreases of deactivation, and the more competent participants displayed less left angular gyrus deactivation than their less competent counterparts in the untrained multiplication task. The functional significance of such deactivations in mental calculation is an increasingly often cited but still unresolved issue [cf. Ansari,2008]. It has been recognized that, different from PET data, activation values in fMRI cannot be interpreted in an absolute way [Raichle,1998]. It is also unclear what the brain does when it rests [Stark and Squire,2001]. For mathematical cognition, some authors argued that the deactivation is evidence for the noninvolvement of the angular gyrus in mental calculation [e.g., Rickard et al.,2000]; others proposed that the angular gyrus probably needs to be inhibited in solving arithmetic problems [e.g., Zago et al.,2001]. In the present study, a high performance level for trained problems or for untrained problems in individuals with higher mathematical competence was observed to be associated with the angular gyrus being neither more or less activated than in a low-level baseline [see also Grabner et al.,2007; Ischebeck et al.,2006]. Interestingly, a similar result was observed in the domain of reading. In a recent fMRI study by Meyler et al. [2007] using a sentence comprehension task, poor readers displayed stronger deactivations in the parieto-temporal regions including the angular gyrus when compared with good readers, who displayed either less deactivation or even a slightly higher activation level.
In conclusion, the present study has added further insights into the role of the angular gyrus in arithmetic problem solving as well as into the relation between brain activation, training, and individual differences in mathematical competence. First, it has been shown that training-related activation increases in the angular gyrus are not specific to the learning of arithmetic facts. Extensive training of solutions to multiplication and figural-spatial problems yielded similar training-related activation increases in the angular gyrus, bilaterally. This suggests that the angular gyrus may support more general processes in fact learning independent of the problem domain.
Second, we have shown that the relation between angular gyrus activation and individual differences in mathematical competence is altered through training. Activation differences between mathematically less and more competent individuals were only observed in untrained multiplication problems. In the trained problems, angular gyrus activation was no longer modulated by mathematical competence. This finding indicates that the relation between mathematical competence and angular gyrus activation in novel or untrained multiplication problems is due to differences in arithmetic fact retrieval.
Acknowledgements
We thank Anna Kanape for organising the test sessions and Elsbeth Stern as well as Andreas Fink for valuable comments on this study.