Nonrigid registration of multiple sclerosis brain images using lesion inpainting for morphometry or lesion mapping
Abstract
Morphometric studies of medical images often include a nonrigid registration step from a subject to a common reference. The presence of white matter multiple sclerosis lesions will distort and bias the output of the registration. In this article, we present a method to remove this bias by filling such lesions to make the brain look like a healthy brain before the registration. We finally propose a dedicated method to fill the lesions and present numerical results showing that our method outperforms current state of the art method. Hum Brain Mapp, 2009. © 2008 Wiley-Liss, Inc.
INTRODUCTION
Nonrigid registration is an essential tool to analyze medical images. For example, it can be used to segment images using a prelabeled atlas [Warfield et al., 1998], to follow the evolution of brain structures in longitudinal studies [Rey et al., 2002] or for morphometry [Ashburner et al., 1998].
In this article, we will focus on the problem caused by white matter lesions in the context of multiple sclerosis (MS). MS is an immune-mediated demyelinating disease affecting both white and grey matter. White matter plaques are easily detected on current conventional images whereas grey matter lesions are still not well appreciated. When one tries to nonlinearly register a brain with MS to a brain without MS, white matter lesions will cause a strong distortion in the output transformation [Brett et al., 2001; Meier et al., 2005]. Indeed, intensity driven nonrigid registration algorithms assume that the two images being registered have the same structures but these lesions are present in the patient and not in the reference image. This distortion of the transformation will be an important problem when nonrigid registration is used for morphometry.
Deformation-based morphometry and tensor-based morphometry allow us to analyze statistical differences in the size or shape of brain structures between two groups of subject. For these techniques, the first step is to find the (nonlinear) mapping between each subject and the reference image and then to do some statistical analysis on the estimated transformations or their derivatives [Ashburner et al., 1998; Chung et al., 2003; Davatzikos et al., 1996; Lepore et al., 2006; Studholme et al., 2004]. It is therefore important for the statistical analysis that the transformation is not distorted by the presence of lesions.
Lesions location can help in the understanding of brain diseases and functions. To perform statistical analysis of lesion location, the lesions of each subject have to be described using a common coordinate system. Different methods have been used to do so. A manual method has been proposed in [Damasio and Frank, 1992] and in [Frank et al., 1997]. An operator has to draw the lesions of each subject in the reference template using anatomical landmarks. The operator has to be an experienced neuro-anatomist, the process is time consuming, and as pointed out in [Fiez et al., 2000], this method is subject to an important inter and intra observer variability. Image registration provides an automated method to perform this task. As nonrigid registration is biased by the presence of lesions, most authors prefer to use affine registration [Narayanan et al., 1997; Charil et al., 2003] or [Enzinger et al., 2006]. Indeed, affine registration is robust to the presence of lesions in the brain but only the global shape of the brain will fit the reference.
In this article, we propose a solution for these two problems and have a nonrigid registration that is not distorted by lesions and an automated method to map MS lesions in a reference brain taking inter subject variability into account.
State of the Art of Pathological Brain Images Registration
Given two images, the aim of registration is to find the transformation that maps the voxels from one image (the reference) to the voxels of the other (the floating image). To restrict the search space and find a realistic transformation, one usually requests that the transformation be smooth and/or invertible [Christensen et al., 1993; Rueckert et al., 2006; Sdika, 2008].
For the registration of normal brains, this requirement makes sense when both the reference image and the floating image have the same structures. An invertible transformation guarantees the preservation of the topology of the floating image before and after the transformation.
For the registration of nonhealthy brains, the invertibility of the transformation is no longer a reasonable assumption as abnormal structures such as tumors or lesions can be present. Nevertheless, apart from the regions where the new structures appear, the topology should be preserved.
For the problem of tumors, a biomechanical model of the growth of the lesions can be used prior and after the registration as in [Kyriacou et al., 1999] or a “tumor seed” can be added to the atlas before the registration as in [Dawant et al., 2002]. These methods cannot be used here. Indeed, a tumor will grow and push the surrounding tissues of the brain, whereas multiple sclerosis is more likely to create lesions that “replace” healthy tissues without moving surrounding tissues.
Another approach consists of removing the influence of the pathological voxels during the registration process. The voxels in the lesions are removed from the similarity metric driving the registration: the cost function is masked so that only the voxels from normal structures are used. It has been applied to focal lesions in [Brett et al., 2001] or to tumors in [Radu et al., 2004].
In [Meier and Fisher, 2005], the registration is not based on voxel intensity but works by first segmenting and parameterizing different brain structures and then finding a transformation that makes these binary structures match. In their work, they used the brain surface, the midsagittal plane, and the ventricles surface. As MS lesions do not appear in these structures, they do not affect the registration, but the registration will not make the grey matter structures match either.
In general, three approaches can be distinguished: removing the lesions from the patient image and aligning, adding the lesions to the atlas and aligning, or removing the influence of the lesions during the registration.
Our method consists of inpainting white matter lesions before performing the registration: the intensity in the lesions is replaced to remove them from the original image. Usually, image inpainting is done by smoothly interpolating the image in the inpainting area while continuing the level sets as in [Bertalmio et al., 2000; Oliveira et al., 2001]. One can also try to reproduce the surrounding texture as in [Bertalmio et al., 2003; Drori et al., 2003]. We propose in this article an inpainting algorithm dedicated to the problem of filling white matter lesions in brain images.
Our inpainting based method is adapted to the physiological process of MS, computationally efficient and fully automated once the lesions have been segmented. It allows the registration of an MS patient and the mapping of MS lesions to an atlas or a single case reference template.
In this article, there are three contributions: (i) the introduction of inpainting in biomedical image processing as an effective tool to remove the influence of lesion during nonrigid registration of patients, (ii) the proposition of an inpainting algorithm dedicated to this problem and (iii) the comparison between different inpainting methods using state of the art methods showing that our method improves the registration of MS patient brain MR images.
METHOD
Overall Approach
The method we propose in this article applies to the nonrigid registration of multiple sclerosis brains. This disease causes the formation of lesions mostly visible in the white matter. Some lesions can also be located in the cortical or deep grey matter but are more difficult to appreciate with current imaging technology.
White matter lesions must have already been segmented either manually or with a semi-automated software as binary regions in the patient image. Then, they are removed from the image and the space left is reconstructed to make the image look like a normal brain. We can subsequently use a standard nonrigid registration algorithm that can preserve the topology of the floating image.
An Inpainting Algorithm Using Anatomical Prior
The objective of image inpainting is to fill missing parts in a given image. Most image inpainting techniques found in the literature are applied to 2D images for scratch removal from paintings, photo restoration, object or text removal.
In general, the problem of image inpainting is ill-posed. As the intensity of the voxels in the missing regions is not known, the objective is to fill the regions in a coherent and visually acceptable way by continuing the grey level or texture of surrounding voxels.
In our case, the objective of the inpainting step was to fill the lesions to make the brain look like a healthy brain. As image inpainting will be used for a specific range of images (images of brains with a given modality) and a specific type of inpainting mask (MS lesions), a priori knowledge on the problem can be used to design dedicated inpainting algorithms. We have evaluated three inpainting methods to fill white matter lesions.
Basic inpainting
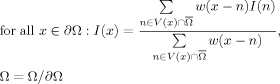
 its complement (the voxels outside Ω), ∂Ω its border (voxels of Ω having on of its 6 neighbours in
its complement (the voxels outside Ω), ∂Ω its border (voxels of Ω having on of its 6 neighbours in  ), V(x) a neighbourhood of x (a 3 × 3 × 3 neighborhood in our implementation) and w a Gaussian kernel.
), V(x) a neighbourhood of x (a 3 × 3 × 3 neighborhood in our implementation) and w a Gaussian kernel.This algorithm will be denoted as BI (basic inpainting) in the rest of this paper
Note that, as some voxels are removed during every iteration, this algorithm is guaranteed to terminate.
Local white matter inpainting
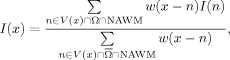
If the segmentation is inexact or inaccurate, the algorithm might not start for some lesions (for example if the lesion is surrounded by GM on the segmentation). In this case, the neighborhood V and the Gaussian kernel w can be dynamically enlarged to make the neighborhood reach the NAWM mask.
Note that, as only the NAWM is used to inpaint the lesion, enlarging V and w is not problematic with LWMI and can be beneficial for the robustness of the method. Indeed, voxels not directly in contact with the lesions (and not affected with partial volume effect, fuzzy boundary or other influence of the lesion) can be used to fill the lesion areas. This is another clear advantage of LWMI over BI for which enlarging V means increasing the chances to use non WM structures to fill the lesions.
In our implementation, a 5 × 5 × 5 neighborhood of x is used for V(x)
Global white matter inpainting
A third possibility to inpaint the white matter lesion was to fill the MS lesions with the mean intensity of the NAWM over the whole brain. This constant is automatically found by computing the average intensity over the NAWM mask provided by FAST.
The Nonrigid Registration
Following the inpainting step, we perform a nonlinear registration using the inpainted image. As the topological changes due to lesions have been removed before the registration, constraints to preserve topology or penalization of nonsmooth transformation can be used during the registration process everywhere in the image.
The algorithm used, as described in [Sdika, 2008], models the registration by a nonlinear optimization problem with nonlinear constraints to prevent the Jacobian to be negative. The constrained optimization problem is solved by using a combination of the multipliers method and the L-BFGS algorithm with a non-monotone line search. The transformation is modeled using cubic splines, making it intrinsically smooth, local, compact, and fast to compute. The cost function is the squared difference between the reference and the deformed version of the floating image, which is adapted to monomodality registration. A multiresolution approach is used to speed-up the registration and to avoid local minima.
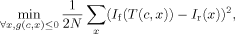
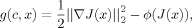
Before the nonrigid registration, a slight Gaussian smoothing (σ = 0.7) is applied to both the reference and the floating image to reduce the effect of whole integer intensity quantitation values and to improve signal to noise ratio (SNR).
EVALUATION
Material
The images we used were T1 weighted 3D gradient echo images with a resolution of 1 × 1 × 1 mm acquired on a 3 Tesla General Electric (GE) MR scanner equipped with an 8-channel receiver coil. The lesion masks of the MS patients have been manually segmented by an experienced MS neurologist.
Lesion Mapping Example
To map lesions from a patient brain to a reference healthy brain using inpainting one needs to: inpaint the patient white matter lesions, perform the nonrigid registration using the inpainted image as the floating image and the healthy brain as reference and then, map the patient lesion mask using the transformation found by the registration.
An example of such a mapping is shown in Figure 1. Note that on this figure, some lesions seem to be created, some others seem to disappear but if you consider them as 3D object and look at few neighboring slices in the patient and the control, no lesions are added or lost.
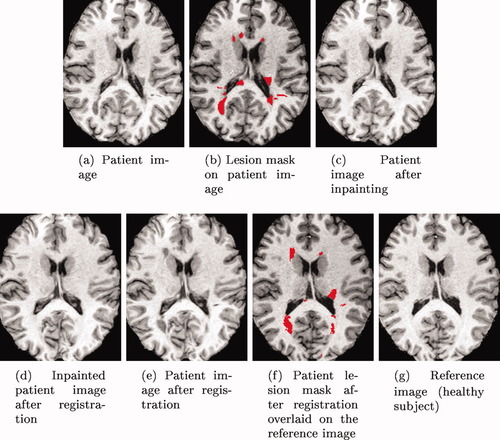
Example of lesion mapping by inpainting white matter lesions before the registration. On the patient image (a) the lesions are segmented out (b) and inpainted using the LWMI method (c). The registration is performed between the inpainted patient (c) and the reference image (g). The output transformation can finally be applied on the inpainted patient (d) the original patient image (e) and on the lesion mask of the patient (f). Note that some lesions appeared and disappeared on this slice but in 3D, no lesion is added or lost. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
Protocol for Numerical Simulation
In this section, we will evaluate quantitatively different ways to register a patient image with white matter MS lesions to a reference template. To compare the different methods, we propose an evaluation procedure similar to the one used in [Brett et al., 2001]. Simulated datasets are created and the output transformations of the different methods are compared to a ground truth.
The simulations are generated as follows. Using a healthy brain c and a patient brain p with its lesion mask lp, an artificial image cp and its lesion mask lcp are created by mapping the lesions of the patient to the control.
For another control c′ and a given registration method with lesions, a transformation T can be estimated between cp with its lesion mask lcp and c′.
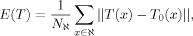
Results
The results of the evaluation are shown on Figure 2 for the error in the whole brain and on Figure 3 for the error in the lesions. Regardless of the lesion mapping method used to create the simulation set, one can see that the LWMI method gives the best results followed by BI, GWMI and CFM, the Naive method comes last.
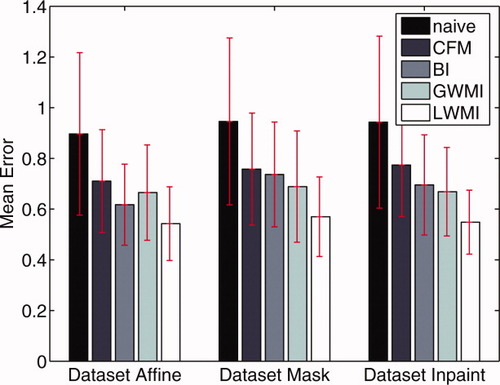
Mean and standard deviation of the error in the whole brain for each set of simulations and each method. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
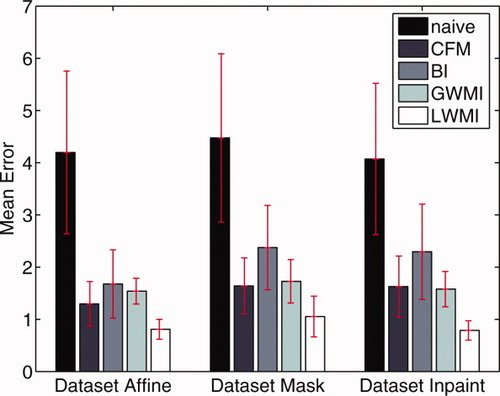
Mean and standard deviation of the error in the lesion mask for each set of simulations and each method. [Color figure can be viewed in the online issue, which is available at www.interscience.wiley.com.]
As already reported in [Brett et al., 2001] for focal lesions or in [Radu et al., 2004] for tumors, the cost function masking approach improves the registration compared to the Naive method. Indeed the lesions are outliers that are removed before the fit of one image to another.
The experiments in this article also show that inpainting the lesions with LWMI before the registration improves the registration over the CFM. The rationale behind the inpainting approach is to try to correct the outliers instead of removing them during the fit. A good outlier correction method provides, in this case, a better fit.
As expected, the difference between the methods is more visible in lesion area and the superiority of LWMI is clearer. Indeed, LWMI is the only method with subvoxel accuracy in the lesion area. Note also that the interval of one standard deviation around the mean do not overlap between LWMI and the second best method (CFM) for the datasets Affine and Inpaint. This emphasizes the need to pay a special attention to the registration method if the object of the study is the spatial distribution of lesions.
Results from statistical analysis show that the superiority of LWMI is highly significant. Tables I and II present the P-values of right tail T-tests between the output of LWMI and the other methods for the three datasets. With a significance threshold of 0.05 all the tests show the significance of the superiority of LWMI over the other methods presented.
| Naïve | CFM | BI | GWMI | |
|---|---|---|---|---|
| Dataset affine | 3.8e-12 | 2.5e-09 | 5.6e-04 | 6.5e-07 |
| Dataset mask | 4.9e-12 | 1.7e-08 | 1.3e-06 | 1.1e-04 |
| Dataset inpaint | 4.3e-12 | 2.7e-11 | 7.8e-07 | 3.4e-06 |
| Naïve | CFM | BI | GWMI | |
|---|---|---|---|---|
| Dataset affine | 4.7e-19 | 1.9e-11 | 3.8e-13 | 3.6e-25 |
| Dataset mask | 5.7e-19 | 3.6e-08 | 9.7e-14 | 1.8e-23 |
| Dataset inpaint | 5.1e-20 | 2.4e-13 | 2.1e-14 | 6.9e-24 |
DISCUSSION
In this work, an original approach was proposed to perform nonlinear registration between two brain images when at least one of them has MS lesions. It consists of inpainting white matter lesions; the inpainted image is then used for nonlinear registration in lieu of the original patient image. Secondly, a dedicated inpainting algorithm has been proposed to fill the lesions, using the properties of the images to inpaint (images of the brain) and the inpainting mask (MS lesions). The lesions are inpainted using the intensity of surrounding normal appearing white matter voxels.
Since our lesion inpainting approach is an easy preprocessing step before the registration, any standard nonrigid registration algorithm can be used without modification. Besides, any brain with white matter lesions can be used as the reference image or the floating image of the registration algorithm. This is not the case with the CFM method. Indeed, if a mask is used to remove the influence of a region of the floating image, the voxels of the reference mapped to this region will have a null cost. Consequently, the algorithm will tend to map voxels of the reference to the area of the floating image with no cost and the lesions in the floating image would have the tendency to attract the surrounding tissue. So, with the cost function masking approach, the brain with lesions has to be used as the reference of the registration. As for morphometry or lesion mapping, the reference image of the registration should be the reference template (a control subject or an average of a group of controls), a solution would be to do the registration with the patient as reference and the lesions masked, and then, to invert the transformation. The inpainting method does not raise this issue. The lesions of the patient are inpainted, and then, the patient image can be used as either the reference or the floating image (or both) during the registration.
The evaluation of the different methods, summarized in Figures 2 and 3, favors the LWMI method over CFM. The mean error obtained with the LWMI method is clearly reduced compared to the other methods, especially in the lesion area. This is of importance when the spatial distribution of the lesions is the object of the study.
Instead of removing the outliers as the CFM method does, the inpainting method tries to reconstruct the cost function as it would be without the lesions. The registration algorithm is then driven to a better solution with this reconstruction than when no information is available at the lesion location. The GWMI method uses the a priori knowledge that the lesions are in the white matter and BI fills the lesions with surrounding voxels, using local information for the inpainting. The LWMI method combines these two properties to inpaint the lesions using the local values of the white matter and consequently, produces the best results of the evaluation. With a better reconstruction method, the solution found by the registration is also better.
The inpainting method we proposed (LWMI) uses the output of the segmentation of the brain in CSF, GM, and NAWM. A high accuracy is not required for this segmentation. Indeed, we only need the intensity of the NAWM in the neighbourhood of the inpainted area. If we are not confident in the segmentation accuracy or if the lesion boundary is fuzzy or if we want to improve the robustness of the method, a good prescription would be to erode the NAWM mask and to increase the size of the neighborhood V(x) used in the inpainting method.
We assume in this article that grey matter lesions have only a minor influence on the registration. If this assumption is considered too strong, grey matter lesions can also be inpainted the same way white matter lesions are inpainted, by filling them with the surrounding grey matter voxel intensities.
Our LWMI inpainting method can be applied to different contrast modalities (T1, T2, proton density…) and other neurological diseases affecting the white matter. The only requirement is that intensity in the lesions must be uniform, without details to reconstruct, create or extend from the neighborhood. The extension of our inpainting based approach to DTI images will be the object of future work.
Acknowledgements
The authors would like to thank Dr Hélène Ratiney, PhD and Alan Evangelista, BA for reviewing the manuscript and Dr Roland Henry, PhD and Dr Hélène Ratiney for helpful discussion.




