More “mapping” in brain mapping: Statistical comparison of effects
Abstract
The term “mapping” in the context of brain imaging conveys to most the concept of localization; that is, a brain map is meant to reveal a relationship between some condition or parameter and specific sites within the brain. However, in reality, conventional voxel-based maps of brain function, or for that matter of brain structure, are generally constructed using analyses that yield no basis for inferences regarding the spatial nonuniformity of the effects. In the normal analysis path for functional images, for example, there is nowhere a statistical comparison of the observed effect in any voxel relative to that in any other voxel. Under these circumstances, strictly speaking, the presence of significant activation serves as a legitimate basis only for inferences about the brain as a unit. In their discussion of results, investigators rarely are content to confirm the brain's role, and instead generally prefer to interpret the spatial patterns they have observed. Since “pattern” implies nonuniform effects over the map, this is equivalent to interpreting results without bothering to test their significance, a practice most of the experimentally-trained would eschew in other contexts. In this review, we appeal to investigators to adopt a new standard of data presentation that facilitates comparison of effects across the map. Evidence for sufficient effect size difference between the effects in structures of interest should be a prerequisite to the interpretation of spatial patterns of activation. Hum. Brain Mapping 19:90–95, 2003. © 2003 Wiley-Liss, Inc.
INTRODUCTION
To many, modern brain mapping represents the premier scientific paradigm for examining the relationship between activity in specific neural systems and mental processes. Indeed, never before has it been possible to measure levels of brain activity or tissue characteristics with such fine spatial sampling. The recent acceleration in the number of brain mapping reports appearing in the literature is testament to the wide acceptance that the technique has received in neuroscientific circles. It would be specious to contend that this large body of new data has not substantially enriched our understanding of the functional anatomy of mental processes, or that it will not continue to do so. However, it is the premise here that the most common approaches to “mapping” brain functions actually reveal almost nothing about the spatial distribution of the effects of the experimental manipulations, and in this way the most critical information relevant to localizing the functions in question is concealed. Many investigators focus almost exclusively on only one bit of information about the variability in effect size across the field of view (in this case, across the brain); namely, whether the effects do or do not reach the investigator's criterion for significance. The argument advanced here is that in presenting brain mapping results, investigators should display, at the least, in addition to the positions at which the estimated effect size (EES) meets this criterion, enough additional information about the distribution of EES that a reader could reasonably examine the map to determine whether the effects in specific structures or regions are likely to differ reliably. The term EES is used here to refer to the statistic computed for each voxel (typically, a t-statistic, though a variety of other statistics can, and have been, substituted). We also argue that, in the interpretation of the results of mapping studies, inferences about the “specificity” of the relationship between the experimental variable and activated structures, circuits, or systems, should be referenced to the roles of particular other structures in which the EES has been shown to differ substantially.
EVIDENCE FOR LOCALIZATION OF FUNCTION IN NEUROPSYCHOLOGY
In the long history of neuropsychology, theorists have distinguished between three levels of evidence for localization of function (sometimes referred to as functional segregation) in the brain: association, dissociation, and double dissociation [Jones, 1983; Shallice, 1988; Teuber, 1995]. A classical example of a simple association is an observation that degree of damage to a brain structure (S1) is correlated with degree of functional impairment on a test of a specific function (F1). It has long been acknowledged, however, that such an observation, by itself, provides no evidence for localization of function, because it does not preclude either the possibility that damage to S1 impairs many, if not all, functions, nor that damage to many, if not all, structures impairs F1. Stronger evidence for localization is the observation that damage in S1 impairs F1 to a greater extent than does damage to a second structure (S2). This represents an anatomical dissociation. Note that comparing statistically the association of S1 with F1 and the association of S2 with F1 and finding a significant difference establishes such a dissociation. Of course, evidence that damage to S1 is significantly more strongly associated with F1 impairment than to impairment of a second function (F2) is also a dissociation, generally referred to as a functional dissociation.
Neuroscientists are familiar with dissociations, and most are also well aware of their pitfalls. Considering the first example above, it is possible that the stronger association with F1 impairment of damage to S1 than of damage to S2 was due, not to a specific relation between S1 and F1 but to the relative insensitivity of the measure of S2. In other words, it is possible that a more sensitive measure of the damage to S2 would have revealed an equally large effect on F1. Similarly, the dissociation given in the second example could have occurred because of “unequal” measurement sensitivity of the F1 and F2 measures. Traditionally, neuroscientists have attempted to counter the weaknesses of “single” dissociations such as these by establishing “double dissociations.” The example of double dissociation is obvious: here it must be true both that damage to S1 is significantly more strongly associated with impairment of F1 than F2, and also that damage to S2 is significantly more strongly associated with impairment of F2 than F1. In this case, the investigator is more confident concluding that differences between the functional demands of the F1 and F2 measures lead to different levels of dependence on the integrity of S1 and S2.
BRAIN MAPPING EXPERIMENT
These examples have been cast in terms of the classical “lesion model” in neuropsychology. It is not the intent here to argue the merits of such models; however, the logic could equally apply to relationships between brain activity measures and task manipulations or functional parameters. Consider a typical brain mapping result. Usually the level of activity (BOLD, blood flow, electrical current, etc.) in a large number of brain voxels is measured while the subject is in differing states, and then the activity levels in different states are contrasted statistically. In other cases, the level of some parameter of interest is in effect correlated with the level of activity in the brain voxels. The question often posed by the investigator is whether the EES in any voxel, or set of voxels, exceeds that expected by chance, given the number of voxels examined. If the answer is yes, the permissible conclusion is that a significant “brain activation” effect has occurred. The locations of those voxels in which the EES exceeds the criterion implicate the tissue in these locations as encompassed within this “brain activation” effect. However, note that what has been demonstrated here is, in the parlance of the previous section, a simple association. All of the statistical tests involve only S1; there is no S2. In no case is the effect in one voxel compared statistically to that in another. Therefore, there is no test of dissociation, let alone double dissociation.
The problem can be illustrated with a simple example: Suppose that a voxel t statistic >3.5 is required for a voxel to be considered to be “activated.” Using this criterion, a voxel with t = 3.0 would not be considered to be “activated.” The effects in these two voxels with ts of 3 and 3.5, however, would not be significantly different from each other, and therefore no inference of a distinction between the effects in the two voxels would be justified.
The convention in brain mapping is to display the map of “activated” voxels superimposed in color on an image that reveals the underlying anatomy. For example, 21 articles published in Human Brain Mapping in 2001 reported voxel-based analyses of functional effects observed with PET or fMRI, and exhibited the regional pattern using a color-mask superimposed on structural images. Two of these articles [Crespo-Facorro et al., 2001; Grabowski et al., 2001], both from Iowa City, provided informative effect size maps meeting the criteria suggested in this article. In the remaining 19 of 21 articles, however, only the positions of voxels with EES exceeding the investigators' criteria for significance were displayed. Many investigators apparently infer that a distinction between the colored voxels and the uncolored voxels has been demonstrated, despite the fact that no comparison of the effects in different locations has occurred (i.e., location is not a factor in the analysis model). Investigators exhibit a strong tendency to interpret the “pattern” of the activation by ascribing different functional characteristics to the particular structures that underlie the colored voxels than to those that do not. One need only read a few brain mapping reports to find evidence that this is the case. The literature is replete with discussion sections attempting to explain, for example, the fact that a previous study with a similar design yielded “an additional site of activation in location x,” revealed bilateral rather than unilateral activation within some Brodmann's area, or did not produce “the activation in structure X observed in the present study.” In fact, many would say that explaining such discrepancies is the real grist for the mill in the brain mapping field. In reality, the typical brain map contains almost no information about the spatial distribution of EESs. Commonly, the information amounts to one bit; i.e., the map reveals for each voxel, whether the EES exceeded or did not exceed the criterion chosen by the investigator. On some occasions, investigators color-code the range of the values of the mapped statistic above the criterion, though often no legend is included to permit quantitative comparison of the regions distinguished by this code. There is very often no evidence presented, either in the reported results or in the map, to preclude the possibility that the EES in every uncolored voxel hovers just below the criterion value, and, therefore, differs only trivially from that present in the colored voxels. This, of course, is very unlikely; but it is likely that the effects in many voxels are of magnitudes that are not statistically distinguishable from those in the colored voxels. Knowing which voxels do and which do not have substantially less association with the experimental variable would provide evidence for dissociation in the classic sense, since this would represent statistical evidence for different effect sizes in different parts of the map.
It should perhaps be noted that a statistically defensible dissociation relies upon a significant region by condition interaction. Such a “spatial” effect can (theoretically) be estimated within a mass univariate model, in which each voxel is treated independently, or within a multivariate model, in which voxels are regarded as components of a single (whole brain) multivariate observation. These issues have been discussed in the brain mapping literature by others [Friston et al., 1995, 1996; Worsley et al., 1997]. However, the major point raised here is that present standards in the field encourage inferences and discussion of what are in reality region by condition interactions in the absence of any statistical evidence for such interaction effects in the results.
EXAMPLES OF EFFECT SIZE MAPS (ESM)
Two typical “mapping” results are shown in Figures 1 and 2 (top). Both maps were generated from data collected during an fMRI (BOLD) experiment in which 8 normal volunteers participated. The subjects' task involved performing different simple finger movements with the right hand when prompted by verbal instructions displayed on a screen. The instructions read, “REST,” “TAP,” “SEQUENCE,” and “ALTERNATE.” The tap condition was simple repetitive tapping of the index finger and thumb, and the sequence and alternate conditions were a simple sequence of the fingers to the thumb, and a more complex sequence of the fingers to the thumb, respectively. Contrasts of BOLD response under different conditions were performed with AFNI (Robert Cox, NIMH). The specific results of these contrasts are of little interest here, though the pattern of brain activation is consistent with others obtained with simple motor tasks. The maps are presented for illustrative purposes only.
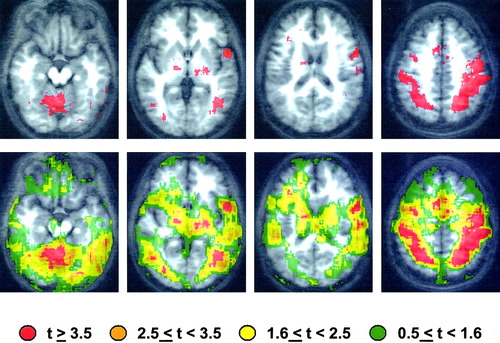
Contrast of the tap with the rest condition: Top: The voxels for which the tap condition response exceeded the rest condition response with t ≥ 3.5 are color-washed in red.
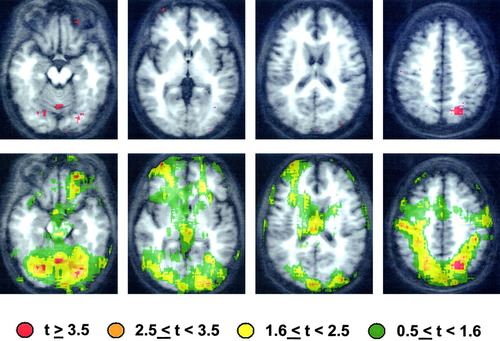
Contrast of the alternate with the tap condition.
In Figure 1 (top), the voxels for which the tap condition response exceeded the rest condition response with t ≥ 3.5 (a typical criterion) are color-washed in red. No clustering (i.e., selection based on cluster size) was performed. The pattern suggests “significant” cerebellar and motor strip activation, frontal opercular activation, and some evidence for additional activation in left posterior temporal cortex and subcortical structures. The map shown in Figure 1 (bottom) displays, in addition to the positions of voxels with t ≥ 3.5 (shown again in red), positions of voxels with effect sizes in different ranges. Arguably, the effects in many of these voxels are not significantly smaller than those in the voxels with t = 3.5; i.e., they are not smaller than what has been defined as a “significant” effect. Similar maps are presented in Figure 2 for the contrast of the alternate with the tap condition. In this case, the voxels shown in red had higher BOLD responses during the more complex alternate task (in spite of a lower response rate) with t ≥ 3.5, and again, effect sizes in different ranges are color-coded in Figure 1 (bottom).
The assertion here is that an investigator implying that effects observed in the red voxels are distinct from those in orange voxels is making a statistically unsupported inference. For example, describing the results shown in Figure 1 (top) as “lateralized left frontal opercular activation” would be misleading. The map shown in Figure 1 (bottom) suggests that the effects in many homologous right hemisphere voxels are not statistically lower in magnitude than those in the left hemisphere. In other words, the “laterality” effect is unlikely to be statistically significant for this contrast. Similarly, for the tap/alternate contrast, an area of activity increase in homologous right-hemisphere areas that is statistically similar in magnitude to the left-sided effects accompanies the apparently unilateral left-sided increase in activity in the peri-rolandic cortex.
To give another example, one might be tempted to “interpret” results shown in Figure 2 (top) as revealing cerebellar and cortical, but not subcortical, increases associated with task complexity. However, examination of Figure 2 (bottom) suggests that complexity-related activation in subcortical regions within diencephalic and striatal structures may not be statistically different in magnitude from that in the cerebellar and cortical voxels shown in red. Any discussion of these results that contrasted the role of left motor cortex, for example, with that of the thalamus, in relation to motor complexity, would clearly be suspect given the maps shown in Figure 2 (bottom).
These examples do not represent a proposed “specific method” for examining and displaying effect size differences across maps. The design of appropriate estimates of the statistical reliability of effect size differences is likely to be a long-term and contentious process. Various approaches will probably yield useful results, and a discussion of the relevant statistical issues is beyond the scope of this article. However, any method that displays effect-size information in a form that allows those interpreting the map to estimate the degree to which the effects in one structure of interest differ statistically from those in another structure of interest should help to establish true functional dissociations.
ADVANTAGES OF ESMS
As noted above, even when ESMs reveal statistically reliable differences between effects in different regions or structures, the results represent single, rather than double, dissociations. However, in some cases, the results of multiple experiments satisfy the conditions for double dissociations. In particular, this is true when a structure in an activated zone and a structure in a zone with statistically lower EES “trade zones” in another experiment. Without ESMs, investigators cannot distinguish double dissociations from disparities in activation patterns that are statistically consistent with sampling error.
An implication of the argument here is that when archiving the results of brain mapping studies for future use (such as in meta-analyses), care should be taken to preserve the entire map of effects, rather than a map of the location of significant activations. Only with the full maps can meaningful between-experiment analyses be performed for detecting reliable pattern disparities across conditions.
It may also be useful to identify regions that are rarely “activated” but instead frequently are the sites of effects not statistically distinguishable from the smallest significant estimated effect size. While this could occur because these neural structures contribute little to the functions under investigation, it could also occur because the mapping technique in use has relatively lower sensitivity in the region. Consistent failure to observe dissociation of the function of such an area from the functions of other areas may prompt researchers to examine more carefully the local sensitivity of the method in this region.
SUMMARY AND CONCLUSIONS
The assertion here is that present standards for conveying the results of brain mapping experiments, because they do not require investigators to provide information about spatial variability in effect sizes, conceal most of the information relevant to inferences about localization of functions. A suggested remedy for this is to display, and to compare statistically when appropriate, the experimental effects in different parts of the map. The recommendation is that results of mapping experiments be visualized in a manner that permits a more detailed assessment of the regional variability in EES, i.e., with ESMs. When investigators wish to make inferences about the roles of specific structures or regions, vis-à-vis the roles of others, such inferences should be accompanied by statistical evidence for meaningful variation in EES in the different regions of interest.
Acknowledgements
We thank Dr. Greg Brown and anonymous reviewers for helpful critiques of earlier versions of this article.




