A General Framework for Association Tests With Multivariate Traits in Large-Scale Genomics Studies
ABSTRACT
Genetic association studies often collect data on multiple traits that are correlated. Discovery of genetic variants influencing multiple traits can lead to better understanding of the etiology of complex human diseases. Conventional univariate association tests may miss variants that have weak or moderate effects on individual traits. We propose several multivariate test statistics to complement univariate tests. Our framework covers both studies of unrelated individuals and family studies and allows any type/mixture of traits. We relate the marginal distributions of multivariate traits to genetic variants and covariates through generalized linear models without modeling the dependence among the traits or family members. We construct score-type statistics, which are computationally fast and numerically stable even in the presence of covariates and which can be combined efficiently across studies with different designs and arbitrary patterns of missing data. We compare the power of the test statistics both theoretically and empirically. We provide a strategy to determine genome-wide significance that properly accounts for the linkage disequilibrium (LD) of genetic variants. The application of the new methods to the meta-analysis of five major cardiovascular cohort studies identifies a new locus (HSCB) that is pleiotropic for the four traits analyzed.
Introduction
Pleiotropy, the influence of one gene on multiple traits, is a widespread phenomenon in complex human diseases [Sivakumaran et al., 2011]. Recent years have seen a heightened interest in discovering genetic variants with pleiotropic effects [Gottesman et al., 2012; Lawson et al., 2011; Paaby and Rockman, 2012; Watanabe et al., 2000]. The joint analysis of multiple traits can increase statistical power by aggregating multiple weak effects and provide new biological insights by revealing pleiotropic variants [Amos and Laing, 1993; Jiang and Zeng, 1995].
The advent of large-scale genetic association studies, particularly genome-wide association studies (GWAS), poses tremendous challenges in analyzing multiple traits. First, there are a huge number of genetic variants to be tested, which may entail considerable computation burden. The inclusion of covariates (e.g., ancestry variables to account for population stratification) may make the computation even more intensive. Second, complex diseases are characterized by a wide variety of traits, some of which are continuous (i.e., quantitative) and some of which are discrete. Third, it is desirable to combine results from multiple studies, some of which may consist of unrelated individuals and some of which may consist of families; the genetic variants and the traits may not be uniformly measured in all studies. Fourth, it is necessary to adjust for multiple testing, but the conventional Bonferroni correction may be overly conservative.
There exist several statistical methods for association analysis of multiple traits, but none of them addresses all the above issues. Ferreira and Purcell [2009] suggested canonical correlation analysis, which is computationally fast but does not accommodate covariates. Liu et al. [2009] suggested a Wald statistic based on generalized estimating equations (GEE) [Liang and Zeger, 1986] for the mixture of one continuous trait and one binary trait. Their method does not accommodate family data, and the Wald statistic requires fitting a regression model for each genetic variant, which can be time consuming. Yang et al. [2010] suggested a linear combination of univariate test statistics with data-dependent weights by estimating the weights from part of the data and calculating the test statistic from the remaining data. The P-values are assessed by permutation, which is computationally demanding. Maity et al. [2012] proposed a kernel machine method for joint analysis of multiple genetic variants, which is equivalent to testing the variance component in a multivariate linear mixed model. Recently, van der Sluis et al. [2013] proposed a method called “trait-based association test that uses extended Simes procedure” (TATES). The Simes procedure was originally designed to alleviate the conservativeness of the Bonferroni correction; the TATES extends the Simes procedure to the multivariate-trait analysis by harnessing the correlations among the traits.
In this paper, we provide a very general framework for association analysis of multiple traits, which simultaneously tackles all the aforementioned challenges. Our framework covers both studies of unrelated individuals and family studies and allows any type/mixture of traits. To enhance robustness, we relate the marginal distributions of multivariate traits to genetic variants and covariates through generalized linear models without parametric modeling of the dependence among the traits or family members; we account for the dependence in constructing the test statistics by estimating the correlations empirically from the data. We develop score-type statistics, which are computationally fast and numerically stable even in the presence of covariates and which can be combined efficiently across studies with different designs and arbitrary patterns of missing data. We consider various types of multivariate test statistics and compare their power both theoretically and empirically. We provide a strategy to determine genome-wide significance that properly accounts for the linkage disequilibrium (LD) of genetic variants. We demonstrate the usefulness of the new methods through extensive simulation studies and an application to five GWAS studies involving cardiovascular traits.
Methods
In this section, we present our general framework for association tests with multivariate traits. We first construct the marginal models and the corresponding score-type statistics. We then show how to combine those statistics to form multivariate test statistics. Finally, we discuss meta-analysis and genome-wide significance thresholds.
Calculating Score Statistics and Their Covariance Matrix
We consider a single study with a total of n unrelated individuals, K (potentially correlated) traits, and p covariates (including the unit component). For 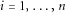 and
and  , let
, let  be the kth trait of the ith individual. For
be the kth trait of the ith individual. For 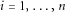 , let
, let  be the p-vector of covariates for the ith individual, and let
be the p-vector of covariates for the ith individual, and let  denote the number of minor alleles (or the imputed dosage) the ith individual carries at a particular test locus.
denote the number of minor alleles (or the imputed dosage) the ith individual carries at a particular test locus.
We assume that the marginal distribution of  is related to
is related to  and
and  through a generalized linear model with mean
through a generalized linear model with mean 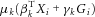 and dispersion parameter
and dispersion parameter  , where
, where  is a specific function, and
is a specific function, and  and
and  are unknown regression parameters. We adopt natural link functions such that
are unknown regression parameters. We adopt natural link functions such that  for continuous traits and
for continuous traits and 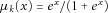 for binary traits.
for binary traits.
To accommodate missing data, we let  indicate, by the values 1 versus 0, whether
indicate, by the values 1 versus 0, whether  is observed or missing, and let
is observed or missing, and let 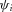 indicate, by the values 1 versus 0, whether
indicate, by the values 1 versus 0, whether  is observed or missing. It is assumed that the covariates have no missing values. (We recommend to exclude the covariates with substantial missingness and to replace the missing values with their sample means for the remaining covariates.)
is observed or missing. It is assumed that the covariates have no missing values. (We recommend to exclude the covariates with substantial missingness and to replace the missing values with their sample means for the remaining covariates.)
 takes the form
takes the form

 is
is
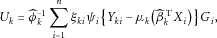
 solves the equation
solves the equation
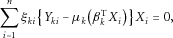
 is a sample estimator of
is a sample estimator of  . For continuous traits,
. For continuous traits,
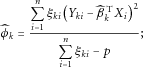
 . Note that the construction of the
. Note that the construction of the 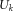 s makes full use of the available data by estimating
s makes full use of the available data by estimating  and
and  from all individuals with nonmissing trait values and is more efficient than the traditional complete-case analysis.
from all individuals with nonmissing trait values and is more efficient than the traditional complete-case analysis. at
at  and applying the law of large numbers, we can show that
and applying the law of large numbers, we can show that 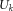 is asymptotically equivalent to the following sum of n-independent terms:
is asymptotically equivalent to the following sum of n-independent terms:
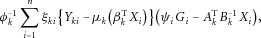
 and
and  are the limits of
are the limits of 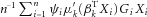 and
and 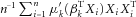 , respectively, and
, respectively, and  . Define the score vector
. Define the score vector
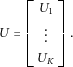

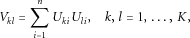


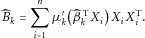
Note that  and
and 
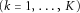 do not depend on the SNP genotypes and thus need to be calculated only once (before looping through all the SNPs). Note also that, given the
do not depend on the SNP genotypes and thus need to be calculated only once (before looping through all the SNPs). Note also that, given the  s, the calculations of U and V do not involve solving any equations. Thus, the implementation of the proposed score-type statistics is orders of magnitude faster than that of the conventional Wald statistics. In addition, the score-type statistics are numerically more stable and statistically more accurate than the Wald statistics, especially when the minor allele frequency (MAF) is low [Lin and Tang, 2011].
s, the calculations of U and V do not involve solving any equations. Thus, the implementation of the proposed score-type statistics is orders of magnitude faster than that of the conventional Wald statistics. In addition, the score-type statistics are numerically more stable and statistically more accurate than the Wald statistics, especially when the minor allele frequency (MAF) is low [Lin and Tang, 2011].
We now extend the above results to family studies. Suppose that we have a total of n families, with  members in the ith family. For
members in the ith family. For 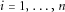 ,
, 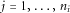 and
and 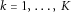 , let
, let 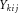 denote the kth trait for the jth member of the ith family,
denote the kth trait for the jth member of the ith family,  denote the p-vector of covariates for the jth member of the ith family, and
denote the p-vector of covariates for the jth member of the ith family, and  denote the number of minor alleles (or the imputed dosage) which the jth member of the ith family carries at a particular test locus. We assume that the marginal distribution of
denote the number of minor alleles (or the imputed dosage) which the jth member of the ith family carries at a particular test locus. We assume that the marginal distribution of 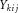 is related to
is related to  and
and  through the same marginal generalized linear regression model as in the case of unrelated individuals.
through the same marginal generalized linear regression model as in the case of unrelated individuals.
 indicate whether
indicate whether 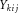 is observed or missing, and let
is observed or missing, and let  indicate whether
indicate whether  is observed or missing. It is assumed that there are no missing values in the covariates. Under the independence working assumption [Liang and Zeger, 1986], the (pseudo-likelihood) score statistic for testing the null hypothesis that
is observed or missing. It is assumed that there are no missing values in the covariates. Under the independence working assumption [Liang and Zeger, 1986], the (pseudo-likelihood) score statistic for testing the null hypothesis that  is
is
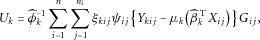
 solves the equation
solves the equation
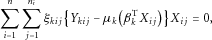
 for continuous traits, and
for continuous traits, and  for binary traits. Again, define
for binary traits. Again, define 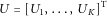 . It follows from the above arguments for the case of unrelated individuals that U is asymptotically K-variate normal with mean 0 and a covariance matrix that can be estimated by
. It follows from the above arguments for the case of unrelated individuals that U is asymptotically K-variate normal with mean 0 and a covariance matrix that can be estimated by  , where
, where
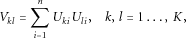
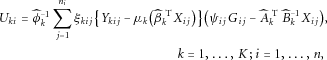
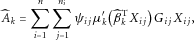
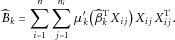
 s.
s.Performing Multivariate Association Tests
 , we calculate the quadratic form
, we calculate the quadratic form


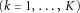 and
and 
 . We then calculate
. We then calculate
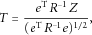
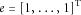 . This test statistic is asymptotically standard normal.
. This test statistic is asymptotically standard normal. s. Note that the score test statistic
s. Note that the score test statistic  is asymptotically equivalent to the Wald test statistic, i.e., the estimate of
is asymptotically equivalent to the Wald test statistic, i.e., the estimate of  divided by its standard error. Thus, T is optimal if the limits of the
divided by its standard error. Thus, T is optimal if the limits of the  s or the standardized
s or the standardized  s are the same. To detect alternative hypotheses under which the original
s are the same. To detect alternative hypotheses under which the original  s are the same, we define
s are the same, we define 
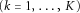 and
and 
 . Note that the limit of
. Note that the limit of 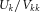 is approximately
is approximately  . We then calculate
. We then calculate
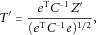
 and
and  . This test statistic is also asymptotically standard normal. When using this test statistic, it is important to use comparable scales for the K traits such that it is plausible for the
. This test statistic is also asymptotically standard normal. When using this test statistic, it is important to use comparable scales for the K traits such that it is plausible for the  to be equal. When using either T or
to be equal. When using either T or  , it is important to code the trait values in such a way that the genetic effects on the K traits are plausibly in the same direction.
, it is important to code the trait values in such a way that the genetic effects on the K traits are plausibly in the same direction.If the effects of the SNP are similar among the K traits, then T and  will tend to be more powerful than Q. If the effects are very different, then Q will likely be more powerful than T and
will tend to be more powerful than Q. If the effects are very different, then Q will likely be more powerful than T and  . In the Appendix, we derive the asymptotic distributions of Q, T, and
. In the Appendix, we derive the asymptotic distributions of Q, T, and  under alternative hypotheses for the important special case of two continuous traits.
under alternative hypotheses for the important special case of two continuous traits.
Combining Results From Multiple Studies
We wish to combine results from L-independent studies. For 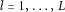 , let
, let  and
and 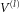 denote the score vector and its (estimated) covariance matrix from the lth study. Then the overall score vector is
denote the score vector and its (estimated) covariance matrix from the lth study. Then the overall score vector is  , and its covariance matrix is estimated by
, and its covariance matrix is estimated by  . Note that
. Note that  is the (pseudo-likelihood) score statistic in the joint analysis of the individual-level data of the L studies (allowing nuisance parameters to be different among the studies). Thus, meta-analysis of score statistics is equivalent to the joint analysis of individual-level data. When there are multiple studies, K pertains to the total number of distinct traits, some of which may not be measured in certain studies. (For
is the (pseudo-likelihood) score statistic in the joint analysis of the individual-level data of the L studies (allowing nuisance parameters to be different among the studies). Thus, meta-analysis of score statistics is equivalent to the joint analysis of individual-level data. When there are multiple studies, K pertains to the total number of distinct traits, some of which may not be measured in certain studies. (For  , we may have four traits that are common between the two studies, two traits that are measured only in the first study, and three traits that are measured only in the second study. Then
, we may have four traits that are common between the two studies, two traits that are measured only in the first study, and three traits that are measured only in the second study. Then  .) Given U and V, we can calculate Q, T, and
.) Given U and V, we can calculate Q, T, and  in the same manner as in the case of a single study.
in the same manner as in the case of a single study.
Determining Genome-Wide Significance
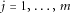 , let
, let 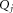 be the value of Q for the jth SNP. If the critical value q0 for the m test statistics satisfies
be the value of Q for the jth SNP. If the critical value q0 for the m test statistics satisfies


 are independent standard normal random variables. Let
are independent standard normal random variables. Let 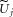 and
and  be the values of
be the values of  and V for the jth SNP. Define
and V for the jth SNP. Define

 can be approximated by that of
can be approximated by that of  [Lin, 2005]. Thus, we determine q0 by the following equation
[Lin, 2005]. Thus, we determine q0 by the following equation

 10,000 times while holding the observed data fixed and set q0 to be the 10,000
10,000 times while holding the observed data fixed and set q0 to be the 10,000 th largest value of the resulting
th largest value of the resulting  's. We may convert the critical value q0 to the P-value threshold p0 by referring q0 to the chi-squared distribution with K degrees of freedom. We can determine the genome-wide significance thresholds for T,
's. We may convert the critical value q0 to the P-value threshold p0 by referring q0 to the chi-squared distribution with K degrees of freedom. We can determine the genome-wide significance thresholds for T,  and
and 
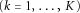 in a similar manner.
in a similar manner.Results
Simulation Studies
We conducted simulation studies to evaluate the performance of the proposed test statistics. We set G to be the number of minor alleles for a SNP with MAF of 0.4 and set X to be normal with mean 0.1G and unit variance. We generated two continuous traits under the bivariate linear model:  and
and  where ε1 and ε2 are zero-mean normal with variances
where ε1 and ε2 are zero-mean normal with variances  and
and  , respectively, and with correlation
, respectively, and with correlation  . We set α to 10−4. To evaluate the type I error, we simulated 10 million data sets under
. We set α to 10−4. To evaluate the type I error, we simulated 10 million data sets under  . To evaluate the power, we simulated 10,000 data sets under various combinations of γ1 and γ2. Each simulated data set consists of 1,000 unrelated individuals. In addition to the three multivariate test statistics,
. To evaluate the power, we simulated 10,000 data sets under various combinations of γ1 and γ2. Each simulated data set consists of 1,000 unrelated individuals. In addition to the three multivariate test statistics,  and
and  , we considered two versions of univariate tests, Uni-B and Uni-corr, which adjust for multiple testing (between the traits) by adopting the Bonferroni correction (i.e., dividing the nominal significance level by the number of traits) and by accounting for the correlation between Z1 and Z2 (using the multivariate normal distribution of U), respectively. We also included the TATES method (van der Sluis et al., 2013).
, we considered two versions of univariate tests, Uni-B and Uni-corr, which adjust for multiple testing (between the traits) by adopting the Bonferroni correction (i.e., dividing the nominal significance level by the number of traits) and by accounting for the correlation between Z1 and Z2 (using the multivariate normal distribution of U), respectively. We also included the TATES method (van der Sluis et al., 2013).
The results are summarized in Table 1. The type I error for the TATES is inflated by about 12%. The type I errors for the other five tests are below the nominal significance level. The Q test has reasonable power against all 12 alternatives. As expected,  is more powerful than the other tests when γ1 is close to γ2, and T is more powerful than the others when
is more powerful than the other tests when γ1 is close to γ2, and T is more powerful than the others when 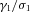 and
and 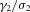 are close to each other. The Uni-B is expected to have lower power than Uni-corr, but the two tests perform very similarly due to the relatively weak correlation between the two traits. The differences between the two tests become more pronounced as the correlation increases; see supplementary Table SI. The TATES has slightly higher power than Uni-B and Uni-corr but also has inflated type I error, especially when the correlation is high.
are close to each other. The Uni-B is expected to have lower power than Uni-corr, but the two tests perform very similarly due to the relatively weak correlation between the two traits. The differences between the two tests become more pronounced as the correlation increases; see supplementary Table SI. The TATES has slightly higher power than Uni-B and Uni-corr but also has inflated type I error, especially when the correlation is high.
 )
) |
 |
Uni-B | Uni-corr | TATES | Q | T |  |
|---|---|---|---|---|---|---|---|
| (0, 0) | (0, 0) | 8.6 |
8.7 |
1.12 |
9.0 |
9.0 |
8.8 |
| (0.3, 0) | (0.21, 0) | 0.6861 | 0.6865 | 0.714 | 0.854 | 0.095 | 0.003 |
| (0.3, 0.1) | (0.21, 0.1) | 0.6865 | 0.6869 | 0.715 | 0.638 | 0.487 | 0.187 |
| (0.25, 0.18) | (0.18, 0.18) | 0.5714 | 0.5723 | 0.606 | 0.594 | 0.700 | 0.641 |
| (0.3, 0.25) | (0.21, 0.25) | 0.9358 | 0.936 | 0.945 | 0.942 | 0.967 | 0.966 |
| (0.2, 0.2) | (0.14, 0.2) | 0.6222 | 0.6229 | 0.651 | 0.594 | 0.632 | 0.702 |
| (0.2, 0.25) | (0.14, 0.25) | 0.9054 | 0.9056 | 0.917 | 0.881 | 0.828 | 0.922 |
| (0.25, 0.25) | (0.18, 0.25) | 0.9128 | 0.913 | 0.925 | 0.906 | 0.917 | 0.947 |
| (0, 0.25) | (0, 0.25) | 0.9034 | 0.9036 | 0.915 | 0.977 | 0.197 | 0.701 |
| (0, 0.3) | (0, 0.3) | 0.9902 | 0.9903 | 0.992 | 0.999 | 0.402 | 0.914 |
| (0.1, 0.25) | (0.07, 0.25) | 0.9034 | 0.9036 | 0.915 | 0.907 | 0.523 | 0.841 |
| (0.1, 0.3) | (0.07, 0.3) | 0.9902 | 0.9903 | 0.992 | 0.994 | 0.742 | 0.968 |
| (0.2, 0.3) | (0.14, 0.3) | 0.9903 | 0.9904 | 0.992 | 0.987 | 0.940 | 0.990 |
We also considered the mixture of a binary trait and a continuous trait. We simulated the binary trait under the logistic regression model  and simulated the continuous trait under the linear model
and simulated the continuous trait under the linear model 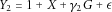 , where ε is normal with mean 2Y1 and unit variance. (The Pearson correlation between the two traits is about 0.65.) As shown in Table 2, Q tends to have higher power than the two univariate tests. As expected,
, where ε is normal with mean 2Y1 and unit variance. (The Pearson correlation between the two traits is about 0.65.) As shown in Table 2, Q tends to have higher power than the two univariate tests. As expected,  is more powerful than the other tests when
is more powerful than the other tests when  , and T outperforms the others when the means of Z1 and Z2 are similar. Again, the TATES has higher power than Uni-B and Uni-corr but at the expense of inflated type I error.
, and T outperforms the others when the means of Z1 and Z2 are similar. Again, the TATES has higher power than Uni-B and Uni-corr but at the expense of inflated type I error.
 |
 * * |
Uni-B | Uni-corr | TATES | Q | T |  |
|---|---|---|---|---|---|---|---|
| (0, 0) | — | 8.7 |
9.0 |
1.02 |
8.7 |
9.7 |
9.3 |
| (0.3, 0) | (3.07, 2.09) | 0.171 | 0.173 | 0.171 | 0.141 | 0.141 | 0.026 |
| (0.3, 0.1) | (3.07, 3.65) | 0.377 | 0.380 | 0.398 | 0.334 | 0.410 | 0.382 |
| (0.25, 0.18) | (2.54, 4.52) | 0.685 | 0.687 | 0.709 | 0.664 | 0.488 | 0.758 |
| (0.3, 0.25) | (3.07, 5.88) | 0.973 | 0.973 | 0.977 | 0.975 | 0.845 | 0.986 |
| (0.2, 0.2) | (2.02, 4.49) | 0.676 | 0.678 | 0.700 | 0.709 | 0.372 | 0.764 |
| (0.2, 0.25) | (2.02, 5.24) | 0.892 | 0.893 | 0.907 | 0.938 | 0.534 | 0.937 |
| (0.25, 0.25) | (2.54, 5.56) | 0.943 | 0.944 | 0.952 | 0.958 | 0.707 | 0.967 |
| (0, 0.25) | (0.02, 4.02) | 0.489 | 0.493 | 0.519 | 0.880 | 0.046 | 0.655 |
| (0, 0.3) | (0.02, 4.79) | 0.782 | 0.784 | 0.808 | 0.987 | 0.104 | 0.888 |
| (0.1, 0.25) | (1.01, 4.62) | 0.722 | 0.725 | 0.750 | 0.899 | 0.210 | 0.832 |
| (0.1, 0.3) | (1.01, 5.37) | 0.917 | 0.919 | 0.930 | 0.990 | 0.347 | 0.960 |
| (0.2, 0.3) | (2.02, 5.97) | 0.979 | 0.979 | 0.984 | 0.994 | 0.688 | 0.992 |
- *
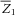 and
and 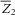 are the sample means of Z1 and Z2, respectively.
are the sample means of Z1 and Z2, respectively.
We also considered four continuous traits with a compound-symmetry correlation structure for the error terms. The results are shown in supplementary Table SII. The basic conclusions remain the same. We added the MANOVA method implemented in R to the case of no covariates. As shown in supplementary Table SIII, MANOVA has slightly higher type I error and power than the Q test. This is consistent with the general phenomenon that the likelihood ratio test is more liberal than the score test [Lin and Zeng, 2011]. Finally, we considered family studies with 250 families (two parents and two children in each family) and two continuous traits. As shown in supplementary Table SIV, the conclusions are similar to the case of unrelated subjects.
Cardiovascular Studies
We analyzed the GWAS data on the Caucasian samples from the Atherosclerosis Risk in Communities (ARIC) study, the Coronary Artery Risk Development in Young Adults (CARDIA) study, the Cardiovascular Health Study (CHS), the Multi-Ethnic Study of Atherosclerosis (MESA), and the Framingham Heart Study (FHS), the sample sizes being 9,068, 1,433, 3,892, 2,286, and 2,789, respectively. The FHS is a family study, and the others consist of unrelated individuals. Each individual was genotyped on 250,000 SNPs. We considered four cardiovascular traits: diabetes status, high-density lipoprotein (HDL), low-density lipoprotein (LDL), and triglycerides; the first trait is binary whereas the other three are continuous. These traits are major players in the development of coronary artery diseases and metabolic syndrome [Grundy, 2012; Holmes et al., 1981]. We aimed to identify genetic factors underlying these traits. Since the HDL is “good” cholesterol, we used negative values of HDL in the analysis.
We performed single-SNP analysis with the following covariates: age, gender, study centers, and the top 10 principle components for ancestry. We calculated the score-type statistics and their covariance matrices for each study and then combined the results of the five studies. The (unadjusted) P-values of the univariate and multivariate tests are displayed in Figures 1 and 2, respectively. The genome-wide significance thresholds based on the Bonferroni correction and the Monte Carlo procedure are marked in both figures.
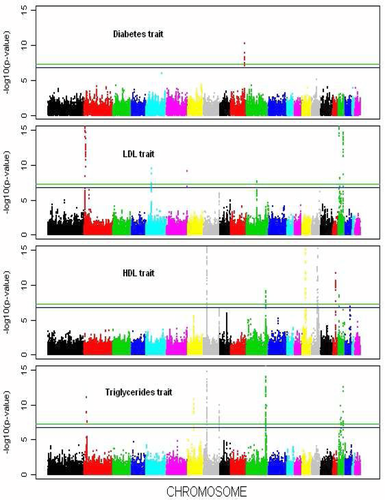
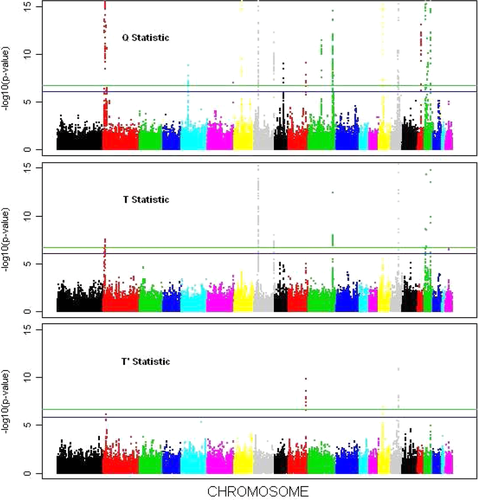
We first examine the results based on the Bonferroni correction. For the four traits, more than 10 regions are above the Bonferroni threshold in the Uni-B test (Fig. 1). Compared to Uni-B, the Q test identifies one new signal that is located on chromosome (Chr) 9 (Fig. 2). The signal on Chr9 identified by the Q test is an accumulation of weak/moderate signals for individual traits. The gene at this locus encodes a protein called ABCA1, which is involved in cellular cholesterol removal (Lawn et al., 1999). This gene was previously found to be associated with metabolic syndrome (Avery et al., 2011). Table 3 lists all the loci discovered by the Q test. (The P-values from the univariate-trait analysis are also shown.) The T and  tests did not identify any additional signals that achieve genome-wide significance, but the two tests yielded more extreme P-values for several SNPs than the univariate tests.
tests did not identify any additional signals that achieve genome-wide significance, but the two tests yielded more extreme P-values for several SNPs than the univariate tests.
| P-values of single-trait analysis | ||||||||
|---|---|---|---|---|---|---|---|---|
| Chr | SNP | Gene | P-value of Q test | Diabetes | LDL | HDL | Trig | |
| 2 | rs515135 | APOB | 6.3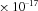 |
4.0 |
3.4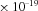 |
5.8 |
3.1 |
|
| 2 | rs1260326 | GCKR | 2.2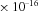 |
3.7 |
3.6 |
6.1 |
8.9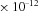 |
|
| 5 | rs12916 | HMGCR | 1.7 |
8.2 |
3.0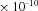 |
2.0 |
9.4 |
|
| 6 | rs10455872 | LPA | 1.1 |
9.3 |
8.7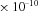 |
1.8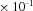 |
8.7 |
|
| 7 | rs7777102 | MLXIPL | 2.2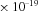 |
4.6 |
8.4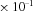 |
3.8 |
1.2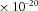 |
|
| 8 | rs1011685 | LPL | 5.3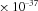 |
5.2 |
7.6 |
2.3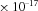 |
4.6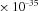 |
|
| 8 | rs2954021 | TRIB1 | 5.9 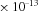 |
6.4  |
1.1 |
2.0 |
1.1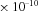 |
|
| 9 | rs2575876 | ABCA1 | 9.5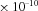 |
2.4 |
1.9 |
2.0 |
4.8 |
|
| 10 | rs7903146 | TCF7L2 | 8.4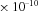 |
5.8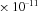 |
8.0 |
8.3 |
6.4 |
|
| 11 | rs174538 | FEN1 | 3.5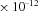 |
1.9 |
2.9 |
3.2 |
6.6 |
|
| 11 | rs964184 | ZNF259 | 2.7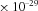 |
8.6 |
2.9 |
3.6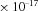 |
3.3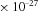 |
|
| 15 | rs1077835 | LIPC | 1.1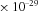 |
2.2 |
2.9 |
5.2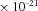 |
3.1 |
|
| 16 | rs247616 | CETP | 6.7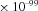 |
7.3 |
5.5 |
3.5 |
2.5 |
|
| 18 | rs4121823 | LIPG | 8.0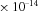 |
5.3 |
7.3 |
2.4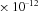 |
8.2 |
|
| 19 | rs6511720 | LDLR | 5.8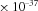 |
8.6 |
3.3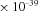 |
6.6 |
6.0 |
|
| 19 | rs10401969 | SUGP1 | 2.4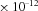 |
5.1 |
1.1 |
3.5 |
1.6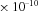 |
|
| 19 | rs445925 | APOC1 | 2.1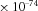 |
8.6 |
2.2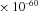 |
6.3 |
1.1 |
|
Not surprisingly, the Monte Carlo procedure reduced the genome-wide significance thresholds for all tests. For the univariate test on the HDL, one SNP on Chr20 becomes significant by the Monte Carlo criterion. For the T test, one SNP (rs5752792) on Chr22 is above the Monte Carlo threshold. This SNP resides near gene HSCB, which is mainly expressed in liver, muscle and heart [Sun et al., 2003] and is involved in the biogenesis of an elementary metabolic function unit [Rouault and Tong, 2008]. The expression pattern and biological function of HSCB strongly suggest that this gene is pleiotropic.
We have provided a very general and flexible approach to association testing with multivariate traits. An earlier version of this approach (focusing on the Q test for continuous traits) was recently used to successfully identify genes associated with metabolic syndrome [Avery et al., 2011]. The new application presented in this paper further demonstrates the usefulness of the proposed approach. It only took several hours to calculate all the P-values shown in Figures 1 and 2. We have posted our software online at http://dlin.web.unc.edu/software.
When the number of traits is very large, we recommend to reduce the dimension through principal component analysis [Avery et al., 2011]. Although we have focused on main effects of genetic variants, our approach can be easily modified to test gene–environment interactions. It can also be extended to perform burden tests on rare variants (Lin and Tang, 2011).
Univariate-trait analysis and multivariate-trait analysis are complementary to each other. The former is easier to implement and can be used to rapidly screen a large number of genetic variants. The multivariate-trait analysis provides a useful tool to uncover pleiotropic variants that have weak or moderate effects on individual traits. This is particularly important for dissecting the genetic basis of complex diseases, as most of the genetic variants with strong effects and high MAFs might have already been identified.
There is no uniformly most powerful test for analyzing multivariate traits. If the effects of a genetic variant are similar across the traits, then T and  are generally preferable. If the effects are considerably different or even in opposite directions, then Q is preferable. The theoretical results of the Appendix offer useful insights into the relative power of the three test statistics and can be used to determine the power and sample size for future studies.
are generally preferable. If the effects are considerably different or even in opposite directions, then Q is preferable. The theoretical results of the Appendix offer useful insights into the relative power of the three test statistics and can be used to determine the power and sample size for future studies.
For family data, we adopted the marginal models with an independence working correlation matrix. A more efficient approach would be a random-effect model which utilizes the family relationships. We adopted marginal models instead of random-effects models for several reasons. First, the association tests under marginal models are more robust to model misspecification. Second, it is much faster to fit marginal models than random-effects models. Third, marginal models can easily handle mixtures of continuous and binary traits.
Adjustment for multiple testing is an important issue in genetic association analysis. The Monte Carlo procedure considered in this paper accounts for the correlations among the test statistics and is thus less conservative than the conventional Bonferroni correction. Some existing methods, such as the TATES, may yield inflated type I error. We have focused on determining the genome-wide significance threshold rather than calculating individual adjusted P-values. The former only requires several thousands Monte Carlo samples whereas the latter would entail millions of Monte Carlo samples to estimate extremely small P-values. If the number of SNPs is small, the joint distribution of the test statistics can be evaluated through numerical integration [Conneely and Boehnke, 2007, 2010].
Acknowledgments
This research was supported by the National Institutes of Health grants R01 CA082659, U01 HG004803, and R00-HL-098458. We thank two reviewers for their helpful comments.
Appendix
Asymptotic Distributions of Q, T,  for Two Quantitative Traits
for Two Quantitative Traits

 and
and 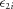 are bivariate zero-mean normal with covariance matrix
are bivariate zero-mean normal with covariance matrix
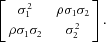
 takes the form
takes the form
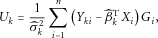
 and
and  are the least-squares estimators of
are the least-squares estimators of  and
and 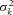 . Simple algebraic manipulation yields
. Simple algebraic manipulation yields
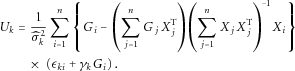
 is in the order of
is in the order of  . By the multivariate central limit theorem and the law of large numbers,
. By the multivariate central limit theorem and the law of large numbers,  is approximately bivariate normal with mean
is approximately bivariate normal with mean
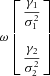
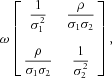
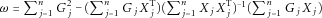 .
.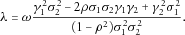
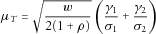
 is approximately normal with mean
is approximately normal with mean
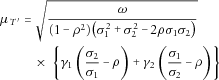
 ,
,
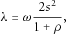

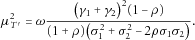
 . It can be shown that
. It can be shown that  , where the equality holds if and only if
, where the equality holds if and only if  (assuming that
(assuming that  ).
). ,
,
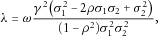
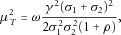
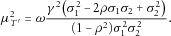
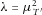 . It can be shown that
. It can be shown that  , where the equality holds if and only if
, where the equality holds if and only if  (assuming that
(assuming that  ).
).



