Genetic Association Test for Multiple Traits at Gene Level
Contact grant sponsor: National Institute on Drug Abuse; Contact grant number: R01 DA016750-09; Contact grant sponsor: NIH Genes, Environment and Health Initiative [GEI]; Contact grant numbers: U01 HG004422 and U01HG004438; Contact grant sponsor: GENEVA Coordinating Center; Contact grant number: U01 HG004446; Contact grant sponsor: Collaborative Study on the Genetics of Alcoholism; Contact grant number: U10 AA008401; Contact grant sponsor: Collaborative Genetic Study of Nicotine Dependence; Contact grant number: P01 CA089392; Contact grant sponsor: Family Study of Cocaine Dependence; Contact grant number: R01 DA013423; Contact grant sponsor: National Institute on Alcohol Abuse and Alcoholism; Contact grant sponsor: National Institute on Drug Abuse; Contact grant sponsor: NIH contract; Contact grant number: HHSN268200782096C.
Abstract
Genome-wide association studies (GWASs) at the gene level are commonly used to understand biological mechanisms underlying complex diseases. In general, one response or outcome is used to present a disease of interest in such studies. In this study, we consider a multiple traits association test from the gene level. We propose and examine a class of test statistics that summarizes the association information between single nucleotide polymorphisms (SNPs) and each of the traits. Our simulation studies demonstrate the advantage of gene-based multiple traits association tests when multiple traits share common genes. Using our proposed tests, we reanalyze the dataset from the Study of Addiction: Genetics and Environment (SAGE). Our result validates previous findings while presenting stronger evidence for consideration of multiple traits.
INTRODUCTION
Taking advantage of high-throughput genomic data, genome-wide association studies (GWASs) have become efficient tools in linking genetic variants and phenotypes [Burton et al., 2007; McCarthy et al., 2008]. Most GWASs employ the case-control design by recruiting a group of cases (diseased individuals) and a group of controls (healthy individuals). The single nucleotide polymorphisms (SNPs) are genotyped for all study participants. The most convenient analysis approach is to test the association between the disease and every SNP. Because a large number of SNPs requires a large number of tests, it becomes imperative to carefully control the false discovery rate [Dudbridge and Gusnanto, 2008]. Typically, a stringent threshold with P-value  is used as the threshold to declare a genome-wide significance. Such a small significance level is at the cost of missing many SNPs that are important to the disease but do not reach this threshold. Furthermore, due to locus heterogeneity, diseases could result from alleles at different loci in different populations, making it difficult to replicate results based on a single SNP [Neale and Sham, 2004]. Recently, multiple-locus methods have emerged as powerful approaches for complementing the traditional single-locus tests in identifying susceptible loci. Among these multiple-locus approaches, gene-based methods are one of popular choices thanks to some appealing features. Because genes are functional units, gene-based analysis may have a better chance in revealing functional mechanisms underlying complex traits [Wang et al., 2010]. From the statistical perspective, the gene-based analysis reduces the number of tests by more than 10-folds, alleviating the multiple comparisons problem. In addition, unlike the heterogeneity of a single locus, the functions of a gene are highly consistent across populations [Neale and Sham, 2004], enhancing the likelihood of replication.
is used as the threshold to declare a genome-wide significance. Such a small significance level is at the cost of missing many SNPs that are important to the disease but do not reach this threshold. Furthermore, due to locus heterogeneity, diseases could result from alleles at different loci in different populations, making it difficult to replicate results based on a single SNP [Neale and Sham, 2004]. Recently, multiple-locus methods have emerged as powerful approaches for complementing the traditional single-locus tests in identifying susceptible loci. Among these multiple-locus approaches, gene-based methods are one of popular choices thanks to some appealing features. Because genes are functional units, gene-based analysis may have a better chance in revealing functional mechanisms underlying complex traits [Wang et al., 2010]. From the statistical perspective, the gene-based analysis reduces the number of tests by more than 10-folds, alleviating the multiple comparisons problem. In addition, unlike the heterogeneity of a single locus, the functions of a gene are highly consistent across populations [Neale and Sham, 2004], enhancing the likelihood of replication.
Many gene-based association tests have been developed, and they belong to two broad groups: one based on the raw data and the other based on summary statistics. The key idea among gene-based tests is to combine the results of SNP-based test statistics within a gene. As part of the first group, the PLINK gene-based test [Purcell et al., 2007] chooses a subset of SNPs within a gene or pathway below a threshold and then averages the P-values of the remaining SNPs. Unlike the PLINK gene-based test, Lehne, in 2011 [Lehne et al., 2011], proposed three different methods that averaged the test statistics rather than the P-values of the individual SNPs. Another approach is to use the extreme test statistic, or the smallest P-value of SNPs within a gene, as the gene level score [Wang et al., 2007]. Due to the complex linkage disequilibrium (LD) structure among SNPs, permutation is usually required to obtain the P-values from such tests, and there are efforts to speed up the computation [Li et al., 2011]. It is reported that the raw data based algorithms perform better in a comprehensive comparison of seven algorithms for gene/pathway analysis using the Well Trust Case Control Consortium (WTCCC) Crohn disease (CD) dataset [Gui et al., 2011].
All of the existing approaches focus on a single trait, and hence it is important to extend them to the analysis of multiple correlated traits because comorbidity is a significant phenomenon in the genetic study of mental disorders. In this article, we consider multiple trait association tests at the gene level based on the raw data. Specifically, we first calculate the signals from individual SNPs. Second, we summarize the moderate signals within a gene or pathway. Finally, we use permutation to obtain the gene-based P-value. If there exists a common genetic predisposition in multiple traits, these traits will enhance the overall signal and further increase the power of detecting the association. The permutation enables us to consider the LD among SNPs.
MATERIALS AND METHODS
NONPARAMETRIC ASSOCIATION TEST BASED ON GENERALIZED KENDALL'S TAU
 and
and  denote the kth trait and a genotypic score, respectively. The test statistic is defined as
denote the kth trait and a genotypic score, respectively. The test statistic is defined as
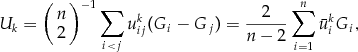
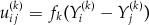 ,
, 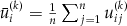 , and the link
, and the link  can be an identity function for the quantitative and binary traits or the sign function for the ordinal trait [Zhang et al., 2006]. According to the results in [Rabinowitz and Laird, 2000], conditional on the available phenotypes and under the null hypothesis,
can be an identity function for the quantitative and binary traits or the sign function for the ordinal trait [Zhang et al., 2006]. According to the results in [Rabinowitz and Laird, 2000], conditional on the available phenotypes and under the null hypothesis, 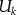 follows an normal distribution asymptotically with mean zero and variance
follows an normal distribution asymptotically with mean zero and variance
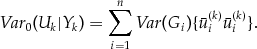
 (1)
(1)MULTIPLE-TRAIT GENE-BASED TEST
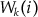 be the
be the  in (1) for SNPi. To assess the gene-based association, we employ the following three summary statistics
in (1) for SNPi. To assess the gene-based association, we employ the following three summary statistics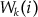 :
:
- M-MeanStat: the mean of
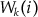 is chosen for the L SNPs and denoted by
is chosen for the L SNPs and denoted by  . Then, the statistic for multiple traits is
. Then, the statistic for multiple traits is 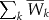 .
. - M-MaxStat: the maximum of
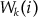 is chosen among the L SNPs and denoted by
is chosen among the L SNPs and denoted by 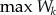 . Then, the statistic for multiple traits is
. Then, the statistic for multiple traits is 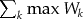
- M-TopQ25Stat: the mean among the largest 25% of the L
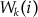 calculated and denoted by
calculated and denoted by 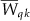 . Then, the statistic for multiple traits is
. Then, the statistic for multiple traits is 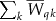 .
.
DERIVING THE EMPIRICAL P-VALUE FOR EACH GENE
Because the distributions of the test statistics have not been well characterized, a common practice is to use permutation to compute an empirical P-value for each gene in the dataset. We use a subject-based permutation schedule in order to preserve the correlation structure among traits and the LD within each gene while eliminating the association across the traits and genes. Specifically, we consider the multivariate outcome as one unit of a subject and then randomly permute the multivariate outcome vectors among all subjects. By permuting the multivariate outcome vectors, we do not need to permute the genotypes anymore, hence simplifying the computation; more importantly, this approach protects the dependence structure among the traits. The test statistics were calculated for each permuted dataset, giving rise to the empirical distributions of the test statistics under the null hypothesis that can be used to obtain the empirical P-value.
There are about 20,000 protein coding genes in the human genome, so by Bonferroni correction a genome-wide significance of 0.05 requires the individual P-values at the gene level to be smaller than 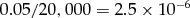 . To ensure that we can accurately approximate the P-values, we may need to permute the dataset at least 500,000 times. Taking advantage of the fact that there are usually a small number of significant genes, we employed a faster algorithm similar to the adaptive permutation schedule [Purcell et al., 2007] to prune genes in the permutation procedure. Instead of performing 500,000 permutations, we carry out the permutation adaptively and in multiple iterations. Let
. To ensure that we can accurately approximate the P-values, we may need to permute the dataset at least 500,000 times. Taking advantage of the fact that there are usually a small number of significant genes, we employed a faster algorithm similar to the adaptive permutation schedule [Purcell et al., 2007] to prune genes in the permutation procedure. Instead of performing 500,000 permutations, we carry out the permutation adaptively and in multiple iterations. Let  be the P-value threshold and
be the P-value threshold and 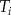 be the total number of permutations at and prior to the i-th iteration. Specifically, we choose
be the total number of permutations at and prior to the i-th iteration. Specifically, we choose 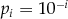 and
and 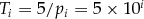 ,
,  . The number of additional permutations at the i-th iteration is actually
. The number of additional permutations at the i-th iteration is actually  , for
, for  . At the end of the five iterations, we will have performed a total of 500,000 permutations. This is similar to but simpler than the procedure in Purcell et al. [2007]. Although the total number of required permutations is the same, we save huge computational time because we only need to test a small number of genes in the later iterations.
. At the end of the five iterations, we will have performed a total of 500,000 permutations. This is similar to but simpler than the procedure in Purcell et al. [2007]. Although the total number of required permutations is the same, we save huge computational time because we only need to test a small number of genes in the later iterations.
SIMULATION STUDIES OF TYPE I ERROR AND STATISTICAL POWER
In this section, we investigate the power of gene-based multiple traits association tests. Because our methods test one gene (or one gene set) at a time, for computational reasons, in each dataset we simulated only one gene (or one gene set) that consists of a number of SNPs in LD. For assessing type I errors, this gene does not affect any of the traits. To evaluate the power, one SNP within this gene is used to define the penetrance. To simulate SNPs in LD, we followed the simulation experiment proposed by Wang and Abbott [2008].
Specifically, we generated an underlying multinormal random vector,X with the dimension equal to the number of SNPs in LD. Then, we used two cutoff values, c1 and c2, to convert the values into genotype scores such that 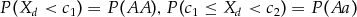 , and
, and  , where
, where  is the d-th element of X and determines the d-th SNP genotype. We set the mean and variance of
is the d-th element of X and determines the d-th SNP genotype. We set the mean and variance of  to 0 and 1, respectively. Hardy-Weinberg equilibrium was attained by choosing proper cutoff values, c1 and c2. Specifically, for minor allele frequency (MAF) 0.1, we chose
to 0 and 1, respectively. Hardy-Weinberg equilibrium was attained by choosing proper cutoff values, c1 and c2. Specifically, for minor allele frequency (MAF) 0.1, we chose 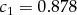 and
and  ; for MAF 0.15, we chose
; for MAF 0.15, we chose 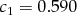 and
and  . It is easy to verify the Hardy-Weinberg equilibrium in these simulation settings. In addition, we consider two patterns of MAF: (1) 0.1 for all SNPs and (2) 0.15 for the first half of SNPs, and 0.1 for second half SNPs.
. It is easy to verify the Hardy-Weinberg equilibrium in these simulation settings. In addition, we consider two patterns of MAF: (1) 0.1 for all SNPs and (2) 0.15 for the first half of SNPs, and 0.1 for second half SNPs.
We considered three different scenarios of LD structure: (1) The SNPs are in strong LD. Specifically, the correlation coefficients among 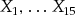 are set to 0.95, and the correlation coefficients among
are set to 0.95, and the correlation coefficients among  are set to 0.6. The cross correlation coefficient between
are set to 0.6. The cross correlation coefficient between  and
and  is set to 0.6. (2) The SNPs are in moderate LD. Specifically, the correlation coefficients among
is set to 0.6. (2) The SNPs are in moderate LD. Specifically, the correlation coefficients among  all equal to 0.6 and the correlation coefficients among
all equal to 0.6 and the correlation coefficients among  are set to 0.4. The cross correlation coefficient between
are set to 0.4. The cross correlation coefficient between  and
and  is set to 0.4. (3) The SNPs are in linkage equilibrium (LE). After we defined the correlation matrix of the latent variable
is set to 0.4. (3) The SNPs are in linkage equilibrium (LE). After we defined the correlation matrix of the latent variable  , we were able to obtain the SNPs with the desired LD.
, we were able to obtain the SNPs with the desired LD.
Another variety of our simulation is the number of traits: two and three. These choices are simple, yet representative. For the simulation with two traits, the second SNP is the disease locus for trait 1, and the third SNP for trait 2. For the simulation with three traits, the second SNP, third SNP, and fourth SNP are chosen as the disease locus for one of the three traits, respectively. The trait values are determined by underlies penetrance function:  with
with 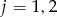 or
or 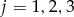 ,
,  . The correlation between ε1 and ε2 or ε1, ε2 and ε3 is set to 0.2. In addition,
. The correlation between ε1 and ε2 or ε1, ε2 and ε3 is set to 0.2. In addition,  denotes as the number of the corresponding minor allele. For the case with two traits, we fix the effect size of one trait and then consider the effect size of the other trait from 0 to 1. Specifically, we use three different settings for
denotes as the number of the corresponding minor allele. For the case with two traits, we fix the effect size of one trait and then consider the effect size of the other trait from 0 to 1. Specifically, we use three different settings for 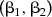 : (1, 0), (1, 0.5), and (1, 1), implying that the two traits have no common genetic variation, moderate common genetic variation, and strong common variation within this gene, respectively. Similarly, for the case with three traits, we assume that the disease gene has strong and moderate effect sizes on the first and second trait, respectively, and the effect size on the third trait varies from 0 to 1. The settings for
: (1, 0), (1, 0.5), and (1, 1), implying that the two traits have no common genetic variation, moderate common genetic variation, and strong common variation within this gene, respectively. Similarly, for the case with three traits, we assume that the disease gene has strong and moderate effect sizes on the first and second trait, respectively, and the effect size on the third trait varies from 0 to 1. The settings for 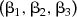 are (1, 0.5, 0), (1, 0.5, 0.5), and (1, 0.5, 1).
are (1, 0.5, 0), (1, 0.5, 0.5), and (1, 0.5, 1).
Furthermore, the number of individuals was set to 500 in each simulated dataset. The significant threshold was set at 0.01 and we replicated the simulation 1,000 times for the power analysis and 3,000 times for calculating type I error.
The multiple trait gene-based association tests, namely M-MeanStat, M-MaxStat, and M-TopQ25Stat, were used in the simulation. To investigate whether the power and type I error would be affected by the percentile of the chosen SNPs, we evaluated the performance for 50% and 75% percentiles, which are denoted by M-TopQ50Stat and M-TopQ75Stat. As a comparison, we also analyzed a single trait by using test statistics: MeanStat, MaxStat, TopQ25Stat, TopQ50Stat, and TopQ75Stat. To take into account the multiple testing problem when we test one trait at a time, we employed the Bonferroni correction for the significance threshold of the single-trait test.
STUDY OF ADDICTION: GENETICS AND ENVIRONMENT (SAGE) DATA
We used the data from Study of Addiction: Genetics and Environment (SAGE) [Bierut et al., 2008, 2010; Hartel et al., 2006; Luo et al., 2008; Reich et al., 1998] that we obtained from the database of Genotype and Phenotype (dbGap). The SAGE dataset is a large case-control study that aims to detect susceptible genetic variant for addiction. The original dataset included 4,121 individuals with various well-defined addiction outcomes including six categories of substance dependence data: alcohol, cocaine, marijuana, nicotine, opiates, and other dependence on other drugs. Lifetime dependence on the six substances was diagnosed by Diagnostic and Statistical Manual of Mental Disorders Manual, Fourth Edition (DSM-IV). The genomic-wide SNP data were collected by using the ILLUMINA Human 1 M platform, and were cleaned by setting quality control thresholds for MAF (>5%) and call rate (>90%). In addition, we deleted 60 duplicate genotype samples and nine individuals whose ethnicities were neither African-origin nor European-origin. As a result, there were 3,627 unrelated participants with 830,696 autosomal SNPs for our final analysis. To avoid population stratification, the samples were stratified into four sub-samples: 1,393 white women, 1,131 white men, 568 black women, and 535 black men. In a previous genome-wise association study of the same data [Chen et al., 2011], the PKNOX2 gene was reported to be significantly associated with substance dependence in European-origin women. This finding has been subsequently and independently confirmed in other studies. Because those reports focused on SNP-based association, we reanalyzed the same region of PKNOX2 in European-origin women at the gene level. SNPs were considered to be mapped to a gene if their physical locations are within 20 kilobases(kb) 5′ upstream and 20 kilobases(kb) 3′ downstream of the coding regions for the gene [Menashe et al., 2012]. Meanwhile, we would include additional SNPs to the gene if they are in strong LD ( ) with the initially mapped SNPs within the gene [Christoforou et al., 2012]. In the end, we included 131 SNPs in the PKNOX2 gene. MeanStat, MaxStat, and TopQ25Stat statistics were used to test the association for the six individual addiction traits, and M-MeanStat, M-MaxStat, and M-TopQ25Stat statistics for the joint analysis of the six addiction traits.
) with the initially mapped SNPs within the gene [Christoforou et al., 2012]. In the end, we included 131 SNPs in the PKNOX2 gene. MeanStat, MaxStat, and TopQ25Stat statistics were used to test the association for the six individual addiction traits, and M-MeanStat, M-MaxStat, and M-TopQ25Stat statistics for the joint analysis of the six addiction traits.
RESULTS
SIMULATION STUDIES OF TYPE I ERROR AND STATISTICAL POWER
Table I reports the type I error rates when the nominal significance levels were set at 0.01. All of the type I error rates are very close to the nominal values. Figures 1 and 2 present the power of two traits and three traits, respectively, when the significance level was set 0.01. In our simulation, the power of M-TopQ50Stat and M-TopQ75Stat is always between that of M-TopQ25Stat and M-MeanStat. Hence, we only presented the results from M-TopQ25Stat and M-MeanStat only.
| Number of traits | MAF pattern | LD structure | MeanStat | M-MeanStat | MaxStat | M-MaxStat | TopQ25Stat | M-TopQ25Stat |
|---|---|---|---|---|---|---|---|---|
| 2 | 1 | Strong | 0.0097 | 0.0087 | 0.0117 | 0.0093 | 0.0093 | 0.0093 |
| 1 | Moderate | 0.0090 | 0.0110 | 0.0093 | 0.0107 | 0.0090 | 0.0090 | |
| 1 | LE | 0.0100 | 0.0100 | 0.0090 | 0.0093 | 0.0103 | 0.0083 | |
| 2 | Strong | 0.0100 | 0.0100 | 0.0113 | 0.0107 | 0.0097 | 0.0097 | |
| 2 | Moderate | 0.0093 | 0.0087 | 0.0100 | 0.0080 | 0.0093 | 0.0073 | |
| 2 | LE | 0.0107 | 0.0107 | 0.0117 | 0.0107 | 0.0100 | 0.0107 | |
| 3 | 1 | Strong | 0.0117 | 0.0100 | 0.0110 | 0.0107 | 0.0113 | 0.0087 |
| 1 | Moderate | 0.0103 | 0.0080 | 0.0107 | 0.0080 | 0.0103 | 0.0090 | |
| 1 | LE | 0.0097 | 0.0077 | 0.0093 | 0.0103 | 0.0087 | 0.0087 | |
| 2 | Strong | 0.0113 | 0.0083 | 0.0123 | 0.0117 | 0.0107 | 0.0087 | |
| 2 | Moderate | 0.0107 | 0.0113 | 0.0083 | 0.0083 | 0.0103 | 0.0103 | |
| 2 | LE | 0.0083 | 0.0060 | 0.0103 | 0.0090 | 0.0073 | 0.0097 |
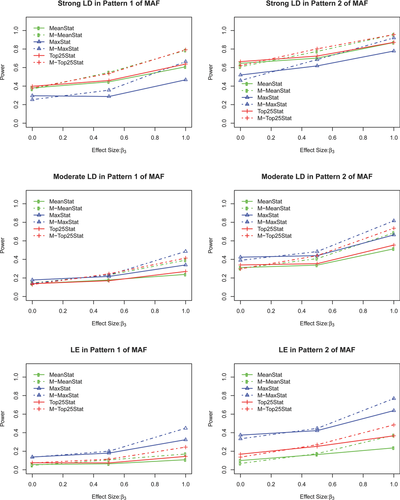
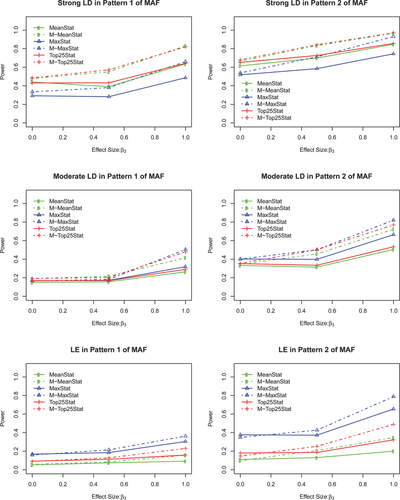
Figure 1 demonstrates the advantage of gene-based multiple traits association tests when multiple traits share a common genetic component. First of all, we can observe that when there is no common genetic variation between two traits, the power of single trait tests is slightly better than the power of multiple traits tests. If there exists a moderate common genetic variation between the two traits, multiple trait tests gain higher power than single trait tests. The advantage of the multiple traits tests becomes more obvious when the two traits have a strong common genetic variation.
In addition, the LD structures impact the performance of methods in the following two situations. (1) When the disease locus is in a strong LD block of other observed SNPs, the power of statistic M-TopQ25Stat is comparable to M-MeanStat, while M-TopQ25Stat performs slightly better than M-MeanStat in nearly all settings. M-MaxStat is the least powerful among the three multiple trait tests. This observation is consistent with Gui et al. [2011] that compared seven algorithms in pathway analysis and found that Plink-Average method was superior to Plink-Max method. (2) When the disease locus is in moderate LD with other observed SNPs, the M-MaxStat performed better than the other two methods. The advantages of M-MaxStat became more obvious when the disease locus was located in a LE block.
These findings can be partially explained as follows. When the disease locus is in a strong LD block of the observed SNPs, the average test statistic such as the M-TopQ25Stat or M-MeanStat can borrow information from the other loci within the LD block of disease locus; however, the extreme test statistic: M-MaxStat neglects the information among the LD block. When the disease locus and other SNPs are in weak LD, the noise in the loci masks the genetic effect in the average test statistic, and hence reduces its power. The M-MaxStat is less affected by the LD because only the strongest signal is included. That is why M-MaxStat performs better than M-MeanStat and M-TopQ25Stat in the cases with moderate LD or LE.
Lastly, the power of our proposed methods depends on the minor allele patterns and LD structures. Specifically, the power increases as the MAF of the disease locus increases or when the LD of the observed SNPs with the disease locus increases.
Figure 2 reveals similar patterns to Figure 1. Even when the third trait is independent of the gene, the power of multiple traits tests is still higher than the single-trait tests. The advantage becomes more obvious as the effect size of the disease gene on the third trait increases.
APPLICATION TO GWAS
Table II presents the matrix consisting of the pairwise odds ratio between the six traits. The odds ratio between any pair of substance dependence is consistently much higher than 1, indicating strong comorbidity among the six substance dependence. Table III displays the results of various association tests between PKNOX2 gene and the six substance addictions. The P-values are calculated from 500,000 permutations. Except for the MaxStat method, the P-values obtained by multiple trait gene-based association tests are consistently smaller than the values obtained when analyzing each trait individually, which suggested that the proposed multiple-trait gene-based tests are more powerful than the single trait gene-based tests, even before we adjusted for the trait-based multiple comparisons. For the MaxStat method in Table III, the P-value (4.00 × 10–04) of the multiple traits tests is slightly larger than the smallest P-value of single-trait tests (3.80 × 10–04, alcohol dependence). However, if we apply the Bonferroni correction for single-trait test, the P-value for multiple traits will be smaller than the single trait test. Among the multiple-trait tests, TopQ25Stat consistently yielded smaller P-values than the other two methods, as what we observed in the simulation study.
| Alcohol | Cocaine | Marijuana | Nicotine | Opiates | Others | |
|---|---|---|---|---|---|---|
| Alcohol | – | 38.2 | 35.6 | 7.2 | 167.3 | 45.7 |
| Cocaine | 38.2 | – | 30.1 | 8.2 | 30.2 | 40.1 |
| Marijuana | 35.6 | 30.1 | – | 12.4 | 12.1 | 21.0 |
| Nicotine | 7.2 | 8.2 | 12.4 | – | 8.4 | 7.1 |
| Opiates | 167.3 | 30.2 | 12.1 | 8.4 | – | 47.9 |
| Others | 45.7 | 40.1 | 21.0 | 7.1 | 47.9 | – |
| Alcohol | Cocaine | Marijuana | Nicotine | Opiates | Others | Combined | |
|---|---|---|---|---|---|---|---|
| MeanStat | 3.40 × 10–04 | 8.70 × 10–03 | 4.90 × 10–03 | 2.20 × 10–01 | 1.30 × 10–02 | 9.40 × 10–04 | 8.00 × 10–05 |
| MaxStat | 3.80 × 10–04 | 6.50 × 10–03 | 4.80 × 10–03 | 6.10 × 10–02 | 2.20 × 10–01 | 9.10 × 10–03 | 4.00 × 10–04 |
| TopQ25Stat | 1.40 × 10–04 | 1.90 × 10–03 | 1.90 × 10–03 | 1.60 × 10–01 | 9.70 × 10–03 | 1.80 × 10–04 | 6.00 × 10–06 |
| GATE | 1.80 × 10–04 | 2.40 × 10–03 | 8.70 × 10–04 | 8.10 × 10–02 | 1.10 × 10–01 | 9.80 × 10–04 | – |
To further evaluate our methods, we also considered a commonly used gene-based association test for a single-trait based association. It uses an extended Simes procedure (GATES) to summarize the P-values of the SNPs within a gene [Li et al., 2011]. Table III also presents the results from GATES and reveals, interestingly, that TopQ25Stat and GATES yields comparable results, although four of the six P-values from TopQ25Stat are smaller than those from GATES. Thus, our data analysis suggests that TopQ25Stat is a reliable test for single-trait-based associations.
Although the P-values of the multiple-trait gene-based association test did not reach the conservative significance level of  , the P-value from the M-TopQStat is
, the P-value from the M-TopQStat is 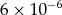 .
.
DISCUSSION
Comorbidity is an important issue in mental and behavioral research, and to study comorbidity we need to consider relevant traits simultaneously. In this article, we proposed a novel approach for conducting multiple-trait association test at gene level. Borrowing the strength of the nonparametric association test based on generalized Kendall's tau, the proposed multiple-trait gene-based test is applicable for any combinations of binary traits, continuous traits, and/or ordinal traits. It is useful to note that the proposed multiple-trait gene-based tests are nonparametric-based tests. Although we used the Kendall's tau test, our idea can be generalized for other multiple-trait based tests.
We investigated the properties of our proposed multiple traits gene-based methods through extensive simulation experiments. First, compared with the single-trait gene-based methods, multiple-traits gene-based methods performed better when there is a common genetic variation between traits. As expected, if the common genetic variation between traits is weak, multiple-traits gene-based methods have no advantage. Second, the performance of our proposed methods depend on the LD structures. This is reasonable because the observed SNPs need to be in LD with the disease locus for us to detect any association. The power improves as the LD gets stronger. When the disease locus is in strong LD of the observed SNPs, the average test statistics are better than extreme-based methods (M-MaxStat). However, if the disease locus is in weak LD of the observed SNPs, extreme test statistics are more powerful. Overall, the performance of M-TopQ25Stat is better than M-MeanStat. Thirdly, a higher MAF leads to a higher power.
Although our proposed test statistics do not include the comorbidity in their formation, the comorbidity among the traits is not neglected in the hypothesis testing. When the P-value is computed through the permutation, the vector of the traits is permuted together and hence the comorbidity is kept intact. In other words, the comorbidity is taken into account in the distribution of a test statistic under the null hypothesis. The efficiency of the test varies according to the data and genetic models; our simulation suggested that different tests are more powerful under different settings.
It is useful to note that estimating correlation is challenging and involves a great deal of uncertainty. Although it is a natural to incorporate the correlation in a test, the performance is not uniformly improved due to the extra level of uncertainty. One could consider log-linear models to accommodate multiple discrete traits [Christensen et al., 1997], but they cannot accommodate continuous covariates and become too complicated as the number of the traits or covariates increases. Principal component analysis (PCA) [Jolliffe et al., 2003] is also often used for dimension reduction. PCA may produce a combination of the traits representing the great variation of the traits, but the direction of the maximum variation is not unnecessary related to the genetic effect. For example, we can theoretically construct examples in which the leading PCA is totally irrelevant to a risk factor (such as gene) of interest [Bair et al., 2006]. Furthermore, for binary or ordinal traits, the definition of their linear combination may be meaningless and at least difficult to interpret.
Our data analysis suggests several advantages of the multiple-trait gene-based tests. First, the computation algorithm is a relatively straightforward extension of the algorithms from the single-trait tests. Second, although the permutation procedure is computationally intensive, it is flexible in accommodating complicated LD structure among SNPs and various sizes of the gene or gene set as well as unknown dependence among the traits. Third, the multiple-trait gene-based tests can be incorporated into gene set enrichment studies, which would improve the understanding of molecular mechanisms between traits. Lastly, but importantly, when there exist common genetic variants among the traits, the multiple-trait gene-based tests are more powerful than the single-trait based test. However, when this assumption is violated, we do not expect the multiple-trait gene-based tests to have this advantage [Yu et al., 2010].
ACKNOWLEDGMENTS
This work was supported by grant R01 DA016750-09 from the National Institute on Drug Abuse. Funding support for the SAGE was provided through the NIH Genes, Environment and Health Initiative [GEI] (U01 HG004422). SAGE is one of the GWASs funded as part of the Gene Environment Association Studies (GENEVA) under GEI. Assistance with phenotype harmonization and genotype cleaning, as well as with general study coordination, was provided by the GENEVA Coordinating Center (U01 HG004446). Assistance with data cleaning was provided by the National Center for Biotechnology Information. Support for the collection of datasets and samples was provided by the Collaborative Study on the Genetics of Alcoholism (COGA; U10 AA008401), the Collaborative Genetic Study of Nicotine Dependence (COGEND; P01 CA089392), and the Family Study of Cocaine Dependence (FSCD; R01 DA013423). Funding support for genotyping, which was performed at the Johns Hopkins University Center for Inherited Disease Research, was provided by the NIH GEI (U01HG004438), the National Institute on Alcohol Abuse and Alcoholism, the National Institute on Drug Abuse, and the NIH contract “High throughput genotyping for studying the genetic contributions to human disease” (HHSN268200782096C). The datasets used for the analyses described in this manuscript were obtained from dbGaP at http://www.ncbi.nlm.nih.gov/projects/gap/cgibin/study.cgi?studyid=phs000092.v1.p1 through dbGaP accession number phs000092.v1.p. The authors have no conflict of interest.




