GAMM-Mitteilungen
Volume 44, Issue 1 e202100004
ORIGINAL PAPER
Open Access

Classification and image processing with a semi-discrete scheme for fidelity forced Allen–Cahn on graphs

Jeremy Budd, 

Corresponding Author

Jeremy Budd

Delft Institute of Applied Mathematics (DIAM), Technische Universiteit Delft, Delft, The Netherlands

Correspondence Jeremy Budd, Mathematics and Computer Science, EWI, TU Delft, Van Mourik Broekmanweg 6, Delft 2628 XE, The Netherlands. Email: [email protected]

Search for more papers by this author
Yves van Gennip, 

Yves van Gennip

Delft Institute of Applied Mathematics (DIAM), Technische Universiteit Delft, Delft, The Netherlands

Search for more papers by this author
Jonas Latz, 

Jonas Latz

Department of Applied Mathematics and Theoretical Physics (DAMTP), University of Cambridge, Cambridge, UK

Search for more papers by this author
First published: 17 March 2021
https://doi.org/10.1002/gamm.202100004
Citations: 4

Abstract

This paper introduces a semi-discrete implicit Euler (SDIE) scheme for the Allen-Cahn equation (ACE) with fidelity forcing on graphs. The continuous-in-time version of this differential equation was pioneered by Bertozzi and Flenner in 2012 as a method for graph classification problems, such as semi-supervised learning and image segmentation. In 2013, Merkurjev et. al. used a Merriman-Bence-Osher (MBO) scheme with fidelity forcing instead, as heuristically it was expected to give similar results to the ACE. The current paper rigorously establishes the graph MBO scheme with fidelity forcing as a special case of an SDIE scheme for the graph ACE with fidelity forcing. This connection requires the use of the double-obstacle potential in the ACE, as was already demonstrated by Budd and Van Gennip in 2020 in the context of ACE without a fidelity forcing term. We also prove that solutions of the SDIE scheme converge to solutions of the graph ACE with fidelity forcing as the discrete time step converges to zero. In the second part of the paper we develop the SDIE scheme as a classification algorithm. We also introduce some innovations into the algorithms for the SDIE and MBO schemes. For large graphs, we use a QR decomposition method to compute an eigendecomposition from a Nyström extension, which outperforms the method used by, for example, Bertozzi and Flenner in 2012, in accuracy, stability, and speed. Moreover, we replace the Euler discretization for the scheme's diffusion step by a computation based on the Strang formula for matrix exponentials. We apply this algorithm to a number of image segmentation problems, and compare the performance with that of the graph MBO scheme with fidelity forcing. We find that while the general SDIE scheme does not perform better than the MBO special case at this task, our other innovations lead to a significantly better segmentation than that from previous literature. We also empirically quantify the uncertainty that this segmentation inherits from the randomness in the Nyström extension.

1 INTRODUCTION

In this paper, we investigate the Allen-Cahn gradient flow of the Ginzburg-Landau functional on a graph, and the Merriman-Bence-Osher (MBO) scheme on a graph, with fidelity forcing. We extend the definition of the semi-discrete implicit Euler (SDIE) scheme (introduced in 13 for the graph Allen-Cahn equation (ACE)) to the case of fidelity forcing, and prove that the key results of 13 hold true in the fidelity forced setting, that is
  • the MBO scheme with fidelity forcing is a special case of the SDIE scheme with fidelity forcing; and
  • the SDIE solution converges to the solution of Allen-Cahn with fidelity forcing as the SDIE time step tends to zero.

We then demonstrate how to employ the SDIE scheme as a classification algorithm, making a number of improvements upon the MBO-based classification in 32. In particular, we have developed a stable method for extracting an eigendecomposition or singular value decomposition (SVD) from the Nyström extension 21, 36 that is both faster and more accurate than the previous method used in 6, 32. Finally, we test the performance of this scheme as an alternative to graph MBO as a method for image processing on the “two cows” segmentation task considered in 6, 32.

Given an edge-weighted graph, the goal of two-class graph classification is to partition the vertex set into two subsets in such a way that the total weight of edges within each subset is high and the weight of edges between the two subsets is low. Classification differs from clustering by the addition of some a priori knowledge, that is, for certain vertices the correct classification is known beforehand. Graph classification has many applications, such as semi-supervised learning and image segmentation 6, 15.

All programming for this paper was done in Matlab R2019a. Except within algorithm environments and URLs, all uses of typewriter font indicate built-in Matlab functions.

1.1 Contributions of this work

In this paper we have:
  • Defined a double-obstacle ACE with fidelity forcing (Definition 2.6), and extended the theory of 13 to this equation (Theorem 2.7).
  • Defined an SDIE scheme for this ACE (Definition 2.8) and following 13 proved that this scheme is a generalization of the fidelity forced MBO scheme (Theorem 2.9), derived a Lyapunov functional for the SDIE scheme (Theorem 2.12), and proved that the scheme converges to the ACE solution as the time-step tends to zero (Theorem 2.17).
  • Described how to employ the SDIE scheme as a generalization of the MBO-based classification algorithm in 32.
  • Developed a method, inspired by 3, using the QR decomposition to extract an approximate SVD of the normalized graph Laplacian from the Nyström extension (Algorithm 1), which avoids the potential for errors in the method from 6, 32 that can arise from taking the square root of a non-positive-semi-definite matrix, and empirically produces much better performance than the 6, 32 method (Figure 4) in accuracy, stability, and speed.
  • Developed a method using the quadratic error Strang formula for matrix exponentials 39 for computing fidelity forced graph diffusion (Algorithm 2), which empirically incurs a lower error than the error incurred by the semi-implicit Euler method used in 32 (Figure 6), and explored other techniques with the potential to further reduce error (Table 1).
  • Demonstrated the application of these algorithms to image segmentation, particularly the “two cows” images from 6, 32, compared the quality of the segmentation to those produced in 6, 32 (Figure 11), and investigated the uncertainty in these segmentations (Figure 14), which is inherited from the randomization in Nyström.
TABLE 1. Comparison of the relative ℓ2 errors from the methods for approximating b on the image from Figure 5
Relative ℓ2 error for τ = 0 . 5 Relative ℓ2 error for τ = 4
Method |V|=1600, K = 1600 |V|=1600, K = 40 |V|=6400, K = 40 |V|=1600, K = 1600 |V|=1600, K = 40 |V|=6400, K = 40
Semi-implicit Euler 32 1.434 × 10−4 0.4951 0.4111 2.882 × 10−4 0.2071 0.1721
Woodbury identity 2.292 × 10−8 0.5751 0.4607 1.038 × 10−7 0.1973 0.1537
Midpoint rule (3.3) 0.0279 0.1290 0.1110 0.4279 0.6083 0.6113
Simpson's rule (m = 500) via Strang formula 2.592 × 10−9 0.1335 0.1136 5.845 × 10−7 0.5124 0.4827
Matlab integrate via Strang formula n/a 0.1335 0.1136 n/a 0.5124 0.4827
Simpson's rule (m = 500) via Yoshida method 8.381 × 10−14 0.1335 0.1136 9.335 × 10−12 0.5124 0.4827
Matlab integrate via Yoshida method n/a 0.1335 0.1136 n/a 0.5124 0.4827
  • Note: We did not compute integrate for K = 1600 as it ran too slowly. Bold entries indicate the smallest error in that column.

This work extends the work in 13 in four key ways. First, introducing fidelity forcing changes the character of the dynamics, for example, making graph diffusion affine, which changes a number of results/proofs, and it is thus of interest that the SDIE link continues to hold between the MBO scheme and the ACE. Second, this work for the first time considers the SDIE scheme as a tool for applications. Third, in developing the scheme for applications we have made a number of improvements to the methods used in the previous literature 32 for MBO-based classification, which result in a better segmentation of the “two cows” image than that produced in 32 or 6. Fourth, we quantify the randomness that the segmentation inherits from the Nyström extension.

1.2 Background

In the continuum, a major class of techniques for classification problems relies upon the minimization of total variation (TV), for example, the famous Mumford-Shah 34 and Chan-Vese 16 algorithms. These methods are linked to Ginzburg-Landau methods by the fact that the Ginzburg-Landau functional Γ -converges to TV 29, 33 (a result that continues to hold in the graph context 23). This motivated a common technique of minimizing the Ginzburg-Landau functional in place of TV, for example, in 20 two-class Chan-Vese segmentation was implemented by replacing TV with the Ginzburg-Landau functional; the resulting energy was minimized by using a fidelity forced MBO scheme.

Inspired by this continuum work, in 6 a method for graph classification was introduced based on minimizing the Ginzburg-Landau functional on a graph by evolving the graph ACE. The a priori information was incorporated by including a fidelity forcing term, leading to the equation
d u d t = − Δ u − 1 ε W ′ ∘ u − μ ^ P Z ( u − f ˜ ) ,
where u is a labeling function which, due to the influence of a double-well potential (eg, W(x) = x2(x − 1)2) will take values close to 0 and 1, indicating the two classes. The a priori knowledge is encoded in the reference f ˜ which is supported on Z, a subset of the node set with corresponding projection operator PZ. In the first term Δ denotes the graph Laplacian and ε , μ ^ > 0 are parameters. All these ingredients will be explained in more detail in Sections 1.3 and 2.

In 32 an alternative method was introduced: a graph MBO scheme with fidelity forcing. The original MBO scheme, introduced in a continuum setting in 4 to approximate motion by mean curvature, is an iterative scheme consisting of diffusion alternated with a thresholding step. In 32 this scheme was discretized for use on graphs and the fidelity forcing term − M ( u − f ˜ ) (where M is a diagonal nonnegative matrix, see Section 2 for details) was added to the diffusion. Heuristically, this MBO scheme was expected to behave similarly to the graph ACE as the thresholding step resembles a “hard” version of the “soft” double-well potential nonlinearity in the ACE.

In 13 it was shown that the graph MBO scheme without fidelity forcing could be obtained as a special case of a SDIE scheme for the ACE (without fidelity forcing), if the smooth double-well potential was replaced by the double-obstacle potential defined in (1.2), and that solutions to the SDIE scheme converge to the solution of the graph ACE as the time step converges to zero. This double-obstacle potential was studied for the continuum ACE in 8-10 and was used in the graph context in 11. In 14 a result similar to that of 13 was obtained for a mass-conserving graph MBO scheme. In this paper such a result will be established for the graph MBO scheme with fidelity forcing.

In 24 it was shown that the graph MBO scheme pins (or freezes) when the diffusion time is chosen too small, meaning that a single iteration of the scheme will not introduce any change as the diffusion step will not have pushed the value at any node past the threshold. In 13 it was argued that the SDIE scheme for graph ACE provides a relaxation of the MBO scheme: the hard threshold is replaced by a gradual threshold, which should allow for the use of smaller diffusion times without experiencing pinning. The current paper investigates what impact that has in practical problems.

1.3 Groundwork

We briefly summarize the framework for analysis on graphs, following the summary in 13 of the detailed presentation in 24. A graph G = (V, E) will henceforth be defined to be a finite, simple, undirected, weighted, and connected graph without self-loops with vertex set V, edge set E ⊆ V2, and weights { ω i j } i , j ∈ V with ω i j ≥ 0 , ω i j = ω j i , ω i i = 0 , and ω i j > 0 if and only if ij ∈ E. We define the following function spaces on G (where X ⊆ ℝ , and T ⊆ ℝ an interval):
𝒱 ≔ u : V → ℝ , 𝒱 X ≔ u : V → X , ℰ ≔ φ : E → ℝ . 𝒱 t ∈ T ≔ u : T → 𝒱 , 𝒱 X , t ∈ T ≔ u : T → 𝒱 X .
Defining d i ≔ ∑ j ∈ V ω i j to be the degree of vertex i ∈ V, we define inner products on 𝒱 (or 𝒱 X ) and ℰ (where r ∈ [0, 1]):
⟨ u , v ⟩ 𝒱 ≔ ∑ i ∈ V u i v i d i r , ⟨ φ , ϕ ⟩ ℰ ≔ 1 2 ∑ i , j ∈ V φ i j ϕ i j ω i j ,
and define the inner product on 𝒱 t ∈ T (or 𝒱 X , t ∈ T )
( u , v ) t ∈ T ≔ ∫ T u ( t ) , v ( t ) 𝒱 d t = ∑ i ∈ V d i r ( u i , v i ) L 2 ( T ; ℝ ) .
These induce inner product norms ‖ · ‖ 𝒱 , ‖ · ‖ ℰ , and ‖ · ‖t ∈ T. We also define on 𝒱 the norm
‖ u ‖ ∞ ≔ max i ∈ V | u i | .
Next, we define the L2 space:
L 2 ( T ; 𝒱 ) ≔ u ∈ 𝒱 t ∈ T | ‖ u ‖ t ∈ T < ∞ ,
and, for T an open interval, we define the Sobolev space H 1 ( T ; 𝒱 ) as the set of u ∈ L 2 ( T ; 𝒱 ) with weak derivative d u / d t ∈ L 2 ( T ; 𝒱 ) defined by
∀ φ ∈ C c ∞ ( T ; 𝒱 ) u , d φ d t t ∈ T = − d u d t , φ t ∈ T ,
where C c ∞ ( T ; 𝒱 ) is the set of φ ∈ 𝒱 t ∈ T that are infinitely differentiable with respect to time t ∈ T and are compactly supported in T. By [13, Proposition 2.1], u ∈ H 1 ( T ; 𝒱 ) if and only if u i ∈ H 1 ( T ; ℝ ) for each i ∈ V. We define the local H1 space on any interval T (and likewise define the local L2 space L l o c 2 ( T ; 𝒱 ) ):
H l o c 1 ( T ; 𝒱 ) ≔ u ∈ 𝒱 t ∈ T | ∀ a , b ∈ T , u ∈ H 1 ( ( a , b ) ; 𝒱 ) .
For A ⊆ V, we define the characteristic function of A, χ A ∈ 𝒱 , by
( χ A ) i ≔ 1 , if i ∈ A , 0 , if i ∉ A .
Next, we introduce the graph gradient and Laplacian:
( ∇ u ) i j ≔ u j − u i , i j ∈ E , 0 , otherwise, ( Δ u ) i ≔ d i − r ∑ j ∈ V ω i j ( u i − u j ) .
Note that Δ is positive semi-definite and self-adjoint with respect to 𝒱 . As shown in 24, these operators are related via:
⟨ u , Δ v ⟩ 𝒱 = ⟨ ∇ u , ∇ v ⟩ ℰ .
We can interpret Δ as a matrix. Define D ≔ diag ( d ) (ie, Dii ≔ di, and Dij ≔ 0 otherwise) to be the diagonal matrix of degrees. Then writing ω for the matrix of weights ω i j we get
Δ ≔ D − r ( D − ω ) .
From Δ we define the graph diffusion operator:
e − t Δ u ≔ ∑ n ≥ 0 ( − 1 ) n t n n ! Δ n , u
where v ( t ) = e − t Δ u is the unique solution to d v / d t = − Δ v with v(0) = u. Note that e − t Δ 1 = 1 , where 1 is the vector of ones. By [13, Proposition 2.2] if u ∈ H 1 ( T ; 𝒱 ) and T is bounded below, then e − t Δ u ∈ H 1 ( T ; 𝒱 ) with
d d t e − t Δ u = e − t Δ d u d t − e − t Δ Δ u .
We recall from functional analysis the notation, for any linear operator F : 𝒱 → 𝒱 ,
σ ( F ) ≔ { λ : λ an eigenvalue of F } ρ ( F ) ≔ max { | λ | : λ ∈ σ ( F ) } | | F | | ≔ sup | | u | | 𝒱 = 1 | | F u | | 𝒱
and recall the standard result that if F is self-adjoint then | | F | | = ρ ( F ) .

Finally, we recall some notation from 13: for problems of the form argmin x f ( x ) we write f ≃ g and say f and g are equivalent when g(x) = af(x) + b for a > 0 and b independent of x. As a result, replacing f by g does not affect the minimizers.

Lastly, we define the non-fidelity-forced versions of the graph MBO scheme, the graph ACE, and the SDIE scheme.

The MBO scheme is an iterative, two-step process, originally developed in 4 to approximate motion by mean curvature. On a graph, it is defined in 32 by the following iteration: for u n ∈ 𝒱 { 0 , 1 } , and τ > 0 the time step,
  1. v n ≔ e − τ Δ u n , that is, the diffused state of un after a time τ .
  2. u n + 1 ≔ Θ ( v n ) where Θ is defined by, for all i ∈ V and v ∈ 𝒱 ,
    ( Θ ( v ) ) i ≔ 1 , if v i ≥ 1 / 2 , 0 , if v i < 1 / 2 . ()
To define the graph ACE, we first define the graph Ginzburg-Landau functional as in 13 by
GL ε ( u ) ≔ 1 2 ∇ u ℰ 2 + 1 ε W ∘ u , 1 𝒱
where W is a double-well potential and ε > 0 is a scaling parameter. Then the ACE results from taking the ⟨· , ·⟩ gradient flow of GL ε , which for W differentiable is given by the ODE (where ∇ 𝒱 is the Hilbert space gradient on 𝒱 ):
d u d t = − ∇ 𝒱 GL ε ( u ) = − Δ u − 1 ε W ′ ∘ u .
To facilitate the SDIE link from 13 between the ACE and the MBO scheme, we will henceforth take W to be defined as:
W ( x ) ≔ 1 2 x ( 1 − x ) , for 0 ≤ x ≤ 1 , ∞ , otherwise, ()
the double-obstacle potential studied by Blowey and Elliott 8-10 in the continuum and Bosch et al. 11 on graphs. As W is not differentiable, we redefine the ACE via the subdifferential of W. As in 13 we say that a pair ( u , β ) ∈ 𝒱 [ 0 , 1 ] , t ∈ T × 𝒱 t ∈ T is a solution to the double-obstacle ACE on an interval T if u ∈ H l o c 1 ( T ; 𝒱 ) and for a.e. t ∈ T
ε d u d t ( t ) + ε Δ u ( t ) + 1 2 1 − u ( t ) = β ( t ) , β ( t ) ∈ ℬ ( u ( t ) ) ,
where ℬ ( u ) is the set (for I[0, 1](x) ≔ 0 if x ∈ [0, 1] and I[0, 1](x) ≔ ∞ otherwise)
ℬ ( u ) ≔ α ∈ 𝒱 | ∀ i ∈ V , α i ∈ − ∂ I [ 0 , 1 ] ( u i ) . ()
That is, ℬ ( u ) = ∅ if u ∉ 𝒱 [ 0 , 1 ] , and for u ∈ 𝒱 [ 0 , 1 ] it is the set of β ∈ 𝒱 such that
β i ∈ [ 0 , ∞ ) , u i = 0 , { 0 } , 0 < u i < 1 , ( − ∞ , 0 ] , u i = 1 .
Finally, the SDIE scheme for the graph ACE is defined in 13 by the formula
u n + 1 = e − τ Δ u n − τ ε W ′ ∘ u n + 1
or more accurately, given the above detail with the subdifferential,
( 1 − λ ) u n + 1 − e − τ Δ u n + λ 2 1 = λ β n + 1 ,
where λ ≔ τ / ε and β n + 1 ∈ ℬ ( u n + 1 ) . The key results of 13 are then that:
  • When τ = ε , this scheme is exactly the MBO scheme.
  • For ε fixed and τ ↓ 0 , this scheme converges to the solution of the double-obstacle ACE (which is a well-posed ODE).

1.4 Paper outline

The paper is structured as follows. In Section 1.3 we introduced important concepts and notation for the rest of the paper. Section 2 contains the main theoretical results of this paper. It defines the graph MBO scheme with fidelity forcing, the graph ACE with fidelity forcing, and the SDIE scheme for graph ACE with fidelity forcing. It proves well-posedness for the graph ACE with fidelity forcing and establishes the rigorous link between a particular SDIE scheme and the graph MBO with fidelity forcing. Moreover, it introduces a Lypunov functional for the SDIE scheme with fidelity forcing and proves convergence of solutions of the SDIE schemes to the solution of the graph ACE with fidelity forcing. In Section 3 we explain how the SDIE schemes can be used for graph classification. In particular, the modifications to the existing MBO-based classification algorithms based on the QR decomposition and Strang formula are introduced. Section 4 presents a comparison of the SDIE and MBO scheme for image segmentation applications, and an investigation of the uncertainty in these segmentations. In Appendix A it is shown that the application of the Euler method used in 32 can be seen as an approximation of the Lie product formula.

2 THE ACE, THE MBO SCHEME, AND THE SDIE SCHEME WITH FIDELITY FORCING

2.1 The MBO scheme with fidelity forcing

Following 20, 32, we introduce fidelity forcing into the MBO scheme by first defining a fidelity forced diffusion.

Definition 2.1. (Fidelity forced graph diffusion)For u ∈ H l o c 1 ( [ 0 , ∞ ) ; 𝒱 ) and u 0 ∈ 𝒱 we define fidelity forced diffusion to be:

d u d t ( t ) = − Δ u ( t ) − M ( u ( t ) − f ˜ ) = : − A u ( t ) + M f ˜ , u ( 0 ) = u 0 , ()
where M ≔ diag ( μ ) for μ ∈ 𝒱 [ 0 , ∞ ) ∖ { 0 } the fidelity parameter, A ≔ Δ + M , and f ˜ ∈ 𝒱 [ 0 , 1 ] is the reference. We define Z ≔ supp ( μ ) ≠ ∅ , which is the reference data we enforce fidelity on. Note that μ i parameterizes the strength of the fidelity to the reference at vertex i. For the purposes of this section we shall treat μ and f ˜ (and therefore M and Z) as fixed and given. Moreover, since f ˜ only ever appears in the presence of M, we define f ≔ M f ˜ which is supported only on Z. Note that f i ≔ μ i f ˜ i ∈ [ 0 , μ i ] .

Note.This fidelity term generalizes slightly the one used (for ACE) in 6, in which μ ≔ μ ^ χ Z for μ ^ > 0 a parameter (ie, fidelity was enforced with equal strength on each vertex of the reference data) yielding M = μ ^ P Z where PZ is the projection map:

( P Z u ) i = u i , if i ∈ Z , 0 , if i ∉ Z .
This generalization has practical relevance, for example if the confidence in the accuracy of the reference were higher at some vertices of the reference data than at others it might be advantageous to use a fidelity parameter that is nonconstant on the reference data. This is due to the link between the value of the fidelity parameter at a vertex and the statistical precision (ie, the inverse of the variance of the noise) of the reference at that vertex (see [7, Section 3.3] for details).

Proposition 2.2.A is invertible with σ ( A ) ⊆ ( 0 , | | Δ | | + | | μ | | ∞ ] .

Proof.For the lower bound, we show that A is strictly positive definite. Let u ≠ 0 be written u = v + α 1 for v ⊥ 1. Then

⟨ u , A u ⟩ 𝒱 = ⟨ v , Δ v ⟩ 𝒱 + ⟨ u , M u ⟩ 𝒱
and note that both terms on the right-hand side are nonnegative. Next, if v ≠ 0 then
⟨ u , A u ⟩ 𝒱 ≥ ⟨ v , Δ v ⟩ 𝒱 = | | ∇ v | | ℰ 2 > 0
since v ⊥ 1 and hence ∇v ≠ 0, since G is connected. Else, v = 0 so α ≠ 0 and
⟨ u , A u ⟩ 𝒱 = α 2 ⟨ 1 , μ ⟩ 𝒱 > 0 .
For the upper bound: A is the sum of self-adjoint matrices, so is self-adjoint and hence has largest eigenvalue equal to | | A | | = | | Δ + M | | ≤ | | Δ | | + | | M | | = | | Δ | | + | | μ | | ∞ .

Theorem 2.3.For given u 0 ∈ 𝒱 , (2.1) has a unique solution in H l o c 1 ( [ 0 , ∞ ) ; 𝒱 ) . The solution u to (2.1) is C 1 ( ( 0 , ∞ ) ; 𝒱 ) and is given by the map (where I denotes the identity matrix):

u ( t ) = 𝒮 t u 0 ≔ e − t A u 0 + A − 1 ( I − e − t A ) f . ()
This solution map has the following properties:

  1. If u0 ≤ v0 vertexwise, then for all t ≥ 0, 𝒮 t u 0 ≤ 𝒮 t v 0 vertexwise.

  2. 𝒮 t : 𝒱 [ 0 , 1 ] → 𝒱 [ 0 , 1 ] for all t ≥ 0, that is, if u 0 ∈ 𝒱 [ 0 , 1 ] then u ( t ) ∈ 𝒱 [ 0 , 1 ] .

Proof.It is straightforward to check directly that (2.2) satisfies (2.1) and is C1 on (0, ∞). Uniqueness is given by a standard Picard-Lindelöf argument (see eg, [40, Corollary 2.6]).

  1. By definition, 𝒮 t v 0 − 𝒮 t u 0 = e − t A ( v 0 − u 0 ) . Thus it suffices to show that e−tA is a nonnegative matrix for t ≥ 0. Note that the off-diagonal elements of −tA are nonnegative: for i ≠ j, − t A i j = − t Δ i j = t d i r ω i j ≥ 0 . Thus for some a > 0, Q ≔ aI − tA is a nonnegative matrix and thus eQ is a nonnegative matrix. It follows that e−tA = e−aeQ is a nonnegative matrix.

  2. Let u 0 ∈ 𝒱 [ 0 , 1 ] and recall that f ˜ ∈ 𝒱 [ 0 , 1 ] . Suppose that for some t > 0 and some i ∈ V, ui(t) < 0. Then

    min t ′ ∈ [ 0 , t ] min i ∈ V u i ( t ′ ) < 0
    and since each ui is continuous this minimum is attained at some t∗ ∈ [0, t] and i∗ ∈ V. Fix such a t∗. Then for any i∗ minimizing u(t∗), since u i ∗ ( t ∗ ) < 0 we must have t∗ > 0, so u i ∗ is differentiable at t∗ with d u i ∗ / d t ( t ∗ ) = 0 . However by (2.1)
    d u i ∗ d t ( t ∗ ) = − ( Δ u ( t ∗ ) ) i ∗ + μ i ∗ ( f ˜ i ∗ − u i ∗ ( t ∗ ) ) .
    We claim that we can choose a suitable minimizer i∗ such that this is strictly positive. First, since any such i∗ is a minimizer of u(t∗), and f ˜ i ≥ 0 for all i, it follows that each term is nonnegative. Next, suppose such an i∗ has a neighbor j such that u j ( t ∗ ) > u i ∗ ( t ∗ ) , then it follows that ( Δ u ( t ∗ ) ) i ∗ < 0 and we have the claim. Otherwise, all the neighbors of that i∗ are also minimizers of u(t∗). Repeating this same argument on each of those, we either have the claim for the above reason or we find a minimizer i∗ ∈ Z, since G is connected. But in that case μ i ∗ ( f ˜ i ∗ − u i ∗ ( t ∗ ) ) ≥ − μ i ∗ u i ∗ ( t ∗ ) > 0 , since μ is strictly positive on Z, and we again have the claim. Hence d u i ∗ / d t ( t ∗ ) > 0 , a contradiction. Therefore ui(t) ≥ 0 for all t. The case for ui(t) ≤ 1 is likewise.

Definition 2.4. (Graph MBO with fidelity forcing)For u 0 ∈ 𝒱 [ 0 , 1 ] we follow 20, 32, and define the sequence of MBO iterates by diffusing with fidelity for a time τ ≥ 0 and then thresholding, that is

( u n + 1 ) i = 1 , if ( 𝒮 τ u n ) i ≥ 1 / 2 , 0 , if ( 𝒮 τ u n ) i < 1 / 2 , ()
where 𝒮 τ is the solution map from (2.2). Note that (2.3) has variational form similar to that given for graph MBO in 24, which we can then re-write as in 13:
u n + 1 ∈ argmin u ∈ 𝒱 [ 0 , 1 ] ⟨ 1 − 2 𝒮 τ u n , u ⟩ 𝒱 ≃ 1 2 τ ⟨ 1 − u , u ⟩ 𝒱 + u − 𝒮 τ u n 𝒱 2 2 τ . ()

2.2 The ACE with fidelity forcing

To derive the ACE with fidelity forcing, we re-define the Ginzburg-Landau energy to include a fidelity term (recalling the potential W from (1.2)):
GL ε , μ , f ˜ ( u ) ≔ 1 2 ∇ u ℰ 2 + 1 ε W ∘ u , 1 𝒱 + 1 2 ⟨ u − f ˜ , M ( u − f ˜ ) ⟩ 𝒱 . ()
Taking the ⟨· , ·⟩𝒱 gradient flow of (2.5) we obtain the ACE with fidelity:
ε d u d t ( t ) + ε ( Δ u ( t ) + M ( u ( t ) − f ˜ ) ) + 1 2 1 − u ( t ) = β ( t ) , β ( t ) ∈ ℬ ( u ( t ) ) . ()
Where ℬ ( u ( t ) ) is defined as in (1.3). Recalling that A ≔ Δ + M and f ≔ M f ˜ , we can rewrite the ODE in (2.6) as
ε d u d t ( t ) + ε A u ( t ) − ε f + 1 2 1 − u ( t ) = β ( t ) .
As in 13, we can give an explicit expression for β given sufficient regularity on u.

Theorem 2.5.Let ( u , β ) obey (2.6) at a.e. t ∈ T, with u ∈ H l o c 1 ( T ; 𝒱 ) ∩ C 0 ( T ; 𝒱 ) ∩ 𝒱 [ 0 , 1 ] , t ∈ T . Then for all i ∈ V and a.e. t ∈ T,

β i ( t ) = 1 2 + ε ( Δ u ( t ) ) i − ε f i , u i ( t ) = 0 , 0 , u i ( t ) ∈ ( 0 , 1 ) , − 1 2 + ε ( Δ u ( t ) ) i + ε ( μ i − f i ) , u i ( t ) = 1 . ()
Hence at a.e. t ∈ T,
β ( t ) ∈ 𝒱 [ − 1 / 2 , 1 / 2 ] .

Proof.Follows as in [13, Theorem 2.2] mutatis mutandis.

Thus following 13 we define the double-obstacle ACE with fidelity forcing.

Definition 2.6. (Double-obstacle ACE with fidelity forcing)Let T be an interval. Then a pair ( u , β ) ∈ 𝒱 [ 0 , 1 ] , t ∈ T × 𝒱 t ∈ T is a solution to double-obstacle ACE with fidelity forcing on T when u ∈ H l o c 1 ( T ; 𝒱 ) ∩ C 0 ( T ; 𝒱 ) and for almost every t ∈ T,

ε d u d t ( t ) + ε A u ( t ) − ε f + 1 2 1 − u ( t ) = β ( t ) , β ( t ) ∈ ℬ ( u ( t ) ) . ()
We frequently will refer to just u as a solution to (2.8), since β is a.e. uniquely determined as a function of u by (2.7).

We now demonstrate that this has the same key properties, mutatis mutandis, as the ACE in 13.

Theorem 2.7.Let T = [0, T0] or [0, ∞). Then:

  1. (Existence) For any given u 0 ∈ 𝒱 [ 0 , 1 ] , there exists a ( u , β ) as in Definition 2.6 with u(0) = u0.

  2. (Comparison principle) If ( u , β ) , ( v , γ ) ∈ 𝒱 [ 0 , 1 ] , t ∈ T × 𝒱 t ∈ T with u , v ∈ H l o c 1 ( T ; 𝒱 ) ∩ C 0 ( T ; 𝒱 ) satisfy

    ε d u d t ( t ) + ε A u ( t ) − ε f + 1 2 1 − u ( t ) ≥ β ( t ) , β ( t ) ∈ ℬ ( u ( t ) ) , ()
    and
    ε d v d t ( t ) + ε A v ( t ) − ε f + 1 2 1 − v ( t ) ≤ γ ( t ) , γ ( t ) ∈ ℬ ( v ( t ) ) , ()
    vertexwise at a.e. t ∈ T, and v(0) ≤ u(0) vertexwise, then v(t) ≤ u(t) vertexwise for all t ∈ T.

  3. (Uniqueness) If ( u , β ) and ( v , γ ) are as in Definition 2.6 with u(0) = v(0) then u(t) = v(t) for all t ∈ T and β ( t ) = γ ( t ) at a.e. t ∈ T.

  4. (Gradient flow) For u as in Definition 2.6, GL ε , μ , f ˜ ( u ( t ) ) monotonically decreases.

  5. (Weak form) u ∈ 𝒱 [ 0 , 1 ] , t ∈ T ∩ H l o c 1 ( T ; 𝒱 ) ∩ C ( T ; 𝒱 ) (and associated β ( t ) = ε d u d t ( t ) + ε A u ( t ) − ε f + 1 2 1 − u ( t ) a.e.) is a solution to (2.8) if and only if for almost every t ∈ T and all η ∈ 𝒱 [ 0 , 1 ]

    ε d u d t + ε A u ( t ) − ε f + 1 2 1 − u ( t ) , η − u ( t ) 𝒱 ≥ 0 . ()

  6. (Explicit form) ( u , β ) ∈ 𝒱 [ 0 , 1 ] , t ∈ T × 𝒱 t ∈ T satisfies Definition 2.6 if and only if for a.e. t ∈ T, β ( t ) ∈ ℬ ( u ( t ) ) , β ( t ) ∈ 𝒱 [ − 1 / 2 , 1 / 2 ] and (for B ≔  A − ε−1I and ε − 1 ∉ σ ( A ) ):

    u ( t ) = e − t B u ( 0 ) + B − 1 I − e − t B f − 1 2 ε 1 + 1 ε ∫ 0 t e − ( t − s ) B β ( s ) d s . ()

  7. (Lipschitz regularity) For u as in Definition 2.6, if ε − 1 ∉ σ ( A ) , then u ∈ C 0 , 1 ( T ; 𝒱 ) .

  8. (Well-posedness) Let u 0 , v 0 ∈ 𝒱 [ 0 , 1 ] define the ACE trajectories u, v as in Definition 2.6, and suppose ε − 1 ∉ σ ( A ) . Then, for ξ 1 ≔ min σ ( A ) ,

    | | u ( t ) − v ( t ) | | 𝒱 ≤ e − ξ 1 t e t / ε | | u 0 − v 0 | | 𝒱 . ()

Proof.

  1. We prove this as Theorem 2.17.

  2. We follow the proof of [13, Theorem B.2]. Letting w ≔ v − u and subtracting (2.9) from (2.10), we have that

    ε d w d t ( t ) + ε A w ( t ) − w ( t ) ≤ γ ( t ) − β ( t )
    vertexwise at a.e. t ∈ T. Next, take the inner product with w + ≔ max ( w , 0 ) , the vertexwise positive part of w:
    ε d w d t ( t ) , w + ( t ) 𝒱 + ε ⟨ A w ( t ) , w + ( t ) ⟩ 𝒱 − ⟨ w ( t ) , w + ( t ) ⟩ 𝒱 ≤ ⟨ γ ( t ) − β ( t ) , w + ( t ) ⟩ 𝒱 .
    As in the proof of [13, Theorem B.2], the RHS ≤ 0. For the rest of the proof to go through as in that theorem, it suffices to check that ⟨Aw(t), w+(t)⟩ ≥ ⟨Aw+(t), w+(t)⟩. But by [13, Proposition B.1], ⟨ Δ w ( t ) , w + ( t ) ⟩ 𝒱 ≥ ⟨ Δ w + ( t ) , w + ( t ) ⟩ 𝒱 , and ⟨Mw(t), w+(t)⟩ = ⟨Mw+(t), w+(t)⟩ since M is diagonal, so the proof follows as in [13, Theorem B.2].

  3. Follows from (b): if ( u , β ) and ( v , γ ) have u(0) = v(0) and both solve (2.8), then applying the comparison principle in both directions gives that u(t) = v(t) at all t ∈ T. Then (2.7) gives that β ( t ) = γ ( t ) at a.e. t ∈ T.

  4. We prove this in Theorem 2.20 for the solution given by Theorem 2.17, which by uniqueness is the general solution.

  5. Let u solve (2.8). Then for a.e. t ∈ T, β ( t ) ∈ ℬ ( u ( t ) ) , and at such t we have ⟨ β ( t ) , η − u ( t ) ⟩ 𝒱 ≥ 0 for all η ∈ 𝒱 [ 0 , 1 ] as in the proof of [13, Theorem 3.8], so u satisfies (2.11). Next, if u satisfies (2.11) at t ∈ T, then as in the proof of [13, Theorem 3.8], β ( t ) ≔ ε d u d t ( t ) + ε A u ( t ) − ε f + 1 2 1 − u ( t ) ∈ ℬ ( u ( t ) ) , as desired.

  6. Let ( u , β ) ∈ 𝒱 [ 0 , 1 ] , t ∈ T × 𝒱 t ∈ T . If: We check that (2.12) satisfies (2.8). Note first that we can rewrite (2.8) as

    d u d t ( t ) + B u ( t ) − f + 1 2 ε 1 = 1 ε β ( t ) .
    Next, let u be as in (2.12). Then it is easy to check that
    d u d t ( t ) = − B e − t B u ( 0 ) + e − t B f − 1 2 ε 1 + 1 ε β ( t ) − 1 ε B ∫ 0 t e − ( t − s ) B β ( s ) d s
    and that this satisfies (2.8). Next, we check the regularity of u. The continuity of u is immediate, as it is a sum of two smooth terms and the integral of a locally bounded function. To check that u ∈ H l o c 1 : u is bounded, so is locally L2, and by above du/dt is a sum of (respectively) two smooth functions, a bounded function and the integral of a locally bounded function, so is locally bounded and hence locally L2.

    Only if: We saw that (2.12) solves (2.8) with β ( t ) ∈ ℬ ( u ( t ) ) and β ( t ) ∈ 𝒱 [ − 1 / 2 , 1 / 2 ] , and by (c) such solutions are unique.

  7. We follow the proof of [13, Theorem 3.13]. Let 0 ≤ t1 < t2. Since (2.8) is time-translation invariant, we have by (f) that

    u ( t 2 ) = e − ( t 2 − t 1 ) B u ( t 1 ) + B − 1 I − e − ( t 2 − t 1 ) B f − 1 2 ε 1 + 1 ε ∫ 0 t 2 − t 1 e − s B β ( t 2 − s ) d s
    and so, writing Bs ≔ (e−sB − I)/s for s > 0 (which we note commutes with B),
    u ( t 2 ) − u ( t 1 ) = ( t 2 − t 1 ) B t 2 − t 1 u ( t 1 ) − B − 1 f − 1 2 ε 1 + 1 ε ∫ 0 t 2 − t 1 e − s B β ( t 2 − s ) d s .
    Note that Bs is self-adjoint, and as −B has largest eigenvalue less than ε−1 we have ||Bs||< (es/ε − 1)/s, with RHS monotonically increasing in s for s > 0.Since f ∈ 𝒱 [ 0 , | | μ | | ∞ ] and for all t, β ( t ) ∈ 𝒱 [ − 1 / 2 , 1 / 2 ] and u ( t ) ∈ 𝒱 [ 0 , 1 ] , we have for t2 − t1 < 1:
    u ( t 2 ) − u ( t 1 ) 𝒱 t 2 − t 1 ≤ | | B t 2 − t 1 | | · 1 + | | μ | | ∞ | | B − 1 | | + 1 2 ε | | B − 1 | | | | 1 | | 𝒱 + 1 ε ess sup s ∈ [ 0 , t 2 − t 1 ] e − s B β ( t 2 − s ) 𝒱 < e ( t 2 − t 1 ) / ε − 1 t 2 − t 1 · 1 + | | μ | | ∞ | | B − 1 | | + 1 2 ε | | B − 1 | | | | 1 | | 𝒱 + 1 ε sup s ∈ [ 0 , t 2 − t 1 ] e − s B · 1 2 | | 1 | | 𝒱 ≤ e ( t 2 − t 1 ) / ε − 1 t 2 − t 1 · 1 + | | μ | | ∞ | | B − 1 | | + 1 2 ε | | B − 1 | | | | 1 | | 𝒱 + 1 ε e ( t 2 − t 1 ) / ε · 1 2 | | 1 | | 𝒱 < 1 + | | μ | | ∞ | | B − 1 | | + 1 2 ε | | B − 1 | | e 1 / ε − 1 + 1 2 ε e 1 / ε | | 1 | | 𝒱
    and for t2 − t1 ≥ 1 we simply have
    u ( t 2 ) − u ( t 1 ) 𝒱 t 2 − t 1 ≤ u ( t 2 ) − u ( t 1 ) 𝒱 ≤ | | 1 | | 𝒱
    completing the proof.

  8. We prove this as Theorem 2.21 for the solution given by Theorem 2.17, which by uniqueness is the general solution.

Note.Given the various forward references in the above proof, we take care to avoid circularity by not using the corresponding results until they have been proven.

2.3 The SDIE scheme with fidelity forcing and link to the MBO scheme

Definition 2.8. (SDIE scheme with fidelity forcing, cf. [[13], Definition 4.1])For u 0 ∈ 𝒱 [ 0 , 1 ] , n ∈ ℕ , and λ ≔ τ / ε ∈ [ 0 , 1 ] we define the SDIE scheme iteratively:

( 1 − λ ) u n + 1 − 𝒮 τ u n + λ 2 1 = λ β n + 1 ()
for a β n + 1 ∈ ℬ ( u n + 1 ) to be characterized in Theorem 2.9.

As in 13, we have the key theorem linking the MBO scheme and the SDIE schemes for the ACE.

Theorem 2.9. (Cf. [[13], Theorem 4.2])For λ ∈ [ 0 , 1 ] , the pair ( u n + 1 , β n + 1 ) is a solution to the SDIE scheme (2.14) for some β n + 1 ∈ ℬ ( u n + 1 ) if and only if un + 1 solves:

u n + 1 ∈ argmin u ∈ 𝒱 [ 0 , 1 ] λ u , 1 − u 𝒱 + u − 𝒮 τ u n 𝒱 2 . ()
Note that for λ = 1 (2.15) is equivalent to the variational problem (2.4) that defines the MBO scheme. Furthermore, (2.15) has unique solution for λ ∈ [ 0 , 1 )
( u n + 1 ) i = 0 , if 𝒮 τ u n i < 1 2 λ , 1 2 + 𝒮 τ u n i − 1 / 2 1 − λ , if 1 2 λ ≤ 𝒮 τ u n i < 1 − 1 2 λ , 1 , if 𝒮 τ u n i ≥ 1 − 1 2 λ , ()
with corresponding β n + 1 = λ − 1 ( 1 − λ ) u − 𝒮 τ u n + λ 2 1 , and solutions for λ = 1
( u n + 1 ) i ∈ { 1 } , ( 𝒮 τ u n ) i > 1 / 2 , [ 0 , 1 ] , ( 𝒮 τ u n ) i = 1 / 2 , { 0 } , ( 𝒮 τ u n ) i < 1 / 2 . ()
(ie, the MBO thresholding) with corresponding β n + 1 = 1 2 1 − 𝒮 τ u n .

Proof.Identical to the proof of [13, Theorem 4.2] with the occurrences of “ e − τ Δ ” in each instance replaced by “ 𝒮 τ .”

As in [13, Figure 1], we can plot (2.16) to visualize the SDIE scheme (2.14) as a piecewise linear relaxation of the MBO thresholding rule. Next, we note that we have the same Lipschitz continuity property from [13, Theorem 4.4].

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Plot of the SDIE updates un + 1 (blue, left axis, see (2.16)) and β n + 1 (orange, right axis) at vertex i for 0 ≤ λ < 1 as a function of the fidelity forced diffused value at i. Cf. [13, Figure 1]

Theorem 2.10. (Cf. [[13], Theorem 4.4])For λ ∈ [ 0 , 1 ) and all n ∈ ℕ , if un and vn are defined according to Definition 2.8 with initial states u 0 , v 0 ∈ 𝒱 [ 0 , 1 ] and ξ 1 ≔ min σ ( A ) then

| | u n − v n | | 𝒱 ≤ e − n ξ 1 τ ( 1 − λ ) − n | | u 0 − v 0 | | 𝒱 . ()

Proof.Follows as in [13, Theorem 4.4] mutatis mutandis.

2.4 A Lyapunov functional for the SDIE scheme

Lemma 2.11. (Cf. [[24], Lemma 4.6])The functional on 𝒱

J ( u ) ≔ ⟨ u , 1 − 2 A − 1 ( I − e − τ A ) f − e − τ A u ⟩ 𝒱
has the following properties:

  1. It is strictly concave.

  2. It has first variation at u

    L u ( v ) ≔ v , 1 − 2 A − 1 ( I − e − τ A ) f − 2 e − τ A u 𝒱 = v , 1 − 2 𝒮 τ u 𝒱 .

Proof.Let w ≔ 1 − 2 A − 1 ( I − e − τ A ) f . We expand around u:

J ( u + t v ) = ⟨ u + t v , w − e τ A ( u + t v ) ⟩ 𝒱 = ⟨ u , w − e τ A u ⟩ 𝒱 + t ⟨ v , w − e τ A u ⟩ 𝒱 − t ⟨ u , e − t A v ⟩ 𝒱 − t 2 ⟨ v , e − τ A v ⟩ 𝒱 .

  1. d 2 d t 2 J ( u + t v ) = − 2 ⟨ v , e − τ A v ⟩ 𝒱 < 0 for v ≠ 0.

  2. Since e−tA is self-adjoint, J ( u + t v ) = J ( u ) + t L u ( v ) + 𝒪 ( t 2 ) .

Theorem 2.12. (Cf. [[13], Theorem 4.9])For 0 ≤ λ ≤ 1 we define on 𝒱 [ 0 , 1 ] the functional

H ( u ) ≔ J ( u ) + ( λ − 1 ) ⟨ u , 1 − u ⟩ 𝒱 . ()
This has uniform lower bound
H ( u ) ≥ − 2 τ | | f | | 𝒱 | | 1 | | 𝒱 ()
and is a Lyapunov functional for (2.14), that is, H(un + 1) ≤ H(un) with equality if and only if un + 1 = un for un + 1 defined by (2.14). In particular, we have that
H ( u n ) − H ( u n + 1 ) ≥ ( 1 − λ ) u n + 1 − u n 𝒱 2 . ()

Proof.We can rewrite H as:

H ( u ) = λ ⟨ u , 1 − u ⟩ 𝒱 + ⟨ u , u − 2 A − 1 ( I − e − τ A ) f − e − τ A u ⟩ 𝒱 ≥ ⟨ u , ( I − e − τ A ) u ⟩ 𝒱 − 2 ⟨ u , A − 1 ( I − e − τ A ) f ⟩ 𝒱 since u ∈ 𝒱 [ 0 , 1 ] ≥ − 2 ⟨ u , A − 1 ( I − e − τ A ) f ⟩ 𝒱 since I − e − τ A is positive definite ≥ − 2 | | f | | 𝒱 | | u | | 𝒱 A − 1 ( I − e − τ A ) ≥ − 2 | | f | | 𝒱 | | 1 | | 𝒱 A − 1 ( I − e − τ A ) ≥ − 2 τ | | f | | 𝒱 | | 1 | | 𝒱 ,
where the final line follows since A − 1 ( I − e − τ A ) is self-adjoint (since A is) and has eigenvalues
1 − e − τ λ λ | λ ∈ σ ( A )
so we have by Proposition 2.2 that
A − 1 ( I − e − τ A ) ≤ sup x ∈ ( 0 , | | Δ | | + | | μ | | ∞ ] 1 − e − τ x x = lim x → 0 1 − e − τ x x as x ↦ x − 1 ( 1 − e − τ x ) is monotonically decreasing 3 = τ .
Nextwe show that H is a Lyapunov functional. By the concavity of J:
H ( u n ) − H ( u n + 1 ) = J ( u n ) − J ( u n + 1 ) + ( 1 − λ ) ⟨ u n + 1 , 1 − u n + 1 ⟩ 𝒱 − ( 1 − λ ) ⟨ u n , 1 − u n ⟩ 𝒱 ≥ L u n ( u n − u n + 1 ) + ( 1 − λ ) ⟨ u n + 1 , 1 − u n + 1 ⟩ 𝒱 − ( 1 − λ ) ⟨ u n , 1 − u n ⟩ 𝒱 ∗ = ⟨ u n − u n + 1 , 1 − 2 𝒮 τ u n ⟩ 𝒱 + ( 1 − λ ) ⟨ u n + 1 , 1 − u n + 1 ⟩ 𝒱 − ( 1 − λ ) ⟨ u n , 1 − u n ⟩ 𝒱 = ⟨ u n − u n + 1 , 1 − 2 𝒮 τ u n ⟩ 𝒱 + ( 1 − λ ) ( ⟨ u n + 1 − u n , 1 ⟩ 𝒱 + ⟨ u n , u n ⟩ 𝒱 − ⟨ u n + 1 , u n + 1 ⟩ 𝒱 ) = ⟨ u n − u n + 1 , λ 1 − 2 𝒮 τ u n + ( 1 − λ ) u n + 1 + ( 1 − λ ) u n ⟩ 𝒱 = ⟨ u n − u n + 1 , 2 λ β n + 1 + ( 1 − λ ) ( u n − u n + 1 ) ⟩ 𝒱 by (2.14) ≥ ( 1 − λ ) u n + 1 − u n 𝒱 2 ≥ 0
with equality in (∗) if and only if un + 1 = un as the concavity of J is strict, and where the last line follows since by β n + 1 ∈ ℬ ( u n + 1 )
( β n + 1 ) i ( ( u n ) i − ( u n + 1 ) i ) = “ ≥ 0 ” · ( u n ) i , ( u n + 1 ) i = 0 0 , ( u n + 1 ) i ∈ ( 0 , 1 ) “ ≤ 0 ” · ( u n ) i − 1 , ( u n + 1 ) i = 1 ≥ 0
and so ⟨ u n − u n + 1 , β n + 1 ⟩ 𝒱 ≥ 0 .

Corollary 2.13.For λ = 1 (ie, the MBO case) the sequence un defined by (2.14) is eventually constant.

For 0 ≤ λ ≤ 1 , the sum

∑ n = 0 ∞ | | u n + 1 − u n | | 𝒱 2
converges, and hence
lim n → ∞ | | u n + 1 − u n | | 𝒱 = 0 .

Proof.For the first claim, the proof follows as in [24, Proposition 4.6] mutatis mutandis. For the second claim, the proof follows as in [13, Corollary 4.10] mutatis mutandis.

2.5 Convergence of the SDIE scheme with fidelity forcing

Following 13, we first derive the nth term for the semi-discrete scheme.

Proposition 2.14. (Cf. [[13], Proposition 5.1])For the sake of notation, define:

w ≔ − 1 2 λ 1 + A − 1 ( I − e − τ A ) f .
Then for λ ∈ [ 0 , 1 ) the sequence generated by (2.14) is given by:
u n = ( 1 − λ ) − n e − n τ A u 0 + ∑ k = 1 n ( 1 − λ ) − k e − ( k − 1 ) τ A w + λ 1 − λ ∑ k = 1 n ( 1 − λ ) − ( n − k ) e − ( n − k ) τ A β k . ()

Proof.We can rewrite (2.14) as

( 1 − λ ) u n + 1 = e − τ A u n + A − 1 ( I − e − t A ) f − 1 2 λ 1 + λ β n + 1 = e − τ A u n + w + λ β n + 1 .
We then check (2.22) inductively. The n = 0 case is trivial, and we have that
( 1 − λ ) − 1 e − τ A u n + ( 1 − λ ) − 1 w + λ 1 − λ β n + 1 = ( 1 − λ ) − ( n + 1 ) e − ( n + 1 ) τ A u 0 + ∑ k = 1 n ( 1 − λ ) − ( k + 1 ) e − k τ A w + λ 1 − λ ∑ k = 1 n ( 1 − λ ) − ( ( n + 1 ) − k ) e − ( ( n + 1 ) − k ) τ A β k + ( 1 − λ ) − 1 w + λ 1 − λ β n + 1 = ( 1 − λ ) − ( n + 1 ) e − ( n + 1 ) τ A u 0 + ∑ k = 0 n ( 1 − λ ) − ( k + 1 ) e − k τ A w + λ 1 − λ ∑ k = 1 n + 1 ( 1 − λ ) − ( ( n + 1 ) − k ) e − ( ( n + 1 ) − k ) τ A β k = u n + 1
completing the proof.

Next, we consider the asymptotics of each term in (2.22).

Theorem 2.15.Considering 𝒪 relative to the limit of τ ↓ 0 and n → ∞ with n τ − t ∈ [ 0 , τ ) for some fixed t ≥ 0 and for fixed ε > 0 (with ε − 1 ∉ σ ( A ) ), and recalling that λ ≔ τ / ε , B ≔ A − ε−1I and w ≔ − 1 2 λ 1 + A − 1 ( I − e − τ A ) f :

  1. ( 1 − λ ) − n e − n τ A u 0 = e t / ε e − t A u 0 + 𝒪 ( τ ) = e − t B u 0 + 𝒪 ( τ ) .

  2. ∑ k = 1 n ( 1 − λ ) − k e − ( k − 1 ) τ A w = B − 1 ( I − e − t B ) f − 1 2 ε B − 1 ( I − e − t B ) 1 + 𝒪 ( τ ) .

  3. λ 1 − λ ∑ k = 1 n ( 1 − λ ) − ( n − k ) e − ( n − k ) τ A β k = λ ∑ k = 1 n e − ( n − k ) τ B β k + 𝒪 ( τ ) .

Hence by (2.22), the SDIE term obeys

u n = e − t B u 0 + B − 1 ( I − e − t B ) f − 1 2 ε B − 1 ( I − e − t B ) 1 + λ ∑ k = 1 n e − ( n − k ) τ B β k + 𝒪 ( τ ) . ()

Proof.Let n τ − t = : η n = 𝒪 ( τ ) . Note that e η n X = I + 𝒪 ( τ ) for any bounded matrix X.

Note that 𝒪 ( τ ) is the same as 𝒪 ( λ ) , and also that, for bounded (in τ ) invertible matrices X and Y with bounded (in τ ) inverses, X = Y + 𝒪 ( τ ) if and only if X − 1 = Y − 1 + 𝒪 ( τ ) .

  1. | | ( 1 − λ ) − n e − n τ A u 0 − e − t B u 0 | | 𝒱 ≤ | | ( 1 − λ ) − n e − n τ A − e − t B | | · | | u 0 | | 𝒱 , so it suffices to consider ( 1 − λ ) − n e − n τ A − e − t B . Since ( 1 − λ ) − n = e n λ + 𝒪 ( τ 2 ) we infer that

    ( 1 − λ ) − n e − n τ A = e t / ε e η n / ε e − t A e − η n A + 𝒪 ( τ 2 ) = e − t B + 𝒪 ( τ ) .

  2. We note that

    ∑ k = 1 n ( 1 − λ ) − k e − ( k − 1 ) τ A = ( ( 1 − λ ) I − e − τ A ) − 1 ( I − ( 1 − λ ) − n e − n τ A ) = ( ( 1 − λ ) I − e − τ A ) − 1 ( I − e − t B ) + 𝒪 ( τ ) .
    We next consider each term of w individually. First, we seek to show that
    ( ( 1 − λ ) I − e − τ A ) − 1 ( I − e − t B ) A − 1 ( I − e − τ A ) f = B − 1 ( I − e − t B ) f + 𝒪 ( τ )
    so it suffices to show that
    ( ( 1 − λ ) I − e − τ A ) − 1 A − 1 ( I − e − τ A ) = B − 1 + 𝒪 ( τ ) .
    This holds if and only if
    B = ( ( 1 − λ ) I − e − τ A ) A ( I − e − τ A ) − 1 + 𝒪 ( τ ) = A − λ A ( I − e − τ A ) − 1 + 𝒪 ( τ ) = A − ε − 1 τ A τ A − 1 2 τ 2 A 2 + − ⋯ − 1 + 𝒪 ( τ ) = A − ε − 1 I − 1 2 τ A + − ⋯ − 1 + 𝒪 ( τ ) = A − ε − 1 I + 𝒪 ( τ )
    and since B = A − ε−1I the result follows. Next we seek to show that
    ( ( 1 − λ ) I − e − τ A ) − 1 ( I − e − t B ) 1 2 λ 1 = 1 2 ε B − 1 ( I − e − t B ) 1 + 𝒪 ( τ )
    so it suffices to show that
    ( ( 1 − λ ) I − e − τ A ) − 1 τ = B − 1 + 𝒪 ( τ )
    which holds if and only if
    B = τ − 1 ( ( 1 − λ ) I − e − τ A ) + 𝒪 ( τ ) = A − ε − 1 I + 𝒪 ( τ )
    and since B = A − ε−1I the result follows.

  3. We follow [13, Proposition 5.1] and consider the difference

    λ 1 − λ ∑ k = 1 n ( 1 − λ ) − ( n − k ) e − ( n − k ) τ A β k − λ ∑ k = 1 n e − ( n − k ) τ B β k 𝒱 = λ ∑ k = 1 n ( 1 − λ ) − ( n − k + 1 ) − e ( n − k ) λ e − ( n − k ) τ A β k 𝒱 = λ ∑ ℓ = 0 n − 1 ( 1 − λ ) − ( ℓ + 1 ) − e ℓ λ e − ℓ τ A β k 𝒱 ≤ λ ∑ ℓ = 0 n − 1 ( 1 − λ ) − ( ℓ + 1 ) − e ℓ λ e − ℓ τ A β k 𝒱 as ( 1 − λ ) − ( ℓ + 1 ) − e ℓ λ ≥ 0 ≤ 1 2 λ | | 1 | | 𝒱 ∑ ℓ = 0 n − 1 ( 1 − λ ) − ( ℓ + 1 ) − e ℓ λ as | | e − ℓ τ A | | ≤ 1 and | | β k | | 𝒱 ≤ 1 2 | | 1 | | 𝒱 = 1 2 λ | | 1 | | 𝒱 ( 1 − λ ) − n − 1 1 − ( 1 − λ ) − e n λ − 1 e λ − 1 = 1 2 | | 1 | | 𝒱 ( 1 − λ ) − n − e n λ + 𝒪 ( τ ) as λ / ( e λ − 1 ) = 1 + 𝒪 ( τ ) = 𝒪 ( τ )
    as desired.

Following 13 we define the piecewise constant function z τ : [ 0 , ∞ ) → 𝒱
z τ ( s ) ≔ e τ B β 1 [ τ ] , 0 ≤ s ≤ τ e k τ B β k [ τ ] , ( k − 1 ) τ < s ≤ k τ for k ∈ ℕ
and the function
γ τ ( s ) ≔ e − s B z τ ( s ) = e ( τ − s ) B β 1 [ τ ] , 0 ≤ s ≤ τ e ( k τ − s ) B β k [ τ ] , ( k − 1 ) τ < s ≤ k τ for k ∈ ℕ
following the bookkeeping notation of 13 of using the superscript [ τ ] to keep track of the time-step governing un and β n . Next, we have weak convergence of z, up to a subsequence, as in 13.

Theorem 2.16.For any sequence τ n ( 0 ) ↓ 0 with τ n ( 0 ) < ε for all n, there exists a function z : [ 0 , ∞ ) → 𝒱 and a subsequence τ n such that z τ n converges weakly to z in L l o c 2 . It follows that:

  • (A)

    γ τ n ⇀ γ in L l o c 2 , where γ ( s ) = e − s B z .

  • (B)

    For all t ≥ 0,

    ∫ 0 t z τ n ( s ) d s → ∫ 0 t z ( s ) d s .

  • (C)

    Passing to a further subsequence of τ n , we have strong convergence of the Cesàro sums, that is, for all bounded T ⊆ [0, ∞)

    1 N ∑ n = 1 N z τ n → z and 1 N ∑ n = 1 N γ τ n → γ in L 2 ( T ; 𝒱 )
    as N → ∞.

Proof.Follows as in [13, Proposition 5.2] and [13, Corollary 5.3] mutatis mutandis.

We thus infer convergence of the SDIE iterates as in 13. Taking τ to zero along the sequence τ n , we can define for all t ≥ 0:
û ( t ) ≔ lim n → ∞ , m = ⌈ t / τ n ⌉ u m [ τ n ] . ()
By the above discussion, we can rewrite this as:
û ( t ) = e − t B u 0 + B − 1 ( I − e − t B ) f − 1 2 ε B − 1 ( I − e − t B ) 1 + lim n → ∞ τ n ε ∑ k = 1 m e − ( m − k ) τ n B β k [ τ n ] = e − t B u 0 + B − 1 ( I − e − t B ) f − 1 2 ε B − 1 ( I − e − t B ) 1 + 1 ε lim n → ∞ e − m τ n B ∫ 0 m τ n z τ n ( s ) d s .
Next, note that m τ n = τ n ⌈ t / τ n ⌉ = : t + η n where η n ∈ [ 0 , τ n ) . Therefore
lim n → ∞ e − m τ n B ∫ 0 m τ n z τ n ( s ) d s = lim n → ∞ e − η n B e − t B ∫ 0 t z τ n ( s ) d s + e − η n B e − t B ∫ t t + η n z τ n ( s ) d s = lim n → ∞ e − t B ∫ 0 t z τ n ( s ) d s + e − t B ∫ t t + η n z τ n ( s ) d s as e − η n B = I + 𝒪 ( τ n ) = lim n → ∞ e − t B ∫ 0 t z τ n ( s ) d s as z τ n ( s ) is bounded on [ t , t + max n ′ η n ′ ] uniformly in n = e − t B ∫ 0 t z ( s ) d s by Theorem 2.16(B) .
So we have that
û ( t ) = e − t B u 0 + B − 1 ( I − e − t B ) f − 1 2 ε B − 1 ( I − e − t B ) 1 + 1 ε ∫ 0 t e − ( t − s ) B γ ( s ) d s . ()
Note the similarity between (2.25) and the explicit form for ACE solutions (2.12). Thus, to prove that û is a solution to (2.8) it suffices to show that:

  1. û ( t ) ∈ 𝒱 [ 0 , 1 ] for all t ≥ 0,

  2. û ∈ H l o c 1 ( [ 0 , ∞ ) ; 𝒱 ) ∩ C 0 ( [ 0 , ∞ ) ; 𝒱 ) , and

  3. γ ( t ) ∈ ℬ ( û ( t ) ) for a.e. t ≥ 0.

These results follow as in 13. Item (a) follows immediately from the fact that for all n, u m [ τ n ] ∈ 𝒱 [ 0 , 1 ] .

Towards (b), note that each term in (2.25) except for the integral is C ∞ ( [ 0 , ∞ ) ; 𝒱 ) , and that ∫ 0 t z ( s ) d s is continuous since z is locally bounded as a weak limit of locally uniformly bounded functions. Hence û is continuous. By (a), û is bounded so is locally L2. Finally, it is easy to check that û has weak derivative
d û d t = − B e − t B u 0 + e − t B f − 1 2 ε 1 + 1 ε e − t B z ( t ) − 1 ε B e − t B ∫ 0 t z ( s ) d s .
This is locally L2 since (for T a bounded interval) B and e−tB are bounded operators from L 2 ( T ; 𝒱 ) to L 2 ( T ; 𝒱 ) , z is a weak limit of locally L2 functions so is locally L2, and ∫ 0 t z ( s ) d s is continuous so is locally bounded.
Towards (c), by Theorem 2.16(C) and [13, p. 25] mutatis mutandis there is a sequence Nk → ∞, independent of t, with
γ ( t ) = lim k → ∞ 1 N k ∑ n = 1 N k β m [ τ n ]
for a.e. t ≥ 0. Then, at each such t, γ ( t ) ∈ ℬ ( û ( t ) ) follows from u m [ τ n ] → û ( t ) and β m [ τ n ] ∈ ℬ ( u m [ τ n ] ) as in [13, p. 25]. Hence we can infer the following convergence theorem.

Theorem 2.17. (Cf. [[13], Theorem 5.4])For any given u 0 ∈ 𝒱 [ 0 , 1 ] , ε > 0 (with ε − 1 ∉ σ ( A ) ) and τ n ↓ 0 , there exists a subsequence τ n ′ of τ n with τ n ′ < ε for all n, along which the SDIE iterates ( u m [ τ ′ n ] , β m [ τ ′ n ] ) given by (2.14) with initial state u0 converge to the ACE solution with initial condition u0 in the following sense: For each t ≥ 0, as n → ∞ and m = ⌈ t / τ n ′ ⌉ , u m [ τ ′ n ] → û ( t ) , and there is a sequence Nk → ∞ such that for almost every t ≥ 0, 1 N k ∑ n = 1 N k β m [ τ n ′ ] → γ ( t ) , where ( û , γ ) is the solution to (2.8) with û ( 0 ) = u 0 .

Corollary 2.18.Let u 0 ∈ 𝒱 [ 0 , 1 ] , ε > 0, ε − 1 ∉ σ ( A ) , and τ n ↓ 0 with τ n < ε for all n. Then for each t ≥ 0, as n → ∞, u ⌈ t / τ n ⌉ [ τ n ] → û ( t ) .

Proof.Let x n : t ↦ u ⌈ t / τ n ⌉ [ τ n ] and let τ n k be any subsequence of τ n . Then by the theorem there is a subsubsequence τ n k l such that x n k l → ũ pointwise where ũ is a solution to (2.8) with initial condition ũ ( 0 ) = u 0 . By Theorem 2.7(c) such solutions are unique, so ũ = û . Thus there exists x (in particular, x = û ) such that every subsequence of xn has a convergent subsubsequence with limit x. It follows by a standard fact of topological spaces that x n → û pointwise as n → ∞.

Finally, we follow 13 to use Theorem 2.17 to deduce that the Ginzburg-Landau energy monotonically decreases along the ACE trajectories by considering the Lyapunov functional H defined in (2.19). We also deduce well-posedness of the ACE.

Proposition 2.19. (Cf. [[13], Proposition 5.6])Let H τ ( u ) ≔ 1 2 τ H ( u ) . Then for u ∈ 𝒱 [ 0 , 1 ]

H τ ( u ) = GL ε , μ , f ˜ ( u ) − 1 2 ⟨ f ˜ , M f ˜ ⟩ 𝒱 + 1 2 τ ⟨ u , Q τ ( u − 2 A − 1 f ) ⟩ 𝒱 ,
where Q τ ≔ τ − 2 ( I − τ A − e − τ A ) . Hence H τ + 1 2 ⟨ f ˜ , M f ˜ ⟩ 𝒱 → GL ε , μ , f ˜ uniformly on 𝒱 [ 0 , 1 ] as τ → 0 , and furthermore if u τ → u in 𝒱 [ 0 , 1 ] then H τ ( u τ ) + 1 2 ⟨ f ˜ , M f ˜ ⟩ 𝒱 → GL ε , μ , f ˜ ( u ) .

Proof.Expanding and collecting terms in (2.5), we find that for u ∈ 𝒱 [ 0 , 1 ]

GL ε , μ , f ˜ ( u ) = 1 2 ε ⟨ u , 1 − u ⟩ 𝒱 + 1 2 ⟨ u , A u − 2 f ⟩ 𝒱 + 1 2 ⟨ f ˜ , M f ˜ ⟩ 𝒱 .
Then by (2.19) and recalling that λ ≔ τ / ε
H τ ( u ) = 1 2 ε ⟨ u , 1 − u ⟩ 𝒱 + 1 2 τ ⟨ u , ( I − e − τ A ) u − 2 A − 1 ( I − e − τ A ) f ⟩ 𝒱 = 1 2 ε ⟨ u , 1 − u ⟩ 𝒱 + 1 2 τ ⟨ u , ( τ A + τ 2 Q τ ) u − 2 A − 1 ( τ A + τ 2 Q τ ) f ⟩ 𝒱 = 1 2 ε ⟨ u , 1 − u ⟩ 𝒱 + 1 2 ⟨ u , A u − 2 f ⟩ 𝒱 + 1 2 τ ⟨ u , Q τ ( u − 2 A − 1 f ) ⟩ 𝒱 .
To show the uniform convergence, note that | | u | | 𝒱 and | | u − 2 A − 1 f | | 𝒱 are uniformly bounded in u for u ∈ 𝒱 [ 0 , 1 ] . Thus it suffices to prove that | | Q τ | | is uniformly bounded in τ . But Q τ is self-adjoint, and if ξ k is an eigenvalue of A then Q τ has corresponding eigenvalue τ − 2 ( 1 − τ ξ k − e − τ ξ k ) ∈ [ − 1 2 ξ k 2 , 0 ] , so | | Q τ | | ≤ 1 2 | | A | | 2 . Finally, it suffices to show that H τ ( u τ ) − H τ ( u ) → 0 , since
H τ ( u τ ) + 1 2 ⟨ f ˜ , M f ˜ ⟩ 𝒱 − GL ε , μ , f ˜ ( u ) = H τ ( u τ ) − H τ ( u ) + H τ ( u ) + 1 2 ⟨ f ˜ , M f ˜ ⟩ 𝒱 − GL ε , μ , f ˜ ( u ) .
Then by the above expression for H τ
H τ ( u τ ) − H τ ( u ) = 1 2 u τ − u , 1 ε 1 − u τ − u + ( A + τ Q τ ) ( u τ + u ) − 2 ( I + τ Q τ A − 1 ) f 𝒱 → 0
since the right-hand entry in the inner product is bounded uniformly in τ .

Theorem 2.20. (Cf. [[13], Theorem 5.7, Remark 5.8])Suppose and ε − 1 ∉ σ ( A ) . Then the ACE trajectory u defined by Definition 2.6 has GL ε , μ , f ˜ ( u ( t ) ) monotonically decreasing in t. More precisely: for all t > s ≥ 0,

GL ε , μ , f ˜ ( u ( s ) ) − GL ε , μ , f ˜ ( u ( t ) ) ≥ 1 2 ( t − s ) u ( s ) − u ( t ) 𝒱 2 . ()
Furthermore, this entails an explicit C0, 1/2 condition for u
u ( s ) − u ( t ) 𝒱 ≤ | t − s | 2 GL ε , μ , f ˜ ( u ( 0 ) ) . ()

Proof.The proof is identical to that in [13, Theorem 5.7] and [13, Remark 5.8].

Theorem 2.21. (Cf. [[13], Theorem 3.11])Let u 0 , v 0 ∈ 𝒱 [ 0 , 1 ] define ACE trajectories u, v by Definition 2.6, and suppose ε − 1 ∉ σ ( A ) . Then, if ξ 1 ≔ min σ ( A ) , then

| | u ( t ) − v ( t ) | | 𝒱 ≤ e − ξ 1 t e t / ε | | u 0 − v 0 | | 𝒱 . ()

Proof.Fix t ≥ 0 and let m ≔ ⌈ t / τ n ⌉ . By Corollary 2.18, we take τ n ↓ 0 such that u m [ τ n ] → u ( t ) and v m [ τ n ] → v ( t ) as n → ∞. Then by (2.18):

| | u m [ τ n ] − v m [ τ n ] | | 𝒱 ≤ e − m ξ 1 τ n ( 1 − τ n / ε ) − m | | u 0 − v 0 | | 𝒱
and taking n → ∞ gives (2.28).

3 THE SDIE SCHEME AS A CLASSIFICATION ALGORITHM

As was noted in the introduction, trajectories of the ACE and of the MBO scheme on graphs can be deployed as classification algorithms, as was originally done in work by Bertozzi and coauthors in 6, 32. In the above, we have shown that the SDIE scheme (2.14) introduced in 13 generalizes the MBO scheme into a family of schemes, all of the same computational cost as the MBO scheme, and which as τ ↓ 0 become increasingly more accurate approximations of the ACE trajectories. In the remainder of this paper, we will investigate whether the use of these schemes can significantly improve on the use of the MBO scheme to segment the “two cows” images from 6, 32. We will also discuss other potential improvements to the method of 32.

3.1 Groundwork

In this section, we will describe the framework for applying graph dynamics to classification problems, following 6, 32.

The individuals that we seek to classify we will denote as a set V, upon which we have some information x : V → ℝ q . For example, in image segmentation V is the pixels of the image, and x is the grayscale/RGB/etc values at each pixel. Furthermore, we have labeled reference data which we shall denote as Z ⊆ V and binary reference labels f ˜ supported on Z. Supported on Z we have our fidelity parameter μ ∈ 𝒱 [ 0 , ∞ ) ∖ { 0 } , and we recall the notation M ≔ diag ( μ ) and f ≔ M f ˜ (recall that the operator diag sends a vector to the diagonal matrix with that vector as diagonal, and also vice versa).

To build our graph, we first construct feature vectors z : V → ℝ ℓ . The philosophy behind these is that we want vertices which are “similar” (and hence should be similarly labeled) to have feature vectors that are “close together.” What this means in practice will depend on the application, for example, 41 incorporates texture into the features and 6, 15 give other options.

Next, we construct the weights on the graph by deciding on the edge set E (eg, E = V2 ∖ {(i, i) | i ∈ V}) and for each ij ∈ E computing ω i j ≔ Ω ( z i , z j ) (and for ij ∉ E, ω i j ≔ 0 ). There are a number of standard choices for the similarity function Ω , see for example 6, 12, 43, 45. The similarity function we will use in this paper is the Gaussian function:
Ω ( z , w ) ≔ e − | | z − w | | 2 ℓ σ 2 .
Finally, from these weights we compute the graph Laplacian so that we can employ the graph ODEs discussed in the previous sections. In particular, we compute the normalized (a.k.a. random walk) graph Laplacian, that is, we will henceforth take r = 1 and so Δ = I − D − 1 ω . We will also consider the symmetric normalized Laplacian Δ s ≔ I − D − 1 / 2 ω D − 1 / 2 , though this does not fit into the above framework (extending the above theory to the symmetric normalized Laplacian case is a topic for future research). This normalization matters because, as discussed in 6, the segmentation properties of diffusion-based graph dynamics are linked to the segmentation properties of the eigenvectors of the corresponding Laplacian. As shown in [6, Figure 2.1], normalization vastly improves these segmentation properties. As that figure looked at the symmetric normalized Laplacian, we include Figure 2 to show the difference between the symmetric normalized and the random walk Laplacian.
Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Second, third, and fourth eigenvectors of the random walk Laplacian (left) and symmetric normalized Laplacian (right) for the graph built on one of the “two cows” images from Section 4, computed using Algorithm 1

3.2 The basic classification algorithm

For some time step 0 < τ ≤ ε note that
𝒮 τ u = e − τ A u + b ,
where b ≔ A − 1 ( I − e − τ A ) f is independent of u.
  1. Input: Vector x : V → ℝ q , reference data Z, and labels f supported on Z.
  2. Convert x into feature vectors z : V → ℝ ℓ .
  3. Build a weight matrix ω = ( ω i j ) on V2 via ω i j ≔ Ω ( z i , z j ) .
  4. Compute A and therefore b.
  5. From some initial condition u0, compute the SDIE sequence un until it meets a stopping condition at some n = N.
  6. Output: uN thresholded to lie in 𝒱 { 0 , 1 } , that is, we output Θ ( u N ) where Θ is as in (1.1).

Unfortunately, as written this algorithm cannot be feasibly run. The chief obstacle is that in many applications A is too large to store in memory, yet we need to quickly compute e − τ A u , potentially a large number of times. We also need to compute b accurately . Moreover, in general A does not have low numerical rank, so it cannot be well approximated by a low-rank matrix. In the rest of this section we describe our modifications to this basic algorithm that make it computationally efficient.

3.3 Matrix compression and approximate SVDs

We will need to compress Δ into something we can store in memory. Following 6, 32, we employ the Nyström extension 21, 36. We choose K ≪ |V| to be the rank to which we will compress Δ , and choose nonempty Nyström interpolation sets X1 ⊆ V ∖ Z and X2 ⊆ Z at random such that |X|=K where X ≔ X1 ∪ X2. We write |X1| ≕ K1 and |X2| ≕ K2. Then using the function i j ↦ ω i j we compute ω V X ≔ ω ( V , X ) (ie, ω V X ≔ ( ω i j ) i ∈ V , j ∈ X ) and ω X X ≔ ω ( X , X ) and then the Nyström extension is the approximation:
ω ≈ ω V X ω X X − 1 ω V X T .
Note that this avoids having to compute the full matrix ω which in many applications is too large to store in memory. We next compute an approximation for the degree vector d and degree matrix D ≔ diag ( d ) of our graph
d ≈ d ^ ≔ ω V X ω X X − 1 ω V X T 1 , D ≈ D ^ ≔ diag d ^ .
We thus approximately normalize ω
ω ˜ ≔ D − 1 / 2 ω D − 1 / 2 ≈ D ^ − 1 / 2 ω V X ω X X − 1 ω V X T D ^ − 1 / 2 = ω ˜ V X ω X X − 1 ω ˜ V X T ,
where ω ˜ V X ≔ D ^ − 1 / 2 ω V X .

Following 6, 32, we next compute an approximate eigendecomposition of ω ˜ . We here diverge from the method of 6, 32. The method used in those papers requires taking the matrix square root of ω X X , but unless ω X X is the zero matrix it will not be positive semi-definite.While this clearly does not prevent the method of 6, 32 from working in practice, it is a potential source of error and we found it conceptually troubling. We here present an improved method, adapted from the method from 3 for computing a SVD from an adaptive cross approximation (ACA) (see 3 for a definition of ACA).

First, we compute the thin QR decomposition (see [25, Theorem 5.2.2])
ω ˜ V X = Q R ,
where Q ∈ ℝ | V | × K is orthonormal and R ∈ ℝ K × K is upper triangular. Next, we compute the eigendecomposition
R ω X X − 1 R T = Φ ∑ Φ T ,
where Φ ∈ ℝ K × K is orthogonal and ∑ ∈ ℝ K × K is diagonal. It follows that ω ˜ has approximate eigendecomposition:
ω ˜ ≈ Q Φ ∑ Φ T Q T = U s ∑ U s T ,
where U s ≔ Q Φ is orthonormal. This gives an approximate eigendecomposition of the symmetric normalized Laplacian
Δ s = I − ω ˜ ≈ U s ( I K − ∑ ) U s T = U s Λ U s T ,
where IK is the K × K identity matrix and Λ ≔ I K − ∑ , and so we get an approximate SVD of the random walk Laplacian
Δ = D − 1 / 2 Δ s D 1 / 2 ≈ U 1 Λ U 2 T ,
where U 1 ≔ D ^ − 1 / 2 U s and U 2 ≔ D ^ 1 / 2 U s . As in 3, it is easy to see that this approach is 𝒪 ( K | V | ) in space and 𝒪 ( K 2 | V | + K 3 ) in time. We summarize this all as Algorithm 1.

Algorithm 1. QR decomposition-based Nyström method for computing an approximate SVD of Δ , inspired by [3].

gamm202100004-gra-1000-b

3.3.1 Numerical assessment of the matrix compression method

We consider the accuracy of our Nyström-QR approach for the compression of the symmetric normalized Laplacian Δ s built on the simple image in Figure 3, containing |V| = 6400 pixels, which is small enough for us to compute the true value of Δ s to high accuracy. For K ∈ {50, 100, ⋯ , 500}, we compare the rank K approximation U s Λ U s T with the true Δ s in terms of the relative Frobenius distance, that is, | | U s Λ U s T − Δ s | | F / | | Δ s | | F . Moreover, we compare these errors to the errors incurred by other low-rank approximations of Δ s , namely the Nyström method used in 6, 32, the Halko-Martinsson-Tropp (HMT) method 26, and the optimal rank K approximation of Δ s with respect to || · ||F, which (by the Eckart-Young theorem 19; see also [25, Theorem 2.4.8]) is obtained by setting all but the K leading singular values of Δ s to 0. In addition to the methods' accuracy, we measure their complexity via the runtimes of Matlab R2019a implementations of them on the set-up as in Section 4.2.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
The 80 × 80 image on which the Laplacian Δ s is constructed to test the low-rank approximations

We report the relative Frobenius distance in Figure 4. As the Nyström (and HMT) methods are randomized, we repeat the experiments 1000 times and plot the mean error in the far-left figure and the standard deviations in the center-right figure. To expose the difference between the methods for K ≥ 100, we plot the percentage increase of the other errors above the SVD error (ie, [error/errorSVD − 1] × 100%) and show this percentage in the center-left figure. In the far-right figure, we compare the complexity of the algorithms in terms of their average runtime. The SVD timing is constant in K as we always computed a full SVD and kept the largest K singular values.

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Error of the low-rank approximations of Δ s in terms of their relative Frobenius distance to the true Δ s (far-left), percentage increase above the optimal error reached with the SVD (center-left), and standard deviations (StD) of the errors (center-right). Timings of the methods in seconds (far-right). In the far-left figure the red and cyan lines are both plotted but cannot be distinguished from each other by the eye

We observe that the Nyström-QR method outperforms the Nyström method from 6, 32: it is faster, more accurate, and is stable for small K. In terms of accuracy, the Nyström-QR error is only about 0.012% larger than the optimal low-rank error. Notably, this additional error is (almost) constant, indicating that the Nyström-QR method and the SVD converge at a similar rate. The Nyström-QR randomness has hardly any effect on the error; the standard deviation of the relative error ranges from 8.87 × 10−7 (K = 50) to 5.00 × 10−8 (K = 500). By contrast, for the Nyström method from 6, 32 we see much more random variation. The bump in the HMT error at K = 450 is an outlier that is present (though not always for the same K) in many repeats of this experiment.

3.4 Implementing the SDIE scheme: a Strang formula method

To compute the iterates of our SDIE scheme, we will need to compute an approximation for 𝒮 τ u n . In 32, at each iteration 𝒮 τ u n was approximated via a semi-implicit Euler method, which therefore incurred a linear (in the time step of the Euler method, that is, δ t in the below notation) error in both the e − τ A u n and b terms (plus a spectrum truncation error). In Appendix A1 we show that the method from 32 works by approximating a Lie product formula approximation (see [27, Theorem 2.11]) of e − τ A , therefore we propose as an improvement a scheme that directly employs the superior Strang formula to approximate e − τ A u n —with quadratic error (plus a spectrum truncation error). We also consider potential improvements of the accuracy of computing b: by expressing b as an integral and using quadrature methods; by expressing b as a solution to the ODE from (2.1) with initial condition 0, and using the Euler method from 32 with a very small time step (or a higher-order ODE solver); or by computing the closed form solution for b directly using the Woodbury identity. We therefore improve on the accuracy of computing 𝒮 τ u at low cost.

The Strang formula for matrix exponentials 39 is given, for k > 0 a parameter and 𝒪 relative to the limit k → ∞, by
e X + Y = ( e 1 2 Y / k e X / k e 1 2 Y / k ) k + 𝒪 ( k − 2 ) .
Given Δ ≈ U 1 Λ U 2 T as in Algorithm 1 (the case for Δ s is likewise) for any u ∈ 𝒱 we compute (writing δ t ≔ τ / k )
e − τ A u = e − 1 2 τ / k M e − τ / k Δ e − 1 2 τ / k M k u + 𝒪 ( k − 2 ) = e − 1 2 δ t M I + U 1 ( e − δ t Λ − I K ) U 2 T e − 1 2 δ t M k u + E + 𝒪 ( δ t 2 ) = v k + E + 𝒪 ( δ t 2 ) , ()
where E is a spectrum truncation errorand vk is defined by v0 ≔ u, and vr for r ∈ {1, …, k} is defined iteratively by
v r + 1 = e − δ t M v r + e − 1 2 δ t M U 1 ( e − δ t Λ − I K ) U 2 T e − 1 2 δ t M v r = a 1 ( δ t ) ⊙ v r + a 3 ( δ t ) ⊙ U 1 a 2 ( δ t ) ⊙ U 2 T a 3 ( δ t ) ⊙ v r = : S ( δ t ) v r , ()
where ⊙ is the Hadamard (ie, elementwise) product, a 1 ( δ t ) ≔ exp ( − δ t μ ) , a 2 ( δ t ) ≔ exp ( − δ t diag ( Λ ) ) − 1 K , and a 3 ( δ t ) ≔ exp ( − 1 2 δ t μ ) is the elementwise square root of a 1 ( δ t ) (where exp is applied elementwise, and 1K is the vector of K ones). In Figure 6, we verify on a simple image that this method has quadratic error (plus a spectrum truncation error) and outperforms the 32 Euler method. Furthermore (3.2) is as fast as (A2) (ie, a step of the 32 Euler method). This is because by defining ã 1 ≔ 1 − δ t μ and ã 2 ≔ ( 1 K + δ t diag ( Λ ) ) − 1 (applying the reciprocation elementwise), we can rewrite (A2) as
v r + 1 = U 1 ã 2 ⊙ U 2 T ã 1 ⊙ v r + μ δ t f
and so both (3.2) and (A2) involve two 𝒪 ( N K ) matrix multiplications and the vectors in (3.2) and (A2) and are at most N-dimensional, hence the Hadamard products in (3.2) and (A2) are all at most 𝒪 ( N ) and so are not rate-limiting.
At the cost of extra 𝒪 ( N K ) matrix multiplications, one can employ the method of Yoshida 44 to increase the order of the (non-spectrum-truncation) error by 2. If we set α 0 ≔ − 2 3 / ( 2 − 2 3 ) and α 1 ≔ 1 / ( 2 − 2 3 ) then we can define the map
Y ( δ t ) ≔ S ( α 1 δ t ) ∘ S ( α 0 δ t ) ∘ S ( α 1 δ t )
which gives Y k ( δ t ) u = e − τ A u + 𝒪 ( δ t 4 ) plus a spectrum truncation error.However, as can be seen in Figure 6C,D, the spectrum truncation error can make negligible any gain from using the Yoshida method over the Strang formula.
It remains to compute an approximation for b ≔ A − 1 ( I − e − τ A ) f . It is easy to show that b can be rewritten as the integral
b = ∫ 0 τ e − t A f d t
which we can approximate via a quadrature, for example, applying respectively the trapezium, midpoint, or Simpson's rules we get
b = 1 2 τ ( I + e − τ A ) f + 𝒪 ( τ 3 ) = τ e − 1 2 τ A f + 𝒪 ( τ 3 ) = 1 6 τ ( I + 4 e − 1 2 τ A + e − τ A ) f + 𝒪 ( τ 5 ) ()
any of which we can approximate efficiently via the above methods. Furthermore, as we only need to compute b once, we can take a large value, kb, for k in those methods. As is standard for quadrature methods, the accuracy can often be improved by subdividing the interval. For example, using Simpson's rule and subdividing into intervals of length h ≔ τ / ( 2 m ) we get
b = 1 3 h I + 2 ∑ j = 1 m − 1 e − 2 j h A + 4 ∑ j = 1 m e − ( 2 j − 1 ) h A + e − τ A f + 𝒪 ( τ h 4 )
which if kb = 2m, that is, the Simpson subdivision equals the Strang/Yoshida step number, can be approximated efficiently by
b = 1 3 h f + 2 ∑ j = 1 m − 1 v 2 j + 4 ∑ j = 1 m v 2 j − 1 + v 2 m + E 1 + E 2 + 𝒪 ( τ h 4 ) ,
where vr ≔ Sr(h)f with E 1 = 𝒪 ( τ 2 h ) or vr ≔ Yr(h)f with E 1 = 𝒪 ( τ 2 h 3 ) , and E2 is the spectrum truncation error. Finally, we can also let Matlab compute its preferred quadrature using the built-in integrate function, using either the Strang formula or Yoshida method to compute the integrand. However, we found this to be very slow.
Another method to compute b is to solve an ODE. We note that, by (2.2), b is the fidelity forced diffusion of 0 at time τ , that is,
d v d t ( t ) = − Δ v ( t ) − M v ( t ) + f , v ( 0 ) = 0 ,
has v ( τ ) = b . Hence we can approximate b by solving
d v ^ d t ( t ) = − U 1 Λ ( U 2 T v ^ ( t ) ) − μ ⊙ v ^ ( t ) + f , v ^ ( 0 ) = 0 ,
via the semi-implicit Euler method from 32. Since we only need to compute b once we can choose a small time step, that is, a time step of τ / k b for kb large, for this Euler method. One could also choose a higher-order ODE solver for this same reason, however as 32 notes this ODE is stiff, which we found causes standard solvers such as ode45 (ie, Dormand-Prince-(4, 5) 18) to be inaccurate, and we ran into the issue of the Matlab stiff solvers requiring matrices too large to fit in memory.
Finally, we can try to compute the formula for b directly. By the Strang formula or Yoshida method, we can efficiently compute g ≔ f − e − τ A f . It remains to compute b = A−1g. Given our approximation Δ ≈ U 1 Λ U 2 T , by the Woodbury identity 42
A − 1 = ( Δ + M ) − 1 ≈ ( I − U 1 ∑ U 2 T + M ) − 1 = Y − 1 − Y − 1 U 1 − ∑ + + U 2 T Y − 1 U 1 − 1 U 2 T Y − 1 .
where Y ≔ I + M, superscript + denotes the pseudoinverse, and recall that ∑ = I K − Λ . Then
b = y ⊙ g − U 1 x ,
where y ≔ ( 1 + μ ) − 1 , reciprocation applied elementwise, and x is given by solving
− ∑ + + U 2 T ( y ⊙ U 1 ) x = U 2 T ( y ⊙ g ) ,
where we define y ⊙ U1 as columnwise Hadamard multiplication, that is, (y ⊙ U1)ij ≔ yi(U1)ij. We compare the accuracy of these approximations of b in Table 1, and observe that no method is hands-down superior. Table 1 also indicates that the likely reason for methods like Simpson's rule not performing as well as expected is that the spectrum truncation error is dominating.

Given these ingredients, it is then straightforward to compute the SDIE scheme sequence via Algorithm 2.

Algorithm 2. The SDIE scheme via a Strang formula method.

gamm202100004-gra-1001-b

Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
The 40 × 40 or 80 × 80 image that we build our graphs on, using feature vectors as described in Section 4.2

3.4.1 Numerical assessment of methods

In this section, we will build our graphs on the image in Figure 5, which is small enough for us to compute the true values of e − τ A u (with A here given by Δ s + M ) and b to high accuracy. First, in Figure 6 we investigate the accuracy of the Strang formula and Yoshida method vs the 32 Euler method. We take |V|=1600, τ = 0 . 5 , u a random vector given by Matlab's rand(1600,1), and μ as the characteristic function of the left two quadrants of the image. We consider two cases: one where K = |V| (ie, full-rank) and one where K = | V | . We observe that the Strang formula and Yoshida method are more accurate than the Euler method in both cases, and that the Yoshida method is more accurate than the Strang formula, but only barely in the rank-reduced case. Furthermore, the log-log gradients of the Strang formula error and the Yoshida method error (excluding the outliers for small k values and the outliers caused by errors from reaching machine precision) in Figure 6(b) are respectively 2.000 and 3.997 (computed using polyfit), confirming that these methods achieve their theoretical orders of error in the full-rank case.

Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
Comparison of the ℓ2 error from approximating e − τ A u via the semi-implicit Euler method (blue), Strang formula (red), and Yoshida method (green) approximations for e − τ A u on the graph built on the image in Figure 5. A,B, K = |V|. C,D, K = | V | . The gradient of the line in (D), excluding outliers for small k, is 2.000. In (C), the green and red lines are both plotted but cannot be distinguished by the eye

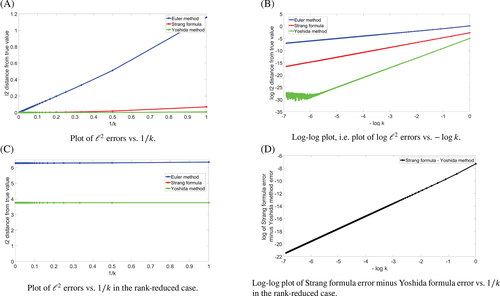
Next, in Table 1 we compare the accuracy of the different methods for computing b. We take Z as the left two quadrants of the image, μ = χ Z , f ˜ as equal to the image on Z, and kb = 1000 in the Strang formula/Yoshida method approximations for e−tAf and in the 32 Euler scheme. We observe that the rank reduction plays a significant role in the errors incurred, and that no method is hands-down superior. In the “two cows” application (Example 4.1), we have observed that (interestingly) the 32 Euler method yields the best segmentation. A topic for future research can be whether this is generally true for large matrices.

4 APPLICATIONS IN IMAGE PROCESSING

4.1 Examples

We consider three examples, all using images of cows from the Microsoft Research Cambridge Object Recognition Image Database (available at https://www.microsoft.com/en-us/research/project/image-understanding/). Some of these images have been used before by 6, 32 to illustrate and test graph-based segmentation algorithms.

Example 4.1. (Two cows)We first introduce the two cows example familiar from 6, 32. We take the image of two cows in the top left of Figure 7 as the reference data Z and the segmentation in the bottom left as the reference labels f ˜ , which separate the cows from the background. We apply the SDIE scheme to segment the image of two cows shown in the top right of Figure 7, aiming to separate the cows from the background, and compare to the ground truth in the bottom right. Both images are RGB images of size 480 × 640 pixels, that is, the reference data and the image are tensors of size 480 × 640 × 3.

Details are in the caption following the image
FIGURE 7
Open in figure viewerPowerPoint
Two cows: the reference data image, the image to be segmented, the reference f ˜ , and the ground truth segmentation associated to Example 4.1. Note. During proofing, the authors noticed that a mistake during the hand-segmentation had caused 35 pixels in the bottom-left of the data segmentation to be mislabelled as “cow”. The figures in this paper were produced with this slightly misclassified reference data. Test runs with this mistake fixed suggest that its impact was negligible. Both segmentations were drawn by hand by the authors
We will use Example 4.1 to illustrate the application of the SDIE scheme. Moreover, we will run several numerical experiments on this example. Namely, we will:
  • study the influence of the parameters ε and τ , comparing non-MBO SDIE ( τ < ε ) and MBO SDIE ( τ = ε );
  • compare different normalizations of the graph Laplacian, that is, the symmetric vs random walk normalization;
  • investigate the influence of the Nyström-QR approximation of the graph Laplacian in terms of the rank K; and
  • quantify the inherent uncertainty in the computational strategy induced by the randomized Nyström approximation.

Example 4.2. (Grayscale)This example is the grayscale version of Example 4.1. Hence, we map the images in Figure 7 to grayscale using rgb2gray. We show the grayscale images in Figure 8. We use the same segmentation of the reference data image as in Example 4.1. The grayscale images are matrices of size 480 × 640.

Details are in the caption following the image
FIGURE 8
Open in figure viewerPowerPoint
Two cows grayscale: the reference data image and the image to be segmented associated to Example 4.2. Note that the reference f ˜ and the ground truth segmentation are identical to those in Figure 7

The grayscale image is much harder to segment than the RGB image, as there is no clear color separation. With Example 4.2, we aim to illustrate the performance of the SDIE scheme in a harder segmentation task.

Example 4.3. (Many cows)In this example, we have concatenated four images of cows that we aim to segment as a whole. We show the concatenated image in Figure 9. Again, we shall separate the cows from the background. As reference data, we use the reference data image and labels as in Example 4.1. Hence, the reference data is a tensor of size 480 × 640 × 3. The image consists of approximately 1.23 megapixels. It is represented by a tensor of size 480 × 2560 × 3.

Details are in the caption following the image
FIGURE 9
Open in figure viewerPowerPoint
Many cows: the image to be segmented associated to Example 4.3. Note that the reference data image and labels are identical to those in Figure 7 (left)

With Example 4.3, we will illustrate the application of the SDIE scheme to large scale images, as well as the case where the image and reference data are of different sizes.

Note.In each of these examples we took as reference data a separate reference data image. However, our algorithm does not require this, and one could take a subset of the pixels of a single image to be the reference data, and thereby investigate the impact of the relative size of the reference data on the segmentation, which is beyond the scope of this paper but is explored for the 32 MBO segmentation algorithm and related methods in [37, Figure 4].

4.2 Set-up

AlgorithmsWe here use the Nyström-QR method to compute the rank K approximation to the Laplacian, and we use the 32 semi-implicit Euler method (with time step τ / k b ) to compute b (as we found that in practice this worked best for the above examples).

Feature vectors Let 𝒩 ( i ) denote the 3 × 3 neighborhood of pixel i ∈ V in the image (with replication padding at borders performed via padarray) and let 𝒦 be a 3 × 3 Gaussian kernel with standard deviation 1 (computed via fspecial(‘gaussian’,3,1)). Thus x | 𝒩 ( i ) can be viewed as a triple of 3 × 3 matrices x J | 𝒩 ( i ) for J ∈ {R, G, B} (ie, one in each of the R, G, and B channels). Then in each channel we define
z i R ≔ 9 𝒦 ⊙ x R | 𝒩 ( i ) , z i G ≔ 9 𝒦 ⊙ x G | 𝒩 ( i ) , z i B ≔ 9 𝒦 ⊙ x B | 𝒩 ( i ) ,
and thus define z i ≔ ( z i R , z i G , z i B ) ∈ ℝ 3 × 3 × 3 , which we reshaped (using reshape) so that z ∈ ℝ | V | × 27 .

Interpolation sets For the interpolation sets X1, X2 in Nyström we took K1 = K2 = K/2. That is, we took K/2 vertices from the reference data image and K/2 vertices from the image to be segmented, chosen at random using randperm. We experimented with choosing interpolation sets using ACA (see 3), but this showed no improvement over choosing random sets, and ran much slower.

Initial condition We took the initial condition, that is, u0, to equal the reference f ˜ on the reference data vertices and to equal 0.49 on the vertices of the image to be segmented (where f ˜ labels “cow” with 1 and “not cow” with 0). We used 0.49 rather than the more natural 0.5 because the latter led to much more of the background (eg, the grass) getting labeled as “cow.” This choice can be viewed as incorporating the slight extra a priori information that the image to be segmented has more non-cow than cow.

Note.It is not an improvement to initialize with the exact proportion of cow in the image (about 0.128), as in that case the thresholding is liable to send every ui for i ∈ V ∖ Z to zero. If one has access to that a priori information, one should use such an initial condition alongside a mass-conserving scheme. We investigate a semi-discrete scheme for mass-conserving Allen-Cahn (without fidelity forcing) in 14, which can be extended to the fidelity-forced case in a manner similar to that of this paper. What the 0.49 initial condition does is more modest. After the initial diffusion, some pixels will have a value very close to 0.5; by lowering the value of the initial condition, we lower the diffused values, introducing a bias towards classifying these borderline pixels as “not cow.” As there is more non-cow than cow in the image, this bias improves the accuracy. It is unknown to the authors why this was necessary for us but was not necessary for 32 nor for 6.

Fidelity parameterWe followed 32 and took μ = μ ^ χ Z , for μ ^ > 0 a parameter.

Computational set-up All programming was done in Matlab R2019a with relevant toolboxes the Computer Vision Toolbox Version 9.0, Image Processing Toolbox Version 10.4, and Signal Processing Toolbox Version 8.2. All reported runtimes are of implementations executed serially on a machine with an Intel® Core™ i7-9800X @ 3.80 GHz [16 cores] CPU and 32 GB RAM of memory.

4.3 Two cows

We begin with some examples of segmentations obtained from the SDIE scheme. Based on these, we illustrate the progression of the algorithm and discuss the segmentation output qualitatively. We will give a quantitative analysis in Section 4.3.1. Note that we give here merely typical realizations of the random output of the algorithm—the output is random due to the random choice of interpolation sets in the Nyström approximation. We investigate the stochasticity of the algorithm in Section 4.3.2.

We consider three different cases: the MBO case τ = ε and two non-MBO cases, where τ ≪ ε , and τ < ε . We show the resulting reconstructions from these methods in Figure 10. Moreover, we show the progression of the algorithms in Figure 12. The parameters not given in the captions of Figure 10 are μ ^ = 30 , σ = 35 , kb = 1, k = 1, δ = 1 0 − 10 , and K = 70.

Details are in the caption following the image
FIGURE 10
Open in figure viewerPowerPoint
MBO SDIE and non-MBO SDIE segmentations for the two cows segmentation task. In the top left figure, we show the reference data image, the image to be segmented, and the image masked with the segmentation we consider the ground truth, see also Figure 7. The other figures (B-D) show the labels on the reference data, the segmentation returned by the respective algorithm, and the original images masked with the segmentation

Note.The regime τ > ε is not of much interest since, by [13, Remark 4.8] mutatis mutandis, in this regime the SDIE scheme has nonunique solution for the update, of which one is just the MBO solution.

Comparing the results in Figure 10, we see roughly equivalent segmentations and segmentation errors. Indeed, the cows are generally nicely segmented in each of the cases. However, the segmentation also labels as “cow” a part of the wall in the background and small clumps of grass, while a small part of the left cow's snout is cut out. This may be because the reference data image does not contain these features and so the scheme is not able to handle them correctly.

In Figure 11 we compare the result of Figure 10(d) (our best segmentation) with the results of the analogous experiments in 6, 32. We observe significant qualitative improvement. In particular, our method achieves a much more complete identification of the left cow's snout, complete identification of the left cow's eyes and ear tag, and a slightly more complete identification of the right cow's hind. However, our method does misclassify more of the grass than the methods in 6, 32 do. Note that as well as the change in method, the reference that we hand-drew (see Figure 7, bottom-left) is different from both the reference used in [6, Figure 4.6] and the reference [32, Figure 2(e)].

Details are in the caption following the image
FIGURE 11
Open in figure viewerPowerPoint
Comparison of our segmentation (using the set-up in Figure 10D) with the analogous segmentations from the previous literature 6, 32, both reproduced with permission from SIAM and the authors. Note that unfortunately in reproduction the color balances and aspect ratios have become slightly inconsistent, but we can still make qualitative comparisons

We measure the computational cost of the SDIE scheme through the measured runtime of the respective algorithm. We note from Figure 10 that the MBO scheme ( τ = ε ) outperforms the non-MBO schemes ( τ < ε ); the SDIE relaxation of the MBO scheme merely slows down the convergence of the algorithm, without improving the segmentation. This can especially be seen in Figure 12, where the SDIE scheme needs many more steps to satisfy the termination criterion. At least for this example, the non-MBO SDIE scheme is less efficient than the MBO scheme. Thus, in the following sections we focus on the MBO case.

Details are in the caption following the image
FIGURE 12
Open in figure viewerPowerPoint
Progression of MBO and non-MBO SDIE for the two cows example. In each subfigure: the first row shows the reference data, image, and ground truth, as in Figure 10. The middle rows, showing the reshaped label vector un and the image masked by the thresholded label, each represent one iteration of the considered algorithm, to be read from top to bottom. The last row gives the state returned by the scheme, that is, the state satisfying the termination criterion, which correspond to the subfigures in Figure 10. For layout reasons, we have squashed the figure in (A)

4.3.1 Errors and timings

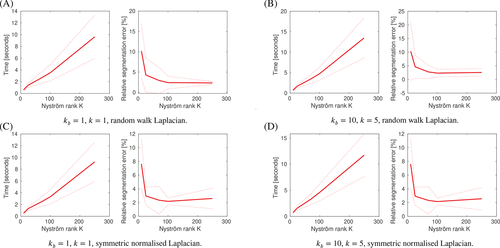
We now quantify the influence, on the accuracy and computational cost of the segmentation, of the Nyström rank K, the number of discretization steps kb and k in the Euler method and the Strang formula respectively, and the choice of normalization of the graph Laplacian. To this end, we segment the two cows image using the following parameters: ε = τ = 0 . 003 , μ ^ = 30 , σ = 35 , and δ = 1 0 − 10 . We take K ∈ {10, 25, 70, 100, 250}, (kb, k) ∈ {(1, 1), (10, 5)}, and use the random walk Laplacian Δ and the symmetric normalized Laplacian Δ s .

We plot total runtimes (ie, the time elapsed from the loading of the image to be segmented, the reference data image, and the reference, to the output of the segmentation) and relative segmentation errors in Figure 13. As our method has randomness from the Nyström extension, we repeat every experiment 100 times and show means and standard deviations. We make several observations. Starting with the runtimes, we indeed see that these are roughly linear in K, verifying numerically the expected complexity. The runtime also increases when increasing kb and k. That is, increasing the accuracy of the Euler method and Strang formula does not lead to faster convergence, and also does not increase the accuracy of the overall segmentation. Finally, we see that the symmetric normalized Laplacian incurs consistently low relative segmentation error for small values of K. This property is of the utmost importance to scale up our algorithm for very large images. Interestingly, the segmentations using the symmetric normalized Laplacian seem to deteriorate for a large K. The random walk Laplacian has diametric properties in this regard: the segmentations are only reliably accurate when K is reasonably large.

Details are in the caption following the image
FIGURE 13
Open in figure viewerPowerPoint
Error and timing of 100 independent segmentations of the two cows image (Example 4.1) with the MBO SDIE scheme. The solid lines represent the means averaged over 100 runs, the dotted lines show means ±standard deviations

4.3.2 Uncertainty in the segmentation

Due to the randomized Nyström approximation, our approximation of the SDIE scheme is inherently stochastic. Therefore, the segmentations that the algorithm returns are realizations of random variables. We now briefly study these random variables, especially with regard to K. We show pointwise mean and standard deviations of the binary labels in each of the left two columns of the four subfigures of Figure 14. In the remaining figures, we weight the original two cows image with these means (varying continuously between label 1 for “cow” and label 0 for “not cow”) and standard deviations. For these experiments we use the same parameter set-up as Section 4.3.1.

Details are in the caption following the image
FIGURE 14
Open in figure viewerPowerPoint
Mean, standard deviation, and images weighted by mean and standard deviation of 100 independent segmentations of Example 4.1 with the MBO SDIE scheme, with set-up as in Section 4.3.1

We make several observations. First, as K increases we see less variation. This is what we expect, as when K = |V| the method is deterministic so has no variation. Second, the type of normalization of the Laplacian has an effect: the symmetric normalized Laplacian leads to less variation than the random walk Laplacian. Third, the parameters kb and k appear to have no major effect within the range tested. Finally, looking at the figures with rather large K, we observe that the standard deviation of the labels is high in the areas of the figure in which there is indeed uncertainty in the segmentation, namely the boundaries of the cows and the parts of the wall with similar color to the dark cow. Determining the exact position of the boundary of a cow on a pixel-by-pixel level is indeed also difficult for a human observer. Moreover, the SDIE scheme usually confuses the wall in the background for a cow. Hence, a large standard deviation here reflects that the estimate is uncertain.

This is of course not a rigorous Bayesian uncertainty quantification, as for instance is given in 7, 37 for graph-based learning. However the use of stochastic algorithms for inference tasks, and the use of their output as a method of uncertainty quantification, has for instance been motivated by 31.

4.4 Grayscale

We now move on to Example 4.2, the grayscale problem. We will especially use this example to study the influence of the parameters μ ^ and σ . The parameter μ ^ > 0 determines the strength of the fidelity term in the ACE. From a statistical point of view, we can understand a choice of μ ^ as an assumption on the statistical precision (ie, the inverse of the variance of the noise) of the reference  f ˜ (see [7, Section 3.3] for details). Thus, a small μ ^ should lead to a stronger regularization coming from the Ginzburg-Landau functional, and a large μ ^ leads to more adherence to the reference. The parameter σ > 0 is the “standard deviation” in the Gaussian kernel Ω used to build the weight matrix ω . For our methods we must not choose too small a σ , as otherwise the weight matrix becomes sparse (up to some precision), and so the Nyström submatrix ω X X has a high probability of being ill-conditioned. In such a case this sparsity can be exploited using Rayleigh-Chebyshev 2 methods as in 32, or Matlab sparse matrix algorithms as in 6, but this lies beyond the scope of this paper. If σ is too large then the graph structure no longer reflects the features of the image.

Details are in the caption following the image
FIGURE 15
Open in figure viewerPowerPoint
MBO SDIE segmentations for the grayscale segmentation task. In the centered top figure, we show the reference data image, the image to be segmented, and the image masked with the ground truth segmentation, cf. Figure 7. The other figures show the reference f ˜ , the segmentation returned by the algorithm, and the original images masked with the segmentation

In the following, we set ε = τ = 0 . 00024 , kb = 10, k = 5, and δ = 1 0 − 10 . To get reliable results we choose a rather large K, K = 200, and therefore (by the discussion in Section 4.3.2) we use the random walk Laplacian. We will qualitatively study single realizations of the inherently stochastic SDIE algorithm. We vary μ ^ ∈ { 50 , 100 , 150 , 200 } and σ ∈ { 2 , 35 , 1 0 3 , 1 0 4 } . We show the best results from these tests in Figure 15. Moreover, we give a comprehensive overview of all tests and the progression of the SDIE scheme in Figure 16.

Details are in the caption following the image
FIGURE 16
Open in figure viewerPowerPoint
Progression of the MBO SDIE scheme for the grayscale segmentation task. In each subfigure: The first row shows the reference data, the image to be segmented, and the ground truth segmentation. The middle rows, showing the reshaped label vector un and the image masked by the label, each represent one iteration of the considered algorithm, to be read from top to bottom. The last row gives the state returned by the scheme, that is, the state satisfying the termination criterion

We observe that this segmentation problem is indeed considerably harder than the two cows problem, as we anticipated after stating Example 4.2. The difference in shade between the left cow and the wall is less visible than in Example 4.1, and the left cow's snout is less identifiable as part of the cow. Thus, the segmentation errors we incur are about three times larger than before. There is hardly any visible influence from changing σ in {35, 103}. However, σ = 2 and σ = 1 0 4 lead to significantly worse results. For σ = 2 , the sparsity (up to some precision) of the matrix deteriorates the results and the method becomes unstable; for σ = 1 0 4 , the weight matrix does not sufficient distinguish pixels of different shade, which is why the method labels everything as “not cow.”

Given σ in {35, 103}, the strength of the fidelity term μ ^ has a significant impact on the result, as well. Indeed, for μ ^ = 50 the algorithm does not find any segmentation. For μ ^ ≥ 100 , we get more practical segmentations. Interestingly, for μ ^ = 150 and μ ^ = 200 we get almost all of the left cow, but misclassify most of the wall in the background; for μ ^ = 100 , we miss a large part of the left cow, but classify more accurately the wall. The interpretation of μ ^ as the statistical precision of the reference explains this effect well. For μ ^ = 100 , we assume that the reference is less precise, leading us (due to the smoothing effect of the Ginzburg-Landau regularization) to classify accurately most of the wall. With μ ^ ≥ 150 , we assume that the reference is more precise, leading us to misclassify the wall (due to its similarity to the cows in the reference data image) but classify accurately more of the cows. At μ ^ = 200 , this effect even leads to a larger total segmentation error. The runtime varied throughout the experiments: the standard seems to be between 6 and 7 seconds. By doing an additional step in the iteration, the times for σ = 2 as well as ( μ ^ , σ ) = ( 50 , 35 ) are significantly increased. We also see a larger runtime in the case of ( μ ^ , σ ) = ( 150 , 35 ) .

4.5 Many cows

We finally study the many cows example, that is, Example 4.3. The main differences to the earlier examples are the larger size of the image that is to be segmented and the variety within it. We first comment on the size. The image is given by a 480 × 2560 × 3 tensor, which is a manageable size. The graph Laplacian, however, is a dense matrix with 1.536 × 106 rows and columns. A matrix of this size requires 17.6 TB of memory to be constructed in MatlabR2019a. This image is much more difficult to segment than the previous examples, in which the cows in the image to be segmented are very similar to the cows in the reference data. Here, we have concatenated images of cows that look very different, for example, cows with a white blaze on their nose.

As the two cows image is part of the many cows image, we first test the algorithmic set-up that was successful at segmenting the former. We show the result (and remind the reader of the set-up) in Figure 17(a). The segmentation obtained in this experiment is rather mediocre—even the two cows part is only coarsely reconstructed. We present two more attempts at segmenting the many cows image in Figure 17: we choose ε = τ = 0 . 00025 , a slightly larger Nyström rank K = 100, and vary ( k b , k , μ ^ ) ∈ { ( 1 , 1 , 500 ) , ( 10 , 10 , 400 ) } . In both cases, we obtain a considerably better segmentation of the image. In the case where μ ^ = 500 , we see a good, but slightly noisy segmentation of the brown and black parts of the cows. In the case where μ ^ = 400 , we reduce the noise in the segmentation, but then also misclassify some parts of the cows. The blaze (and surrounding fur) is not recognized as “cow” in any of the segmentations, likely because the blaze is not represented in the reference data image. The influence of the set-up on the runtimes is now much more pronounced. For the given segmentations, however, all the runtimes are at most a factor of eight larger than the smallest runtimes in the previous examples, despite the larger image size.

Details are in the caption following the image
FIGURE 17
Open in figure viewerPowerPoint
Segmentations of the MBO scheme for the many cows segmentation task. In each subfigure: the top row shows the reference data image and twice the image that is to be segmented, and the bottom row shows the reference f ˜ , the segmentation returned by the respective algorithm, and the original image masked with the segmentation

5 CONCLUSION

Extending the set-up and results in 13, we defined the continuous-in-time graph ACE with fidelity forcing as in 6 and a SDIE time discretization scheme for this equation. We proved well-posedness of the ACE and showed that solutions of the SDIE scheme converge to the solution of the ACE. Moreover, we proved that the graph MBO scheme with fidelity forcing 32 is a special case of an SDIE scheme.

We provided an algorithm to solve the SDIE scheme, which—besides the obvious extension from the MBO scheme to the SDIE scheme—differs in two key places from the existing algorithm for graph MBO with fidelity forcing: it implements the Nyström extension via a QR decomposition and it replaces the Euler discretization of the diffusion step with a computation based on the Strang formula for matrix exponentials. The former of these changes appears to have been a quite significant improvement: in experiments the Nyström-QR method proved to be faster, more accurate, and more stable than the Nyström method used in previous literature 6, 32, and it is less conceptually troubling than that method, as it does not involve taking the square root of a non-positive-semi-definite matrix.

We applied this algorithm to a number of image segmentation examples concerning images of cows from the Microsoft Research Cambridge Object Recognition Image Database. We found that while the SDIE scheme yielded no improvement over the MBO scheme (and took longer to run in the non-MBO case) the other improvements that we made led to a substantial qualitative improvement over the segmentations of the corresponding examples in 6, 32. We furthermore investigated empirically various properties of this numerical method and the role of different parameters. In particular:
  • We found that the symmetric normalized Laplacian incurred consistently low segmentation error when approximated to a low rank, while the random walk Laplacian was more reliably accurate at higher ranks (where “higher” is still less than 0.1% of the full rank). Thus for applications that require scalability, and thus very low-rank approximations, we recommend using the symmetric normalized Laplacian.
  • We investigated empirically the uncertainty inherited from the randomization in the Nyström extension. We found that the rank reduction and the normalization of the graph Laplacian had the most influence on the uncertainty, and we furthermore observed that at higher ranks the segmentations had high variance at those pixels which are genuinely difficult to classify, for example, the boundaries of the cows.
  • We noted that the fidelity parameter μ corresponds to ascribing a statistical precision to the reference data. We observed that when the reference data were not fully informative, as in Examples 4.2 and 4.3, it was important to tune this parameter to get an accurate segmentation.

To conclude, we give a number of directions we hope to explore in future work, in no particular order.

We seek to investigate the use of the very recent method of 5 combined with methods such as the HMT method 26 or the (even more recent) generalized Nyström method 35 to further increase the accuracy of the low-rank approximations to the graph Laplacian. Unfortunately, we became aware of these works too near to finalizing this paper to use those methods here.

We will seek to extend both our theoretical and numerical framework to multiclass graph-based classification, as considered for example in 22, 28, 37. The groundwork for this extension was laid by the authors in [14, Section 6].

This work dovetails with currently ongoing work of the authors with Carola-Bibiane Schönlieb and Simone Parisotto exploring graph-based joint reconstruction and segmentation with the SDIE scheme. In practice, we often do not observe images directly, but must reconstruct an image from what we observe. For example, when the image is noisy, blurred, has regions missing, or we observe only a transform of the image, such as the output of a CT or MRI scanner. “Joint reconstruction and segmentation” (see 1, 17) is the task of simultaneously reconstructing and segmenting an image, which can reduce computational time and improve the quality of both the reconstruction and the segmentation.

We will also seek to develop an SDIE classification algorithm that is scalable towards larger data sets containing not just one, but hundreds or thousands of reference data images. This can be attempted via data subsampling: rather than evolving the SDIE scheme with regard to the full reference data set, we use only a data subset that is randomly replaced by a different subset after some time interval has passed. Data subsampling is the fundamental principle of various algorithms used in machine learning, such as stochastic gradient descent 38. A subsampling strategy that is applicable in continuous-in-time algorithms has recently been proposed and analyzed by 30.

ACKNOWLEDGEMENTS

We thank Andrea Bertozzi, Arjuna Flenner, and Arieh Iserles for very helpful comments. This work dovetails with ongoing work of the authors joint with Carola-Bibiane Schönlieb and Simone Parisotto, whom we therefore also thank for many indirect contributions. The work of Jeremy Budd and Yves van Gennip was supported by the European Union's Horizon 2020 research and innovation program under Marie Skłodowska-Curie grant 777826. The work of the Jonas Latz was supported by the EPSRC grant EP/S026045/1.

    Appendix A: An analysis of the method from 32

    In 32, the authors approximated 𝒮 τ u by a semi-implicit Euler method for fidelity forced diffusion. That is, since 𝒮 τ u is defined to equal v ( τ ) where v is defined by
    d v d t = − Δ v − M ( v − f ˜ ) , v ( 0 ) = u ,
    the authors of 32 approximate trajectories of this ODE by a semi-implicit Euler method with time step δ t > 0 (such that τ / δ t ∈ ℕ ), that is, v0 ≔ u and
    v k + 1 − v k δ t = − Δ v k + 1 − M ( v k − f ˜ )
    with solution (recalling that f ≔ M f ˜ )
    v k + 1 = I + δ t Δ − 1 v k − δ t M ( v k − f ˜ ) = I + δ t Δ − 1 I − δ t M v k + δ t I + δ t Δ − 1 f ()
    and then (A1) leads to the approximation 𝒮 τ u ≈ v τ / δ t . To compute (A1), they use the Nyström decomposition to compute the leading eigenvectors and eigenvalues of Δ .

    Note.In fact, in 32 the authors use Δ s not Δ . It makes no difference to this analysis which Laplacian is used.

    Given Δ ≈ U 1 Λ U 2 T , an approximate SVD of low rank, the authors approximate (A1) by
    v ^ k + 1 = U 1 ( I K + δ t Λ ) − 1 U 2 T ( v ^ k − δ t M ( v ^ k − f ˜ ) ) = U 1 ( I K + δ t Λ ) − 1 U 2 T ( I − δ t M ) v ^ k + δ t U 1 ( I K + δ t Λ ) − 1 U 2 T f . ()
    Therefore, the final approximation for 𝒮 τ u in 32 is computed by setting v ^ 0 = u and 𝒮 τ u ≈ v ^ τ / δ t .

    A.1 Analysis

    Both (A1) and (A2) are of the form
    v k + 1 = 𝒜 v k + g .
    By induction, this has kth term
    v k = 𝒜 k v 0 + ∑ r = 0 k − 1 𝒜 r g = 𝒜 k v 0 + ( 𝒜 − I ) − 1 ( 𝒜 k − I ) g . ()
    Thus taking k = τ / δ t and v0 = u, we get successive approximations
    𝒮 τ u ≈ I + δ t Δ − 1 I − δ t M k u ()
    + I + δ t Δ − 1 I − δ t M − I − 1 I + δ t Δ − 1 I − δ t M k − I δ t I + δ t Δ − 1 f ≈ U 1 ( I K + δ t Λ ) − 1 U 2 T ( I − δ t M ) k u + U 1 ( I K + δ t Λ ) − 1 U 2 T I − δ t M − I − 1 U 1 ( I K + δ t Λ ) − 1 U 2 T I − δ t M k − I δ t U 1 ( I K + δ t Λ ) − 1 U 2 T f . ()
    To see what these approximations are doing, note that
    I + δ t X = e δ t X + 𝒪 ( δ t 2 )
    and note the Lie product formula [27, Theorem 2.11]
    e ( X + Y ) / k = e X / k e Y / k + 𝒪 ( k − 2 ) and therefore e X + Y = e X / k e Y / k k + 𝒪 ( k − 1 ) .
    Then, since k δ t = τ ,
    I + δ t Δ − 1 I − δ t M k = e − δ t Δ e − δ t M + 𝒪 ( δ t 2 ) k = e − δ t Δ e − δ t M k + 𝒪 ( k δ t 2 ) = e − τ ( Δ + M ) + 𝒪 ( k δ t 2 ) + 𝒪 ( k δ t 2 ) = e − τ A + 𝒪 ( δ t ) ()
    and the second term in (A4) becomes
    I − I + δ t Δ − 1 I − δ t M − 1 I − e − τ A + 𝒪 ( δ t ) δ t I + δ t Δ − 1 = Δ + M − 1 ( I + δ t Δ ) I − e − τ A + 𝒪 ( δ t ) I + δ t Δ − 1 = A − 1 ( I − e − τ A ) + E + 𝒪 ( δ t )
    where (writing [X, Y] ≔ XY − YX for the commutator of X and Y)
    E ≔ A − 1 ( I + δ t Δ ) I − e − τ A , ( I + δ t Δ ) − 1 = − A − 1 ( I + δ t Δ ) e − τ A , ( I + δ t Δ ) − 1 = A − 1 e − τ A , ( I + δ t Δ ) ( I + δ t Δ ) − 1 = δ t A − 1 e − τ A , Δ ( I + δ t Δ ) − 1 = 𝒪 ( δ t )
    is the commutation error. Hence the overall error for (A4) is 𝒪 ( δ t ) . The error for (A5) is similar but also contains an extra error from the spectrum truncation.
    We can also relate this Euler method to a modified quadrature rule. It is easy to see from (2.2) that
    S τ u = e − τ A u + ∫ 0 τ e − t A f d t .
    We understand the Euler approximation for the e − τ A u term by (A6). By (A3), we can write the Euler approximation for the integral term as
    ∫ 0 τ e − t A f d t ≈ δ t ∑ r = 0 k − 1 I + δ t Δ − 1 I − δ t M r I + δ t Δ − 1 f ()
    ≈ δ t ∑ r = 0 k − 1 U 1 ( I K + δ t Λ ) − 1 U 2 T ( I − δ t M ) r U 1 ( I K + δ t Λ ) − 1 U 2 T f . ()
    We note that, since M = diag ( μ ) (and assuming that δ t | | μ | | ∞ < 1 ),
    ( I − δ t M ) − 1 = diag ( 1 − δ t μ ) − 1
    applying the reciprocation elementwise. Therefore, we can rewrite (A7) as
    b ≔ ∫ 0 τ e − t A f d t ≈ δ t ∑ r = 0 k − 1 I + δ t Δ − 1 I − δ t M r + 1 ( 1 − δ t μ ) − 1 ⊙ f = δ t ∑ r = 1 k e − r δ t A ( 1 − δ t μ ) − 1 ⊙ f + 𝒪 ( r δ t 2 ) by (A6) and relabeling r = δ t ∑ r = 1 k e − r δ t A ( 1 − δ t μ ) − 1 ⊙ f + 𝒪 ( τ 2 δ t )
    recalling that k δ t = τ . This can be seen to be a quadrature by the right-hand rule of the integral
    ∫ 0 τ e − t A ( 1 − δ t μ ) − 1 ⊙ f d t .
    Likewise, we can rewrite (A8) as
    ∫ 0 τ e − t A f d t ≈ δ t ∑ r = 1 k U 1 ( I K + δ t Λ ) − 1 U 2 T ( I − μ δ t P Z ) r ( 1 − δ t μ ) − 1 ⊙ f
    where going from (A7) to (A8) has incurred an extra error from the spectrum truncation alongside the quadrature and Lie product formula errors.

    A.2 Conclusions from analysis

    The key takeaway from these calculations (besides the verification that we have the usual 𝒪 ( δ t ) Euler error) concerns (A6). That equation shows that the Euler approximation for the e − τ A term is in fact an approximation of a Lie product formula approximation for e − τ A . This motivates our method of cutting out the middleman and using a matrix exponential formula directly, and furthermore motivates our replacement of the linear error Lie product formula with the quadratic error Strang formula.

    We have also shown how the Euler method approximation for b can be written as a form of quadrature, motivating our investigation of other quadrature methods as potential improvements for computing b.

    • 1 d d s ( ( e s / ε − 1 ) / s ) = s − 2 e s / ε e − s / ε − 1 + s / ε > 0 for s > 0.
    • 2 For the MBO case λ = 1 the thresholding is discontinuous so we do not get an analogous property.
    • 3 d d x ( x − 1 ( 1 − e − τ x ) ) = x − 2 e − τ x ( 1 + τ x − e τ x ) ≤ 0 .
    • 4 More precisely, we will say for real (matrix) valued g, g ( τ , n ) = 𝒪 ( τ ) if and only if limsup | | g ( τ , n ) / τ | | < ∞ as ( τ , n ) → ( 0 , ∞ ) in { ( ρ , m ) | ρ > 0 , m ρ − t ∈ [ 0 , ρ ) } with the subspace topology induced by the standard topology on ( 0 , ∞ ) × ℕ .
    • 5 Suppose X − 1 = Y − 1 + 𝒪 ( τ ) . Then X = ( Y − 1 + 𝒪 ( τ ) ) − 1 = Y ( I + 𝒪 ( τ ) ) − 1 = Y ( I + 𝒪 ( τ ) ) = Y + 𝒪 ( τ ) .
    • 6 Suppose x n 9 x . Then there exists U which is open in the topology of pointwise convergence such that x ∈ U and infinitely many xn ∉ U. Choose x n k such that for all k, x n k ∉ U . This subsequence has no further subsubsequence converging to x.
    • 7 It is easy to see that nonzero ω X X has negative eigenvalues, as it has zero trace.
    • 8 The case of the random walk Laplacian is similar (due to the similarity of the matrices) except for a small additional error incurred by the approximation of D.
    • 9 The HMT results serve only to give an additional benchmark for the Nyström methods: HMT requires matrix-vector-products with Δ s , which was infeasible for us in applications. However, as we were finalizing this paper we were made aware of the recent work of 5, which may make computing the HMT-SVD of Δ s feasible.
    • 10 We owe the suggestion to use this formula to Arieh Iserles, who also suggested to us the Yoshida method that we consider below.
    • 11 We again thank Arieh Iserles for also making this suggestion.
    • 12 We can afford to do this for b, but not generally for the 𝒮 τ u n , because b only needs to be computed once rather than at each n.
    • 13 Specifically, E = ( e − 1 2 δ t M e − δ t Δ e − 1 2 δ t M ) k u − ( e − 1 2 δ t M ( I + U 1 ( e − δ t Λ − I K ) U 2 T ) e − 1 2 δ t M ) k u is incurred by the spectrum truncation in the middle of the latter term.
    • 14 This method can be extended to give higher-order formulae of any even order, but consideration of those formulae is beyond the scope of this paper.
    • 15 Accessed 20 October 2020.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.