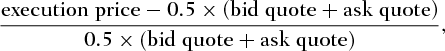Dynamic Dependence Between Liquidity and the S&P 500 Index Futures-Cash Basis
The authors are grateful for helpful comments and suggestions by an anonymous referee, the editor, Bob Webb, and participants at the 2009 FMA Meetings. Li Yang gratefully acknowledges the financial support of the Australian School of Business at University of New South Wales. Chunyang Zhou would like to acknowledge NSFC funding support (no. 71001071).
Abstract
Roll, Schwartz, and Subrahmanyam (2007) investigate the linear relationship between stock market liquidity and index futures-cash basis. We extend their work and examine nonlinear relationship between the two variables of interests, in particular, tail dependence. We find that the tail dependence is asymmetric and varies significantly over times. The lower tail dependence between changes in (il) liquidity measured by bid–ask spread of S&P 500 index and changes in absolute value of S&P 500 index futures-cash basis is almost zero and the upper tail dependence is positive and significantly different from zero. The results suggest that an increase in liquidity is not always associated with a decrease in basis. However, a reduction in liquidity is significantly associated with an increase in basis. At the extreme situation, the link between changes in basis and changes in liquidity can break down. Arbitrage profits cannot be realized and hedging becomes less effective. © 2012 Wiley Periodicals, Inc. Jrl Fut Mark 33:327-342, 2013
1. INTRODUCTION
Liquidity is a broad term in finance, which refers to an asset's ability to be easily converted through the course of buying or selling in large quantities without causing significant price movements and with minimum loss of value. Numerous studies on liquidity have shed light on the importance of this economic fundamental. Amihud and Mendelson (1986) show that stock returns are positively related to the bid–ask spread (i.e., one of liquidity measures). Pastor and Stambaugh (2004) find that stocks with higher sensitivities to fluctuations in liquidity (i.e., liquidity risk) earn higher returns on average. Chordia, Roll, and Subrahmanyam (2002) find that liquidity plummets significantly in down markets.
More recently, liquidity is linked to arbitrage activities in derivatives markets, which cause market prices to converge to the fair values. For example, Deville and Riva (2010) examine the determinants of the time it takes for an index options market to return to the no-arbitrage value in the presence of put–call parity deviations. They show that liquidity-linked variables are associated with a faster reversion of arbitrage profits after controlling for conventional impediments to arbitrage. Roll, Schwartz, and Subrahmanyam (2000) argue that deviations from the no-arbitrage condition, particularly the zero futures-cash basis induced by the cost-of-carry relation, should be related to market liquidity, because illiquidity impedes arbitrage activities. At the same time, a large futures-cash basis may trigger arbitrage trades and thereby affect liquidity. They test the conjecture by investigating the joint dynamic structure of aggregate NYSE market liquidity and the NYSE composite index futures-cash basis with a vector autoregression (VAR) model and find a two-way Granger causality between liquidity and basis.
However, a VAR model would not be able to capture the causality between liquidity and the futures-cash basis under extreme conditions, which is very important for hedgers in the futures markets. As suggested by Chordia et al. (2002), liquidity changes more significantly in down markets than in up markets. The asymmetric responses of liquidity to the direction of the market movement imply that the interdependence between liquidity and the futures-cash basis in down markets may differ from that in up markets. This calls for an alternative approach in order to incorporate any nonlinear dependence between basis and liquidity.
In this study, we employ a copula modeling approach to examine the dynamic and asymmetric dependence between liquidity and the futures-cash basis of S&P 500 index. The copula approach enables us to identify the dependence structures and to capture the potential nonlinear relation between the basis and liquidity. Copula theory was first introduced in Sklar (1959). The capabilities of copula models to capture the dependence structure between variables led to growing interest from both practitioners and academic researchers in recent years. In short, copulas are multivariate distributions that can be decomposed into the marginal density function of each variable and a component known as the copula density, which contains all information of the dependence structure. This property offers the flexibility to model the dependence structure of related variables independently from their marginal distributions, highlighting the advantage of the copula theory over standard classical methods.
Using bid–ask spread of the S&P 500 index as a proxy measure for market (il)liquidity, we model the dynamic dependence between changes in the S&P 500 index futures-cash basis and changes in (il)liquidity through the copula modeling approach. As expected, we find that the linear dependence coefficient between the two variables varies through time, ranging from −0.0719 to 0.1050. Contrast to Roll et al. (2000), a large increase in liquidity is not always associated with a large reduction in the deviation from the zero futures-cash basis. Further analysis shows that the upper tail dependence is significantly different from the lower tail dependence, that is, an asymmetric dependence. The upper tail dependence is significantly positive whereas the lower tail dependence is always close to zero. Thus, as market liquidity decreases, the absolute basis increases. The dependence structure between the two variables may break down. On the other hand, as market liquidity increases, the absolute basis does not necessarily reduce. In these situations, arbitragers incur a great uncertainty when attempting to reap the risk-free profits, because the deviation from the no-arbitrage condition is persistent causing a delay in the convergence. Hedging becomes less effective. Consequently, the time varying and asymmetric dependence structure documented in this study provides more information for market participants.
The remainder of the study is organized as follows. In Section 2., we briefly discuss the copula approach to model the dependence between two variables and different copula models we adopt to specify the dynamic relationship between changes in the basis and changes in (il)liquidity. Marginal models for changes in the basis and changes in (il)liquidity are described in Section 3.. A summary of the findings is presented in Section 4.. The conclusion is given in Section 5..
2. MODELING DYNAMIC DEPENDENCE BETWEEN CHANGES IN BASIS AND CHANGES IN MARKET (IL)LIQUIDITY
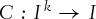 , where
, where  and satisfy the following three conditions:
and satisfy the following three conditions:
- For all
 , if
, if  , then
, then  ;
; - For

 ,
,  ;
; - For all
 ,
,  -->.
-->.
Theorem 1.Let F be the distribution function of k random variables,  , with corresponding marginal distributions (cumulative density function)
, with corresponding marginal distributions (cumulative density function)  , respectively. There exists a copula function C such that
, respectively. There exists a copula function C such that
 (1)
(1) , are continuous, then C is unique.
, are continuous, then C is unique.
 as the quasi-inverse of
as the quasi-inverse of  , such that
, such that  . Upon taking the partial derivatives of Equation1 with respect to each variable and noting
. Upon taking the partial derivatives of Equation1 with respect to each variable and noting  , we have the multivariate density as follows:
, we have the multivariate density as follows:
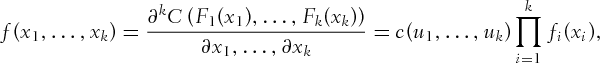 (2)
(2)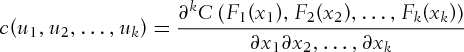
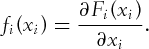
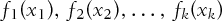 and a copula density,
and a copula density,  . Any dependence structure between the variables is then embedded in the copula density. Equation 2 is a useful result as it allows the univariate dynamic structure to be separated from the dependence structure between the random variables. It also implies that one could more flexibly model the univariate distributions and link them with a copula function that best describes the dependence structures of the random variables. Thus, more flexible multivariate distributions could be easily introduced.
. Any dependence structure between the variables is then embedded in the copula density. Equation 2 is a useful result as it allows the univariate dynamic structure to be separated from the dependence structure between the random variables. It also implies that one could more flexibly model the univariate distributions and link them with a copula function that best describes the dependence structures of the random variables. Thus, more flexible multivariate distributions could be easily introduced.We consider the following two copula functions in this study: (i) the normal copula and (ii) the symmetrized Joe-Clayton (SJC) copula. The normal copula measures the linear dependence between two variables and imposes a symmetric dependence structure, whereas the SJC specification allows for the asymmetric dependence in either direction and measures the tail dependence. In addition, it nests symmetric dependence as a special case. Thus, the normal copula may be considered as a benchmark.
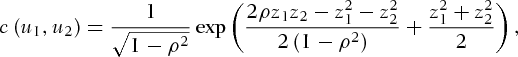 (3)
(3)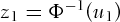 ,
, 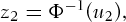 and
and 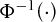 is the inverse of the standard normal cumulative distribution function (CDF). For the normal copula, ρ is the only parameter of the normal copula and measures the linear correlation between the two random variables. Implementing the above model allows us to examine the linear dependence between the two random variables, and because the function is parameterized through the correlation parameter, it is rather easier to interpret. However, it is important to note that the correlation parameter does not represent the linear dependence when the underlying variables are not normally distributed.
is the inverse of the standard normal cumulative distribution function (CDF). For the normal copula, ρ is the only parameter of the normal copula and measures the linear correlation between the two random variables. Implementing the above model allows us to examine the linear dependence between the two random variables, and because the function is parameterized through the correlation parameter, it is rather easier to interpret. However, it is important to note that the correlation parameter does not represent the linear dependence when the underlying variables are not normally distributed.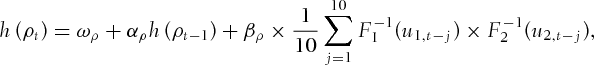 (4)
(4)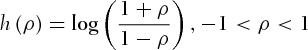
 captures possible persistence in the correlation parameter, while the average of the past ten lags of
captures possible persistence in the correlation parameter, while the average of the past ten lags of  incorporates possible variation in the dependence pattern into the correlation parameter.
incorporates possible variation in the dependence pattern into the correlation parameter.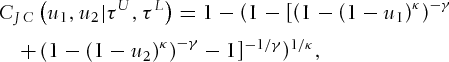 (5)
(5) , and
, and  measure upper and lower tail dependences, respectively. To elaborate, it is the probability of observing a large (small) value for one variable given a large (small) value for the other variable. The drawback of the “BB7” copula is that the asymmetry behavior in the tail dependence is always enforced even when the tail dependence is de facto symmetric. The SJC copula corrects for this possible bias with the following modification:
measure upper and lower tail dependences, respectively. To elaborate, it is the probability of observing a large (small) value for one variable given a large (small) value for the other variable. The drawback of the “BB7” copula is that the asymmetry behavior in the tail dependence is always enforced even when the tail dependence is de facto symmetric. The SJC copula corrects for this possible bias with the following modification:
 (6)
(6) is the “BB7” copula defined as Equation 5. The SJC copula is only a slight modification of the original Joe-Clayton copula, but by construction it is symmetric when the upper and lower tail dependencies are the same, that is,
is the “BB7” copula defined as Equation 5. The SJC copula is only a slight modification of the original Joe-Clayton copula, but by construction it is symmetric when the upper and lower tail dependencies are the same, that is,  .
.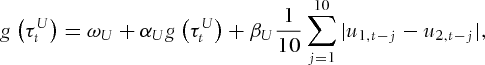 (7)
(7)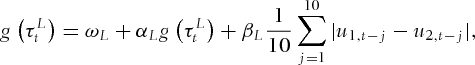 (8)
(8)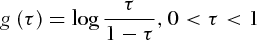
3. MARGINAL DISTRIBUTIONS OF CHANGES IN BASIS AND CHANGES IN LIQUIDITY
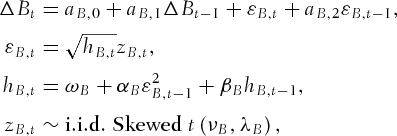 (9)
(9) is the futures-cash basis at time t and defined as a percentage term.
is the futures-cash basis at time t and defined as a percentage term.  and
and  are the futures and spot prices, respectively. Roll et al. (2000) link time variation in the basis to stock market liquidity.
are the futures and spot prices, respectively. Roll et al. (2000) link time variation in the basis to stock market liquidity. 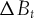 in the mean equation, that is, Equation 6, denotes the change in the basis from time
in the mean equation, that is, Equation 6, denotes the change in the basis from time  to time t, and it follows an ARMA(1,1) process. Equations 7 and 8 assume that the error term follows a GARCH(1,1) process.
to time t, and it follows an ARMA(1,1) process. Equations 7 and 8 assume that the error term follows a GARCH(1,1) process.  is assumed to follow a skewed Student's t-distribution proposed by Hansen (1997) with zero mean and unit variance. The distribution is defined as follows:
is assumed to follow a skewed Student's t-distribution proposed by Hansen (1997) with zero mean and unit variance. The distribution is defined as follows:
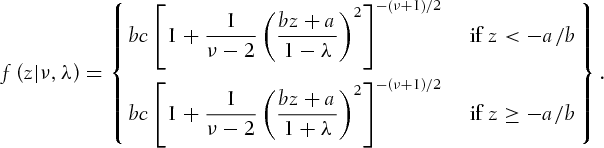
 is the degree of freedom, and
is the degree of freedom, and 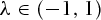 is the skewness parameter.
is the skewness parameter. 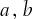 , and c are three constants, given by
, and c are three constants, given by
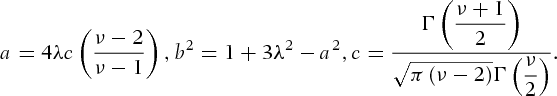
 , it nests to Student's t-distribution.
, it nests to Student's t-distribution.As mentioned above, Chen et al. (1999) assume that the standardized residuals  follow a normal distribution. However, it is well known that financial variables, especially when measured over short time intervals (i.e., daily or weekly), are characterized by nonnormality. In particular, return series exhibit fat tails (excess kurtosis) and are often skewed (Jondeau & Rockinger, 2003; Patton, 2006). Bollerslev (1987) combines the GARCH model with standard Student's t-density to account for fat tails. In addition, asymmetric GARCH model incorporates the leverage effects to generate asymmetric conditional densities. However, this model often fails to adequately describe the asymmetry effect in equity returns (see, e.g., Patton, 2006, 2007). We assume that
follow a normal distribution. However, it is well known that financial variables, especially when measured over short time intervals (i.e., daily or weekly), are characterized by nonnormality. In particular, return series exhibit fat tails (excess kurtosis) and are often skewed (Jondeau & Rockinger, 2003; Patton, 2006). Bollerslev (1987) combines the GARCH model with standard Student's t-density to account for fat tails. In addition, asymmetric GARCH model incorporates the leverage effects to generate asymmetric conditional densities. However, this model often fails to adequately describe the asymmetry effect in equity returns (see, e.g., Patton, 2006, 2007). We assume that  follows the Hansen's (1997) skewed Student's t-distribution for its analytical tractability and its past success in fitting changes in the basis.2 For comparison purpose, we also fit the data with the standard normal distribution despite that, given the non-normality of spot and futures returns, we expect changes in the basis to be nonnormal as well. Based upon distribution adequacy tests, the standard normal is found to be misspecified in terms of uniformity of the probability integral transform3 whereas skewed Student's t-distribution is deemed adequate.
follows the Hansen's (1997) skewed Student's t-distribution for its analytical tractability and its past success in fitting changes in the basis.2 For comparison purpose, we also fit the data with the standard normal distribution despite that, given the non-normality of spot and futures returns, we expect changes in the basis to be nonnormal as well. Based upon distribution adequacy tests, the standard normal is found to be misspecified in terms of uniformity of the probability integral transform3 whereas skewed Student's t-distribution is deemed adequate.
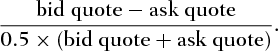 (10)
(10)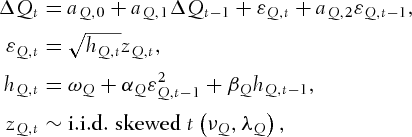 (11)
(11) is the scaled bid–ask spread at time t and
is the scaled bid–ask spread at time t and  is the change in the scaled bid–ask spread from time
is the change in the scaled bid–ask spread from time  to time t. The conditional variance of changes in the spread follows a GARCH(1, 1) process.
to time t. The conditional variance of changes in the spread follows a GARCH(1, 1) process.4. DATA AND ESTIMATION RESULTS
We collect the data on spot and futures prices of the S&P 500 index from Datastream. The sample period covers from January 1, 2002 to December 31, 2008. The futures contracts5 are cash settled in March, June, September, and December. To generate a continuous futures price series from the traded contracts, we first use the nearest to maturity contract and then switch to the next nearest to maturity contracts during the delivery month. In the literature, some studies choose to rollover the contract in the first day of the delivery month (e.g., Bessembinder, 1992; Roon, Nijman, & Veld, 2007), a few days before the expiration of current contract, or at expiration day (e.g., MacKinlay & Ramaswamy, 1994; Roll et al., 2000). There is no single rule of when the contract should be switched. In this study, we use two different switching rules: (i) switching the contract five working days (i.e., one week) prior to the expiration of the contract and (ii) switching the contract ten working days (i.e., two weeks) prior to the expiration of the contract. The results with both (i) and (ii) switching rules are similar. Thus, we only report the results based on the five working-day switching rule. The results based on the ten working-day switching rule are available upon request.
Summary statistics of changes in the basis and changes in the scaled bid–ask spread are provided in Table I. Nonnormality is evident from sample skewness and kurtosis. Moreover, the Jarque–Bera test rejects normality at the 1% level of significance for both variables. The ARCH Lagrange multiplier (ARCH LM) tests indicate that significant ARCH effects prevail in the data. The correlation between changes in the basis and changes in the scaled bid–ask spread is positive, suggesting that the higher stock market liquidity, the smaller the deviations of the futures-cash basis from zero.
| Changes in Basis | Changes in Spread | |
|---|---|---|
| Mean | 0.0007 | 0.0000 |
| Standard deviation | 0.2015 | 0.0032 |
| Skewness | 0.3178 | −0.2691 |
| Kurtosis | 9.9959 | 53.2256 |
| Jarque–Bera | 0.0010 | 0.0010 |
| Ljung–Box Q | 0.0000 | 0.0000 |
| ARCH LM statistic | 0.0000 | 0.0000 |
| Correlation coefficient | 0.0716 |
- Note. The null hypothesis under the Jarque–Bera test assumes normality with test statistic follows a χ2(2)-distribution. The Ljung–Box Q test and the ARCH LM test of Engle (1982) is conducted with ten lags. For Jarque-Bera test, Ljung-Box Q test, and the ARCH test, the numbers reported are the corresponding p-values.
4.1. Dynamics of Changes in the Basis and Changes in the Bid–ask Spread
 is negative and significantly different from zero at the 10% level, and
is negative and significantly different from zero at the 10% level, and  is negative but significantly different from zero at the 1% level. Given the estimated coefficients of
is negative but significantly different from zero at the 1% level. Given the estimated coefficients of  and
and  , we can calculate the first-order autocorrelation of
, we can calculate the first-order autocorrelation of  for an ARMA(1,1) process as
for an ARMA(1,1) process as
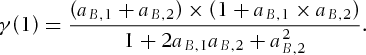 (12)
(12) is about −0.4865, implying that changes in the basis is reduced by a proportional amount of the previous changes in the basis. The result suggests a mean reversion in changes in the basis, which is consistent with the findings by Miller, Muthuswamy, and Whaley (1999) and Garrett and Taylor (1994). Estimation results for the conditional variance indicate that strong GARCH effects prevail with the sum of estimated coefficients (
is about −0.4865, implying that changes in the basis is reduced by a proportional amount of the previous changes in the basis. The result suggests a mean reversion in changes in the basis, which is consistent with the findings by Miller, Muthuswamy, and Whaley (1999) and Garrett and Taylor (1994). Estimation results for the conditional variance indicate that strong GARCH effects prevail with the sum of estimated coefficients (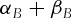 ) being very close to one.
) being very close to one.In columns 4–5 in Table II, we present the parameter estimates and standard errors for the marginal model of changes in the bid–ask spread, given in Equations 14–17. We find that  is positive and
is positive and  is negative, both of which are significantly different from zero at the 1% significance level. The first-order autocorrelation of
is negative, both of which are significantly different from zero at the 1% significance level. The first-order autocorrelation of  calculated using the above formula is about −0.3383, implying that the spread change is reduced by a proportional amount of the previous spread change. Estimation results for the conditional variance indicate strong GARCH effects.
calculated using the above formula is about −0.3383, implying that the spread change is reduced by a proportional amount of the previous spread change. Estimation results for the conditional variance indicate strong GARCH effects.
| Changes in Basis | Changes in Spread | |||
|---|---|---|---|---|
| Coefficient | Standard Error | Coefficient | Standard Error | |
| Mean equation | ||||
 ,0 ,0 |
−0.0009 | 0.0008 | 0.0000 | 0.0000 |
 ,1 ,1 |
 |
0.0288 | 0.1961*** | 0.0432 |
 ,2 ,2 |
 |
0.0190 | 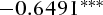 |
0.0333 |
| Variance equation | ||||
| ωi | 0.0015*** | 0.0003 | 0.0000*** | 0.000 |
| αi | 0.1851*** | 0.0310 | 0.2040*** | 0.0325 |
 |
0.7862*** | 0.0259 | 0.7960*** | 0.0219 |
| Distribution parameters | ||||
| νi | 4.3951*** | 0.4319 | 3.7936*** | 0.3514 |
| λi | 0.3635*** | 0.0317 | 0.1680*** | 0.0337 |
- Note. The asterisks, *, and *** represent the 10%, 5%, and 1% significance levels, respectively. Note that
 or Q.
or Q.
If a distribution is correctly specified for an underlying variable, the probability integral transform of the variable should be an independently and identically distributed uniform random variable with a range [0,1]. This property provides a test for distribution adequacy. To proceed, we first test whether the standardized residuals are serially correlated using the LM test conducted by regressing the four central moments of the probability integral transform on its own 20 lags. We then test if the probability integral transform of the standardized residuals are uniformly distributed using the Kolmogorov–Smirnov (KS) test statistics. The p-values of the test results for changes in the basis and changes in the bid–ask spreads are reported in the second and third columns of Table III, respectively. It is shown that serial independence and uniformity of PITs cannot be rejected at the 10% significance level for both marginal models.
| Changes in Basis | Changes in Spread | |
|---|---|---|
| First moment LM test | 0.4361 | 0.3392 |
| Second moment LM test | 0.9820 | 0.9995 |
| Third moment LM test | 1.0000 | 1.0000 |
| Fourth moment LM test | 1.0000 | 1.0000 |
| KS test | 0.1534 | 0.6746 |
- Note. The LM test is carried out by regressing
 on its own 20 lags for k = 1,2,3,4, where
on its own 20 lags for k = 1,2,3,4, where  represents the standardized residuals. The test statistic is (
represents the standardized residuals. The test statistic is ( 20)R2 , where N is the sample size and R2 is the explained sum of squares from the regressions. The KS test refers to the Kolmogorov–Smirnov The null hypothesis is that the standardized residuals of changes in the basis or spread follow skewed Student's t-distribution with the estimated degree of freedom and skewness parameter.
20)R2 , where N is the sample size and R2 is the explained sum of squares from the regressions. The KS test refers to the Kolmogorov–Smirnov The null hypothesis is that the standardized residuals of changes in the basis or spread follow skewed Student's t-distribution with the estimated degree of freedom and skewness parameter.
4.2. Dynamic Dependence Between Changes in the Basis and Changes in the Bid–ask Spread
In Table IV, we present the parameter estimates from the copula models between changes in the basis and changes in the bid–ask spread. The correlation estimate from the constant normal copula model is 0.0066 and statistically insignificantly different from zero. The lower and upper tail dependence estimates from the constant SJC copula are very close to zero, of which the lower tail dependence is statistically insignificant, but the upper tail dependence is statistically significant at the 1% significance level.
| Coefficient | Standard Error | |
|---|---|---|
| Constant normal copula | ||
| ρ | 0.0066 | 0.0240 |
| Copula likelihood | 0.0999 | |
| Constant SJC copula | ||
| τL | 0.0000 | 0.0000 |
| τU | 0.0000*** | 0.0000 |
| Copula likelihood | 0.0883 | |
| Time-varying normal copula | ||
| ωp | 0.0022 | 0.0072 |
| αp | 0.8870*** | 0.2209 |
| βp | 0.0187 | 0.0270 |
| Copula likelihood | 0.5335 | |
| Time-varying SJC copula | ||
| ωL − | 1.2185 | 43.9169 |
| αL | 0.9948*** | 0.2274 |
| βL | 0.8106 | 96.1327 |
| ωU − | 0.5176 | 0.9968 |
| αU | 0.9982*** | 0.0024 |
| βU | 3.3625 | 1.6669 |
| Copula likelihood | 2.7673 | |
- Note. The asterisks, *, **, and *** represent the 10%, 5%, and 1% significance levels, respectively.
Under the time-varying normal copula, the autoregressive term  is estimated to be 0.8870, different from zero at the 1% significance level, and the average past dependence term
is estimated to be 0.8870, different from zero at the 1% significance level, and the average past dependence term  is estimated to be 0.0187, insignificantly different from zero. Figure 1 displays conditional correlation between changes in the basis and changes in the bid–ask spread based on the time-varying normal copula. The value fluctuates mildly around its unconditional value 0.0066. Thus, an increase in the S&P 500 index liquidity is not always associated with a reduction in the basis as suggested in Roll et al. (2000).
is estimated to be 0.0187, insignificantly different from zero. Figure 1 displays conditional correlation between changes in the basis and changes in the bid–ask spread based on the time-varying normal copula. The value fluctuates mildly around its unconditional value 0.0066. Thus, an increase in the S&P 500 index liquidity is not always associated with a reduction in the basis as suggested in Roll et al. (2000).

Under the time-varying SJC copula, the two autoregressive terms  and
and  are estimated to be 0.9948 and 0.9982, respectively, and they are significantly different from zero at the 1% significance level. The two average past dependence terms are estimated to be 0.8102 and 1.6669, respectively, however they are both insignificantly different from zero. Figure 2 displays the time-varying upper tail dependences from the SJC copula model. The lower tail dependences are very close to zero over time, which suggests that a large increase in liquidity is not always associated with a large reduction in basis. The upper tail dependences vary through time. Especially during the financial crisis, there are huge variations in the upper tail dependences. Thus, an asymmetric dependence structure prevails. A positive upper tail dependence suggests that when the absolute basis becomes larger, the bid–ask spread becomes larger as well. In this situation, the deviation of the futures-cash basis from zero may be strongly persistent as there is a great uncertainty for arbitragers to enter the market to take the arbitrage positions.
are estimated to be 0.9948 and 0.9982, respectively, and they are significantly different from zero at the 1% significance level. The two average past dependence terms are estimated to be 0.8102 and 1.6669, respectively, however they are both insignificantly different from zero. Figure 2 displays the time-varying upper tail dependences from the SJC copula model. The lower tail dependences are very close to zero over time, which suggests that a large increase in liquidity is not always associated with a large reduction in basis. The upper tail dependences vary through time. Especially during the financial crisis, there are huge variations in the upper tail dependences. Thus, an asymmetric dependence structure prevails. A positive upper tail dependence suggests that when the absolute basis becomes larger, the bid–ask spread becomes larger as well. In this situation, the deviation of the futures-cash basis from zero may be strongly persistent as there is a great uncertainty for arbitragers to enter the market to take the arbitrage positions.

5. CONCLUSION
This study investigates the joint dynamics between changes in the S&P 500 futures-cash basis and changes in liquidity of S&P 500 index using a copula modeling approach. Copula theory differentiates from the classical method by allowing one to model the dynamics of the individual variables separately from their dependence structure.
The main results documented in this study are (1) the dependence between changes in the basis and changes in liquidity varies through time, and (2) the tail dependence is asymmetric with significant positive upper tail dependence and zero lower tail dependence. The results suggest that the deviation of the futures-cash basis from zero may be strongly persistent, which discourages arbitragers from entering into the market to exploit arbitrage opportunities. Meanwhile, hedging becomes more costly and less effective.
BIBLIOGRAPHY