This paper introduces an extended multivariate EGARCH model that overcomes the zero-return problem and allows for negative news and volatility spillover effects, making it an attractive tool for multivariate volatility modeling. Despite limitations, such as noninvertibility and unclear asymptotic properties of the QML estimator, our Monte Carlo simulations indicate that the standard QML estimator is consistent and asymptotically normal for larger sample sizes (i.e., $T \geq 2500$ ). Two empirical examples demonstrate the model's superior performance compared to multivariate GJR-GARCH and Log-GARCH models in volatility modeling. The first example analyzes the daily returns of three stocks from the DJ30 index, while the second example investigates volatility spillover effects among the bond, stock, crude oil, and gold markets. Overall, this extended multivariate EGARCH model offers a flexible and comprehensive framework for analyzing multivariate volatility and spillover effects in empirical finance research.

1 Introduction

In financial decision-making, multivariate GARCH models, especially the CCC or DCC-GARCH model, are indispensable tools for portfolio selection, risk management, and volatility spillover analysis. Multivariate modeling of the conditional variance is the first step in this type of model. However, positive definiteness of the conditional variance must be guaranteed almost surely at all points in time, which requires all coefficients to be positive. These conditions may be too restrictive and may exclude some crucial stylized facts such as negative volatility spillovers. Conrad and Karanasos (2010) proposed less restrictive nonnegativity conditions, which were further extended by Karanasos et al. (Forthcoming) in the context of the MEM model¹, allowing some elements of the GARCH coefficients to be negative. However, these conditions are often violated in practice.

If the nonnegativity conditions are violated in a multivariate model estimation, several solutions are available. One is to ignore the positivity condition and specify an unrestricted model (e.g., Engle and Gallo 2006). However, this can result in an invalid model, leading to negative volatility forecasts (see Karanasos et al. Forthcoming for details). Another solution is to use a multivariate exponential type of GARCH model, which models logarithmic transformations. Two types of models are available: the multivariate EGARCH model, inspired by Nelson (1982), and the multivariate Log-GARCH (LGARCH) model, inspired by Geweke (1986) and Bauwens and Giot (2000).

The exponential specification does not require nonnegativity constraints, allowing the ARCH and GARCH own and cross coefficients to be negative. This enables not only negative volatility (conditional) spillovers but also negative shock (unconditional) spillover effects, making it more flexible than the GARCH formulation. While the multivariate LGARCH (or Log-MEM) model has been used empirically in several recent papers, such as Sucarrat, Grønneberg, and Escribano (2016), Francq and Sucarrat (2017), Taylor and Xu (2017) and Xu (2024b), the literature on multivariate EGARCH is limited. The term “multivariate” EGARCH found in the literature (e.g., Koutmos and Booth 1995; Jane and Ding 2009; Hansen and Huang 2016; Asai and McAleer 2022) typically refers to univariate EGARCH-X models, where X signifies the inclusion of additional exogenous variables.

To fill the gap in the literature, we propose an extended multivariate EGARCH model. We use the term “extended” following He and Teräsvirta (2004) and Conrad and Karanasos (2010), because the off-diagonal coefficients of the ARCH term and the GARCH term are not restricted to zero. It is also notable the proposed model serves as an exponential version of Conrad and Karanasos (2010)'s multivariate GARCH model and can be seen as a special case within Karanasos et al. (Forthcoming)'s mixture model. To estimate the model, we propose a QML estimation. Similar to the univariate EGARCH model, establishing consistency and asymptotic normality of QML estimates is infeasible, due to the difficulty with the invertibility condition, which involves writing $l n (h_{t})$ as a well-defined function of past observables (see, for example, Wintenberger 2013for the EGARCH(1, 1) model discussion). Instead of establishing asymptotic properties, we use Monte Carlo simulations to examine the finite sample properties of the QML estimator. Our simulation results demonstrate that the QML estimator approaches consistency and normality when the sample size is relatively large (i.e., $T \geq 2,500$ ). However, when the sample size is small (i.e., $T \leq 1,000$ ), the QML estimator can be biased and deviate from normality. Fortunately, GARCH models are often used in empirical finance, where daily data are available, and sample sizes are sufficiently large. For example, for daily data from 2000 to 2021, the sample size is close to 5000, making QML estimators approach consistency and normality. If estimation is not an issue, the multivariate EGARCH model offers distinct benefits. Compared to the multivariate GARCH model, it allows for negative news and volatility spillover effects. Additionally, it does not suffer from problems caused by zero-valued observations that plague the multivariate LGARCH model. Therefore, we conclude that the multivariate EGARCH model is a more attractive model for studying volatility in empirical finance.

We include two empirical examples to illustrate the multivariate EGARCH model. In the first example, we compare the forecasting performance of the multivariate GARCH, LGARCH, and EGARCH models with a DCC structure for conditional correlation for the daily returns of three stocks from the DJ30 index. Our results show that the multivariate EGARCH model outperforms the GARCH and LGARCH models in forecasting volatility and covariance. In the second example, we illustrate how the multivariate EGARCH model can be used to study volatility spillover effects. With bond, stock, crude oil, and gold markets, we find significant negative news and volatility spillover effects. We also observe more than 100 zero-valued observations in the return series, indicating that the multivariate EGARCH model is more suitable for studying (negative) volatility spillover effects in this case.

The remainder of the paper is organized as follows. Section 2 introduces the multivariate EGARCH models. Section 3 discusses the QML estimation and the properties of the QML estimator. Section 4 presents Monte Carlo simulations. Section 5 includes two empirical examples. Section 6 concludes the paper. A Supporting Information appendix provides additional theoretical results.

2 Multivariate Exponential GARCH Model

Following He and Teräsvirta (2004) and Nakatani and Teräsvirta (2009), consider the following vector stochastic process:

r_{t} = ε_{t},

(1)

ε_{t} = D_{t} e_{t},

(2)

where

r_{t}

is a stochastic

(N \times 1)

vector of financial returns and

D_{t} = diag (h_{1, t}^{1 / 2}, \dots, h_{N, t}^{1 / 2}

) is a diagonal matrix of conditional standard deviations of

ε_{t}

. The sequence

\{e_{t}\}

with the stochastic vector

e_{t} = {[e_{1, t}, \dots, e_{N, t}]}^{'}

is a sequence of independent and identically distributed variables with mean

0

and time-invariant positive definite correlation matrix

P = [ρ_{i j}]

with ones on the main diagonal. With these assumptions,

E [ε_{t} | F_{t - 1}] = 0 and E [ε_{t} ε_{t}^{'} | F_{t - 1}] = H_{t} = h_{i, t}^{1 / 2} h_{j, t}^{1 / 2} ρ_{i j},

(3)

where

F_{t}

is the information set up to and including time

t

, and

H_{t} = D_{t} P D_{t}

. Matrix

H_{t}

is the conditional covariance matrix, and

P

is the constant conditional correlation matrix of the process

\{ε_{t}\}

This specification is independent from the specification of a conditional correlation matrix. It can therefore be employed for CCC as well as for DCC GARCH models, leading to the same estimators of the individual volatilities. In the empirical analysis, an example is provided to demonstrate the inclusion of dynamic conditional correlation estimation.

The extended multivariate EGARCH(

p, q

) model of

ε_{t}

takes the form

\ln h_{t} = ω + \sum_{i = 1}^{p} A_{i} | e_{t - i} | + \sum_{j = 1}^{q} B_{j} \ln h_{t - j} + \sum_{i = 1}^{p} Γ_{i} e_{t - i},

(4)

where

ω

is an

(N \times 1)

vector and

A_{i}, B_{j}

and

Γ_{i}

are

(N \times N)

matrices.

If we define

B (L) = (I - \sum_{j = 1}^{q} B_{j} L^{j})

and

A (L) = \sum_{i = 1}^{p} (A_{i} L^{i})

and

Γ (L) = \sum_{i = 1}^{p} (Γ_{i} L^{i})

, Equation (4) can also be written as

B (L) \ln h_{t} = ω + A (L) | e_{t} | + Γ (L) e_{t} .

(5)

Equations (1), (2), and (4) jointly define the $N$ -dimensional extended CCC-EGARCH $(p, q)$ model. In the multivariate EGARCH model, $h_{t}$ is guaranteed to have positive elements for all $t$ , without any restriction on the elements in $A_{i}$ and $B_{j}$ for each $i$ and $j$ . This guarantees that, together with the positive definiteness of $P$ , the conditional variance matrix $H_{t}$ is positive definite for all $t$ .

For comparison purpose, we also suggest the multivariate asymmetric LGARCH(

p, q

) model for

ε_{t}

, which takes the form

\ln h_{t} = ω + \sum_{i = 1}^{p} (A_{i} + Γ_{i} s_{t - i}) \ln ε_{t - i}^{2} + \sum_{j = 1}^{q} B_{j} \ln h_{t - j} .

(6)

where

s_{t} = 0

r_{t} \leq 0

If we define

B (L) = (I - \sum_{j = 1}^{q} B_{j} L^{j})

and

A (L) = \sum_{i = 1}^{p} (A_{i} + Γ_{i} s_{t - i}) L^{i}

, Equation (6) can also be written as

B (L) \ln h_{t} = ω + A (L) \ln ε_{t}^{2} .

(7)

Equations (1), (2), and (6) jointly define the $N$ -dimensional extended CCC-LGARCH $(p, q)$ model. It should be noted that if both $A_{i}$ and $B_{j}$ are diagonal for all $i$ and $j$ , the variance equation in (4) collapses into the $N$ univariate EGARCH $(p, q)$ models of Nelson (1982), the variance equation in (6) collapses into the $N$ univariate LGARCH $(p, q)$ models of Geweke (1986).

To simplify our discussion and because first-order models adequately describe many heteroskedastic time series in most empirical applications, we will focus on the case of $p = q = 1$ and a diagonal $Γ$ , unless otherwise stated. The CCC-EGARCH(1, 1) model has $N (5 N + 2) / 2$ parameters, with $N (2 N + 2)$ parameters appearing in $h_{t}$ and the remaining $N (N - 1) / 2$ in $P$ .

The multivariate EGARCH process defined in (4) is considered stationary if the modulus of the roots of $| I - {\tilde{B}}_{1} z - {\tilde{B}}_{2} z^{2} \dots \tilde{B} q z^{q} | = 0$ are all greater than one. In the case of the univariate EGARCH(1,1) process, the stationarity condition is that the largest eigenvalue of $B$ is smaller than unity. However, the invertibility condition, which is to express $\ln (h_{t})$ as a well-defined function of past observables, cannot be verified analytically². The stationarity and invertibility conditions of the multivariate LGARCH model are well established and can be found in Appendix A.2 of Taylor and Xu (2017).

3 Quasi-Maximum Likelihood Estimation (QMLE)

In this section, we will derive a quasi-maximum likelihood (QML) estimation method for the multivariate EGARCH model.

We assume that

e_{t}

in Equation (2) follows a multivariate normal distribution,

e_{t} {| F}_{t - 1} \sim N (0, P)

. Let

θ^{'} = [θ_{1}^{'}, θ_{2}^{'}]

, where

θ_{1}^{'} = v e c h (P)

, operator

v e c h

stacks the lower triangular (without diagonal) elements of a symmetric (

N \times N

) matrix into a

N \times (N - 1) / 2

vector and

θ_{2}^{'}

contains the parameters in

ε_{t}

. The log-likelihood function is given by the following:

l (θ) = \sum_{t = 1}^{T} \ln f (ε_{t} | θ),

where

\begin{matrix} \ln f (ε_{t} | θ) = & - \frac{N}{2} \ln (2 π) - \frac{1}{2} \ln | D_{t} {PD}_{t} | - \frac{1}{2} ε_{t}^{'} {(D_{t} {PD}_{t})}^{- 1} ε_{t} \\ = & - \frac{N}{2} \ln (2 π) - \frac{1}{2} \ln | D_{t} | - \frac{1}{2} \ln | P | \\ - \frac{1}{2} ε_{t}^{'} D_{t}^{- 1} P^{- 1} D_{t}^{- 1} ε_{t} \\ = & - \frac{N}{2} \ln (2 π) - \frac{1}{2} \ln | D_{t} | - \frac{1}{2} \ln | P | - \frac{1}{2} e_{t}^{'} P^{- 1} e_{t}, \end{matrix}

(8)

where

D_{t} = d i a g (\sqrt{h_{1, t}}, \sqrt{h_{2, t}}, \dots, \sqrt{h_{N, t}})

Additionally, if the DCC specification is employed for the conditional correlation, the correlation matrix

P

can be replaced by the identity matrix in this stage estimation. The log-likelihood function at time

t

is then

\begin{matrix} \ln f (ε_{t} | θ_{1}) & = - \frac{k}{2} \ln (2 π) \\ - \frac{1}{2} \ln | D_{t} | - \frac{1}{2} e_{t}^{'} e_{t} . \end{matrix}

(9)

In the second stage, the dynamic correlation matrix $P_{t}$ can be estimated using ${\hat{e}}_{t}$ , where ${\hat{e}}_{t} = ε_{t} ⊙ {\hat{h}}_{t}^{- 1 / 2}$ and ${\hat{h}}_{t}$ is the estimated conditional variance evaluated at $θ_{1} = {\hat{θ}}_{1}$ , which is obtained from the first stage estimation.

This is a standard log-likelihood estimation approach, which can also be applied to multivariate GARCH and LGARCH models. The consistency and asymptotic normality of the QML estimator $\hat{θ}$ for GARCH and LGARCH models are derived from a more general maximum likelihood theory, as found in Nakatani and Teräsvirta (2009) and Francq, Wintenberger, and Zakoan (2013). Detailed asymptotic properties are provided in the Supporting Information appendix of this paper.

However, the consistency and asymptotic properties of the QML estimator $\hat{θ}$ for the multivariate EGARCH model are not available under general conditions. A limitation in the development of asymptotic properties lies in the lack of an invertibility condition, which would allow expressing $\ln h_{t}$ as a well-defined function of past observables. Wintenberger (2013) and Kyriakopoulou (2015) demonstrate the invertibility conditions for the univariate EGARCH(1,1), while Hafner and Linton (2017) and Martinet and McAleer (2018) present the invertibility conditions for the univariate EGARCH( $p, q$ ). These conditions are complex and require strong assumptions, which are often nonverifiable analytically. Xu (2024b), through Monte Carlo simulations, shows that the QML estimator of the exponential HEAVY model exhibits good finite sample properties when the sample size is sufficiently large. Given these challenges, instead of relying solely on asymptotic theory, we conduct Monte Carlo simulations to investigate the finite sample properties of the QML estimator.

4 Monte Carlo Simulation

As the asymptotic properties of the QML estimator of the multivariate LGARCH model are well established (Sucarrat et al. 2016; Francq and Sucarrat 2017; Taylor and Xu 2017), we will estimate both the multivariate EGARCH and LGARCH models and compare their finite sample properties in a Monte Carlo simulation. We adopt the bivariate EGARCH and LGARCH models given by (4) and (6), respectively. We use sample sizes of 1000, 2500, 5000, and 10,000 for each data-generating process (DGP), and the disturbance term is generated under a multivariate Gaussian distribution. We conduct a Monte Carlo simulation experiment with 1000 repetitions.

The simulations are carried out for three different multivariate DGPs, corresponding to three levels of persistence. The intercept vector $ω =$ ${[0.1, 0.1]}^{'}$ , the correlation parameter $ρ$ = 0.5, and asymmetric parameter matrix $Γ = (\begin{array}{cc} - 0.02 & 0 \\ 0 & - 0.02 \end{array})$ for the EGARCH model and $- Γ$ for the LGARCH model. The remaining parameter values in the DGPs are detailed in Table 1. The multivariate EGARCH DGPs exhibit the following dynamic properties: DGP 1 has moderate volatility persistence, DGP 2 has very high persistence, and DGP 3 has low persistence. In DGPs 1 and 2, one of the off-diagonal coefficients has a negative value ( $β_{21} = - 0.02$ ). In DGP 3, this off-diagonal coefficient has a large negative value ( $β_{21} = - 0.2$ ). For the multivariate LGARCH model, the parameter values in each DGP are the same as the corresponding EGARCH DGP, except for the diagonal elements in matrix B, which are selected to ensure that the persistence level of the LGARCH model is similar to that of the EGARCH model in each DGP. Notably, these parameter values satisfy the stationary condition and are consistent with Nakatani and Teräsvirta (2009)'s experiments.

TABLE 1. Simulation—Data-generating process.

Panel A. EGARCH model data-generating process
	DGP 1	DGP 2	DGP 3
$A$	$(\begin{array}{cc} 0.10 & 0.01 \\ 0.03 & 0.20 \end{array})$	$(\begin{array}{cc} 0.03 & 0.01 \\ 0.03 & 0.05 \end{array})$	$(\begin{array}{cc} 0.10 & 0.01 \\ 0.03 & 0.20 \end{array})$
$B$	$(\begin{array}{cc} 0.90 & 0.04 \\ - 0.02 & 0.90 \end{array})$	$(\begin{array}{cc} 0.98 & 0.04 \\ - 0.02 & 0.95 \end{array})$	$(\begin{array}{cc} 0.55 & 0.04 \\ - 0.20 & 0.60 \end{array})$

Panel B. LGARCH model data-generating process
	DGP 1	DGP 2	DGP 3
$A$	$(\begin{array}{cc} 0.10 & 0.01 \\ 0.03 & 0.20 \end{array})$	$(\begin{array}{cc} 0.03 & 0.01 \\ 0.03 & 0.05 \end{array})$	$(\begin{array}{cc} 0.10 & 0.01 \\ 0.03 & 0.20 \end{array})$
$B$	$(\begin{array}{cc} 0.80 & 0.04 \\ - 0.02 & 0.70 \end{array})$	$(\begin{array}{cc} 0.95 & 0.04 \\ - 0.02 & 0.90 \end{array})$	$(\begin{array}{cc} 0.45 & 0.04 \\ - 0.20 & 0.60 \end{array})$

After generating the return data, we estimate the model parameters using the QML method proposed in the previous section. Tables 2–4 present the Monte Carlo simulation results. We observe that the QML estimates of the parameters in the LGARCH model are generally unbiased, even when the sample size is small ( $T = 1000$ ). As the sample size increases, the biases tend to approach zero, and the standard deviation decreases. However, the QML estimates of the parameters in the EGARCH model exhibit some degree of bias when the sample size is small ( $T = 1000$ ). In particular, the persistent parameters ( $β_{11}$ and $β_{22}$ ) are underestimated, and the bias can be significant, as observed in GDP 2 and GDP 3. Additionally, the estimates of $a_{11}$ and $a_{22}$ are downward biased. As the sample size increases ( $T ≽$ 2500), most of the biases disappear. It is also worth noting that the standard deviation of the estimated EGARCH parameters is much larger than that of LGARCH.

TABLE 2. Simulation results: DGP1.

EGARCH simulation results
		$T = 1000$		$T = 2500$		$T = 5000$		$T = 10,000$
	True	Mean	Std.	Mean	Std.	Mean	Std.	Mean	Std.
$a_{11}$	0.100	0.086	0.071	0.097	0.033	0.099	0.022	0.099	0.015
$a_{12}$	0.010	0.005	0.076	0.009	0.035	0.009	0.023	0.010	0.016
$a_{21}$	0.030	0.029	0.071	0.029	0.034	0.030	0.024	0.030	0.016
$a_{22}$	0.200	0.183	0.071	0.195	0.034	0.199	0.023	0.200	0.017
$β_{11}$	0.900	0.874	0.155	0.886	0.070	0.894	0.033	0.897	0.021
$β_{12}$	0.040	0.053	0.091	0.046	0.043	0.043	0.023	0.041	0.015
$β_{21}$	−0.020	−0.014	0.197	−0.023	0.076	−0.023	0.039	−0.022	0.024
$β_{22}$	0.900	0.887	0.099	0.896	0.045	0.898	0.024	0.899	0.017
$γ_{1}$	−0.020	−0.020	0.062	−0.021	0.016	−0.020	0.010	−0.020	0.008
$γ_{2}$	−0.020	−0.020	0.049	−0.021	0.017	−0.021	0.012	−0.020	0.008

LGARCH simulation results
		$T = 1000$		$T = 2500$		$T = 5000$		$T = 10,000$
	True	Mean	Std.	Mean	Std.	Mean	Std.	Mean	Std.
$a_{11}$	0.100	0.100	0.017	0.099	0.010	0.100	0.007	0.100	0.005
$a_{12}$	0.010	0.009	0.014	0.010	0.009	0.009	0.006	0.010	0.004
$a_{21}$	0.030	0.030	0.016	0.030	0.010	0.030	0.007	0.030	0.005
$a_{22}$	0.200	0.199	0.019	0.200	0.012	0.200	0.008	0.200	0.006
$β_{11}$	0.800	0.798	0.030	0.800	0.017	0.799	0.012	0.800	0.009
$β_{12}$	0.040	0.043	0.023	0.041	0.015	0.041	0.010	0.040	0.007
$β_{21}$	−0.020	−0.024	0.035	−0.022	0.022	−0.021	0.015	−0.021	0.010
$β_{22}$	0.700	0.701	0.027	0.700	0.017	0.700	0.012	0.700	0.008
$γ_{1}$	0.020	0.020	0.018	0.020	0.010	0.020	0.007	0.020	0.005
$γ_{2}$	0.020	0.020	0.021	0.019	0.013	0.021	0.009	0.020	0.007

TABLE 3. Simulation results: DGP2.

EGARCH simulation results
		$T = 1000$		$T = 2500$		$T = 5000$		$T = 10,000$
	True	Mean	Std.	Mean	Std.	Mean	Std.	Mean	Std.
$a_{11}$	0.030	0.142	0.182	0.074	0.023	0.049	0.011	0.037	0.007
$a_{12}$	0.010	−0.042	0.153	−0.004	0.075	0.006	0.012	0.009	0.008
$a_{21}$	0.030	0.040	0.156	0.038	0.080	0.033	0.015	0.031	0.010
$a_{22}$	0.050	0.085	0.105	0.066	0.029	0.057	0.016	0.053	0.011
$β_{11}$	0.980	0.883	0.315	0.962	0.110	0.975	0.033	0.979	0.009
$β_{12}$	0.004	0.081	0.243	0.023	0.092	0.012	0.036	0.005	0.011
$β_{21}$	−0.020	−0.033	0.211	−0.038	0.100	−0.029	0.063	−0.024	0.015
$β_{22}$	0.950	0.914	0.174	0.929	0.111	0.940	0.069	0.946	0.018
$γ_{1}$	−0.020	0.021	0.027	0.020	0.010	0.020	0.006	0.020	0.004
$γ_{1}$	−0.020	0.021	0.030	0.020	0.013	0.020	0.008	0.020	0.005

LGARCH simulation results
		$T = 1000$		$T = 2500$		$T = 5000$		$T = 10,000$
	True	Mean	Std.	Mean	Std.	Mean	Std.	Mean	Std.
$a_{11}$	0.030	0.052	0.008	0.040	0.004	0.035	0.003	0.032	0.002
$a_{12}$	0.010	0.009	0.008	0.010	0.005	0.010	0.003	0.010	0.002
$a_{21}$	0.030	0.031	0.010	0.029	0.005	0.030	0.004	0.030	0.003
$a_{22}$	0.050	0.057	0.012	0.053	0.007	0.052	0.005	0.051	0.003
$β_{11}$	0.950	0.925	0.014	0.939	0.006	0.944	0.005	0.947	0.003
$β_{12}$	0.004	−0.002	0.021	0.000	0.010	0.002	0.006	0.004	0.004
$β_{21}$	−0.020	−0.007	0.018	−0.014	0.010	−0.017	0.006	−0.019	0.004
$β_{22}$	0.900	0.888	0.024	0.895	0.012	0.897	0.008	0.898	0.006
$γ_{1}$	0.020	0.020	0.006	0.020	0.003	0.020	0.002	0.020	0.001
$γ_{2}$	0.020	0.020	0.011	0.020	0.006	0.020	0.004	0.020	0.003

TABLE 4. Simulation results: DGP3.

EGARCH simulation results
		$T = 1000$		$T = 2500$		$T = 5000$		$T = 10,000$
	True	Mean	Std.	Mean	Std.	Mean	Std.	Mean	Std.
$a_{11}$	0.100	0.087	0.073	0.091	0.044	0.096	0.033	0.098	0.022
$a_{12}$	0.010	0.014	0.079	0.012	0.042	0.010	0.030	0.010	0.020
$a_{21}$	0.030	0.031	0.068	0.029	0.046	0.032	0.030	0.029	0.020
$a_{22}$	0.200	0.179	0.072	0.194	0.039	0.198	0.027	0.199	0.018
$β_{11}$	0.550	0.457	0.462	0.506	0.349	0.508	0.268	0.536	0.177
$β_{12}$	0.040	0.046	0.220	0.044	0.112	0.047	0.079	0.039	0.050
$β_{21}$	−0.200	−0.242	0.521	−0.261	0.389	−0.230	0.276	−0.217	0.158
$β_{22}$	0.800	0.788	0.185	0.787	0.106	0.792	0.070	0.798	0.040
$γ_{2}$	−0.020	0.020	0.038	0.019	0.024	0.019	0.017	0.020	0.011
$γ_{2}$	−0.020	0.021	0.035	0.021	0.020	0.020	0.013	0.020	0.009

LGARCH simulation results
		$T = 1000$		$T = 2500$		$T = 5000$		$T = 10,000$
	True	Mean	Std.	Mean	Std.	Mean	Std.	Mean	Std.
$a_{11}$	0.100	0.101	0.024	0.101	0.014	0.100	0.010	0.100	0.007
$a_{12}$	0.010	0.010	0.017	0.010	0.011	0.010	0.008	0.010	0.005
$a_{21}$	0.030	0.030	0.019	0.030	0.012	0.030	0.008	0.030	0.006
$a_{22}$	0.200	0.200	0.019	0.200	0.012	0.200	0.008	0.200	0.006
$β_{11}$	0.450	0.427	0.134	0.442	0.081	0.449	0.055	0.448	0.040
$β_{12}$	0.040	0.042	0.045	0.041	0.028	0.040	0.019	0.040	0.013
$β_{21}$	−0.200	−0.217	0.137	−0.203	0.081	−0.203	0.056	−0.199	0.040
$β_{22}$	0.600	0.594	0.044	0.598	0.026	0.599	0.018	0.600	0.013
$γ_{1}$	0.020	0.021	0.029	0.020	0.017	0.020	0.012	0.020	0.008
$γ_{2}$	0.020	0.020	0.019	0.020	0.011	0.020	0.008	0.020	0.006

We then construct histograms for two persistence parameters ( $a_{11}$ and $β_{11}$ ) and two volatility spillover parameters ( $a_{21}$ and $β_{21}$ ) derived from DGP 1 for various sample sizes³, as displayed in Figures 1-4. The $p$ -values of the Jarque–Bera (JB) normality test are reported alongside each histogram. For smaller sample sizes (i.e., $T = 1000$ ), the LGARCH model estimates exhibit closer approximation to normality than their EGARCH counterparts. As demonstrated by the JB test, the estimated $a_{11}$ and $a_{21}$ from the LGARCH model are normally distributed, while they are not in the case of the EGARCH model. As the sample size increases ( $T \geq 2500$ ), histograms reveal that both EGARCH and LGARCH parameter estimates approach normality, which is further supported by the results of the JB test. The sole exception is the estimated $β_{11}$ from the EGARCH model. The histogram of $β_{11}$ estimates derived from the EGARCH model deviates significantly from normality, particularly when the sample size is 1000; the histogram exhibits left-skewedness and resembles an exponential distribution. In numerous instances, the estimated $β_{11}$ reaches the upper bound (0.9999). The JB test rejects the normality of $β_{11}$ for all sample sizes.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

The histogram of DGP1, $T = 1000$ This figure contains histogram plots of the estimated parameters from simulation. The first row of panels contain plots of estimates of $α$ s and $β$ s from EGARCH model simulation; the second row of panels contain plots of estimates of $α$ s and $β$ s from LGARCH model simulation. JB normality test denotes Jarque–Bera normality test.

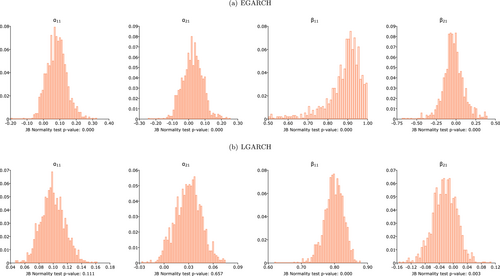
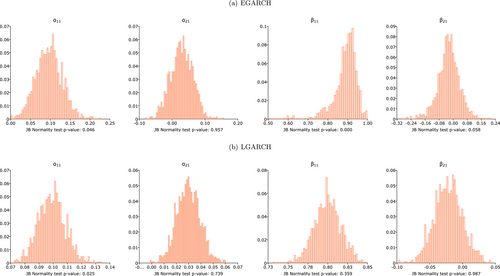
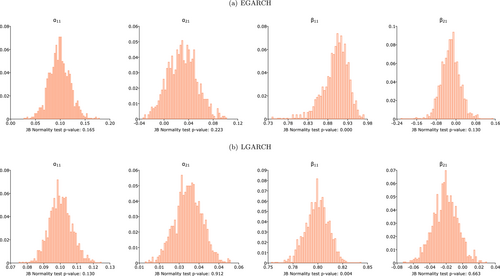
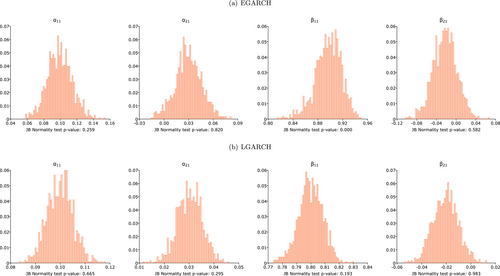
In summary, the simulation results reveal that (1) LGARCH model estimates are consistent and approximate normality even for small samples, (2) the LGARCH model exhibits a smaller standard deviation than the EGARCH model, (3) EGARCH model estimates display bias in small samples but become unbiased for relatively large samples, and (4) EGARCH model estimates approach normality only for sample sizes of 2500 or greater. Overall, the LGARCH model proves more tractable than the EGARCH model (as also corroborated by Francq, Wintenberger, and Zakoan 2013) in small samples. For sufficiently large sample sizes, both LGARCH and EGARCH models' estimates are consistent and asymptotically normal.

We also generated disturbance terms from a multivariate $t$ distribution with varying degrees of freedom and conducted the Monte Carlo simulation again. The outcomes were generally in line with our previous findings, with the sole distinction being an increased standard deviation for all cases, as anticipated.

5 Empirical Analysis

In this section, we present two empirical examples.

5.1 Example 1: Conditional Covariance Matrix of Returns of Three Stocks From DJ30

In our first example, we estimate a three-dimensional EGARCH model with a DCC for the conditional correlation. We analyze daily stock returns of three stocks from the DJ30 index (AXP, GE, IBM) within the timeframe of 02/01/2001 to 16/04/2018, comprising 4092 trading days. For comparison purposes, we also estimate four additional multivariate volatility models. Models 1 and 2 are extended multivariate GARCH models. We adopt the GJR-GARCH type for asymmetry, resulting in multivariate GJR-GARCH models. Model 1 is a GJR-GARCH model with all parameters restricted to be nonnegative, following the constraints imposed by Bollerslev. This model is denoted as GJR-GARCH1. Model 2 is a multivariate GJR-GARCH model with constraints imposed by Karanasos et al. (Forthcoming), allowing at most two parameters in matrix B to be negative. We denote this model as GJR-GARCH2. Model 3 is the multivariate asymmetric power GARCH (APGARCH) model, with the same constraints as Model 2. Model 4 is the multivariate LGARCH model, and Model 5 is the multivariate EGARCH model. For Models 4 and 5, no restrictions are imposed on the parameter set. After estimating the variance process for the multivariate GARCH models, we estimate the correlation process using the DCC model. Subsequently, we use these models to forecast volatility, correlation, and covariance, comparing their forecasting performance.

In estimation, we follow Francq, Wintenberger, and Zakoan (2013) and impose a lower bound (1e-5) for the $r_{t}$ so that $l n (r_{t})$ can be calculated in the multivariate LGARCH model. The estimation results are reported in Tables 5 and 6. Based on the log-likelihood comparison, the EGARCH model exhibits the best fit with the volatility data, as it possesses the smallest Bayesian information criterion (BIC). From the LGARCH and EGARCH model estimates, we identify negative elements in matrix B, suggesting negative interactions between the volatilities of the three assets. The second-stage estimate are remarkably close between the four models. Once again, the EGARCH model demonstrates a superior fit to the correlation data compared to the other models, having the smallest BIC values in the dynamic conditional correlation estimation. It is worth noting that the LGARCH and EGARCH models have the same number of parameters; thus, any model selection criterion (e.g., BIC) comparison is equivalent to the log-likelihood comparison.

TABLE 5. Multivariate asymmetric GARCH models estimation results.

	GJR-GARCH1			GJR-GARCH2			APGARCH
$A$	0.003	0.008	0.010	0.005	0.000	0.036	0.008	0.000	0.034
	(0.26)	(1.07)	(0.98)	(0.89)	( .)	(3.02)	(1.78)	( .)	(5.14)
	0.000	0.050	0.036	0.000	0.046	0.040	0.000	0.137	0.024
	( .)	( 1.22)	(2.20)	( .)	(2.20)	(3.01)	( .)	(12.48)	(3.09)
	0.000	0.000	0.049	0.003	0.000	0.079	0.028	0.000	0.075
	( .)	( .)	(-2.56)	(0.58)	( .)	(3.58)	(1.06)	( .)	(10.02)
$B$	0.921	0.000	0.000	0.865	0.146	-0.100	0.885	0.155	-0.104
	(36.37)	( .)	( .)	(25.12)	(2.36)	(2.60)	(51.50)	(3.86)	(4.51)
	0.057	0.769	0.000	0.238	0.469	0.043	0.247	0.434	0.092
	(1.36)	(8.16)	( .)	(3.47)	(4.11)	(0.69)	(4.85)	(6.31)	(1.62)
	0.000	0.114	0.628	-0.103	0.216	0.718	-0.147	0.276	0.762
	( .)	(1.62)	(4.83)	(2.46)	(3.15)	(15.92)	(4.49)	(4.57)	(29.49)
$Γ$	0.119	0.134	0.154	0.081	0.182	0.062	0.074	0.081	0.051
	(4.23)	(3.71)	(2.77)	(4.87)	(6.75)	(1.76)	(12.45)	(5.84)	(6.20)
$δ$							0.95	0.964	1.312
							(13.34)	(13.02)	(17.10)
$B I C$		44650			44622			44570

	Conditional correlation		Conditional correlation		Conditional correlation
	$α_{c}$	$β_{c}$	$α_{c}$	$β_{c}$	$α_{c}$	$β_{c}$
	0.060	0.762	0.0553	0.7683	0.0511	0.7830
	(4.18)	(11.57)	(4.38)	(12.12)	(4.28)	(9.88)
$B I C$		32031		32006		31965

Note: Bollerslev–Wooldridge robust $t$ -statistics in parentheses. Variables significant at the 5% confidence level formatted in bold. $δ$ denotes the power transform parameter in the AP-GARCH model. BIC notes the Bayesian information criterion.

TABLE 6. Multivariate LGARCH and EGARCH model estimation results.

	LGARCH			EGARCH
$A$	0.028	0.011	0.046	0.096	0.048	0.089
	(9.07)	(3.52)	(14.75)	(10.88)	(6.75)	(8.69)
	0.003	0.020	0.012	0.015	0.068	0.101
	(1.09)	(8.13)	(4.84)	(1.13)	(9.70)	(13.61)
	0.031	0.012	0.043	0.024	0.113	0.139
	(1.62)	(4.17)	(15.18)	(1.63)	(12.89)	(18.01)
$B$	0.939	0.063	-0.133	0.984	0.035	-0.052
	(89.88)	(2.01)	(3.88)	(228.66)	(8.36)	(7.95)
	0.021	0.959	-0.047	0.009	1.012	-0.053
	(1.27)	(121.31)	(2.14)	(1.38)	(503.58)	(11.06)
	-0.061	0.065	0.872	0.006	0.026	0.922
	(1.84)	(2.12)	(79.19)	(0.58)	(9.20)	(181.99)
$Γ$	0.009	0.024	0.003	-0.089	-0.038	-0.020
	(1.98)	(6.53)	(1.53)	(8.98)	(4.49)	(8.69)
$B I C$	44724			44565

	Conditional correlation		Conditional correlation
	$α_{c}$	$β_{c}$	$α_{c}$	$β_{c}$
	0.0511	0.783	0.0631	0.7594
	(4.28)	(9.87)	(5.08)	(12.29)
$B I C$	31945		31941

Note: Bollerslev–Wooldridge robust $t$ -statistics in parentheses. Variables significant at the 5% confidence level formatted in bold. BIC notes the Bayesian information criterion.

A comprehensive comparison among nonnested models can be conducted by evaluating the one-step ahead in-sample and out-of-sample forecasting performance of the models, using the model confidence set (MCS) of Hansen et al. (2011) with the aim of detecting a set of models exhibiting the best forecasting performance. For this purpose, we adopt two statistical loss functions: The first loss function is the root-mean-square error (RMSE) based on the Frobenius norm (see Chiriac and Voev 2011; Golosnoy, Gribisch, and Liesenfeld 2012; Bauwens and Xu 2023) of the forecast error, while the second is a quasi-likelihood (QLIK) loss function (see Noureldin et al., 2012). Since conditional covariance is unobservable, our analysis relies on the realized covariance matrix as a proxy. This approach provides a consistent ranking of volatility models in the sense of Patton (2011) and Laurent, Rombouts, and Violante (2013). The realized covariance is calculated using 5-min intraday returns, such that

R C_{t} = \sum_{j = 1}^{m} r_{j, t} r_{j, t}^{'} .

(10)

where

r_{j, t}

is the corresponding

j

-th intradaily return vector at time

j

on day

t

, where

j = 1,2, \dots, m

. Assuming, for instance, six and a half hours of trading per day and 5-min returns,

m = 78

⁴. It is important to note that with the log-linear specification, one would need to account for distributional aspects of log volatility to produce an unbiased forecast of volatility. However, this should not pose a significant challenge since the log-linear Gaussian specification appears to work well with the data. To compute out-of-sample forecasts, each model is re-estimated every fifth observation based on rolling sample windows of 3000 observations, resulting in a total of 1092 out-of-sample forecasts.

The loss values and MCS test results are reported in Tables 7 and 8. For the in-sample forecasting of conditional covariance, only the EGARCH model is included in the MCS. The LGARCH and APGARCH models rank second, while GJR-GARCH2 performs better than GJR-GARCH1. Similar results are observed when forecasting conditional variance. The in-sample forecast comparisons indicate that the EGARCH model outperforms the other models, a finding consistent with the in-sample likelihood statistics.

TABLE 7. In sample forecast comparison.

	Conditional covariance				Conditional variance
	RMSE	MCS	QLIK	MCS	RMSE	MCS	QLIK	MCS
GRJ-GARCH1	5.196	0.048	3.392	0.000	4.805	0.025	0.380	0.002
GRJ-GARCH2	5.129	0.063	3.398	0.000	4.679	0.028	0.382	0.002
APGARCH	5.078	0.063	3.392	0.000	4.739	0.049	0.377	0.000
LGARCH	5.095	0.063	3.404	0.000	4.740	0.049	0.384	0.002
EGARCH	4.828	1.000	3.368	1.000	4.214	1.000	0.372	1.000

Note: Values of loss functions in bold identify the models in the 90% level MCS. The loss values for variance are the average of foretasted variance cross the three assess.

TABLE 8. Out-of-sample forecast comparison.

	Conditional covariance				Conditional variance
	RMSE	MCS	QLIK	MCS	RMSE	MCS	QLIK	MCS
GRJ-GARCH1	2.984	0.005	2.019	0.002	2.013	0.017	0.522	0.000
GRJ-GARCH2	2.905	0.005	2.042	0.002	1.855	0.017	0.531	0.000
APGARCH	2.435	0.450	1.878	0.906	1.542	0.061	0.474	0.106
LGARCH	2.328	1.000	1.864	1.000	1.281	1.000	0.475	0.106
EGARCH	2.513	0.446	1.878	0.906	1.493	0.061	0.475	1.000

Note: Values of loss functions in bold identify the models in the 90% level MCS. The loss values for variance are the average of foretasted variance cross the three assess.

For out-of-sample forecasting of conditional covariance, the EGARCH, LGARCH, and APGARCH models are included in the MCS when using the RMSE or QLIK loss functions. The two GJR-GARCH models are not included in the MCS. Similar results are observed when forecasting conditional variance. The out-of-sample forecast comparisons indicate that the EGARCH model still performs best, but LGARCH and APGARCH perform equally well.

In summary, the forecasting comparison reveals that the exponential specification of multivariate volatility models performs better than the linear specification when forecasting conditional variance and conditional covariance. The multivariate EGARCH model, proposed in this study, is among the best-performing models for both in-sample and out-of-sample forecasting.

5.2 Example 2: Volatility Spillover Effects Between Stock, Bond, Crude Oil, and Gold Market

In this empirical analysis, we apply a CCC-EGARCH model to study the volatility spillover effects among four financial markets: Bond, Stock, Crude Oil, and Gold. These markets/assets form a straightforward portfolio for risk hedging. Considering that negative volatility spillover might be present in both ARCH and GARCH terms (Baur and Lucey 2010; Arouri, Lahiani, and Nguyen 2011), we use a multivariate EGARCH model to account for potential negative news and volatility spillover effects. The multivariate LGARCH model is not employed due to the presence of numerous zero return observations in the sample (see Table 9).

TABLE 9. Data descriptive statistics.

	Bond	Stock	Crude oil	Gold
Min	−2.87	−12.77	−44.16	−10.16
Max	4.05	10.96	21.51	6.87
Mean	0.72	1.99	2.09	3.18
Std	0.46	1.22	2.28	1.06
Skewness	−0.07	−0.4	−1.2	−0.4
Kurtosis	6.12	14.57	33.93	9.11
$L B^{2} (15)$	1132	6998	835.9	837.7
No. zero	261	204	171	293

Note: This table provides descriptive statistics for the four assets. Std denotes standard deviations. $L B^{2} (15)$ denotes the Ljung–Box test statistic based on 15 lags for the squared returns. The 95% critical value associated with the LB test statistic equals 25.00. No. zero denotes the number of zero observations in the sample. Total observation in the sample is 5689.

The data, priced in USD, are obtained from DataStream. We use the S&P 500 composite index to represent the US stock market and the US 10-year Treasury bond yield for bonds. Crude oil and gold prices correspond to the spot prices of Brent Crude Oil and the London bullion market, respectively. The sample period ranges from January 3, 2001 to October 20, 2021, comprising 5689 trading days.

Table 9 reports the statistics of the four return series, while Figure 5 displays their time series plots. Bonds exhibit the lowest average return at 0.72%, while Gold presents the highest at 3.18%. Crude oil demonstrates the most substantial negative and positive returns (−44.16% during the Covid-19 crisis) and greater volatility compared to the other markets. The skewness and kurtosis statistics reveal that all return series are negatively skewed and highly leptokurtic. The Ljung–Box (LB) statistics for squared return series up to 15 lags indicate significant serial autocorrelations. There are 261, 204, 171, and 293 zero return series observations in the sample for bond, stock, crude oil, and gold markets, respectively, suggesting that the LGARCH model is not suitable for studying volatility spillover effects.

The estimation results, reported in Table 10, show several individually significant effects, including the link from Bond to Stock markets and vice versa. Bidirectional spillovers appear in both ARCH and GARCH terms. We also detect some negative and significant effects. For instance, the Bond market has a negative and significant ( $a_{12} = - 0.027$ ) news spillover effect on the Stock market. The Gold market exerts a negative and significant ( $β_{34} = - 0.007$ ) volatility spillover effect on the Crude Oil market, while the Crude Oil market has a negative and significant ( $β_{43} = - 0.011$ ) volatility spillover effect on the Gold market. Additionally, Bond and Gold display significant news spillover effects on all three markets. The negative spillovers from bonds and gold to other markets align with the stabilizing role of bonds and gold in financial markets. For example, increased volatility in bonds could potentially be associated with reduced volatility in the stock market. This aligns with the safe-haven feature of bonds (Bredin, Conlon, and Potí 2015). Investors seeking safety in bonds may interpret stock market crashes as buying signals in the bond market. Asymmetric effects are observed in the Stock, Crude Oil, and Gold markets but not in the Bond market. The last row reports the largest eigenvalues of the companion matrix ( $B$ ), equal to 0.9958, suggesting that the estimated models are stationary.

TABLE 10. Multivariate EGARCH estimates.

	Bond	Stock	Crude Oil	Gold
$A$	0.056	0.029	−0.008	0.022
	(5.71)	(3.56)	(0.94)	(2.71)
	−0.027	0.134	0.018	0.036
	(2.09)	(10.48)	(1.18)	(2.79)
	0.035	−0.001	0.105	0.023
	(3.52)	(0.13)	(10.32)	(2.32)
	0.037	−0.001	0.019	0.098
	(3.69)	(0.10)	(1.68)	(10.37)
$B$	0.987	0.005	−0.001	0.000
	(279.37)	(2.13)	(0.27)	(0.18)
	0.043	0.948	0.004	−0.004
	(3.74)	(144.79)	(0.75)	(0.63)
	−0.004	0.010	0.986	−0.007
	(0.77)	(2.85)	(373.78)	(2.35)
	−0.006	0.011	−0.011	0.988
	(1.25)	(3.16)	(4.10)	(337.84)
$Γ$	0.008	−0.173	−0.047	0.019
	(1.86)	(15.71)	(8.18)	(3.80)
Eigen( $B$ )	0.9427	0.9781	0.992	0.9958
$L B^{2} (15)$	29.21	16.85	15.59	43.04

Note: Robust standard $t$ -statistics reported in bracket. Parameters significance at the 5% level is indicated by boldcase. Eigen(B) denotes the eigenvalue values of B matrix. $L B^{2} (15)$ denotes the Ljung–Box test statistic based on 15 lags for the squared standardized returns.The 95% critical value associated with the LB(15) test statistic equals 25.00.

A total of seven estimated elements in matrices A and B are negative, and three of these are significant. This finding implies that employing a multivariate GARCH model with nonnegativity constraints may lead to the omission of crucial information related to negative spillover effects. The multivariate LGARCH model requires positivity for all observations, which is not fulfilled in this example. Consequently, the multivariate EGARCH model emerges as a superior alternative, as it accommodates both negative spillover effects and the occurrence of zero returns.

6 Conclusion

In conclusion, this paper presents an extended multivariate EGARCH model, which offers considerable advantages in empirical finance research. This model accommodates negative news and volatility spillover effects while handling zero-valued observations, giving it a clear edge over multivariate GARCH and Log-GARCH models. Despite the model's promising features, one must acknowledge its limitations, particularly regarding the asymptotic properties of the QML estimator and the model's invertibility. Our Monte Carlo simulations reveal that the standard quasi-maximum likelihood estimator performs well when sample sizes are large (i.e., $T \geq 2500$ ). However, it can exhibit significant bias in smaller samples (i.e. $, T \leq 1000$ ).

Our empirical examples showcase the multivariate EGARCH model's potential in practical applications, highlighting its superior performance compared to other models. Nevertheless, further research is necessary to address its limitations in small-sample contexts. One potential avenue for future work involves developing a mixture GARCH model that combines LGARCH and GARCH specifications, utilizing GARCH when zero observations are present and LGARCH in other cases. This mixture model is still a work in progress (Karanasos, Xu, and Yfanti 2024). It is also notable that the multivariate GARCH, EGARCH, and LGARCH models would be special cases of this mixture model.

Overall, the extended multivariate EGARCH model presented in this paper contributes to the empirical finance literature by providing a more comprehensive and flexible framework for analysing multivariate volatility and spillover effects.

Conflicts of Interest

The author declares no conflicts of interest.

Endnotes

¹ MEM denotes Multiplicative Error Model, which was originally proposed by Engle and Gallo (2006) and extended to the multivariate MEM by Cipollini et al. (2013) and multivariate Log-MEM by Taylor and Xu (2017).

² See Wintenberger (2013) and Martinet and McAleer (2018) for further discussion in the univariate context.

³ Histograms of parameters from other DGPs, which are similar in nature, can be provided upon request.

⁴ We use the same data as Bauwens and Xu (2023) and the data description can be found in Appendix 1 of Bauwens and Xu (2023).

Open Research

Data Availability Statement

The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

Supporting Information

References

Arouri, M. E. H., A. Lahiani, and D. K. Nguyen. 2011. “Return and Volatility Transmission Between World Oil Prices and Stock Markets of the GCC Countries.” Economic Modelling 28, no. 4: 1815–1825.
10.1016/j.econmod.2011.03.012
Web of Science® Google Scholar
Asai, M., and M. McAleer. 2022. “Bayesian Analysis of Realized Matrix-Exponential GARCH Models.” Computational Economics 59, no. 1: 103–123.
10.1007/s10614-020-10074-6
Web of Science® Google Scholar
Baur, D. G., and B. M. Lucey. 2010. “Is Gold a Hedge or a Safe Haven? An Analysis of Stocks, Bonds and Gold.” Financial Review 45, no. 2: 217–229.
10.1111/j.1540-6288.2010.00244.x
Google Scholar
Bauwens, L., and P. Giot. 2000. “The Logarithmic ACD Model: An Application to the Bid-Ask Quote Process of Three NYSE Stocks.” Annales d'Economie et de Statistique 60: 117–149.
10.2307/20076257
Google Scholar
Bauwens, L., and Y. Xu. 2023. “DCC-and DECO-HEAVY: Multivariate GARCH Models Based on Realized Variances and Correlations.” International Journal of Forecasting 39, no. 2: 938–955.
10.1016/j.ijforecast.2022.03.005
Web of Science® Google Scholar
Bredin, D., T. Conlon, and V. Potí. 2015. “Does Gold Glitter in the Long-Run? Gold as a Hedge and Safe Haven Across Time and Investment Horizon.” International Review of Financial Analysis 41: 320–328.
10.1016/j.irfa.2015.01.010
Web of Science® Google Scholar
Chiriac, R., and V. Voev. 2011. “Modelling and Forecasting Multivariate Realized Volatility.” Journal of Applied Econometrics 26: 922–947.
10.1002/jae.1152
Web of Science® Google Scholar
Conrad, C., and M. Karanasos. 2010. “Negative Volatility Spillovers in the Unrestricted CCC-GARCH Model.” Econometric Theory 26, no. 3: 838.
10.1017/S0266466609990120
Google Scholar
Engle, R. F., and G. M. Gallo. 2006. “A Multiple Indicator Model for Volatility Using Intra-Daily Data.” Journal of Econometrics 131: 3–27.
10.1016/j.jeconom.2005.01.018
Web of Science® Google Scholar
Francq, C., and G. Sucarrat. 2017. “An Equation-by-Equation Estimator of a Multivariate Log-GARCH-X Model of Financial Returns.” Journal of Multivariate Analysis 153: 16–32.
10.1016/j.jmva.2016.09.010
Web of Science® Google Scholar
Francq, C., O. Wintenberger, and J.-M. Zakoan. 2013. “GARCH Models Without Positivity Constraints: Exponential or Log GARCH?.” Journal of Econometrics 177, no. 1: 34–46.
10.1016/j.jeconom.2013.05.004
Web of Science® Google Scholar
Geweke, J. 1986. “Modeling the Persistence of Conditional Variances: A Comment.” Econometric Reviews 5, no. 1: 57–61.
10.1080/07474938608800097
Google Scholar
Golosnoy, V., B. Gribisch, and R. Liesenfeld. 2012. “The Conditional Autoregressive Wishart Model for Multivariate Stock Market Volatility.” Journal of Econometrics 167: 211–223.
10.1016/j.jeconom.2011.11.004
Web of Science® Google Scholar
Hafner, C. M., and O. Linton. 2017. “An Almost Closed Form Estimator for the EGARCH Model.” Econometric Theory 33, no. 4: 1013–1038.
10.1017/S0266466616000256
Web of Science® Google Scholar
Hansen, P. R., and Z. Huang. 2016. “Exponential GARCH Modeling With Realized Measures of Volatility.” Journal of Business and Economic Statistics 34, no. 2: 269–287.
10.1080/07350015.2015.1038543
Web of Science® Google Scholar
Hansen, P. R., A. Lunde, and J. M. Nason. 2011. “The Model Confidence Set.” Econometrica 79: 453–497.
10.3982/ECTA5771
Web of Science® Google Scholar
He, C., and T. Teräsvirta. 2004. “An Extended Constant Conditional Correlation GARCH Model and Its Fourth-Moment Structure.” Econometric Theory 20, no. 5: 904–926.
10.1017/S0266466604205059
Web of Science® Google Scholar
Jane, T. D., and C. G. Ding. 2009. “On the Multivariate EGARCH Model.” Applied Economics Letters 16, no. 17: 1757–1761.
10.1080/13504850701604383
Web of Science® Google Scholar
Karanasos, M., Y. Xu, and S. Yfanti. 2024. “ Some New (mixture) Formulations for Vector (Asymmetric Power) GARCH/HEAVY Models and MEM.” Cardiff Economics Working Papers Cardiff University, Cardiff Business School, Economics Section.
Google Scholar
Karanasos, M., Y. Xu, S. Yfanti, and C. Zopounidis. Forthcoming. “Constrained QML Estimation for Vector MEM: The Practicality of Matrix Inequalities.” Journal of Financial Econometrics.
Google Scholar
Koutmos, G., and G. G. Booth. 1995. “Asymmetric Volatility Transmission in International Stock Markets.” Journal of International Money and Finance 14, no. 6: 747–762.
10.1016/0261-5606(95)00031-3
Web of Science® Google Scholar
Kyriakopoulou, D. 2015. “ Asymptotic Normality of the QML Estimator of the EGARCH (1, 1) Model.” Available at SSRN 2236055.
Google Scholar
Laurent, S., J. V. Rombouts, and F. Violante. 2013. “On Loss Functions and Ranking Forecasting Performances of Multivariate Volatility Models.” Journal of Econometrics 173, no. 1: 1–10.
10.1016/j.jeconom.2012.08.004
Web of Science® Google Scholar
Martinet, G. G., and M. McAleer. 2018. “On the Invertibility of EGARCH (p, q).” Econometric Reviews 37, no. 8: 824–849.
10.1080/07474938.2016.1167994
Web of Science® Google Scholar
Nakatani, T., and T. Teräsvirta. 2009. “Testing for Volatility Interactions in the Constant Conditional Correlation GARCH Model.” Econometrics Journal 12, no. 1: 147–163.
10.1111/j.1368-423X.2008.00261.x
Web of Science® Google Scholar
Patton, A. J. 2011. “Volatility Forecast Comparison Using Imperfect Volatility Proxies.” Journal of Econometrics 160, no. 1: 246–256.
10.1016/j.jeconom.2010.03.034
Web of Science® Google Scholar
Sucarrat, G., S. Grønneberg, and A. Escribano. 2016. “Estimation and Inference in Univariate and Multivariate log-GARCH-X Models When the Conditional Density Is Unknown.” Computational Statistics and Data Analysis 100: 582–594.
10.1016/j.csda.2015.12.005
Web of Science® Google Scholar
Taylor, N., and Y. Xu. 2017. “The Logarithmic Vector Multiplicative Error Model: An Application to High Frequency NYSE Stock Data.” Quantitative Finance 17, no. 7: 1021–1035.
10.1080/14697688.2016.1260756
Web of Science® Google Scholar
Wintenberger, O. 2013. “Continuous Invertibility and Stable QML Estimation of the EGARCH (1, 1) Model.” Scandinavian Journal of Statistics 40, no. 4: 846–867.
10.1111/sjos.12038
Web of Science® Google Scholar
Xu, Y. 2024a. “Quasi Maximum Likelihood Estimation of Vector Multiplicative Error Model Using the ECCC-GARCH Representation.” Journal of Time Series Econometrics 16, no. 1: 1–27.
10.1515/jtse-2022-0018
CAS Web of Science® Google Scholar
Xu, Y. 2024b. “The Exponential HEAVY Model: An Improved Approach to Volatility Modeling and Forecasting.” Review of Quantitative Finance and Accounting 2024: 1–22.
Web of Science® Google Scholar

Volume44, Issue4

July 2025

Pages 1266-1279

Extended Multivariate EGARCH Model: A Model for Zero-Return and Negative Spillovers

ABSTRACT

1 Introduction

2 Multivariate Exponential GARCH Model

3 Quasi-Maximum Likelihood Estimation (QMLE)

4 Monte Carlo Simulation

5 Empirical Analysis

5.1 Example 1: Conditional Covariance Matrix of Returns of Three Stocks From DJ30

5.2 Example 2: Volatility Spillover Effects Between Stock, Bond, Crude Oil, and Gold Market

6 Conclusion

Conflicts of Interest

Endnotes

Open Research

Data Availability Statement

Supporting Information

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Extended Multivariate EGARCH Model: A Model for Zero-Return and Negative Spillovers

ABSTRACT

1 Introduction

2 Multivariate Exponential GARCH Model

3 Quasi-Maximum Likelihood Estimation (QMLE)

4 Monte Carlo Simulation

5 Empirical Analysis

5.1 Example 1: Conditional Covariance Matrix of Returns of Three Stocks From DJ30

5.2 Example 2: Volatility Spillover Effects Between Stock, Bond, Crude Oil, and Gold Market

6 Conclusion

Conflicts of Interest

Endnotes

Open Research

Data Availability Statement

Supporting Information

References

Figures

References

Related

Information