Development and Validation of Multiple Linear Regression Models for Predicting Chronic Zinc Toxicity to Freshwater Microalgae
Abstract
Multiple linear regression (MLR) models were developed for predicting chronic zinc toxicity to a freshwater microalga, Chlorella sp., using three toxicity-modifying factors (TMFs): pH, hardness, and dissolved organic carbon (DOC). The interactive effects between pH and hardness and between pH and DOC were also included. Models were developed at three different effect concentration (EC) levels: EC10, EC20, and EC50. Models were independently validated using six different zinc-spiked Australian natural waters with a range of water chemistries. Stepwise regression found hardness to be an influential TMF in model scenarios and was retained in all final models, while pH, DOC, and interactive terms had variable influence and were only retained in some models. Autovalidation and residual analysis of all models indicated that models generally predicted toxicity and that there was little bias based on individual TMFs. The MLR models, at all effect levels, performed poorly when predicting toxicity in the zinc-spiked natural waters during independent validation, with models consistently overpredicting toxicity. This overprediction may be from another unaccounted for TMF that may be present across all natural waters. Alternatively, this consistent overprediction questions the underlying assumption that models developed from synthetic laboratory test waters can be directly applied to natural water samples. Further research into the suitability of applying synthetic laboratory water–based models to a greater range of natural waters is needed. Environ Toxicol Chem 2023;42:2630–2641. © 2023 The Authors. Environmental Toxicology and Chemistry published by Wiley Periodicals LLC on behalf of SETAC.
INTRODUCTION
Zinc toxicity to aquatic organisms is dependent on its bioavailability, which is influenced by water quality parameters, such as pH, hardness, and dissolved organic carbon (DOC). For example, pH determines zinc speciation, and protons (H+) and hardness ions (Ca2+ and Mg2+) compete with zinc for biological uptake at the biotic ligand, while DOC complexes zinc, thereby altering its bioavailability (Adams et al., 2020).
Currently, the Australian and New Zealand water quality guidelines for zinc only account for the influence of hardness on bioavailability via a hardness algorithm (Australian and New Zealand Governments, 2018). This algorithm is largely based on acute toxicity data derived from North American fish species and has recently been shown to not be appropriate for freshwater microalgae (Price, Stauber, Holland et al., 2022). Increased attention has focused on bioavailability-based water quality guidelines with the development of the biotic ligand model (BLM), which predicts the toxicity of a metal to a species based on water quality parameters. The model predicts the amount of accumulation that occurs at the biotic ligand by accounting for changes in metal speciation and the presence of competitive effects from other ions in solution (Di Toro et al., 2001). More recently, there has been interest in the development of simpler empirical bioavailability models, such as multiple linear regression (MLR) models, because they can be easier to use. Brix et al. (2017) suggested that there may be perceptions among regulators that BLM approaches are too complicated and not sufficiently transparent.
To date, several studies have developed MLR models for predicting bioavailability-based toxicity of metals to freshwater organisms (Brix et al., 2017, 2021, 2023; Croteau et al., 2021; DeForest et al., 2018, 2023; Peters et al., 2021). From the current literature two approaches to data sourcing have been used. Several studies have aggregated large data sets from multiple sources and laboratories (Brix et al., 2017, 2021; Croteau et al., 2021; DeForest et al., 2023; Peters et al., 2021). Others have used data from a single study or laboratory, and therefore all toxicity data for a particular species are derived from the same culture and tested under the same conditions using synthetic laboratory test waters (Brix et al., 2023; DeForest et al., 2018). Both approaches have merit. Utilizing large, aggregated data sets provides more statistical power in model development and often does not require any additional laboratory work. However, pooling data from different sources also reduces confidence in the comparability of data between studies and introduces issues of colinearity because often studies varied multiple toxicity-modifying factors (TMFs) simultaneously. In addition, pooling studies can result in an imbalance in the representation of different TMF effects. For example, generally, fewer DOC studies are available compared to hardness studies. Relying on data from a single study typically means smaller data sets for model development but often greater confidence in the consistency of data given that they were collected under the same testing conditions and from the one culture. However, of the two MLR models developed using single data sets, neither has been independently validated using natural waters, and the MLR models have only previously been developed for one microalga, Raphidocelis subcapitata (Brix et al., 2023; DeForest et al., 2018).
The present study is the first to develop a zinc bioavailability MLR model for a different freshwater microalga and the first to be independently validated with natural waters. The objective of the present study was to use recently published zinc toxicity data under varying pH, hardness, and DOC conditions for the microalga Chlorella sp. (Price, Stauber, Holland et al., 2022; Price et al., 2021, 2023) to develop empirical models that predict zinc toxicity as a function of these parameters. Models were independently validated using six different zinc-spiked Australian natural waters with a range of water chemistries. Previously developed zinc MLR models for R. subcapitata were also validated using the natural waters toxicity data to assess the suitability of these models under Australian water chemistry conditions. These data, together with those presented in the companion paper by Stauber et al. (2023), will be used to develop bioavailability-based zinc water quality guidelines for Australia and New Zealand (Australian and New Zealand Governments, 2018).
METHODS
Model development
Data sources
The chronic toxicity of zinc has been tested over a wide range of water chemistries for the freshwater microalga Chlorella sp. These data were sourced from Price et al. (2021, 2023) and Price, Stauber, Holland et al. (2022), with each source providing a detailed description of the tests carried out. All tests were conducted using laboratory-prepared synthetic freshwaters with pH levels ranging from 6.7 to 8.3, hardness concentrations from 5 to 400 mg CaCO3 L–1, and DOC concentrations of 0–15 mg C L–1. Tests were performed at a constant alkalinity (~40 mg L–1) and calcium to magnesium ratio (~0.7) as described in Price, Stauber, Holland et al. (2022). The toxicity data used met the acceptability criteria outlined by Warne et al. (2018) for use in development of Australian water quality guidelines. All zinc effect concentrations used in the present study are expressed as dissolved zinc (measured as <0.45 µm) and are provided in Supporting Information, Tables S1 and S2.
MLR analysis
In Equation (1), toxicity is an effect level (i.e., EC10, EC20, or EC50), in micrograms of zinc per liter; b0 is the y-intercept; and b1, b2, and b3 are the slope parameters for pH, ln(hard), and ln(DOC), respectively, with hardness and DOC in milligrams per liter.
Both the Akaike information criterion (AIC) and the Bayesian information criterion (BIC) were used in stepwise MLR analyses to determine which terms to include in the model to create the most parsimonious model at each effect level. Both criteria achieve parsimony and balance specificity and generality through penalizing the goodness-of-fit of a model in relation to the number of parameters present in the model. The BIC also accounts for the sample size used in the analysis and is described in further detail by DeForest et al. (2018).
Variance inflation factors (VIFs) were calculated for all independent variables to assess colinearity. The VIF is a quotient that measures the amount of variance in an estimated regression coefficient that is changed by colinearity between parameters used in the model. A low VIF means low colinearity, with VIFs <3 considered acceptable (Zuur et al., 2010). In controlled experiments using laboratory-prepared media, each independent variable can be carefully controlled, and therefore correlation among independent variables is unlikely. In contrast, studies that use field samples may see higher levels of correlation because these independent variables cannot be as easily controlled.
Stepwise regressions were run using the stepAIC function from the MASS library (Venables & Ripley, 2002) and assessed using both AIC and BIC. Variance inflation factors were determined using the vif function in the usdm library (Naimi et al., 2014). Predictive R2 values were calculated using leave-one-out cross-validation via the caret package (method = “LOOCV”; Kuhn et al., 2021). The predicted R2 summarizes a model's predictive capacity and will always be lower than the corresponding adjusted R2. A predicted R2 value that is much smaller than the adjusted R2 is indicative of model overfitting or a model that is heavily reliant on individual data points.
Four models were developed and considered for each of the EC10, EC20, and EC50 data sets. These four models (at each effect level) were those developed with parameters based on the stepwise regression analysis using either AIC or BIC test statistics with and without interaction terms. For the EC50 data set an additional four models were developed and considered using a subset of data (n = 18 EC50 values) in which data from zinc toxicity experiments using DOC sourced from Appletree Creek and Manton Dam (Price et al., 2023) were excluded. These data were excluded because Price et al. (2023) found that the presence of Appletree Creek dissolved organic matter (DOM) increased toxicity at the EC50 level, which is contrary to principles described by the BLM. As such, it was considered that these toxicity-enhancing effects are unlikely to be representative of the influence of all Australian DOM, and additional models were developed for comparison. In total, 16 models across the three effect levels were developed and considered in the present study. Models developed using all data as described above (see Data sources) are referred to as “full data models,” and the EC50 models developed excluding the DOM data, as described above, are referred to as “subset data models” throughout.
Validation methods followed procedures described by Garman et al. (2020), Besser et al. (2021), and DeForest et al. (2023). Autovalidation assesses the fit of data used to develop the model. Observed toxicity was plotted versus predicted toxicity data on a 1:1 plot as a visual means to understand how closely the model was predicting the observed data. Performance was assessed based on the percentage of observed data that fell within a factor of 2 or 3 of the predicted toxicity values. The factor of 2 is based on intertest variability on median lethal concentration values for Pimephales promelas exposed to copper (Erickson et al., 1996) and Daphnia magna exposed to cadmium, copper, nickel, or zinc (Meyer et al., 2018; Santore & Ryan, 2015). From these studies, the factor of 2 has become a standard metric for assessing model predictive capability. A recent study by Price, Stauber, Stone et al. (2022) found that the factor of 2 metric may not be appropriate for low effect levels (e.g., EC10 and EC20 values), with a factor of 3 metric being more appropriate. This is attributable to the greater uncertainty at EC10 and EC20 values in a concentration–response model (Peters et al., 2018; Price, Stauber, Stone et al., 2022). Price et al. (2022) also found that both the factor of 2 and the factor of 3 metrics were suitable for microalgae at all effect levels. Based on this, the current study has assessed model performance at all effect levels based on both the factor of 2 and factor of 3 metrics.
Model residual analysis, as described by Garman et al. (2020) and implemented by Brix et al. (2021, 2023) and Croteau et al. (2021), was used as an additional metric of performance in model validation. Model residuals were calculated using Equation (3). Geometric means and regression slopes of residuals of the observed versus predicted values as a function of either observed and predicted toxicity were assessed to test for consistent over- or underprediction of the model.
MLR independent validation
Natural water collection and analysis
Natural surface freshwaters were collected from six unimpacted waterways across Australia: Woronora River (Tharawal Country) from New South Wales, Ovens River (Waveroo Country) from Victoria, Teatree Creek and Limestone Creek (Darumbal Country) from Queensland, Magela Creek (Mirrar Country) from Northern Territory, and Blackwood River (Bibbulman Noongar Country) from Western Australia (Supporting Information, Figure S1). Global Positioning System coordinates of the sample locations are given in Supporting Information, Table S3. The waterways were selected to cover a range of climatic, geographical, and state jurisdictions. Selection was also based on water quality previously recorded, taking into account TMFs, that is, hardness, pH, and DOC concentrations. The hardness, pH, DOC concentration, and conductivity of the natural waters were estimated from online real-time water data sources, if available, and from previously published data (Holland et al., 2014; Stauber et al., 2021, 2023). These sites chosen for sampling were targeted for their water chemistries, which were generally representative of typical Australian water chemistry ranges.
A YSI multiprobe meter (YSI DSS PRO) was used at each site to confirm that pH and conductivity were within acceptable limits before river water was collected. Water was stored in 5-L high-density polyethylene containers which had been previously acid-washed and rinsed in ultrapure water (18 MΩ cm; Milli-Q®; Millipore) and associated river water. Approximately 25 L of water was collected from each site and kept on ice until arrival at the laboratory. The river water was then filtered through a prerinsed 0.45-μm in-line flowthrough polyethersulfone filter (Waterra). Filters were prerinsed with acid, ultrapure water, and associated river water. The samples were stored at 4 °C in the dark until they were used in the bioassays. All bioassays were conducted within 1 month of water collection. Additional samples were taken at the time of collection for chemical analysis, which are detailed in the the Supporting Information. Subsamples of the stored freshwaters were collected and analyzed for total hardness, cations, and organic carbon immediately prior to and during toxicity testing (methods provided in Supporting Information).
Toxicity testing
Toxicity testing using collected natural waters was conducted to develop an additional data set for independent validation of MLR models developed in the present study and those available in the literature. The 72-h growth inhibition bioassays were conducted following the same methods used to generate the development data set (Price et al., 2021), except that natural freshwaters were used instead of a synthetic laboratory water. A buffered test (0.5 g 3-morpholinopropanesulfonic acid [MOPS] L–1) and an unbuffered test were conducted in each natural water, except Teatree Creek water, where only an unbuffered test was conducted because the natural pH of the water was below the range of MOPS. An additional test was conducted on an Ovens River water sample where the pH was increased (named “Ovens River—Adjusted”) to create potentially high-bioavailability conditions. Each test consisted of a zinc concentration series between 0 and 10,000 µg L–1, with five control replicates and 22 individual zinc treatments with a single replicate per treatment. A zinc reference toxicant test in synthetic water was run concurrently with each natural water test. Reference toxicant test water had no additional DOC added. The test was considered acceptable if algal growth rates in reference toxicant tests were 1.7 ± 0.4 doublings per day (mean ± SD), control growth rates had a coefficient of variation <20%, and the zinc reference EC50 was within internal database limits of 85 ± 40 µg Zn L–1.
RESULTS AND DISCUSSION
MLR models
The VIFs for pH, ln(hardness), and ln(DOC) across all models ranged from 1.0 to 1.1, indicating very low correlation between independent variables. This was expected given that all data used came from controlled experiments, where an individual parameter was varied while the others were held constant. This is consistent with models developed from other controlled experiment studies (Brix et al., 2023; DeForest et al., 2018, 2020), where VIFs are generally lower than for models developed from larger databases derived from a range of sources (Brix et al., 2017, 2021).
All models retained hardness as a term, whereas only seven of the 16 retained DOC and only four retained pH. Only two models retained the interactive term of ln(DOC) × pH (Table 1). This contrasts with the zinc models of DeForest et al. (2023) developed for R. subcapitata, in which only pH and DOC were retained (not hardness) as a significant parameter. On three occasions AIC and BIC methods retained the same model terms and coefficients (shown in Table 1 on a single line). On two occasions (EC50 with data subset) there were no differences between models with and without interactive terms, but AIC-selected and BIC-selected models retained different terms and coefficients (Table 1).
| Slopes | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Endpoint | n | Data used | Model | Intercept | pH | ln(Hard) | ln(DOC) | ln(DOC) × pH | Adj. R2 | Pred. R2 | AIC | BIC |
| EC10 | 30 | All data | No interaction (AIC) | −0.189 | – | 0.276 (p = 0.006) | 0.177 (p = 0.06) | – | 0.32 | 0.27 | −30.7 | – |
| No interaction (BIC) | −0.189 | – | 0.276 (p = 0.006) | 0.177 (p = 0.06) | – | 0.32 | 0.27 | – | −26.5 | |||
| With interaction (AIC) | 0.160 | −0.055 (p = 0.78) | 0.288 (p = 0.005) | −2.137 (p = 0.15) | 0.302 (p = 0.12) | 0.34 | 0.28 | −29.7 | – | |||
| With interaction (BIC) | −0.189 | – | 0.276 (p = 0.006) | 0.177 (p = 0.06) | – | 0.32 | 0.27 | – | 26.5 | |||
| EC20 | 30 | All data | No interaction (AIC and BIC) | 0.142 | – | 0.446 (p < 0.001) | – | – | 0.41 | 0.37 | −27.7 | −24.9 |
| With interaction (AIC) | 0.189 | −0.009 (p = 0.97) | 0.432 (p < 0.001) | −2.114 (p = 0.18) | 0.289 (p = 0.16) | 0.42 | 0.34 | −25.6 | – | |||
| With interaction (BIC) | 0.142 | – | 0.446 (p < 0.001) | – | – | 0.41 | 0.37 | – | −24.9 | |||
| EC50 | 30 | All data | No interaction (AIC and BIC) | 1.17 | – | 0.628 (p < 0.001) | – | – | 0.47 | 0.43 | −14.6 | −11.6 |
| With interaction (AIC and BIC) | 1.17 | – | 0.628 (p < 0.001) | – | – | 0.47 | 0.43 | −14.6 | −11.6 | |||
| 18 | Subset data only | No interaction (AIC) | 3.97 | −0.359 (p = 0.17) | 0.673 (p < 0.001) | 0.351 (p = 0.080) | – | 0.75 | 0.66 | −14.4 | – | |
| No interaction (BIC) | 1.15 | – | 0.684 (p < 0.001) | – | – | 0.70 | 0.64 | – | −10.4 | |||
| With interaction (AIC) | 3.97 | −0.359 (p = 0.17) | 0.673 (p < 0.001) | 0.351 (p = 0.080) | – | 0.75 | 0.66 | −21.8 | – | |||
| With interaction (BIC) | 1.15 | – | 0.684 (p < 0.001) | – | – | 0.70 | 0.64 | – | −14.8 | |||
- Adj. R2 = adjusted R2; AIC = Akaike information criterion; BIC = Bayesian information criterion; Hard = hardness; DOC = dissolved organic carbon; EC10/20/50 = 10%, 20%, and 50% effective concentrations, respectively; Pred. R2 = predicted R2; – = term not retained in stepwise regression analysis.
In general, model adjusted R2 values were low, ranging from 0.3 to 0.5 for models using the full data set. Adjusted R2 values improved in the EC50 models using the subset data, ranging from 0.7 to 0.8. Predicted R2 values ranged from 0.3 to 0.7, with EC10 models having the lowest (0.3) and EC50 models having the highest (0.7) values. All predicted R2 values were only slightly lower than their respective adjusted R2 values, indicating the models were not overfitted. The inclusion of interaction terms either did not improve or only marginally improved model adjusted R2 and predicted R2 values for all EC levels. Therefore, both types of models, with and without interaction terms, were retained for autovalidation.
Autovalidation
Autovalidation was used to validate and assess the fit of data used in the model development data set. Data were considered acceptable if agreement between observed and predicted EC20 and EC50 values was within a factor of 2. For all values, including EC10 values, agreement within a factor of 3 was also considered (Peters et al., 2018; Price, Stauber, Stone et al., 2022).
Observed toxicity versus predicted toxicity plots are shown for all models in Figures 1 and 2. For the EC10 and EC20 models, both models with and without interaction terms generally provided good fit of the data. The inclusion of interaction terms in EC10 models improved the factor of 2 and factor of 3 percentages from 57% and 77% to 80% and 93%, respectively (Figure 1, left-hand panel; Supporting Information, Table S4). Inclusion of interaction terms in EC20 models did not improve the percentage of predictions within a factor of 2, with 77% for both models, but did improve predictions within a factor of 3 marginally from 93% to 97%. The EC50 models did not predict data as well as the EC10 and EC20 models. The full data set (n = 30) model had 53% and 93% of predictions within a factor of 2 and 3, respectively.
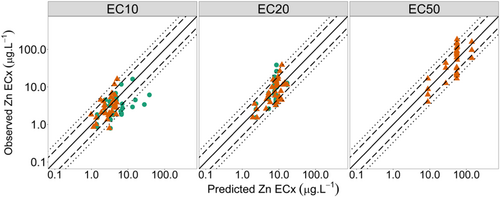

To assess the EC50 subset data models, factor of 2 and 3 performances were firstly assessed using only the observed data used to develop the model (n = 18). The AIC-selected model had factor of 2 and factor of 3 percentages of 72% and 100%, respectively, while the BIC-selected model had 61% and 94%. Secondly, the subset data models were assessed using the full development data set (n = 30). As expected, performance was reduced, with the AIC-selected model having factor of 2 and factor of 3 percentages of 57% and 73%, respectively. The BIC-selected model had a slightly lower factor of 2 percentage of 50% but a slightly higher factor of 3 percentage of 87% relative to the AIC-selected model (Supporting Information, Table S4).
Model residuals (Equation 3) were used as an additional metric of performance. Residuals were not homogenous across the entire range of observed and predicted toxicity (Supporting Information, Figures S2–S6), with residual slope directionality (i.e., positive, negative) for residuals versus observed ECx tending to be positive at all effect levels. This suggests that there may be a bias in the MLRs leading to underprediction of EC values at higher EC values, which in turn results in overprediction of toxicity. This trend was not observed for residuals versus TMFs (Supporting Information, Figures S2–S6), indicating that the models were accurately capturing the effects of each TMF. Interestingly, the same trend in residuals versus observed ECx was reported by DeForest et al. (2023).
Patterns in model residuals versus TMFs were generally consistent between models with and without interaction terms, except for the EC10 models (Supporting Information, Figure S2). Differences were particularly strong for EC10 DOC residuals, where the model with interaction terms had a slope of 0.0, while the model without interaction terms had a slope of –0.36. This indicates that at increased concentrations of DOC there was a bias to underpredict toxicity, attributing too great a protective effect to the DOC.
Final MLR models
For EC10 and EC20 model comparisons, where models with and without interaction terms were considered, MPS values were consistently higher when interactive terms were included. The MPS values for models with interaction terms were higher than those for models without interactive terms for MPS using a factor of 2 or a factor of 3 percentage score (Supporting Information, Table S4). Based on the higher MPS value, both the EC10 and EC20 models with interaction terms were selected for further independent validation.
The AIC-selected EC50 model (with or without interaction terms because they were the same; Table 1), using the subset data, had the highest MPS and was selected for further independent validation. All full data set EC50 models provided the same terms and coefficients and therefore the same MPS value; as such, this model was carried through for independent validation.
The models selected are shown below (Equations 66-9), with ECx values expressed in micrograms per liter and DOC and hardness expressed in milligrams per liter.
Independent validation using natural waters
Test acceptability
Test acceptability criteria for ecotoxicology tests with zinc-spiked natural waters were achieved (data provided in Supporting Information). Several unbuffered water tests had slightly higher pH variability compared to buffered tests and were above the desired ±0.1 unit pH change, with Limestone Creek (unbuffered) and Magela Creek (unbuffered) having a ±0.2 pH variation and Teatree Creek having ±0.3 variation in pH over the test duration. This is still considered very low for chronic algal studies, and the data were included in the validation analysis. Further test acceptability data are provided in the Supporting Information.
Measured toxicity
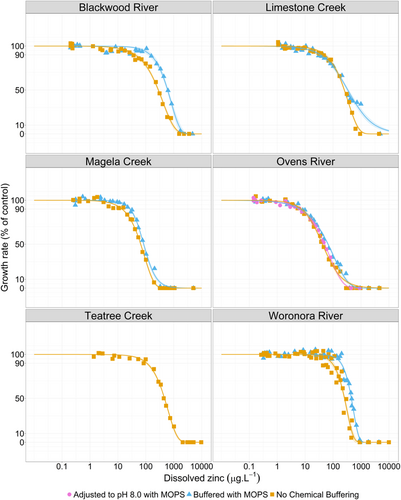
Zinc was toxic to Chlorella sp. in all zinc-spiked natural waters tested (Figure 3), with EC10 values ranging from 6.3 to 193 µg L–1 and EC50 values ranging from 42 to 603 µg L–1 (Table 2). Control growth rates were consistent across buffered and unbuffered tests, with differences being small between EC10 values and larger for EC50 values. Where larger differences in toxicity between buffered and unbuffered tests were observed (i.e., Blackwood River and Woronora River), the unbuffered tests were consistently more toxic. This was likely attributable to the increase in pH in the unbuffered tests in the 24-h preequilibration period, which is consistent with findings by Price et al. (2021), who showed that the toxicity of zinc to this Chlorella sp. strain increased with increasing pH. Similar conclusions around the influence of organic buffers on zinc toxicity were found by DeForest et al. (2023) when preparing data sources for MLR development. Based on this, buffered and unbuffered tests were pooled for independent validation. All toxicity data from the natural water testing is provided in Supporting Information, Table S5.
| Water | pH | DOC (mg L–1) | Hardness (mg L–1) | EC10 (µg L–1) | EC20 (µg L–1) | EC50 (µg L–1) |
|---|---|---|---|---|---|---|
| Blackwood River buffered | 8.05 (±0.04) | 4.2 | 355 | 145 (111–179) | 256 (216–295) | 603 (553–652) |
| Blackwood River unbuffered | 8.2 (±0.1) | 4.2 | 355 | 42 (34–50) | 89 (78–101) | 280 (260–299) |
| Limestone Creek buffered | 7.42 (±0.02) | 20 | 89 | 35 (27–43) | 81 (68–94) | 337 (299–374) |
| Limestone Creek unbuffered | 8.0 (±0.2) | 20 | 89 | 51 (42–60) | 96 (85–108) | 254 (238–269) |
| Magela Creek buffered | 6.38 (±0.03) | 6.0 | 3 | 27 (24–30) | 41 (38–44) | 84 (79–89) |
| Magela Creek unbuffered | 6.7 (±0.2) | 6.0 | 3 | 14 (12–16) | 26 (24–28) | 66 (63–69) |
| Ovens River buffered | 7.47 (±0.02) | <1 | 11 | 6.6 (5.3–7.9) | 16 (14–19) | 66 (61–71) |
| Ovens River unbuffered | 7.7 (±0.1) | <1 | 11 | 7.4 (6.1–8.7) | 14 (12–16) | 42 (39–45) |
| Ovens River (pH-adjusted) buffered | 8.01 (±0.02) | <1 | 11 | 6.3 (5.5–7.0) | 14 (13–15) | 50 (48–52) |
| Teatree Creek Unbuffered | 6.1 (±0.3) | 25 | 13 | 109 (93–124) | 194 (176–213) | 467 (445–489) |
| Woronora River buffered | 7.11 (±0.02) | 5.3 | 18 | 193 (172–213) | 271 (251–290) | 452 (433–470) |
| Woronora River unbuffered | 7.4 (±0.1) | 5.3 | 18 | 92 (75–109) | 139 (121–156) | 257 (238–276) |
- Summary of water chemistry and toxicity of zinc; pH is test average ± standard deviation; 95% confidence intervals are shown in parentheses.
- DOC = dissolved organic carbon; EC10/20/50 = 10%, 20%, and 50% effective concentrations, respectively.
Ovens River tests showed the lowest ECx values at all effect levels, and this was expected given that there was no measurable DOC, low hardness (11 mg CaCO3 L–1), and high pH (7.47; relative to other waters tested). However, the increased pH in the adjusted Ovens River test did not increase toxicity at any effect level as expected based on pH terms and the coefficient in the MLR models. Magela Creek tests had the second lowest ECx values at all effect levels, despite having a low pH (6.4–6.7) and moderate DOC concentration (6.0 mg L–1); however, this water did have very low hardness (3 mg CaCO3 L–1 at the time of testing). These results suggest that low hardness may lead to increased zinc toxicity, and this is in general agreement with the inclusion of a hardness term in each MLR model.
In agreement with this were the relatively high ECx values in Blackwood River, which had a high hardness of 355 mg CaCO3 L–1, moderate DOC concentration (4.2 mg C L–1), and high pH (8.0–8.2). While Teatree Creek had a relatively low hardness of 13 mg CaCO3 L–1, the relatively high ECx values are likely explained by its high DOC concentration of 25 mg L–1.
Woronora River results were contrary to the expected results based on this hardness dependency. With a low hardness of 18 mg CaCO3 L–1, moderate DOC concentration of 5.3 mg L–1, and a moderate pH of 7.1 to 7.4, toxicity was expected to be relatively high. However, the Woronora River buffered test had the highest EC10 and EC20 values (193 and 271 µg L–1, respectively) and the second highest EC50 value (467 µg L–1). In addition to these contrasting results based on water chemistry, the relative magnitude of ECx values at all effect levels differed between the natural water results and the synthetic water results from the data sources for MLR development. Zinc EC10 values ranged from 6 to 193 µg L–1 in the natural waters, higher than EC10 values of 0.8 to 5 µg L–1 in synthetic water; EC20 values ranged from 14 to 271 µg L–1 in the natural waters compared to 2 to 19 µg L–1 in synthetic water, and EC50 values ranged from 42 to 603 µg L–1 in the natural waters compared to 18 to 185 µg L–1 in synthetic water.
Predicted toxicity
In addition to the MLR models developed for Chlorella sp. in the present study, other models have previously been developed for R. subcapitata, a different species of green microalga. These models (Table 3) were assessed for their suitability for predicting Chlorella sp. toxicity in natural Australian freshwaters and to assess the suitability of cross-species models for microalgae.
| Slope | |||||||
|---|---|---|---|---|---|---|---|
| Species | Model reference | Effect level | Intercept | pH | ln(Hard) | ln(DOC) | ln(DOC) × pH |
| Chlorella sp. | Current study | EC10 | 0.16 | −0.055 | 0.288 | −2.137 | 0.302 |
| EC20 | 0.189 | −0.009 | 0.432 | −2.114 | 0.289 | ||
| EC50 | 1.17 | – | 0.628 | – | – | ||
| EC50a | 3.97 | −0.359 | 0.673 | 0.351 | – | ||
| Raphidocelis subcapitata | Canadian Council of Ministers of the Environment (2018) | EC50 | 11.8 | −1.122 | – | n/e | n/e |
| Stauber et al. (2023) | EC50 | 8.28 | −0.75 | 0.296 | 0.468 | – | |
| DeForest et al. (2023) | EC10 | 10.307 | −0.992 | – | 0.378 | – | |
| DeForest et al. (2023) | EC20 | 11.950 | −1.172 | – | 0.342 | – | |
| DeForest et al. (2023) | EC50 | 10.925 | −0.865 | – | 0.209 | – | |
- a Subset model.
- DOC = dissolved organic carbon; EC10/20/50 = 10%, 20%, and 50% effective concentrations, respectively; Hard = hardness; n/e = not evaluated because of insufficient data; – = term not retained in stepwise regression analysis.
Chlorella sp. MLRs
The developed Chlorella sp. MLRs (Table 3) performed poorly at predicting toxicity in the natural waters. The EC10 and EC20 models consistently overpredicted zinc toxicity, predicting 0% of the data within a factor of 2 or 3 (Figure 4). Both EC50 models also predicted natural water toxicity poorly, where the full data set (n = 30) model predicted 0% and 17% of data within a factor of 2 and 3, respectively. The subset data (n = 18) EC50 model predicted 25% and 33% of data within a factor of 2 and 3, respectively.
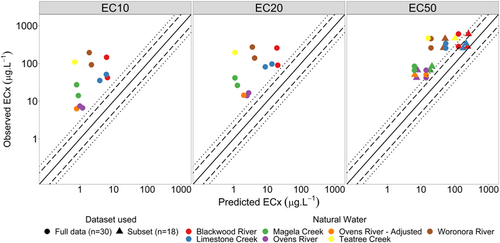
Given that all models consistently overpredicted toxicity, sensitivity coefficients (y-intercept) were recalibrated using the natural waters’ zinc toxicity data according to methods outlined by Peters et al. (2021). Observed versus predicted plots with original and updated sensitivity coefficients are shown in Figures 4 and 5, respectively; and revised coefficient values are provided in Supporting Information, Table S7.
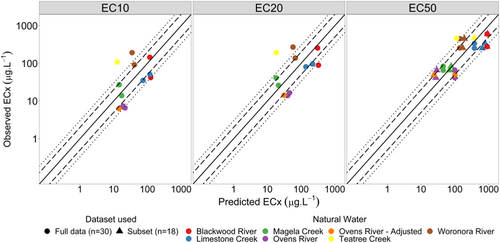
The recalibrated models provided an improved fit to the data, with both the revised EC10 and EC20 models predicting 25% and 75% of data within a factor of 2 and 3, respectively. Both EC50 models were also improved, with the full data set model predicting 58% and 75% of data within a factor of 2 and 3, respectively. The subset data model predicted 50% and 92% of data within a factor of 2 and 3, respectively. Model residual plots with original and updated sensitivity coefficients are provided in Supporting Information, Figures S7–S14.
While recalibrated sensitivity coefficients did improve the models, it is important to note that this recalibration procedure is typically used for cross-species validation methods (Peters et al., 2021) or when it is believed that the sensitivity of cultures has significantly shifted with time (Van Regenmortel et al., 2017). Based on the consistency of reference toxicant tests used during the current study, shifts in culture sensitivity are unlikely to explain this consistent overprediction in toxicity to Chlorella sp. in the Australian natural waters.
An unaccounted for TMF(s) may be present across all natural waters, causing this consistent overprediction in toxicity. Calcium and magnesium ratios, which are known to be different from those in the Northern Hemisphere (Peters et al., 2021), as a contributor to the overprediction were considered, as were concentrations of sodium, aluminum, iron, and manganese, all of which are known to modify metal speciation. Ratios and concentrations are provided in Supporting Information, Table S8. However, there were no consistent trends in the calcium and magnesium ratios among the natural waters, nor were there any consistently elevated concentrations of the four metals listed above.
Elevated control growth rates in natural water testing relative to the concurrently run reference toxicant tests in synthetic media suggested that nutrient levels may be influencing toxicity. Control growth rates in natural waters ranged from 2.1 to 2.5 doublings per day compared to 1.7 doublings per day in the reference tests. A broad suite of nutrients (i.e., NH3, NO2, NO3, phosphorus, etc.) were analyzed for each natural water prior to testing, to ensure that levels were consistently low. All analytes were consistently below the limit of detection or near the limit of detection (Supporting Information, Table S8) except Limestone Creek water, which had slightly elevated ammonia (0.16 mg L–1) and total nitrogen (1 mg L–1). The highest total phosphorus concentration was 0.04 mg L–1 in Teatree Creek. However, it is important to note that all tests including those in natural waters and those used to develop the MLR models were supplemented with nitrogen and phosphorus at the start of each toxicity test, as part of standard toxicity testing protocols (Organisation for Economic Co-operation and Development, 2011). Final concentrations of supplemental NO3– and PO43− were 1.5 and 0.15 mg L–1, respectively. Therefore, nutrient exposure concentrations for the microalgae were generally consistent across all tests, both natural water and synthetic, and do not explain the relative change in toxicity observed, nor do they likely explain the elevated control growth rates. Iron is also a microalgal micronutrient and, as mentioned above, can modify metal speciation. While dissolved concentrations of iron varied (7–500 µg L–1; Supporting Information, Table S8) in the natural waters, there were no consistent trends that could explain the change in observed toxicity.
Alternatively, rather than the presence of an unidentified TMF or zinc complexing agent, there may be something present in the natural waters that alters the physiology of the microalgae which indirectly affects zinc toxicity, such as by a change in mechanism of toxicity. Such physiological changes may be changes in cell membrane permeability (Wood et al., 2011). Further experimental work is required to test this hypothesis.
Another possible explanation for the overprediction is the underlying assumption that models using zinc toxicity-modifying relationships derived from synthetic laboratory test waters can be directly applied to natural water samples. Natural waters typically contain a more complex matrix than synthetic laboratory waters, and therefore, the presence of unknown TMFs may be ameliorating zinc toxicity (as seen by the overprediction of toxicity by the models). The current study is the third study to develop a microalgal MLR solely from synthetic laboratory water toxicity data (Brix et al., 2023; DeForest et al., 2018) and the first to independently validate the developed MLRs with natural waters. Further research into the suitability of applying synthetic laboratory water–based models to a greater range of natural waters, which potentially include a range of biotic TMFs, is clearly needed.
Comparison to preexisting MLR models
The MLR models developed for R. subcapitata were updated to include Chlorella sp.–specific sensitivity coefficients (Peters et al., 2021). The R. subcapitata models generally provided a better fit than the Chlorella sp. model (with original sensitivity coefficients) for all effect levels and were comparable to the Chlorella sp. model with updated sensitivity coefficients (Figure 6). The DeForest et al. (2023) EC10 model predicted 42% and 67% of data within a factor of 2 and 3, respectively; and the EC20 model predicted 50% and 75% of data with a factor of 2 and 3, respectively. Of the three EC50 models, the CCME (2018) MLR performed the poorest for both factor of 2 and factor of 3 predictions, with 33% and 58%, respectively. The Stauber et al. (2023) and DeForest et al. (2023) EC50 models performed similarly, with 50% and 83% and with 67% and 75% of data predicted within a factor of 2 and 3, respectively.
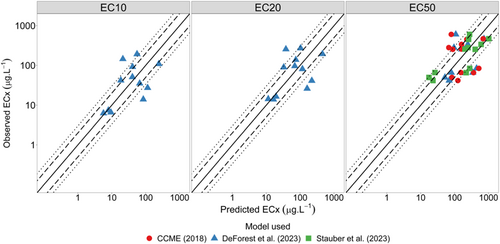
Residual analysis of all R. subcapitata models found general biases across all models. The EC10 and EC20 models by DeForest et al. (2023) had low residual bias when plotted against DOC, with slopes of −0.031 and −0.043, respectively. The DeForest et al. (2023) EC50 model had a slightly larger model bias when plotted against DOC, with a slope of −0.28. The CCME (2018) EC50 model had biased slopes for all three TMFs (DOC = 0.21, hardness = 0.72, pH = 1.1), while the Stauber et al. (2023) EC50 model had low residual bias for DOC, with a slope of 0.045 (Supporting Information, Figures S15–S17).
Peters et al. (2021) recommended acceptability criteria requiring 50% of data to lie within a factor of 2 and 90% of data within a factor 3. Based on these criteria, none of the tested models would be deemed acceptable; however, both the Stauber et al. (2023) model and the EC20 and EC50 models by DeForest et al. (2023) would pass the 50% within a factor of 2 criterion.
This generally poor performance of the Chlorella sp. and R. subcapitata models during independent and cross-species validation using natural waters suggests that relative changes in zinc toxicity as a function of pH, hardness, and DOC may not be consistent across microalgal species and that these three TMFs might not be the only significant modifiers of toxicity in Australian natural waters.
Examples of cross-species validation of MLR models for microalgae are limited given that the majority of microalgal toxicity data use a single species (R. subcapitata), whereas cross-species comparisons are more common for invertebrates and fish because large toxicity data sets often exist for multiple species (Croteau et al., 2021; Peters et al., 2021). Peters et al. (2021) reported good cross-species validation using Chlorella sp. (different strain from present study) for R. subcapitata–derived nickel MLRs; however, the validation data set was small (n = 5), and the range of hardness values used was low.
CONCLUSION
Our study presents the first Chlorella sp. zinc toxicity MLR models and the first metal toxicity MLR models for microalgae using a development species other than R. subcapitata. It was highlighted that while developed models can perform well during autovalidation procedures, assessment of independent data sets using natural waters is critical for assessing the predictive power of MLRs.
The findings of the present study showed that zinc toxicity to algae is difficult to predict, even when using species-specific MLRs. Neither the Chlorella sp. MLRs nor the existing R. subcapitata model accurately predicted zinc toxicity to Chlorella sp. in Australian natural waters. Poor independent validation of the Chlorella sp. models also suggests that models derived from laboratory waters may not be suitable for predicting toxicity in far more complex matrices like natural waters, and further investigation is needed to elucidate this, such as expanding the natural water toxicity testing data set.
The present study is part of a larger investigation examining the applicability of a range of bioavailability models in Australian and New Zealand waters and is discussed in the companion paper (Stauber et al., 2023).
Supporting Information
The Supporting Information is available on the Wiley Online Library at https://doi.org/10.1002/etc.5749.
Acknowledgment
The present study was funded by the International Zinc Association and an Australian Government Research Training Program Scholarship for Gwilym Price. We thank Sarah Stone and Kitty McKnight for providing technical advice during method development and Anthony Evans, Ceiwen Pease, and Andrew Harford for assistance with sample collection and preparation.
Author Contributions Statement
Gwilym A. V. Price: Data curation; Formal analysis; Investigation; Methodology; Software; Visualization; Writing–original draft; Writing–review & editing. Jenny L. Stauber: Conceptualization; Investigation; Writing–review & editing; Supervision; Project Management; Funding acquisition. Dianne F. Jolley: Conceptualization; Investigation; Writing–review & editing; Supervision. Darren J. Koppel: Investigation; Writing–review & editing; Supervision. Eric J. Van Genderen: Conceptualization; Funding acquisition. Adam C. Ryan: Writing–review & editing; Funding acquisition. Aleicia Holland: Conceptualization; Investigation; Writing–review & editing; Supervision.
Open Research
Data Availability Statement
All raw and calculated data relating to the present study including development and validation toxicity data sets are included in the Supporting Information. If further information regarding coding used to conduct statistical analyses is needed, this can be made available on request to the corresponding author.




