A micelle inhibition model for the bioavailability of polycyclic aromatic hydrocarbons in aquatic systems
Abstract
A mathematical model was developed to quantify micelle suppression on the bioavailability of hydrophobic organic compounds in aquatic systems. The model was based on a three-compartment dynamic system in which the hydrophobic compounds are taken up and eliminated by organisms with an equilibrium partitioning between water and micelle. The model was validated against data obtained from in vitro studies of the bioaccumulation of naphthalene, anthracene, and chrysene into the gills of the freshwater mussel (Ellipto complanata) in the presence of a surfactant (Tween 80). The model predictions agreed well with the experimental results for all three chemicals. Sensitivity analyses were performed to examine model responses to the surfactant parameters. From the model, we derive an equation for a bioconcentration factor in aquatic surfactant systems to predict the maximum concentration of polycyclic aromatic hydrocarbons (PAHs) in aquatic organisms. From these results, we also propose a micelle inhibition factor for bioconcentration that is a function of the surfactant concentration, critical micelle concentration, and partition coefficient of hydrophobic compounds between water and micelle. Knowledge of these parameters may improve understanding of the partitioning of PAHs into organisms in the presence of surfactants.
INTRODUCTION
Polycyclic aromatic hydrocarbons (PAHs) are ubiquitous hydrophobic compounds found throughout air, soil, and aquatic systems. Because of the carcinogenic and mutagenic effects of some of their metabolites in some organisms, some are considered to be major pollutants in those three media [1]. In aquatic systems, the major sources of PAHs include atmospheric deposition of combustion particles, runoff from watershed, and petroleum spills. The fate and effect of PAHs in aquatic systems are mainly determined by low water solubility and high liphophilicity. The solubility of PAHs decreases with increasing molecular weight. Larger PAHs can be strongly sorbed to soot and other particles such that they are less available to organisms [2, 3]. The lipophilicity of higher-molecularweight PAHs, however, results in their accumulation in the fatty tissues of aquatic organisms [3].
Surfactants as well as dissolved organic matter play an important role in controlling the fate of the hydrophobic compounds in aquatic systems [4] as well as in aiding the bioremediation of contaminated soils and sediments [5, 6]. Application of surfactants to enhance aqueous concentrations of hydrophobic contaminants could affect the bioavailability of pollutants to microbial degradation. To the macroorganisms, however, the surfactants would suppress the bioavailability and, therefore, reduce the risk to aquatic ecosystems [7-10]. These various roles of surfactants indicate the potential for future applications in the remediation of aquatic ecosystems contaminated by hydrophobic compounds.
To examine the effect of surfactants on the bioavailability of hydrophobic compounds, bioaccumulation models that in- corporate major factors are very useful [11]. Several bioaccumulation models have been developed and used for prediction of toxicant effect in aquatic organisms [12]. At present, however, no mathematical model is available that incorporates the role of surfactants in bioaccumulation [13].
In the present study, we developed a bioaccumulation model for hydrophobic organic compounds in an aqueous surfactant system in which the micelle formation is correlated with the bioavailability of hydrophobic compounds. Micelles with fluorocarbon-like counterions are larger in size than those with metallic counterions. The developed model was validated with data obtained from the bioaccumulation of three PAHs (naphthalene, anthracene, and chrysene) in the gills of freshwater mussels in the presence of a surfactant (Tween 80) and was used to analyze the various roles of surfactants in bioavailability of PAHs to higher organisms in water systems. The PAHs used in the present study are classified as priority pollutants by the U.S. Environmental Protection Agency because of their mutagenic effects on aquatic organisms [14]. The surfactant Tween 80 was used in this work to mimic the presence of naturally occurring surfactant molecules that would affect the partitioning of PAHs in aquatic systems. Freshwater mussels are representative of a general lipid membrane and accumulate PAHs from the water column and not via ingestion. Thus, we examined the excised gills rather than the whole organism, because the gill tissue is the primary site of uptake, shows great sensitivity to poisons that contact their surface, and is the initial route of accumulation in the organism.
MATERIALS AND METHODS
Model development
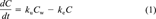 (1)
(1)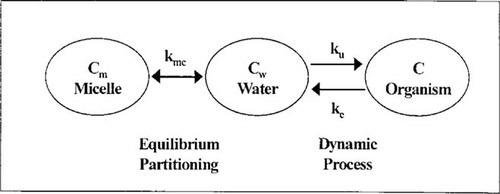
Schematic diagram of bioaccumulation in micelle-emulsified system. See Materials and Methods for definitions.
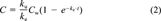 (2)
(2)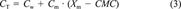 (3)
(3) (4)
(4)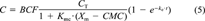 (5)
(5)| Naphthalene | Anthracene | Chrysene | |
|---|---|---|---|
| Molecular weight | 128.2 | 178.2 | 228.3 |
| No. of aromatic rings | 2 | 3 | 4 |
| Octanol-water partition coefficient (log Kow) | 3.37 | 4.54 | ∼5.0 |
| Concentration (μmole/L) | 100.0 | 100.0 | 1.0 |
| Micelle concentration (mg/L) | 200 | 200 | 200 |
Specimens and solutions
To validate this model, bioaccumulation experiments were performed with selected PAHs and the gills of freshwater mussels in micelle-emulsified systems. Freshwater mussels (Ellipto complanata) were obtained from Connecticut Valley Biological Supply (Southampton, MA, USA). Mussels were maintained at 18°C in aerated freshwater and allowed to acclimate for one week before use. The [14C]naphthalene, [14C]anthracene, and [14C]chrysene were obtained from Sigma (St. Louis, MO, USA). All unlabeled PAHs (naphthalene, anthracene, and chrysene) were obtained from Aldrich Chemical (Milwaukee, MI, USA). Stock solutions of PAHs were prepared by using dimethyl formamide as solvent. An aliquot (1.0 ml) of PAH solution was further diluted into 99 ml of Tween 80 (200 mg/L) to limit loss by volatilization and sorption to the container. The net experimental solution by volume contained approximately 1% (v/v) dimethyl formamide, 0.02% Tween 80 surfactant, and greater than 98% (v/v) distilled water.
Uptake experiments
For the uptake of naphthalene and anthracene, the experimental solution (100 ml) contained 10−4M of either compound (or 12.8 and 17.8 mg/L, respectively) of either compound or 10−6 M chrysene (0.228 mg/L), because of its solubility, plus the surfactant Tween 80 (200 mg/L) with a small amount (∼10−8 M) of the 14C-labeled radioactive tracer. A low concentration of the surfactant Tween 80 was used in our studies to simulate the presence of naturally occurring surfactant molecules that would be present in the aquatic environment and that would affect the partitioning behavior of hydrophobic compounds such as PAHs in this environment [18]. The chemical properties and experimental conditions are summarized in Table 1.
Before the experiments, excised gills (all of the gill) were incubated in distilled water and placed on a shaker table for 20 min to minimize the trauma (gills stay viable for a period of up to 4 h, as evidenced by their ciliary activity). The gills were then allowed to drain, were dried lightly on a paper towel, and were then placed in a closed container (capacity, 125 ml) containing 100 ml of the experimental solution. The container was then placed on a shaker table. Gills were removed from the solution at selected intervals of time (from 2–120 min), rinsed for a few seconds in a solution devoid of organics, and blotted dry on filter paper. At both 0 and 120 min, 1.0 ml of the experimental solution was withdrawn to calculate a mass balance of radioactivity and the quenching factor. The final concentrations of the 14C-labeled PAHs were on the order of 4,440 disintegrations per minute (DPM)/ml for naphthalene, 5,060 DPM/ml for anthracene, and 4,720 DPM/ml for chrysene. A control experiment indicated very little absorption of PAHs on the Teflonr̀ liner of the container. The gills were then placed in tared scintillation vials, covered with activated carbon filters obtained from VWR Scientific (Bridge Port, NJ, USA), dried overnight at 65°C, and weighed to the nearest 0.1 mg. Two milliliters of 0.1 M nitric acid were added to each dry gill tissue sample and allowed to stand for 4 h, after which 8 ml of scintillation fluid were added to each gill sample and incubated for at least 12 h. The carbon filters were necessary to ensure quantification of any surface-associated PAH that volatilized during drying and were treated in the manner described above. After incubation, the radioactivity of the vials and the carbon filters was counted in the Beckman liquid scintillation counter (model LS6500; Fullerton, CA, USA) and converted to micromoles per gram dry weight of sample using a known activity of the tracer/milliliter of solution and a known concentration of PAH in solution.
| Parametera | Naphthalene | Anthracene | Chrysene |
|---|---|---|---|
| BCFa (ml/g) | 1.6 × 103 | 2.1 × 103 | 2.6 × 103 |
| ke (1/h) | 3.5 | 2.0 | 1.5 |
| Kmc (L/kg) | 5.00 × 103 | 5.5 × 103 | 6.0 × 103 |
- a BCF = bioconcentration factor; ke = elimination rate constant; Kmc = partition coefficient.
For the uptake of PAHs in the absence of surfactant, the same procedure as described above was followed except that the experimental solution did not contain the surfactant Tween 80.
RESULTS AND DISCUSSION
 (6)
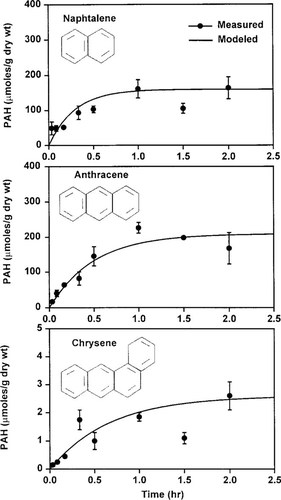
(6)Based on the calibrated values of BCF and ke, the model was applied to the bioaccumulation data obtained from the micelle emulsion system. Comparisons of model results to experimental data for each PAH are presented in Figure 3. Experimental data are displayed as maximum, mean, and minimum values of six measured points. Because the CMC value is 13 mg/L [15] and the Xm value is 200 mg/L for all chemicals, only Kmc values were calibrated based on the experimental data (Table 2). Figure 3 shows that the model results agree with the experimental data quite well (r2 = 0.86–0.92). From an examination of Figures Fig. 2., Fig. 3., better agreement is noted between the model results and the experimental data for the micelle-containing system (Fig. 3) than for the system containing no micelles. (Fig. 2). This can be attributed to the observation that the micelle appears to increase the solubility and affinity of the PAHs to the lipid component of the gill tissue.
Comparison of model predictions with experimental data in the absence of surfactant. PAH = polycyclic aromatic hydrocarbon. The error bars represent ± 1 SD of the mean.
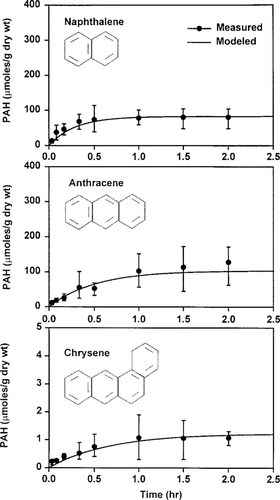
To examine the role of surfactants on the bioavailability of PAHs, model sensitivity analyses were performed by varying the model parameters BCF, Kmc, and Xm. Because BCF and Kmc are closely related to the lipophilicity of the chemicals, they can be presented as a function of the octanol-water partition coefficient (Kow), as shown in Figure 4. Utilizing the regression lines, the model responses were tested against Kow, and the results are presented in Figure 5a, in which differences in bioaccumulation between nonsurfactant and surfactant-containing systems are plotted. This figure shows that the role of surfactant as an inhibitor of bioaccumulation increases with the increase in Kow. The inhibition effects of surfactants on bioaccumulation nearly tripled with an increase in the log Kow from three to six and doubled with an increase from four to six, as shown in this figure.
The model was executed under various concentrations of surfactants (Fig. 5b). The input conditions for naphthalene in the absence of surfactants were used as the control conditions and acted as a reference case. As shown in this figure, the surfactant significantly lowers the amount of PAHs available to the mussels, even at low micelle concentration. At high micelle concentration, the rate of accumulation is quite low at the time of first exposure and quickly reaches steady state compared to the no-micelle condition.
Comparison of model predictions with experimental data in the presence of surfactant. PAH 5 polycyclic aromatic hydrocarbon. The error bars represent + 1 SDM.
Regression lines of bioconcentration factor (BCF) and partition coefficient.
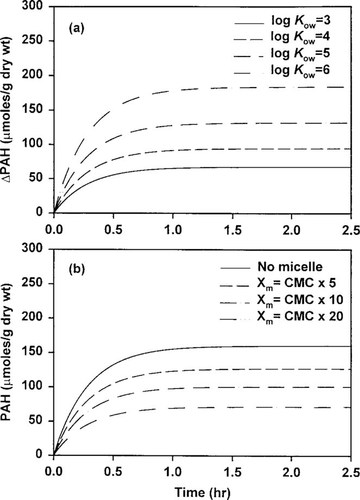
Results of sensitivity analyses: (a) effect of octanol-water partition coefficient (Kow) and (b) effect of surfactant concentration. CMC = critical micelle concentration; PAH = polycyclic aromatic hydrocarbon; Xm = concentration of micelles.
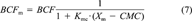 (7)
(7)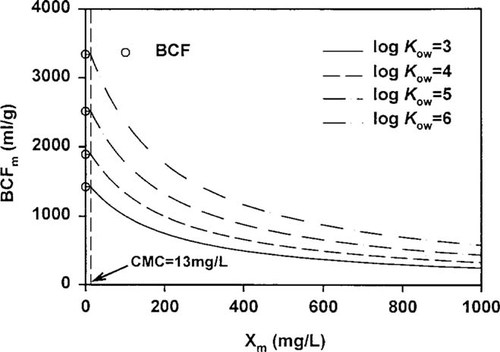
Changes of bioconcentration factor (BCF) in surfactant-containing system. BCFm = BCF with micelle; CMC = critical micelle concentration; Kow = octanol-water partition coefficient; Xm = concentration of micelles.
Acknowledgements
The authors wish to thank all who have contributed directly and/or indirectly through insightful discussions and reviews. Thanks to Jerry Kukor. This research was supported in part by Hatch/McIntire-Stenis Grants 07139 and 07149, the NJAES-Program Revitalization Initiatives, and by Korea Ministry of Science and Technology through the National Research Program (00-B-WB-06-A-02) for Women's University.




