Concentration-dependent kinetics of pollutant desorption from soils
Abstract
Sorption-desorption kinetics play a major role in transport and bioavailability of pollutants in soils. Contaminant concentration is a potentially important factor controlling kinetics. A previous paper dealt with the effect of solute concentration on fractional uptake rates of phenanthrene and pyrene from a finite aqueous source. In this study we determined the effect of initial phenanthrene sorbed concentration (q0) on the fractional mass desorption rates from each of six soils to a zero-concentration solution, approximated by including a polymer adsorbent (Tenax™) as a third-phase sink. The soils were preequilibrated with phenanthrene for 180 d. Consistent with theory, the fractional desorption rates determined by empirical curve fitting increased with q0 provided the isotherm was nonlinear. After 500 to 600 d of desorption at the steepest possible concentration gradient, all soils retained a highly resistant fraction, which ranged from 4 to 31% of q0, except for one soil at a high q0. The highly resistant fraction decreased with increasing q0 for nonlinear isotherm cases, but increased with q0 for linear or nearly linear isotherm cases. Application of a nonlinear diffusion model, the dual-mode diffusion model (DMDM), to the nonresistant fraction gave reasonably good fits. The DMDM attributes the increase with concentration of the apparent diffusivity to a decrease in the proportion of sorbate occupying immobile sites (holes) in soil organic matter. The concentration-dependent term in the expression for the apparent diffusivity correlated with either of two indices that reflect the linearity of the sorption isotherm. Bunker C oil present in one soil acted as a partition domain. The findings of this study are consistent with heterogeneous models of soil organic matter, and indicate that concentration effects should be taken into account whenever desorption rate is important.
INTRODUCTION
The transport and bioavailability of organic compounds in soil or sediment are often controlled by their rates of sorption and desorption [1-5]. This is especially true for large and hydrophobic compounds such as polycyclic aromatic hydrocarbons (PAHs). Understanding the conditions that govern sorption and desorption rates is crucial for predicting the fate and toxicity of contaminants and may be helpful in assigning mechanisms for hindered intraparticle diffusion.
A potentially important condition influencing sorption or desorption rates is the contaminant concentration. Although the absolute rate (mass taken up or released per unit time) obviously ordinarily increases with concentration, the question here is whether the fractional rate (fraction of total initial mass taken up or released per unit time) is concentration-dependent. Compounds that have a linear sorption isotherm in a sorbent are expected to show fractional sorption and desorption rate curves that are coincident and concentration-independent [6]. But such symmetry is not expected to hold when the isotherm is nonlinear [7]. Nonlinear isotherms in natural solids are typically concave-down to the solute concentration axis. For such systems, the apparent diffusivity of the sorbate is expected to increase with absolute concentration, reflecting a corresponding decline in the affinity of the sorbate for the solid [7]. Therefore, the fractional sorption or desorption rate is predicted to increase with absolute concentration [7].
Although predicted by theory, the demonstration of a concentration effect on kinetics in geosorbents heretofore has been ambiguous and in some cases has been challenged [8]. Braida et al. [8] described new experiments on the influence of initial solute concentration on phenanthrene or pyrene uptake rates in various soils. They found that when the isotherm is nonlinear, a concentration effect exists in the direction expected from theory. However, they showed that the observed effect is often small when, as is commonly the case, the experiment is carried out at constant soil to water ratio in a solution of finite source. This is due to an opposing effect called the shrinking gradient effect that is operative under such conditions. The shrinking gradient effect applies to compounds that sorb nonlinearly. The shrinking gradient effect is due to the decreasing fraction of total chemical finally taken up by the solid with increasing solute concentration because of the nonlinearity of the isotherm; as this fraction declines, the normalized rate also declines, regardless of other effects, as a result of the changing gradient driving force [7]. The conclusion was made that the conflicting results in the literature on the question of concentration-dependent uptake kinetics was likely the result of these two opposing effects on observed rates. Braida et al. [8] proposed simple models to computationally place upper and lower bounds on the shrinking gradient component so as to isolate the intrinsic concentration-dependence of sorption kinetics.
The present study focuses on the concentration-dependence of desorption and is an extension of the first study by Braida et al. [8] and White et al. [9]. To date, little information apparently is available on the effect of concentration on fractional desorption rates. Schlebaum et al. [10] observed faster pentachlorobenzene desorption from soil after sorbing at the higher of two initial solute concentrations, but maintained that the effect was due to the system having been closer to equilibrium at the higher concentration before the desorption step. Johnson et al. [11] observed concentration-dependent rates of release; however, their study was focused on a comparison of six empirical models in fitting the experimental data and not on explaining the source of the concentration effect. In the present study, fractional phenanthrene desorption rates at different concentrations from each of five soils (and one modified soil) were measured and compared independently of any model. An empirical approach is necessary to avoid bias by the choice of a particular model, because no consensus has been reached among researchers about the most appropriate model for sorption and desorption of hydrophobic chemicals to and from natural particles. Desorption commenced after an uptake period of 180 d, by which time equilibrium was assumed to be achieved, or closely approached, in all soils. Desorption was carried out to a solution at infinite dilution, which was approximated by including a third-phase sink, Tenax™ polymeric beads (Supelco, Bellefonte, PA, USA). This eliminates the opposing shrinking gradient effect seen for uptake rates, allowing an assessment of whether intrinsic concentration effects exist. This study also permits a determination of the effect of initial concentration on the magnitude of a highly resistant sorbed fraction, which formed in all soils tested.
MATERIALS AND METHODS
Materials
The soils and their organic carbon (OC) contents (g/100 g dry wt basis) were Cheshire (CT, USA) fine sandy loam (1.4), Pahokee (FL, USA) (43.9), Seal Beach (CA, USA) (1.5), Mount Pleasant silt loam (NY, USA) (4.5), and Port Hueneme (CA, USA) (0.62). The source and additional physical properties of each soil are given elsewhere [3, 8, 12, 13]. Because Seal Beach soil was known to be heavily contaminated with Bunker C oil, a modified Seal Beach soil was prepared by extracting Seal Beach soil with pentane [8] to address the potential effects of this oil contamination. Modified Seal Beach soil has 0.74 g of OC per 100 g soil. All soils were air dried, sieved through a 0.5- or 2-mm sieve, and sterilized by gamma irradiation [14]. [9-14C]Phenanthrene (>98%, 46.9 mCi/mmol) and unlabeled phenanthrene were purchased from Sigma Chemical (St. Louis, MO, USA). The aqueous phase for all experiments was an inorganic salts solution at pH 7.1 [14] containing NaN3 (0.2 g/L) to inhibit aerobic degradation.
Desorption kinetics
Uptake curves of phenanthrene in the listed soils have been given elsewhere [8]. After 180 d of sorption, sample vials were centrifuged as described in that study [8] and 60 to 90% of the supernatant liquid was discarded. The remaining suspension was transferred to a 30-ml crimp-cap separatory funnel with a Teflonr̀ stopcock (Fisher Scientific, Pittsburgh, PA, USA) or a 60-ml vial with Teflon-lined closure (Fisher Scientific), and the discarded supernatant was replaced. The replacement fluid consisted of the supernatant from a PAH-free soil suspension prepared at the same soil to water ratio as used in the individual sorption experiments and equilibrated for 60 to 90 d. This was done to ensure continuity in water chemistry (colloids, ions, pH, and so on) between the sorption and desorption stages of the experiment. Each vessel was amended with 200 mg of Tenax (20/35 mesh), which serves as an infinite sink for phenanthrene [15, 16]. This amount of Tenax corresponded to 15 to 80 times the mass of soil organic matter (SOM). Kinetic studies (D. Zhao, J.J. Pignatello, unpublished data) have confirmed that phenanthrene concentrations reach and are maintained at undetectable levels within minutes at the employed Tenax to water ratios.
The vessels were mixed end-over-end at 21 ± 0.2°C. At timed intervals, the soil was transferred to new vessels containing fresh Tenax and desorption was continued. Acetonitrile was used to rinse the previous portion of Tenax into a vial, which was placed on a rotary shaker at 21°C for 16 h. An aliquot of the extract was then assayed for radioactivity. For desorption experiments conducted in 60-ml vials, the vials were centrifuged at 1,350 to 2,200 rpm, depending on the soil, and the Tenax (which floats) was removed with a spatula. Fresh Tenax was added to each vial and shaking was continued. The Tenax was extracted as above. The amount desorbed from the soil at each time was calculated from the initial amount sorbed and the cumulative amount taken up by the Tenax.
At the end of desorption, selected samples were separated from the final Tenax portion and extracted with methanol at 70°C for 4 h. The total 14C recovery from the soil and all Tenax portions was 96 ± 8 % (average of 18 vials). For 8 of the 18 methanol extracts, phenanthrene was phase-transferred to hexane containing naphthalene as internal standard and its concentration was determined by gas chromatography with a Supelco PTE 5™ column and a flame ionization detector. The resistant fraction calculated on the basis of gas chromatography analysis was always higher than that calculated on the basis of scintillation counting (by a factor ranging from 1.1 to 2.8). Although the reason for the disagreement is unclear, the conclusion can be made that the resistant fraction is phenanthrene itself and not degradation products.
RESULTS AND DISCUSSION
Isotherms
Representative examples of 180-d phenanthrene sorption isotherms are shown in Figure 1. These data were obtained in a previous study [8]. The concentration-dependence of desorption should be related to a parameter that expresses the degree of linearity of the isotherm. The uptake data for the isotherms previously obtained were fit in this study to two models from which indices of linearity can be obtained. Fits to these models are included in Figure 1 and model parameters for all soils are listed in Table 1.
 (1)
(1)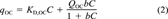 (2)
(2)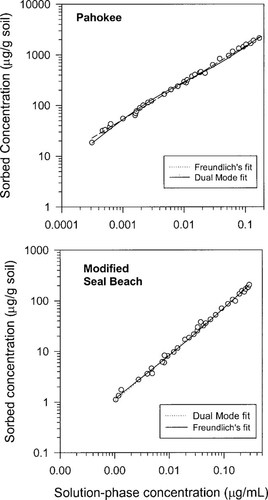
Phenathrene uptake isotherms after 180 d of equilibration for Pahokee (FL, USA) and modified Seal Beach (CA, USA) soils along with dual-mode and Freundlich model fits. Sorbed concentration is based on whole soil dry weight.
 ) and hole domain (f
) and hole domain (f ) are
) are
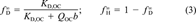 (3)
(3)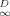 , ranging from 0 to 1, may be taken as an index of linearity. Values of f
, ranging from 0 to 1, may be taken as an index of linearity. Values of f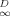 are included in Table 1.
are included in Table 1.One can see that f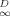 and N correlate. This correlation is evaluated later. Regardless of which index is used, the degree of linearity of phenanthrene sorption in soils follows the order Pahokee ∼ Mount Pleasant < Cheshire < modified Seal Beach ∼ Port Hueneme < Seal Beach (linear). Because Mount Pleasant has much less OC than Pahokee, one can see that nonlinearity is not necessarily related to OC content.
and N correlate. This correlation is evaluated later. Regardless of which index is used, the degree of linearity of phenanthrene sorption in soils follows the order Pahokee ∼ Mount Pleasant < Cheshire < modified Seal Beach ∼ Port Hueneme < Seal Beach (linear). Because Mount Pleasant has much less OC than Pahokee, one can see that nonlinearity is not necessarily related to OC content.
Kinetics
Desorption of phenanthrene in the presence of Tenax was followed in each of the soils at selected high and low initial absolute sorbed concentrations after the 180-d sorption period. The desorption curves are plotted in Figure 2. Sorbed concentrations are normalized to the initial value, q0.
Empirical analysis of concentration-dependent rates. The first objective was to evaluate concentration-dependent kinetics empirically to avoid bias that might occur through the choice of a kinetic model based on a particular mechanism. A consensus on the most appropriate model for uptake of contaminants by soils and sediments has so far been lacking.
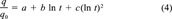 (4)
(4)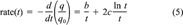 (5)
(5)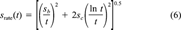 (6)
(6)| Soil | Solute concn. range (μg/ml | n | log KF,OC (μg/g OC)-(μg/ml)−n | KD,OC (ml/g OC) | QOC (μg/g OC) | b (ml/μg) | f |
|---|---|---|---|---|---|---|---|
| Pahokee (FL, USA) | 0.0003–0.181 | 0.72 | 4.3 | 26,788 | 617 | 179 | 0.196 |
| Mt. Pleasant (NY, USA) | 0.001–0.686 | 0.73 | 3.9 | 9,689 | 564 | 65.9 | 0.209 |
| Cheshire (CT, USA) | 0.002–0.769 | 0.79 | 4.2 | 16,786 | 736 | 55 | 0.293 |
| Port Hueneme (CA, USA) | 0.001–0.455 | 0.91 | 4.7 | 52,903 | 226 | 218 | 0.518 |
| Modified Seal Beach (CA, USA) | 0.001–0.290 | 0.92 | 4.9 | 95,270 | 216 | 378 | 0.538 |
| Seal Beach (CA, USA) | 0.002–0.312 | 1.0 | 4.9b | 73,133b | ∼0 | ∼0 | ∼1 |
- a Data from Braida et al. [8].
- b Values are based on organic carbon (OC) content from both natural organic matter and Bunker C oil.

Effect of initial sorbed concentration on the desorption of phenanthrene from soils. Curves represent best fit to Equation 4. Phenanthrene concentrations in the legend are based on the organic carbon content of the soil (including Bunker C oil in the case of Seal Beach [CA, USA]). Regression r2 and standard error of estimate are as follows: Pahokee (FL, USA) 4,100 (0.988, 1.8), Pahokee 250 (0.964, 3.0), Mount Pleasant (NY, USA) 4,900 (0.806, 4.1), Mount Pleasant 280 (0.989, 1.6), Cheshire (CT, USA) 13,000 (0.915, 2.3), Cheshire 2,000 (0.901, 3.5), Cheshire 160 (0.986, 1.6), Seal Beach (CA, USA) 25,000 (0.147, 7.6), Seal Beach 240 (0.765, 1.4), modified Seal Beach 25,000 (0.947, 2.1), modified Seal Beach 530 (0.998, 0.5), Port Hueneme (CA, USA) 21,000 (0.995, 0.9), and Port Hueneme 980 (0.996, 2.8).
The fitted curves according to Equation 4 are displayed in Figure 2, where it can be seen that the fits in most cases are good; this is indicated by the high r2 values and low standard errors (legend to Fig. 2). A notable exception is Seal Beach at 25,000 μg/g OC, where replicate data inexplicably showed wide variation. The time-zero datum and final datum in each data set were not included in the regression; therefore, the interpretation of the results is limited to the range of included data.
The fractional rates as a function of percent remaining sorbed, together with error bars at selected points representing ±Srate(t), are presented in Figure 3. Examination of the results shows that the effect of initial absolute phenanthrene concentration on fractional desorption rate is inversely related to the degree of linearity in the isotherm. For soils in which the isotherm is nonlinear (Pahokee, Mount Pleasant, and Cheshire), desorption at the highest concentration is relatively faster than desorption at the lowest concentration. For two of the three soils in which the isotherm is linear or nearly linear (modified Seal Beach and Port Hueneme), desorption is significantly unaffected by concentration, even for very high differences in the initial phenanthrene loading. For the third soil in which the isotherm is linear (Seal Beach), the results are inconclusive principally because of the large errors in the rate for the high concentration case (see the high degree of scatter in those data, Fig. 2). Cheshire soil, with intermediate indices of linearity, shows a significant difference in fractional rate between 160 and 2,000 or 13,000 μg/g OC, but no significant difference in fractional rate between the two higher concentrations.
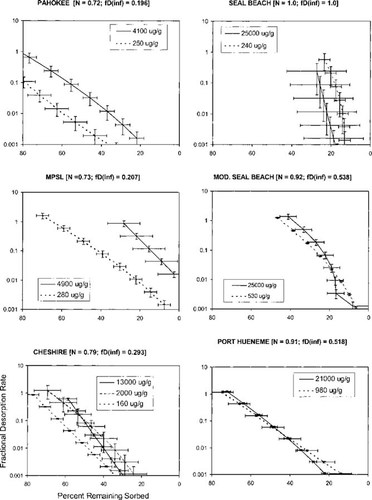
Resistant fraction. With only one exception, a substantial fraction of phenanthrene (4–31% of initial) strongly resisted desorption in the presence of the infinite sink by the end of the desorption period, which lasted up to 606 d (Fig. 4, which replots data from Fig. 2). The exception is Mount Pleasant soil; in this soil, desorption appeared to be complete after 30 d at the higher of the two concentrations, whereas a 4% resistant fraction remained after 566 d at the lower concentration. As will be discussed later, this may be due to the modification of the SOM by high concentrations of sorbate. Calculations based on the isotherm of phenanthrene in Tenax (D. Zhao, J.J. Pignatello, unpublished data) show that in the last desorption step, the hypothetical soil concentrations in equilibrium with the Tenax and the aqueous phase is three orders of magnitude or more smaller than the actual soil concentrations. This clearly indicates that the resistant fraction arises from a rate limitation.
Previous studies have shown that the fraction resistant to exhaustive aqueous extraction is inversely concentration-dependent. An inverse relationship between initial or applied concentration and resistant fraction was found for tetrachloroethene, trichloroethene, and 1,2-dibromo-3-chloropropane in the Cheshire soil [12] and for trichloroethene in various model and natural porous materials [20]. In the latter cases [20], the authors concluded that the resistant fraction is related qualitatively to the inverse value of the Freundlich N.
The results of the present study confirm the trend toward decreasing resistant fraction with increasing initial sorbed concentration for nonlinear cases, but indicate that as the isotherm tends toward linearity, this concentration dependence may even reverse. For soils in which isotherm nonlinearity is relatively high (Pahokee and Mount Pleasant) the resistant fraction is inversely related to initial sorbed concentration. For soils in which nonlinearity is relatively low (Seal Beach, modified Seal Beach, and Port Hueneme), the relationship does not vanish but rather is reversed and the resistant fraction is greater for the higher concentration. Cheshire soil, with an intermediate degree of nonlinearity, shows decreasing resistant fraction between 160 and 2,000 μg/g OC, then increasing resistant fraction between 2,000 and 13,000 μg/g OC.
Application of a nonlinear mechanistic kinetic model. Having demonstrated concentration-dependent desorption kinetics empirically, we now wish to test the applicability of a nonlinear radial diffusion model based on the DMM that was developed earlier [19]. The dual-mode diffusion model (DMDM) assumes Fickian diffusion of molecules in the dis-solution domain and immobilization of molecules in the holes of natural organic matter.
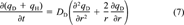 (7)
(7)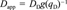
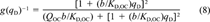 (8)
(8)The DMDM was solved numerically by using the same algorithms as used by Zhao et al. [19] except for the following modifications. The boundary condition was modified to accommodate the presence of the infinite sink Tenax by assuming zero solution-phase phenanthrene at all times. A desorption-resistant fraction, Fr, was introduced to account for the amount of phenanthrene that remains sorbed after several months of desorption. The assumption was made that Fr is governed by a different diffusivity or a different rate law. The value of Fr, which for each soil was chosen as the concentration remaining at the last experimental point, was subtracted from all data before application of the model. Fits of the data by the DMDM without subtracting Fr (not shown) were poor.
The sole fitting parameter of the DMDM is the diffusion rate parameter, DD/r , where r0 represents a characteristic diffusion length, which is unknown. Each set of desorption data was fitted separately to obtain the best DD/r
, where r0 represents a characteristic diffusion length, which is unknown. Each set of desorption data was fitted separately to obtain the best DD/r . The best-fit curves were obtained by minimizing the mean weighted square error as described by Zhao et al. [19] and they are shown in Figure 4. Values of DD/r
. The best-fit curves were obtained by minimizing the mean weighted square error as described by Zhao et al. [19] and they are shown in Figure 4. Values of DD/r for all soils and concentrations are given in Table 2. The DMDM could not be used for Seal Beach soil because the isotherm is linear.
for all soils and concentrations are given in Table 2. The DMDM could not be used for Seal Beach soil because the isotherm is linear.
The fits tend to slightly underpredict desorption at very early times and slightly overpredict desorption at intermediate times. The values of DD/r for two of the soils agree well with those published earlier (1.6 × 10−3/h for Cheshire, and 1.5 × 10−4/h for Pahokee [19]) where phenanthrene desorption was performed by using a sequential dilution technique (desorption to a finite bath) rather than the present technique (desorption to an infinite bath). The DMDM predicts DD/r
for two of the soils agree well with those published earlier (1.6 × 10−3/h for Cheshire, and 1.5 × 10−4/h for Pahokee [19]) where phenanthrene desorption was performed by using a sequential dilution technique (desorption to a finite bath) rather than the present technique (desorption to an infinite bath). The DMDM predicts DD/r to be independent of initial sorbed concentration provided the sorbed concentration is below the amount that would soften (plasticize) the SOM. This expectation is met for most soils. The ratio between DD/r
to be independent of initial sorbed concentration provided the sorbed concentration is below the amount that would soften (plasticize) the SOM. This expectation is met for most soils. The ratio between DD/r at low and high concentration ranges between 0.81 and 0.9; the exception is Mount Pleasant silt loam for which DD/r
at low and high concentration ranges between 0.81 and 0.9; the exception is Mount Pleasant silt loam for which DD/r increases significantly (a factor of three) with concentration. Plasticization, which is well known for polymers [21], can result in faster diffusion within the solid. Hence, the concentration dependence of DD/r
increases significantly (a factor of three) with concentration. Plasticization, which is well known for polymers [21], can result in faster diffusion within the solid. Hence, the concentration dependence of DD/r for Mount Pleasant may be due to plasticization at high concentrations.
for Mount Pleasant may be due to plasticization at high concentrations.
As the instantaneous local dissolution-domain concentration qD increases, g(qD)−1, and therefore Dapp, increases (Fig. 5a). As qD reaches very high values, the holes become saturated and g(qD)−1 approaches unity. As qD approaches zero, g(qD)−1 approaches KD/(KD + Qb), which is just the local fraction of dissolution-type sorption and is equal to f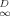 . Figure 5b shows that limqD.0 g(qD)−1 (hence, f
. Figure 5b shows that limqD.0 g(qD)−1 (hence, f ) correlates with the Freundlich N. In other words, Dapp for desorption is concentration-dependent to the degree that the isotherm is nonlinear. The data for Cheshire soil (Fig. 3) reflect the sigmoidal shape of g(qD)−1 versus qD curve, in that a strong concentration effect is found between 160 and 2,000 μg/g OC but little concentration effect is found between 2,000 and 13,000 μg/g OC.
) correlates with the Freundlich N. In other words, Dapp for desorption is concentration-dependent to the degree that the isotherm is nonlinear. The data for Cheshire soil (Fig. 3) reflect the sigmoidal shape of g(qD)−1 versus qD curve, in that a strong concentration effect is found between 160 and 2,000 μg/g OC but little concentration effect is found between 2,000 and 13,000 μg/g OC.
Implications
We have demonstrated that normalized desorption rates are dependent on the absolute concentration when the isotherm is nonlinear. The magnitude of the concentration effect is inversely related to the degree of linearity as represented by f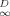 of the DMM (Eqn. 3) or by N of the Freundlich model. Nonlinearity is a function of the quality of the organic matter. Concentration-dependent kinetics arises from the heterogeneity of natural organic matter as a sorbent. Heterogeneous models for organic matter that have been proposed include rubbery/glassy polymer models such as the DMM [1, 13, 17], hard carbon/soft carbon models [22, 23], and models based on the assumption of fixed, activated carbonlike pores present in materials such as soot and charcoal [22-27]. Variations in the character of organic matter phases, the size of organic matter particles or coatings, and different accessibility of organic particles or coatings within the interstices of inorganic aggregates all may play a role in determining soil-specific rates [1]. The present desorption study and the earlier uptake study [8] indicate a consequence of nonideal sorption behavior in the kinetic realm, and suggest that concentration effects should be taken into account whenever sorption and desorption rates are a consideration. The DMDM ascribes the increase in apparent diffusivity with concentration in terms of progressive population of the dissolution domain at the expense of the hole domain, that is, as immobile sites (holes) become filled up.
of the DMM (Eqn. 3) or by N of the Freundlich model. Nonlinearity is a function of the quality of the organic matter. Concentration-dependent kinetics arises from the heterogeneity of natural organic matter as a sorbent. Heterogeneous models for organic matter that have been proposed include rubbery/glassy polymer models such as the DMM [1, 13, 17], hard carbon/soft carbon models [22, 23], and models based on the assumption of fixed, activated carbonlike pores present in materials such as soot and charcoal [22-27]. Variations in the character of organic matter phases, the size of organic matter particles or coatings, and different accessibility of organic particles or coatings within the interstices of inorganic aggregates all may play a role in determining soil-specific rates [1]. The present desorption study and the earlier uptake study [8] indicate a consequence of nonideal sorption behavior in the kinetic realm, and suggest that concentration effects should be taken into account whenever sorption and desorption rates are a consideration. The DMDM ascribes the increase in apparent diffusivity with concentration in terms of progressive population of the dissolution domain at the expense of the hole domain, that is, as immobile sites (holes) become filled up.
Fractional desorption rate calculated according to Equation 5 as a function of the percent remaining sorbed. The numbers appearing alongside the soil name represent the indices of linearity for phenanthrene in that soil based on the Freundlich and dual-mode models. Phenanthrene concentrations in legends are based on the organic carbon content of the soil (including Bunker C oil in the case of Seal Beach [CA, USA]).
Fits of experimental desorption data in Figure 2 by the dualmode diffusion model. Error bars represent 95% confidence limits of three to four replicates.
The magnitude of the concentration effect can be expected to vary with experimental conditions and whether sorption or desorption is being observed. Uptake from an infinite bath (i.e., at constant solute concentration) or release to infinite dilution (i.e., in the presence of an infinite sink such as Tenax) will be subject to an intrinsic concentration effect on the apparent diffusivity, if one exists. Uptake from a finite bath where the soil to water ratio is held constant will be subject additionally to the shrinking gradient effect [8], which, when the isotherm is concave-down, will oppose the intrinsic concentration dependence of the apparent diffusivity and reduce the observed concentration effect. For the sequential-dilution batch method of measuring desorption rates, in which the supernatant liquid is repeatedly diluted with clean liquid to achieve desorption, the shrinking gradient effect reinforces the intrinsic concentration effect on diffusivity, rather than opposing it as in uptake in a finite bath. This was illustrated by White and Pignatello [28] and also by Zhao et al. [19] in their study of batch uptake and batch sequential dilution desorption of phenanthrene in the presence of a competing cosolute, pyrene. There, increasing the concentration of a competing cosolute was regarded as fulfilling a similar function as increasing the solute concentration.
| Soil | q0 (μg/gOC) | Resistant fraction Fr | DD/r (h−1) (h−1) |
MWSEb |
|---|---|---|---|---|
| Pahokee (FL, USA) | 250 ± 25 | 0.38 ± 0.06 | 3.8 × 10−4 | 0.00217 |
| 4,100 ± 25 | 0.25 ± 0.05 | 4.2 × 10−4 | 0.0114 | |
| Mt. Pleasant (NY, USA) | 280 ± 31 | 0.10 ± 0.03 | 1.3 × 10−3 | 0.0530 |
| 4,900 ± 270 | 0.01 ± 0.08 | 4.0 × 10−3 | 0.1230 | |
| Cheshire (CT, USA) | 160 ± 28 | 0.36 ± 0.03 | 1.3 × 10−3 | 0.00978 |
| 2,000 ± 250 | 0.26 ± 0.08 | 1.6 × 10−3 | 0.0192 | |
| 13,000 ± 930 | 0.29 ± 0.03 | 1.4 × 10−3 | 0.0201 | |
| Port Hueneme (CA, USA) | 980 ± 73 | 0.19 ± 0.03 | 5.1 × 10−4 | 0.0265 |
| 21,000 ± 65 | 0.26 ± 0.02 | 5.8 × 10−4 | 0.0182 | |
| Modified Seal Beach (CA, USA) | 530 ± 74 | 0.09 ± 0.01 | 1.8 × 10−3 | 0.0956 |
| 25,000 ± 130 | 0.16 ± 0.04 | 2.0 × 10−3 | 0.0907 | |
| Seal Beach (CA, USA) | 240 ± 67 | 0.13 ± 0.04 | NA | NA |
| 25,000 ± 1,900 | 0.17 ± 0.11 | NA | NA |
- a OC = organic carbon. NA = not applicable. Values are standard deviations with 95% confidence limits.
-
b Mean weighted square error, MWSE = 1/M ∑
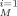 (C
(C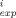 - C
- C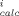 /C
/C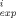 )2 where C
)2 where C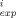 and C
and C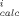 are experimental and calculated aqueous phase concentrations of the ith point of M total points.
are experimental and calculated aqueous phase concentrations of the ith point of M total points.
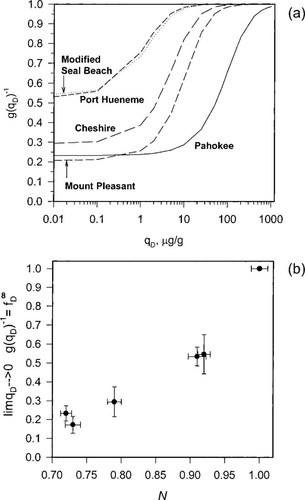
(a) Variation in the concentration-dependent component of the apparent diffusivity with local instantaneous dissolution-domain concentration. (b) Correlation between the limit of g(qD)−1 at infinite dilution (=f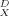 ) and the Freundlich exponent as an index of linearity.
) and the Freundlich exponent as an index of linearity.
In many cases, natural solids may harbor a fraction of the originally sorbed chemical in a highly resistant state [1, 12, 20, 28, 29]. All soils in the present study displayed such a fraction. This fraction can be very large. In the Pahokee soil at the lower concentration, about 31% of the initial phenanthrene was still sorbed after 20 months of continuous desorption at the maximum possible rate (i.e., to a zero-concentration bath). In contrast to the results of others [20], the highly resistant fraction in the samples in the present study was not necessarily related to the degree of isotherm linearity, because all three of the cases showing linear or nearly linear isotherms (Seal Beach, modified Seal Beach, and Port Hueneme) gave substantial resistant fractions. The existence of a highly resistant fraction in such cases is remarkable because hysteresis is not characteristic of a partitionlike, homogeneous-potential sorbent, as SOM is often regarded to be, and is implied by the linearity. The identity, or identities, of microscopic soil structures responsible for highly hindered diffusion occurring on net desorption are still a matter of debate [1, 13, 22-27, 30, 31]. Xia and Pignatello [13] have given evidence for irreversible deformation of pores, presumably located in organic matter, during net sorption that gives rise to hysteresis. Thus, structural relaxation of the solid, in addition to molecular diffusion, may regulate desorption rates.
Sorbed molecules have been demonstrated [13] to be able to plasticize SOM at sufficiently high concentrations, just as they can synthetic and natural polymers [21]. This can result in faster sorbate diffusion within the solid phase. Consistent with this, Mount Pleasant soil gives a higher DD/r2 at the higher of the two initial sorbed concentrations.
The modified Seal Beach soil behaves as if the removed Bunker C oil, which comprises about one half of the OC in the parent soil, was an additional partition medium for phenanthrene. Because the isotherm parameters based on total OC content (from natural organic matter and oil) are nearly the same for Seal Beach as for Modified Seal Beach, removal of the oil lowers the amount sorbed per gram of whole soil by about one half. Removal of the oil also decreases the linearity consistent with the oil acting like a partition domain.
Acknowledgements
This work was supported by grants from the U.S. Environmental Protection Agency's STAR Program (Joint Program on Bioremediation, R 82595–01–0) and the Office of Navel Research Harbor Processes Program (N00014–99–1–0095). W.J. Braida, currently at Center for Environmental Engineering, Stevens Institute of Technology, and D. Zhao, currently at Department of Civil Engineering, Auburn University, are grateful for support during revision of the manuscript from their respective institutions. Although the research described in this article has been funded in part by the U.S. Environmental Protection Agency, it has not been subjected to the Agency's required peer and policy review and therefore does not necessarily reflect the views of the Agency and no official endorsement should be inferred.




