Minimum data required for deriving soil quality criteria from invertebrate ecotoxicity experiments
Abstract
The suitability of a new method to determine the minimum number of data required to stabilize a calculation is studied. Five different calculations have been computed, changing the order of data randomly. The statistical reliability of numerical values has also been calculated depending on the successive increase in the number of data included. In our study, when few data are considered, a great variation in the estimations is observed depending on the individual data included. The calculation is stabilized for a sample size between 5 and 15 data points, and the sample can therefore be considered representative enough. Results are in agreement with those presented by other authors.
INTRODUCTION
Statistics generally deals with populations or groups of individuals, that is, with quantities of information. Thus, the measurement of a single animal or the response from a single biochemical test will not generally be of interest. Unless a sample of animals is measured or several such tests are performed, ordinary statistics can play no role. So what sample size is needed? It is obvious that the more heterogeneous a population is the larger should be the sample size required to obtain a given level of accuracy. The less variable (the more homogeneous) a population, the smaller the sample size. If variability within measurements is great, many samples will be needed to empirically determine a representative mean (or median) value, and this will also imply that it will probably be difficult to predict such a mean value by models since this will be influenced by many sources of variability [1].
However, the optimal size of predictive models is generally achieved with a surprisingly small number of dependant variables. The results presented by Hakanson [1] indicate that predictive models should not have more than two to six x variables (or compartments). Although it is evident that there may be many specific cases where more x variables would do more good than harm, it is also important to note that the potential model uncertainty would then increase, too [1].
This paper deals with the reliability of the calculation procedure followed in the Basque country to derive soil quality criteria aiming at protecting ecosystems. These values, designated with the acronym VIE (indicative values for assessment) have been drawn up as a tool for risk assessment. They have been formulated so that they delimit clearly differentiated areas with regard to risk along the pollutant concentration gradient [2, 3]. Two different values with two different meanings have been established. In this paper, we will focus on the so-called VIE-C, defined as the level above which the risk becomes unacceptable. From an ecotoxicological point of view, this level implies a potential hazard for 50% of the ecosystem species [4] and the subsequent impairment in the ecological function.
The suitability of a new probabilistic method to determine minimum data needs in order to stabilize the VIE-C values for four metals (cadmium, copper, lead, and zinc) is studied and compared with the results obtained following the method proposed by Carral et al. [5].
MATERIAL AND METHODS
Data were collected by an extensive literature review and were selected based on sublethal effects of long-duration exposure (NOECs) tests on invertebrates. Priority was given to parameters affecting reproduction and growth as well as other attributes important to population dynamics (see Appendix 1). The VIE-C values for Cd, Cu, Pb, and Zn were calculated following the method of Van Straalen and Denneman [6] and Denneman and Van Gestel [7] adapted to the soil characteristics of the Basque country [3]. These values are of the same order of magnitude, although 12 to 33% higher, than the equivalent ones established in The Netherlands [8]. The reliability index of the calculation was established according to Denneman and Van Gestel [7] and Van den Berg and Roels [8], who take into account the number of both species and taxonomic groups for which data are available. The four metals were selected because they showed a good reliability from this point of view as well as a great number of available ecotoxicity data.
To check the mathematical robustness of the derived VIE-C values, successive calculations were carried out in which the number of ecotoxicity data included was progressively increased randomly to minimize factors of variability [9]. For each of the four heavy metals (Cd, Cu, Pb, and Zn), the computation was repeated five times, changing randomly the order in which data were added in each of the runs in order to avoid bias in the stabilization interpretation.
| Species | T (d) | Pter | [C] | % OM | % Clay | Reference |
|---|---|---|---|---|---|---|
| Acrobeloides nanus | 10 | NOEC | 0.05 | — | — | [16] |
| 14 | NOEC-d | 2 | — | — | [17] | |
| 35 | NOEC-c | 10 | — | — | [18] | |
| Aphelenchus avenae | 21 | NOEC-cpo | 0.094 | — | — | [19] |
| 21 | NOEC-po | 0.01 | — | — | [19] | |
| Dendrobaena rubida | 14 | NOEC | 100 | 5.7 | — | [20] |
| 90 | NOEC-h | 101 | 9.7 | 5 | [20] | |
| Eisenia andrei | 21 | NOEC-c | 100 | 10 | 20 | [21] |
| 21 | NOEC-r | 100 | 10 | 20 | [21] | |
| 21 | NOEC-c | 10 | 10 | 20 | [21] | |
| 21 | NOEC-h | 10 | 10 | 20 | [21] | |
| 84 | NOEC-c | 10 | 8 | 10 | [22] | |
| 84 | NOEC-c | 18 | 8 | 10 | [23] | |
| 21 | NOEC-j | 108 | 38 | 5 | [24] | |
| 21 | NOEC-j | 100 | 10 | 20 | [21] | |
| Eisenia fetida | 56 | NOEC-l | 300 | 10 | 20 | [25] |
| 14 | NOEC | 25 | 50 | — | [26] | |
| 56 | NOEC-h | 39.2 | 10 | 20 | [25] | |
| 56 | NOEC-h | 25 | 50 | 5 | [26] | |
| 21 | NOEC-h | 152 | 20 | 10 | [27] | |
| 21 | NOEC-c | 207 | 20 | 10 | [27] | |
| 21 | NOEC-l | 300 | 20 | 10 | [27] | |
| 56 | NOEC-c | 50 | 50 | 5 | [26] | |
| Folsomia candida | 63 | NOEC-h | 323 | — | — | [28] |
| 50 | NOEC-c | 148 | 95 | — | [29] | |
| 50 | NOEC-po | 326 | 95 | — | [29] | |
| 63 | NOEC-c | 324 | — | — | [28] | |
| Helix aspersa | 30 | NOEC-c | 10 | 86 | — | [30] |
| 30 | NOEC-con | 50 | 86 | — | [30] | |
| 14 | NOEC | 10 | 86 | — | [30] | |
| 21 | NOEC | 50 | — | — | [31] | |
| Lumbricus rubellus | 12 | NOEC-h | 10 | 3.4 | 17 | [32] |
| 14 | NOEC | 10 | 3.4 | — | [32] | |
| Mesorhabditis monhystera | 22 | NOEC-cpo | 0.23 | — | — | [19] |
| Orchesella cincta | 61 | NOEC-l | 56 | 95 | 0 | [33] |
| 42 | NOEC-l | 56 | 95 | — | [34] | |
| 61 | NOEC-c | 4 | 95 | 0 | [33] | |
| 84 | NOEC-r | 56 | 95 | — | [34] | |
| 63 | NOEC-r | 56 | 95 | — | [35] | |
| 63 | NOEC-c | 4.7 | 95 | — | [35] | |
| 14 | NOEC | 56 | 95 | — | [35] | |
| 84 | NOEC-c | 4 | 95 | — | [34] | |
| 63 | NOEC-po | 56 | 95 | — | [35] | |
| 63 | NOEC-con | 56 | 95 | — | [35] | |
| 61 | NOEC-pd | 56 | 95 | — | [33] | |
| Platynothrus peltifer | 63 | NOEC-h | 1 | 51 | — | [28] |
| 14 | NOEC | 2.9 | 95 | — | [35] | |
| 84 | NOEC-con | 27.3 | 95 | — | [35] | |
| 84 | NOEC-po | 2.9 | 95 | — | [35] | |
| 84 | NOEC-l | 117 | 95 | — | [35] | |
| 84 | NOEC-r | 2.9 | 95 | — | [35] | |
| Plectus acuminatus | 21 | NOEC-po | 32 | 10 | 20 | [36] |
| Porcellio scaber | 67 | NOEC-r | 10 | 95 | 0 | [37] |
| 67 | NOEC-con | 2.25 | 95 | 0 | [37] | |
| 67 | NOEC-c | 2.25 | 95 | 0 | [37] | |
| 67 | NOEC-t | 10.1 | 95 | 0 | [37] | |
| 28 | NOEC-con | 10 | 86 | 0 | [38] | |
| 28 | NOEC-aa | 10 | 86 | 0 | [38] | |
| 14 | NOEC | 10 | 95 | — | [37] | |
| 28 | NOEC-c | 4 | 86 | 0 | [38] | |
| 308 | NOEC-l | 95 | — | — | [28] |
- aT (d) = test duration (in days); Pter = parameter considered (see Appendix); [C] = concentration in mg/kg; % OM = organic matter in percent; — = no data specified.
RESULTS
Tables 1 through 4 show the toxicity data for cadmium, copper, lead, and zinc, respectively, and the different parameters considered in the calculations. Figure 1 displays the regression curve slopes for the VIE-C values according to the succesive addition of data included in the calculations. According to this figure, it can be concluded that the stabilization of the values for the four metals arises within the range of 5 to 15 data points, at around 10 data points Curve shapes are unpredictable for calculations based on few data points, which is reasonable if we take into account the high standard deviations observed in these initial sectors.
| Species | T (d) | Pter | [C] | % OM | % Clay | Reference |
|---|---|---|---|---|---|---|
| Aporrectodea caliginosa | 14 | NOEC-c | 100 | 2 | 5 | [39] |
| 15 | NOEC-h | 50 | 5 | 2 | [39] | |
| 14 | NOEC-l | 500 | 2 | 5 | [39] | |
| 28 | NOEC-h | 28 | 6 | 4 | [32] | |
| 28 | NOEC-h | 27 | 6 | 4 | [32] | |
| Arion ater | 27 | NOEC-con | 25 | 86 | 0 | [40] |
| Dendrobaena rubida | 90 | NOEC-h | 22 | 9.7 | 5 | [20] |
| Eisenia andrei | 21 | NOEC-po | 306 | 8 | 10 | [41] |
| 84 | NOEC-c | 62 | 8 | 10 | [22] | |
| 84 | NOEC | 106 | 8 | 10 | [22] | |
| 21 | NOEC-h | 120 | 8 | 10 | [41] | |
| — | NOEC-c | 56 | 8 | 10 | [23] | |
| 7 | NOEC-h | 60 | 8 | 10 | [41] | |
| Eisenia fetida | 21 | NOEC-l | 293 | 20 | 10 | [27] |
| 56 | NOEC-l | 210 | 10 | 20 | [25] | |
| 42 | NOEC-c | 1,000 | 38 | 5 | [42] | |
| 42 | NOEC-h | 1,000 | 38 | 5 | [42] | |
| 56 | NOEC-c | 500 | 50 | 5 | [26] | |
| 56 | NOEC-c | 1,700 | — | — | [43] | |
| 21 | NOEC-h | 29 | 20 | 10 | [27] | |
| 56 | NOEC-h | 32 | 10 | 20 | [25] | |
| 56 | NOEC-h | 500 | 50 | 5 | [26] | |
| Lumbricus rubellus | 84 | NOEC-hj | 63 | 3.4 | 17 | [44] |
| 84 | NOEC-h | 30 | 3.4 | 17 | [32] | |
| 84 | NOEC-h | 13 | 3.4 | 17 | [44] | |
| 84 | NOEC-c | 373 | 3.4 | 17 | [44] | |
| 28 | NOEC-h | 80 | 6 | 4 | [32] | |
| 84 | NOEC-h | 130 | 5.7 | 2 | [44] | |
| Octolasium cyaneum | 14 | NOEC-l | 153 | 24.1 | — | [45] |
| 14 | NOEC-l | 1,214 | — | — | [45] | |
| Onychiurus armatus | 119 | NOEC-c | 2,608 | 95 | 0 | [20] |
| Platynothrus peltifer | 84 | NOEC-c | 598 | 95 | 0 | [46] |
| 84 | NOEC-r | 168 | 95 | 0 | [46] | |
| 84 | NOEC-r | 200 | 20 | 10 | [47] | |
| 84 | NOEC-c | 200 | 20 | 10 | [47] | |
| Plectus acuminatus | 21 | NOEC-po | 32 | 10 | 20 | [36] |
- aT (d) = test duration (in days); Pter = parameter considered (see Appendix); [C] = concentration in mg/kg; % OM = organic matter in percent; — = no data specified.
| Species | T (d) | Pter | [C] | % OM | % Clay | Reference |
|---|---|---|---|---|---|---|
| Aiolopus thalassinus | 35 | NOEC-c | 50 | — | — | [18] |
| 14 | NOEC-nf | 50 | — | — | [17] | |
| 14 | NOEC | 100 | — | — | [17] | |
| Aporrectodea caliginosa | — | NOEC | 1,000 | 1 | 0 | [39] |
| Aphelenchus avenae | 21 | NOEC-po | 0.01 | — | — | [19] |
| Arion ater | 27 | NOEC-con | 1,000 | 86 | 0 | [40] |
| Dendrobaena rubida | 90 | NOEC-r | 564 | 9.7 | 5 | [20] |
| 90 | NOEC-r | 130 | 9.7 | 5 | [20] | |
| 90 | NOEC-r | 560 | 9.7 | 5 | [20] | |
| Eisenia fetida | 140 | NOEC-h | 1,000 | 50 | 5 | [26] |
| 140 | NOEC-c | 1,000 | 50 | 5 | [26] | |
| 56 | NOEC-c | 36,000 | — | — | [43] | |
| 42 | NOEC-c | 5,000 | 38 | 5 | [42] | |
| 56 | NOEC-l | 2,190 | 10 | 20 | [25] | |
| 56 | NOEC-h | 1,810 | 10 | 20 | [25] | |
| 21 | NOEC-c | 1,966 | 20 | 10 | [27] | |
| 21 | NOEC-l | 4,793 | 20 | 10 | [27] | |
| 21 | NOEC-h | 608 | 20 | 10 | [27] | |
| Lumbricus rubellus | 12–84 | NOEC-c | 1,000 | 8 | 17 | [32] |
| 42 | NOEC-l | 3,000 | 8 | 17 | [32] | |
| 84 | NOEC-h | 200 | 3.4 | 17 | [32] | |
| Mesorhabditis monhystera | 22 | NOEC-po | 7.6 | — | — | [19] |
| Onychiurus armatus | 119 | NOEC-r | 1,096 | 95 | 0 | [20] |
| 119 | NOEC-c | 1,096 | 95 | 0 | [20] | |
| Platynothrus peltifer | 84 | NOEC-c | 430 | 95 | 0 | [46] |
| 84 | NOEC-r | 430 | 95 | 0 | [46] | |
| Porcellio scaber | — | NOEC | 40 | 95 | 0 | [48] |
| 448 | NOEC-po | 6,400 | 95 | 0 | [48] |
- aT (d) = test duration (in days); Pter = parameter considered (see Appendix); [C] = concentration in mg/kg; % OM = organic matter in percent; — = no data specified.
| Species | T (d) | Pter | [C] | % OM | % Clay | Reference |
|---|---|---|---|---|---|---|
| Arion ater | 27 | NOEC-con | 10 | 86 | 5 | [40] |
| Arion lusitanicus | — | NOEC-r | 98 | — | — | [34] |
| Eisenia andrei | 21 | NOEC-h | 320 | 38 | 5 | [24] |
| Eisenia fetida | 56 | NOEC-c | 2,400 | — | — | [43] |
| 42 | NOEC-h | 1,000 | 38 | 5 | [50] | |
| 42 | NOEC-c | 2,500 | 38 | 5 | [50] | |
| 56 | NOEC-1 | 289 | 10 | 20 | [25] | |
| 56 | NOEC-h | 199 | 10 | 20 | [25] | |
| 21 | NOEC-1 | 702 | 10 | — | [51] | |
| 140 | NOEC-c | 5,000 | 50 | 5 | [26] | |
| 21 | NOEC-1 | 256 | 10 | — | [51] | |
| 21 | NOEC-1 | 274 | 5 | — | [51] | |
| 21 | NOEC-c | 400 | 20 | 10 | [27] | |
| 21 | NOEC-1 | 1,048 | 15 | — | [51] | |
| 21 | NOEC-1 | 366 | 5 | — | [51] | |
| 140 | NOEC-h | 1,000 | 50 | 5 | [26] | |
| 21 | NOEC-h | 85 | 5 | — | [51] | |
| 21 | NOEC-h | 183 | 10 | — | [51] | |
| 21 | NOEC-h | 115 | 5 | — | [51] | |
| 21 | NOEC-h | 161 | 10 | — | [51] | |
| 21 | NOEC-1 | 368 | 15 | — | [51] | |
| 21 | NOEC-h | 414 | 15 | — | [51] | |
| 21 | NOEC-1 | 442 | 20 | 10 | [27] | |
| 21 | NOEC-h | 484 | 15 | — | [51] | |
| 21 | NOEC-h | 237 | 20 | 10 | [27] | |
| 21 | NOEC-h | 553 | 10 | — | [51] | |
| 21 | NOEC-h | 97 | 5 | — | [51] | |
| 21 | NOEC-1 | 184 | 15 | — | [51] | |
| 21 | NOEC-1 | 168 | 10 | — | [51] | |
| 21 | NOEC-1 | 197 | 5 | — | [51] | |
| 21 | NOEC-h | 223 | 15 | — | [51] | |
| Oniscus asellus | 1 | NOEC-a | 2,000 | 95 | 0 | [52] |
| Porcellio scaber | 67 | NOEC | 2,000 | 95 | 0 | [37] |
| 448 | NOEC-po | 800 | 95 | 0 | [48] | |
| 67 | NOEC-con | 1,000 | 95 | 0 | [37] | |
| 67 | NOEC | 2,000 | 95 | 0 | [37] | |
| 42 | NOEC-con | 1,700 | 95 | 0 | [53] | |
| 7 | NOEC-a | 2,000 | 95 | 0 | [52] | |
| 67 | NOEC-c | 398 | 95 | 0 | [37] |
- aT (d) = test duration (in days); Pter = parameter considered (see Appendix 1); [C] = concentration in mg/kg; % OM = organic matter (%); — = no data specified.
Identical results are obtained following the Carral et al. [5] test based on the standard error calculation. Stabilization of the values is also reached for about 10 data points, as Figures 2 a, b, c, and d show. These graphics correspond to the standard error representation for only one of the computation sequence of cadmium, copper, lead, and zinc, respectively.
DISCUSSION
Different criteria are usually followed to determine the appropriate sample size, and these have to consider both mathematical and scientific–technical issues. Among others, Miaoulis and Michener [10] stated three of these criteria that would need to be specified in any study, including (1) the degree of variability within the variables to be measured, (2) the level of accuracy in the estimation, and (3) the level of reliability. The first two can be related to mathematical issues, while the third refers to the scientific reliability of the approach adopted (relevance of parameters, sampling strategies, etc.) for the problem under investigation.
In our study, the reliability of the calculation from the scientific viewpoint was established according to Van den Berg and Roels [8] and Denneman and Van Gestel [7]. The quantitative reliability scale formulated by these authors is based on the availability and representativity of toxicity data, both in terms of number and kind of species and taxonomic goups. The species and groups of interest are previously identified in relation to their biological significance to the soil ecosystem function. So our study has been focused on the statistical aspects and, more specifically, on the number of data required to stabilize the mathemathical calculation.
The two factors considered are the variability of the input data and the variability of the output value as a measure of the degree of accuracy in the calculation. Due to the natural interspecies variations, the range of species sensitivity to the pollutants under test is the most important factor in assessing ecosystem risk on the basis of a few single test data [11]. Nevertheless, variations between laboratories and even variations between tests within a laboratory are generally thought to become a more determining factor. Toxicity values are not constant values but depend on different environmental factors and thus on experimental conditions. In order to minimize as much as possible this source of variability, the selection of input data involved a careful appraisal of test conditions. Only NOEC-type data from nonlethal effects on long-duration exposure tests on soil invertebrates were selected. Moreover, it was considered necessary for toxicity data to have been obtained in standardized or generally well-accepted laboratory test methods. In this sense, these types of data have also been used to study the relationships among VIE-C values derived independently for soil, marine, and freshwater ecosystems, showing a strong correlation between media [12].

Variability on all metal slopes obtained through each of the five different runs on increasing the number of data for all the metals used in the calculations.
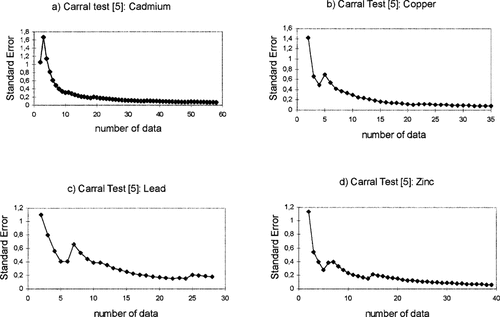
Standard error representation (Carral et al. Sci Total Environ 172:175–178 [5]) for cadmium (a), copper (b), lead (c), and zinc (d) versus number of data points.
With respect to the stabilization topic, Carral et al. [5] consider that minimum sample size is reached when the standard error is small (curve shape becomes flat, i.e., the slope tends to zero). Our results indicate a similar behavior. The addition of new data diminishes the variability of the VIE-C values derived while the curve shape tends to the horizontal. This happens from 10 data points onward.
The use of a similar approach has also been suggested by Solomon [13] for the evaluation of the species sensitivity to many substances. In this study, the decrease and stabilization of the distribution slope was reached with nine data points (one less than our results), which is in very good agreement with our results. The author advocates for this minimum number of data to apply a probabilistic ecological risk assessment.
CONCLUSIONS
The reliability of values estimated from sample data should take into account both scientific and statistical criteria. In our example, the unique use of biological criteria (based on the number of species and taxonomic groups) to establish the reliability of the derived value could have led to incorrect conclusions if mathemathical stability were not considered. As Fobes and Forbes [14] suggested, the rational use of these models as ecotoxicological tools for environmetal regulation requires basic knowledge concerning the relationships between the structure and function of ecosystems and the nature of the statistical distribution. The need to encourage the checking of statistical aspects is not only necessary for scientific purposes but also for management and economic ones. If both biological and statistical criteria are not taken into account, extrapolations can lead to mistaken management decisions. In this sense, to reduce uncertainty, it is necessary to make the tests more realistic by using multispecies tests, by including other toxicants that may occur with the substance of interest, and by using indigenous species [15].
Acknowledgements
This study has been promoted and funded by IHOBE, SA, a public society for environmental management that depends on the Department of Spatial Planning, Housing, and the Environment of the Basque Country.
APPENDIX
| NOEC | no observed effect concentration |
| NOEC-f | feeding |
| NOEC-fa | food assimilation |
| NOEC-g | growth |
| NOEC-con | consumption |
| NOEC-po | population |
| NOEC-ep | egg production |
| NOEC-dj | eggs developed to juveniles |
| NOEC-j | number of juveniles |
| NOEC-l | lethality |
| NOEC-m | mobility |
| NOEC-n | number of nymphs developed |
| NOEC-r | reproduction |
| NOEC-t | trembling |




