Quantitative structure-property relationships for the chemical reactivity of acrylates and methacrylates
Abstract
Reactivity towards three different nucleophiles was measured for a training set of six acrylates and seven methacrylates. The reactions studied were neutral and base-catalyzed hydrolysis and Michael addition of reduced glutathione (GSH). A linear free energy relationship (LFER) was established for the base-catalyzed hydrolysis rate constants of methacrylates, with the Taft parameter σ* as single descriptor. The GSH reactivity could be modeled with a partial least square regression (PLS) using four quantum chemical ground state parameters describing the difference in frontier orbital interaction and coulombic forces within the training set. Literature data for GSH reactivity was used to test the applicability of the PLS model. Differences in acute fish toxicity for structurally similar acrylates and methacrylates could be explained by their different potency as Michael-type acceptors.
INTRODUCTION
Acrylic and methacrylic acid esters are chemicals that are produced in large quantities. Their toxicity for humans and rodents as well as for aquatic organisms has been documented [1]. In ecotoxicological research, acrylates and methacrylates are either classified together in one group as unspecific reactive chemicals [2] or as two groups, the acrylates as electrophiles and the methacrylates as ester narcotics [3]. Structure activity relationships have been established for acute fish toxicity of acrylates based on empirical [4] as well as quantum-chemical parameters [5]. An important link between chemical structure and toxicity for these electrophilic compounds is their chemical reactivity [6], which influences both their toxicokinetic and toxicodynamic behaviors. Modeling of reaction rates can therefore help to explain differences in toxicity. Data about chemical reactivity can furthermore be used to predict the fate of compounds in the environment.
Chemical reactivity has been modeled successfully for a number of chemical classes using quantum chemical parameters [7]. Quantitative structure–property relationships (QSPRs) for organic electrophiles have been proposed among others for small chlorinated alkenes by Verhaar et al. [8], for organophosphorus esters by Hermens et al. [9] and Schüürmann [10], and for epoxides by Eriksson et al. [11] and Purdy [12]. For the reactivity of chlorinated alkenes, activation energies were calculated. For the other compounds, semiempirical molecular orbital (MO) parameters or empirical substituent constants proved to be successful.
In this work, a training set of six acrylates and seven methacrylates was created to gain more insight into the reactivity of acrylic and methacrylic acid esters. Quantum chemical descriptors of electronic structure that were hypothesized to bear a relationship to the test compounds’ reactivity or empirical descriptors were used to establish QSPRs with experimental reaction rates. Because acrylates and methacrylates are both electrophilic chemicals, their reactivities were tested against three nucleophiles of different strength, including water (H2O), the hydroxyl anion (OH), and reduced glutathione (GSH). From a toxicological point of view, reaction rates of electrophilic compounds with biological nucleophiles are of special interest. In combination with effect data, they provide information about target sites within the cell and possibly about their mode of action [13-15]. Glutathione is a nucleophile that is often used as a model for cellular thiol groups. It has an important function in the phase 2 metabolism of xenobiotic compounds, where it acts as scavengerof free electrophiles and as cosubstrate of glutathione transferases. In the literature, GSH reaction rates towards different electrophiles have been reported along with a number of QSARs [16-20]. Michael addition, a nucleophilic addition on Cβ (Fig. 1) is suggested as the predominant reaction mechanism of negatively charged thiols with α, β unsaturated carboxyl groups such as acrylates and methacrylates [5, 21].
MATERIAL AND METHODS
Material
Chemicals were used as received were o-phthalaldehyde from Acros (DBs, Hertogenbosch, The Netherlands); ethyl acrylate, 2-hydroxyethyl acrylate, diethyl fumarate, isobutyl acrylate, lauryl acrylate, isobutyl methacrylate, methyl methacrylate, allyl methacrylate, hydroxypropyl acrylate (mixture of isomers), hexyl acrylate, benzyl methacrylate, tetrahydrofurfuryl methacrylate, and reduced glutathione from Fluka, Sigma-Aldrich (Zwijndrecht, The Netherlands); and isopropyl methacrylate from Pfaltz and Bauer (Waterbury, CT, USA). Deionized water was treated with a Millipore filter system before use. Methanol, acetone, sodium citrate, citric acid, KH2PO4, Na2HPO4, sodium-tetraborate decahydrate, and sodium-EDTA were of analytical grade.
Assay to measure the neutral and base-catalyzed hydrolysis
Stock solutions of acrylates and methacrylates were prepared in acetone or in methanol. Aqueous buffer solutions were prepared with a pH 7.0 (1.0 mM H2PO4/HPO4) and a pH 10 (1 mM sodium-tetraborate decahydrate). Mixtures of two or three compounds were used in the determination of the hydrolysis rates. The choice for the composition of the mixture was based on the retention time on the HPLC column of the individual compounds in order to assure proper identification and quantification. To achieve final concentrations of 100 μM of the electrophile (maximum 1.5% organic solvent), 50 μl stock solution of the mixture were added to 10 ml aqueous buffer solution. The reaction vials were kept at 20°C. Samples were taken in duplicate immediately after mixing and after 24 and 48 h (after 1 and 2 h for diethyl fumarate at pH 10). The disappearance of the parent compound was used to calculate the hydrolysis rates.
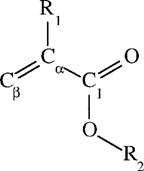
Chemical structure of acrylic and methacrylic acid esters. R1: H for acrylates, C for methacrylates; R2: alcohol moiety.
High-pressure liquid chromatography analysis for hydrolysis rate measurements
Reversed phase HPLC separations of the mixtures were performed on an Inertsil C-18 bonded silica column 100 mm in length and 3 mm internal diameter (Chrompack, Bergen op Zoom, The Netherlands). Isocratic elution at 0.4 ml/min with a 20 to 40% water in methanol mobile phase was used depending on the hydrophobicity of the most hydrophobic compound in the mixture. Analyte detection was with a UV detector using a wavelength of 215 nm. Concentrations were quantified using standard solutions of the compounds in methanol.
Assay to measure the reactivity with reduced glutathione
Stock solutions of reduced glutathione (GSH; 1 mM) were made every second day. The GSH was dissolved in water containing 50 μM sodium-EDTA to prevent oxidation. Because the deprotonated form of glutathione, GS−, is a much stronger nucleophile, the reaction was carried out at a pH of 8.8. Therefore, 1 ml of GSH stock solution was diluted with 9 ml of a 1mM sodium-tetraborate buffer solution, resulting in a final GSH concentration of 100 μM. To start the reaction, 0.1 ml of a methanol stock solution of an acrylate or methacrylate was added. The reaction temperature was 20°C. Electrophile concentrations ranged from 0.4 to 1.6 mM. Immediately after adding the electrophile, as well as after a given reaction time (1 h for acrylates and 24 h for methacrylates), a 0.1 ml sample was taken and diluted with 0.9 ml of a buffer with pH 3.9 (2.5 mM citric acid/2.5 mM sodium citrate) to stop the reaction with GS−. The GSH concentration of the samples was subsequently analyzed on the HPLC as described below. All reaction rates were measured in duplicate. No decrease of reduced GSH within 24 h was found in control incubations spiked with methanol only.
High-pressure liquid chromatography analysis for glutathione depletion
Reduced glutathione was separated from the reactive test chemical and the GSH conjugate on a C-18 column, as described above, using isocratic elution at 0.4 ml/min with 10% methanol in an aqueous phosphate buffer (5 mM, pH 3.0) as mobile phase. An RDR-1 reagent delivery unit (Timberline, Boulder, CO, USA) was used for the postcolumn derivatization of reduced glutathione with o-phthalaldehyde. Reaction conditions according to Cohn and Lyle [22] and by Fujita et al. [23] were used with some modifications, including the aqueous derivatization solution contained 7.5 mM o-phthalaldehyde and 5% (v/v) methanol and was buffered at pH 8.0 with 35 mM phosphate buffer. The solution was delivered at 0.3 ml/min in a thermostated reaction coil (1 m, 60°C). The fluorescence of the formed isoindole was monitored at λex = 350 nm and λem = 420 nm. The GSH concentrations were quantified with standard solutions of GSH in citric acid/sodium-citrate buffer.
Calculation of kinetic parameters
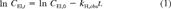 (1)
(1)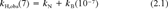 (2)
(2)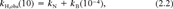 (3)
(3)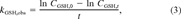 (4)
(4) (5)
(5)| kN | kB | |||||
|---|---|---|---|---|---|---|
| Chemicals | Chemical Abstract no. | s−1 | %SE | s−1M−1 | %SE | Half-life at pH 8.8 (days) |
| 2-Hydroxyethyl acrylate | 818611 | NDb | 1.1E−01 | 14 | 12 | |
| Hydroxypropyl acrylate | 999611 | ND | 3.2E−02 | 48 | 40 | |
| Diethyl fumarate | 623916 | 5.3E−07 | 14 | 2.9E+00 | 7 | 0.4 |
| Ethyl acrylate | 140855 | ND | 5.0E−02 | 3 | 25 | |
| Hexyl acrylate | 2499958 | ND | 8.7E−02 | 1 | 15 | |
| Isobutyl acrylate | 106638 | 1.6E−07 | 101 | 2.0E−02 | 9 | 28 |
| 2-Ethoxyethyl methacrylate | 2370630 | ND | 3.8E−02 | 0.1 | 33 | |
| Allyl methacrylate | 96059 | 7.9E−07 | 62 | 5.9E−02 | 9 | 7 |
| Benzyl methacrylate | 2495376 | ND | 1.1E−01 | 9 | 12 | |
| Isobutyl methacrylate | 97869 | 4.3E−07 | 9 | 7.1E−03 | 15 | 17 |
| Isopropyl methacrylate | 4655349 | 9.2E−07 | 16 | 7.7E−03 | 75 | 8 |
| Methyl methacrylate | 80626 | 9.0E−07 | 30 | 2.6E−02 | 28 | 8 |
| Tetrahydrofurfuryl methacrylate | 2455245 | 3.9E−07 | 4 | 4.4E−02 | 1 | 12 |
- aRate constants were calculated according to Equation 2 from measured hydrolysis rates.
- bND = no significant decrease measured.
Relative deviations from the average of two measurements were reported as %SE.
Quantum chemical calculations
Quantum chemical descriptors were calculated for both the training set and the test set acrylates and methacrylates. Individual structures were built manually, using the SPARTAN builder subprogram, and preoptimized using a modified MM2 force field [26]. Global minimum conformations were located manually using this force field. Optimized structures were subsequently submitted to a full AM1 minimization using either SPARTAN or AMSOL [27]. Results from both programs should be the same within machine precision. Properties were derived from the fully minimized eigenvector matrix. Additionally, AM1-optimized structures were submitted to a single point energy ab initio calculation at the Hartree-Fock/3-21G(*) level, and the same properties as for the semiempirical results were extracted from the ab initio results. Parameters used as descriptors were electrostatic potential fitted charges on selected atoms (q(Ci)) and εLUMO, the energy of the lowest unoccupied molecular orbital.
Quantitative structure–property relationship models and statistical analysis
All QSPR modeling and statistical analysis were performed with the chemometrics package SCAN (Minitab, State College, PA, USA). A partial least square (PLS) model was favored over a multiple regression (MLR) model because descriptor variables were correlated. The cross validated r2 (Q2) was calculated with a leave-one-out procedure.
RESULTS AND DISCUSSION
Quantitative structure–property relationship for hydrolysis
The measured neutral (kN) and base-catalyzed (kB) hydrolysis rate constants of the training set are presented in Table 1 along with their predicted hydrolysis half-lives in the GSH assay reaction buffer at a pH of 8.8. For all but one acrylate (isobutyl acrylate), the neutral hydrolysis rate was below the detection limit of our assay. Methacrylates generally have a higher neutral hydrolysis rate, but the differences between them is small. We found this data set too small to establish a QSPR for the reactivity of the training set compounds toward H2O.
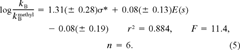 (6)
(6)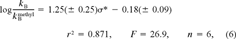 (7)
(7)The estimated hydrolysis rate at pH 8.8 (Table 1) shows that, for all but one compound, hydrolysis does not interfere with the GSH reactivity assay. Half-lives between 4 and 30 d were predicted. Only diethyl fumarate, a diester, had a much higher base-catalyzed hydrolysis rate and consequently a low half-life at pH 8.8. It was therefore excluded from the GSH reactivity assay.
| Chemicals | σ*a | E(s) | log(kB/kmethylB) |
|---|---|---|---|
| Isobutyl methacrylate | −0.19 | −0.93 | −0.565 |
| Benzyl methacrylate | 0.75 | −1.62 | 0.616 |
| Allyl methacrylate | 0.23 | −1.60 | 0.350 |
| Methyl methacrylate | 0.00 | 0.00 | 0.000 |
| Isopropyl methacrylate | −0.19 | −1.71 | −0.534 |
| 2-Ethoxyethyl methacrylate | 0.27 | −2.21 | 0.161 |
| kGSH | Charge density (au) | log kGSH | ||||||
|---|---|---|---|---|---|---|---|---|
| Training set | M−1 min−1 | %SE | Cβ | Cα | C1 | ∈LUMO (eV) | Measured | Predicted |
| Ethyl acrylate | 39.7 | 4.7% | −0.21 | −0.51 | 1.06 | 0.0981 | 1.60 | 1.37 |
| 2-Hydroxyethyl acrylate | 50.9 | 4.4% | −0.21 | −0.50 | 1.04 | 0.0935 | 1.71 | 1.51 |
| Hydroxypropyl acrylate | 42.1 | 13.6% | −0.19 | −0.53 | 1.08 | 0.0880 | 1.47 | 2.01 |
| Isobutyl acrylate | 29.3 | 11.4% | −0.19 | −0.49 | 1.04 | 0.0975 | 1.62 | 1.35 |
| Hexyl acrylate | 20.3 | 8.5% | −0.22 | −0.48 | 1.03 | 0.0988 | 1.31 | 1.16 |
| Isobutyl methacrylate | 0.19 | 18.9% | −0.40 | −0.09 | 0.91 | 0.1042 | −0.73 | −0.52 |
| Isopropyl methacrylatea | NDb | −0.45 | −0.03 | 0.88 | 0.1056 | −1.00 | −0.91 | |
| Benzyl methacrylate | 0.33 | 14.7% | −0.40 | −0.09 | 0.88 | 0.1040 | −0.49 | −0.61 |
| Methyl methacrylate | 0.20 | 17.8% | −0.37 | −0.15 | 0.97 | 0.1045 | −0.70 | −0.17 |
| Allyl methacrylate | 0.51 | 42.9% | −0.44 | −0.07 | 0.94 | 0.1030 | −0.29 | −0.49 |
| Tetrahydrofurfuryl methacrylate | 0.30 | 8.7% | −0.43 | −0.05 | 0.84 | 0.1014 | −0.52 | −0.76 |
| 2-Ethoxyethyl methacrylate | 0.25 | 15.8% | −0.43 | −0.07 | 0.92 | 0.1036 | −0.60 | −0.57 |
- aFor the PLS model, the log kGSH of isobutyl methacrylate was set to −1.00.
- bND = no significant decrease measured.
Quatitative structure–property relationship for reactivity with reduced glutathione
A clear separation in reaction rates toward GSH could be seen between the readily reacting acrylates and the slowly reacting methacrylates (Table 3). Our aim was to derive one QSPR that could describe the reactivity of both groups. Calculated partial charges on the attacked electrophilic carbon as well as Hammett constants have been used successfully by VanderAar et al. [17] to describe the chemical reactivity of a series of 2-substituted 4-nitrobenzenes with GSH. Frontier orbital energies (εLUMO) have been used recently by Soffers et al. [16] to describe the reaction rate of fluorinated nitrobenzenes with glutathione. The rather small variability in reaction rate within the methacrylates, respectively acrylates, in our training set indicates that the electronic effect of the alcohol moiety is less important than the effect of the substitution pattern on the α carbon. The unsaturated β-carbon atom in the acid group is the most probable site of attack in the Michael addition. Therefore, we used local descriptors of this part of the molecule to establish a QSPR for the reactivity with GS−. Based on frontier orbital theory [21, 32], an equation containing two terms can be used to explain differences in reactivity of electrophiles toward a nucleophile. The two terms are a coulombic attraction/repulsion term and the overlap of the frontier orbitals (the highest occupied [HOMO] of the nucleophile and the lowest unoccupied [LUMO] of the electrophile). This framework led us to choose quantum chemical descriptors for a QSPR for the reaction rate with GS− (log kGSH). For the first term, we used the charge densities (q(Ci)) on the three carbon atoms in the acid part of the esters (Cβ, Cα and C1 in Fig. 1). For the second term, we used the energy of εLUMO of the electrophilic acrylates and methacrylates as a single descriptor for orbital overlap in terms of energy. According to Fleming [21], a lower εLUMO of the electrophiles correlates with a smaller difference between the energy of the two interacting molecular orbitals, which in turn yields more energy for bond formation.
| q(Cβ) | q(Cα) | q(C1) | ∈LUMO | |
|---|---|---|---|---|
| Ab initio 3-21G(*) | ||||
| q(Cα) | −0.995 | |||
| q(C1) | 0.930 | −0.943 | ||
| ∈LUMO | −0.835 | 0.847 | −0.791 | |
| log kGSH | 0.968 | −0.98 | 0.902 | −0.848 |
| Semiempirical AM1 | ||||
| q(Cα) | −0.94 | |||
| q(C1) | 0.500 | −0.517 | ||
| ∈LUMO | −0.667 | 0.669 | −0.418 | |
| log kGSH | 0.853 | −0.939 | 0.384 | −0.682 |
These four parameters, q(Cβ), q(Cα), q(C1), and εLUMO, were calculated within two quantum chemical formalisms, semiempirical (AM1) and ab initio (3–21G(*)). Correlation matrices for resulting parameters calculated with the two different approaches as well as for log kGSH are given in Table 4. Generally, the ab initio results correlated better with log kGSH. The two algorithms yielded very similar energies for the εLUMO‘s of the training set. For the charge densities, however, the ab initio algorithm revealed a pronounced difference between acrylates and methacrylates, whereas the semiempirical algorithm (data not shown) did not. Therefore, and because we expected the ab initio calculations to be more precise than semiempirical ones, ab initio results were used in the QSPR. High reactivity of the acrylates correlated with less negative charge density on Cβ, more negative charge density on Cα, and a high positive charge density on C1. These correlations indicate the importance of the coulombic interaction of the thiol anion with the carbon in the β position. As predicted by the theory, a lower εLUMO correlates with higher reactivity toward GS−. The full descriptor set, calculated with the ab initio algorithm, is given in Table 3. All four descriptor variables correlate with each other, so the use of a MLR model might give misleading results [33]. Hence, we used a PLS model to derive a relation between these four descriptors and the reaction rate. In a PLS model, the descriptor variables are transformed to orthogonal (noncorrelating) latent variables [34]. For isopropyl methacrylate, with a reaction rate below the detection limit of our assay, we used a kGSH of 0.10 (/M/min) for the PLS modeling.
| Descriptor | Regression coefficient | Relative importance |
|---|---|---|
| q(Cβ) | 2.65 | 0.264 |
| q(Cα) | −1.37 | −0.267 |
| q(C1) | 3.39 | 0.246 |
| ∈LUMO | −49.33 | −0.231 |
| r2 = 0.932 Q2 = 0.872 n = 12 |
| Charge density (au) | log kGSH (M−1 min−1) | ||||||
|---|---|---|---|---|---|---|---|
| Test set | Chemical Abstract no. | Cβ | Cα | C1 | ∈LUMO (eV) | Literature dataa | Predicted |
| Methyl acrylate | 96333 | −0.15 | −0.57 | 1.14 | 0.1040 | 1.72 | 1.56 |
| Ethyl acrylate | 140885 | −0.21 | −0.51 | 1.06 | 0.0981 | 1.42 | 1.37 |
| Butyl acrylate | 141322 | −0.21 | −0.51 | 1.15 | 0.1053 | 1.59 | 1.31 |
| Methyl methacrylate | 80626 | −0.37 | −0.15 | 0.97 | 0.1045 | −0.48 | −0.17 |
| Ethyl methacrylate | 97632 | −0.36 | −0.14 | 0.92 | 0.1066 | −0.85 | −0.46 |
| Butyl methacrylate | 97881 | −0.36 | −0.16 | 0.98 | 0.1073 | 0.00 | −0.23 |
- a[20].
The PLS model with one latent variable is given in Table 5.
The resulting predictions for log kGSH are given in Table 3. The selected PLS model (Table 5) contains only one latent variable, and all four descriptor importances are almost equal. The proposed site of attack of a thiol anion is the β carbon but, as pointed out by Fleming [21], the molecular orbitals in an allyl system are strongly influenced by electron withdrawing or donating substituents on C1, so it is not surprising that all three carbon atoms in the allyl system are included in the PLS model.
Validation of the quantitative structure–property relationship with a test set of literature data
Although GSH reactivity of acrylic compounds has been measured by several researchers [19, 20, 35], we only found one data set containing different acrylates and methacrylates. We used this data, reported by McCarthy et al. [20], to test the validity of the QSPR presented above (Table 5). Two compounds of this test set, ethyl acrylate and methyl methacrylate, were also present in the training set. The quantum chemical descriptors for all six test set chemicals were calculated as described above using the ab initio formalism and are presented in Table 6. The reaction rates of this literature test set were given at 37°C in an aqueous buffer solution of pH 7, whereas we used a temperature of 20°C and a pH of 8.8. The two chemicals, which are both in the training and the test set, allowed us to compare the influence of the different reaction conditions. Their reaction rates for both conditions, given in Tables 3 and 6, show that the effect of a lower pH (lower concentration of GS−) is partially compensated by a higher temperature. The reported reaction rates of the test set were therefore used without correction, although it is clear that model predictions for this test set could not be as accurate as for the training set. Table 6 shows the predicted reaction rates of the test set calculated with the PLS model (Table 5). It can be concluded that the model is able to predict the large difference in GSH reactivity between methacrylates and acrylates for the four compounds not included in the training set.
Quantum chemical ground state parameters, like the ones used in Table 5, generally give information about the first step of a reaction. For the Michael addition, this step would be the approach of a thiol anion toward the electrophilic carbon Cβ. Due to the good correlation of our PLS model, we think that this is the rate-limiting step. This conclusion is strengthened by the findings of Osman [36], who evaluated the relative reactivity of acrylic and methacrylic acid toward the fluoride anion with ab initio calculations. He found that differences in charge distribution of the ground state structures can explain the difference in reactivity.
Reduced glutathione reactivity and toxicity
Because chemical reactivity is often mentioned as a cause of toxicity [1-6], we compared the measured reaction rates with reported LC50 values for 4-d acute fish toxicity. For this comparison, we used two acrylates and two methacrylates that were very similar regarding hydrophobicity and alcoholic moiety. Log Kow and acute LC50 values were taken from Karabunarliev et al. [5]. Predicted baseline toxicity and toxic ratios (TR) were calculated according to Russom et al. [3]. This data for the four compounds is given in Table 7. Based on an expert classification system to predict modes of action from chemical structure [3], acrylates and methacrylates are supposed to act by different modes of action. Our experimental results show that the low Michael-type acceptor potency of the methacrylates corresponds with their low TR values, which in turn suggests that baseline toxicity (also referred to as narcosis 1) is the predominant mode of action. For the acrylates, which are good Michael-type acceptors, the high TR reveals that they are much more toxic than baseline toxicity would imply. We conclude that reaction rates with glutathione can be used to discriminate between different modes of action.
| Chemicals | log Kowa | LC50a (μM) | Baseline LC50b (μM) | TRc | log kGSH (M−1 min−1 |
|---|---|---|---|---|---|
| Methyl methacrylate | 1.38 | 2,588 | 2,841 | 1.1 | 0.20 |
| Isopropyl methacrylate | 2.25 | 296 | 436 | 1.5 | NDd |
| Ethyl acrylate | 1.32 | 25 | 3,234 | 129 | 39.7 |
| Isobutyl acrylate | 2.22 | 16 | 465 | 28 | 29.3 |
| Allyl methacrylate | 1.57 | 8 | 1,885 | 240 | 0.51 |
The comparison was made with four compounds that have simple aliphatic alcohol groups. It should be noted, however, that the alcohol moiety of the ester may be of toxicological importance. This is shown for allyl methacrylate, for which the relevant data is included in Table 7. This compound has a low kGSH value but is much more toxic than predicted by the baseline QSAR [3, 5]. The hydrolysis product of allyl methacrylate is allyl alcohol, which is known to be a potent hepatotoxin in mammals and fish [37, 38].
CONCLUSION
Two approaches have been used to describe the reactivity of acrylates and methacrylates toward different nucleophiles. For the base-catalyzed hydrolysis of the methacrylates, a linear free energy relationship could be established based on Taft's substituent constants for the leaving alcohols. Two problems were identified for this approach. First, a substituent constantbased QSPR is only valid within structure analogues so that an equation for methacrylates is not a priori valid for acrylates. Second, although many substituent values have been reported in the literature, these compilations are not complete, which hampers the general use of the fragment-based approach.
For the reactivity with glutathione, quantum chemical descriptors were calculated from the three-dimensional structure of the compounds. For a reaction like Michael addition to unsaturated carboxylates, substituent values of the alcohol moiety are less useful because the site of addition is far away from the substituent and there is no large delocalized II-system, as e.g., in benzene rings, that could communicate electronic effects. The presented data shows that ab initio calculations of the electronic structure in the ground state can produce descriptors, that are able to explain the observed reaction rates. The QSPRs based on these parameters can then be used to predict the reactivity of closely related chemicals. Recent investigations in toxicity of ethyl acrylate and other acrylic acid esters in rodents [39, 40] and in fish show that the reactions described above are relevant for the toxicity. Measuring and understanding the reactivity of organic electrophilic compounds will help to identify their predominant modes of toxic action.
Acknowledgements
The financial support of the Swiss National Foundation, grant 83EU-046316, is gratefully acknowledged. This work was, in part, carried out within the EC project Fate and Activity Modeling of Environmental Pollutants Using Structure–Activity Relationships under contract ENV4-CT96-0221.




