MOSAIC_SSD: A new web tool for species sensitivity distribution to include censored data by maximum likelihood
Abstract
Censored data are seldom taken into account in species sensitivity distribution (SSD) analysis. However, they are found in virtually every dataset and sometimes represent the better part of the data. Stringent recommendations on data quality often entail discarding a lot of these meaningful data, resulting in datasets of reduced size which lack representativeness of any realistic community. However, it is reasonably simple to include censored data in SSD by using an extension of the standard maximum likelihood method. The authors detail this approach based on the use of the R-package fitdistrplus, dedicated to the fit of parametric probability distributions. The authors present the new Web tool MOSAIC_SSD, that can fit an SSD on datasets containing any type of data, censored or not. The MOSAIC_SSD Web tool predicts any hazardous concentration and provides bootstrap confidence intervals on the predictions. Finally, the authors illustrate the added value of including censored data in SSD, taking examples from published data. Environ Toxicol Chem 2014; 33:2133–2139. © 2014 SETAC
INTRODUCTION
The species sensitivity distribution (SSD) is a central tool for risk assessment in ecotoxicology. It provides a subtle way to define hazardous concentrations for the environment compared with using arbitrary safety factors. However, the approach is still subject to heated debates regarding its optimal implementation, and no consensus has been reached. As a result, environmental regulatory bodies often advocate country- or region-specific approaches 1-5. In studying SSD, methodological choices based on very theoretical arguments have a direct impact on legislation and significant economic and ecological outcomes. The purposes of the SSD approach are to model interspecies sensitivity variability and to provide a protective concentration for a group of species. Species sensitivity distribution uses sensitivity data as input, such as no-effect concentration, no-observed-effect concentration (NOEC), or x% effective concentration (ECx) for a group of tested species. These can be called critical effect concentrations, which are obtained through acute or chronic toxicity bioassays. The SSD approach is based on the hypothesis that variability in species sensitivity follows a probability distribution. This distribution is extrapolated from the sample of tested species to infer a group-wide protective concentration, the hazardous concentration for p% of the group (HCp). In general, a parametric distribution is assumed. However, assumptions about the distribution can be avoided using distribution-free methods 6.
The SSD approach has many issues 7, ranging from ecological to statistical concerns. Despite the difficulty of addressing all of them, specific aspects can be improved. Throughout the body of work mentioning SSD, there are very few occurrences of properly taking into account missing data, nondetects, or censored data in general. On those rare occurrences, this is achieved in a Bayesian framework 8, which requires statistical expertise not accessible to untrained users. However, censored data contain crucial information, and ignoring or transforming them alters the quality of the predictions based on the remaining data 9. It is possible to deal with censored data in the more familiar frequentist framework using standard maximum likelihood methods. This also offers several advantages over common SSD approaches. In the present study, we present a Web tool, MOSAIC_SSD (http://pbil.univ-lyon1.fr/software/mosaic/ssd/), to easily include censored data in an SSD analysis. The MOSAIC_SSD Web tool relies on the existing R package fitdistrplus10.
In the following sections, we first review the methods to fit a distribution to data to position our tool among the existing SSD approaches. Then, we explain how to include censored data in SSD and present the Web tool we have designed for this purpose, MOSAIC_SSD. Finally, we illustrate the added value of including censored data in SSD using example datasets from published literature.
REVIEW OF METHODS TO FIT AN SSD
Two steps are required to fit an SSD. The first step is to choose a distribution that seems appropriate to describe the data. Possible options include a Weibull distribution 11 to emphasize the tails of the distribution; a triangular distribution 11 with a finite-size support when no species are more sensitive/resilient than a certain threshold value; or a multimodal distribution 12, 13 for an assemblage of several taxons, for example. Log-normal 14 and log-logistic 15 distributions are the customary choices 16, although an extensive list of distributions have been applied to SSD. Alternatively, distribution-free methods can be used to avoid the subjective choice of a distribution for the data. This approach has been used for SSD in various works 6, 8, 17. Among these distribution-free methods, the Kaplan-Meier estimator is a means to include censored data in SSD 8. However, it is restricted to certain types of censored data. One difference between parametric and distribution-free methods is that when fitting a parametric distribution, the possibilities of shapes are restricted to a certain class of distributions, and the shape is refined by adding information from the data. In a distribution-free approach, however, any kind of shape is allowed, and the result emerges solely from the data. Therefore, distribution-free methods do not use any sort of exterior information and often require more data than parametric methods 16, 17. Consequently, when dealing with small datasets, it is more reasonable to fit a parametric distribution.
Each parametric distribution is determined by a set of parameters, so the second step is to estimate them. Parameter estimation is performed by optimizing a chosen criterion: the likelihood or some goodness-of-fit distance. The likelihood function gives the probability of observing the data given the parameters. Maximizing the likelihood implies selecting the parameters for which the probability of observing the data is highest. Maximum likelihood is by far the most standard approach to distribution fitting and more generally to model fitting. It is backed with a consequent body of theoretical work ensuring many interesting asymptotic properties 18: the maximum likelihood estimate converges to the true value of the parameters (consistency), it is the fastest estimate to converge (efficiency), and the difference with the true value is normally distributed (normality), which provides confidence intervals on the parameters. This approach is used by the Australian software BurrliOZ 19, for example, which fits a Burr III distribution to the toxicity data. Moreover, a natural extension of the likelihood function makes it possible to take into account censored data 20.
Another popular method to determine the distribution parameters that best describe the data is the least-square regression on the empirical cumulative distribution function (CDF), which minimizes the sum of the squared vertical distances between the CDF and the data. It is also known as the Cramer-Von Mises distance 21. This approach is adopted by the software CADDIS_SSD 22 from the US Environmental Protection Agency (USEPA), which performs a least-square regression on the CDF with a log-probit function. The software SSD MASTER 23 uses the same method but tries several other distributions: normal, logistic, Gompertz, and Fisher-Tippett. However, regression on the CDF is not an easy method to include censored data, because constructing the CDF implies sorting the data, which is not trivial with censored data. In addition, there is no unique way to build a CDF. Several possible plotting positions 1, 24 all have desirable properties, but none of them represents the data more faithfully than any other. Therefore, the resulting SSD and its predictions depend on purely arbitrary decisions regarding the plotting positions, a fact that undermines its scientific credibility.
A third common approach to determine the distribution parameters is to match the moments of the empirical distribution with those of the model. This is numerically easy when there is an analytical formula for the determination of the parameters. Moment matching is equivalent to maximum likelihood for the distributions of the exponential family, such as the normal, exponential, or gamma distributions, but not for the logistic distribution. The free software ETX 25 uses the moment matching method 14, 15. It fits a log-normal and a log-logistic distribution by moment matching and computes confidence intervals. Moment matching is sensitive to outliers and can give unrealistic results 26. However, it can be useful when the maximum likelihood computation is intractable 26. Moment determination with censored data is not trivial. Therefore, this method cannot be straightforwardly extended to include censored data.
This brief review of the classical SSD approaches shows that several methodological choices must be made to fit an SSD: whether to use a nonparametric method, selection of the distribution and of the parameter estimation method. Apart from maximum likelihood, no straightforward approach exists for a nonexpert in statistics to make use of all types of censored data. Indeed, all of the available turn-key software programs for SSD fitting require the use of noncensored data. Yet, there is a possibility to use the R-package fitdistrplus 10 to fit censored data using maximum likelihood, with the following scheme.
MAXIMUM LIKELIHOOD FOR CENSORED DATA
Maximum likelihood provides a single framework to cope with both censored and noncensored data. Censored data is a general name given to data that are not in the form of fixed values but belong to an interval, bounded or not. Censored sensitivity data occur when determining a critical effect concentration for a given species is not possible. Possible reasons are that the highest concentration tested does not have any noticeable effect, that only a tiny amount of contaminant already stamps out all the individuals, or that the measurement is simply too imprecise to be reasonably described by a single value instead of an interval. In such cases, it is only possible to give a lower bound, a higher bound, or an interval to the critical effect concentration. Such data are called right-censored, left-censored, or interval-censored, respectively. Censored data can also occur when there are multiple values for the sensitivity of 1 species to a given toxicant. When the quality of the data seem equivalent, the European Chemical Agency's (ECHA) advice 5 is to use the geometric mean as a replacement for the different values. It might be more cautious to use these multiple values to define an interval containing the sensitivity of that species. Censored data are very different from doubtful or questionable data, obtained from failed experiments. They are produced using a valid experimental procedure, and they contain information as valid as noncensored data. Censorship is very common, especially for rare species for which scant data are available and for which no standard test procedure exists. Discarding censored data has a downside, because these data could represent the larger part of an extended dataset. For instance, in the work by Dowse et al. 8, discarding censored data entails a division of the number of tested species by a factor of 8.
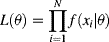 (1)
(1)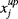 the Nlc upper bounds for left-censored data,
the Nlc upper bounds for left-censored data, 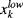 the Nrc lower bounds for right-censored data and
the Nrc lower bounds for right-censored data and 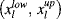 the Nic pairs of bounds for interval-censored data. Then, the previous likelihood function is now extended to
the Nic pairs of bounds for interval-censored data. Then, the previous likelihood function is now extended to
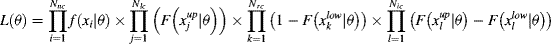 (2)
(2)MOSAIC_SSD
It is possible to use the method described in the previous section using the R-package fitdistrplus 10. R-packages survival 29 and NADA 30 offer the same possibility. However, they require a certain fluency in the R programming language, preventing the widespread use of censored data in ecotoxicology. Minitab 31 is a commercial software with a graphical user interface that fits multiple distributions to censored data rather easily, but there does not seem to be any open-source alternative.
Moreover, fitdistrplus and these other packages and software are not specifically designed for SSD, and their versatility in the choice of distributions and fitting methods might discourage inexperienced users. Thus, we developed a Web interface, MOSAIC_SSD (http://pbil.univ-lyon1.fr/software/mosaic/ssd/), which is a wrap-up of fitdistrplus into an SSD-dedicated online tool. The MOSAIC_SSD tool enables anyone to perform a simple yet statistically sound SSD analysis including censored data without worrying about the conceptually difficult underlying statistical questions. The Web interface is easily accessible via any browser and simple to use; given an input dataset, it sends the calculation to a server and then hands in the result. The input dataset is a text file uploaded by the user with straightforward encoding. A noncensored dataset is given in 1 column. A censored dataset is given as 2 columns: an “NA” in the left column and a number in the right denotes left-censored data, and a number in the left column and an “NA” on the right denotes right-censored data. Two differing numbers denote interval-censored data, and 2 identical numbers represent noncensored data. It is also possible to type in the dataset by copying and pasting it in a text box.
To keep the tool more user-friendly, few options are offered. The user can choose 1 or 2 among the log-normal and log-logistic distributions. These 2 distributions are the most widely used 16, and parameter estimation appears robust enough to accommodate for most datasets, because they contain only 2 parameters. To select which distribution best describes the data, the first step is to perform a qualitative assessment by looking at the representative curves. The value of the likelihood function for each model can then be used as a further decision criterion. The log-logistic distribution has heavier tails than the log-normal and is therefore more conservative in the determination of the 5% hazardous concentration (HC5) 15.
After clicking the run button, the bootstrap 95% confidence intervals are automatically computed. They yield confidence intervals on the parameters of the distribution and on several computed HC5. The bootstrap procedure is not guaranteed to converge, the number of iterations required being strongly dependent on the dataset. Therefore, an automatic check of bootstrap convergence is implemented. The bootstrap procedure is run several times, comparing the magnitude of the results' fluctuations with the span of the confidence interval. This comparison determines whether the bootstrap has converged. In the case that the bootstrap procedure fails to converge, additional computations are launched. If the bootstrap finally converges, or if the process has reached the time limit, the user is advised as to whether the confidence intervals are reliable. Calculating the confidence intervals using a bootstrap method has the advantage of using a unified framework for every distribution. Figure 1 shows a screenshot of the result page of the analysis with an example dataset (provided in MOSAIC_SSD) containing censored data and documenting the salinity tolerance of riverine macro-invertebrates 32 (hereafter referred to as the censored salinity dataset). The dataset contains 72-h 50% lethal concentration (LC50) values for 110 macro-invertebrate species from Australia. Data were collected using rapid toxicity testing 33 and contain noncensored, right-censored, and interval-censored data. The result page shows a graphical representation of the censored data, the distribution parameters, HCp computed for various interesting values of p, and the bootstrap confidence intervals within brackets. Figure 1 also shows the output of an SSD analysis with a noncensored dataset. It actually is a noncensored version of the salinity dataset. The transformation from censored to noncensored dataset follows the customary approach to censored data, which consists of discarding some type of data and transforming others (see Added value of including censored data). An analysis with noncensored data follows identical steps and yields results with the same outline, except that a traditional CDF is used to visualize the data. The obvious difference between the outputs of the censored dataset and the noncensored dataset is the representation of the CDF. For noncensored data, the CDF is represented using the traditional Hazen plotting positions 1. The choice of plotting positions remains arbitrary, and no perfect solution exists 1, 24, so preference was given to the most standard approach. Building a CDF implies defining an ordering for the data. If obvious for noncensored data, such an ordering makes little sense for interval-censored data. They might be ranked according to the median of the interval, the higher bound, or the lower. Adding left- or right-censored data further complicates matters. Within fitdistrplus, the answer to this problem is to use the Turnbull estimate of the CDF, which is a nonparametric maximum likelihood estimator of the CDF 34. This estimate can be obtained through an expectation-maximization algorithm and yields the CDF that predicts the data with the highest probability. The Turnbull estimate is represented as a stepwise curve, as in Figure 1 (top panel).
Finally, MOSAIC_SSD can be used as a stepping stone to perform further analysis with fitdistrplus. The last item on the MOSAIC_SSD result page is not shown on the screenshots. It is an R script offering the possibility to replicate the analysis using fitdistrplus, through a copy and paste operation in R. This script is intended as a stepping stone to using the complete fitdistrplus R-package. It can be adjusted by slightly changing some of the options. For instance, HCp for different values of p can be computed, with an alternative distribution or a different fitting method. Moreover, this script ensures transparency and traceability of the results obtained through MOSAIC_SSD.
ADDED VALUE OF INCLUDING CENSORED DATA
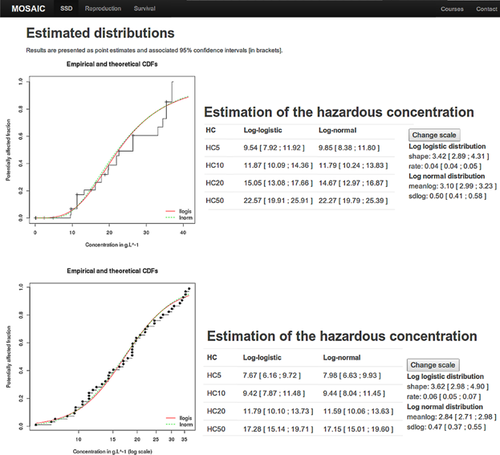
Changing a few parameters in the R script provided within MOSAIC_SSD, it is possible to use fitdistrplus to investigate several fundamental aspects of SSD, such as the influence of including censored data on the prediction. A customary approach when dealing with censored data is to discard or to transform them. More precisely, it is common to discard left- or right-censored data and to take the middle of the interval-censored data as a single value. Two datasets were analyzed to assess the effect of such data transformation on the predicted hazardous concentrations. In the censored salinity dataset, 89 of 108 LC50s (82.4%) are censored, among which 60 (55.6%) are right-censored and 29 (26.8%) interval-censored. Most of the censored data resulted from the testing of rare species, for which the small number of individuals captured prevented the calculation of an LC50 by fitting a concentration–effect model 32. This extensive dataset was collected to be as representative as possible of the species found in nature 32. Therefore, a first asset of taking censored data into account is to abstain from discarding or altering the vast majority of the data. The resulting SSD is therefore more representative of the community it aims to describe. Moreover, using only noncensored data in the analysis introduces a strong selection bias toward abundant species. This is particularly problematic when some rare species are likely to be among those that the environmental manager wishes to protect by carrying out an SSD analysis. The second dataset was published by Koyama 35 and contains vertebral deformity susceptibilities of marine fishes exposed to trifluralin (hereinafter referred to as the censored trifluralin dataset). The measured endpoints are 96-h LC50 on 10 species. Four of the LC50s are censored, among which 2 are right-censored and 2 are left-censored. For this dataset, the obvious advantage of including censored data is that the SSD can be fitted on 10 species, whereas discarding the censored data reduces the size of the dataset to 6 species only. This is below the minimum recommendation of ECHA of 10, preferably 15 36. A noncensored version of the 2 datasets (hereinafter referred to as the transformed salinity and transformed trifluralin datasets) was obtained after the habitual procedure of discarding the right- or left-censored data and taking the middle of the interval-censored data. Fitting the log-normal distribution on the censored and transformed versions of the datasets showed that discarding censored data had an adverse effect on the predicted HC5 (Figure 2). For the salinity dataset, discarding right-censored data induced a clear upward bias for the cumulative curve and therefore a smaller HC5 (Figure 2, left). The estimates for the HC5 and their 95% confidence interval were 9.85 g L−1 (8.38–11.80 g L−1) for the censored dataset and 7.98 g L−1 (6.63–9.93 g L−1) for the transformed dataset, respectively. Underestimating the hazardous concentration might seem a harmless error, because it is more protective to use the transformed salinity dataset. However, that incorrectly low value might motivate the use of costly decontamination measures at a specific location, when efforts could be spared and distributed elsewhere.
The influence of censored data is dataset-dependent, and the bias could be in the opposite direction. This is illustrated on the trifluralin dataset (Figure 2, right). Fitting the log-normal distribution yielded the following estimates and 95% confidence intervals for the HC5: 2.4 × 10−3 mg · L−1 (4.7 × 10−5 − 2.6 × 10−2) for the censored dataset and 1.7 × 10−2 mg · L−1 (8.9 × 10−3 − 4.3 × 10−2 mg · L−1) for the transformed dataset, respectively.
Discarding the censored data led to underestimating the variability in the community sampled by the tested species. Therefore, the width of the distribution was underestimated, and the fifth percentile had a too large value. Discarding the censored data led to an underestimation of the trifluralin real toxicity and of its potential hazard to the environment. Another striking differentiation was that the span of the confidence interval was much larger when censored data were included in the SSD. It reveals that a possible effect of transforming censored datasets is to severely underestimate the width of the confidence interval and to give overconfident predictions on the hazardous concentrations.
To confirm these findings, we studied a published dataset containing 3442 contaminants and 1549 species 37. This dataset contained both censored and noncensored data. Thus, we compared the HC5 obtained on the complete dataset with the HC5 obtained on the transformed dataset including only censored data. To have consistent endpoints for SSDs, we restricted the dataset to LC50 only. We also chose to focus on chemicals for which the proportion of censored data was superior to 10%. The data were aggregated to accommodate for the presence of multiple sensitivity values for the same contaminant, species, and endpoint. The aggregation procedure is detailed in the Supplemental Data. Two subsets of the dataset were considered: 1) a well-documented subset (data-rich), containing more than 10 species per contaminant to produce good quality SSDs, and 2) a poorly documented contaminant dataset (data-poor), containing between 5 and 9 noncensored LC50 after aggregation. This second subset represents a common situation with insufficient precise information on the species sensitivities to the contaminant. On each of these subsets, we studied the ratio of the noncensored HC5 over the censored HC5. We also studied the ratio of the noncensored lower bound of the 95% confidence interval on the HC5 (HC52.5%) over the censored HC52.5% for both datasets. The HC52.5% has been proposed to derive safe concentration levels for contaminants 16. The computation of the confidence intervals is detailed in the Supplemental Data. The study of the large ecotoxicity database revealed that it is risky to discard or transform censored data. When sufficient noncensored data are available, the value of the HC5 might prove relatively insensitive to the degradation of the information induced by arbitrarily transforming censored data into noncensored data. The maximum bias introduced was a factor 5 larger or smaller, which is comparable to the largest safety factors that can be applied to the HC5. When few data are available, however, it appears to be crucially important to include censored data in the determination of the HC5. The bias on the HC5 can lead to an overestimation by a factor of 80, yielding safe concentrations that fail to protect the target communities. The bias on the HC52.5% can be even greater, as it reached 5 orders of magnitude on the dataset studied. Finally, because MOSAIC_SSD provides a transparent method to deal with censored data, there remains no particular reason to transform the data. The detailed results of the analysis, along with the database, are provided in the Supplemental Data.
DISCUSSION
In the present study, we reviewed the general approach to fit an SSD to sensitivity data and explained how it was possible to use maximum likelihood to include censored data in SSD. We presented MOSAIC_SSD, a Web tool that enables any user to perform an SSD analysis including censored data with few very simple steps. The MOSAIC_SSD tool is an interface to a more versatile tool, the R package fitdistrplus 10, and presents only a handful of options to simplify the use. We supported the methodological approach behind MOSAIC_SSD with several arguments and showed the added value of including censored data into the SSD. Discarding or transforming censored data has been shown to alter the results of the SSD analysis. Using MOSAIC_SSD is a convenient way to take censored data into account in the fitting of an SSD. Moreover, the sound general statistical approach is also an asset to perform any sort of SSD. Considering the choice of a distribution, MOSAIC_SSD provides by default 2 standard distributions, the log-normal and log-logistic, but it encourages the use of alternative distributions by providing a stepping stone to using the R package fitdistrplus. The question of which distribution best fits a dataset cannot have a general answer and must be addressed by testing several options. Therefore, the possibility of trying multiple distributions is a valuable asset. For instance, a user might wish to fit a distribution that best describes the tails of the dataset, because determining an HC5 is an extreme quantile estimation problem. In that case, a heavy tailed distribution such as Weibull or exponential is appropriate.
In selecting a distribution, it is important not to pick a distribution with too many parameters. One of the easily accessible software programs for SSD is BurrliOZ 19, which fits the Burr III distribution using maximum likelihood and computes confidence intervals using bootstrap. The Burr III distribution is very flexible 13, but it contains 1 parameter more than the log-normal or log-logistic distributions. Fitting of a distribution with many parameters requires a lot of data, and the Burr III distribution is likely to suffer from strong structural correlation among the parameters 13. Therefore, convergence can be difficult, and the estimates produced are not very reliable. However, BurrliOZ is currently being developed to fit the log-logistic distribution on small datasets and to provide a comparison between at least the log-logistic and the Burr III distribution for larger datasets 3.
Because it is easily accessible and user-friendly, MOSAIC_SSD can encourage the inclusion of censored data in SSD analysis to better use all of the data at hand. We did not address all of the methodological issues relating to the SSD approach but tried to improve the existing methods, with the aim of making the most of the available data given the cost of collecting them. Questions remain as to what might happen if the proportion of censored data is too great and the dataset is small. It is not possible to test this situation thoroughly, because there are many ways to censor data and no trivial way to choose between them. A good practice would be to consider the span of the confidence interval around the hazardous concentration of interest and decide whether the dataset is adequate for predicting such concentrations or whether more data need to be collected. Taking censored data into account would therefore be crucial to have a precise assessment of the confidence interval and not an artificially reduced estimation as in the trifluralin dataset.
We mentioned that censored data might represent an important part of any dataset and that MOSAIC_SSD could be profitably used on many occasions. In particular, inclusion of censored data appeared most important when few noncensored data were available on contaminants. However, this work could have a more general scope, because fundamentally all data with confidence intervals could be considered interval-censored data. Indeed, the confidence interval around any critical effect concentration estimate can be considered as the range that has a 95% probability of containing the real value and could be reported as interval-censored data. Using the confidence intervals on the critical effect concentrations as censored data provides a basic way to propagate the uncertainty on the critical effect concentration into the SSD, a fundamental problem of SSD 3 that is seldom addressed 38.
Moreover, lowest-observed-effect concentration (LOEC) data, which are often reported, are indeed left-censored data. The only information LOEC carries is that the NOEC lies below this concentration 39. Therefore, the SSD approach we propose, which includes censored data, would allow ecotoxicologists to better use the available experimental data used to calculate the NOEC.
However, we reached the limits of a traditional SSD based on critical effect concentrations and still discarded a lot of information. Indeed, a critical effect concentration is only a summary of a full concentration–effect curve. This summary sets aside several aspects of the response of a species to a pollutant, such as the slope of the curve. This slope describes whether the species is gradually affected or there is a sudden drastic effect. Including all the information present in the experimental concentration–effect curve in the SSD by building a hierarchical model of SSD is possible. This hierarchy would model the joint probability of all of the parameters describing a concentration–effect curve, not only the critical effect concentration in the classical SSD 40. Moreover, this would also take proper account of the uncertainty on the species response modeling and propagate uncertainty into the SSD.
SUPPLEMENTAL DATA
Tables S1.
Figures S1–S2. (175 KB DOC).
Acknowledgment
Financial support for the PhD of G. Kon Kam King is provided by the Région Rhône-Alpes. The authors thank C. Poix for English proofreading.




