Full-scale shaking table test and numerical modeling of a 3000-liter legged storage tank isolated with a vertical rocking isolation system
Abstract
This paper presents the numerical and experimental evaluation of a vertical-rocking isolation (VRI). This evaluation is done by 1-D shaking table tests performed on a full-scale legged storage tank of 3000-liters capacity and its representation through a simple yet representative rigid lumped-mass model approach. The isolation system setup consisted of four ISO3D-2G devices, each one placed on each leg of the tank, which uses high-damping natural rubber to generate the restoring and dissipative forces. The ISO3D-2G device is vertically flexible and laterally rigid, enabling the isolation mechanism of the rocking motion of the tank. The experiments were carried out using three white noise for the system identification and 17 ground motions inputs for the system validation. The measured variables included the lateral acceleration and displacement of the tank, and the vertical and rotational behavior of the isolation interface. The identification results showed a vertical-rotational coupled fundamental mode that is highly dependent on the amplitude of deformation, with a period varying from 0.5 to more than 1 s, depending on the intensity of the motion. The maximum displacement of the tank at the top remained below 13 cm with total accelerations of nearly 0.3 g, both for motions with Peak Ground Acceleration (PGA) values ranging from 0.3 to 0.8 g. The mean maximum values were predicted with the simplified model with errors of less than 10% and 21% for displacements and accelerations, respectively. Finally, the results show that the behavior of vertical-rocking isolated structures can be predicted by simplified models with reasonable errors and that the development of simple design guidelines and equations for VRI systems is possible.
1 INTRODUCTION
During the last decades, seismic isolation has been widely applied worldwide to protect structures.1-3 Historically, base isolation has been achieved by placing a horizontally flexible interface underneath the structure to decouple it from the ground, thus elongating its natural period to values where lower spectral accelerations are expected. Several ways of materializing this behavior have already been proposed,4 such as elastomeric bearings, sliding plates, roller or ball bearings, sleeved piles, cable suspension systems, air cushions, and coil springs. Moreover, there have been attempts to develop 3D dimensional seismic isolation concepts that would also protect a structure or an important piece of equipment from vertical ground excitations. This is generally achieved by including an additional device to provide the vertical isolation, which is placed in series to the one that is providing the horizontal isolation. Some common examples are the use of Frictional Pendulum or laminated rubber bearings supported on different vertically flexible systems,5-11 or even vertical helical springs in viscous fluid.12 Most of these studies suppressed the rocking motion caused by the horizontal-vertical coupling.
The focus of seismic isolation has been set on protecting essential buildings (e.g., residential apartments, hospitals, storage facilities, power plants) or bridges.3, 4 However, some individual critical components from industrial facilities and essential services have shown a poor performance on recent earthquakes,13 demonstrating that essential and valuable equipment might also require targeted seismic protection. Although the principle of seismic isolation remains the same irrespective of the size of the isolated object, using devices designed for buildings to isolate equipment is impractical (e.g., due to instability issues of rubber bearings14) or not cost-effective. Consequently, it is necessary to invent isolation mechanisms and devices to better fit the specific requirements of lighter structures and equipment of industrial facilities in a cost-efficient way.
The most widely used method of seismic isolation involves placing a flexible or sliding interface between the structure and the ground that causes the structure to sustain a translational relative to the ground motion. Alternatively, rocking isolation strategies can be used where structures or equipment sustain rotational motions on a rotationally flexible interface, which can even uplift. The uplift works as a mechanical fuse and limits the design forces on the superstructure. Even though rocking isolation for buildings and bridges has not yet found widespread application, such systems have been widely used to protect slender electrical substation equipment, that because of their shape, horizontal base isolation is not the most effective way of protection. Wire ropes devices15 and friction spring dampers16 are typically used for this purpose. For the former, a comprehensive experimental and numerical study was performed on a cabinet and computer equipment almost 30 years ago,17, 18 validating its effectiveness in protecting this type of equipment. This work concluded that there are cases where it is impractical to follow the classical isolation approach of increasing the fundamental period to large values: some equipment can be protected with damping and relatively small isolation periods. Since these devices are anchored to the structure and the ground, when they dynamically reach their maximum displacement—whether in tension or compression—they get locked and transmit impact forces to the structure, which may lead to significant damage and even collapse.
Due to an inherent fear of collapse by overturning, uplift of both structures and equipment is usually restrained (e.g., using large foundations on buildings or anchorages on uplifting equipment). Nevertheless, it is well known that restraining this behavior leads to an increase of the internal forces on the elements which are transmitted to the foundation. For example, observations after the 1960 Mw 9.5 Valdivia earthquake showed that tall “golf-ball-on-a-tee” structures behaved better than fixed-base ones.19, 20
Several industrial equipment have been damaged during seismic events worldwide, often causing additional financial losses due to loss of functionality. For example, damage on substation equipment interrupts the energy distribution to the population,21 damage on rotating machinery generates significant downtimes for companies,13 damage on hospital equipment compromises its healthcare responsiveness capacity,22, 23 while damage in nuclear power plants may have dramatic consequences.24 Legged thin-walled liquid storage tanks have shown a deficient seismic performance during recent earthquakes, generating significant economic losses and calling the industry's attention to adopt a practical solution. For instance, in the 2010 Mw 8.8 Maule, Chile Earthquake, approximately 125 million liters of wine were lost, equivalent to about 250 million US dollars. This loss represented 12.5% of 2009's year production even though the earthquake occurred a few weeks before the 2010 annual grape harvest25 (i.e., not all tanks were at maximum capacity). The same poor performance was observed again in later events, such as the 2011 Christchurch, 2013 Marlborough, and 2016 Kaikōura Earthquakes in New Zealand,26, 27 the 2012 Emilia Earthquake in Italy,28 the 2014 South Napa Earthquake in the USA,29 and again the 2015 Coquimbo Earthquake in Chile. Winery industries were severely affected in all these events, further demonstrating that finding a cost-effective seismic protection system for thin-walled storage tanks is urgently needed since other devices used in buildings are too expensive for this type of structure.
The purpose of this research is to experimentally evaluate the dynamic performance of a Vertical-Rocking Isolation (VRI) system with uplift allowed on a 3000-liters legged storage tank, and to validate a numerical model to represent the behavior of the whole system. The isolation system comprises four ISO3D-2G devices49, which use unbonded rubber to provide restoring and dissipative forces. The whole device can only take compression. However, a compressive deformation of the device causes part of the rubber (i.e., the central annular rubber) to be in compression and part of the rubber (i.e., the rubber bands) to be in tension. Hence, there is a distinction between “tension (or compression) of the device” and “tension (or compression) of the individual rubber parts.” This system is expected to be a relatively low-cost solution due to the unbonded condition of the rubber (no vulcanization or bonding process is needed) and the absence of anchors to the foundation. The tests were carried out on a 1-D shaking table located at the Structural Engineering laboratory of Pontificia Universidad Católica de Chile. The isolated tank was subject to mainly two sets of inputs: (i) a white noise input scaled to three different intensities in order to perform system identification and compare it to the behavior of the fixed-to-the-base tank, and to (ii) 17 consecutive shaking table tests with records scaled at different intensities. These records included natural and artificial ground motions of the 8.8 Mw Maule, Chile earthquake.
This paper starts by presenting the fundamental aspects of the vertical rocking isolation system with its theoretical background. Then, the complete experimental campaign is described, followed by a section with the system identification of the structure performed with the white noise inputs. A simplified rigid-body model is developed to represent the behavior of the tank and isolators. Finally, the results and observations of the tests are presented, as well as the performance of the numerical model to estimate the measured peak responses.
2 FUNDAMENTAL ASPECTS OF THE VERTICAL-ROCKING ISOLATION SYSTEM
2.1 Description of the VRI system
In contrast to traditional base isolation, a VRI system involves a vertically and rotationally flexible yet laterally rigid isolation interface between the structure and the ground; the system is also allowed to uplift freely. To the best of the authors’ knowledge, this isolation concept was first introduced by Almazán et al.30 as a viable alternative to protect wine storage tanks against earthquakes.
The desired flexible degrees of freedom at the isolation interface are two, rotation and vertical translation. Lateral translation and torsional rotation are restricted at the isolation interface. In contrast, isolation effects should be generated entirely by the rotation at the base of the structure. In addition, for large demand, the system allows for the uplifting of the isolation interface to limit the design forces transmitted to the structure.31-33 Allowing for the uplifting of the isolation interface enables easy equipment relocation inside the facility (there is no need to anchor the structure to the floor), and the forces transmitted to the foundations are considerably reduced by lowering their dimension and cost. The vertical flexibility makes this system a three-dimensional isolation system; however, tests involving vertical excitation are not possible since the shake table can only reproduce 1D motions.
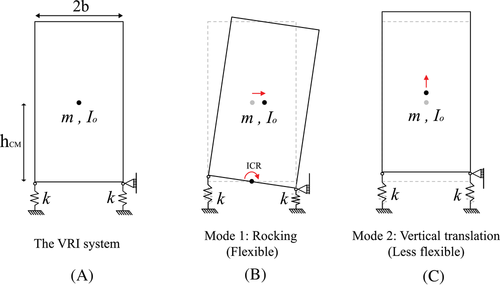
2.2 Rocking behavior of the VRI
Since the isolation system is allowed to uplift, it has two well-defined phases: (i) a pre-uplift phase where all devices are in contact with the ground, with all VRIs in compression; and (ii) a post-uplift phase with some devices uplifting from the ground, and the isolation mechanism due to the rotation as a rigid body. To gain insight on the second phase, this section studies two cases of support of a rigid rocking block on: (i) a rigid surface, and (ii) a two-spring foundation,34-36 with no lateral sliding allowed. Figure 2 illustrates these cases, including the idealized global lateral force-deformation relation at the CM.
Whatever parameters are chosen, there is always an upper bound for the uplifting forces, that is, uplift works as a mechanical fuse. This is why rocking has been suggested as a seismic isolation strategy.32
2.3 Design considerations and device selection
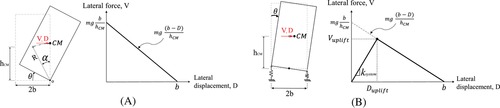
Based on the idealized pushover curve, the main design parameters for the system are two: (i) the vertical stiffness of the devices, and (ii) their position. Therefore, it is interesting to analyze the effect of these variables on the pushover curve by a qualitative parametric analysis. Figure 3A presents the effect on the pushover curve of varying the stiffness of the device, maintaining a fixed separation of b. This variation modifies the pre-uplift stiffness of the system, affecting the necessary force and displacement to produce uplifting. On the other hand, Figure 3B shows the effect of varying the separation b for a fixed value of stiffness of the devices. In this case, in addition to changing the displacement limit, it also affects the uplift force and displacement. In both cases, the pre-uplift stiffness of the system must be positive, and it imposes constraints on the minimum values of devices stiffness, k, and position b.
The devices should reduce the seismic demand by (i) period elongation, and (ii) energy dissipation; and hence, they should have appropriate values of axial stiffness and damping while being laterally stiff. Adding more damping not only has a fundamental role in reducing deformations but also in reducing the base shear, which is highly desirable when no adverse side effects are expected (e.g., increased floor accelerations or inter-story drift when damping is increased as in base-isolated buildings).37 Previous studies on the VRI system suggest that when devices with sufficient energy dissipation capacity are used, it is not strictly necessary to elongate the period of the structure to values larger than 1.5 seconds to reduce the seismic demand considerably. In this context, further studies need to be performed to identify the optimal and physically viable stiffness-damping relation of the devices for a given desired performance through an iso-performance38 or similar method.
Regarding the possible drawbacks of the VRI, two crucial aspects should be carefully considered to achieve a successful performance and assess whether the VRI is a proper system for a specific structure. First, the isolation mechanism is also the vertical supporting system, so the larger the lateral flexibility, the larger the vertical gravitational deformation. For structures with weights over 1000 kN, manufacturing a compact device with controlled self-weight deformation for seismic applications may be too expensive or require too many devices to distribute vertical loads. Instead, this can be handled by precompression of the devices or changing their plan layout to provide a different lateral behavior for the same vertical load. Second, even though rocking isolation systems tend to be more effective on slender structures, avoiding the instabilities resulting from Equation (7) might lead to relatively large design values for the stiffness of the individual devices or their separation.
3 DESCRIPTION OF THE EXPERIMENTAL PROGRAM
The structure used in this paper to validate the VRI system is a typical legged wine storage tank used in the winemaking process. The collapse of these structures during seismic events is due mainly to the low thickness of the vessel walls, which permits local buckling of the mantle or legs of the tank. The latter is the most common failure because the legs support the tank weight and must also directly support the lateral forces induced by the ground motion. Moreover, since the legs are anchored, the tension or uplift generated on the devices of one side by the overturning moment causes compression to increase drastically on the opposite legs. Furthermore, this axial-shear force interaction on the legs can be worsened by the simultaneous action of the earthquake's vertical component,39-41 especially close to the epicenter of the earthquake. Thus, it is of interest to apply a VRI system with the possibility of uplift to these types of structures, which besides reducing the lateral demand, also helps in isolating from the vertical component of the earthquake.
3.1 Experimental setup
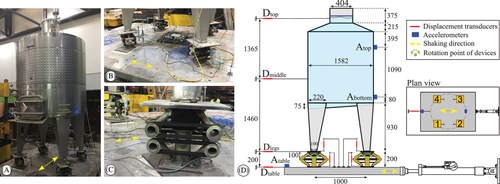
The test structure corresponds to a typical 3000-liter storage tank supported on four ISO3D-2G devices, welded to the four legs of the tank. The tank was placed on a 1-D shaking table installed at the Laboratory of the Department of Structural and Geotechnical Engineering of the Pontificia Universidad Católica de Chile. Therefore, the behavior under 3D excitation is not studied in this work. For 4 tons payload, the maximum velocity and acceleration of the table is 200 mm/s and 0.5 g, respectively; the maximum stroke is ± 500 mm.
A 2 mm neoprene sheet was placed below the devices to increase friction with the table and avoid sliding. The liquid used in the tests was water (similar density to wine), and a baffle was placed in the neck to minimize sloshing. This small-free-surface condition is also consistent with practice in the winemaking process (i.e., tanks fully filled with wine). The total mass of the steel tank (without water inside) is mtank = 250 kg, and its CM is at the height of 1573 mm with respect to the rotation point of the devices (see Figure 4D).
The instrumentation considered (see Figure 4D): (i) three linear variable differential transformers (LVDTs) to measure the absolute lateral displacement at the isolation level (Dlegs), close to the midheight (Dmiddle), and at the top of the structure (Dtop); (ii) an LVDT to measure the absolute lateral displacement of the table; (iii) four LVDTs to measure the vertical displacement at the top of the devices with respect to the shaking table, (iv) two LVDTs to measure the vertical uplift from the table of two diagonally opposite devices; and (v) three piezoelectric accelerometers measuring the horizontal acceleration of the tank at a different height and the horizontal acceleration of the shaking table (all the accelerometers were set up in the direction of the applied motion). All sampling frequencies were set to 100 Hz for the white noise inputs and 200 Hz for the seismic inputs.
3.2 History of loading and testing protocols
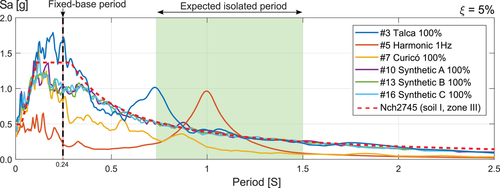
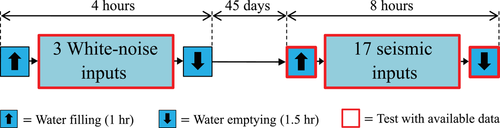
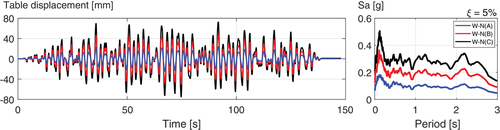
The first excitations were three White-noise (W-N) records scaled to three different intensities, referred to as W-N(A), W-N(B), and W-N(C); with measured PGA values at the shaking table of 0.096, 0.183, and 0.262 g, respectively. After 45 days, and within a time frame of about 8 h, the structure was subjected to 17 consecutive excitations (less than 2 min elapsed between each test of the same record at different scaling). Both artificial, as well as natural excitations recorded from the 2010 Mw 8.8 Maule Earthquake, were used. These records were also used by Colombo and Almazán.42 The target spectrum of the artificial records corresponded to the Chilean code spectrum for seismically isolated structures for 5% damping, soil type I, and seismic zone III. Additionally, one of the records corresponded to a harmonic sinusoidal input with a frequency of 1Hz.
Table 1 presents all input records with their respective identifier number, names, scaling, and measured peak acceleration, velocity, and displacement. Table 1 also presents the spectral acceleration values for a tank fixed-to-the base (T = 0.24s, ξ = 5%) and the total acceleration at the CM of the tank (ACM) measured during the tests (obtained by interpolation between Amiddle and Atop at the position of the CM and after passing the recorded signal through a low-pass filter with a cut-off frequency of 30 Hz), with its respective reduction ratio, which is discussed in Section 6.1. All acceleration records that were used as input for the table were filtered using a low-pass (LP) filter with a cut-off frequency of 40 Hz, and a high-pass (HP) filter with a cut-off frequency of 0.1 Hz. The controller integrates this signal to produce a displacement signal which afterward passes through a HP filter with a cut-off frequency of 0.2 Hz. Since the tested structure was full scale, no time scaling was necessary. Figure 5 presents the response spectra of the records as measured on the table. For reasons of figure clarity, not all spectra are presented, but since the remaining ones are scaled versions of the presented ones, Figure 5 provides enough information to derive the spectra that are not shown. Note, that the spectra of the measured motions that are not shown were indeed scaled versions of the spectra of the measured motions that are shown. Before and after these tests, the tank was filled and emptied, measuring the vertical deformation of the devices. The sequence of all these tests and the timeframe is schematically presented in Figure 6.
| # ID | Record name | Scaling | PGA [g] | PGV [mm/s] | PGD [mm] | Fixed-base CM accel. (numerical prediction) [g] | Isolated CM accel. (test measurement) [g] | |
|---|---|---|---|---|---|---|---|---|
| A | W-N(A) | 33% | 0.096 | 86 | 25.2 | - | - | - |
| B | W-N(B) | 66% | 0.183 | 166 | 50.3 | - | - | - |
| C | W-N(C) | 100% | 0.262 | 243 | 76.0 | - | - | - |
| 1 | Talca | 50% | 0.287 | 202 | 39.2 | 0.81 | 0.12 | 6.8 |
| 2 | Talca | 75% | 0.435 | 307 | 59.9 | 1.20 | 0.15 | 8.0 |
| 3 | Talca | 100% | 0.589 | 408 | 77.4 | 1.65 | 0.18 | 9.2 |
| 4 | Talca | 120% | 0.783 | 464 | 84.1 | 1.96 | 0.19 | 10.3 |
| 5 | Harmonic (1 Hz) | 65% | 0.307 | 191 | 25.2 | - | - | - |
| 6 | Curicó | 75% | 0.303 | 125 | 24.7 | 0.64 | 0.12 | 5.3 |
| 7 | Curicó | 100% | 0.419 | 152 | 31.9 | 0.86 | 0.14 | 6.1 |
| 8 | Curicó | 120% | 0.527 | 182 | 36.5 | 1.04 | 0.15 | 6.9 |
| 9 | Synthetic A | 75% | 0.431 | 186 | 31.3 | 0.77 | 0.14 | 5.5 |
| 10 | Synthetic A | 100% | 0.499 | 260 | 42.5 | 1.03 | 0.17 | 6.1 |
| 11 | Synthetic A | 120% | 0.566 | 314 | 51.9 | 1.25 | 0.18 | 6.9 |
| 12 | Synthetic B | 75% | 0.431 | 187 | 32.6 | 0.69 | 0.14 | 4.9 |
| 13 | Synthetic B | 100% | 0.526 | 241 | 43.6 | 0.95 | 0.16 | 5.9 |
| 14 | Synthetic B | 120% | 0.560 | 283 | 52.0 | 1.14 | 0.18 | 6.3 |
| 15 | Synthetic C | 75% | 0.454 | 204 | 29.7 | 0.77 | 0.13 | 5.9 |
| 16 | Synthetic C | 100% | 0.488 | 276 | 39.7 | 1.03 | 0.16 | 6.4 |
| 17 | Synthetic C | 120% | 0.591 | 307 | 47.8 | 1.27 | 0.18 | 7.1 |
| Mean | 6.7 |
4 SYSTEM IDENTIFICATION
Figure 7 plots the measured displacement of the table and the elastic response spectra for ξ = 5% of damping ratio for the three white noise acceleration records. The identification was performed with two methods: (i) the Empirical Transfer Function Estimate (ETFE) method, and (ii) the analytical Transfer function (TF). The purpose of this identification is to provide the outcome of simple yet effective methods to identify the main structural properties (i.e., fundamental frequency and damping). The input and output signals used for the identification were the measured total acceleration at the shaking table and at the bottom of the mantle.
4.1 Empirical transfer function estimate method
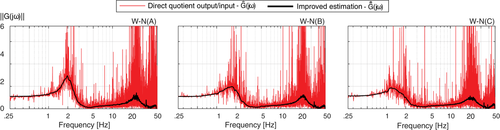
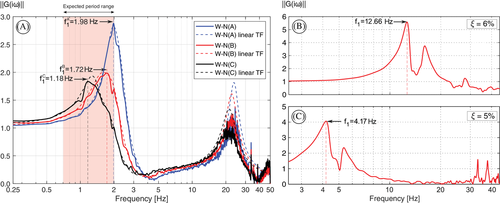
Auad45 previously performed the system identification of the same tank under fixed-base conditions, on the same shaking table, and similar instrumentation. Figure 9A shows the ETF estimations presented in Figure 8, while Figures 9B and C presents the amplitude of the estimated empirical TF for the empty and completely water-filled tank under fixed-base conditions, respectively. These latter two plots were constructed directly from the information provided by Auad, using the same identification method. It can be observed that the empty fixed-base tank presents a fundamental period of 1/12.66 = 0.079 seconds, which increases to 0.24 s when it is filled with water.
A well-accepted way of modeling flat cylindrical tanks with liquid inside is with Mass-Spring Mechanical (MSM) models.46, 47 MSM models separate the mass of the liquid into an impulsive mass that moves rigidly attached to the tank, and several convective masses that move according to different sloshing modes. A spring, a dashpot, and a centroid wall pressure height need to be assigned to each mass. In the fixed-base tests presented in this work, assuming that the increase of the period when the tank is full of water is only due to a rigidly-attached-to-the-wall lumped mass (the “impulsive mass”), the latter can be estimated as approximately 74% of the total water mass. This amount is considerably less than the whole mass of the liquid, even though the reduced top cross-section is expected to have reduced sloshing and the convective contribution of the liquid and make it act almost entirely as an impulsive mass. However, since the geometry of the tank, filled condition, and dynamic behavior (i.e., lateral and rotational elasticity provided by the legs of the tanks) is more complex than the ones analyzed in the literature, there is not enough basis to attribute the 26% remaining missing mass to a convective mass. However, it cannot be overlooked that this value of 74% is very close to the proposed 77% impulsive mass ratio for flat cylindrical tanks of a similar aspect ratio46, 48 (see Section 5.1 for details on determining this 77%). Therefore, further analyses including detailed Fluid-Structure Interaction (FSI) models need to be performed to better understand why these experimental and theoretical values were close.
Figure 9A presents the analytical TFs of the system in dashed line and are discussed in the following subsection. Both the frequency of the fundamental mode and the maximum amplitude of , decrease for higher intensities, representing a highly nonlinear behavior in terms of stiffness and damping dependence on the deformation amplitude.
These insights are consistent with previous findings49, 50 and can be explained by the observed local behavior of the ISO3D-2G devices. The decrease of the eigenfrequencies for stronger excitation is due to a reduction of the effective vertical stiffness of the isolation device at larger deformations. The damping dependence is due to the increased energy dissipation of the dampers for larger deformations, as the dissipated energy increases with the deformation with a power of 1.5.49
Additionally, a second mode with a frequency close to 20–25 Hz was identified. The frequency and amplitude for that mode seem to be relatively unaffected by the intensity of the ground motion. This amplitude-independence suggests that in this mode, the vertical deformation of the devices does not participate and it may be due to the lateral flexibility provided by the leg-device assembly—a mode that is not taken into account when the tank is modeled as a rigid body. The demands obtained with the white noise inputs are lower than those expected during a seismic event, so following the observed trend, it would be expected that the fundamental frequency of the structure during strong earthquakes could still decrease up to values near 1.0 Hz.
The half-power bandwidth (HPB) method51 was employed in the first peak of each TF shown in Figure 9A to estimate the damping of the system; the identified damping was larger than 30% in all cases. These high values are not consistent with the observed behavior of the system during the tests, nor with the expected estimation errors in the HPB method,52 so the observed peaks may represent more than a single mode. Even though a maximum value for the peaks is recognizable, the contribution from a close frequency seems to be present in all three cases. This suggests that two modes with close frequencies may be mixed in the identification, thus explaining the significant errors obtained when estimating the damping with the HPB method. These two mixed modes could represent coupling between the rocking and vertical modes. This coupling is due to the nonlinear behavior of the devices that causes the ICR not to be in the center of the system, as the ICR position depends on the tangent stiffness of the devices. This coupling causes the interaction of these two modes. Consequently, analytical TFs of an equivalent linear system will be identified to estimate the damping and frequencies of the system.
4.2 Analytical transfer function estimation
To perform a quantitative identification of the system, the coefficients of an analytical TF that best fit the observed behavior were obtained. The coefficients of continuous-time TF were obtained directly from the measured discrete-time signal using the Control System Toolbox of Matlab (i.e., tfest() function). The Instrument Variable method53 was used to initialize the parameter values (i.e., the coefficients of the TF) and the Trust-region-reflective algorithm54, 55 for the iterative estimation. The objective function was set to minimize the norm of the prediction error vector. A number of six poles (three modes) were identified in the TF, to observe the two low-frequency-coupled modes and the high-frequency mode. Table 2 presents the properties of the identified TF for each record, including poles, damping, frequency, and goodness of fit. The latter corresponds to the Normalized Root Mean Squared Error (NRMSE) expressed as the percentage 100(1-NRMSE).
| Record | Mode | Conjugate Poles | Damping [%] | Frequency [Hz] | Goodness of fit [%] |
|---|---|---|---|---|---|
| W-N(A) | 1 | −1.95 ± 1.23i | 15.7 | 1.98 | 78.83 |
| 2 | −2.21 ± 14.5i | 15.0 | 2.34 | ||
| 3 | −15.2 ± 148i | 10.2 | 23.73 | ||
| W-N(B) | 1 | −2.59 ± 9.55i | 26.1 | 1.58 | 78.88 |
| 2 | −2.57 ± 12.7i | 19.9 | 2.06 | ||
| 3 | −16.8 ± 142i | 11.8 | 22.70 | ||
| W-N(C) | 1 | −1.81 ± 8.33i | 21.2 | 1.36 | 78.99 |
| 2 | −2.33 ± 11.4i | 20.2 | 1.85 | ||
| 3 | −20.2 ± 134i | 14.9 | 21.60 |
For each case, two modes with a very similar frequency were identified. These modes cannot be clearly differentiated by visual inspection of Figure 9A, and validates the existence of two close modes. In this same plot, the identified linear TFs are plotted with dashed lines, and the match with the empirical identification is reasonably good for the three modes in terms of frequency and amplitude. Figure 10 compares the measured acceleration at the bottom of the mantle and the simulated output with the identified TFs, where some high and low amplitude zones are zoomed in. The results show that the linear system can predict the large and small amplitudes reasonably well and that for a given intensity demand, the isolation system may be linearized. This level of accuracy is sufficient for engineering purposes since only the maximum deformation and acceleration levels are of interest for design; however, the approach is not practical since different TFs would be needed to predict the response for different intensities, which are not known in advance. Also, linear TFs cannot identify possible uplift on the system for higher demand. Therefore, it is necessary to follow a different approach to be able to capture these effects, and in the following section, a simplified structural model is built for the VRI system.
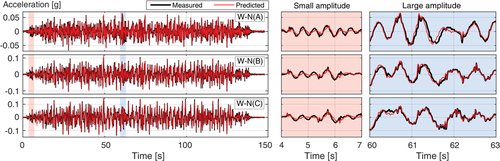
5 SIMPLIFIED NUMERICAL MODELING OF THE VRI SYSTEM
5.1 Simplified equations of motion
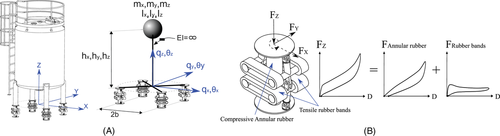
In the above, q(t) is the vector of the six DOF located below the equivalent mass at the isolation interface as shown in Figure 11A; matrices M and Kgeo are the mass and geometric stiffness, respectively; W is the self-weight vector and g the acceleration of gravity. Parameters Mi, hi, and Ii, are the mass, the height, and the RI, respectively, of the equivalent lumped mass in a given direction i = x, y, z; FNL(t) is the vector that contains the local nonlinear forces of the n devices involved in the system, and L is a kinematic transformation matrix from local forces to global coordinates; is the ground acceleration vector where rotational accelerations are neglected, and S is defined in Equation (12) while its physical meaning is to excite the specific DOFs that are excited by each component of the ground motion. All these expressions were obtained by formulating the Euler-Lagrange equation. Notice that the geometric stiffness matrix involves only first-order P-delta effects due to the constant acceleration of gravity g and the additional vertical acceleration of the ground since the restoring forces are provided only by the nonlinear term LTFNL(t). As a legged thin-wall wine tank filled with water was used in these tests, its equivalent properties need to be defined accordingly for the liquid sloshing dynamics theory.58
The periods of the system can be analytically estimated using Equations (14), (15), and linearizing the nonlinear forces of the devices in Equation (16) to obtain an elastic K matrix with positive terms. Then, one obtains the periods given by Equations (1) and (2).
5.2 Equivalent properties of the system CM
In the existing literature, there are widely-accepted tabulated values for the impulsive and convective parameters based on the aspect ratio H/r of a flat cylindrical tank of radius r and filled with water up to a height H subject to lateral acceleration. In most cases, including only the first sloshing mode gives an accurate enough response; however, if the free surface on the tank is minimal, its behavior is usually governed by the impulsive mass.48 Moreover, recent experimental studies59, 60 validated this statement for cylindrical tanks with an aspect ratio similar to the one used in this study. However, it should be noted that some of the assumptions made by Malhotra et al.48 deviate from the experimental conditions of the tests: (i) the tank is elevated by the legs, (ii) rocking motions are involved, (iii) convective modes are suppressed, and (iv) the radius of the free surface is considerably smaller than the main body. Despite the deviation of the tested specimen from the idealized conditions of Malhotra et al.,48 the structural identification presented in Section 4.1 identified a water mass moving together with the tank (i.e., “impulsive mass”) roughly equal to the mass predicted in the mentioned study.48 Therefore, the methods presented in Malhotra et al.48 will be used to determine the part of the mass that is moving together with the tank as well as the height that this should be attached. One could add an extra DOF to model the convective part of the mass, but this was not done in this work for the sake of simplicity. The performance of this simplified approach is evaluated in the next sections.
Considering that the conical roof on the top and the sloped portion at the base (Figure 4) can be approximated as triangular portions with their centroid at 1/3 of the height, the height and radius of an equivalent cylindrical tank are H = 1662 mm and r = 791 mm, respectively. These dimensions give an aspect ratio of H/r ≈ 2.1, which according to the values provided by Malhotra et al.,46, 48 a value of ∼77% of the liquid should be considered as an impulsive mass with its centroid at a height 0.496 H from the base of the equivalent cylindrical tank. This height considers the additional moment produced by the pressure distribution at the base of the tank, since the equilibrium of forces of the considered structural model is made below the base of the tank. The height of the liquid centroid is hwater = 1829 mm, and the height of the CM of the tank is htank = 1573 mm. All heights are taken with respect to the rotation point of the devices at the isolation interface, which is 100 mm below the legs of the tank. Thus, the equivalent lateral CM's height of the whole system is hx = hy = 1804 mm. Notice that the equivalent height in both principal directions is the same due to the radial symmetry of the tank. The height hz for computing vertical reaction forces and the geometric P-delta effects is considered at half of the equivalent cylinder height. The total mass of the water (i.e., mwater = 3000 kg) is considered in the vertical z-direction.
To compute the RI of the system around its CM, one would need to take into account that the water neither rotates with the container as a rigid body nor it stays still. Thus, only a portion of this mass rotates. The accurate solution of this FSI problem is beyond the scope of this work. Therefore, the approximate equations given elsewhere58, 61 are used for this specific geometry and yield an RI equal to 18% of solid volume RI, i.e., , with , and where mwater is the total mass of the water, r is the cylinder radius, and H is the cylinder height. As the tank is not a perfect cylinder and also to include the influence of the mass of the legs, an equivalent cylinder of having a height of 1.2H was considered. This implies . As most of the inertia effects come from Steiner's term, this approximation does not heavily influence the results. The RI about z-direction considers the tank as a hollow cylinder and 5% of the solid volume of water . Table 3 summarizes the equivalent properties used in Equations (12)–(17).
| Parameter expression | Value | Parameter expression | Value |
|---|---|---|---|
| 3000 kg | 3250 kg | ||
| 250 kg | 1.804 m | ||
| hwater | 1.829 m | 1.816 m | |
| htank | 1.573 m | 373.6 kg-m2 | |
| 2560 kg | 203.3 kg-m |
By replacing the values of Table 3 on Equations (1) and (2), considering a device separation of b = 0.5 m, and an equivalent stiffness k = 908,406 N/m,49 the fundamental rocking and vertical mode periods are T1 = 0.933 s (1.07 Hz) and T2 = 0.266 s (3.76 Hz), respectively. The stiffness k used to compute these values correspond to twice (because there are two devices at each side of the tank) the effective stiffness of the cycle #22.2-Phase 2 presented in Table 3 of Reyes & Almazán.49 The deformation amplitude of the devices during these cycles (i.e., cycle #22.2-Phase 2) was slightly larger than those reached during the third white noise test (i.e., W-N(C)) and is the best available estimation in terms of equivalent linear stiffness. Notice that even with this slight difference in the deformation level, the rocking frequency obtained with Equation (1) (1.07 Hz) is very similar to the one observed in the first peak of the identified TF for the input W-N(c) during the system identification (1.17 Hz), and is consistent with the observed trend: a reduction of the frequency for larger displacements.
5.3 The ISO3D-2G isolation device
Any device that complies with the kinematic requirements of being vertically flexible and laterally rigid can be used with the VRI system; however, the list of possible devices is limited since traditional isolation devices behave differently; they are laterally flexible and vertically rigid unless one rotates the device. Thus, the ISO3D-2G49 device is used hereafter.
This device comprises an assembly of steel pieces and two types of high-damping rubber bearings: (i) a central annular rubber that is deformed in compression, and (ii) several rubber bands that are deformed in tension. The steel components create a kinematic mechanism that amplifies the deformation of the tensile rubber bands. The vertical deformation of the device directly compresses the annular rubber, while it stretches the rubber bands in tension. The device can be modeled as a three DOF element as shown in Figure 11B: (i) a vertical DOF associated only with compression forces Fz (the device is freely allowed to uplift, so forces need to be set to zero for tensile forces), and (ii) two coupled horizontal orthogonal DOFs associated with the lateral forces Fx and Fy. The device can be considered hinged at the top, since the moments transmitted by its rotation can be neglected. Figure 11B also schematically presents the individual contribution of the annular rubber and the rubber bands to the global vertical force-deformation relationship of the device.
5.4 Vertical force-deformation relationship
| a1 | α2 | α3 | μ1 | μ2 | μ3 | C1 | Ainitial [cm2] | |
|---|---|---|---|---|---|---|---|---|
| Tensile | 30.15 | −5.68 | 1.94 | 4.5e-8 | −16.73 | −23.47 | 0.6 | 16 |
| Compression | −4.97 | −2.63 | 4.75 | 0.30 | −15.17 | −18.52 | 0.6 | 43.2 |
The evolution in time of Z is modeled using the same differential equation as for the traditional B-W model.62 The yield deformation Y(Y1,Y2,Y3,Y4,Z,u) is selected based on the direction of deformation (i.e., the value of ) and the value of the internal variable Z. With this approach, it is possible to generate different slope branches in the hysterical cycle of fhys.
Table 5 summarizes the parameters used for the hysteretic component.
| Bouc-Wen | Yield deformation Y [cm] | Bounds curves of Bouc-Wena | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| β | γ | n | A | Y1 | Y2 | Y3 | Y4 | C4 | C5 | C2Z>0 | C3Z>0 | C2Z<0 | C3Z<0 | |
| Tensile | 1 | 0 | 1 | 1 | 0.001 | 1.8 | 1.3 | 0.2 | 2.5 | 0.5 | 0.17 | 2.9 | −0.15 | 44 |
| Compression | 1 | 0 | 1 | 1 | 0.15 | 6 | 1 | 0.01 | 0.5 | 0.6 | 0.33 | 1570 | −0.06 | −98 |
- a C3Z>0 and C3Z<0 are in [N] force units
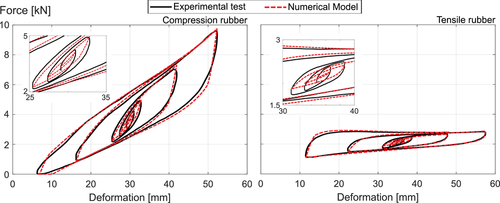
Figure 12 presents the performance of the numerical model for the selected parameters in representing the behavior of the two types of rubber in the device. The target cycles corresponded to phase 2 of the protocol presented in Reyes & Almazán.49 The parameters were selected to fit medium and large-size centered loops, resulting in a lower quality fitting for very small cycles. The difficulty in achieving a good fit for small, medium, and large deformations with the same parameters is a common shortcoming of these types of phenomenological models, and needs to be further studied in future work. Nevertheless, the observed deformation during the tests is consistent with this calibration, especially for the larger motions.
5.5 Horizontal force-deformation relationship
6 EXPERIMENTAL AND NUMERICAL RESULTS
6.1 Main test observations and results
After 17 ground motions, there was no visible damage neither in the tank nor in the isolation devices. Under the ground motions tested, no sliding was observed. It seems that the 2 mm rubber pads that were placed under the isolation devices were enough to provide the necessary friction. In most of the ground motions, no significant uplift was recorded. However, ground motions #5, #11, and #17 did induce uplift, which in all cases, remained smaller than 3 mm and did not cause a noticeable increase of accelerations in the system due to drop-back impact. The maximum uplift values cannot be reported with higher accuracy because the measurements also include the deformation of the rubber pad, which was about ± 1 mm during the records.
The excitations did cause a settlement of the tank. Figure 13A presents the accumulated vertical deformation on the devices after each test, including the initial filling and final emptying of water. Note that when filling the tank with water, the devices do not deform uniformly. This is due to: (a) the variability of the rubber mechanical properties in each device, and (b) the induced eccentricity by the sloped bottom of the tank. The former caused a small leaning of the tank toward devices 4 and 3, while the latter displaced the resultant vertical force almost 20 mm toward devices 1 and 4 (see plan layout on Figure 4). The vertical deformations of the devices for the empty tank were not measured (i.e., when mounting the tank on the devices); however, it was minimal. This is because a pretension was necessary when hooking the tensile rubber bands on the device, which was sufficient to support the empty tank without deformation (i.e., ∼60 kg on each device).
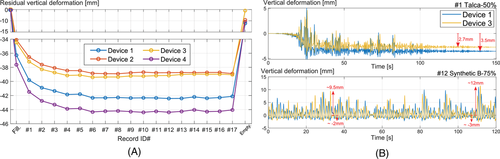
There is an accumulation of residual vertical deformation at the initial tests, stopping after test #6. For instance, Figure 13B shows the time history of the measured vertical deformation on devices 1 and 3 subjected to the records #1 Talca-50% and #12 Synthetic-75%, with the latter having 50% larger PGA than the former. The abrupt settlement in the intense part of record #1 (i.e., around the 25th second of the record) suggests that the vertical creep may be accelerated by large-amplitude deformation cycles. However, this settlement is limited since, after record #12, there is almost no residual deformation.
In all tests, due to the rocking motion, devices at one side (e.g., 1 and 4) deformed out-of-phase with respect to the devices at the opposite side (i.e., 2 and 4), which can be observed in Figure 13B (record #12). However, this out-of-phase deformation was not symmetric. Figure 12 shows that starting from the dead weight equilibrium point (e.g., ∼30 mm of deformation and ∼3 kN of force in the compression rubber), the stiffness for increased compression (i.e., the force required to further compress the rubber) is significantly larger than that for reducing compression. This induced a nonlinearity that breaks the symmetry in displacements, explaining the observed asymmetry. When emptying the tank after the tests, the devices lost compression in approximately 31 mm on average, which is nearly 10 mm less than their average deformation during the tests.
Table 6 shows the peak responses measured in the tests for the lateral accelerations and displacements during the 17 records. The acceleration signals were passed through a low-pass filter with a cut-off frequency of 30 Hz. Figure 14 presents six outputs of interest obtained from the shaking table tests for two of the records, selected due to the observed low and large displacements demand in each: #1 Talca-50% and #17 Synthetic-120%, respectively. The six outputs correspond to the measured (filtered) lateral accelerations (Abottom, Atop), relative lateral displacements (Dmiddle, Dtop), vertical deformation on device 1 (Ddevice 1), and rotation of the isolation interface (θbase). For both records, a close-up is presented around the time instant when the maximum deformation occurred. Deformations and rotations are considered with respect to the initial position (i.e., before the start of each ground motion), so initial conditions of rotation and deformation are shown as zero. Table 6 and Figure 14 also show the results of the numerical model in predicting the response of the system, but this is discussed in the next section.
| Peak shaking table responses | Numerical prediction errors | |||||||
|---|---|---|---|---|---|---|---|---|
| Record | Abottom [g] | Atop [g] | Dmid [mm] | Dtop [mm] | Abottom [%] | Atop [%] | Dmid [%] | Dtop [%] |
| #1 Talca-50% | 0.171 | 0.186 | 24.6 | 42.3 | −19.7 | −15.8 | 18.4 | 24.0 |
| #2 Talca-75% | 0.209 | 0.243 | 37.4 | 64.7 | −11.7 | −13.8 | 6.0 | 12.2 |
| #3 Talca-100% | 0.258 | 0.279 | 56.5 | 95.2 | −8.0 | −7.6 | −8.6 | 1.2 |
| #4Talca-120% | 0.304 | 0.290 | 73.4 | 115.6 | −13.4 | −6.9 | −15.2 | 2.3 |
| #5 Harmonic | 0.217 | 0.263 | 66.4 | 114.5 | −18.6 | −37.9 | −20.5 | -12.2 |
| #6 Curicó-75% | 0.182 | 0.211 | 22.6 | 37.0 | −14.7 | −40.1 | 14.7 | 24.6 |
| #7 Curicó-100% | 0.233 | 0.234 | 24.1 | 44.9 | −23.5 | −31.6 | 24.4 | 23.8 |
| #8 Curicó-120% | 0.269 | 0.274 | 33.0 | 60.7 | −20.0 | −35.4 | 5.7 | 6.3 |
| #9 Synthetic A-75% | 0.223 | 0.214 | 35.7 | 60.6 | −17.4 | −24.8 | −1.8 | 6.9 |
| #10 Synthetic A-100% | 0.264 | 0.241 | 57.4 | 92.7 | −5.4 | −19.4 | −24.6 | −8.7 |
| #11 Synthetic A-120% | 0.302 | 0.274 | 77.6 | 124.0 | −13.9 | −20.1 | −40.6 | −21.2 |
| #12 Synthetic B-75% | 0.206 | 0.222 | 38.9 | 63.8 | 0.9 | −27.4 | −11.0 | 1.4 |
| #13 Synthetic B-100% | 0.259 | 0.262 | 46.1 | 79.7 | −0.8 | −22.2 | 1.6 | 8.2 |
| #14 Synthetic B-120% | 0.328 | 0.287 | 61.4 | 102.0 | −17.7 | −18.8 | −9.4 | 1.9 |
| #15 Synthetic C-75% | 0.222 | 0.220 | 36.7 | 63.7 | −1.9 | −23.8 | 24.1 | 28.6 |
| #16 Synthetic C-100% | 0.250 | 0.245 | 58.6 | 102.6 | −1.8 | −5.2 | 7.0 | 12.1 |
| #17 Synthetic C-120% | 0.271 | 0.289 | 65.5 | 122.7 | 9.1 | −10.0 | 9.3 | 8.5 |
| Min | −23.5 | −40.1 | −40.6 | −21.2 | ||||
| Max | 9.1 | −5.2 | 24.4 | 28.6 | ||||
| Mean | −10.5 | −21.2 | −1.2 | 7.0 | ||||
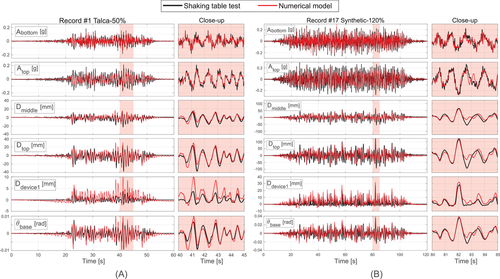
In general, the displacement histories measured at the top and middle of the tank were in phase and proportional to the base rotation. This validates the rotation as a rigid body of the system. Measured accelerations followed a similar trend for the rocking mode. The tests results show that for all records, the total accelerations at the CM remained below 0.19 g, and the maximum displacements at the top of the tank were smaller than 13 cm.
These values are consistent with the desired performance of isolated industrial equipment since the maximum acceleration for the nonisolated case would be on average almost seven times larger (see Table 1). This reduction was computed as the ratio between the expected spectral acceleration for the fixed-base tank (i.e., Sa[T = 0.24s, ξ = 5%] for the spectra presented in Figure 5), and the obtained total acceleration in the CM of the tank during the tests.
6.2 Numerical model performance
The differential vertical deformations observed on devices when filling the tank (due to weight eccentricity and variability of mechanical properties) were included in the numerical model by reducing in 4% and 5% the vertical force of devices 1 and 4, respectively (i.e., the RHS of Equation (21) was multiplied by 0.96 and 0.95 respectively). The reduction value was selected to match the average self-weight rotation at the base from tests #6 through 17#.
Figure 14 shows the prediction of the numerical results for records #1 and #17, for the six mentioned time history outputs. It can be seen that in terms of maximum deformation and accelerations, the numerical model performs relatively better for a more intense record than for a weak one. This trend was observed in all records, and it is consistent with the chosen calibration of the devices shown in Figure 12. Additionally, the model was able to capture the low-frequency rocking mode and the high-frequency modes that source from the high (albeit not infinite) horizontal stiffness of the tank-leg / isolation-device assembly (Figure 9A) well. Neglecting the convective mode of the tank seems to have no considerable negative effects on the performance of the model, further validating the used MSM modeling approach for filled-to-the-top tanks of the considered aspect ratio. However, further studies are needed to extrapolate these conclusions and validate the proposed approach for tanks of different aspect ratios and shapes.
Table 6 includes the relative errors obtained by the prediction of the observed peak responses in the records, together with their mean values. Figure 15 arranges this data in scatterplots as a function of two intensity measures: PGA and peak ground velocity (PGV), respectively. In general, the error and the variability of the predictions are lower for more intense ground motions, irrespective of whether PGA or PGV are chosen as an intensity measure. There is no clear advantage in considering PGA or PGV as intensity measures.
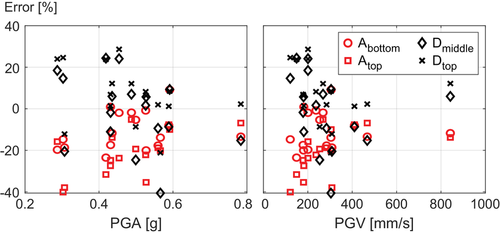
The error in predicting displacement was less than 30% in all but one cases, that is excitation #11 were the error was nearly 40%. The error in predicting accelerations was in general less than 40%. These error values are comparable to other studies of isolation systems17, 18 that did not include Fluid Structure Interaction. Moreover, in terms of average error, the displacements were predicted with a mean error of −1.2% and 7% for the displacements at the middle and the top of the tank, respectively. In terms of total accelerations, they were underestimated with mean errors of −10.5% and −21.2% for the acceleration at the bottom and top of the mantle, respectively. This underestimation is a consequence of neglecting higher modes resulting from the deformability of the structure since the errors obtained in the predicted acceleration in the top (Atop) were generally larger than those predicted in the middle (Amid). This also can be clearly observed in Figures 14A and B, since the main difference in accelerations between the model and the tests are caused by a high-frequency oscillation.
The observed accuracy of these predictions is also consistent with the results obtained by Ipek et al.65 for structures with different seismic isolation systems. The errors of the analyses presented both in this paper and elsewhere65 are the result of uncertainties in the behavior of the tested structures, which can be accounted for in analysis and design using bounding methods of analysis.
7 CONCLUSIONS AND FINAL REMARKS
In this work, the performance of a Vertical Rocking Isolation System based on unbonded rubber was experimentally analyzed using shake table tests. A 3000-liter capacity legged storage tank was supported on four ISO3D-2G devices to generate the vertical rocking isolation mechanism. The tank was subjected to three white noise inputs of different intensities to perform the system identification, and 17 seismic records to evaluate its performance as an isolation system. A numerical model was developed to predict the observed behavior of the tank during the tests. The model considered a rigid superstructure supported on four nonlinear elements representing the isolation devices. The nonlinear force-deformation relation of the devices was represented using a hyperelastic Bouc-Wen model. The liquid on the tank was modeled as an impulsive mass, neglecting convective terms.
The system identification of the structure showed two fundamental modes below the Nyquist frequency. The first mode has a highly nonlinear behavior with a high dependence on the amplitude of deformation. The fundamental period increases for larger demands, varying between 0.5 and 0.8 s for the white noise inputs and reaching values of nearly 1.0 s for stronger seismic inputs. This period elongation is due to the softening of the device for larger deformations. A second identification using empirically estimated TFs showed that this first mode is indeed a coupling of two vertical-rocking modes with very close frequencies. The second identified mode has a higher frequency of about 25 Hz, given by the lateral flexibility of the leg-device assembly. This mode remained practically unaffected by the intensity of the ground motion since the lateral behavior of this assembly can be considered amplitude-independent and linear.
During the seismic record tests, neither the tank nor the isolation devices exhibited any damage. The devices showed an initial settlement due to an induced creep in the rubber; however, this phenomenon is quite limited and should not be a problem in practice. When emptying the water, the devices showed a residual deformation of nearly 10 mm. The tank presented a maximum top displacement of 124 mm, with a maximum total acceleration of approximately 0.33 g, even for intense ground motions recorded during the 2010 Mw 8.8 Maule, Chile earthquake scaled by 1.2. This total acceleration of 0.33 g could also be interpreted as the normalized base shear, which validates the effectiveness of the isolation system.
The time history and peak responses of the system were predicted relatively well with a simple yet representative, rigid lumped-mass model. The maximum errors of peak response predictions were nearly less than 40%; however, they corresponded to specific records, and in general, all prediction errors remained below ±30%. In terms of mean errors, values of less than 10% and 21% were obtained for displacements and accelerations, respectively. These prediction errors are realistic and comparable to recent studies that perform analytical prediction of primary and secondary systems in seismically isolated structures.17, 18 Moreover, the model performed better for larger intensity seismic records, which are of interest in design.
The simplicity of the considered model for the tank is of great advantage for design; however, the assumptions and limitations need to be further studied and validated for tanks of different aspect ratios, shapes, and contained liquid levels.
Finally, it is concluded that using vertically flexible devices at the base of some light structures to generate a rocking isolation mechanism is an effective way to reduce the seismic demand on the structure, even for isolated modes and structural periods shorter than 2.0 s. Although there is no lateral translation at the base, the VRI system isolates the structure by allowing the lateral displacement of the CM.
ACKNOWLEDGMENTS
This research has been supported by the Sawiris Foundation for Social Development and ETH for Development, as well as by Agencia Nacional de Investigación y Desarrollo through the following grants: ANID/FONDEF/VIU19E0130 “ISOVEP: Industrial Solutions for Operational Vibrations and Earthquake Protection”, ANID/FONDECYT/1201841 “Analysis, design and experimentation of solutions to mitigate the effects of impact forces on structures and equipment with two-dimensional and three-dimensional seismic isolation systems”, ANID/FONDAP/15110017 “Research Center for Integrated Disaster Risk Management (CIGIDEN)”, and ANID BASAL FB210015 CENAMAD. The authors are grateful for the support.
Open access funding provided by Eidgenossische Technische Hochschule Zurich.
Open Research
DATA AVAILABILITY STATEMENT
The data that support the findings of this study are available from the corresponding author upon reasonable request.




