1.1 Electrolyte Filling and Wetting of Lithium-Ion Battery Cells

With a growing demand for cheap and reliable lithium-ion batteries, manufacturing processes are being optimized continuously to reduce energy consumption and costs. However, one of the main contributors to the manufacturing cost^{[ 1, 2 ]}the wetting of the porous structure within the battery cell—still needs a gain in process knowledge to enable further acceleration and improvement.^{[ 3 ]} After filling the battery cell with electrolyte, wetting is the next step in the process chain and involves a rest period under controlled conditions.^{[ 4, 5 ]} Unfortunately, there is uncertainty about the degree of wetting achieved and thus a safety margin is often used, which adds to the total time for this step.

The wetting process is usually performed at elevated temperatures and may, depending on cell geometry and type, even involve additional steps of electrolyte dosing. To ensure a high battery cell quality, reliable performance, and safety, the wetting has to be completed before the subsequent formation step is performed. Otherwise, a nonhomogeneous deposition of the initial solid–electrolyte interface (SEI) is expected,^{[ 4, 6 ]} causing an accelerated aging of the battery cells.^{[ 7-9 ]} Therefore, best practice solutions are in place to ensure a sufficiently long wetting time. These solutions are based on experience with the production of battery cells with similar specifications and postmortem studies to visually inspect the wetting degree and the uniformity of the formation process. An in-line testing method to be able to test the wetting degree of each battery cell or to determine the best parameters for sufficient wetting of a battery cell type in preproduction development is highly desirable.^{[ 10 ]} Such a method would enable the process time to be shortened to a minimum without the need for a safety margin.

1.2 Monitoring and Testing of the Wetting Process

There is currently no imaging or testing method, applicable on an industrial scale, able to spatially resolve the electrolyte distribution within a battery cell. Electrochemical impedance spectroscopy (EIS) is used to estimate the wetting degree,^{[ 11, 12 ]} The high-frequency resistance (HFR) is used as a measure for the wet electrode area, which is determined from the intersection in the Nyquist plot with the axis denoting the real part of the impedance, for example, where the imaginary part is zero, in the MHz–kHz frequency range. As the HFR is closely related to the ohmic resistance of the battery cell, which results from the electrical resistance of the cell components and the conductivity of the electrolyte,^{[ 11 ]} its ability to measure the wetting of the microporous surface area of the electrodes is limited. The wetting of this surface is best measured by the charge transfer (CT) resistance, as its magnitude is inversely proportional to the wet, electrochemically active surface area. Unfortunately, the time required to measure the spectra in the low-frequency range (Hz–mHz), hosting the CT, renders EIS inadequate for the measurement of the microporous wetting.

Imaging methods such as infrared thermography,^{[ 11 ]} X-ray,^{[ 10 ]} and neutron radiography^{[ 2, 5, 7, 12 ]} or optical methods applied to battery cells with a transparent window^{[ 13 ]} have been demonstrated to be feasible at the laboratory scale. The advancement of the wetting front within the battery cell as a whole was visualized in a number of reports,^{[ 5, 10, 12, 13 ]} but the degree of wetting of microporous structure could not be accessed. Ultrasound-based imaging methods might bridge this gap. The use of scanning ultrasound microscopy for the imaging of different types of lithium-ion battery cells has been demonstrated.^{[ 14, 15 ]} Pitta Bauermann et al. have shown that by applying different gates, for example, selecting different sections to discriminate the depth within the sample, to the ultrasonic signals returned in pulse-echo geometry, the resolution of the internal structure in different depths is possible.^{[ 14 ]} Deng et al. demonstrated that in transmission geometry, ultrasound can be used to resolve the degree of wetting within a battery cell by evaluating the transmitted amplitude.^{[ 15 ]} The latter method relies on the strong attenuation of ultrasound by the gas volume in its pathway. This means that gas bubbles and dry or “unwet” areas of the battery cell can be made visible by ultrasound.

1.3 Propagation of Ultrasound in Lithium-Ion Battery Cell Materials

The discussion on how to describe the propagation and attenuation of ultrasound in lithium-ion batteries and their constituents is ongoing. The applicable theories might vary depending on the measurement technique and probed frequency range. It was suggested that lithium-ion battery cells in an electrolyte-filled and functional state may be treated like an isotropic, elastic solid, if the wavelength λ of the compressional sound waves, used for interrogation, are much larger than the thickness l of an individual layer within the cell (i.e., λ >> l).^{[ 16 ]} Carcione et al. calculated the ratio, R _EM, of wavelength λ and spatial period d _EM, at which the layered medium can be replaced with an equivalent or effective medium to be between 5 and 8 (R _EM = λ/d _EM).^{[ 17 ]} It is well known that under the assumption of an effective medium, where the layered medium is replaced with a homogenous material of averaged properties of the constituent layers, deviations of up to 20% of the measured sound velocity from the expected sound velocity can be observed. This is known as Backus averaging.^{[ 16, 18 ]}

It was shown that, depending on the measurement frequency, the layered structure of lithium-ion batteries might require the treatment of the sound propagation in individual layers to fully model the sound propagation. Recently, Huang et al. showed that the frequency-selective passing of sound waves through the layered structure of lithium-ion batteries can be modeled layer by layer and thus allows the reflected ultrasonic signal from the echoes generated at the current collector foil–electrode coating interface to be reconstructed.^{[ 19 ]} They showed that in this case, the acoustic properties of the wet separator and electrode coating are similar and thus no significant reflections occur at the separator–electrode coating interface. Therefore, the layering of copper foil (anode current collector), anode coating, separator, cathode coating, and aluminum foil makes up a repetitive unit in which the criteria for resonance through constructive interference are fulfilled at certain frequencies.^{[ 19 ]} Subsequently, the frequency spectrum of the signal in pulse-echo geometry shows peaks at multiples of this resonant frequency.

The propagation of sound waves in the individual battery material layers was discussed in several publications.^{[ 19, 20 ]} For the solid metal layers, that is, the current collector, sound propagation, as described in Equation (1) and (2), can be assumed. It was suggested to use Biot's theory to model the sound propagation in fluid-saturated porous media to describe the ultrasonic waves in lithium-ion batteries.^{[ 21 ]} Huang et al., in contrast, suggested that the slurry model is better suited for the description of the propagation in the electrode coating due to the nature of the electrode, which consists of active material particles elastically linked by the binder and surrounded with electrolyte.^{[ 19 ]} For the separator, they agree with Gold et al. that the sound propagation in the wet separator can be described with Biot's theory.^{[ 19, 21 ]}

The objective of this article is the measurement of ultrasound velocity and spectral analysis of transmitted waves of different frequencies through different pouch cell stacks. The sound wave attenuation and time-dependent change can also be a threshold for unwet and wet regions in the pouch cell stack.

2.1 Development of the Measurement Setup

The measurement setup was designed to ensure the application of homogeneous pressure to the samples while carrying out ultrasonic measurements in transmission geometry. A rigid frame was constructed for this purpose, which is displayed in Figure  1a. Within this frame, pressure plates are mounted on movable sleds, which allows a sample to be comfortably inserted and the transducers to be exchanged. Between the frame and the left sled, a load cell (LC) is mounted to measure the force built up within the frame by operating the jackscrew on the very right. Operating the jackscrew moves the spring-loaded plane (springs: SP) and builds up a force within the frame. As the force is the same on all elements, the resulting pressure on the sample can be calculated by the ratio of measured force and elevated surface of the sample.

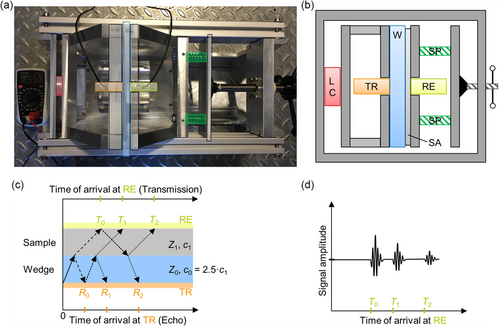
In Figure 1b, a schematic representation of the setup is shown. The left pressure plate serves as a wedge (W). The term “wedge” is used in ultrasonic nondestructive testing synonymously with the term “delay line” and does not make implications about the shape. Therefore, wedges do not have to have surfaces at angle and can also be zero-degree wedges, as in this case. The thickness of the wedge is chosen to exceed the near-field length of the ultrasound in aluminum: the material of the wedge. Thereby, the sample is placed at a distance from the transducer that is considered the far field, in which the ultrasound pressure profile is uniform. In addition, the wedge serves as a delay line, ensuring that the sending waveform, which could be electrically transmitted from transmitter to receiver, does not overlay with the acoustic waveform in the received signal. The transmitting transducer (TR) is mounted on the back of the wedge, while the receiving transmitter (RE) is mounted within a cutout of the right pressure plate. The mount fixes the receiving transmitter horizontally and vertically in a plane parallel to the sample surface but allows it to move slightly in the axis perpendicular to the sample. A compressible silicone rubber foam layer is placed at the back of the transducer and acts as a spring. Without any load applied, the receiver stands out about 0.5 mm against the surrounding pressure plate. When the sample is gradually compressed by the pressure plates, the left pressure plate and the receiver are the first to make contact with the sample. By applying pressure, the silicone rubber layer on the back of the receiver is compressed until the right pressure plate is also fully in contact with the sample. This ensures a good coupling of the receiver while maintaining a homogeneous pressure on the sample.

The intensity at which ultrasound is transmitted at the interface between two media, for example, from a transducer into a sample, depends greatly on the difference in acoustic impedance at that interface. The effective exchange surface between the two media is also highly relevant as surface roughness can contribute greatly to reduced coupling. Therefore, a coupling agent is very often used to fill the voids at the junction of two media. For this purpose and depending on application, a variety of coupling agents can be considered. Common choices are water, gel, natural, or synthetic oil. Here, a natural, biological oil (rapeseed) was chosen due to its compatibility with the materials it was in contact with and the rather low requirements regarding the longevity of a stable contact.

A wave can be reflected multiple times. Therefore, the transmission signal, sketched in Figure 1d, contains wave packages resulting from direct transmission (T ₀) and multiple reflections (T ₁, T ₂, …). This leads to a reduction in intensity with every interface passed. At the receiver (RE), operating in through-transmission mode, only directly transmitted pulses and signals resulting from an even number of reflections can be observed. T ₀ to T ₂ represents the first three possible transmitted pulses, resulting from up to two reflections. At the transmitter (TR), operating in pulse-echo mode, only signals resulting from an odd number of reflections can be observed. R ₀ to R ₂ represents the first three possible signals resulting from up to three reflections.

2.2 Analysis Algorithm to Extract Ultrasonic Signal Properties

In Figure  2 , an exemplary transmission signal is presented. The signal amplitude is plotted as a blue line versus the time after triggering the initial signal. The orange line represents the envelope of the signal, which is calculated via the Hilbert transform (see Experimental Section). The envelope allows a section of the signal, associated with the first acoustic wave package arriving at the receiver, as marked by the vertical dashed lines, to be estimated. For this first signal, the time of flight (ToF) is estimated with a threshold equal to 10% of the maximum amplitude of the signal. The ToF estimated by threshold (τ _th,0.10) and maximum of the envelope (τ _env,max) are plotted as green and red dots, respectively. As pointed out in refs. [23-26], different ToF estimation techniques introduce varying levels of offset, also called bias error, and differ in achievable accuracy. For this contribution, several ToF estimation techniques have been tested and the threshold technique was selected due to its stability and reliability over the measurement frequency range and the variety of samples measured.

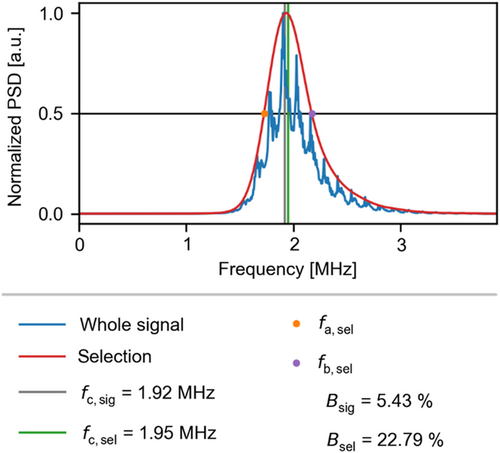
The spectral analysis of this signal is plotted separately in Figure  3 . From the whole signal and the selection, the power spectral density (PSD) is calculated as the squared Fourier transform of the signal amplitude. The selected section of the signal refers to the first arrival at the receiving transducer and contains the first wave package of the signal. As pointed out in ref. 27, the whole signals contains arrivals resulting from a different number of reflections, leading to a different amplitude spectrum of the PSD due to their phase shift with respect to the first arrival. By normalizing the PSD and taking the intersection of the spectrum with the 0.5 line closest to its maximum, the frequencies f _a and f _b are estimated. The distance between f _a and f _b is called absolute bandwidth B _abs. The geometric mean of the two values is called center frequency f _c and is used along with the relative bandwidth B _rel = (f _a–f _b)/f _c to characterize the spectral content of a signal or a section of the signal. As shown in Figure 3, the PSD of the whole signal and the selection deviate significantly in shape, one exhibiting many peaks and the other is very regularly bell shaped. Therefore, the relative bandwidth is also quite different. This shows that the whole signal contains frequency components in different ratios as it results from multiple reflections. To measure the direct transmission alone, the selection containing the first arrival is chosen for the quantification of the PSD. Therefore, the PSD of the selection is the basis for the analysis of the frequency of the transmitted signals throughout this work. The algorithm developed to estimate the signal properties is detailed in the Supporting Information.

2.3 Acoustic Properties of Lithium-Ion Battery Cell Materials

A large number of measurements were carried out on 70 individual samples. The following figures, unless otherwise stated, contain mean values with the standard deviation depicted as error bars. For each sample type, two to six samples were evaluated. As a reference, “baseline measurements” with two layers of the pouch foil as a sample were carried out. Interference patterns originating from closely spaced reflections were present in the resulting signals, which made a systematic ToF estimation not feasible. Therefore, reference “baseline measurements” with the aluminum wedge, but without a sample between the transmitting and receiving transducer ,were chosen instead. To avoid similar effects within the measurement series, a minimum sample thickness of 0.5 mm was selected. The same aluminum wedge is used as a delay line in each measurement. As described above, ToF estimation techniques, such as the threshold technique, introduce an offset. In the reference “baseline measurements”, a correction of the offset is required, which is described in the Supporting Information. The ToF in a sample alone is calculated by subtracting the ToF through the wedge from the ToF through the wedge and a sample. As both terms contain the offset, it is canceled out and no correction is required. Table  1 lists the samples studied, along with the respective legend entries and color labels used in the graphs of this work. The construction of the samples is detailed in Experimental Section. Samples were either kept in a dry state and evacuated state or filled were with electrolyte and evacuated to 50 mbar before sealing. With this sample preparation strategy, the ultrasound propagation at the two extreme points during the wetting process, that is, fully dry and fully wet state, was investigated. The number of layers in each sample was chosen such that the sample thickness exceeds the thickness of the pouch foil by a factor of at least two. To assess the ability of ultrasound to penetrate a battery cell comprising many cell stacks, samples with ten cell stacks were build. A stack is defined by the layer sequence of anode (A), separator (S), cathode (C), separator, represented as A|S|C|S). In this case, anode and cathode refer to a sheet of current collector foil, copper, or aluminum for A and C, respectively, coated on both sides with the respective negative or positive active material-containing electrode mass. The 10× cell stack samples contain 11 anode sheets, 10 cathode sheets, and 22 separator sheets, each with a layering sequence of 10×(S|A|S|C)|S|A|S. To estimate the propagation of ultrasound in each of the constituent, samples consisting of one type of layer were constructed with the same number of sheets. Initially, it was unclear if ultrasound could penetrate ten cell stack samples. Therefore, additional samples with a single cell stack, consisting of three separator sheets and one anode and one cathode sheet each (S|A|S|C|S), were constructed.

Table 1. List of samples with assigned legend entries and color labels

Label	Content of the stack within the sample/description	Color	Number of dry samples	Number of wet samples
11× anodea)	11 anode sheets		5	5
10× cathodea)	10 cathode sheets		5	5
22× FS separatorb)	22 Freudenberg separator sheets		6	6
22× CG separatorb)	22 Celgard separator sheets		3	3
FS 1× cell stackc)	Single cell stack with Freudenberg separator		6	5
CG 1× cell stackc)	Single cell stack with Celgard separator		3	3
FS 10× cell stackd)	Ten cell stacks Freudenberg separator		3	3
CG 10× cell stackd)	Ten cell stacks Celgard separator		2	–
Aluminum wedge	Wedge, cut from a single piece of aluminum		–	–

• All samples are sealed in a pouch bag. Dry samples: sealing at 50 mbar, wet samples: electrolyte dosing and sealing at 50 mbar.
• a) Anode (A) and cathode (C) describes the double-sided electrode sheet;
• b) Separator (S) describes a single sheet of the respective separator;
• c) 1× cell stack describes the layering of S|A|S|C|S sheets;
• d) 10× cell stack describes the layering of 10×(S|A|S|C)|S|A|S sheets.

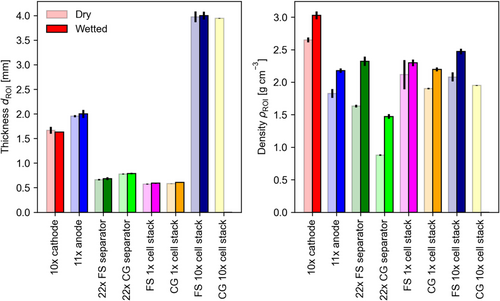
In Figure  4 , the thickness and the density of the samples per sample type is depicted in the dry and wet states. The bars represent the mean values for all samples of a given type and the error bars represent the standard deviation. The thickness of the samples serves as an estimate for the travel distance of the ultrasonic waves from which the sound velocity is calculated in combination with the ToF. The product of density and sound velocity is used to calculate the acoustic impedance of the samples. Since the dry samples were evacuated to a residual of 50 mbar pressure, the pore volume is filled with gas that merely contributes to the weight of the sample. The density of the samples increases due to filling the pore volume with electrolyte. The pouch bag has sufficient dead volume to host the excess electrolyte (40% more than the free pore volume). Therefore, the thickness increase of the samples is expected to arise solely from the swelling of the battery materials due to electrolyte soaking. The properties of the aluminum wedge are not displayed in the figure. Its thickness is 25.0 ± 0.1 mm and the density was estimated to be 2.65 ± 0.01 g cm⁻³.

As the ultrasound passes through the wedge and the sample under investigation, the amplitude of the signal is dampened at specific frequencies more significantly than at others, which depend on sample type. This leads to a change in the frequency distribution, as estimated by PSD, see Experimental Section.

Figure  5 displays the center frequency of the PSD, estimated from the selected section of the transmitted signal. The center frequency is plotted versus the measurement frequency, that is, the nominal frequency of the transmitting transducer. The selected section contains the first wave package and is determined as described in the Experimental Section. The results for the dry and electrolyte-filled samples are displayed in separate subplots. If passing through a particular sample volume did not selectively dampen specific frequency components of the signal, the respective data point would overlay the datapoint of the reference at the measurement frequency in question. In both subplots, the slope for the signals transmitted solely through the aluminum wedge, shown as a reference (black line), remains close to 1 until 4.6 MHz. Only the point at a measurement frequency of 9.5 MHz deviates and is shifted toward a higher frequency of 11.2 MHz. If the data point representing the measurements conducted on one type of sample is shifted toward higher frequency with respect to the reference, higher frequencies pass through the sample or are attenuated less compared to lower frequencies. If the data point is shifted toward lower frequencies, higher frequencies are attenuated selectively, for example, due to scattering at the microstructure. To illustrate this hypothesis, a sketch is provided in Figure S5, Supporting Information. Here, the amplitude modulation of the ultrasound wave by samples with different characteristics is presented in a semilogarithmic intensity spectrum (PSD). The samples, constructed from lithium-ion battery cell materials, are modeled as band stop filters. Depending on the position of the stop band, the center frequency of the PSD can be shifted to higher or lower frequencies, accompanied by an overall decrease in amplitude (intensity).

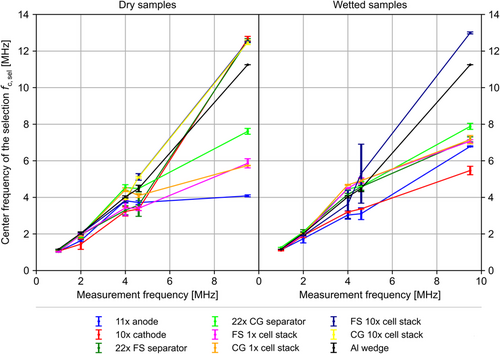
At the measurement frequencies of 1 and 2 MHz, all samples appear to selectively dampen higher frequencies or show little difference in the center frequency of the PSD in comparison with the reference. This trend continues at 4 MHz measurement frequency, except for two of the samples containing Celgard separator sheets, “22× CG separator” and “CG 1× cell stack.” At higher frequencies, the observed trends do not continue.

For the “11× anode” samples, the center frequency remains around 4 MHz at measurement frequencies of 4 MHz and above, suggesting that those frequencies are selectively dampened when ultrasound passes through the sample volume. The resonance model, established by Huang et al.,^{[ 19 ]} could provide an explanation for the observed frequency modulation at these measurement frequencies. They observed a resonance frequency similar to that observed here for cells with very similar dimensions and properties (refer to Supporting Information). The samples containing ten cell stacks as defined above (“CG 10× cell stack” and “FS 10× cell stack”), as well as the “10× cathode” and “22× FS separator,” show a center frequency of about 12.5–12.7 MHz at a measurement frequency of 9.5 MHz. For these measurements, an exemplarily comparison of the intensity spectra (PSD) with the reference is included in the Supporting Information. In Figure S6, Supporting Information, the intensity peak is reduced by several orders of magnitude while being shifted to higher frequencies, with respect to the reference. The remaining samples are located between “11× anode” at about 4 MHz and the reference at 11.5 MHz. The distance to the next lower datapoint is about 4 MHz. To enable a better understanding of the results, the frequency range between 4 and 9.5 MHz should be investigated.

For the wet samples, a similarly heterogeneous picture arises. Here the samples containing electrode sheets alone (“11× anode” and “10 cathode”) show a shift toward lower frequencies. At measurement frequencies up to 4.6 MHz, the center frequencies of the remaining samples are shifted to higher frequencies with respect to the reference. At measurement frequency of 9.5 MHz, all other samples are located between the electrodes and the reference, as expected. Only the “FS 10× cell stack” sample deviates significantly. These samples show very similar behavior for the wet and dry state. This suggests that the respective samples undergo increased gassing or may have taken in air through a defect in the pouch seal over the course of the measurement series, which starts at 2 MHz, followed by 9.5 MHz, and finishes with 4 and 4.6 MHz.

Frequency-selective dampening can originate from several effects. Scattering occurs at every interface within the path of the ultrasonic wave. This includes the boundaries between wedge, sample, and transducer as well as within the sample. Structures within the samples that might scatter sound might be particles, for example, active material particles or ceramic fillers, fibers or layers, for example, the current collector foil and the coating of the electrodes. Depending on wavelength and acoustic impedance, the sound can be scattered at these structures. These two acoustic properties are calculated from the sound velocity.

Figure  6 shows the sound velocity in different sample types in the dry and wet state. The sound velocity c = d _ROI/τ is calculated from the ToF τ of the first wave package, transmitted through the sample and the thickness d _ROI of the sample, measured in the region of interest (ROI), which contains the stacked layers of battery materials. For the results, presented here, the ToF estimated by the threshold technique, where applying 10% of the maximum amplitude of the signal as the threshold, is used. As the ultrasound passes through the wedge and the sample, a separate “baseline measurement” without a sample is performed. The ToF through the wedge is subtracted from the ToF through wedge and sample, which yields the ToF through the sample alone. The “baseline measurement” is plotted as a reference in Figure 6 (black data points). A small increase of sound velocity in aluminum with frequency is observed. This common effect is called dispersion and occurs in most media.^{[ 28 ]}

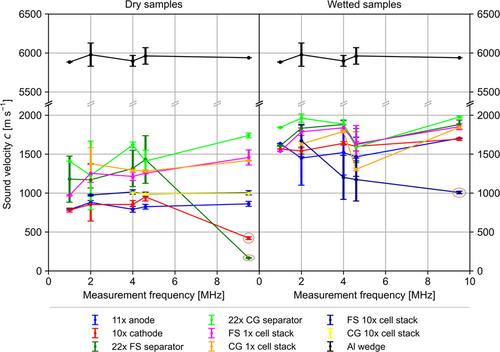
For the dry samples, the sound velocity in different types of samples shows a rather uniform picture, with the exception of the data points for the “22× FS separator” and the “10× cathode” at a measurement frequency of 9.5 MHz. Those two data points are considered outliers as they occur at a sound velocity that is from a physical perspective too low. These two datapoints also show a shift in center frequency with respect to the reference. An increase in sound velocity is expected with increasing measurement frequency. Nevertheless, the recorded transmission signals, which have a low signal-to-noise ratio, did not allow an earlier arrival to be identified, which would have resulted in a sound velocity reasonable for that associated with sound propagation in a solid.

The lowest sound velocity is measured in the electrodes, with exception of the outliers. These consist primarily of the active material particles coated onto thin metal foils. The mechanical properties of the electrodes are known to be dominated by the comparably soft binder since the application of external pressure does not significantly compress the active material particles but rather shifts their position within the elastic binder framework.^{[ 29, 30 ]} Therefore, the overall elastic modulus of the electrode is dominated by the binder properties and not by the properties of the component with the highest mass share, that is, the active material particles. Subsequently, the overall elastic modulus of the electrode lies orders of magnitude lower than the elastic modulus of the active material particles.^{[ 29 ]} As the sound velocity within a material is proportional to the square root of its elastic modulus divided by its density, the observed result is expected.

As the sound velocity is proportional to the square of elastic modulus divided by density, an increase in sound velocity with decreasing density and vice versa is expected. Therefore, the decreasing trend of the density of the first four dry sample types (electrodes and separators) in Figure 4 correlates well with the order of sound velocity of these sample types in Figure 6.

The other types of samples are located in between the electrodes and separators. The samples with one cell stack containing three layers of separator and two electrode layers have higher values than the sample types with ten cell stacks. With one cell stack, the ratio of separator layers to electrode layers is 3:2 = 1.5. In contrast, the samples with ten cell stacks have a ratio of separator layers to electrode layers that is close to one (22:21). Assuming a linear mixing model, a ratio of 1.5 yields a sound velocity closer to that of the separator samples, while a sound velocity closer to that of the electrodes is found with a ratio closer to one.

With the wetting of the materials, differences in behavior can be expected, since the wetting increases the density of the samples due to the filling of the pores. Given that the various sample types have different porosities, the change in density depends on the sample type, as can be seen in Figure 4. Additionally, it is known that the elastic properties of electrodes change due to wetting with electrolyte.^{[ 31, 32 ]} Nevertheless, the elastic modulus of all battery materials in wet state is not easily accessible in the literature. Depending on the binder, the electrodes can soften significantly,^{[ 33, 34 ]} particularly with PVDF, which is known to absorb large quantities of solvent.^{[ 32, 35, 36 ]} Thus, both the change in the elastic modulus and the density will affect the sound velocity due to wetting. The results in Figure 6 show that the order of sample types roughly stays the same after wetting, with exception of the sample “FS 10× cell stack.” In this case, a similar sound velocity as the comparable dry samples has been determined, suggesting that the wet samples might still contain a gas volume in the ultrasonic pathway. The electrodes have the lowest sound velocity, while two separator sample types have the highest and the samples containing cell stacks are in between. The electrodes (C and A) change places, which might be a result of different degrees of softening of the different binders (PVDF vs. a mixture of SBR and CMC). Since the porosity of the electrodes differs only by about 6%, as shown in Table S1, Supporting Information, the softening of the binder probably is the more dominant effect.

Overall, the sound velocity increases by a factor of up to two in the different battery materials from the dry to the wet state. This can be considered a rather large effect and thus is an appropriate figure of merit to be used as a measure for the degree of wetting.

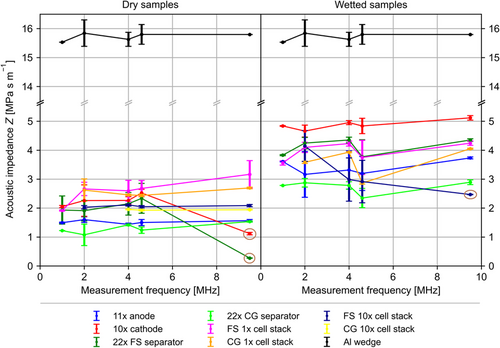
As explained in Section 2.1, the acoustic impedance of the materials to be investigated plays a decisive role for the adaptation of ultrasonic transducers and wedges. The acoustic impedance is also relevant for modeling the reflection and scattering processes within a sample. To act as a stochastic scatterer, an object or structure within a sample has to have a size in the order of magnitude of the wavelength and its acoustic impedance must be significantly different from that of the surrounding material. Figure  7 shows the acoustic impedance calculated by multiplying the density ρ and the sound velocity c of the samples according to Z = ρ·c. Since the sound velocity and the density increases strongly due to electrolyte filling, a corresponding increase in the acoustic impedance is expected and observed here. The behavior of the samples, containing a single-cell stack, is particularly relevant for the subsequent application in battery cell testing. The acoustic impedance of the single-cell stack doubles from ≈2 MPa s m⁻¹ to ≈4 MPa s m⁻¹ (MRayl). Therefore, the acoustic impedance of the wedge and the ultrasonic transducer should be adjusted to 3 MRayl in order to limit the reflected intensity at the interface to 15% (see Equation (6)) for both sample extremes, that is, the dry and wet states, along with everything in between.

The properties derived from the signal center frequency f _c of the PSD and sound velocity c in the samples allow calculating the wavelength λ = c/f _c. The wavelength is plotted against measurement frequency in Figure  8 , with the results for dry and wet samples displayed in separate subplots. With a constant center frequency, the wavelength within the wet sample will increase due to the increase of sound velocity. Since the sound velocity in the dry samples “11× anode” and “22× FS separator” was around 400 m s⁻¹ and the center frequency of these two along with the “CG 10× cell stack” samples was exceptionally high, at about 12.6 MHz. These three have wavelengths below 0.1 mm. Similarly, the measurements on the wet samples of type “FS 10× cell stack” yield a much lower wavelength than the other sample types. Those four should be considered as outliers for previously discussed reasons.

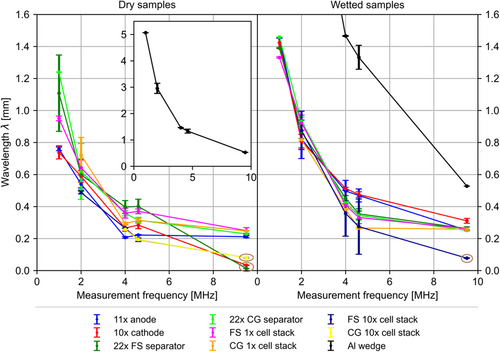
For both, dry and wet samples, a general trend can be observed. The wavelength decreases with measurement frequency, as wavelength is proportional to 1/f _c . As seen before, center frequency f _c increases with measurement frequency. In the dry state, the wavelength varies between 1.25 and 0.2 mm, with the exception of the outliers described. In the wetted state, the wavelength varies between 1.46 and 0.25 mm in the frequency range measured. As described in the Introduction, interaction between the ultrasound waves and the internal structure occurs if the size of the structures is on the order of magnitude of the wavelength and results in scattering and reflections. Therefore, calculating the wavelength at a given measurement frequency allows the interaction of the ultrasound wave with structures within the samples to be estimated. These considerations can be used to identify measurement frequencies useful for accessing averaged properties at comparably large wavelengths or for resolving the microstructure of the battery materials.

For all sample types, the average size of the microstructure (particles, fibers, cracks) is well below 1/10 of the average wavelength in the frequency range presented, with exception of the outliers resulting from particularly low sound velocities or particularly high center frequencies. The periodicity of the stacked samples should also be considered. In particular, the spacing between two adjacent metallic layers is relevant, as these structures generally exhibit a jump in acoustic impedance, compared to the more porous components. The various material specifications are given in the Supplementary Information. The periodicity in samples with layers of electrodes alone can be calculated as 100 and 140 μm, for “10× cathode” and “11× anode,” respectively. In samples containing full battery cell stacks, it is 137–146 μm for the Freudenberg and Celgard separators, respectively. Therefore, the minimum ratio of the wavelength to the periodicity of a medium of 5–8, as described by Carcione et al.,^{[ 37 ]} is not given for all measurement frequencies. Particularly above 2 MHz, where the wavelength lies mostly below 1 mm, theoretical considerations should involve a treatment of the medium layer by layer instead of applying effective medium theory.

Freudenberg and Celgard separators were measured to be 17 and 26 μm thick, respectively (see Table S1, Supporting Information). In the absence of a metallic central layer, as in the electrodes, their acoustic properties are assumed to be uniform throughout their thickness with respect to the measurement frequencies utilized. Therefore, no periodic jump in acoustic impedance is expected within samples containing a stack of separator layers alone.