Quantitative Comparison of Different Approaches for Reconstructing the Carbon-Binder Domain from Tomographic Image Data of Cathodes in Lithium-Ion Batteries and Its Influence on Electrochemical Properties
Abstract
It is well known that the spatial distribution of the carbon-binder domain (CBD) offers a large potential to further optimize lithium-ion batteries. However, it is challenging to reconstruct the CBD from tomographic image data obtained by synchrotron tomography. Herein, several approaches are considered to segment 3D image data of two different cathodes into three phases, namely, active material, CBD, and pores. More precisely, it is focused on global thresholding, a local closing approach based on energy-dispersive X-ray spectroscopy data, a k-means clustering method, and a procedure based on a neural network that has been trained by correlative microscopy, i.e., based on data gained by synchrotron tomography and focused ion beam scanning electron microscopy data representing the same electrode. The impact of the considered segmentation approaches on morphological characteristics as well as on the resulting performance by spatially resolved transport simulations is quantified. Furthermore, experimentally determined electrochemical properties are used to identify an appropriate range for the effective transport parameter of the CBD. The developed methodology is applied to two differently manufactured cathodes, namely, an ultrathick unstructured cathode and a two-layer cathode with varying CBD content in both layers. This comparison elucidates the impact of a specific structuring concept on the 3D microstructure of cathodes.
1 Introduction
Because of their outstanding energy density, low self-discharge rate, and high power density, lithium-ion batteries are the most widely used technology for storing electrical energy.[ 1-4 ] However, further optimization of the performance is necessary due to the continuously growing requirements for electric vehicles and a general need for reducing carbon dioxide emissions to mitigate global warming.[ 5, 6 ] As it is well known that the 3D microstructure of battery electrodes strongly influences the resulting electrochemical performance,[ 7-12 ] tailoring the morphology of the 3D microstructure by specifically developed structuring concepts seems to be a promising approach. Obviously, the manufacturing process consisting, among others, of mixing,[ 13, 14 ] drying,[ 15, 16 ] and calendering[ 17-19 ] has a significant impact on the electrode morphology.[ 20 ] Although the carbon-binder domain (CBD) is regarded as passive constituent of the electrode morphology, its spatial distribution is particularly crucial for the resulting electrochemical properties of cathodes[ 13, 21-23 ] and anodes.[ 24, 25 ] Thus, the segmentation of tomographic image data into three phases, namely, active material, CBD, and pores, is necessary to adequately describe the 3D microstructure of battery electrodes. On the one hand, a high resolution of 3D image data up to the nanometer scale, which can be achieved by focused ion beam scanning electron microscopy (FIB-SEM) tomography, enables for the application of segmentation techniques, which distinguish between these three phases. Disadvantageously, FIB-SEM tomography provides only a small field of view such that the resulting 3D image of the electrode is often not sufficiently representative. On the other hand, X-ray-based imaging techniques such as synchrotron tomography allow for a nondestructive measurement of a comparatively large cutout of the electrode. The technique has been applied successfully for the analysis of a wide range of electrode materials, including transition metal oxides,[ 26-28 ] lithium-iron phosphates,[ 29 ] and organic active materials.[ 30 ] However, the contrast between CBD and pores is comparatively low in many cases such that a frequently used approach is to segment only the active material and its complement (see refs. [29, 31-34]). Several studies then use modeling approaches for inserting the CBD in a subsequent step (see refs. [19, 35–37]).
In the present article, we consider four conceptually different data-driven approaches to reconstruct the microstructure of two differently manufactured cathodes using tomographic image data. While in ref. 37, the CBD is virtually included based on different geometric models for a given segmentation of active material; the novelty of the present article consists of the quantitative comparison between data-driven three-phase reconstructions. These segmentation approaches include global thresholding, k-means clustering, machine learning trained by correlative microscopy, and a reconstruction based on energy-dispersive X-ray spectroscopy (EDX) data. This comparison elucidates the impact of different segmentation approaches on morphological and electrochemical properties of the resulting electrode microstructures. Moreover, we determine the effective transport parameter of the CBD for each segmentation approach by validating the output of spatially resolved half-cell simulations with experimentally determined electrochemical data. This approach allows us to specify a range in which the effective transport parameter is located. Thereby, the presented approach takes the important aspect of uncertainty during the reconstruction process[ 38 ] into account when analyzing the microstructure of battery electrodes based on 3D image data.
This article is organized as follows. In Section 2, we describe the manufacturing process of two different cathodes as well as the tomographic imaging procedure. Next, we present four different approaches of segmenting active material, CBD, and pores from 3D image data in Section 3. The computation of electrochemical properties by spatially resolved numerical simulations is described in Section 4. In Section 5, the influence of the different trinarization approaches on the 3D microstructure is quantitatively investigated by means of statistical image analysis. In addition, we present results regarding simulated electrochemical properties, where a particular focus is put on the effective transport parameter of the CBD, which is fitted via experimentally determined lithiation curves. Finally, the article is concluded with a summary of the main results and an outlook to possible future research.
2 Experimental Section
In this section, manufacturing, material composition and the tomographic imaging of the cathode materials considered in the present article are described.
2.1 Materials and Cathode Manufacturing
We investigate two different cathode samples, the 3D microstructure of which is quantitatively characterized based on different segmentation approaches. Moreover, an additional electrode is considered, which is solely used for the trinarization approach based on correlative microscopy in Section 3. In the following, we describe four different suspensions, denoted by A, B, C, and D, which were used to manufacture these samples. Note that one of the electrodes is a two-layer electrode, where the two layers are prepared with different suspensions. All suspensions share the underlying materials, but differ with regard to their composition.
Commercially available (BASF), shortly denoted by NMC, was mixed and dispersed with carbon black (SuperP, Imerys) and graphite (SFG6L, Imerys) as conducting additive and polyvinylidene fluoride (PVdF, Solvay Solexis) as a binder, where the union of carbon black, graphite, and binder forms the CBD. N-methyl-2-pyrrolidone (NMP, Sigma-Aldrich) was used as a solvent. Note that all materials were utilized as delivered without further treatment. Because two suspensions were needed simultaneously for the manufacturing of the two-layer electrode, different mixers applying the same working principle were used for the preparation of the cathode suspensions. To be precise, a 10 dm3 planetary mixer (Netzsch, Germany) and a 1.6 dm3 planetary mixer (Grieser, Germany) were used. Both mixers were equipped with two agitators, a cross-bar stirrer (CS) and a butterfly stirrer (BS) running at low and high speed, respectively. In the case of the 10 dm3 mixer, an axially double butterfly stirrer was used while the 1.6 dm3 mixer contained a single butterfly stirrer. Transport of the components into the mixing zone was ensured by a wall scraper rotating at slow speed. For each suspension, the solid material composition and the type of mixer used for the preparation are given in Table 1 .
| Suspension | A | B | C | D |
|---|---|---|---|---|
| Content in solid mass | ||||
| NMC | 93.5 | 91.5 | 95.5 | 93.0 |
| Carbon black | 2.0 | 2.0 | 2.0 | 2.0 |
| Graphite | 1.0 | 1.0 | 1.0 | 1.0 |
| PVdF | 3.5 | 5.5 | 1.5 | 4.0 |
| Mixer | Grieser | Netzsch | Grieser | Netzsch |
The suspensions were prepared starting from a binder solution containing 7–10 wt% of PVdF which was dissolved in NMP at room temperature. First, carbon black and then graphite were added to the binder solution and dispersed, respectively. After that, NMC was added stepwise and dispersed after each addition. Finally, the viscosity of each suspension was adjusted for application by thinning with NMP. From the suspensions, ultrathick electrodes were produced using a pilot line coating machine (LACOM, Germany). A single-layer electrode (abbreviated by SL) was prepared from the suspension A using a single slot die. A two-layer electrode (abbreviated by TL) was prepared by simultaneous slot die coating with a double slot die applying suspension B at the bottom and suspension C at the top. The suspensions were cast onto an aluminum foil (Korff, Switzerland). A drying oven with a total length of 8 m, separated into four drying stages, independently adjustable in temperature, was used for evaporation of the solvent. The belt speed was 0.8 m min−1 and the temperatures of the ovens were 50, 70, 95, and 110 °C for both electrodes. The mass loading resulted in 51 and 53 mg cm−2 for the single-layer and the two-layer electrode, respectively. After drying, the electrodes were calendered using a pilot line calender (KKA, Germany) with a line pressure restricted to a maximum value of 208.3 Pa m−1 and rolls heated to 100 °C. The final density of the electrode composites was 3.1. g cm−3 for both electrodes. Note that the single-layer and the two-layer cathode share the following volume fractions: 59.54% active material, 11.54% CBD, and 28.92% pore space. These volume fractions are computed from the density of the electrode as well as the material composition (i.e., the weight percentage as well as the density of the individual solid constituents).
In addition, a third cathode sample is considered, image data of which is solely used in Section 3 for establishing a trinarization approach based on correlative microscopy. This sample is manufactured with suspension D analogously to the single-layer and the two-layer cathode, except for a slower belt speed of 0.6 m min−1 and a slightly lower mass loading of 49.1 mg cm−2.
2.2 Tomographic Imaging
First, we describe the imaging procedure of the single-layer and the two-layer cathode. The tomography measurements of these cathode samples have been conducted at the P05 beamline (Petra III, DESY, Germany).[ 39, 40 ] More precisely, a monochromatic nearly parallel X-ray beam is guided on the rotating sample without the use of X-ray focusing optics. Behind the sample, the transmitting beam is detected with a setup consisting of a CdWO4 scintillator for X-ray to light transformation, an optical microscope, and a CMOS camera. The samples have been measured with an energy of 28 keV to assure an optimal image contrast, where a double crystal monochromator is used for selection. Both samples have been measured as close as possible to the scintillator screen to reduce phase contrast. During the tomography each sample was constantly rotated while 2401 images have been captured using a KIT CMOS camera (5120 × 3840 pixel) with an exposure time of 130 ms. Combined with the 10 times optics this resulted in a voxel size of 0.642 μm. For the reconstruction the normalized data were denoised using a total variation minimization filter[ 41 ] and then reconstructed using the gridrec routine based on the filtered back projection.[ 42 ] Note that all subsequent results regarding the single-layer and the two-layer sample are based on three nonoverlapping equal size cutouts, where the entire thickness is used in through-plane direction.
With regard to the third cathode sample, which is used for establishing the neural network approach based on correlative microscopy, imaging by synchrotron tomography as well as by FIB-SEM tomography has been carried out. First, synchrotron tomography has been conducted at the P05 beamline (Petra III, DESY, Germany) using the μ-CT setup. For the tomography, a beam energy of 25 keV was found to yield optimal transmission contrast. The energy was filtered using a double multilayer monochromator. The sample that was fixated on the translation/rotation stage was positioned 15 mm away from the CdWO4 scintillator. Behind the scintillator the portion of the signal that has been transformed into visible light was magnified (10 times magnification) by the microscope optics and redirected into the camera system. A KIT CMOS camera equipped with a CMOSIS CMV 20 000 sensor (5120 × 3840 pixel) was then used to capture the signal with an exposure time of 130 ms. The whole tomography consisted of 3000 projections; for ring artifact reduction, a center of rotation variation protocol was used. The whole setup yielded a 0.642 μm raw pixel size. The synchrotron tomography was reconstructed using the P05 in-house reconstruction tools based on the filtered back projection algorithm. After reconstruction, an additional nonlocal means denoising step was performed.[ 43, 44 ]
The FIB-SEM tomography has been conducted at Helmholtz-Zentrum Berlin (HZB) using the ZEISS Crossbeam 340. For this purpose, the sample that previously was measured at P05 has been fixated on an aluminum sample holder. For better orientation on the sample, a first low-resolution large-scale surface scan was performed. The scan was then aligned with the 3D synchrotron tomography reconstruction using the SIFT algorithm.[ 45 ] Afterward, using the synchrotron tomography, a suitable ROI has been selected for FIB-SEM tomography. For the FIB-SEM tomography, a Gallium ion milling source with 30 keV and 300 pA ion current was used. The Gemini electron gun was operated at 2 keV. For imaging the SE2 chamber detector (i.e., a detector for low-resolution secondary electrons) with an image capture rate of 30 s per image was used. The pixel size was set to , which also corresponds to the thickness of the slices that have been cut by the FIB. Finally, the 3D image data obtained by FIB-SEM tomography were manually aligned with the synchrotron tomography data set using Fiji/ImageJ.[ 46 ] A 3D rendering of the complete 3D FIB-SEM data together with the image data obtained by synchrotron tomography is shown in Figure 1 .

In addition, 2D EDX data have been gathered for the local closing approach described in Section 3.4. For this purpose, cross sections of electrodes were prepared perpendicular to the electrode surface by a broad ion beam milling device (Hitachi IM4000Plus) at an accelerating voltage of 5 kV for 2–3 h depending on the electrode thickness. A subsequent analysis of the electrode microstructure was conducted with scanning electron microscopy (SEM, accelerating voltage between 4 and 5 kV) using a LEO1530VP (Zeiss) equipped with a thermal field emission gun. To determine the locally resolved elemental distribution of fluorine, EDX (X-Max50, Aztec Advanced Software, Oxford Instruments) was used. Characteristic X-rays of fluorine were used as a measure for the spatial distribution of PVdF within the electrode.
3 Phase-Based Segmentation
This section covers four different approaches to reconstruct the 3D image data obtained by synchrotron tomography. Each of these trinarization methods is designed in such a way that the experimentally determined volume fractions of all three phases can be matched. However, it is not possible to resolve the inner structure of the CBD based on synchrotron image data because the resolution is too low. Thus, we assume that each CBD voxel contains an inner porosity, sometimes called nanoporosity, of 50%, which is close to inner porosities of 47% and 58% reported in refs. [47, 48], respectively. Therefore, a voxel labeled as CBD also contains nanopores, which cannot be resolved by synchrotron tomography, whereas voxels labeled as pores correspond to the larger macropores. Finally, a voxel-based analysis is carried out to obtain a first impression about potential differences between the four segmentation approaches. A visualization of these different segmentation approaches, which are described in detail in the following, is shown in Figure 2 .
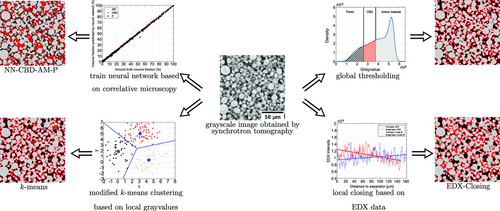
3.1 Global Thresholding
To begin with, we consider the trinarization of 3D image data by two global thresholds,[ 49-51 ] which are chosen in such a way that the experimentally determined volume fractions of all three phases are matched. For this purpose, we choose a sufficiently large sampling window, which does not contain void space outside the electrodes to avoid edge effects. The size of this cutout is given by voxels (two-layer cathode) and voxels (single-layer cathode), respectively. In the following, we refer to this approach as Thresholding. A visualization of the grayvalue histogram together with two thresholds as vertical lines is shown in Figure 2.
3.2 Clustering Approach
3.3 Neural Network
In order to train a neural network that classifies each voxel according to the grayvalues in the synchrotron images, we make use of correlative microscopy. More precisely, a small cutout of the electrode has been imaged by FIB-SEM tomography after measuring the whole electrode sample by synchrotron tomography as described in Section 2.2. This approach relies on the fact that a three-phase reconstruction of 3D FIB-SEM data is possible due to the better contrast compared to image data obtained by synchrotron tomography. More precisely, a global threshold determined by Otsu's method is used to segment the active material,[ 58 ] whereas a U-Net is trained to distinguish between pores and CBD.[ 59 ] Finally, a slicewise flood-filling algorithm has been applied to the active material phase in order to remove inclusions of CBD or pores.[ 50, 51 ] Due to the different voxel sizes of both kinds of image data, each synchrotron voxel corresponds to voxels in the FIB-SEM data. Thus, we can compute the material composition—i.e., a 3D vector containing the volume fractions of active material, CBD, and pore space—for each synchrotron voxel, for which FIB-SEM data are available. This information serves as ground truth for training a feed-forward neural network, which uses the grayvalues of an input voxel and its neighborhood. The neural network is a multilayer perceptron consisting of five hidden layers with 75 units each and a softmax output layer with three units representing the predicted material composition of the input voxel.[ 60, 61 ]
As the physical size of the FIB-SEM cutout is comparatively small (only 2541 voxels as training data), we make use of a data augmentation for the training data, where we flip and/or rotate the neighborhood.[ 61-64 ] As these kind of transformations do not change the material composition, we increase the size of the training data by a factor of 48, which corresponds to the number of elements of the symmetry group of a hexahedron.[ 65 ] The data points are randomly shuffled and split into 60% training data, 20% validation data, and 20% test data. The validation data are used for early stopping in case of ten subsequent epochs with a nondecreasing error on the validation set. The network consists of five hidden layers with 75 nodes each.[ 60, 61 ] The mean squared error, which is used as loss function, has been optimized using Nesterov's accelerated stochastic gradient descent[ 66 ] with a learning rate of 0.01 and a momentum coefficient of 0.99. After training the network is applied to the synchrotron image data of the single-layer and the two-layer sample, respectively. For each sample, this results in a 3D image, where for each voxel the material composition is predicted. This kind of information can be either interpreted as fuzzy membership or as probability of belonging to a certain phase.[ 67, 68 ] The top left plot in Figure 2 shows the prediction accuracy on the test set of the trained neural network for each of the three phases, which indicates that the material composition can be reliably predicted.
In order to transform the output of the neural network into a segmentation with three classes, we consider two procedures. The first approach relies on the experimentally determined material composition as well as on a predefined ordering of the three phases, denoted by , and . More precisely, we assign the voxels with the highest predicted probability of belonging to phase to until the target volume fraction of is matched. This procedure is then repeated for , except that we no longer consider voxels already classified as . In the following, this approach will be abbreviated as NN––– with . For example, first segmenting the active material and then assigning the CBD lead to the trinarization NN–––P. The second possibility for transforming the material composition by the neural network to a trinarization is based on conditional probabilities, where the first phase is obtained analogously to the first approach. However, we then compute the conditional probabilities of voxels belonging to and conditioned on the event that these voxels are not classified as . As these two conditional probabilities add up to one, there is—given that the phase is fixed—exactly one possibility to obtain a trinarization, which matches the experimentally determined material composition. This trinarization method will be denoted by NN––Cond in the following. For example, first classifying the active material and then assigning the CBD and pore space based on the conditional probability that a certain voxel is not classified as active material leads to the trinarization NN––Cond. In total, there exist six different orderings of the three phases required for the first approach, as well as three different trinarizations based on the conditional probability approach, leading to nine different neural network segmentations.
3.4 Local Closing Based on EDX Data
Similar to ref. 13, 2D image data obtained by EDX are used to estimate the corresponding CBD gradient along the transport direction, which is then fitted by a linear function (see Figure 3 ).
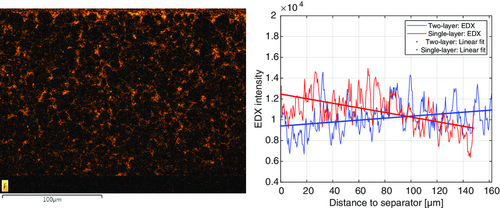
The first step to obtain a 3D segmentation that reflects the linear CBD gradient is to use the active material obtained by the k-means segmentation. Afterward, the CBD is inserted by a morphological closing of the active material phase, where the structuring element is given by a ball with some location-dependent radius .[ 69, 70 ] Note that it has been shown in ref. 37 that using a morphological closing is an appropriate model for inserting the CBD. As described in ref. 13, the closing radius r depends on the distance to the separator such that the slice-dependent amount of CBD is proportional to the estimated CBD gradient, where the known CBD volume fraction is matched by multiplying the EDX intensity values by a constant that is computed with the bisection method.[ 71 ] In the following, we refer to this approach as EDX-Closing.
3.5 Voxel-Based Comparison of Trinarization Approaches
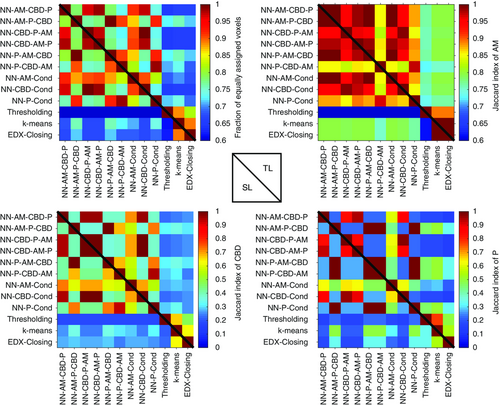
Before investigating the influence of the different trinarization approaches on morphological and electrochemical properties in Section 5, we perform a quantitative voxel-based analysis to obtain a first impression regarding the potential differences between the segmentation approaches described above. Before we quantify the influence of the trinarization approach on geometric descriptors of the resulting 3D microstructures in Section 5.1, we first quantify the difference between the presented three-phase reconstructions by the fraction of equally assigned voxels as well as the Jaccard index[ 72 ] (see Figure 4 ). Both measures take values between zero and one, where lower values correspond to more pronounced differences between two trinarizations. In the present setting, the Jaccard index compares the spatial distribution of a predefined phase between two different trinarizations by computing the ratio of the intersection volume and the volume of the union. Note that the fraction of equally assigned voxels and the Jaccard index corresponding to a certain phase are symmetric characteristics such that the entries below the main diagonal in Figure 4 contain the information regarding the single-layer cathode, whereas the entries above the main diagonal correspond to the two-layer cathode. On the one hand, the top left plot shows that there exist non-negligible differences between the neural network approaches, i.e., the method for converting the output of the neural network to a trinarization has an influence on the resulting three-phase reconstruction. On the other hand, there are even more pronounced differences between the neural network trinarizations and the remaining three approaches, namely, k-means, EDX-Closing, and Thresholding. In addition, the remaining three plots in Figure 4 indicate that the least differences between the trinarization approaches are observed with regard to the segmentation of active material, which is most likely caused by the high contrast between active material and the remaining two phases. Furthermore, there are negligible differences between the single-layer and the two-layer cathode, except for the trinarization obtained by global thresholding.
4 Simulation of Electrochemical Properties
The electrochemical simulations are conducted using the research branch of the framework BEST, which is developed in collaboration between the DLR Institute of Engineering Thermodynamics and the Fraunhofer Institute for Industrial Mathematics (ITWM) (https://www.itwm.fraunhofer.de/best). Focus of this work is on the influence of the CBD on electrochemical reactions and transport. Therefore, we will describe our CBD model and assumptions in more detail in subsequent paragraphs. A derivation of the governing equations and a description of our numerical framework can be found in previous publications.[ 37, 73, 74 ] To provide a systematic overview of the electrochemical simulation approach, we summarize the model equations, boundary conditions, initial conditions, and parameters in the supporting information. More specifically, the governing equations in the different phases are listed in Table S2, Supporting Information. Interface and boundary conditions are given in Table S3, Supporting Information. Interface models between active materials and electrolyte are listed in Table S4, Supporting Information.
As described in the previous section, the 3D image data of both cathodes are segmented into three distinct phases, namely, cathode active material, CBD, and porosity. However, the inner structure of the CBD cannot be resolved by means of synchrotron tomography, which has been also discussed at the beginning of Section 3. Therefore, the CBD in our simulations on the electrode scale actually contains two materials, namely, the solid carbon and binder matrix as well as liquid electrolyte. Similarly, the porous separator contains both the glass-fiber material and liquid electrolyte. In our simulations, we do not resolve the actual microstructure of these materials. We rather use a homogenization approach[ 75 ] to simulate the effective transport through these mixed domains. This approach is computationally much more efficient and enables simulations on the cell scale; however, requires additional input parameters for our model.
The effective tortuosity of the solid part in the CBD and the electrolyte part of the separator are computed likewise. The electrochemical parameters used in the simulations within this article are listed in the Supporting Information (see Table S5, Supporting Information).
The list of all interface conditions can be found in Table S3, Supporting Information.
To evaluate the impact of different methods for CBD reconstruction we performed two different types of virtual experiments: 1) constant current lithiation in half-cell configuration with six different currents (1, 3, 6, 8, 10, and 12 mA cm−2); and 2) impedance spectroscopy in symmetrical cell configuration under blocking condition.
The simulation domains for the lithiation and the symmetrical impedance simulations are shown in Figure 5 .
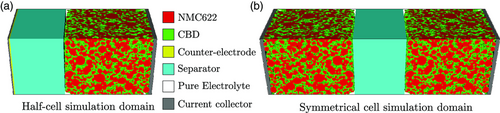
Three different cutouts of the electrode tomography are used as simulation domain for each trinarization approach and electrode type. The trinarized 3D microstructures are cropped to a lateral size of 200 voxels for the electrochemical simulations due to computational constraints. This modifications keeps the thickness of the electrode and areal capacity unchanged.
Impedance spectra are calculated using the step excitation method. Details of the approach are also provided in ref. 37. All electrochemical simulations are conducted using the HPC resources of JUSTUS2.
5 Results and Discussion
This section covers the quantitative analysis of the different trinarization approaches with regard to their morphological properties by means of statistical microstructure analysis as well as the resulting electrochemical behavior based on spatially and temporally resolved numerical simulations.
5.1 Influence of Selected Trinarization Approach on Morphological Descriptors
In this section, we discuss the influence of the different trinarization approaches described in Section 3 on the morphology of the resulting three-phase microstructures. For the sake of clarity, we only discuss the three trinarizations corresponding to the conditional probability approach, whereas the results for the remaining six neural network trinarizations can be found in the Supporting Information. Considering the 2D slices in Figure 2, one can already observe visual differences with regard to the morphological properties of the three phases. The CBD phase determined by morphological closing based on EDX data is accumulated around the active material, which, in turn, leads to the formation of relatively large pores. Thereby, this approach differs clearly from the other approaches. On the other hand, the neural network approach results in a finely structured pore space. Moreover, by visual inspection it is hard to detect differences between the segmentation based on global thresholds and the one obtained by k-means clustering. Recall from Section 3 that all segmentation approaches are calibrated such that the volume fractions of active material and CBD phase coincide with the experimentally determined values. In order to quantitatively evaluate the different trinarization approaches, we consider several microstructure characteristics for each of the three phases, which are considered as random closed sets,[ 76 ] denoted by , and .
We begin with the surface area per unit volume. This quantity is estimated from voxelized 3D image data as described in ref. 77. Besides the surface area per unit volume of each phase, denoted by , and (see Table 2 ), the surface area per unit volume of the interface between active material and the pore space is of interest from an electrochemical point of view because the intercalation takes place at this surface. Due to the inner porosity of the CBD, this characteristic, denoted by , is given by . For this purpose, the surface area per unit volume of the interface between two phases is computed as described in ref. 78. Interestingly, the surface area per unit volume of all three phases does not depend on the underlying trinarization approach. Thus, there are only minor differences between the values of .
| Sample | AM–Cond | CBD–Cond | P–Cond | Thresholding | k-means | EDX-Closing | |
|---|---|---|---|---|---|---|---|
| TL | 0.925 | 0.925 | 0.925 | 0.925 | 0.918 | 0.918 | |
| SL | 0.925 | 0.925 | 0.924 | 0.918 | 0.924 | 0.924 | |
| TL | 0.360 | 0.361 | 0.36 | 0.359 | 0.369 | 0.374 | |
| SL | 0.362 | 0.362 | 0.362 | 0.360 | 0.361 | 0.370 | |
| TL | 0.272 | 0.271 | 0.273 | 0.273 | 0.27 | 0.265 | |
| SL | 0.271 | 0.271 | 0.272 | 0.279 | 0.272 | 0.263 | |
| TL | 0.672 | 0.672 | 0.672 | 0.672 | 0.664 | 0.662 | |
| SL | 0.671 | 0.671 | 0.671 | 0.668 | 0.671 | 0.667 | |
| TL | 1.81 | 1.78 | 1.86 | 1.90 | 2.12 | 2.12 | |
| SL | 1.83 | 1.80 | 1.84 | 1.93 | 2.17 | 2.17 | |
| TL | 0.66 | 0.75 | 0.23 | 0.21 | 0.22 | 0.78 | |
| SL | 0.60 | 0.73 | 0.24 | 0.21 | 0.21 | 0.78 | |
| TL | 0.21 | 0.21 | 0.70 | 0.76 | 0.80 | 0.00 | |
| SL | 0.22 | 0.21 | 0.69 | 0.78 | 0.78 | 0.00 | |
| TL | 3.11 | 2.88 | 3.13 | 3.63 | 3.74 | 3.74 | |
| SL | 3.19 | 3.12 | 3.17 | 3.66 | 3.80 | 3.80 | |
| TL | 1.03 | 1.23 | 0.67 | 0.48 | 0.52 | 1.26 | |
| SL | 0.96 | 1.14 | 0.70 | 0.46 | 0.47 | 1.27 | |
| TL | 0.93 | 0.64 | 1.16 | 1.53 | 1.57 | 2.61 | |
| SL | 0.97 | 0.67 | 1.15 | 1.47 | 1.55 | 2.58 |
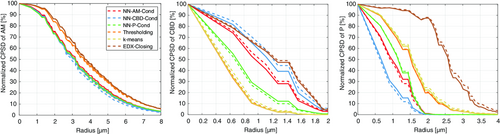
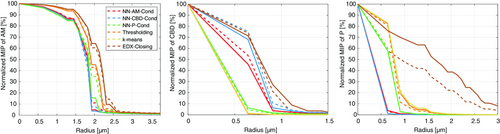
Additionally, the microstructure descriptors and are given in Table 2, where the descriptor denotes the -quantile of the so-called continuous pore size distribution. Similarly, the descriptor denotes the -quantile of a phase size distribution obtained by a geometric simulation of mercury intrusion and can be considered as the radius of the typical bottleneck. By means of and , the constrictivity can be defined, which is a measure for the strength of bottleneck effects and a meaningful characteristic for effective transport properties.[ 79-81 ] With respect to these microstructure descriptors, formally defined in ref. 82, clear differences between the considered trinarization approaches can be observed, whereas there are no significant differences between the single-layer and the two-layer cathode. In particular, Figure 6 shows that EDX-Closing leads to significantly larger pores, which, in turn, leads to the largest value of . Furthermore, k-means and Thresholding lead to nearly identical continuous phase size distributions for all three phases, whereas the neural network trinarizations differ from each other with regard to the continuous phase size distribution of the CBD as well as the pores. It is also interesting to note that with regard to the CBD as well as the pore space, the neural network segmentation based on conditioning on the respective phase leads to larger clusters of this phase. With regard to the simulated mercury intrusion porosimetry (see Figure 7 ), we observe that the curves corresponding to the CBD and the pores are prone to discretization errors. Considering the active material, there are only slight differences, which, in turn, leads to similar values for . Furthermore, the approach based on EDX data is the only case, where clear differences between the single-layer and the two-layer cathode can be observed. These differences are quantified by means of the simulated mercury intrusion porosimetry of the pore space. In Figure 6 and 7, the curves corresponding to the segmentation approaches based on correlative microscopy are shifted to the left compared to the remaining three-phase reconstructions when considering the pore space.
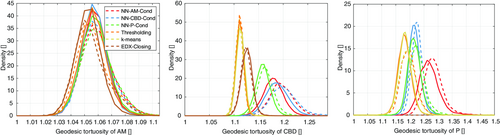
Moreover, the distribution of geodesic tortuosity is considered. This is a purely geometric quantity, in contrast to the effective tortuosity considered in Section 4, providing the distribution of the length of shortest paths through a predefined phase in the electrode divided by the thickness of the electrode (see ref. 82 for a formal definition). Note that different concepts of tortuosity exist in the literature,[ 83-86 ] where in the case of geodesic tortuosity Dijkstra's algorithm is used to estimate this quantity from voxelized image data.[ 87 ] As shown in Figure 8 , the distribution of geodesic tortuosity of the active material neither depends on the selected trinarization approach nor on the considered cathode sample. In contrast, the length of shortest paths through the CBD as well as the pore space is larger for the trinarizations obtained by the neural networks compared to the remaining three segmentation approaches. These differences between the four trinarization approaches considered in this article are stronger than the differences between the single-layer and the two-layer cathode.
In addition, the centered two-point coverage probability function is considered (see Figure 9 ). For stationary and isotropic random closed sets in the 3D Euclidean space with , this characteristic is defined via for any and , where denotes the volume faction of , respectively. This function is also called covariance function in the literature.[ 69, 88 ] Due to the normalization by subtracting the product of the volume fractions, a value of zero implies that the events and are stochastically independent. Positive values of can be interpreted as a positive correlation between those two events, whereas negative values correspond to a negative correlation. Typically, choosing equal phases (i.e., , see top row of Figure 9) leads to a monotonously decreasing function taking non-negative values, which approaches zero for large radii r. On the other hand, considering two different phases (i.e., , see bottom row of Figure 9) leads in most cases to a monotonously increasing function approaching zero from below. Figure 9 shows that there are no differences between both samples regardless of the phases under consideration. Furthermore, the curves in the top row of Figure 9 show the same qualitative behavior as the continuous phase size distribution in Figure 6. The most noticeable effect is the unique behavior of the closing approach based on EDX data with regard to the bottom right plot in Figure 9. More precisely, the remaining segmentation approaches show a peak at around 2 μm, which corresponds to an increased likelihood of observing CBD and pores 2 μm away from each other. The curves corresponding to EDX-Closing show a steadily increasing two-point coverage probability function instead.
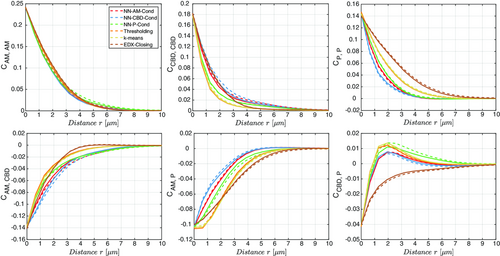
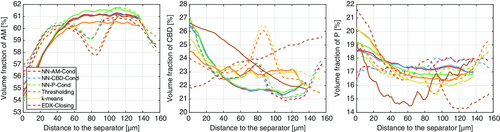
Finally, we consider the volume fraction of each phase in dependence of the distance to the separator (see Figure 10 ). With respect to the spatial distribution of active material, there is a clear difference between the single-layer and the two-layer cathode regardless of the trinarization approach. More precisely, the two-layer sample shows a pronounced drop of the volume fraction of active material at 80 μm, i.e., at the interface between both layers. With regard to the CBD, there are clear differences between the results obtained for each of the trinarization approaches, where all three-phase reconstructions except EDX-Closing indicate a larger amount of CBD at the interface. This peak is most pronounced for k-means and Thresholding. Obviously, EDX-Closing reflects the linear gradient estimated from EDX data. Note that this linear gradient is estimated from a single 2D EDX image and is thus subject to a larger uncertainty compared to the information extracted from 3D image data. Therefore, segmentation approaches not reflecting the linear gradient observed in EDX data are not automatically considered as unrealistic. Interestingly, this does not lead to a linear behavior of the distance-dependent porosity. Except for EDX-Closing, there are comparatively small differences between both samples (see the plots on the right-hand side of Figure 10).
5.2 Influence of Selected Trinarization on Electrochemical Properties
The influence of the selected trinarization approach on the electrochemical simulations is investigated using half-cell lithiation simulations and symmetrical impedance simulations. The only free parameter to achieve a good agreement between experiments and simulations is the effective transport parameter within the electrolyte part of the CBD. Relevant transport mechanisms in a thick NMC electrode are the electronic conductivity through the solid phase and the lithium transport through the electrolyte. Both quantities strongly depend on the distribution and morphology of the CBD. Especially, the electrolyte transport depends on the local effective tortuosity in the CBD. The electronic conductivity depends both on the conductive network of the CBD and the conductivity of the active material, were the latter is additionally dependent on the state of charge. However, at larger CBD contents losses due to electronic transport are minor compared to transport losses in the electrolyte. Therefore, we use the lithiation simulation at a current of 6 mA cm−2 to identify the local effective tortuosity of the CBD that leads to the best agreement between experiment and simulations. Note, at low CBD contents this assumption can be invalid and contribution of the two processes cannot be deconvoluted unambiguously. The best matching effective transport parameters are identified for both electrode types (single-layer cathode and two-layer cathode) with three cutouts each and all trinarization approaches except for NN–CBD–P–AM and NN–P–CBD–AM. In previous studies, we have shown that the EDX-Closing trinarization is able to provide a reasonable agreement between electrochemical measurements and simulations.[ 13, 89 ] Figure 10 visualizes the impact of the effective γ-parameter on the lithiation simulation for the EDX-Closing trinarizations of the two-layer electrode in comparison to the experimental results. Lithiation curves with a current of 6 mA cm−2 serving as target for our parameter optimization are highlighted by the green symbols.
The impact of the spatial distribution of the CBD on the cell voltage and the achievable lihtiation capacity is apparent. A smaller value for the effective transport parameter γ will reduce the achievable lihtiation capacity of the simulated electrode. In turn, increasing the value of γ reduces the transport resistance in the electrolyte allowing to access larger electrode capacity. A value of provides the best match between simulations and experiments for the two-layer electrode created using the EDX-Closing method presented in Figure 11 . This parameter value corresponds to a local effective tortuosity of the electrolyte phase of the CBD of .
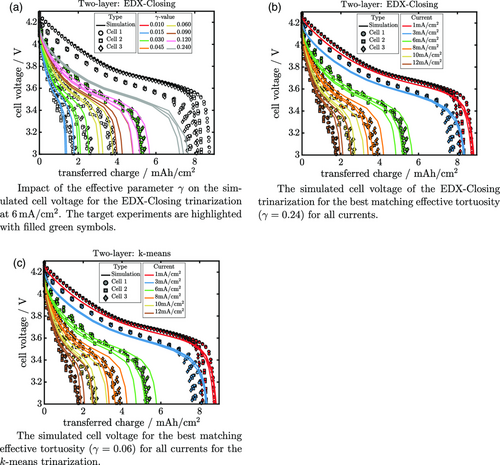
The simulation results for all six currents for the selected effective transport parameter () within the CBD are shown in Figure 11b. The numerical results show some spread for higher currents due to local fluctuations in the three electrode cutouts. Nevertheless, the simulated cell voltages are in excellent agreement with the experimental data for all currents. However, as shown in Figure 11c applying the same procedure to the k-means trinarization will result in a similar match between experiments and simulations. In this case, the resulting effective tortuosity of the CBD is somewhat larger (, 8.3). Similar results can be reported for all cases studied in this work. The figures used for both electrodes and all trinarizations to select the best matching effective tortuosity are shown in the Supporting Information (see Figure S8, Supporting Information). The corresponding values for the ten different trinarizations and the two different electrode types are also listed in Table 3 .
| Method | Single-layer | Two-layer | ||
|---|---|---|---|---|
| k-means | 0.02 | 50 | 0.12 | 8.3 |
| DX-Closing | 0.18 | 5.6 | 0.24 | 4.2 |
| Thresholding | 0.02 | 50 | 0.12 | 8.3 |
| NN–AM–CBD–P | 0.09 | 11.1 | 0.18 | 5.6 |
| NN–AM–Cond | 0.09 | 11.1 | 0.18 | 5.6 |
| NN–AM–P–CBD | 0.03 | 33.3 | 0.18 | 5.6 |
| NN–CBD–AM–P | 0.09 | 11.1 | 0.18 | 5.6 |
| NN–CBD–Cond | 0.09 | 11.1 | 0.18 | 5.6 |
| NN–P–AM–CBD | 0.03 | 33.3 | 0.18 | 5.6 |
| NN–P–Cond | 0.03 | 33.3 | 0.18 | 5.6 |
The impact of the trinarization on the electrode performance differs between the methods investigated in this work. Yet, the two-layer electrode and the single-layer electrode exhibit the same trends. A smaller effective tortuosity indicates that the CBD is distributed in the electrode such that even a small local transport resistance will reduce the overall transport through the electrode. The EDX-Closing trinarization leads to the smallest effective tortuosities for the single-layer and two-layer electrodes due to the distribution of the CBD at the bottlenecks of the active material microstructure. The k-means and thresholding approach, on the other hand, result in the largest effective tortuosities, which implies that the spatial distribution of CBD created by these trinarization methods is not fully covering the bottlenecks for the electrolyte transport. The results obtained for the trinarization based on neural networks are qualitatively in between these two extremes.
Additional analytical techniques are required to probe the influence of the CBD distribution. As shown above, the distribution and corresponding effective tortuosity values have a significant influence on lithium ion transport in the electrolyte. Impedance spectroscopy on symmetrical cells in blocking conditions has become a standard tool for the characterization of the pore transport resistance.[ 90-92 ] Therefore, we additionally performed impedance simulations on symmetrical cells to investigate the impact of the different trinarization methods. The corresponding impedance spectra for the single-layer and two-layer cathode are shown in Figure S6a and S6b, Supporting Information, respectively. However, the different trinarizations result in very similar impedance spectra which will not allow to discern distribution-related effects in corresponding impedance measurements. Therefore, also the electrode impedance does not provide a hint on the most favorable trinarization method.
In summary, we demonstrate that it is possible to identify one effective tortuosity per electrode type and trinarization method such that the simulations are in fair agreement with the experimental data for all currents. However, there are large variations in the effective tortuosity of the CBD between the different trinarization methods. None of the individual techniques is able to provide a consistent representation for all electrode samples investigated in this work. Hence, we could not determine the trinarization method providing the best representation of the electrode microstructure. High-resolution image data of the CBD might yield additional information on the effective CBD conductivity which then eventually will allow to choose the most suitable trinarization technique.
6 Conclusion and Outlook
In the present article, 3D image data of a single-layer and a two-layer cathode obtained by synchrotron tomography have been segmented into active material, the CBD, and the pore space by four different approaches, where the approach based on correlative microscopy allows for nine different trinarizations by altering the way of converting the material composition predicted by the neural network to a three-phase reconstruction. The different segmentation approaches, which are designed to match the experimentally determined volume fractions, are quantitatively compared by means of statistical image analysis as well as spatially and temporally resolved simulations of electrochemical properties. It turns out that there are non-negligible differences between the proposed trinarization approaches. Among others, the geodesic tortuosity as well as the continuous phase size distribution of both - the CBD and the pores - depend on the chosen segmentation approach. Furthermore, it has been shown that there are clear differences between the trinarizations obtained by correlative microscopy. Thus, the rule for converting the material composition predicted by the neural network to a three-phase reconstruction is of importance, even though the differences compared to the remaining three approaches are more pronounced. However, a high level of agreement between the experimental measurements and the lithiation simulations can be achieved for all trinarization methods by adjusting the effective transport parameter of the CBD. Note that using a fixed current for fitting this parameter allows us to match the experimental curves for five different currents, which indicates that each trinarization approach is reasonable. By doing so, the effective tortuosity within the CBD is restricted to the interval . This large range indicates that further research is required to determine the best trinarization approach. For example, the high-resolution 3D FIB-SEM data could be used to quantitatively investigate ionic transport within the nanopores. Nevertheless, this approach based on spatially resolved numerical simulations allows to predict the optimal spatial distribution of the CBD in lithium-ion battery electrodes, leading to an improved electrochemical performance.
Acknowledgements
The presented work was financially supported by the German Ministry “Bundesministerium für Bildung und Forschung” within the projects HighEnergy and HiStructures under the reference numbers 03XP0073C and 03XP0243C/D/E as well as within the framework of the program “Vom Material zur Innovation.” This study contributes to the research performed at CELEST (Center for Electrochemical Energy Storage Ulm Karlsruhe). The work by M.N. was partially funded by the German Research Foundation (DFG) under Project ID 390874152 (POLiS Cluster of Excellence, EXC 2154). The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no. INST 40/575-1 FUGG (JUSTUS 2 cluster). The authors thank Christian Dreer for working out the production process for the single-layer and two-layer electrodes and their manufacturing and Claudia Pfeifer for the preparation and EDX analysis of the electrode cross sections. All responsibility for the content of this publication is assumed by the authors.
Open Access funding enabled and organized by Projekt DEAL.
Conflict of Interest
The authors declare no conflict of interest.
Open Research
Data Availability Statement
Research data are not shared.