Engineering Reports
Volume 7, Issue 7 e70308
RESEARCH ARTICLE
Open Access

Unsteady Radiative MHD Casson Fluid Flow Over an Impulsively Started Porous Plate With Caputo Fractional Derivatives

Mehari Fentahun Endalew, 

Corresponding Author

Mehari Fentahun Endalew

Department of Mathematics, Debre Tabor University, Debre Tabor, Ethiopia

Beijing Institute of Mathematical Sciences and Applications (BIMSA), Beijing, China

Correspondence: Mehari Fentahun Endalew ([email protected])

Contribution: Conceptualization, Methodology, Software, Validation, ​Investigation, Formal analysis

Search for more papers by this author
Xiaoming Zhang, 

Xiaoming Zhang

Beijing Institute of Mathematical Sciences and Applications (BIMSA), Beijing, China

Contribution: Writing - review & editing, Writing - original draft, Conceptualization, Supervision

Search for more papers by this author
First published: 25 July 2025
https://doi.org/10.1002/eng2.70308
Funding: The authors received no specific funding for this work.

ABSTRACT

This study investigates the unsteady natural convection flow of a hydromagnetic Casson fluid past a suddenly accelerated porous plate, incorporating thermal radiation and internal heat generation. The key novelty lies in employing fractional calculus via the Caputo derivative to generalize classical conservation equations, enabling the modeling of memory and hereditary effects crucial for non-Newtonian fluid dynamics. Unlike prior studies focusing on classical or steady-state models, this work develops a fractional-order framework to capture complex unsteady transport phenomena. Exact analytical solutions for momentum, thermal, and concentration equations are derived using Laplace transforms, providing closed-form expressions in the Laplace domain and explicit time-dependent solutions. These serve as rare benchmarks for such systems. The study uniquely integrates thermal radiation and heat generation—often examined separately—while considering porous media and sudden plate motion, enhancing relevance to thermal systems, biomedical flows, and filtration processes. Key findings indicate that increasing the fractional order boosts velocity, temperature, and concentration fields, underscoring the significance of memory effects in transport dynamics. The magnetic field suppresses flow due to Lorentz forces, while thermal radiation and heat generation enhance thermal diffusion. Analytical expressions for skin friction, Nusselt number, and Sherwood number are derived, offering validation benchmarks. A comparison with published results shows strong agreement. The study advances analytical modeling of radiative, magnetized non-Newtonian flows in porous media, with applications in biofluid mechanics, thermal engineering, and industrial processes involving complex fluids. The fractional approach provides a more accurate and generalized framework for such systems.

Abbreviations

  • FPDE
  • fractional partial differential equations
  • MHD
  • magnetohydrodynamics
  • PDE
  • partial differential equation

    • 1 Introduction

    Fractional calculus provides a robust mathematical framework for modeling physical phenomena that exhibit anomalous behavior [1]. Since the latter half of the 20th century, its applications have gained significant traction in engineering literature. Today, fractional calculus plays a central role in diverse fields such as signal processing, physics, fluid mechanics, viscoelasticity, electrochemistry, mathematical biology, and both differential and integral equations [2] highlighted numerous modern applications of fractional calculus across science, engineering, and mathematics. Notably, fractional derivatives have proven to be more effective than integer-order derivatives in capturing complex dynamics in various scenarios [3-5]. In particular, time-fractional derivatives have attracted growing attention for their ability to accurately model fluid flow, heat transfer, and mass transfer processes [6-8].

    Fractional derivatives are widely employed in modeling complex fluid behaviors, particularly for capturing nonlocal interactions and memory effects. Time-fractional derivatives offer a more realistic description in various disciplines, including viscoelastic and non-Newtonian fluids, by accounting for processes where the rate of change depends on both current and past states [9, 10]. For instance, Sadia et al. [11] investigated Casson fluid flow with heat and mass transfer through a porous medium under chemical reactions and slip conditions, demonstrating that memory effects are better captured using fractional models compared to classical approaches. In this context, fractional flow in porous media effectively describes anomalous transport phenomena, where memory and nonlocal dynamics—such as delayed fluid movement due to trapping or adsorption—lead to subdiffusive behavior not adequately modeled by integer-order systems.

    Moreover, the Caputo derivative is preferred here over Riemann–Liouville due to its handling of initial conditions in terms of standard integer-order derivatives, alignment with classical Laplace-transform methods, and the intuitive property that constant functions have zero fractional derivative. These advantages—well-documented in the literature and employed in recent studies such as [12, 13]—provide a clearer and more practical framework for modeling the considered fractional-order phenomena.

    The porous or perforated configuration is characterized by its volume-averaged characteristics through a geometrically defined porous area of volumetric size. Resistance source terms are utilized as closure terms in the momentum equation within this uniform and continuous porous area. In this regard, time fractional derivatives are significant to trace fluid flow through porous medium by replacing classical derivative (i.e., positive integer-order derivatives) with more generalized models, including mass transfer and seepage flow models that use fractional models to capture their complex behaviors more accurately [14-16].

    A powerful mechanism for investigating complicated heat and mass transfer issues, particularly those involving nonlocal interactions, anomalous diffusion, and memory effects, is the fractional model of natural convection [17]. In some circumstances, these models can yield more accurate results, but they can present difficulties because of their processing expense and mathematical complexity. The comprehension of intricate physical phenomena in heat and mass transfer is being improved by the continuous development of fractional calculus and its applications [18, 19]. Moreover, free convection flow of incompressible viscous fluid across the vertical plate under the effect of chemical reaction and Newtonian heating has been investigated by [20] and Vieru et al. [21]. Here, the closed-form solution is obtained via the Laplace transform approach. Recently, mass and heat transfer mechanisms have been investigated by [22, 23].

    Furthermore, another fantastic concept in this investigation is a topic referring to a hydrodynamic Casson fluid flow under the effect of a heat source and thermal radiation, coupled with mass and heat transport in a fractional time model [24]. It is obvious that this is a nontrivial problem, which involves much more complicated and advanced research in viscous fluid flow behavior with thermal and solute transport analysis. This kind of model has numerous scientific and industrial significances, including heat exchangers, biomedical scenarios, plasma dynamics, cooling systems, and heat generation [25-27]. Moreover, time-dependent MHD Casson fluid with magnetic field presence has been performed by [28-33].

    In light of the above literature, it is evident that limited research has addressed the combined influence of magnetic fields, thermal radiation, and internal heat generation in non-Newtonian Casson fluids using fractional calculus. Most existing studies rely on classical integer-order models, which may fail to capture the memory-dependent behavior inherent in complex fluids. Unlike previous works, this study introduces a generalized fractional-order formulation of the governing transport equations using the Caputo derivative, enabling the accurate modeling of viscoelastic memory effects. Furthermore, analytical solutions are derived via Laplace transform techniques and presented in closed-form expressions, providing deeper insights into the transient behavior of velocity, temperature, and concentration fields. A key novelty lies in the quantification of the effects of fractional parameters on the skin friction coefficient, Nusselt number, and Sherwood number, which have not been comprehensively explored in prior analytical studies. This framework significantly enhances the physical understanding of magneto-convective transport phenomena in porous media and offers a rigorous mathematical tool for benchmarking and validating numerical models in applied sciences and engineering.

    2 Model Formulation

    Herein, the incompressible transient radiative MHD Casson fluid flow over an impulsively started porous plate under the effects of buoyancy forces and heat injection/sink is considered. We have surmised that w ( y ′ , 0 ) = 0 $$ w\left({y}^{\prime },0\right)=0 $$ and w ( 0 , t ′ ) = w s $$ w\left(0,{t}^{\prime}\right)={w}_s $$ to specify the respective initial velocity and sudden motion of the plate. Besides, the magnetic field acts perpendicular to the flow direction. Furthermore, the ambient temperature ( T ∞ $$ {T}_{\infty } $$ ) and concentration ( C ∞ $$ {C}_{\infty } $$ ) are maintained constant at a distance from the surface of the plate. The geometrical illustration is provided in Figure 1.

    Details are in the caption following the image
    FIGURE 1
    Open in figure viewerPowerPoint
    Schematic diagram of the flow.
    Rheological circumstances for an isotropic incompressible Casson fluid possess the following form [34, 35]:
    τ i j = P y 2 π + μ B 2 e i j , π > π c , P y 2 π c + μ B 2 e i j , π < π c $$ {\tau}_{ij}=\left\{\begin{array}{c}\hfill \left(\frac{P_y}{\sqrt{2\pi }}+{\mu}_B\right)2{e}_{ij},\pi >{\pi}_c,\\ {}\hfill \left(\frac{P_y}{\sqrt{2{\pi}_c}}+{\mu}_B\right)2{e}_{ij},\pi <{\pi}_c\end{array}\right. $$ (1)
    The dimensionless parameter with inclusion of π c $$ {\pi}_c $$ is given by β = μ B 2 π c P y $$ \beta =\frac{\mu_B\sqrt{2{\pi}_c}}{P_y} $$ .

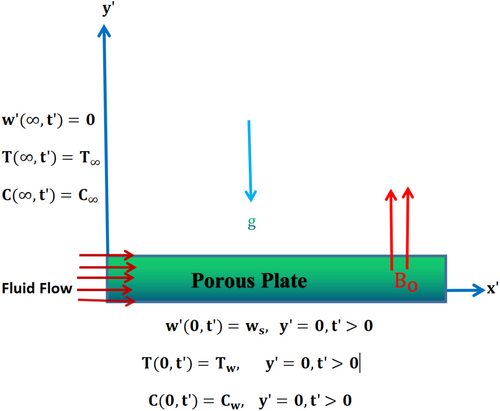
    Here, β $$ \beta $$ is the upper limit apparent coefficient of viscosity and should be smaller compared with the upper limit viscosity coefficient. Moreover, τ i j $$ {\tau}_{ij} $$ represents shear stress, e i j $$ {e}_{ij} $$ is rate of deformation tensor, π = e i j e i j $$ \pi ={e}_{ij}{e}_{ij} $$ , π c $$ {\pi}_c $$ is the critical value of π $$ \pi $$ determined from the non-Newtonian model, μ B $$ {\mu}_B $$ represents the plastic dynamic viscosity and P y $$ {P}_y $$ denotes yield stress.

    Note that P y $$ {P}_y $$ represents the minimum stress needed before any fluid flow occurs. Consequently, the fluid behaves like a solid when the applied shear stress is lower than the yield stress. However, it begins to flow once the shear stress exceeds the yield stress.

    Hence, the model of transient free convection flow radiative MHD Casson fluid over porous plate can be formulated as [36-40]:
    ∂ w ′ ∂ t ′ = ν 1 + 1 β ∂ 2 w ′ ∂ y ′ 2 − σ B o 2 ρ + μ k 1 ρ k o w ′ $$ \frac{\partial {w}^{\prime }}{\partial {t}^{\prime }}=\nu \left(1+\frac{1}{\beta}\right)\frac{\partial^2{w}^{\prime }}{\partial {y}^{\prime 2}}-\left(\frac{\sigma {B}_o^2}{\rho }+\frac{\mu {k}_1}{\rho {k}_o}\right){w}^{\prime } $$ (2)
    + g β T T − T ∞ + g β C C − C ∞ $$ +g{\beta}_T\left(T-{T}_{\infty}\right)+g{\beta}_C\left(C-{C}_{\infty}\right) $$ (3)
    ρ c p ∂ T ∂ t ′ = κ ∂ 2 T ∂ y ′ 2 − ∂ q r ∂ y ′ + S ′ T − T ∞ $$ \rho {c}_p\frac{\partial T}{\partial {t}^{\prime }}=\kappa \frac{\partial^2T}{\partial {y}^{\prime 2}}-\frac{\partial {q}_r}{\partial {y}^{\prime }}+{S}^{\prime}\left(T-{T}_{\infty}\right) $$ (4)
    ∂ C ∂ t ′ = D o ∂ 2 C ∂ y ′ 2 − R c C − C ∞ $$ \frac{\partial C}{\partial {t}^{\prime }}={D}_o\frac{\partial^2C}{\partial {y}^{\prime 2}}-{R}_c\left(C-{C}_{\infty}\right) $$ (5)
    Associated initial and boundary conditions are [36, 37]:
    w ′ ( y ′ , 0 ) = 0 , T ( y ′ , 0 ) = T ∞ , C ( y ′ , 0 ) = C ∞ , ∀ y ′ ≥ 0 $$ {w}^{\prime}\left({y}^{\prime },0\right)=0,T\left({y}^{\prime },0\right)={T}_{\infty },C\left({y}^{\prime },0\right)={C}_{\infty },\forall {y}^{\prime}\ge 0 $$ (6a)
    w ′ ( 0 , t ′ ) = w s , T ( 0 , t ′ ) = T w , C ( 0 , t ′ ) = C w , ∀ t ′ > 0 $$ {w}^{\prime}\left(0,{t}^{\prime}\right)={w}_s,T\left(0,{t}^{\prime}\right)={T}_w,C\left(0,{t}^{\prime}\right)={C}_w,\forall {t}^{\prime }>0 $$ (6b)
    w ′ ( ∞ , t ′ ) = 0 , T ( ∞ , t ′ ) = T ∞ , C ( ∞ , t ′ ) = C ∞ , ∀ t ′ > 0 $$ {w}^{\prime}\left(\infty, {t}^{\prime}\right)=0,T\left(\infty, {t}^{\prime}\right)={T}_{\infty },C\left(\infty, {t}^{\prime}\right)={C}_{\infty },\forall {t}^{\prime }>0 $$ (6c)
    The initial and boundary conditions described in Eqs. (6a-6c) have significant real-world relevance across various engineering and physical systems. The initial condition w ′ ( y ′ , 0 ) = 0 $$ {w}^{\prime}\left({y}^{\prime },0\right)=0 $$ implies that the fluid is initially at rest, while T ( y ′ , 0 ) = T ∞ $$ T\left({y}^{\prime },0\right)={T}_{\infty } $$ and C ( y ′ , 0 ) = C ∞ $$ C\left({y}^{\prime },0\right)={C}_{\infty } $$ indicate that the system begins with uniform ambient temperature and concentration. Such assumptions are typical in startup scenarios of heat and mass transfer processes, for example, when a system is first activated or a fluid begins to flow through a porous medium. The boundary conditions at the wall y ′ = 0 $$ {y}^{\prime }=0 $$ , given by w ′ ( 0 , t ′ ) = w s $$ {w}^{\prime}\left(0,{t}^{\prime}\right)={w}_s $$ , T ( 0 , t ′ ) = T w $$ T\left(0,{t}^{\prime}\right)={T}_w $$ , and C ( 0 , t ′ ) = C w $$ C\left(0,{t}^{\prime}\right)={C}_w $$ , model cases where the wall experiences a constant suction or injection velocity along with fixed thermal and solutal conditions. These are widely encountered in applications like boundary layer control in aerodynamics through suction, controlled cooling or heating in heat exchangers, and mass transfer processes in drying technologies or biomedical drug delivery. Finally, the far-field boundary conditions w ′ ( ∞ , t ′ ) = 0 $$ {w}^{\prime}\left(\infty, {t}^{\prime}\right)=0 $$ , T ( ∞ , t ′ ) = T ∞ $$ T\left(\infty, {t}^{\prime}\right)={T}_{\infty } $$ , and C ( ∞ , t ′ ) = C ∞ $$ C\left(\infty, {t}^{\prime}\right)={C}_{\infty } $$ assume that the fluid velocity vanishes and thermal and concentration profiles return to ambient values at large distances from the wall. This represents open system behavior where wall effects are localized, such as in atmospheric flows, cooling plumes in large fluid reservoirs, or thermal discharge into the environment.

    Note that the nomenclature, presented in Table 1, defines all physical parameters and symbols used in this study.

    TABLE 1. List of symbols and their definitions.
    Symbol Description (SI unit)
    β $$ \beta $$ Casson parameter (dimensionless)
    P y $$ {P}_y $$ Yield stress (Pa or N/m   2 $$ {}^2 $$ )
    ν $$ \nu $$ Kinematic viscosity (m   2 $$ {}^2 $$ /s)
    μ $$ \mu $$ Dynamic viscosity (Pa · $$ \cdotp $$ s)
    ρ $$ \rho $$ Density (kg/m   3 $$ {}^3 $$ )
    σ $$ \sigma $$ Electrical conductivity (S/m)
    w $$ w $$ Fluid velocity (dimensionless)
    w ′ $$ {w}^{\prime } $$ Dimensional vertical fluid velocity (m/s)
    y $$ y $$ Spatial coordinate (dimensionless)
    y ′ $$ {y}^{\prime } $$ Dimensional spatial coordinate normal to the plate (m)
    t $$ t $$ Time (dimensionless)
    t ′ $$ {t}^{\prime } $$ Dimensional time (s)
    T $$ T $$ Temperature (K)
    T w $$ {T}_w $$ Wall (surface) temperature (K)
    T ∞ $$ {T}_{\infty } $$ Ambient (free stream) temperature (K)
    β T $$ {\beta}_T $$ Thermal expansion coefficient (K   − 1 $$ {}^{-1} $$ )
    c p $$ {c}_p $$ Specific heat capacity (J/(kg · $$ \cdotp $$ K))
    κ $$ \kappa $$ Thermal conductivity (W/(m · $$ \cdotp $$ K))
    q r $$ {q}_r $$ Radiative heat flux (W/m   2 $$ {}^2 $$ )
    S ′ $$ {S}^{\prime } $$ Dimensional heat source (W/m   3 $$ {}^3 $$ )
    C $$ C $$ Concentration (mol/m   3 $$ {}^3 $$ )
    C w $$ {C}_w $$ Wall (surface) concentration (mol/m   3 $$ {}^3 $$ )
    C ∞ $$ {C}_{\infty } $$ Ambient (free stream) concentration (mol/m   3 $$ {}^3 $$ )
    β C $$ {\beta}_C $$ Solutal expansion coefficient ((mol · $$ \cdotp $$ m   − 3 $$ {}^{-3} $$ )   − 1 $$ {}^{-1} $$ )
    D o $$ {D}_o $$ Molar diffusion coefficient (m   2 $$ {}^2 $$ /s)
    R c $$ {R}_c $$ Dimensional chemical reaction rate (s   − 1 $$ {}^{-1} $$ )
    B o $$ {B}_o $$ Magnetic field strength (T)
    k 1 $$ {k}_1 $$ Porosity (dimensionless)
    k o $$ {k}_o $$ Permeability (m   2 $$ {}^2 $$ )
    G r $$ Gr $$ Thermal Grashof number (dimensionless)
    G m $$ Gm $$ Molar Grashof number (dimensionless)
    P r $$ \mathit{\Pr} $$ Prandtl number (dimensionless)
    S c $$ Sc $$ Schmidt number (dimensionless)
    R d $$ Rd $$ Thermal radiation parameter (dimensionless)
    Q o $$ {Q}_o $$ Heat generation parameter (dimensionless)
    R $$ R $$ Chemical reaction parameter (dimensionless)
    F p $$ Fp $$ Porosity parameter (dimensionless)
    F m $$ Fm $$ Magnetic field parameter (dimensionless)
    τ s $$ {\tau}_s $$ Skin friction at the wall (N/m   2 $$ {}^2 $$ )
    N u $$ Nu $$ Nusselt number (dimensionless heat transfer rate)
    S h $$ Sh $$ Sherwood number (dimensionless mass transfer rate)
    Depending on Rosseland's assumption, we have the following mathematical expression of radiation flux [41, 42]:
    q r = − 4 σ ′ 3 κ ′ ∂ T 4 ∂ y ′ $$ {q}_r=-\frac{4{\sigma}^{\prime }}{3{\kappa}^{\prime }}\frac{\partial {T}^4}{\partial {y}^{\prime }} $$ (7)

    From the equation as mentioned above, σ ′ $$ {\sigma}^{\prime } $$ symbolizes the Stefan–Boltzmann constant, while κ ′ $$ {\kappa}^{\prime } $$ denotes the heat absorption coefficient.

    By using the Taylor series expansion approach and discarding the higher order terms, T 4 $$ {T}^4 $$ is expanded around T ∞ $$ {T}_{\infty } $$ , yielding:
    T 4 ≅ 4 T − 3 T ∞ T ∞ 3 $$ {T}^4\cong \left(4T-3{T}_{\infty}\right){T}_{\infty}^3 $$ (8)
    Note that the approximation T 4 ≈ ( 4 T − 3 T ∞ ) T ∞ 3 $$ {T}^4\approx \left(4T-3{T}_{\infty}\right){T}_{\infty}^3 $$ used in is based on a first-order Taylor series expansion of T 4 $$ {T}^4 $$ about T = T ∞ $$ T={T}_{\infty } $$ . The truncation introduces an error of the form R 1 ( T ) = 6 ξ 2 ( T − T ∞ ) 2 $$ {R}_1(T)=6{\xi}^2{\left(T-{T}_{\infty}\right)}^2 $$ , where ξ $$ \xi $$ lies between T $$ T $$ and T ∞ $$ {T}_{\infty } $$ . Thus, the error is of order 𝒪 ( ( T − T ∞ ) 2 ) , and this approximation remains valid when | T − T ∞ | $$ \mid T-{T}_{\infty}\mid $$ is sufficiently small. However, for large temperature gradients, the neglected higher-order terms may lead to significant deviations, and a nonlinear treatment of radiative heat flux may be more appropriate. Thus, the radiation heat flux is modified as
    q r = − 16 σ ′ T ∞ 3 3 κ ′ ∂ T ∂ y ′ $$ {q}_r=-\frac{16{\sigma}^{\prime }{T}_{\infty}^3}{3{\kappa}^{\prime }}\frac{\partial T}{\partial {y}^{\prime }} $$ (9)
    Substituting Equation (9) in (4) modifies the energy equation as
    ρ c p ∂ T ∂ t ′ = κ + 16 σ ′ T ∞ 3 3 κ ′ ∂ 2 T ∂ y ′ 2 + S ′ T − T ∞ $$ \rho {c}_p\frac{\partial T}{\partial {t}^{\prime }}=\left(\kappa +\frac{16{\sigma}^{\prime }{T}_{\infty}^3}{3{\kappa}^{\prime }}\right)\frac{\partial^2T}{\partial {y}^{\prime 2}}+{S}^{\prime}\left(T-{T}_{\infty}\right) $$ (10)
    Let us define the dimensionless physical quantities as follows:
    w = w ′ w s , ϕ = C − C ∞ C w − C ∞ , t = w s 2 t ′ ν , θ = T − T ∞ T w − T ∞ , y = y ′ w s ν $$ w=\frac{w^{\prime }}{w_s},\phi =\frac{C-{C}_{\infty }}{C_w-{C}_{\infty }},t=\frac{w_s^2{t}^{\prime }}{\nu },\theta =\frac{T-{T}_{\infty }}{T_w-{T}_{\infty }},y=\frac{y^{\prime }{w}_s}{\nu } $$ (11)
    Therefore, the governing equations above can be simplified into dimensionless form as follows:
    ∂ w ∂ t = C a ∂ 2 w ∂ y 2 − b w + G r θ + G m ϕ $$ \frac{\partial w}{\partial t}={C}_a\frac{\partial^2w}{\partial {y}^2}- bw+ Gr\theta + Gm\phi $$ (12)
    ∂ θ ∂ t = P e f ∂ 2 θ ∂ y 2 + Q o θ $$ \frac{\partial \theta }{\partial t}={P}_{ef}\frac{\partial^2\theta }{\partial {y}^2}+{Q}_o\theta $$ (13)
    S c ∂ ϕ ∂ t = ∂ 2 ϕ ∂ y 2 − S c R ϕ $$ Sc\frac{\partial \phi }{\partial t}=\frac{\partial^2\phi }{\partial {y}^2}- ScR\phi $$ (14)
    Where P e f = 1 + R d P r , b = F p + F m . $$ {P}_{ef}=\frac{1+ Rd}{\mathit{\Pr}},b={F}_p+{F}_m. $$
    Subject to the following initial and boundary conditions:
    w ( y , 0 ) = 0 , θ ( y , 0 ) = 0 , ϕ ( y , 0 ) = 0 , ∀ y ≥ 0 $$ w\left(y,0\right)=0,\theta \left(y,0\right)=0,\phi \left(y,0\right)=0,\forall y\ge 0 $$ (15a)
    w ( 0 , t ) = 1 , θ ( 0 , t ) = ϕ ( 0 , t ) = 1 $$ w\left(0,t\right)=1,\theta \left(0,t\right)=\phi \left(0,t\right)=1 $$ (15b)
    w ( ∞ , t ) = 0 , θ ( ∞ , t ) = 0 , ϕ ( ∞ , t ) = 0 $$ w\left(\infty, t\right)=0,\theta \left(\infty, t\right)=0,\phi \left(\infty, t\right)=0 $$ (15c)
    where
    C a = 1 + 1 β , G r = ν g β T T w − T ∞ w s 3 , G m = ν g β C C w − C ∞ w s 3 , F m = ν 2 k o w o 2 , F p = ν σ B o 2 ρ w o 2 , P r = ρ c p κ , R d = 4 σ ∗ T ∞ 3 κ k ∗ , Q o = S ′ ν ρ c p w o 2 , R = ν R c w s 2 , S c = ν D o $$ {\displaystyle \begin{array}{llll}\hfill {C}_a& =\left(1+\frac{1}{\beta}\right), Gr=\frac{\nu g{\beta}_T\left({T}_w-{T}_{\infty}\right)}{w_s^3}, Gm=\frac{\nu g{\beta}_C\left({C}_w-{C}_{\infty}\right)}{w_s^3},& \kern0em & \\ {}\hfill {F}_m& =\frac{\nu^2}{k_o{w}_o^2},{F}_p=\frac{\nu \sigma {B}_o^2}{\rho {w}_o^2},\mathit{\Pr}=\frac{\rho {c}_p}{\kappa }, Rd=\frac{4\sigma \ast {T}_{\infty}^3}{\kappa k\ast },& \kern0em & \\ {}\hfill {Q}_o& =\frac{S^{\prime}\nu }{\rho {c}_p{w}_o^2},R=\frac{\nu {R}_c}{w_s^2}, Sc=\frac{\nu }{D_o}& & \end{array}} $$ (16)

    3 Fractional Models

    In this section, we have converted the fluid governing equations into fractional models using the Caputo derivative.

    4 Convergence and Truncation Error Analysis

    Most investigations of differential equations, particularly those involving series solutions, require a thorough analysis of convergence and truncation errors. Several researchers, such as [43-46], have conducted detailed studies on the convergence behavior of series-based solutions in this context.

    Theorem 1. (General Convergence and Error Bound)Let

    ϕ ( y , t ) = ∑ k 1 = 0 ∞ ⋯ ∑ k p = 0 ∞ C ( k 1 , … , k p ) F ( y , t , k 1 , … , k p ) $$ \phi \left(y,t\right)=\sum \limits_{k_1=0}^{\infty}\cdots \sum \limits_{k_p=0}^{\infty }C\left({k}_1,\dots, {k}_p\right)F\left(y,t,{k}_1,\dots, {k}_p\right) $$
    be a multiparameter infinite series with the following assumptions:
    • A1.

      For each k i $$ {k}_i $$ , there exists ρ i < 1 $$ {\rho}_i<1 $$ such that:

      C ( k 1 , … , k i + 1 , … , k p ) C ( k 1 , … , k i , … , k p ) ≤ ρ i $$ \left|\frac{C\left({k}_1,\dots, {k}_i+1,\dots, {k}_p\right)}{C\left({k}_1,\dots, {k}_i,\dots, {k}_p\right)}\right|\le {\rho}_i $$

    • A2.

      Basis functions satisfy:

      | F ( y , t , k 1 , … , k p ) | ≤ τ g ( k 1 , … , k p ) , τ < 1 $$ \mid F\left(y,t,{k}_1,\dots, {k}_p\right)\mid \le {\tau}^{g\left({k}_1,\dots, {k}_p\right)},\kern1em \tau <1 $$

    • A3.

      Any Gamma functions Γ ( h ( k 1 , … , k p ) ) $$ \Gamma \left(h\left({k}_1,\dots, {k}_p\right)\right) $$ in the denominator are finite (i.e., h ∉ ℤ − $$ h\notin {\mathbb{Z}}^{-} $$ ).

    Then

    • The series converges absolutely.
    • The truncated version
      ϕ N 1 , … , N p ( y , t ) = ∑ k 1 = 0 N 1 ⋯ ∑ k p = 0 N p C ( k 1 , … , k p ) F ( y , t , k 1 , … , k p ) $$ {\phi}_{N_1,\dots, {N}_p}\left(y,t\right)=\sum \limits_{k_1=0}^{N_1}\cdots \sum \limits_{k_p=0}^{N_p}C\left({k}_1,\dots, {k}_p\right)F\left(y,t,{k}_1,\dots, {k}_p\right) $$
      satisfies the error bound
      ϕ ( y , t ) − ϕ N 1 , … , N p ( y , t ) ≤ ∑ i = 1 p ρ i N i + 1 e ρ i ( N i + 1 ) ! + HOT $$ \left|\phi \left(y,t\right)-{\phi}_{N_1,\dots, {N}_p}\Big(y,t\Big)\right|\le \sum \limits_{i=1}^p\frac{\rho_i^{N_i+1}{e}^{\rho_i}}{\left({N}_i+1\right)!}+\mathrm{HOT} $$
      where HOT = higher order terms.

    Corollary 1. (Double and Triple Series Case)

    • For a double series:
      ϕ − ϕ N , M ≤ ρ 1 N + 1 e ρ 1 ( N + 1 ) ! + ρ 2 M + 1 e ρ 2 ( M + 1 ) ! $$ \left|\phi -{\phi}_{N,M}\right|\le \frac{\rho_1^{N+1}{e}^{\rho_1}}{\left(N+1\right)!}+\frac{\rho_2^{M+1}{e}^{\rho_2}}{\left(M+1\right)!} $$
    • For a triple series:
      w − w N , M , K ≤ ∑ i = 1 3 ρ i N i + 1 e ρ i ( N i + 1 ) ! $$ \left|w-{w}_{N,M,K}\right|\le \sum \limits_{i=1}^3\frac{\rho_i^{N_i+1}{e}^{\rho_i}}{\left({N}_i+1\right)!} $$

    Theorem 2. (Convergence of ϕ ( y , t ) $$ \phi \left(y,t\right) $$ and w ( y , t ) $$ w\left(y,t\right) $$ )Let y , t ∈ ℝ $$ y,t\in \mathbb{R} $$ and parameters S c , R , a , b , c , c 1 , b 1 , b 2 , P e f , Q o , α $$ Sc,R,a,b,c,{c}_1,{b}_1,{b}_2,{P}_{ef},{Q}_o,\alpha $$ be finite with α > 0 $$ \alpha >0 $$ . Then

    • The double series

      ϕ ( y , t ) = ∑ n = 0 ∞ ∑ m = 0 ∞ ( − 1 ) n y n S c n / 2 n ! m ! Γ ( n / 2 + 1 ) Γ ( n / 2 − m + 1 ) R n / 2 − m t − m α Γ ( 1 − m α ) $$ \phi \left(y,t\right)=\sum \limits_{n=0}^{\infty}\sum \limits_{m=0}^{\infty}\frac{{\left(-1\right)}^n{y}^nS{c}^{n/2}}{n!m!}\frac{\Gamma \left(n/2+1\right)}{\Gamma \left(n/2-m+1\right)}{R}^{n/2-m}\frac{t^{- m\alpha}}{\Gamma \left(1- m\alpha \right)}\kern1.00em $$
      converges absolutely for all y , t ∈ ℝ $$ y,t\in \mathbb{R} $$ .

    • The triple series w ( y , t ) $$ w\left(y,t\right) $$ involving terms like

      ∑ q = 0 ∞ ∑ r = 0 ∞ ∑ m = 0 ∞ c m ( − a y ) q b q 2 − r q ! r ! · Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) · t α ( m − r + 1 ) Γ ( α ( m − r + 1 ) + 1 ) $$ \sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\sum \limits_{m=0}^{\infty}\frac{c^m{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\cdotp \frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\cdotp \frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m-r+1\right)+1\right)}\kern1.00em $$
      and their variants also converge absolutely for all y , t ∈ ℝ $$ y,t\in \mathbb{R} $$ .

    Proof.

    • In ϕ ( y , t ) $$ \phi \left(y,t\right) $$ , for each n $$ n $$ , the Gamma denominator is well-defined for all m $$ m $$ . Applying Stirling's approximation to the Gamma functions and noting factorial decay, the series is absolutely convergent.

    • In w ( y , t ) $$ w\left(y,t\right) $$ , all series components include exponential-type decay from factorial and Gamma terms. Using the ratio test for each index, the growth of denominators dominates numerators as q , r , m → ∞ $$ q,r,m\to \infty $$ , ensuring convergence.

    4.1 Some Notes on Truncated Series and Error Estimates

    4.1.1 Truncated Approximation

    In practice, we compute truncated approximations such as
    ϕ N , M ( y , t ) = ∑ n = 0 N ∑ m = 0 M ( − 1 ) n y n S c n / 2 n ! m ! · Γ ( n / 2 + 1 ) Γ ( n / 2 − m + 1 ) R n / 2 − m · t − m α Γ ( 1 − m α ) $$ {\phi}_{N,M}\left(y,t\right)=\sum \limits_{n=0}^N\sum \limits_{m=0}^M\frac{{\left(-1\right)}^n{y}^nS{c}^{n/2}}{n!m!}\cdotp \frac{\Gamma \left(n/2+1\right)}{\Gamma \left(n/2-m+1\right)}{R}^{n/2-m}\cdotp \frac{t^{- m\alpha}}{\Gamma \left(1- m\alpha \right)} $$
    Analogously, w L , Q , R ( y , t ) $$ {w}_{L,Q,R}\left(y,t\right) $$ is truncated in m , q , r $$ m,q,r $$ respectively.

    4.1.2 Error Bound

    Under the assumptions of Theorem 1, we estimate:
    ϕ ( y , t ) − ϕ N , M ( y , t ) ≤ C 1 ρ 1 N + 1 ( N + 1 ) ! + C 2 ρ 2 M + 1 ( M + 1 ) ! $$ \left|\phi \left(y,t\right)-{\phi}_{N,M}\Big(y,t\Big)\right|\le {C}_1\frac{\rho_1^{N+1}}{\left(N+1\right)!}+{C}_2\frac{\rho_2^{M+1}}{\left(M+1\right)!} $$
    and
    w ( y , t ) − w L , Q , R ( y , t ) ≤ C 3 ρ 1 L + 1 ( L + 1 ) ! + ρ 2 Q + 1 ( Q + 1 ) ! + ρ 3 R + 1 ( R + 1 ) ! $$ \left|w\left(y,t\right)-{w}_{L,Q,R}\Big(y,t\Big)\right|\le {C}_3\left(\frac{\rho_1^{L+1}}{\left(L+1\right)!}+\frac{\rho_2^{Q+1}}{\left(Q+1\right)!}+\frac{\rho_3^{R+1}}{\left(R+1\right)!}\right) $$
    for some constants C i $$ {C}_i $$ dependent on y , t , α $$ y,t,\alpha $$ , etc.

    4.1.3 Truncation Strategy

    Choose truncation levels N , M , L , Q , R $$ N,M,L,Q,R $$ such that
    Total Error ≤ ϵ $$ \mathrm{Total}\ \mathrm{Error}\le \epsilon $$
    This balances computational cost with accuracy.

    4.1.4 Numerical Stability

    Truncating beyond moderate index values ensures high precision while preventing overflow in Gamma and factorial evaluations. Convergence is robust for physically relevant ranges of y , t $$ y,t $$ .

    Note that the analysis of the remaining series solutions in this work follows analogously.

    4.2 Fractional Concentration Equation

    Let us define the equation of diffusion balance as follows:
    ∂ C ∂ t = − ∂ M ∂ y $$ \frac{\partial C}{\partial t}=-\frac{\partial M}{\partial y} $$ (17)
    where
    M = − D α C D t 1 − α ∂ C ∂ y , 0 < α ≤ 1 $$ M=-{D}_{\alpha}^C{D}_t^{1-\alpha}\left[\frac{\partial C}{\partial y}\right],0<\alpha \le 1 $$ (18)
    Equation (18) is known as Fick's Law. By putting Equation (18) in to (17) and using Equation (14), we obtained
    S c ∂ ϕ ∂ t =   C D t 1 − α ∂ 2 ϕ ∂ y 2 − S c R ϕ $$ Sc\frac{\partial \phi }{\partial t}={}^C{D}_t^{1-\alpha}\left[\frac{\partial^2\phi }{\partial {y}^2}- ScR\phi \right] $$ (19)
    Equation (19) can be solved using Laplace Transform method.
    It is important to note that   C D t 1 − α $$ {}^C{D}_t^{1-\alpha } $$ represents the Caputo fractional derivative with respect to time, and is defined as
      C D t α ( f ( t ) ) = 1 Γ ( 1 − α ) ∫ 0 x f ( n ) ( x ) ( t − x ) α − 1 + n d x $$ {}^C{D}_t^{\alpha}\left(f(t)\right)=\frac{1}{\Gamma \left(1-\alpha \right)}{\int}_0^x\frac{f^{(n)}(x)}{{\left(t-x\right)}^{\alpha -1+n}} dx $$ (20)
    The Laplace Transform of D t α f ( x , t ) $$ {D}_t^{\alpha }f\left(x,t\right) $$ for t > 0 $$ t>0 $$ is expressed as
    ℒ [ C D t α f ( y , t ) ] = s α ℒ [ f ( y , t ) ] − ∑ n = 0 m − 1 f n ( y , 0 ) s α − n − 1 , ( m − 1 < α < m , m ∈ 𝒩 ) or m − 1 = ⌊ α ⌋ (21)
    When F ( y , s ) $$ F\left(y,s\right) $$ represents the Laplace transform of the function f ( y , t ) $$ f\left(y,t\right) $$ , then f ( x , t ) = ℒ − 1 [ F ( y , s ) ] $$ f\left(x,t\right)={\mathcal{L}}^{-1}\left[F\left(y,s\right)\right] $$ represents inverse Laplace Transform.
    However, the value of α $$ \alpha $$ in this investigation is restricted as 0 < α ≤ 1 $$ 0<\alpha \le 1 $$ . Therefore, Equation (21) is reduced as [47]:
    ℒ [   C D t α f ( y , t ) ] = s α ℒ ( f ( y , t ) ) − s α − 1 ( f ( y , 0 ) ) $$ \mathcal{L}\left[{}^C{D}_t^{\alpha }f\left(y,t\right)\right]={s}^{\alpha}\mathcal{L}\left(f\left(y,t\right)\right)-{s}^{\alpha -1}\left(f\left(y,0\right)\right) $$ (22)
    Note that α $$ \alpha $$ denotes fractional derivative parameter.
    Therefore, by applying Laplace transform and utilizing initial conditions to (19), it reduced into the following second-order ordinary differential equation.
    d 2 ϕ ( y , s ) d y 2 − S c s α + R ϕ ( y , s ) $$ \frac{d^2\phi \left(y,s\right)}{d{y}^2}- Sc\left({s}^{\alpha }+R\right)\phi \left(y,s\right) $$ (23)
    The s $$ s $$ -domain solution becomes
    ϕ ( y , s ) = A e − y S c ( s α + R ) + B e y S c ( s α + R ) $$ \phi \left(y,s\right)=A{e}^{-y\sqrt{Sc\left({s}^{\alpha }+R\right)}}+B{e}^{y\sqrt{Sc\left({s}^{\alpha }+R\right)}} $$ (24)
    From the given boundary conditions, we have the following transformed conditions:
    ϕ ( 0 , s ) = 1 s and ϕ ( ∞ , 0 ) = 0 $$ \phi \left(0,s\right)=\frac{1}{s}\kern0.3em \mathrm{and}\kern0.3em \phi \left(\infty, 0\right)=0 $$ (25)
    Using Equation (25), the fractional concentration in s $$ s $$ -domain remains
    ϕ ( y , s ) = 1 s e − y S c ( s α + R ) $$ \phi \left(y,s\right)=\frac{1}{s}{e}^{-y\sqrt{Sc\left({s}^{\alpha }+R\right)}} $$ (26)
    Note that in the Laplace domain, the general solution to the fractional differential equation involves two exponential terms with unknown constants A $$ A $$ and B $$ B $$ . The boundary conditions ϕ ( 0 , s ) = 1 s $$ \phi \left(0,s\right)=\frac{1}{s} $$ and ϕ ( ∞ , s ) = 0 $$ \phi \left(\infty, s\right)=0 $$ are used to determine these constants. Substituting y = 0 $$ y=0 $$ into the general solution gives A + B = 1 s $$ A+B=\frac{1}{s} $$ . To satisfy the second boundary condition, we examine the behavior as y → ∞ $$ y\to \infty $$ . The term e y S c ( s α + R ) $$ {e}^{y\sqrt{Sc\left({s}^{\alpha }+R\right)}} $$ is always nonzero and increases exponentially with y $$ y $$ since y $$ y $$ , S c $$ Sc $$ , and s α + R $$ {s}^{\alpha }+R $$ are all positive. This means that unless B = 0 $$ B=0 $$ , the solution would diverge at infinity, violating the physical requirement that the concentration must vanish far from the boundary. Therefore, to ensure the solution remains finite, we set B = 0 $$ B=0 $$ , and from the earlier condition, A = 1 s $$ A=\frac{1}{s} $$ . Substituting back yields the final expression ϕ ( y , s ) = 1 s e − y S c ( s α + R ) $$ \phi \left(y,s\right)=\frac{1}{s}{e}^{-y\sqrt{Sc\left({s}^{\alpha }+R\right)}} $$ , which satisfies both boundary conditions and represents the physically meaningful, decaying concentration profile in the Laplace domain. A similar approach works for temperature and velocity fields.
    By employing the exponential series with binomial expansion, we get
    ϕ ( y , s ) = ∑ n = 0 ∞ ∑ m = 0 ∞ ( − 1 ) n y n S c n / 2 n ! m ! Γ ( n / 2 + 1 ) Γ ( n / 2 − m + 1 ) R n / 2 − m s m α − 1 $$ \phi \left(y,s\right)=\sum \limits_{n=0}^{\infty}\sum \limits_{m=0}^{\infty}\frac{{\left(-1\right)}^n{y}^nS{c}^{n/2}}{n!m!}\frac{\Gamma \left(n/2+1\right)}{\Gamma \left(n/2-m+1\right)}{R}^{n/2-m}{s}^{m\alpha -1} $$ (27)
    By taking Laplace transform inverse of both sides of Equation (27), the final exact solution of fractional concentration remains
    ϕ ( y , t ) = ∑ n = 0 ∞ ∑ m = 0 ∞ ( − 1 ) n y n S c n / 2 n ! m ! Γ ( n / 2 + 1 ) Γ ( n / 2 − m + 1 ) R n / 2 − m t − m α Γ ( 1 − m α ) $$ \phi \left(y,t\right)=\sum \limits_{n=0}^{\infty}\sum \limits_{m=0}^{\infty}\frac{{\left(-1\right)}^n{y}^nS{c}^{n/2}}{n!m!}\frac{\Gamma \left(n/2+1\right)}{\Gamma \left(n/2-m+1\right)}{R}^{n/2-m}\frac{t^{- m\alpha}}{\Gamma \left(1- m\alpha \right)} $$ (28)
    Note that Γ ( . ) $$ \Gamma (.) $$ denotes the gamma function.

    4.3 Fractional Temperature Equation

    Thermal balance equation can be provided as
    ∂ T ∂ t = − ∂ B ∂ y $$ \frac{\partial T}{\partial t}=-\frac{\partial B}{\partial y} $$ (29)
    where
    B = − κ α C D t 1 − α ∂ T ∂ y , 0 < α ≤ 1 $$ B=-{\kappa}_{\alpha}^C{D}_t^{1-\alpha}\left[\frac{\partial T}{\partial y}\right],0<\alpha \le 1 $$ (30)
    Now putting Equation (30) into Equation (29) and using the relations in Equation (13), we get
    ∂ θ ∂ t = P e f C D t 1 − α ∂ 2 θ ∂ y 2 + Q o θ $$ \frac{\partial \theta }{\partial t}={P}_{ef}^C{D}_t^{1-\alpha}\left[\frac{\partial^2\theta }{\partial {y}^2}+{Q}_o\theta \right] $$ (31)
    By employing Laplace transform on Equation (31), we get
    d 2 θ ( y , s ) d y 2 − P e f s α − Q o θ ( y , s ) $$ \frac{d^2\theta \left(y,s\right)}{d{y}^2}-{P}_{ef}\left({s}^{\alpha }-{Q}_o\right)\theta \left(y,s\right) $$ (32)
    The s $$ s $$ -domain solution becomes
    θ ( y , s ) = A e − y P e f ( s α − Q o ) + B e y P e f ( s α − Q o ) $$ \theta \left(y,s\right)=A{e}^{-y\sqrt{P_{ef}\left({s}^{\alpha }-{Q}_o\right)}}+B{e}^{y\sqrt{P_{ef}\left({s}^{\alpha }-{Q}_o\right)}} $$ (33)
    By applying the boundary conditions such that θ ( 0 , s ) = 1 s $$ \theta \left(0,s\right)=\frac{1}{s} $$ and θ ( ∞ , s ) = 0 $$ \theta \left(\infty, s\right)=0 $$ , we get the solution
    θ ( y , s ) = 1 s e − y P e f ( s α − Q o ) $$ \theta \left(y,s\right)=\frac{1}{s}{e}^{-y\sqrt{P_{ef}\left({s}^{\alpha }-{Q}_o\right)}} $$ (34)
    By employing the exponential series with binomial expansion, we get
    θ ( y , s ) = ∑ n = 0 ∞ ∑ m = 0 ∞ ( − 1 ) n y n P e f n / 2 n ! m ! Γ ( n / 2 + 1 ) Γ ( n / 2 − m + 1 ) − Q o n / 2 − m s m α − 1 $$ \theta \left(y,s\right)=\sum \limits_{n=0}^{\infty}\sum \limits_{m=0}^{\infty}\frac{{\left(-1\right)}^n{y}^n{P}_{ef}^{n/2}}{n!m!}\frac{\Gamma \left(n/2+1\right)}{\Gamma \left(n/2-m+1\right)}{\left(-{Q}_o\right)}^{n/2-m}{s}^{m\alpha -1} $$ (35)
    By taking Laplace transform inverse to both sides of Equation (35), the final exact result of fractional concentration remains
    θ ( y , t ) = ∑ n = 0 ∞ ∑ m = 0 ∞ ( − 1 ) n y n P e f n / 2 n ! m ! Γ ( n / 2 + 1 ) Γ ( n / 2 − m + 1 ) − Q o n / 2 − m t − m α Γ ( 1 − m α ) $$ \theta \left(y,t\right)=\sum \limits_{n=0}^{\infty}\sum \limits_{m=0}^{\infty}\frac{{\left(-1\right)}^n{y}^n{P}_{ef}^{n/2}}{n!m!}\frac{\Gamma \left(n/2+1\right)}{\Gamma \left(n/2-m+1\right)}{\left(-{Q}_o\right)}^{n/2-m}\frac{t^{- m\alpha}}{\Gamma \left(1- m\alpha \right)} $$ (36)

    4.4 Fractional Velocity Model

    Based on the momentum balance, the velocity equation can be formulated as
    ∂ w ∂ t =   C D t 1 − α ν 1 + 1 β ∂ 2 w ∂ y 2 − σ B o 2 ρ + ν k 1 ρ k o w + β T T − T ∞ + β C C − C ∞ ρ g $$ {\displaystyle \begin{array}{ll}\hfill \frac{\partial w}{\partial t}& ={}^C{D}_t^{1-\alpha}\left[\nu \left(1+\frac{1}{\beta}\right)\frac{\partial^2w}{\partial {y}^2}-\left(\frac{\sigma {B}_o^2}{\rho }+\frac{\nu {k}_1}{\rho {k}_o}\right)w\right.\\ {}\hfill & \kern1em \left.+\left({\beta}_T\left(T-{T}_{\infty}\right)+{\beta}_C\left(C-{C}_{\infty}\right)\right)\rho g\right]\end{array}} $$ (37)
    After making some mathematical calculation of Equation (37) and comparing with Equation (12), we get
    ∂ α w ∂ t α = C a ∂ 2 w ∂ y 2 − b w + G r θ + G m ϕ $$ \frac{\partial^{\alpha }w}{\partial {t}^{\alpha }}={C}_a\frac{\partial^2w}{\partial {y}^2}- bw+ Gr\theta + Gm\phi $$ (38)
    By applying Laplace transform of both sides of Equation (38) and incorporating the initial condition, we get
    d 2 w ( y , s ) d y 2 − 1 C a s α + b w ( y , s ) = − 1 C a ( G r θ ( y , s ) + G m ϕ ( y , s ) ) $$ \frac{d^2w\left(y,s\right)}{d{y}^2}-\frac{1}{C_a}\left({s}^{\alpha }+b\right)w\left(y,s\right)=-\frac{1}{C_a}\left( Gr\theta \left(y,s\right)+ Gm\phi \left(y,s\right)\right) $$ (39)
    Here, let us denote a = 1 C a , a 1 = G r C a $$ a=\frac{1}{C_a},{a}_1=\frac{Gr}{C_a} $$ , and a 2 = G m C a $$ {a}_2=\frac{Gm}{C_a} $$ ; the Equation (39) remains
    d 2 w ( y , s ) d y 2 − a s α + b w ( y , s ) = − a 1 θ ( y , s ) − a 2 ϕ ( y , s ) $$ \frac{d^2w\left(y,s\right)}{d{y}^2}-a\left({s}^{\alpha }+b\right)w\left(y,s\right)=-{a}_1\theta \left(y,s\right)-{a}_2\phi \left(y,s\right) $$ (40)
    By applying variations of parameters on Equation (40) and using boundary conditions, the s-domain solution for velocity is
    w ( y , s ) = 1 s e − a ( s α + b ) y + G r ( C a P e f − 1 ) ( s α − c ) e − a ( s α + b ) y s − e − P e f ( s α − Q o ) y s + G m ( C a S c − 1 ) ( s α − c 1 ) e − a ( s α + b ) y s − e − S c ( s α + R ) y s $$ {\displaystyle \begin{array}{cc}\hfill w\left(y,s\right)& =\frac{1}{s}{e}^{-\left(\sqrt{a\left({s}^{\alpha }+b\right)}\right)y}\\ {}& \hfill \kern1em +\frac{Gr}{\left({C}_a{P}_{ef}-1\right)\left({s}^{\alpha }-c\right)}\left[\frac{e^{-\left(\sqrt{a\left({s}^{\alpha }+b\right)}\right)y}}{s}-\frac{e^{-\left(\sqrt{P_{ef}\left({s}^{\alpha }-{Q}_o\right)}\right)y}}{s}\right]\\ {}& \hfill \kern1em +\frac{Gm}{\left({C}_a Sc-1\right)\left({s}^{\alpha }-{c}_1\right)}\left[\frac{e^{-\left(\sqrt{a\left({s}^{\alpha }+b\right)}\right)y}}{s}-\frac{e^{-\left(\sqrt{Sc\left({s}^{\alpha }+R\right)}\right)y}}{s}\right]\end{array}} $$ (41)
    Here, c = C a P e f + b C a P e f − 1 $$ c=\frac{C_a{P}_{ef}+b}{C_a{P}_{ef}-1} $$ and c 1 = − C a S c + b C a S c − 1 $$ {c}_1=-\frac{C_a Sc+b}{C_a Sc-1} $$ . When we apply series with binomial expansion of (41), we find
    w ( y , s ) = ∑ q = 0 ∞ ∑ r = 0 ∞ ( − a y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) s r α − 1 + b 1 ( s α − c ) ∑ q = 0 ∞ ∑ r = 0 ∞ ( − a y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) s r α − 1 − ∑ q = 0 ∞ ∑ r = 0 ∞ ( − P e f y ) q ( − Q o ) q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) s r α − 1 + b 2 ( s α − c 1 ) ∑ q = 0 ∞ ∑ r = 0 ∞ ( − a y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) s r α − 1 − ∑ q = 0 ∞ ∑ r = 0 ∞ ( − S c y ) q ( R ) q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) s r α − 1 $$ {\displaystyle \begin{array}{ll}w\left(y,s\right)& =\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}{s}^{r\alpha -1}\\ {}& \kern1em +\frac{b_1}{\left({s}^{\alpha }-c\right)}\left[\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}{s}^{r\alpha -1}\right.\\ {}& \kern1em \left.-\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{{\left(-\sqrt{P_{ef}}y\right)}^q{\left(-{Q}_o\right)}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}{s}^{r\alpha -1}\right]\\ {}& \kern1em +\frac{b_2}{\left({s}^{\alpha }-{c}_1\right)}\left[\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}{s}^{r\alpha -1}\right.\\ {}& \kern1em \left.-\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{{\left(-\sqrt{Sc}y\right)}^q{(R)}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}{s}^{r\alpha -1}\right]\end{array}} $$ (42)
    Here, b 1 = G r C a P e f − 1 $$ {b}_1=\frac{Gr}{C_a{P}_{ef}-1} $$ and b 2 = G m C a S c − 1 $$ {b}_2=\frac{Gm}{C_a Sc-1} $$ . By applying geometric series on 1 s α − c $$ \frac{1}{s^{\alpha }-c} $$ and 1 s α − c 1 $$ \frac{1}{s^{\alpha }-{c}_1} $$ , the above equation remains
    w ( y , s ) = ∑ q = 0 ∞ ∑ r = 0 ∞ ( − a y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) s r α − 1 + b 1 ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c m ( − a y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) s α ( r − m − 1 ) − 1 − ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c m ( − P e f y ) q ( − Q o ) q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) s α ( r − m − 1 ) − 1 + b 2 ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c 1 m ( − a y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) s α ( r − m − 1 ) − 1 − ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c 1 m ( − S c y ) q ( R ) q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) s α ( r − m − 1 ) − 1 $$ {\displaystyle \begin{array}{cc}w\left(y,s\right)& =\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}{s}^{r\alpha -1}\\ {}& \kern1em +{b}_1\left[\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c^m{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}{s}^{\alpha \left(r-m-1\right)-1}\right.\\ {}& \left.-\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c^m{\left(-\sqrt{P_{ef}}y\right)}^q{\left(-{Q}_o\right)}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}{s}^{\alpha \left(r-m-1\right)-1}\right]\\ {}& +{b}_2\left[\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c_1^m{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}{s}^{\alpha \left(r-m-1\right)-1}\right.\\ {}& \left.-\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c_1^m{\left(-\sqrt{Sc}y\right)}^q{(R)}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}{s}^{\alpha \left(r-m-1\right)-1}\right]\end{array}} $$ (43)
    Now, by taking inverse Laplace transform on Equation (43), we get
    w ( y , t ) = ∑ q = 0 ∞ ∑ r = 0 ∞ ( − a y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t − r α Γ ( 1 − r α ) + b 1 ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c m ( − a y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t α ( m − r + 1 ) Γ ( α ( m − r + 1 ) + 1 ) − ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c m ( − P e f y ) q ( − Q o ) q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t α ( m − r + 1 ) Γ ( α ( m − r + 1 ) + 1 ) + b 2 ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c 1 m ( − a y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t α ( m − r + 1 ) Γ ( α ( m − r + 1 ) + 1 ) − ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c 1 m ( − S c y ) q ( R ) q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t α ( m − r + 1 ) Γ ( α ( m − r + 1 ) + 1 ) $$ {\displaystyle \begin{array}{cc}\hfill w\left(y,t\right)& =\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{- r\alpha}}{\Gamma \left(1- r\alpha \right)}\\ {}& \hfill \kern1em +{b}_1\left[\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c^m{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m-r+1\right)+1\right)}\right.\\ {}& \hfill \kern1em \left.-\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c^m{\left(-\sqrt{P_{ef}}y\right)}^q{\left(-{Q}_o\right)}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m-r+1\right)+1\right)}\right]\\ {}& \hfill \kern1em +{b}_2\left[\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c_1^m{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m-r+1\right)+1\right)}\right.\\ {}& \hfill \kern1em \left.-\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c_1^m{\left(-\sqrt{Sc}y\right)}^q{(R)}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m-r+1\right)+1\right)}\right]\end{array}} $$ (44)

    Fundamental engineering coefficients are described below:

    4.5 Surface Friction Coefficient

    The surface friction coefficient is a dimensionless quantity used in fluid dynamics to quantify the frictional forces exerted by a fluid motion on a solid surface. Here, it is calculated from Equation (44), and is expressed as

    τ s = C a ∂ w ( y , t ) ∂ y | y = 0 = ∑ q = 0 ∞ ∑ r = 0 ∞ ( − a ) q ( q y q − 1 ) b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t − r α Γ ( 1 − r α ) + b 1 ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c m ( − a ) q ( q y q − 1 ) b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t α ( m − r + 1 ) Γ ( α ( m − k r + 1 ) + 1 ) − ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c m ( − P e f ) q ( q y q − 1 ) ( − Q o ) q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t α ( m − r + 1 ) Γ ( α ( m − r + 1 ) + 1 ) + b 2 ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c 1 m ( − a ) q ( q y q − 1 ) b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t α ( m − r + 1 ) Γ ( α ( m − r + 1 ) + 1 ) − ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c 1 m ( − S c ) q ( q y q − 1 ) ( R ) q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t α ( m − r + 1 ) Γ ( α ( m − r + 1 ) + 1 ) | y = 0 $$ {\displaystyle \begin{array}{cccc}\hfill {\tau}_s& {\left.={C}_a\frac{\partial w\left(y,t\right)}{\partial y}\right|}_{y=0}=\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{{\left(-\sqrt{a}\right)}^q\left(q{y}^{q-1}\right){b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{- r\alpha}}{\Gamma \left(1- r\alpha \right)}& \kern0em & \\ {}& \hfill \kern1em +{b}_1\left[\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c^m{\left(-\sqrt{a}\right)}^q\left(q{y}^{q-1}\right){b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m- kr+1\right)+1\right)}\right.& \kern0em & \\ {}& \hfill \kern1em \left.-\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c^m{\left(-\sqrt{P_{ef}}\right)}^q\left(q{y}^{q-1}\right){\left(-{Q}_o\right)}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m-r+1\right)+1\right)}\right]& \kern0em & \\ {}& \hfill \kern1em +{b}_2\left[\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c_1^m{\left(-\sqrt{a}\right)}^q\left(q{y}^{q-1}\right){b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m-r+1\right)+1\right)}\right.& \kern0em & \\ {}& \hfill {\left.\kern1em \left.-\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c_1^m{\left(-\sqrt{Sc}\right)}^q\left(q{y}^{q-1}\right){(R)}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m-r+1\right)+1\right)}\right]\right|}_{y=0}& & \end{array}} $$ (45)
    For the term to remain, we need q = 1 $$ q=1 $$ , since for q > 1 $$ q>1 $$ , the factor y q − 1 $$ {y}^{q-1} $$ vanishes at y = 0 $$ y=0 $$ . Hence, we consider only q = 1 $$ q=1 $$ term.
    τ s = ∂ w ( y , t ) ∂ y | y = 0 = − a π 2 ∑ r = 0 ∞ b 1 2 − r r ! Γ ( 3 2 − r ) t − r α Γ ( 1 − r α ) − b 1 a π 2 ∑ m = 0 ∞ ∑ r = 0 ∞ c m b 1 2 − r r ! Γ ( 3 2 − r ) t α ( m − r + 1 ) Γ ( α ( m − r + 1 ) + 1 ) + P e f π 2 ∑ m = 0 ∞ ∑ r = 0 ∞ c m ( − Q o ) 1 2 − r r ! Γ ( 3 2 − r ) t α ( m − r + 1 ) Γ ( α ( m − r + 1 ) + 1 ) − b 2 a π 2 ∑ m = 0 ∞ ∑ r = 0 ∞ c 1 m b 1 2 − r r ! Γ ( 3 2 − r ) t α ( m − r + 1 ) Γ ( α ( m − r + 1 ) + 1 ) + S c π 2 ∑ m = 0 ∞ ∑ r = 0 ∞ c 1 m ( R ) 1 2 − r r ! Γ ( 3 2 − r ) t α ( m − r + 1 ) Γ ( α ( m − r + 1 ) + 1 ) $$ {\displaystyle \begin{array}{ccc}\hfill {\left.{\tau}_s=\frac{\partial w\left(y,t\right)}{\partial y}\right|}_{y=0}=\frac{-\sqrt{a\pi}}{2}\sum \limits_{r=0}^{\infty}\frac{b^{\frac{1}{2}-r}}{r!\Gamma \left(\frac{3}{2}-r\right)}\frac{t^{- r\alpha}}{\Gamma \left(1- r\alpha \right)}& \kern0em & \\ {}\hfill \kern1em -{b}_1\left[\frac{\sqrt{a\pi}}{2}\sum \limits_{m=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c^m{b}^{\frac{1}{2}-r}}{r!\Gamma \left(\frac{3}{2}-r\right)}\frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m-r+1\right)+1\right)}\right.& \kern0em & \\ {}\hfill \kern1em \left.+\frac{\sqrt{P_{ef}\pi }}{2}\sum \limits_{m=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c^m{\left(-{Q}_o\right)}^{\frac{1}{2}-r}}{r!\Gamma \left(\frac{3}{2}-r\right)}\frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m-r+1\right)+1\right)}\right]& \kern0em & \\ {}\hfill \kern1em -{b}_2\left[\frac{\sqrt{a\pi}}{2}\sum \limits_{m=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c_1^m{b}^{\frac{1}{2}-r}}{r!\Gamma \left(\frac{3}{2}-r\right)}\frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m-r+1\right)+1\right)}\right.& \kern0em & \\ {}\hfill \kern1em \left.+\frac{\sqrt{Sc\pi}}{2}\sum \limits_{m=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c_1^m{(R)}^{\frac{1}{2}-r}}{r!\Gamma \left(\frac{3}{2}-r\right)}\frac{t^{\alpha \left(m-r+1\right)}}{\Gamma \left(\alpha \left(m-r+1\right)+1\right)}\right]& & \end{array}} $$ (46)
    Note that Γ ( 3 2 ) = π 2 $$ \Gamma \left(\frac{3}{2}\right)=\frac{\pi }{2} $$ .

    4.6 Heat Transfer Rate

    Heat transfer rate or Nusselt number can be obtained from the temperature equation as follows:
    N u = − ∂ θ ( y , t ) ∂ y | y = 0 = P e f π 2 ∑ m = 0 ∞ ( − Q o ) 1 2 − m m ! Γ ( 3 2 − m ) t − α m Γ ( 1 − α m ) $$ {\left. Nu=-\frac{\partial \theta \left(y,t\right)}{\partial y}\right|}_{y=0}=\frac{\sqrt{P_{ef}\pi }}{2}\sum \limits_{m=0}^{\infty}\frac{{\left(-{Q}_o\right)}^{\frac{1}{2}-m}}{m!\Gamma \left(\frac{3}{2}-m\right)}\frac{t^{-\alpha m}}{\Gamma \left(1-\alpha m\right)} $$ (47)

    4.7 Mass Transfer Rate

    Finally, the local Sherwood number or mass transfer rate is given by
    S h = − ∂ θ ( y , t ) ∂ y | y = 0 = S c π 2 ∑ m = 0 ∞ R 1 2 − m m ! Γ ( 3 2 − m ) t − α m Γ ( 1 − α m ) $$ {\left. Sh=-\frac{\partial \theta \left(y,t\right)}{\partial y}\right|}_{y=0}=\frac{\sqrt{Sc\pi}}{2}\sum \limits_{m=0}^{\infty}\frac{R^{\frac{1}{2}-m}}{m!\Gamma \left(\frac{3}{2}-m\right)}\frac{t^{-\alpha m}}{\Gamma \left(1-\alpha m\right)} $$ (48)

    5 Special Cases

    5.1 Classical or Normal Derivative Case

    When α = 1 $$ \alpha =1 $$ , the equations for velocity, temperature, and concentration revert to their classical counterparts.

    w ( y , t ) = ∑ q = 0 ∞ ∑ r = 0 ∞ ( − a y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t − r Γ ( 1 − r ) + b 1 ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c m ( − a y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t m − r + 1 Γ ( m − r + 2 ) − ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c m ( − P e f y ) q ( − Q o ) q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t m − r + 1 Γ ( m − r + 2 ) + b 2 ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c 1 m ( − a y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t m − r + 1 Γ ( m − r + 2 ) − ∑ m = 0 ∞ ∑ q = 0 ∞ ∑ r = 0 ∞ c 1 m ( − S c y ) q ( R ) q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t m − r + 1 Γ ( m − r + 2 $$ {\displaystyle \begin{array}{cccc}\hfill w\left(y,t\right)& =\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{-r}}{\Gamma \left(1-r\right)}& \kern0em & \\ {}& \hfill \kern1em +{b}_1\left[\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c^m{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{m-r+1}}{\Gamma \left(m-r+2\right)}\right.& \kern0em & \\ {}& \hfill \kern1em \left.-\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c^m{\left(-\sqrt{P_{ef}}y\right)}^q{\left(-{Q}_o\right)}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{m-r+1}}{\Gamma \left(m-r+2\right)}\right]& \kern0em & \\ {}& \hfill \kern1em +{b}_2\left[\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c_1^m{\left(-\sqrt{a}y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{m-r+1}}{\Gamma \left(m-r+2\right)}\right.& \kern0em & \\ {}& \hfill \kern1em \left.-\sum \limits_{m=0}^{\infty}\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{c_1^m{\left(-\sqrt{Sc}y\right)}^q{(R)}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{m-r+1}}{\Gamma \Big(m-r+2}\right]& & \end{array}} $$ (49)
    θ ( y , t ) = ∑ n = 0 ∞ ∑ m = 0 ∞ ( − 1 ) n y n P e f n / 2 n ! m ! Γ ( n / 2 + 1 ) Γ ( n / 2 − m + 1 ) − Q o n / 2 − m t − m Γ ( 1 − m ) $$ \theta \left(y,t\right)=\sum \limits_{n=0}^{\infty}\sum \limits_{m=0}^{\infty}\frac{{\left(-1\right)}^n{y}^n{P}_{ef}^{n/2}}{n!m!}\frac{\Gamma \left(n/2+1\right)}{\Gamma \left(n/2-m+1\right)}{\left(-{Q}_o\right)}^{n/2-m}\frac{t^{-m}}{\Gamma \left(1-m\right)} $$ (50)
    ϕ ( y , t ) = ∑ n = 0 ∞ ∑ m = 0 ∞ ( − 1 ) n y n S c n / 2 n ! m ! Γ ( n / 2 + 1 ) Γ ( n / 2 − m + 1 ) R n / 2 − m t − m Γ ( 1 − m ) $$ \phi \left(y,t\right)=\sum \limits_{n=0}^{\infty}\sum \limits_{m=0}^{\infty}\frac{{\left(-1\right)}^n{y}^nS{c}^{n/2}}{n!m!}\frac{\Gamma \left(n/2+1\right)}{\Gamma \left(n/2-m+1\right)}{R}^{n/2-m}\frac{t^{-m}}{\Gamma \left(1-m\right)} $$ (51)

    5.2 Newtonian Fluid and Omission of Free Convection Cases

    When β → ∞ $$ \beta \to \infty $$ and G r = G m = 0 $$ Gr= Gm=0 $$ , the velocity solution (49) is reduced to as follows:
    w ( y , t ) = ∑ q = 0 ∞ ∑ r = 0 ∞ ( − y ) q b q 2 − r q ! r ! Γ ( q / 2 + 1 ) Γ ( q / 2 − r + 1 ) t − r Γ ( 1 − r ) $$ w\left(y,t\right)=\sum \limits_{q=0}^{\infty}\sum \limits_{r=0}^{\infty}\frac{{\left(-y\right)}^q{b}^{\frac{q}{2}-r}}{q!r!}\frac{\Gamma \left(q/2+1\right)}{\Gamma \left(q/2-r+1\right)}\frac{t^{-r}}{\Gamma \left(1-r\right)} $$ (52)
    Equation (52) can be rewritten in exact form as
    w ( y , t ) = 1 2 erfc ( y 2 t − b t ) e − y b + erfc ( y 2 t + b t ) e y b $$ w\left(y,t\right)=\frac{1}{2}\left[\operatorname{erfc}\left(\frac{y}{2\sqrt{t}}-\sqrt{bt}\right){e}^{-y\sqrt{b}}+\operatorname{erfc}\left(\frac{y}{2\sqrt{t}}+\sqrt{bt}\right){e}^{y\sqrt{b}}\right] $$ (53)
    Note that both Equations (52) and (53) are equivalent. Equation (53) is further confirmed with the result obtained by Pattnaik et al. [48] by putting a = G r = G c = 0 $$ a= Gr= Gc=0 $$ in their velocity equation.
    Note that if we assume a nonporous flat plate and nonhydromagnetic incompressible viscous fluid, the momentum Equation (12) reduces to the famous problem named Stokes first kind problem [49], whose solution is same with Equation (53) by putting b = F p + F m = 0 $$ b={F}_p+{F}_m=0 $$ . Therefore, the Equation (53) can be stated by
    w ( y , t ) = erfc ( y 2 t ) $$ w\left(y,t\right)=\operatorname{erfc}\left(\frac{y}{2\sqrt{t}}\right) $$ (54)

    6 Results and Discussion

    The study of time-dependent free convection flow of a hydromagnetic Casson fluid over an impulsively started porous plate, incorporating the Caputo-type fractional derivative, examines the combined effects of various physical and mechanical factors on fluid flow, heat, and mass transfer. This research seeks to improve the understanding of fluid flow, heat, and mass transfer mechanisms along different surfaces along with non-Newtonian properties, fractional time effects, thermal radiation, and magnetic field, which are crucial in several areas such as biomedical flows, material processing, and environmental systems. The exact solution of the problem is derived using the Laplace transform method, which is a powerful technique to solve differential equations with initial and boundary conditions. The numerical results for physical parameters, obtained in closed form, are demonstrated in figures and tables and discussed from a physical point of view. Moreover, the ranges of the physical parameters considered in this study are chosen based on realistic and physically admissible values as follows:

    0 < Gr , Gm ≤ 10 , 0 < F p , F m ≤ 5 , 0 < α ≤ 1 , 0 . 1 ≤ R d ≤ 1 0 2 $$ 0<\mathrm{Gr},\kern0.3em \mathrm{Gm}\le 10,\kern1em 0<{F}_p,\kern0.3em {F}_m\le 5,\kern1em 0<\alpha \le 1,\kern1em 0.1\le {R}_d\le 1{0}^2 $$
    0 < Q o ≤ 10 , 0 . 01 ≤ S c ≤ 10 , 0 < R ≤ 5 , 0 . 3 ≤ P r ≤ 10 , 0 < β ≤ 10 $$ {\displaystyle \begin{array}{lll}\hfill 0<{Q}_o\le 10,\kern1em 0.01\le Sc\le 10,\kern1em 0<R\le 5,& \kern0em & \\ {}\hfill \kern1em 0.3\le \mathit{\Pr}\le 10,\kern1em 0<\beta \le 10& & \end{array}} $$
    These ranges are selected to capture the typical behavior of heat and mass transfer processes in Casson fluid systems influenced by magnetic fields, porous media, and thermal radiation.

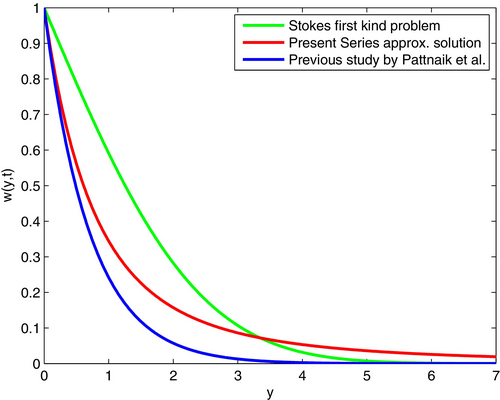
    Figure 2 presents a comparison between the classical Stokes' first problem solution, the exact solution derived by [48], and the present series approximation of the velocity profile w ( y , t ) $$ w\left(y,t\right) $$ for b = 2 $$ b=2 $$ and t = 3 $$ t=\sqrt{3} $$ . The curve labeled “Stokes first kind problem” corresponds to the solution w ( y , t ) = erfc ( y / ( 2 t ) ) $$ w\left(y,t\right)=\operatorname{erfc}\left(y/\left(2\sqrt{t}\right)\right) $$ , which applies in the absence of body forces ( b = 0 $$ b=0 $$ ). This solution exhibits a smooth, monotonic decay typical of viscous diffusion in a quiescent fluid. The curve labeled “Previous study by Pattnaik et al.” represents the exact solution given by Equation (53), capturing the effects of buoyancy and magnetic forces through the parameter b $$ b $$ . As expected, this solution decays more rapidly with increasing y $$ y $$ , indicating stronger momentum diffusion under the influence of body forces. The third curve, “Present Series approx. solution,” corresponds to the truncated series representation given by Equation (52), limited to the r = 0 $$ r=0 $$ case. This series matches the exact solution closely for small values of y $$ y $$ (up to about y = 4 $$ y=4 $$ ), confirming their analytical equivalence in that regime. However, the approximation diverges significantly for larger y $$ y $$ , highlighting the limitations of the truncated series in capturing long-range behavior. Overall, the plot validates the accuracy of the series solution in the near-wall region and emphasizes the importance of including body force effects in the full expression for extended spatial domains.

    Details are in the caption following the image
    FIGURE 2
    Open in figure viewerPowerPoint
    Comparison of the results.

    It is evident that the momentum Equation (3) is influenced by temperature and concentration gradients, where the fluid motion is primarily driven by buoyancy forces. The velocity field is mainly affected by the thermal Grashof number ( G r $$ Gr $$ ), associated with thermal buoyancy, and the mass (solutal) Grashof number ( G m $$ Gm $$ ), associated with concentration-induced buoyancy. These dimensionless quantities represent the relative importance of buoyancy forces compared to viscous forces in free or natural convection flows. Their physical influence is illustrated in Figures 3 and 4, where it is observed that fluid velocity increases with rising values of both G r $$ Gr $$ and G m $$ Gm $$ . This numerical trend aligns well with the theoretical interpretation of these parameters. For generating the corresponding graphs, the physical parameters are set as β = α = 0 . 5 $$ \beta =\alpha =0.5 $$ , F m = F p = 0 . 2 $$ Fm= Fp=0.2 $$ , P r = 0 . 9 $$ \mathit{\Pr}=0.9 $$ , Q o = 2 $$ {Q}_o=2 $$ , S c = 0 . 01 $$ Sc=0.01 $$ , R = 1 $$ R=1 $$ , R d = 30 $$ Rd=30 $$ , and t = 2 $$ t=2 $$ . Additionally, with a baseline of G r = G m = 0 . 2 $$ Gr= Gm=0.2 $$ , we analyzed the effect of each parameter by varying one while keeping the other fixed.

    Details are in the caption following the image
    FIGURE 3
    Open in figure viewerPowerPoint
    Velocity profiles for different values of G r $$ Gr $$ .
    Details are in the caption following the image
    FIGURE 4
    Open in figure viewerPowerPoint
    Velocity profiles for different values of G m $$ Gm $$ .

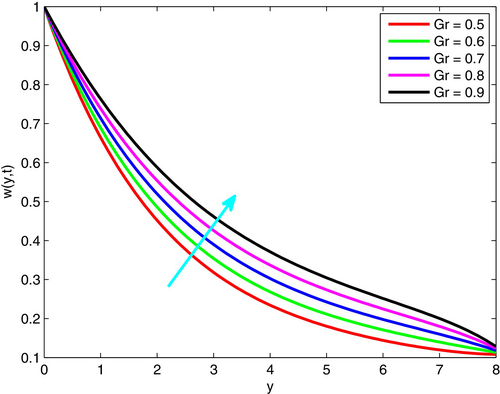
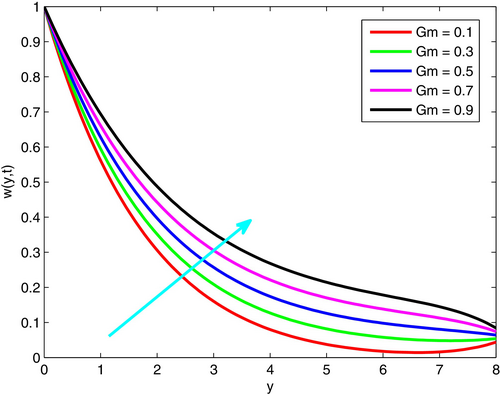
    The thermal Grashof number ( G r $$ Gr $$ ) and the solutal Grashof number ( G m $$ Gm $$ ) quantify buoyancy effects due to thermal and concentration gradients, respectively. G r $$ Gr $$ is significant in natural convection applications such as solar collectors, electronic cooling, and HVAC systems. G m $$ Gm $$ plays an important role in mass transfer processes, including chemical vapor deposition, drying of porous media, and pollutant dispersion. Both parameters influence the intensity of natural convection, thereby affecting heat and mass transfer performance in various engineering and environmental systems.

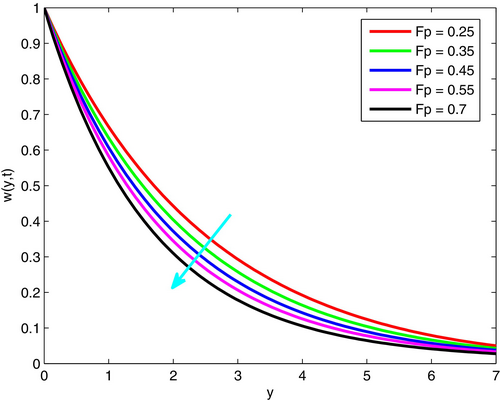
    The effects of ( F p $$ Fp $$ ) on fluid motion are revealed in Figure 5. Here, the velocity of Casson fluid diminishes with enhanced porosity parameter due to existing much more spaces in the plate for the fluid to move. Physically, if the porosity of the medium becomes too high, its structure becomes slightly interconnected, decreasing the whole permeability. Note that decreasing permeability implies high porosity which leads to reduced velocity. Hence, if the fluids have less interconnected pathways to move in, then the velocity leads to diminish in the regime. Here, the numerical assignment of parameters is β = α = 0 . 5 , G r = G m = 0 . 05 , P r = 0 . 9 , Q o = 2 , F m = 0 . 2 , S c = 0 . 01 , R = 1 , R d = 30 $$ \beta =\alpha =0.5, Gr= Gm=0.05,\mathit{\Pr}=0.9,{Q}_o=2, Fm=0.2, Sc=0.01,R=1, Rd=30 $$ and t = 2 $$ t=2 $$ .

    Details are in the caption following the image
    FIGURE 5
    Open in figure viewerPowerPoint
    Velocity profiles for variation of F p $$ Fp $$ .

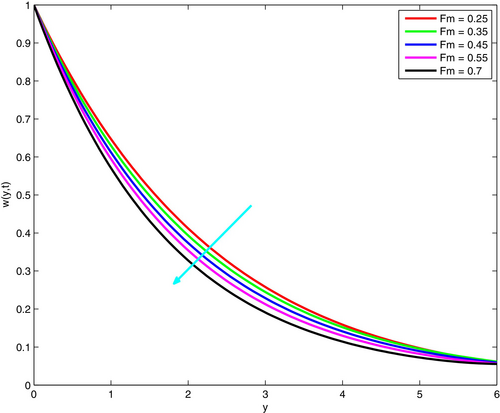
    This investigation deals with the presence of magnetic field, which is a nondimensional quantity that expresses the influence on the flow behaviors of electrically conducting fluids. It is worthy to note that magnetic field has direct relation to flow resistive force named Lorentz force. Due to this, the fluid motion reduces with an increase in the magnetic field parameter (see Figure 6). Here, the parameters are assigned as β = α = 0 . 5 , G r = G m = 0 . 05 , P r = 0 . 9 , Q o = 2 , F p = 0 . 2 , S c = 0 . 01 , R = 0 . 5 , R d = 30 $$ \beta =\alpha =0.5, Gr= Gm=0.05,\mathit{\Pr}=0.9,{Q}_o=2, Fp=0.2, Sc=0.01,R=0.5, Rd=30 $$ and t = 2 $$ t=2 $$ .

    Details are in the caption following the image
    FIGURE 6
    Open in figure viewerPowerPoint
    Velocity profiles for variation of F m $$ Fm $$ .

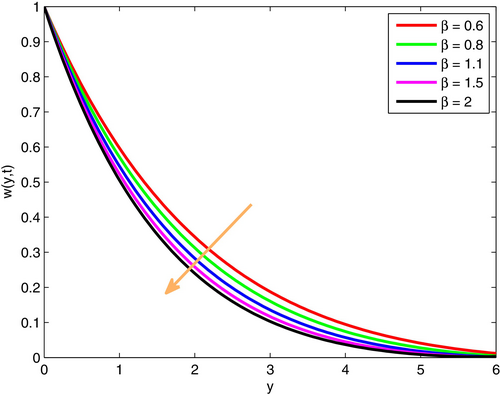
    The numerical values for rest physical parameters in the plot of Casson parameter are fixed as α = 0 . 5 , G r = G m = 0 . 01 , P r = 0 . 9 , Q o = 2 , F p = 0 . 1 , S c = 0 . 01 , R = 0 . 5 , F m = 0 . 2 , R d = 10 $$ \alpha =0.5, Gr= Gm=0.01,\mathit{\Pr}=0.9,{Q}_o=2, Fp=0.1, Sc=0.01,R=0.5, Fm=0.2, Rd=10 $$ and t = 3 $$ t=3 $$ . Here, for the sake of saving time, the maximum value for summation indices is assigned as N m a x = 10 $$ Nmax=10 $$ for each. As shown in Figure 7, elevation in Casson parameter causes immediate reduction on fluid velocity. It is worthy to mention that increasing Casson parameter results enhanced yield stress, which in turn opposes the fluid motion in the system. Thus, the flow diminishes as the Casson parameter increases.

    Details are in the caption following the image
    FIGURE 7
    Open in figure viewerPowerPoint
    Velocity profiles for variation of β $$ \beta $$ .

    Porosity and magnetic field parameters are critical in modeling fluid flow through porous and electrically conducting media. Porosity effects are significant in geothermal reservoirs, insulation materials, oil recovery, and filtration systems, where the porous structure influences flow resistance and transport properties. The magnetic field parameter is essential in magnetohydrodynamic (MHD) applications such as electromagnetic pumps, MHD generators, plasma confinement, and cooling of nuclear reactors, where magnetic forces are used to control or stabilize fluid motion.

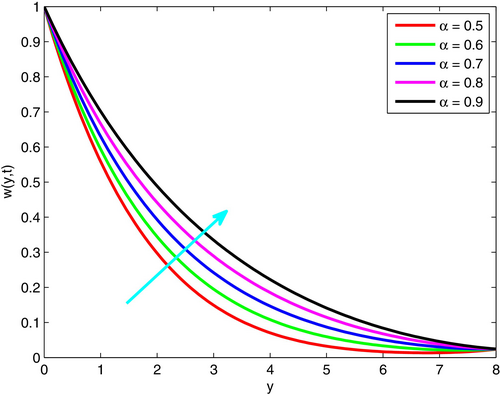
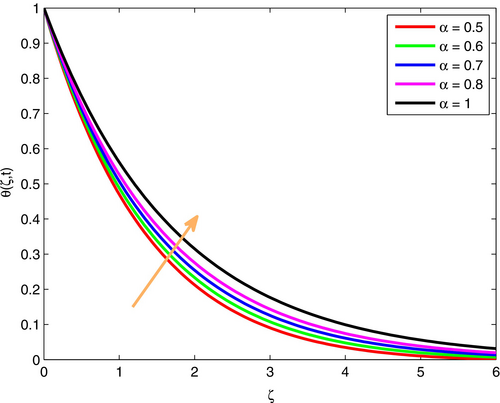
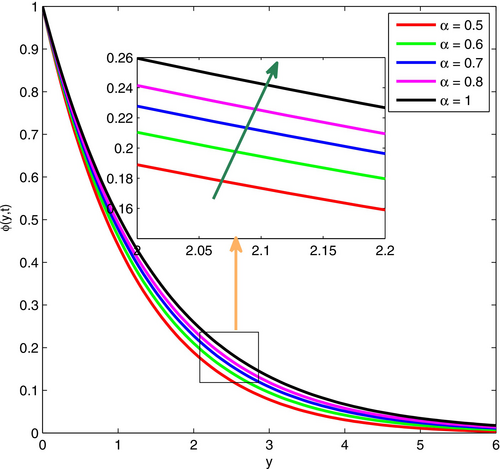
    The impact of the fractional order parameter ( α $$ \alpha $$ ) on velocity, temperature, and concentration is illustrated in Figures 8-10, respectively. In this condition, we have considered the values of α $$ \alpha $$ in the range of 0 < α < 1 $$ 0<\alpha <1 $$ with time t = 2 $$ t=2 $$ . Therefore, it falls under the category of subdiffusive behavior. If α $$ \alpha $$ grows up in the range of 0 < α < 1 $$ 0<\alpha <1 $$ , the fluid velocity rises with time t = 2 $$ t=2 $$ . This condition happens due to α $$ \alpha $$ with a higher value that provides much more weight to the history of the flow, which basically causes a faster development of velocity. Furthermore, higher α $$ \alpha $$ means the behavior of fluid closely related to the classical (integer order) model, where the velocity response is faster and easily predicable. Moreover, as the fractional derivative order α $$ \alpha $$ increases, the system can react to changes in thermal or mass transit more rapidly, which raises the fluid's temperature and concentration. This is because the system has fewer memory effects.

    Details are in the caption following the image
    FIGURE 8
    Open in figure viewerPowerPoint
    Velocity profiles for variation of α $$ \alpha $$ .
    Details are in the caption following the image
    FIGURE 9
    Open in figure viewerPowerPoint
    Temperature profiles for variation of α $$ \alpha $$ .
    Details are in the caption following the image
    FIGURE 10
    Open in figure viewerPowerPoint
    Concentration profiles for variation of α $$ \alpha $$ .

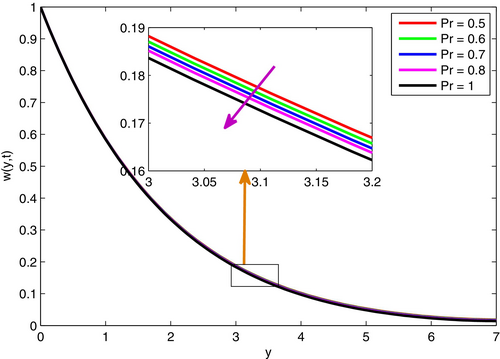
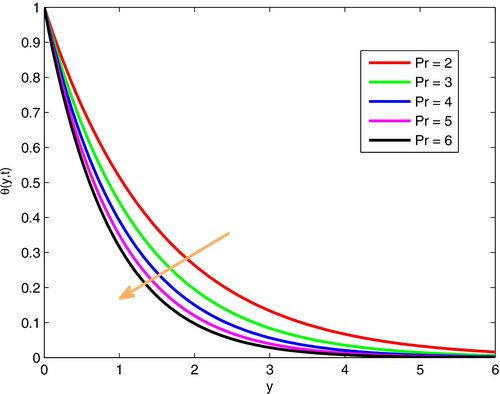
    The impact of the Prandtl number P r $$ \mathit{\Pr} $$ on fluid velocity and temperature is exhibited in n Figures 11 and 12. It is well-known that P r = ν α $$ \mathit{\Pr}=\frac{\nu }{\alpha } $$ , where ν $$ \nu $$ is the kinematic viscosity (characterized by viscous force) and α $$ \alpha $$ symbolizes thermal diffusivity. From this relation, one can see that P r $$ \mathit{\Pr} $$ is directly related to the viscous force and inversely related to the thermal diffusivity. Therefore, as P r $$ \mathit{\Pr} $$ increases, the velocity and temperature decrease within the flow system. The Prandtl number ( P r $$ \mathit{\Pr} $$ ) and Schmidt number ( S c $$ Sc $$ ) characterize heat and mass transfer, respectively. P r $$ \mathit{\Pr} $$ is important in thermal systems like heat exchangers and insulation, with low P r $$ \mathit{\Pr} $$ fluids enhancing heat conduction. S c $$ Sc $$ is key in mass transfer applications such as pollutant dispersion, chemical reactors, and drug delivery, where higher S c $$ Sc $$ indicates slower species diffusion.

    Details are in the caption following the image
    FIGURE 11
    Open in figure viewerPowerPoint
    Velocity profiles for variation of P r $$ \mathit{\Pr} $$ .
    Details are in the caption following the image
    FIGURE 12
    Open in figure viewerPowerPoint
    Temperature profiles for variation of P r $$ \mathit{\Pr} $$ .

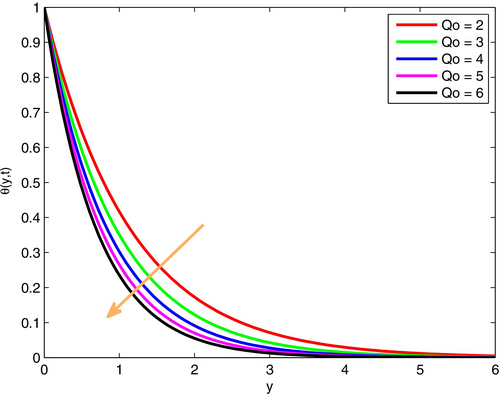
    The effects of Q o $$ {Q}_o $$ on velocity and distribution of temperature are given in n Figures 13 and 14. As indicated in these figures, both fluid velocity and distribution of temperature reduce as values of Q o $$ {Q}_o $$ increase. It is obvious that heat generation expresses the amount of heat production in the flow system due to different sources, including internal processes. Hence, this amount of heat generation causes a high amount of fluid viscosity, which in turn results in reduced velocity. Moreover, it also produces a thicker thermal boundary layer, which causes an immediate reduction on temperature. Heat source and thermal radiation effects play crucial roles in various engineering applications. Internal heat sources arise in nuclear reactors, electronic components, and exothermic chemical processes, influencing thermal distribution. Thermal radiation is dominant in high-temperature systems such as solar collectors, combustion chambers, space vehicles, and metal processing industries like glass and steel manufacturing.

    Details are in the caption following the image
    FIGURE 13
    Open in figure viewerPowerPoint
    Velocity profiles for variation of Q o $$ {Q}_o $$ .
    Details are in the caption following the image
    FIGURE 14
    Open in figure viewerPowerPoint
    Temperature profiles for variation of Q o $$ {Q}_o $$ .

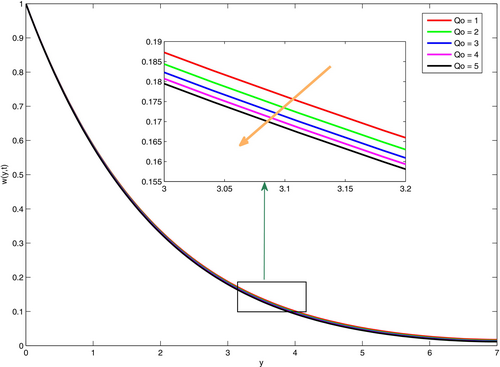
    Figures 15 and 16 demonstrate the variation of fluid velocity and temperature profiles. Here, one can comprehend that increased thermal radiation causes an increase in both velocity profiles and temperature profiles. This increased thermal radiation leads to the expansion of thermal energy, which results from the increased fluid temperature. On other hand, it causes lower density and higher buoyancy force, which produce an increased fluid velocity, particularly in free convection.

    Details are in the caption following the image
    FIGURE 15
    Open in figure viewerPowerPoint
    Velocity profiles for variation of R d $$ Rd $$ .
    Details are in the caption following the image
    FIGURE 16
    Open in figure viewerPowerPoint
    Temperature profiles for variation of R d $$ Rd $$ .

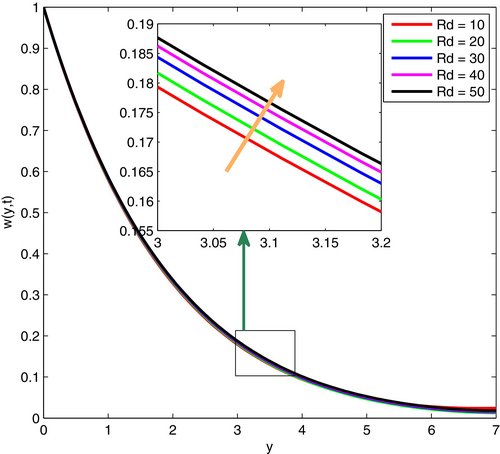
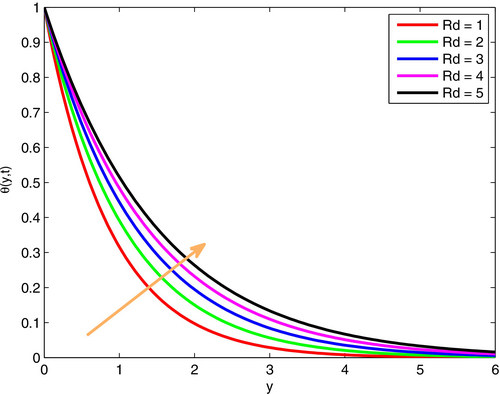
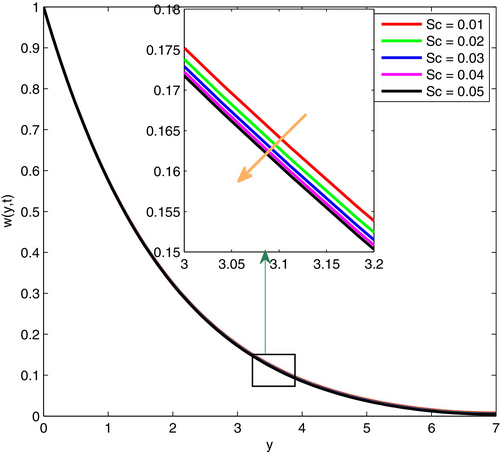
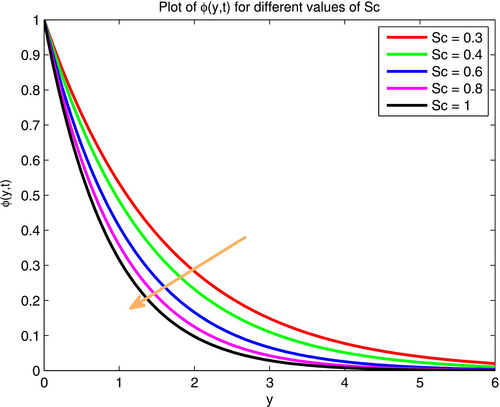
    Figures 17 and 18 illustrate the effects of the Schmidt number ( S c $$ Sc $$ ) on fluid velocity and temperature profiles. It is well-known that S c = ν D $$ Sc=\frac{\nu }{D} $$ , where ν $$ \nu $$ represents viscous force and D $$ D $$ symbolizes molar diffusivity. From this relation, one can see that S c $$ Sc $$ is directly related with viscous force and inversely related with molar diffusivity. As a result, with an increase in S c $$ Sc $$ , the fluid velocity and temperature decrease in the system.

    Details are in the caption following the image
    FIGURE 17
    Open in figure viewerPowerPoint
    Velocity profiles for variation of S c $$ Sc $$ .
    Details are in the caption following the image
    FIGURE 18
    Open in figure viewerPowerPoint
    Concentration profiles for variation of S c $$ Sc $$ .

    The impact of chemical reaction on fluid velocity and concentration are shown in Figures 19 and 20, receptively. Chemical reaction is the process of consumption or production of substances, which directly affects species concentration in the fluid. This process causes either a change in density or loss of buoyancy force in the system, which produces reduced concentration and velocity in the regime. Chemical reactions in fluid flow have important real-time applications in industrial, environmental, and biomedical systems. They influence heat and mass transfer in processes such as combustion, polymerization, pollutant degradation, and drug delivery. Reactions are also critical in microfluidic and lab-on-chip devices for diagnostics and biochemical processing. Including chemical reaction effects in models enables the accurate prediction of concentration profiles, heat generation, and flow behavior.

    Details are in the caption following the image
    FIGURE 19
    Open in figure viewerPowerPoint
    Velocity profiles for variation of R $$ R $$ .
    Details are in the caption following the image
    FIGURE 20
    Open in figure viewerPowerPoint
    Concentration profiles for variation of R $$ R $$ .

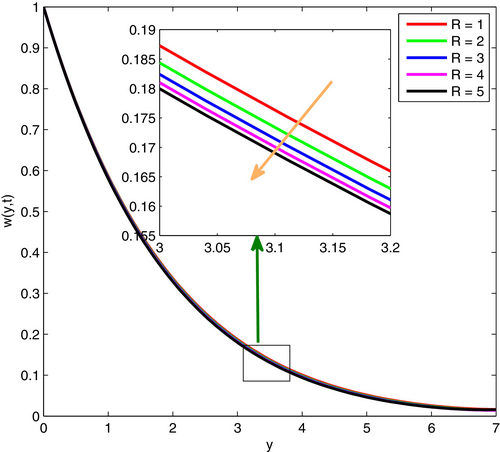
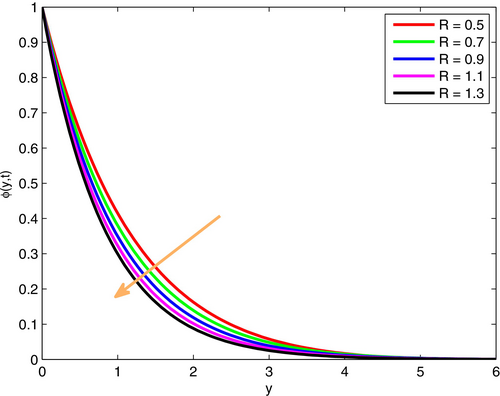
    Table 2 presents the effects of various parameters, including β , F m , F p , G r , G m , P r , R d , Q o , S c , R , α $$ \beta, Fm, Fp, Gr, Gm,\mathit{\Pr}, Rd, Qo, Sc,R,\alpha $$ , and t $$ t $$ on fluid motion at the surface of the plate, as well as on the heat and mass transfer rates.

    TABLE 2. Variations in skin friction, Nusselt number, and Sherwood number.
    β $$ \beta $$ F m $$ Fm $$ F p $$ Fp $$ G r $$ Gr $$ G m $$ Gm $$ P r $$ \mathit{\Pr} $$ R d $$ Rd $$ Q o $$ Qo $$ S c $$ Sc $$ R $$ R $$ α $$ \alpha $$ t $$ t $$ τ s $$ {\tau}_s $$ N u $$ Nu $$ S h $$ Sh $$
    0.5 0.2 0.2 0.1 0.1 0.75 5 2 0.1 2 0.5 2 0.76956 — —
    1 0.2 0.2 0.1 0.1 0.75 5 2 0.1 2 0.5 2 0.94882 — —
    0.5 0.1 0.2 0.1 0.1 0.75 5 2 0.1 2 0.5 2 0.84336 — —
    0.5 0.2 0.2 0.1 0.1 0.75 5 2 0.1 2 0.5 2 0.76956 — —
    0.5 0.1 0.1 0.1 0.1 0.75 5 2 0.1 2 0.5 2 0.84336 — —
    0.5 0.1 0.2 0.1 0.1 0.75 5 2 0.1 2 0.5 2 0.76956 — —
    0.5 0.1 0.2 0.1 0.1 0.75 5 2 0.1 2 0.5 2 0.76956 — —
    0.5 0.1 0.2 0.2 0.1 0.75 5 2 0.1 2 0.5 2 0.82404 — —
    0.5 0.1 0.2 0.2 0.1 0.75 5 2 0.1 2 0.5 2 0.82404 — —
    0.5 0.1 0.2 0.2 0.2 0.75 5 2 0.1 2 0.5 2 0.88059 — —
    0.5 0.1 0.2 0.2 0.1 0.5 5 2 0.1 2 0.5 2 0.78235 1.7037 —
    0.5 0.1 0.2 0.2 0.1 0.95 5 2 0.1 2 0.5 2 0.73668 1.6351 —
    0.5 0.1 0.2 0.2 0.1 0.75 5 2 0.1 2 0.5 2 0.76956 1.6557 —
    0.5 0.1 0.2 0.2 0.1 0.75 10 2 0.1 2 0.5 2 0.77548 1.7504 —
    0.5 0.1 0.2 0.2 0.1 0.75 5 2 0.1 2 0.5 2 0.76956 1.6557 —
    0.5 0.1 0.2 0.2 0.1 0.75 5 4 0.1 2 0.5 2 0.87864 2.2353 —
    0.5 0.1 0.2 0.2 0.1 0.75 5 2 0.1 2 0.5 2 0.76956 — 0.65597
    0.5 0.1 0.2 0.2 0.1 0.75 5 2 0.15 2 0.5 2 0.73389 — 0.92768
    0.5 0.1 0.2 0.2 0.1 0.75 5 2 0.1 2 0.5 2 0.76956 — 0.48047
    0.5 0.1 0.2 0.2 0.1 0.75 5 2 0.1 4 0.5 2 0.88151 — 0.65597
    0.5 0.1 0.2 0.2 0.1 0.75 5 2 0.1 2 0.5 2 0.76956 1.6557 0.49182
    0.5 0.1 0.2 0.2 0.1 0.75 5 2 0.1 2 0.6 2 0.78993 1.6175 0.48047
    0.5 0.1 0.2 0.2 0.1 0.75 5 2 0.1 2 0.5 2 0.76956 1.6175 0.48047
    0.5 0.1 0.2 0.2 0.1 0.75 5 2 0.1 2 0.5 3 0.79641 1.5933 0.47329

    Notably, skin friction exhibits an increasing trend with higher values of β , G r , G m , R d , Q o , R , α $$ \beta, Gr, Gm, Rd, Qo,R,\alpha $$ and t $$ t $$ , indicating enhanced resistance to fluid motion in these cases. However, skin friction decreases as F m , F p , P r $$ Fm, Fp,\mathit{\Pr} $$ and S c $$ Sc $$ increase, suggesting a reduction in the fluid's shear stress at the surface.

    The Nusselt number, which represents the rate of heat transfer, is observed to increase with rising values of R d $$ Rd $$ and Q o $$ Qo $$ , implying intensified thermal transport. Conversely, it decreases with increasing values of P r , α $$ \mathit{\Pr},\alpha $$ and t $$ t $$ , indicating a reduction in heat transfer efficiency.

    Finally, the Sherwood number, which signifies mass transfer, increases with higher values of S c $$ Sc $$ and R $$ R $$ , suggesting enhanced species diffusion. However, it decreases with increasing α $$ \alpha $$ and t $$ t $$ , indicating a reduction in mass transfer efficiency under these conditions. This study is highly relevant in engineering, environmental science, and biomedical fields. By understanding these influences, engineers can optimize cooling systems, design efficient pipelines, and control chemical reactions.

    7 Conclusion

    This research investigated the transient free convection flow of a radiative hydromagnetic Casson fluid over a suddenly moving porous plate, incorporating the effects of chemical reaction and heat source within the framework of Caputo fractional derivatives. The use of fractional calculus allowed for capturing memory effects and anomalous diffusion behavior in the fluid flow, offering a more generalized and realistic description compared to classical integer-order models. This advanced modeling approach provides valuable insights that can enhance the prediction and optimization of heat and mass transfer processes in various engineering and industrial systems involving complex fluids.

    Key qualitative findings include:
    • Thermal and solutal Grashof numbers enhance velocity and boundary layer thickness due to stronger buoyancy-driven convection.
    • Magnetic field and porosity parameters expand velocity profiles, indicating their combined influence can promote fluid motion.
    • Increasing fractional order elevates velocity, temperature, concentration, and their boundary layers, highlighting the role of fluid memory.
    • Higher Prandtl number reduces velocity and thermal boundary layers, reflecting decreased thermal diffusivity.
    • Increased Schmidt number diminishes velocity and concentration profiles, indicating that slower mass diffusion restricts solutal convection.

    These results deepen the understanding of fractional hydromagnetic Casson fluid flows and can guide the design and optimization of related engineering systems.

    8 Limitations and Future Scope

    8.1 Limitations

    While this study provides significant insights into fractional MHD Casson fluid flow, several limitations should be acknowledged:
    • Computational Complexity: The analytical solutions involve infinite series with gamma functions, which become computationally intensive for long-time simulations or high-precision requirements.
    • Linearization Assumptions: The Rosseland approximation for radiation and Taylor series linearization of T 4 $$ {T}^4 $$ may introduce errors in high-temperature gradient scenarios.
    • Constant Properties: The model assumes constant fluid properties (viscosity, thermal conductivity), which may not hold for large temperature variations.
    • Simplified Geometry: The analysis is limited to one-dimensional flow over an infinite plate, neglecting edge effects and three-dimensional flow characteristics.

    8.2 Future Research Directions

    To address these limitations and extend the current work, the following research directions are proposed:
    • Numerical Implementation: Development of efficient numerical algorithms (e.g., finite difference schemes) for the fractional equations to handle more complex boundary conditions and nonlinearities.
    • Variable-Order Calculus: Investigation of variable-order fractional derivatives to model time-dependent memory effects and rheological changes.
    • Coupled Multiphysics: Extension to coupled thermal-stress analysis and electroosmotic effects for biomedical applications.
    • Experimental Validation: Design of laboratory experiments with yield-stress fluids to validate the fractional models under controlled MHD conditions.
    • Machine Learning Integration: Development of hybrid physics-informed neural networks (PINNs) for parameter estimation and solution acceleration.

    These extensions would significantly enhance the practical utility of fractional calculus approaches in non-Newtonian fluid mechanics while addressing current theoretical and computational challenges.

    Author Contributions

    Mehari Fentahun Endalew: conceptualization; methodology; software; validation; investigation; formal analysis. Xiaoming Zhang: writing – review and editing; writing – original draft; conceptualization; supervision.

    Conflicts of Interest

    The authors declare no conflicts of interest.

    Data Availability Statement

    We now proclaim that any scientist who wishes to use the resources detailed in the publication for noncommercial reasons without violating participant confidentiality may do so without restriction, including any pertinent raw data.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.