Engineering Reports
Volume 7, Issue 7 e70277
RESEARCH ARTICLE
Open Access

Novel Unit Distribution for Enhanced Modeling Capabilities: Healthcare and Geological Applications

Amal S. Hassan, 

Amal S. Hassan

Faculty of Graduate Studies for Statistical Research, Cairo University, Giza, Egypt

Contribution: Conceptualization, Writing - original draft, Writing - review & editing, Methodology

Search for more papers by this author
Gaber Sallam Salem Abdalla, 

Gaber Sallam Salem Abdalla

Department of Insurance and Risk Management, Faculty of Business, Imam Mohammad Ibn Saud Islamic University (IMSIU), Riyadh, Saudi Arabia

Contribution: Writing - original draft, Writing - review & editing, Conceptualization

Search for more papers by this author
Abdoulie Faal, 

Corresponding Author

Abdoulie Faal

Mathematics Unit, Department Physical and Natural Sciences, School of Arts and Sciences, University of The Gambia, The Gambia

Correspondence: Abdoulie Faal ([email protected])

Contribution: Writing - original draft, Writing - review & editing, Methodology

Search for more papers by this author
Omar A. Saudi, 

Omar A. Saudi

Department of Basic Sciences, Higher Institute of Management Sciences (HIMS), Cairo, Egypt

Contribution: Conceptualization, Methodology, Software, Formal analysis, Writing - original draft

Search for more papers by this author
First published: 10 July 2025
https://doi.org/10.1002/eng2.70277

Funding: This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2501).

ABSTRACT

In statistical modeling, unit distributions are essential for evaluating proportional or rate-based data in domains including public health, environmental science, and finance. While there are many different unit distributions, a scalable model is required to capture unique features in various data environments. This article introduces the unit inverse exponentiated Pareto (UIEP) distribution, a novel two-parameter model. Unimodal, inverted J-shaped, left-skewed, and right-skewed probability density functions, as well as rising, J-shaped, or U-shaped hazard rate functions, are some of the different shapes of the UIEP. Because of these adaptable features, it is more suited for unit data modeling. Stochastic ordering, quantiles, moments, probability-weighted moments, significant uncertainty measures, Lorenz and Bonferroni curves, and stress-strength reliability are among the key statistical features that are analytically generated. Statistical inference employed a number of methods, such as maximum likelihood, weighted least squares, Anderson-Darling, least squares, and Kolmogorov, to estimate distribution parameters and assess different entropy measures. These statistical techniques make up an effective tool for academics and data analysts. Among these, simulation results indicated that the Kolmogorov method was the most effective for parameter estimation, particularly when combined with Arimoto, Rényi, Havrda-Charvát, and Tsallis entropy measures. Furthermore, for low and high entropy orders, respectively, Arimoto and Rényi entropies performed better when maximum likelihood estimation was used. This result demonstrates a strong correlation between the most efficient estimator and the entropy order. Our results show that both the absolute bias and the mean squared error consistently decrease as the sample size increases. This pattern confirms that the provided estimation methods are reliable and consistent. To validate the proposed distribution, we applied it to two real-world datasets: health data related to COVID-19 and geological data from petroleum rock samples. These applications demonstrated improved model fit compared to alternative distributions.

1 Introduction

The literature has lately suggested a wide range of statistical distributions as alternatives for the current models. Creating new distributions is primarily done to provide more flexibility in modeling and capturing the statistical features of real-world data. In order to enhance the field, a lot of academics work to introduce novel distributions. One efficient method for generating new distributions is the inverse transformation method applied to a baseline variable. Distributions using this method frequently have a parsimonious parameter structure. Inverse distributions are essential for statistical modeling and analysis, especially when working with skew or heavy-tailed data. An inverse transformation is used to generate these distributions. Specifically, if X represents the baseline distribution and Y is defined as the reciprocal of X (i.e., Y = 1/X), then the resulting new distribution of the random variable Y exhibits distinct characteristics. Often, this transformation is required in order to precisely model the special characteristics of particular datasets, including those found in industries like reliability engineering, insurance, and finance. Some of the suggested inverted distributions are the inverse Lindley distribution [1], the inverse power Lindley distribution ([2], the inverse exponentiated Weibull distribution [3], the inverse Nakagami-m distribution [4], the inverse Kumaraswamy (KW) distribution [5], the inverse power Lomax distribution [6], the inverse Nadarajah–Haghighi distribution [7], the inverse exponentiated Lomax distribution [8], the inverse xgamma distribution [9], the inverse Weibull generator [10, 11], the inverse Maxwell distribution [12], the inverse Topp-Leone distribution [13], the inverse Pareto distribution [14], the inverse Ishita distribution [15], the inverse-power logistic-exponential distribution [16], the inverse power Cauchy distribution [17], the inverse power Ramos-Louzada distribution [18], the inverse Shanker distribution [19], the sine inverse exponentiated Weibull distribution [20], the inverse power Zeghdoudi distribution [21], and the arcsine inverse Weibull generator [22], among others.

This study focuses on the inverse exponentiated Pareto (IEP) distribution introduced by Ghitany et al. [23]. The IEP distribution is the inverse form of the exponentiated Pareto distribution (Gupta et al. [24]). The probability density function (PDF) of the IEP distribution is given by:
f ( x ) = δ 1 δ 2 x δ 2 − 1 ( 1 + x ) − δ 2 + 1 1 − 1 + 1 x − δ 2 δ 1 − 1 ; x > 0 , $$ f(x)={\delta}_1{\delta}_2{x}^{\delta_2-1}\kern0.5em {\left(1+x\right)}^{-\left({\delta}_2+1\right)}{\left[1-{\left(1+\frac{1}{x}\right)}^{-{\delta}_2}\right]}^{\delta_1-1};\kern0.36em x>0, $$ (1)
where δ 1 > 0 $$ {\delta}_1>0 $$ and δ 2 > 0 $$ {\delta}_2>0 $$ are the shape parameters. The cumulative distribution function (CDF) is
F ( x ) = 1 − 1 − 1 + 1 x − δ 2 δ 1 ; x > 0 . $$ F(x)=1-{\left[1-{\left(1+\frac{1}{x}\right)}^{-{\delta}_2}\right]}^{\delta_1};\kern0.36em x>0. $$ (2)

The IEP distribution's hazard rate function (HRF) is notably flexible, capable of displaying increasing, decreasing, reversed J-shaped, upside-down, or non-monotonic characteristics. The IEP distribution is a good paradigm for lifetime and reliability modeling with a broad variety of potential applications ranging from analysis of fatigue failure and degradation tests to mechanical, electrical, and even mortality data estimation. Its properties align with other popular distributions like the generalized exponential, exponentiated moment exponential, and inverse exponential Rayleigh distributions, as mentioned by Pradhan and Kundu [25]. Recent work keeps on enhancing its application; for example, Maurya et al. [26] discussed the estimation of parameters under Type-II progressive censoring. Shaikh and Patel [27] focused on estimation via record values. The multicomponent stress-strength reliability (S-SR) estimation under censored samples was examined by [28, 29].

Distributions with support limited to the interval [0, 1] have grown significantly in the last few years. As fractions, rates, or percentages, these distributions are essential for modeling data in this range. This type of data is commonly encountered in many disciplines, such as risk analysis, psychology, economics, medicine, and engineering. Regression, semiparametric, and parametric model building are highly desired in order to examine this data efficiently across a variety of application fields. Notably, a significant portion of today's unit distributions are derived by appropriately transforming existing distributions with support (0,∞). As a result, several different unit distributions have been created. The unit Lindley distribution [30], the unit-Gompertz distribution [31, 32], the unit-Weibull distribution [33], the unit exponentiated half logistic (UEHL) distribution [34], the unit modified Burr-III distribution [35], the unit exponentiated Lomax (UEL) distribution [36], the unit generalized half normal distribution [37], the unit log logistic (ULL) distribution [38], the unit power-skew-normal distribution [39], the unit inverse exponentiated Weibull distribution [40], the unit Burr-XII distribution [41], the unit-power Burr X unit distribution [42], the unit half-logistic geometric distribution [43], the unit xgamma distribution [44], the unit power Lomax (UPL) distribution [45], the unit Teissier distribution [46], the mixture of log-Bilal distributions [47], the generalized exponentiated unit Gompertz [48], the unit Gumbel Type-II distribution [49], the half-logistic unit-Gompertz Type-I distribution [50], the unit Bilal distribution [51], and the unit inverse power Lomax distribution [52] are noteworthy examples.

This work introduces a UIEP distribution, a newly developed unit probability distribution from the IEP. The proposed two-parameter UIEP distribution is derived by using the transformation Y = 1 1 + X $$ Y=\frac{1}{1+X} $$ where X is an IEP distribution with PDF (1) and CDF(2). The following are the reasons that inspired us to introduce the UIEP distribution:
  • The UIEP distribution shows high flexibility and can model different datasets with values ranging between zero and one. Its density function takes on diverse shapes, including unimodal, reversed J-shaped, left-skewed, and right-skewed. The UIEP hazard function may have increasing, J-shaped, or bathtub hazard rate patterns.
  • Explore a number of statistical structure, including moments, quantile function (QF), incomplete moments (IMs), stochastic ordering (SO), probability- weighted moments (PWM), some measures of uncertainty, and S-SR.
  • To discuss the challenges of estimating the model parameters with certain uncertainty measures, i.e., Rényi (Ré), Havrda and Charvát (H–C), Tsallis (TS), and Arimoto (AR).
  • The UIEP distribution estimators are discussed utilizing some estimation techniques like the maximum likelihood (ML), least squares (LS), Kolmogorov (KO), weighted LS (WLS), and Anderson–Darling (AD).
  • To assess the performance and accuracy of the suggested parameter and entropies estimation techniques, a comprehensive simulation study is carried out.
  • Statistically, compared with other rival models, the UIEP model has been compared with some well-known distributions, including unit exponential Pareto (UEP) distribution, UEL distribution, UEHL distribution, KW distribution, and exponentiated Topp-Leone (ETL) distribution.

The remaining parts of this paper's sections are structured as follows: Section 2 gives the description of the UIEP distribution. Section 3 presents the statistical properties of the UIEP distribution, i.e., QF, PWM, moments, IMs, Lorenz and Bonferroni curves, SO, and S-SR. Section 4 gives expressions for the proposed entropy measures. Section 5 discusses the estimation of UIEP distribution parameters and gives estimators of the proposed entropy measures. Section 6 gives an overview of the simulation study, and Monte Carlo simulation was utilized to compare different results of entropy estimates. Two real datasets in Section 7 demonstrate the UIEP distribution's flexibility and usefulness. The paper finally concludes with an overview of the main conclusions and findings in Section 8.

2 The Unit Inverse Exponentiated Pareto Distribution

This section's goal is to determine the UIEP's PDF and CDF. It explores the survival function, HRF, and reversed HRF. Also, it includes a graphical representation of both the PDF and HRF of the UIEP distribution.

The UIEP distribution is derived by applying the transformation to a random variable X following the IEP distribution. Specifically, Y = 1 1 + X $$ Y=\frac{1}{1+X} $$ , where X has the CDF of the IEP distribution given in Equation (2). The resulting CDF of the UIEP distribution is derived as follows:
H ( y ) = P ( Y ≤ y ) = P ( 1 ≤ y + yX ) = P 1 − y y ≤ X = 1 − P X ≤ 1 − y y = 1 − H X 1 − y y , $$ {\displaystyle \begin{array}{cc}H(y)& =P\left(Y\le y\right)=P\left(1\le y+ yX\right)=P\left(\frac{1-y}{y}\le X\right)\\ {}& =1-P\left(X\le \frac{1-y}{y}\right)=1-{H}_X\left(\frac{1-y}{y}\right),\end{array}} $$ (3)
then,
H X 1 − y y = 1 − 1 − 1 + y 1 − y − δ 2 δ 1 = 1 − 1 − 1 1 − y − δ 2 δ 1 = 1 − 1 − ( 1 − y ) δ 2 δ 1 . $$ {\displaystyle \begin{array}{cc}{H}_X\left(\frac{1-y}{y}\right)& =1-{\left[1-{\left(1+\frac{y}{1-y}\right)}^{-{\delta}_2}\right]}^{\delta_1}\\ {}& =1-{\left[1-{\left(\frac{1}{1-y}\right)}^{-{\delta}_2}\right]}^{\delta_1}=1-{\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{\delta_1}.\end{array}} $$ (4)
Then, from Equations (3 and 4), the CDF of the UIEP distribution, with shape parameters δ 1 > 0 $$ {\delta}_1>0 $$ and δ 2 > 0 $$ {\delta}_2>0 $$ , is given by:
H ( y ) = 1 − ( 1 − y ) δ 2 δ 1 ; δ 1 , δ 2 > 0 , y ∈ ( 0 , 1 ) , $$ H(y)={\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{\delta_1};\kern1.56em {\delta}_1,{\delta}_2>0,y\in \left(0,1\right), $$ (5)
where H(y) = 0, for y ≤ 0, and H(y) = 1, for y ≤ 1. The PDF of the UIEP distribution is as below:
h ( y ) = δ 1 δ 2 ( 1 − y ) δ 2 − 1 1 − ( 1 − y ) δ 2 δ 1 − 1 ; δ 1 , δ 2 > 0 , y ∈ ( 0 , 1 ) , $$ h(y)={\delta}_1{\delta}_2{\left(1-y\right)}^{\delta_2-1}{\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{\delta_1-1};{\delta}_1,{\delta}_2>0,y\in \left(0,1\right), $$ (6)
and h(y) = 0 for y ∉ [0, 1]. A random variable with PDF (6) is represented by UIEP δ 1 , δ 2 $$ \left({\delta}_1,{\delta}_2\right) $$ . For δ 1 = 1 $$ {\delta}_1=1 $$ , the PDF (6) provides the unit inverse Pareto distribution as a new sub-model.
The survival function, HRF, and cumulative HRF (for y ∈ ( 0 , 1 ) ) $$ y\in \left(0,1\right)\Big) $$ are, respectively, given by:
H ‾ ( y ) = 1 − 1 − ( 1 − y ) δ 2 δ 1 , z ( y ) = δ 1 δ 2 ( 1 − y ) δ 2 − 1 1 − ( 1 − y ) δ 2 δ 1 − 1 1 − 1 − ( 1 − y ) δ 2 δ 1 , $$ {\displaystyle \begin{array}{cc}\overline{H}(y)& =1-{\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{\delta_1},\\ {}z(y)& =\frac{\delta_1{\delta}_2{\left(1-y\right)}^{\delta_2-1}{\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{\delta_1-1}}{1-{\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{\delta_1}},\end{array}} $$ (7)
and,
κ ( y ) = − log 1 − 1 − ( 1 − y ) δ 2 δ 1 . $$ \kappa (y)=-\log \left[1-{\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{\delta_1}\right]. $$

To visualize the shapes of the PDF (6) and HRF (7), Figures 1 and 2 depict their plots for varying values of the parameters δ 1 $$ {\delta}_1 $$ and δ 2 . $$ {\delta}_2. $$ The PDF graphs, in Figure 1, for different combinations of parameters show a range of shapes, including reversed J-shaped, left-skewed, right-skewed, and unimodal. Significantly, depending on the parameter values, the HRF exhibits remarkable flexibility, showing growing, decreasing, bathtub, and j-shaped patterns (see Figure 2). This illustrates the great level of flexibility needed for various unit data analysis.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Shapes of the PDF of the UIEP distribution for varying parameter values.
Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Shapes of the HRF of the UIEP distribution for varying parameter values.

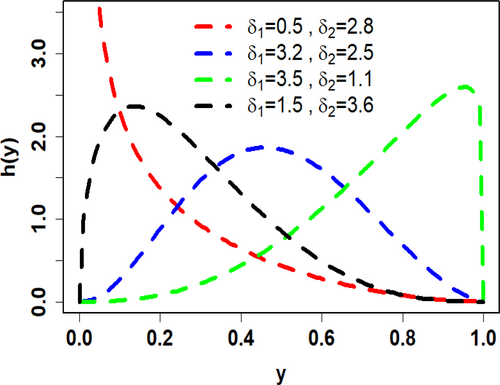
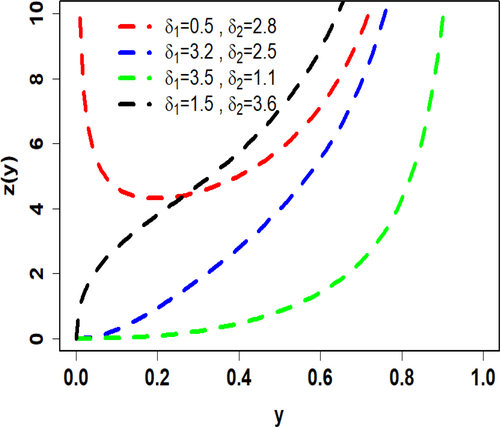
3 Characteristics of UIEP Distribution

Several important statistical properties of the UIEP distribution are examined in this section. Moments, IMs, QF, SO, PWM, and S-SR are some of these properties.

3.1 Probability Weighted Moments

Greenwood et al. [53] first proposed the idea of the PWM, which has since led to a major advance in parameter estimation for a variety of probability distributions. The PWM is typically favored over ordinary moments when dealing with distributions that exhibit heavy tails or extreme values. The PWM is less sensitive to extreme values. According to Ref. [53], the class of PWM, for a random variable Y with a real number l and h, is defined as follows:
η l , h = E Y l H ( y ) h = ∫ − ∞ ∞ y l ( H ( y ) ) h h ( y ) dy . $$ {\eta}_{l,h}=E\left[{Y}^lH{(y)}^h\right]=\int_{-\infty}^{\infty }{y}^l{\left(H(y)\right)}^hh(y) dy. $$ (8)
The PWM of the UIEPL distribution is given by inserting CDF (5) and the PDF (6) in Equation (8).
η l , h = ∫ 0 1 y l δ 1 δ 2 ( 1 − y ) δ 2 − 1 1 − ( 1 − y ) δ 2 h δ 1 + δ 1 − 1 dy . $$ {\eta}_{l,h}=\int_0^1{y}^l{\delta}_1{\delta}_2{\left(1-y\right)}^{\delta_2-1}{\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{h{\delta}_1+{\delta}_1-1} dy. $$ (9)
Using the binomial expansion
( 1 − u ) v = ∑ j = 0 ∞ v j ( − 1 ) j u j , | u | < 1 , $$ {\left(1-u\right)}^v=\sum \limits_{j=0}^{\infty}\left(\begin{array}{c}v\\ {}j\end{array}\right)\;{\left(-1\right)}^j{u}^j,\kern1.56em \mid u\mid <1, $$ (10)
in Equation (9), then we have
η l , h = ∑ j = 0 ∞ ( − 1 ) j δ 1 δ 2 δ 1 ( h + 1 ) − 1 j B l + 1 , δ 2 ( j + 1 ) , $$ {\eta}_{l,h}=\sum \limits_{j=0}^{\infty }{\left(-1\right)}^j{\delta}_1{\delta}_2\left(\begin{array}{c}{\delta}_1\left(h+1\right)-1\\ {}j\end{array}\right)B\left(l+1,{\delta}_2\left(j+1\right)\right), $$
where B (.,.) is the beta function.

3.2 Moments Measures

To comprehend the essential characteristics of a distribution, it is essential to look at moments and related measures. They offer important insights into shape, dispersion, and central tendency, all of which are essential for efficient statistical analysis and hypothesis testing. The mth moment of the UIEP distribution is derived as
μ m ′ = δ 1 δ 2 ∫ 0 1 y m ( 1 − y ) δ 2 − 1 1 − ( 1 − y ) δ 2 δ 1 − 1 dy . $$ {\mu}_m^{\prime }={\delta}_1{\delta}_2\int_0^1{y}^m{\left(1-y\right)}^{\delta_2-1}{\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{\delta_1-1} dy. $$ (11)
Using the binomial expansion (10) in Equation (11) gives
μ m ′ = δ 1 δ 2 ∑ j = 0 m ( − 1 ) j δ 1 − 1 j B m + 1 , δ 2 ( j + 1 ) , $$ {\mu}_m^{\prime }={\delta}_1{\delta}_2\sum \limits_{j=0}^m{\left(-1\right)}^j\left(\begin{array}{c}{\delta}_1-1\\ {}j\end{array}\right)B\left(m+1,{\delta}_2\left(j+1\right)\right), $$
where, B(.,.) is the beta function. Furthermore, the mth central moment of a given random variable Y is defined by
μ m = E Y − μ 1 ′ m = ∑ h = 0 m ( − 1 ) h m h μ 1 ′ h μ m − h ′ . $$ {\mu}_m=E{\left(Y-{\mu}_1^{\prime}\right)}^m=\sum \limits_{h=0}^m{\left(-1\right)}^h\left(\begin{array}{c}m\\ {}h\end{array}\right){\left({\mu}_1^{\prime}\right)}^h{\mu}_{m-h}^{\prime }. $$

Numerical values for certain parameter values, (a) δ 1 = 0.5 , δ 2 = 0.5 $$ \left({\delta}_1=0.5,{\delta}_2=0.5\right) $$ , (b) δ 1 = 0.5 , δ 2 = 1.5 $$ \left({\delta}_1=0.5,{\delta}_2=1.5\right) $$ , (c) δ 1 = 0.5 , δ 2 = 2 $$ \left({\delta}_1=0.5,{\delta}_2=2\right) $$ , (d) δ 1 = 0.5 , δ 2 = 3 $$ \left({\delta}_1=0.5,{\delta}_2=3\right) $$ of the first four moments μ 1 ′ , μ 2 ′ , μ 3 ′ , μ 4 ′ $$ \left({\mu}_1^{\prime },{\mu}_2^{\prime },{\mu}_3^{\prime },{\mu}_4^{\prime}\right) $$ variance ( σ 2 $$ {\sigma}^2 $$ ), coefficient of Skewness (CS) and coefficient of Kurtosis (CK) of the UIEL distribution are listed in Table 1.

TABLE 1. Some moments of UIEP distribution.
Measures Parameters
δ 1 $$ {\delta}_1 $$ δ 2 $$ {\delta}_2 $$ μ 1 ′ $$ {\mu}_1^{\prime } $$ μ 2 ′ $$ {\mu}_2^{\prime } $$ μ 3 ′ $$ {\mu}_3^{\prime } $$ μ 4 ′ $$ {\mu}_4^{\prime } $$ σ 2 $$ {\sigma}^2 $$ CS CK
0.5 0.5 0.4667 0.3397 0.2781 0.2403 0.1219 0.1353 1.5386
1.5 0.2608 0.1335 0.0847 0.0600 0.0655 0.9396 2.8384
2 0.2146 0.0959 0.0548 0.0355 0.0498 1.1513 3.4939
3 0.1587 0.0566 0.0269 0.0150 0.0314 1.4389 4.6253
3 0.5 0.9000 0.8286 0.7738 0.7299 0.0186 −2.1073 7.8661
1.5 0.6318 0.4417 0.3295 0.2573 0.0425 −0.3642 2.3694
2 0.5429 0.3357 0.2262 0.1619 0.0410 −0.0711 2.2658
3 0.4214 0.2110 0.1188 0.0728 0.0334 0.2798 2.4776

Table 1 shows that the moment values increase, but the CS and σ 2 $$ {\sigma}^2 $$ values decrease when δ 1 $$ {\delta}_1 $$ increases and δ 2 $$ {\delta}_2 $$ keeps constant. Both platykurtic and leptokurtic distributions, as well as left- and right-skewed distributions, are possible for the UIEP. Figure 3 displays these patterns for 3D plots of μ 1 ′ $$ {\mu}_1^{\prime } $$ , σ 2 $$ {\sigma}^2 $$ , CS, and CK.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
The 3D plots for UIEP distribution of mean, variance, skewness, and kurtosis.

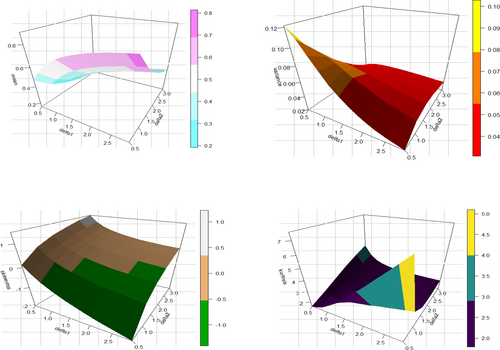
Figure 3 shows how the UIEP distribution is flexible in skewness and kurtosis. The skewness ranges from about −2 to 1, showing a wide variety of options. Furthermore, kurtosis can have both small and large values, allowing the distribution to display all three kurtosis types: leptokurtic, mesokurtic, and platykurtic. These results show how the PDF and HRF of the UIEP distribution may take on various forms.

3.3 Incomplete Moments

A distribution's IM offers important information beyond just means and variances. They highlight extreme occurrences by capturing the dynamics of tails and asymmetries. For thorough risk assessment and decision-making, this knowledge is essential. We can improve the efficacy of our statistical analysis and obtain a deeper knowledge of the underlying data by accepting IMs.

The mth IM of the UIEP distribution is derived as
μ m ′ ( t ) = δ 1 δ 2 ∫ 0 t y m ( 1 − y ) δ 2 − 1 1 − ( 1 − y ) δ 2 δ 1 − 1 dy . $$ {\mu}_m^{\prime }(t)={\delta}_1{\delta}_2\int_0^t{y}^m{\left(1-y\right)}^{\delta_2-1}{\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{\delta_1-1} dy. $$ (12)
Using the binomial expansion (10) in Equation (12) gives
μ m ′ = δ 1 δ 2 ∑ j = 0 m ( − 1 ) j δ 1 − 1 j B m + 1 , δ 2 ( j + 1 ) , t , $$ {\mu}_m^{\prime }={\delta}_1{\delta}_2\sum \limits_{j=0}^m{\left(-1\right)}^j\left(\begin{array}{c}{\delta}_1-1\\ {}j\end{array}\right)B\left(m+1,{\delta}_2\left(j+1\right),t\right), $$
where B(.,.,x) is the incomplete beta function. The Lorenz curve given by LF (t) = μ 1 ′ ( t ) / μ 1 ′ $$ ={\mu}_1^{\prime }(t)/{\mu}_1^{\prime } $$ and the Bonferroni curve given by and BF (t) = L ( t ) / H ( t ) $$ =L(t)/H(t) $$ , respectively, are notable applications of the first IM. These curves have significant utility in various fields, including economics, demographics, insurance, engineering, and medicine, for analyzing inequality, wealth distribution, and other crucial aspects.

Figure 4 shows inequality differences between the Lorenz and Bonferroni curves for five groups that have different δ 1 $$ {\delta}_1 $$ and δ 2 $$ {\delta}_2 $$ values. The green curve, which represents the greatest inequality, is the farthest off the equality line in the Lorenz plot and has the lowest Bonferroni curve, particularly in the lower tail, showing that the lowest 20% of the population receives the smallest amount of income. Conversely, the gold curve displays the lowest inequality, with both curves closer to the equality line, showing a more balanced income distribution. Cods of Lorenz and Bonferroni curves are given in Appendix B.

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Lorenz and Bonferroni curves of the UIEP distribution.

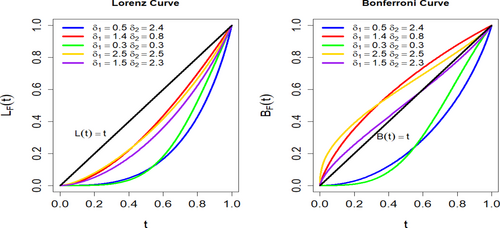
3.4 Quantile Function

The QF of the UIEP distribution, for p∈(0, 1), is derived by inverting its CDF (5) as follows:
Q ( p ) = 1 − 1 − ( p ) 1 / δ 1 1 / δ 2 . $$ Q(p)=1-{\left(1-{(p)}^{1/{\delta}_1}\right)}^{1/{\delta}_2}. $$
The QF yields a number of important statistical metrics. For instance, at p = 0.5 gives the median (second quartile, denoted as Q 2 $$ {Q}_2 $$ ), while at p = 0.75 provides the third quartile (denoted by Q 3 $$ {Q}_3 $$ ) and at p = 0.25 gives the first quartile (denoted by Q 1 $$ {Q}_1 $$ ). We can use the following expression to create the random numbers for the UIEP distribution.
y p = 1 − 1 − ( p ) 1 / δ 1 1 / δ 2 . $$ {y}_p=1-{\left(1-{(p)}^{1/{\delta}_1}\right)}^{1/{\delta}_2}. $$

3.5 Stochastic Ordering

A foundational idea in probability theory, SO has been studied and used extensively for more than 40 years. Numerous domains, such as biological sciences, economics, insurance, survival analysis, queueing theory, and reliability engineering, find use for it. A useful tool for evaluating the robustness and performance of system components, this framework allows the comparison of non-negative continuous random variables.

Let Y 1 $$ {Y}_1 $$ has the UIEP δ 1 , δ 2 $$ \left({\delta}_1,{\delta}_2\right) $$ with PDF h 1 ( y ) $$ {h}_1(y) $$ and Y 2 $$ {Y}_2 $$ has the UIEP δ 3 , δ 4 $$ \left({\delta}_3,{\delta}_4\right) $$ with PDF h 2 ( y ) $$ {h}_2(y) $$ . In terms of likelihood ratio order; Y 1 $$ {Y}_1 $$ is said to be stochastically less than Y 2 $$ {Y}_2 $$ (written as Y 1 ≤ lr Y 2 $$ {Y}_1{\le}_{lr}{Y}_2 $$ ) if h 1 ( y ) / h 2 ( y ) $$ {h}_1(y)/{h}_2(y) $$ is a decreasing function ∀ y $$ \forall y $$ . The following is likelihood ratio ordering:
h 1 ( y ) h 2 ( y ) = δ 1 δ 2 ( 1 − y ) δ 2 − 1 1 − ( 1 − y ) δ 2 δ 1 − 1 δ 3 δ 4 ( 1 − y ) δ 4 − 1 1 − ( 1 − y ) δ 4 δ 3 − 1 . $$ \frac{h_1(y)}{h_2(y)}=\frac{\delta_1{\delta}_2{\left(1-y\right)}^{\delta_2-1}{\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{\delta_1-1}}{\delta_3{\delta}_4{\left(1-y\right)}^{\delta_4-1}{\left[1-{\left(1-y\right)}^{\delta_4}\right]}^{\delta_3-1}}. $$

It is obtained d dy log h 1 ( y ) / h 2 ( y ) < 0 $$ \frac{d}{dy}\left[\log \left({h}_1(y)/{h}_2(y)\right)\right]<0 $$ , at δ 1 > δ 3 $$ {\delta}_1>{\delta}_3 $$ and δ 2 > δ 4 , ∀ y ≥ 0 $$ {\delta}_2>{\delta}_4,\forall y\ge 0 $$ , hence d dy log h 1 ( y ) / h 2 ( y ) < 0 $$ \frac{d}{dy}\left[\log \left({h}_1(y)/{h}_2(y)\right)\right]<0 $$ is a decreasing function ∀ y $$ \forall y $$ and hence Y 1 ≤ Ir Y 2 $$ {Y}_1{\le}_{Ir}{Y}_2 $$ . Conclusions can also be made for various SO, like: hazard rate order Y 1 ≤ hr Y 2 $$ \left({Y}_1{\le}_{hr}{Y}_2\right) $$ , mean residual life order Y 1 ≤ mrl Y 2 $$ \left({Y}_1{\le}_{mrl}{Y}_2\right) $$ , SO Y 1 ≤ st Y 2 $$ \left({Y}_1{\le}_{st}{Y}_2\right) $$ , and reversed hazard rate order Y 1 ≤ rhr Y 2 $$ \left({Y}_1{\le}_{rhr}{Y}_2\right) $$ .

3.6 Stress-Strength Model

This subsection establishes the S-SR parameter for the UIEP model. The S-SR model is a popular method for estimating reliability that has important uses in many fields of physics and engineering. The mathematical expression for reliability ( R $$ R $$ ) in this model is R = P r Y 2 < Y 1 $$ R={P}_r\left({Y}_2<{Y}_1\right) $$ , which is a probability that the system's strength Y 1 $$ \left({Y}_1\right) $$ will be greater than the enforced stress Y 2 $$ \left({Y}_2\right) $$ . When the applied stress exceeds the system's strength Y 2 > Y 1 $$ \left({Y}_2>{Y}_1\right) $$ , the system fails. On the other hand, when Y 1 > Y 2 $$ {Y}_1>{Y}_2 $$ , the component performs adequately. In electrical and electronic systems, reliability ( R $$ R $$ ) is especially significant as a metric for system performance. It can also be thought of as a probability that the system is strong enough to bear the stress that has been applied to it. Suppose that Y 1 $$ {Y}_1 $$ is the strength random variable having UIEP δ 1 , δ 2 $$ \left({\delta}_1,{\delta}_2\right) $$ and Y 2 $$ {Y}_2 $$ is the stress random variable having UIEP δ 3 , δ 2 $$ \left({\delta}_3,{\delta}_2\right) $$ , where Y 1 $$ {Y}_1 $$ and Y 2 $$ {Y}_2 $$ are independent; the S-SR can be determined as follows:
R = ∫ 0 1 δ 1 δ 2 ( 1 − y ) δ 2 − 1 1 − ( 1 − y ) δ 2 δ 1 + δ 3 − 1 dy = δ 1 δ 1 + δ 3 . $$ R=\int_0^1{\delta}_1{\delta}_2{\left(1-y\right)}^{\delta_2-1}{\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{\delta_1+{\delta}_3-1} dy=\frac{\delta_1}{\delta_1+{\delta}_3}. $$ (13)

Note that the formula of S-SR of the UIEP given in Equation (13) is a function of the parameters δ 1 , δ 3 $$ \left({\delta}_1,{\delta}_3\right) $$ .

4 Information Measures

Entropy, an essential idea in information theory, quantifies the uncertainty associated with a random variable. It determines how much information should be present in that variable. In many disciplines, such as statistics, physics, chemistry, economics, insurance, finance, and biological sciences, entropy is essential. Entropy often increases with decreasing information content in a sample. This section gives, expressions of some entropy measures, including Ré, H–C, TS, and AR. The Ré entropy of order b $$ b $$ , presented by Rényi [54], is defined by.
χ 1 = 1 1 − b log ∫ − ∞ ∞ h ( y ) b dy , b > 0 , b ≠ 1 . $$ {\chi}_1=\frac{1}{1-b}\log \left[\int_{-\infty}^{\infty }h{(y)}^b dy\right],b>0,b\ne 1. $$ (14)
Inserting PDF (6) in Equation (14), then the Ré entropy of the UIEP distribution is obtained as follows:
χ 1 = 1 1 − b log ∫ 0 1 δ 1 δ 2 b ( 1 − y ) b δ 2 − 1 1 − ( 1 − y ) δ 2 b δ 1 − 1 dy . $$ {\chi}_1=\frac{1}{1-b}\log \left[\int_0^1{\left({\delta}_1{\delta}_2\right)}^b{\left(1-y\right)}^{b\left({\delta}_2-1\right)}{\left[1-{\left(1-y\right)}^{\delta_2}\right]}^{b\left({\delta}_1-1\right)} dy\right]. $$ (15)
Using the transformation z = ( 1 − y ) δ 2 ⇒ dz = − δ 2 ( 1 − y ) δ 2 − 1 d y $$ z={\left(1-y\right)}^{\delta_2}\Rightarrow dz=-{\delta}_2{\left(1-y\right)}^{\delta_2-1} dy $$ in Equation (15) gives
χ 1 = 1 1 − b log δ 1 b δ 2 b − 1 B b δ 2 − 1 δ 2 + 1 δ 2 , b δ 1 − 1 + 1 , $$ {\chi}_1=\frac{1}{1-b}\log \left[{\delta}_1^b{\delta_2}^{b-1}\mathrm{B}\left(\frac{b\left({\delta}_2-1\right)}{\delta_2}+\frac{1}{\delta_2},b\left({\delta}_1-1\right)+1\right)\right], $$ (16)
where B(.,.) is the beta function. The H–C entropy measure, presented by Ref. [55], is defined by:
χ 2 = 1 2 1 − b − 1 ∫ - ∞ ∞ h ( y ) b dy − 1 , b > 0 , b ≠ 1 . $$ {\chi}_2=\frac{1}{2^{1-b}-1}\left[\int_{\hbox{-} \infty}^{\infty }h{(y)}^b dy-1\right],b>0,b\ne 1. $$ (17)
Inserting PDF(6) in Equation (17) and using the transformation z = ( 1 − y ) δ 2 $$ z={\left(1-y\right)}^{\delta_2} $$ , then the H–C entropy of the UIEP distribution is obtained as follows:
χ 2 = 1 2 1 − b − 1 δ 1 b δ 2 b − 1 B b δ 2 − 1 δ 2 + 1 δ 2 , b δ 1 − 1 + 1 − 1 , $$ {\chi}_2=\frac{1}{2^{1-b}-1}\left[{\delta}_1^b{\delta_2}^{b-1}\mathrm{B}\left(\frac{b\left({\delta}_2-1\right)}{\delta_2}+\frac{1}{\delta_2},b\left({\delta}_1-1\right)+1\right)-1\right], $$ (18)
where B(.,.) is the beta function. The TS entropy measure, presented by Tsallis [56], is defined by:
χ 3 = 1 b − 1 1 − ∫ - ∞ ∞ h ( y ) b dy ; b > 0 , b ≠ 1 . $$ {\chi}_3=\frac{1}{b-1}\left[1-\int_{\hbox{-} \infty}^{\infty }h{(y)}^b dy\right];b>0,b\ne 1. $$ (19)
Inserting PDF(6) in Equation (19) and using the transformation z = ( 1 − y ) δ 2 $$ z={\left(1-y\right)}^{\delta_2} $$ , then the TS entropy of the UIEP distribution is obtained as follows:
χ 3 = 1 b − 1 1 − δ 1 b δ 2 b − 1 B b δ 2 − 1 δ 2 + 1 δ 2 , b δ 1 − 1 + 1 , $$ {\chi}_3=\frac{1}{b-1}\left[1-{\delta}_1^b{\delta_2}^{b-1}\mathrm{B}\left(\frac{b\left({\delta}_2-1\right)}{\delta_2}+\frac{1}{\delta_2},b\left({\delta}_1-1\right)+1\right)\right], $$ (20)
where B(.,.) is the beta function. The AR entropy measure, presented by Arimoto [57], is defined by
χ 4 = b b − 1 ∫ - ∞ ∞ h ( y ) b dy 1 / b − 1 ; b > 0 , b ≠ 1 . $$ {\chi}_4=\frac{b}{b-1}\left[{\left(\int_{\hbox{-} \infty}^{\infty }h{(y)}^b dy\right)}^{1/b}-1\right];b>0,b\ne 1. $$ (21)
Inserting PDF (4) of the UIEP distribution in Equation (21) and using the transformation z = ( 1 − y ) δ 2 $$ z={\left(1-y\right)}^{\delta_2} $$ , then the AR entropy is obtained as follows
χ 4 = b b − 1 δ 1 b δ 2 b − 1 B b δ 2 − 1 δ 2 + 1 δ 2 , b δ 1 − 1 + 1 1 / b − 1 , $$ {\chi}_4=\frac{b}{b-1}\left[{\left({\delta}_1^b{\delta_2}^{b-1}\mathrm{B}\left(\frac{b\left({\delta}_2-1\right)}{\delta_2}+\frac{1}{\delta_2},b\left({\delta}_1-1\right)+1\right)\right)}^{1/b}-1\right], $$ (22)
where B(.,.) is the beta function.

5 Estimation Methods

In order to estimate parameters for the UIEP distribution, this section looks at five distinct approaches: ML, KO, AD, WLS, and LS. It also investigates the estimation of four entropy metrics for the UIEP distribution: AR, TS, Ré, and H–C. Each of these methods provides a unique method for estimating entropy measures and model parameters.

5.1 Maximum Likelihood Method

To estimate the unknown parameters and entropy measures of the UIEP distribution, the ML technique is used. Consider an observed simple random sample of size n, denoted by y1, y2,…, yn taken from the UIEP distribution. The log-likelihood function of the observed sample is given by

l * = n log δ 1 δ 2 + δ 2 − 1 ∑ i = 1 n log 1 − y i + δ 1 − 1 ∑ i = 1 n log 1 − 1 − y i δ 2 . $$ {l}^{\ast }=n\log \left({\delta}_1{\delta}_2\right)+\left({\delta}_2-1\right)\sum \limits_{i=1}^n\log \left(1-{y}_i\right)+\left({\delta}_1-1\right)\sum \limits_{i=1}^n\log \left[1-{\left(1-{y}_i\right)}^{\delta_2}\right]. $$
The ML estimators of δ 1 $$ {\delta}_1 $$ and δ 2 $$ {\delta}_2 $$ can be determined by solving the following two non-linear equations:
∂ l * ∂ δ 1 = n δ 1 + ∑ i = 1 n log 1 − 1 − y i δ 2 = 0 , $$ \frac{\partial {l}^{\ast }}{\partial {\delta}_1}=\frac{n}{\delta_1}+\sum \limits_{i=1}^n\log \left[1-{\left(1-{y}_i\right)}^{\delta_2}\right]=0, $$ (23)
and
∂ l * ∂ δ 2 = n δ 2 + ∑ i = 1 n log 1 − y i − ∑ i = 1 n δ 1 − 1 log 1 − y i 1 − y i − δ 2 − 1 = 0 . $$ \frac{\partial {l}^{\ast }}{\partial {\delta}_2}=\frac{n}{\delta_2}+\sum \limits_{i=1}^n\log \left(1-{y}_i\right)-\sum \limits_{i=1}^n\frac{\left({\delta}_1-1\right)\log \left(1-{y}_i\right)}{\left[{\left(1-{y}_i\right)}^{-{\delta}_2}-1\right]}=0. $$ (24)

Notably, there are no closed-form solutions for Equations (23 and 24). Therefore, in order to derive the ML estimators δ ^ 1 $$ {\hat{\delta}}_1 $$ of δ 1 $$ {\delta}_1 $$ and δ ^ 2 $$ {\hat{\delta}}_2 $$ of δ 2 $$ {\delta}_2 $$ , numerical approaches using optim function in the R programming language are required. Furthermore, based on invariance property, the ML estimators of different entropy measures are produced after substituting δ ^ 1 $$ {\hat{\delta}}_1 $$ and δ ^ 2 $$ {\hat{\delta}}_2 $$ in Equations (16, 18, 20, and 22) to produce χ ^ 1 , χ ^ 2 , χ ^ 3 $$ {\hat{\chi}}_1,{\hat{\chi}}_2,{\hat{\chi}}_3 $$ and χ ^ 4 $$ {\hat{\chi}}_4 $$ .

5.2 Least Squares and Weighted Least Squares

In this sub-section, the LS and WLS estimators of the parameters are obtained. Let y(1) < y(2) < … < y(n) represent the ordered observed sample of size n from the UIEP distribution. The LS and WLS estimators of unknown parameters of the UIEP distribution are obtained by minimizing the error of sum squares.
E * δ 1 , δ 2 = ∑ j = 1 n υ j 1 − 1 − y ( j ) δ 2 δ 1 − j n + 1 2 . $$ {E}^{\ast}\left({\delta}_1,{\delta}_2\right)=\sum \limits_{j=1}^n{\upsilon}_j{\left[{\left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right]}^{\delta_1}-\frac{j}{n+1}\right]}^2. $$
The LS estimators δ ‾ 1 $$ {\overline{\delta}}_1 $$ of δ 1 $$ {\delta}_1 $$ and δ ‾ 2 $$ {\overline{\delta}}_2 $$ of δ 2 $$ {\delta}_2 $$ can be determined for υ j = 1 $$ {\upsilon}_j=1 $$ . While the WLS estimators δ ⌢ 1 $$ {\overset{\frown }{\delta}}_1 $$ of δ 1 $$ {\delta}_1 $$ and δ ⌢ 2 $$ {\overset{\frown }{\delta}}_2 $$ of δ 2 $$ {\delta}_2 $$ can be determined for υ j = ( n + 1 ) 2 ( n + 2 ) j ( n − j + 1 ) $$ {\upsilon}_j=\frac{{\left(n+1\right)}^2\left(n+2\right)}{j\left(n-j+1\right)} $$ . These estimates can also be obtained by solving the equations below using an iterative method:
∂ E * δ 1 , δ 2 ∂ δ 1 = ∑ j = 1 n υ j 1 − 1 − y ( j ) δ 2 δ 1 − j n + 1 ϑ δ 1 = 0 , $$ \frac{\partial {E}^{\ast}\left({\delta}_1,{\delta}_2\right)}{\partial {\delta}_1}=\sum \limits_{j=1}^n{\upsilon}_j\left[{\left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right]}^{\delta_1}-\frac{j}{n+1}\right]{\vartheta}_{\delta_1}=0, $$
∂ E * δ 1 , δ 2 ∂ δ 2 = δ 1 ∑ j = 1 n υ j 1 − 1 − y ( j ) δ 2 δ 1 − j n + 1 ϑ δ 2 = 0 , $$ \frac{\partial {E}^{\ast}\left({\delta}_1,{\delta}_2\right)}{\partial {\delta}_2}={\delta}_1\sum \limits_{j=1}^n{\upsilon}_j\left[{\left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right]}^{\delta_1}-\frac{j}{n+1}\right]{\vartheta}_{\delta_2}=0, $$
where
ϑ δ 1 = 1 − 1 − y ( j ) δ 2 δ 1 log 1 − 1 − y ( j ) δ 2 , ϑ δ 2 = − δ 1 1 − 1 − y ( j ) δ 2 δ 1 − 1 1 − y ( j ) δ 2 log 1 − y ( j )   . $$ {\displaystyle \begin{array}{ll}{\vartheta}_{\delta_1}& ={\left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right]}^{\delta_1}\log \left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right],\\ {}{\vartheta}_{\delta_2}& =-{\delta}_1{\left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right]}^{\delta_1-1}{\left(1-{y}_{(j)}\right)}^{\delta_2}\log \left(1-{y}_{(j)}\right).\end{array}} $$ (25)

Furthermore, the LS estimators of Ré, H–C, TS, and AR measures are produced, following the same procedure presented by Jha et al. [58], after substituting δ ‾ 1 $$ {\overline{\delta}}_1 $$ and δ ‾ 2 $$ {\overline{\delta}}_2 $$ in Equations (16, 18, 20, and 22) to produce χ ‾ 1 , χ ‾ 2 , χ ‾ 3 $$ {\overline{\chi}}_1,{\overline{\chi}}_2,{\overline{\chi}}_3 $$ and χ ‾ 4 $$ {\overline{\chi}}_4 $$ . Similarly, Furthermore, the WLS estimators of Ré, H–C, TS, and AR measures are produced after substituting δ ⌢ 1 $$ {\overset{\frown }{\delta}}_1 $$ and δ ⌢ 2 $$ {\overset{\frown }{\delta}}_2 $$ in Equations (16, 18, 20, and 22) to produce χ ⌢ 1 , χ ⌢ 2 , χ ⌢ 3 $$ {\overset{\frown }{\chi}}_1,{\overset{\frown }{\chi}}_2,{\overset{\frown }{\chi}}_3 $$ and χ ⌢ 4 $$ {\overset{\frown }{\chi}}_4 $$ .

5.3 Anderson–Dalring & Kolmogorov

This subsection presents the AD estimation method for the parameters δ 1 $$ {\delta}_1 $$ and δ 2 $$ {\delta}_2 $$ of the UIEP distribution based on minimizing a goodness-of-fit statistic. This approach relies on comparing the estimated CDF to the empirical CDF of the observed data. Let y(1) < y(2) < … < y(n) represent the ordered observed sample of size n from the UIEP distribution. The AD estimators of δ ⃛ 1 $$ {\overset{\dddot{}}{\delta}}_1 $$ of δ 1 $$ {\delta}_1 $$ and δ ⃛ 2 $$ {\overset{\dddot{}}{\delta}}_2 $$ of δ 2 $$ {\delta}_2 $$ are obtained by minimizing the following function
E 1 * δ 1 , δ 2 = − n − 1 n ∑ j = 1 n ( 2 j − 1 ) log 1 − 1 − y ( j ) δ 2 δ 1 + log 1 − 1 − 1 − y ( n − j + 1 ) δ 2 δ 1 . $$ {\displaystyle \begin{array}{cc}{E}_1^{\ast}\left({\delta}_1,{\delta}_2\right)& =-n-\frac{1}{n}\sum \limits_{j=1}^n\left(2j-1\right)\left[\log \left({\left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right]}^{\delta_1}\right.\right.\\ {}& \kern1em \left.\left.+\log \left(1-{\left[1-{\left(1-{y}_{\left(n-j+1\right)}\right)}^{\delta_2}\right]}^{\delta_1}\right)\right)\right].\end{array}} $$

The following non-linear equations are solved using an iterative method implemented in R, yielding the AD estimators δ ⃛ 1 $$ {\overset{\dddot{}}{\delta}}_1 $$ and δ ⃛ 2 $$ {\overset{\dddot{}}{\delta}}_2 $$

∂ E 1 * δ 1 , δ 2 ∂ δ 1 = − 1 n ∑ j = 1 n ( 2 j − 1 ) ϑ δ 1 1 − 1 − y ( j ) δ 2 δ 1 − ϑ δ 1 1 − 1 − 1 − y ( j ) δ 2 δ 1 = 0 , $$ \frac{\partial {E}_1^{\ast}\left({\delta}_1,{\delta}_2\right)}{\partial {\delta}_1}=-\frac{1}{n}\sum \limits_{j=1}^n\left(2j-1\right)\left[\frac{\vartheta_{\delta_1}}{{\left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right]}^{\delta_1}}-\frac{\vartheta_{\delta_1}}{1-{\left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right]}^{\delta_1}}\right]=0, $$
∂ E 1 * δ 1 , δ 2 ∂ δ 2 = − 1 n ∑ j = 1 n ( 2 j − 1 ) ϑ δ 2 1 − 1 − y ( j ) δ 2 δ 1 − ϑ δ 2 1 − 1 − 1 − y ( j ) δ 2 δ 1 = 0 , $$ \frac{\partial {E}_1^{\ast}\left({\delta}_1,{\delta}_2\right)}{\partial {\delta}_2}=-\frac{1}{n}\sum \limits_{j=1}^n\left(2j-1\right)\left[\frac{\vartheta_{\delta_2}}{{\left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right]}^{\delta_1}}-\frac{\vartheta_{\delta_2}}{1-{\left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right]}^{\delta_1}}\right]=0, $$
where ϑ δ 1 $$ {\vartheta}_{\delta_1} $$ and ϑ δ 2 $$ {\vartheta}_{\delta_2} $$ are defined in Equation (25). Furthermore, the AD estimators of Ré, H–C, TS, and AR measures are produced after substituting δ ⃛ 1 $$ {\overset{\dddot{}}{\delta}}_1 $$ and δ ⃛ 2 $$ {\overset{\dddot{}}{\delta}}_2 $$ in Equations (16, 18, 20, and 22) to produce χ ⃛ 1 , χ ⃛ 2 , χ ⃛ 3 $$ {\overset{\dddot{}}{\chi}}_1,{\overset{\dddot{}}{\chi}}_2,{\overset{\dddot{}}{\chi}}_3 $$ and χ ⃛ 4 $$ {\overset{\dddot{}}{\chi}}_4 $$ .

Finally, the parameters δ 1 $$ {\delta}_1 $$ and δ 2 $$ {\delta}_2 $$ of the UIEP distribution are determined using the KO method. Maximizing the following equation, with respect to the parameters δ 1 $$ {\delta}_1 $$ and δ 2 $$ {\delta}_2 $$ to produce the KO estimators' parameters δ ¨ 1 $$ {\ddot{\delta}}_1 $$ and δ ¨ 2 $$ {\ddot{\delta}}_2 $$ is the aim of the following estimating procedure:

E 2 * δ 1 , δ 2 = Max 1 ≤ j ≤ n ∑ j = 1 n j n − 1 − 1 − y ( j ) δ 2 δ 1 , 1 − 1 − y ( j ) δ 2 δ 1 − j − 1 n . $$ {E}_2^{\ast}\left({\delta}_1,{\delta}_2\right)=\underset{1\le j\le n}{\mathit{\operatorname{Max}}}\kern.2em \sum \limits_{j=1}^n\left[\frac{j}{n}-{\left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right]}^{\delta_1},{\left[1-{\left(1-{y}_{(j)}\right)}^{\delta_2}\right]}^{\delta_1}-\frac{j-1}{n}\right]. $$

Also, the KO estimators χ ¨ 1 , χ ¨ 2 , χ ¨ 3 $$ {\ddot{\chi}}_1,{\ddot{\chi}}_2,{\ddot{\chi}}_3 $$ and χ ¨ 4 $$ {\ddot{\chi}}_4 $$ are produced after inserting δ ¨ 1 $$ {\ddot{\delta}}_1 $$ and δ ¨ 2 $$ {\ddot{\delta}}_2 $$ in Equations (16, 18, 20, and 22).

6 Numerical Simulation

A simulation study was conducted to evaluate the effectiveness of multiple estimation strategies for Ré, H–C, TS, and AR entropy measures and parameters δ 1 , δ 2 $$ {\delta}_1,{\delta}_2 $$ in UIEP distribution. The study considered sample sizes n of 25, 50, 75, 100, and 200, with N = 1000 replication numbers. Specifically, the UIEP distribution was constructed by choosing the following parameter values as
  • The true values on Table A1 are set1 =  ( δ 1 = 0.5 , δ 2 = 1.4 , b = 0.9 ) $$ \left({\delta}_1=0.5,{\delta}_2=1.4,b=0.9\right) $$ , while the corresponding true values of entropy measures are Ré = −0.40489, H–C = −0.55285, TS = −0.39680, and AR = −0.39592.
  • The true values on Table A2 are set 2 =  ( δ 1 = 2 , δ 2 = 0.6 , b = 0.9 ) $$ \left({\delta}_1=2,{\delta}_2=0.6,b=0.9\right) $$ , white the associated true values of entropy measures are Ré = −0.61617, H–C = −0.83257, TS = − $$ - $$ 0.59757, and AR = −0.59555.
  • The true values on Table A3 are set 3 =  ( δ 1 = 0.8 , δ 2 = 2 , b = 1.5 ) $$ \left({\delta}_1=0.8,{\delta}_2=2,b=1.5\right) $$ , while the associated true values of entropy measures are Ré = −0.38956, H–C = −0.73420, TS = −0.43008, and AR = −0.41598.
  • The true values Table A4. are set 4 =  ( δ 1 = 2.2 , δ 2 = 0.8 , b = 1.5 ) $$ \left({\delta}_1=2.2,{\delta}_2=0.8,b=1.5\right) $$ , while the associated true values of entropy measures are Ré = − $$ - $$ 0.54937, H–C = −1.07929, TS = − $$ - $$ 0.63223, and AR = −0.60289.
were carefully selected to ensure a wide range of entropy levels. Furthermore, this study employed four distinct entropy measures: Ré, TS, AR, and H–C. Five estimating approaches: ML, KO, LS, WLS, and AD were examined. Uniform random numbers between 0 and 1 were created, and sample size n of the UIEP distribution was obtained with the QF. The performance of entropy measures and parameters has been evaluated using absolute biases (ABs) and mean squared errors (MSEs).
All simulations were implemented in the R programming language, employing the “optim” function for estimation. The findings are summarized in Tables A1–A4 (see Appendix A) and Figures 5 and 6.
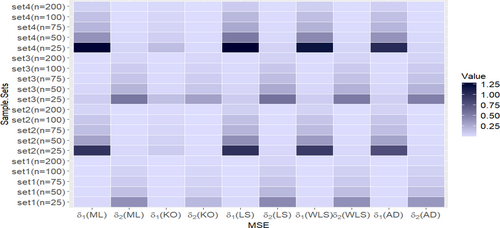
  • As n increases, the ABs and MSEs of each estimate decrease.
  • The KO method is the most efficient compared to all other estimation methods for the parameters of the UIEP distribution.
  • As true values of δ 1 $$ {\delta}_1 $$ and δ 2 $$ {\delta}_2 $$ increase, the estimates for δ 1 $$ {\delta}_1 $$ and δ 2 $$ {\delta}_2 $$ generally show an increase in MSE across all methods.
  • At b = 1.5 $$ b=1.5 $$ , under the LS method, when δ 1 $$ {\delta}_1 $$ is less than δ 2 $$ {\delta}_2 $$ , the H–C entropy estimates show a higher increase in MSE than the TS entropy estimates. However, when δ 2 $$ {\delta}_2 $$ is less than δ 1 $$ {\delta}_1 $$ , the TS entropy estimate shows a higher increase in MSE than the H–C entropy estimate.
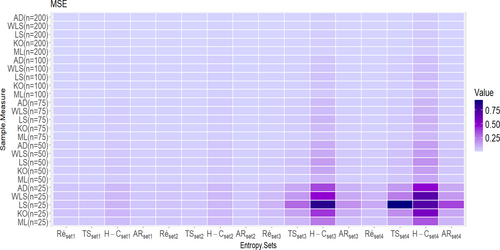
  • At b = 0.9 $$ b=0.9 $$ , the AR entropy estimation is the best compared to all other entropy estimation methods for the UIEP distribution.
  • At b = 1.5 $$ b=1.5 $$ , the Ré entropy estimation is the best compared to all other entropy estimation methods for the UIEP distribution.
  • Both the AR and Ré entropy estimators are found to be best when using ML estimation. The AR estimate is preferred for low-entropy order value, whereas Ré is the superior choice for high-entropy order value.
Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
Heatmaps of MSE values for parameters of the UIEP distribution with different methods.
Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
Heatmaps of MSE values for entropy measures of the UIEP distribution with different methods.

7 Real Data Application

This section investigates the UIEP distribution by comparing it to well-known unit distributions available in the literature. For this comparison, two datasets are used: one with coronavirus data and one with rock samples from a petroleum reserve. The following distributions are examined for comparison: UEP distribution, UEL distribution, UEHL distribution, KW distribution, ETL distribution (Pourdarvish et al. [59]), ULL distribution, and UPL distribution.

The ML method was employed to parameterize competing distributions. The KO, LS, WLS, and AD techniques are used to estimate the parameters for the UIEP distribution. The model selection process used the log-likelihood-derived are the Akaike information criterion ( ƛ 1 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_1 $$ ), Bayesian information criterion ( ƛ 2 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_2 $$ ), consistent Akaike information criterion ( ƛ 3 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_3 $$ ), Hannan–Quinn information criterion ( ƛ 4 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_4 $$ ). The AD statistic ( ƛ 5 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_5 $$ ), the Cramér–von Mises statistic ( ƛ 6 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_6 $$ ), the Kolmogorov–Smirnov statistic ( ƛ 7 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_7 $$ ), and the p-value ( ƛ 8 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_8 $$ ) were used to evaluate goodness-of-fit. Superior fit is indicated by lower ƛ 1 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_1 $$ , ƛ 2 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_2 $$ , ƛ 3 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_3 $$ , ƛ 4 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_4 $$ , ƛ 5 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_5 $$ , ƛ 6 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_6 $$ , and ƛ 7 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_7 $$ values as well as a higher ƛ 8 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_8 $$ . This method compares UIEP with other distributions provided. All cods are given in Appendix B.
  1. COVID Data

For an 82-day period in 2021, from May 1 to July 16, COVID-19 death rates were recorded in England (see Abu El Azm et al. [60]). The data are as follows: 0.0023, 0.0023, 0.0023, 0.0046, 0.0065, 0.0067, 0.0069, 0.0069, 0.0091, 0.0093, 0.0093, 0.0093, 0.0111, 0.0115, 0.0116, 0.0116, 0.0119, 0.0133, 0.0136, 0.0138, 0.0138, 0.0159, 0.0161, 0.0162, 0.0162, 0.0162, 0.0163, 0.0180, 0.0187, 0.0202, 0.0207, 0.0208, 0.0225, 0.0230, 0.0230, 0.0239, 0.0245, 0.0251, 0.0255, 0.0255, 0.0271, 0.0275, 0.0295, 0.0297, 0.0300, 0.0302, 0.0312, 0.0314, 0.0326, 0.0346, 0.0349, 0.0350, 0.0355, 0.0379, 0.0384, 0.0394, 0.0394, 0.0412, 0.0419, 0.0425, 0.0461, 0.0464, 0.0468, 0.0471, 0.0495, 0.0501, 0.0521, 0.0571, 0.0588, 0.0597, 0.0628, 0.0679, 0.0685, 0.0715, 0.0766, 0.0780, 0.0942, 0.0960, 0.0988, 0.1223, 0.1343, and 0.1781.

The COVID-19 data's key descriptive statistics are tabulated in Table 2 and visualized in Figure 7.

TABLE 2. Summary statistics for COVID-19 data.
Minimum Q 1 $$ {Q}_1 $$ Q 2 $$ {Q}_2 $$ μ 1 ′ $$ {\mu}_1^{\prime } $$ Q 3 $$ {Q}_3 $$ Maximum σ 2 $$ {\sigma}^2 $$ SK KU
0.002 0.014 0.027 0.036 0.046 0.178 0.001 2.021 8.176
Details are in the caption following the image
FIGURE 7
Open in figure viewerPowerPoint
Descriptive visualizations of COVID-19 data.

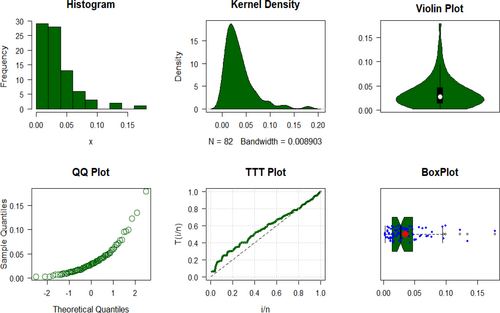
Figure 7 examines the total test time (TTT) plot and its relationship to HRF, demonstrating an excellent fit with the UIEP distribution. The PDF analysis shows asymmetrical data distribution. Quantile–quantile (QQ) and box plots are used to test normality and observe outliers, with the mean in red and outliers shown by blue rings on the plots. The left-hand panel of Table 3 shows the results of KO, LS, WLS, and AD estimation, along with their associated SEs, calculated specifically for the UIEP distribution. The right-hand panel of Table 3 presents the results of the ML estimation, including standard errors (SEs), for all distributions. Figure 8 illustrates a comparison of the SEs of different estimates for the UIEP distribution.

TABLE 3. The estimates associated with the SEs derived from different distributions for COVID-19 data.
Distribution UIEP UEP UEL UEHL UG ETL ULL UPL
Methods ML KO LS WLS AD ML
δ ^ 1 $$ {\hat{\delta}}_1 $$ 1.604 0.203 1.484 1.611 1.622 1.186 0.033 29.313 55.316 1.256 7.195 4.120
δ ^ 2 $$ {\hat{\delta}}_2 $$ 36.161 1.139 35.381 37.499 37.613 0.087 41.763 1.251 1.238 24.979 3.597 1.868
δ ^ 3 $$ {\hat{\delta}}_3 $$ — — — — — 2.462 71.919 — — — — 356.314
SE ( δ ^ 1 $$ {\hat{\delta}}_1 $$ ) 0.257 0.026 1.222 0.054 0.481 0.096 0.016 9.285 18.084 0.111 0.662 0.383
SE ( δ ^ 2 $$ {\hat{\delta}}_2 $$ ) 4.725 0.111 23.935 1.023 8.819 0.343 18.526 0.103 0.105 6.944 0.096 0.665
SE ( δ ^ 3 $$ {\hat{\delta}}_3 $$ ) — — — — — 11.530 26.624 — — — — 115.113
Details are in the caption following the image
FIGURE 8
Open in figure viewerPowerPoint
Comparison of SEs for the UIEP distribution across COVID-19 data.

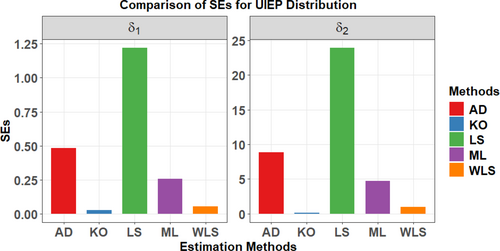
Table 4 and Figure 8 collectively indicate that the KO method offers the most reliable estimates, validating the simulation outcomes for the UIEP distribution. The goodness of fit measures as ƛ 1 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_1 $$ , ƛ 2 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_2 $$ , ƛ 3 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_3 $$ , ƛ 4 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_4 $$ , ƛ 5 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_5 $$ , ƛ 6 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_6 $$ , ƛ 7 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_7 $$ , and ƛ 8 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_8 $$ for the COVID-19 data are also shown in Table 4.

TABLE 4. Measurements of goodness of fit for COVID-19 data.
Name UIEP UEP UEL UEHL KW ETL ULL UPL
ƛ 1 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_1 $$ −387.304 −369.451 −381.515 −385.054 −384.669 −384.877 −387.076 −370.001
ƛ 2 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_2 $$ −382.491 −362.231 −374.295 −380.241 −379.856 −380.063 −382.063 −362.781
ƛ 3 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_3 $$ −387.152 −369.143 −381.208 −384.902 −384.517 −384.725 −387.025 −369.693
ƛ 4 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_4 $$ −385.372 −366.552 −378.617 −383.122 −382.737 −382.944 −385.144 −367.102
ƛ 5 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_5 $$ 0.032 0.071 0.074 0.055 0.060 0.058 0.079 0.012
ƛ 6 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_6 $$ 0.244 0.494 0.509 0.393 0.421 0.411 0.749 0.109
ƛ 7 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_7 $$ 0.053 0.064 0.063 0.058 0.060 0.059 0.054 0.963
ƛ 8 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_8 $$ 0.974 0.886 0.901 0.949 0.931 0.938 0.969 0.054

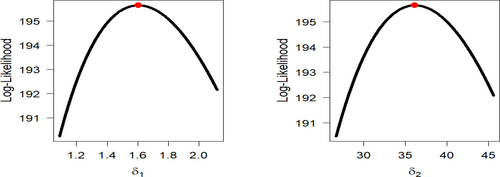
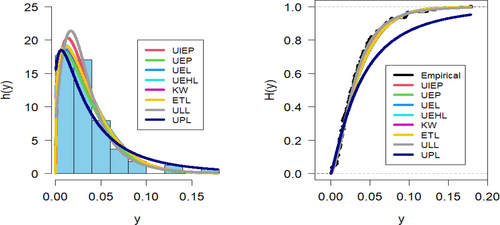
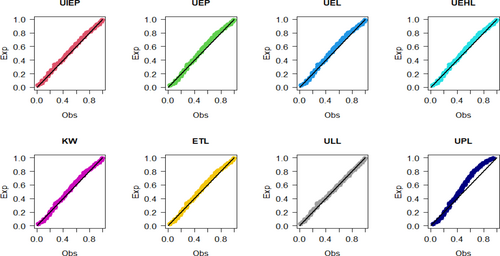
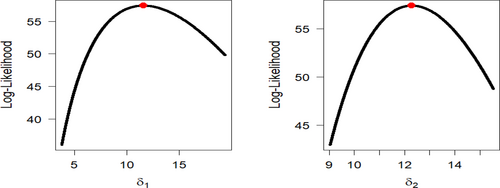
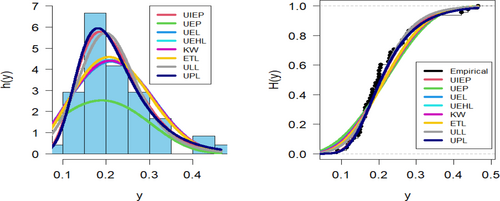
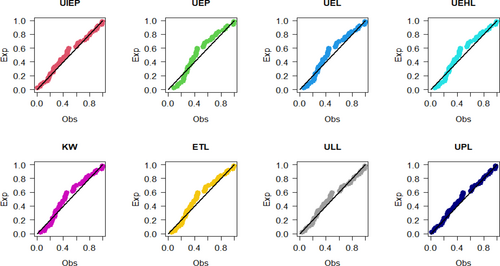
Figures 9-11 assess the UIEP distribution's fit to the COVID-19 data. Figure 9 shows the log-likelihood curve parameters for the UIEP distribution, which proves the estimators' maximizing. Figure 10 compares the estimated and empirical CDFs and the estimated PDFs with a histogram. Figure 11 displays a P–P plot of the UIEP distribution demonstrating the model's sufficiency.

Details are in the caption following the image
FIGURE 9
Open in figure viewerPowerPoint
Profile-Log-likelihood for parameters δ 1 $$ {\delta}_1 $$ and δ 2 $$ {\delta}_2 $$ of COVID-19 data.
Details are in the caption following the image
FIGURE 10
Open in figure viewerPowerPoint
PDF and CDF estimates for the COVID-19 data.
Details are in the caption following the image
FIGURE 11
Open in figure viewerPowerPoint
PP plots for different distributions of COVID-19 data.
  1. Petroleum Reservoir Data

There are 48 rock samples in the dataset, all taken from a petroleum reservoir discussed by Cordeiro and Brito [61]. The values for these samples are 0.0903296, 0.2036540, 0.2043140, 0.2808870, 0.1976530, 0.3286410, 0.1486220, 0.1623940, 0.2627270, 0.1794550, 0.3266350, 0.2300810, 0.1833120, 0.1509440, 0.2000710, 0.1918020, 0.1541920, 0.4641250, 0.1170630, 0.1481410, 0.1448100, 0.1330830, 0.2760160, 0.4204770, 0.1224170, 0.2285950, 0.1138520, 0.2252140, 0.1769690, 0.2007440, 0.1670450, 0.2316230, 0.2910290, 0.3412730, 0.4387120, 0.2626510, 0.1896510, 0.1725670, 0.2400770, 0.3116460, 0.1635860, 0.1824530, 0.1641270, 0.1534810, 0.1618650, 0.2760160, 0.2538320, and 0.2004470.

The petroleum reservoir data's key descriptive statistics are tabulated in Table 5 and visualized in Figure 12.

TABLE 5. Summary statistics for petroleum reservoir data.
Minimum Q 1 $$ {Q}_1 $$ Q 2 $$ {Q}_2 $$ μ 1 ′ $$ {\mu}_1^{\prime } $$ Q 3 $$ {Q}_3 $$ Maximum σ 2 $$ {\sigma}^2 $$ SK KU
0.090 0.162 0.199 0.218 0.263 0.464 0.007 1.169 4.110
Details are in the caption following the image
FIGURE 12
Open in figure viewerPowerPoint
Descriptive visualizations of petroleum reservoir data.

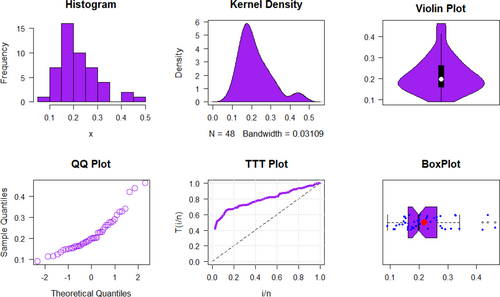
Following a summary of the petroleum reservoir data, Figure 12 examines the TTT plot and its relationship to HRF, demonstrating an excellent fit with the UIEP distribution. The PDF analysis shows asymmetrical data distribution. QQ and box plots are used to test normality and observe outliers, with the mean in red and outliers shown by blue rings on the plots. Table 6 displays the results of ML, KO, LS, WLS, and AD estimation, along with their associated SEs Figure 13 shows a comparison of the SEs of estimation methods for the UIEP distribution.

TABLE 6. The estimates associated with the SEs derived from the distribution of petroleum reservoir data.
Distribution UIEP UEP UEL UEHL UG ETL ULL UPL
Methods ML KO LS WLS AD ML
δ ^ 1 $$ {\hat{\delta}}_1 $$ 11.564 0.854 10.847 10.908 10.905 1.968 0.045 23.694 44.440 3.136 7.404 5.644
δ ^ 2 $$ {\hat{\delta}}_2 $$ 12.285 2.291 12.373 12.267 12.235 0.298 63.783 2.746 2.715 13.641 1.582 4.164
δ ^ 3 $$ {\hat{\delta}}_3 $$ — — — — — 0.792 49.538 — — — — 74.019
SE ( δ ^ 1 $$ {\hat{\delta}}_1 $$ ) 3.891 0.065 21.015 1.058 7.149 0.199 0.035 8.954 17.444 0.364 0.898 0.870
SE ( δ ^ 2 $$ {\hat{\delta}}_2 $$ ) 1.625 0.115 8.936 0.461 2.990 2.942 45.985 0.285 0.293 4.199 0.053 3.389
SE ( δ ^ 3 $$ {\hat{\delta}}_3 $$ ) — — — — — 15.365 20.603 — — — — 52.583
Details are in the caption following the image
FIGURE 13
Open in figure viewerPowerPoint
Comparison of SEs for the UIEP distribution across petroleum reservoir data.

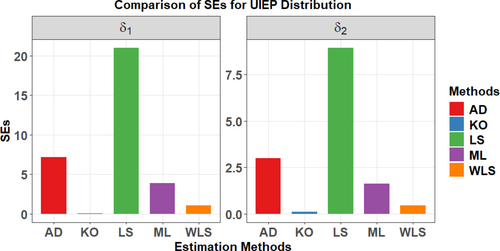
Analysis of Table 6 and Figure 13 demonstrates that the KO method provides the most accurate estimation, corroborating the simulation results for the UIEP distribution. The goodness of fit measures as ƛ 1 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_1 $$ , ƛ 2 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_2 $$ , ƛ 3 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_3 $$ , ƛ 4 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_4 $$ , ƛ 5 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_5 $$ , ƛ 6 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_6 $$ , ƛ 7 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_7 $$ , and ƛ 8 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_8 $$ for the petroleum reservoir data are also shown in Table 7.

TABLE 7. Measurements of goodness of fit for petroleum reservoir data.
Name UIEP UEP UEL UEHL UG ETL ULL UPL
ƛ 1 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_1 $$ −110.825 −45.004 −98.266 −101.451 −100.983 −102.712 −106.497 −110.169
ƛ 2 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_2 $$ −107.083 −39.391 −92.653 −97.709 −97.241 −98.969 −102.755 −104.555
ƛ 3 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_3 $$ −110.559 −44.459 −97.721 −101.184 −100.716 −102.445 −106.230 −109.623
ƛ 4 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_4 $$ −109.411 −42.883 −96.145 −100.037 −99.569 −101.298 −105.083 −108.047
ƛ 5 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_5 $$ 0.072 0.281 0.218 0.201 0.208 0.187 0.127 0.096
ƛ 6 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_6 $$ 0.428 1.737 1.337 1.230 1.279 1.142 0.748 0.731
ƛ 7 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_7 $$ 0.117 0.159 0.154 0.150 0.153 0.153 0.212 0.389
ƛ 8 $$ {\mathtt{{\mathchar'26\mkern-9mu \lambda}}}_8 $$ 0.524 0.177 0.206 0.229 0.210 0.215 0.487 0.370

Figures 14-16 assess the UIEP distribution's fit to the COVID-19 data. Figure 14 shows the log-likelihood curve parameters for the UIEP distribution, which proves the estimators' maximizing. Figure 15 compares the estimated and empirical CDFs and the estimated PDFs with a histogram. Figure 16 displays a P–P plot of the UIEP distribution demonstrating the model's sufficiency.

Details are in the caption following the image
FIGURE 14
Open in figure viewerPowerPoint
Profile-Log-likelihood for parameters δ 1 $$ {\delta}_1 $$ and δ 2 $$ {\delta}_2 $$ of for petroleum reservoir data.
Details are in the caption following the image
FIGURE 15
Open in figure viewerPowerPoint
PDF and CDF estimates for petroleum reservoir data.
Details are in the caption following the image
FIGURE 16
Open in figure viewerPowerPoint
PP plots for different distributions of petroleum reservoir data.

8 Concluding Remarks

Unit distributions serve a key role in statistical modeling and are essential for assessing variables that are restricted to the interval [0,1]. In this study, we present the UIEP distribution, a new two-parameter model. Numerous forms are displayed by the UIEP, such as rising, J-shaped, or U-shaped hazard rate functions, as well as unimodal, reversed J-shaped, left-skewed, and right-skewed density functions. Its applicability for modeling unit data is improved by this flexibility. Quantiles, moments, PWM, SO, important uncertainty measures, Lorenz and Bonferroni curves, and the S-SR parameter are among the important statistical features that we derive analytically. To estimate distribution parameters and evaluate entropy measures, the statistical analysis uses a number of estimation approaches, such as ML, WLS, AD, LS, and KO. According to simulation data, the KO technique is the most successful estimation strategy among those studied for the parameters and entropy measures of the UIEP distribution. For lower entropy orders, the AR entropy typically performs better under ML estimation, whereas Ré entropy works better for higher entropy orders. This observation highlights a clear relationship between the entropy order and the optimal estimator. In order to verify the suggested distribution, we apply it to two real-world datasets: geological data from petroleum rock samples and health data associated with COVID-19. The model fit of these applications is better than that of other distributions. This study, although useful, has one drawback that should be noted. Primarily, this study utilizes four traditional estimation techniques along with large sample sizes. These methods are sensitive to small sample sizes, which can produce fewer stable estimates. The reliability of our conclusions may be impacted when working with smaller datasets, as this could result in less stable estimates or potentially prevent the model from converging. Future research could significantly benefit from exploring Bayesian estimation techniques. This approach is advantageous, especially when dealing with smaller samples, because it allows the use of informative priors and hierarchical modeling. Furthermore, implementing the UIEP distribution on real-world datasets with more complex structures would be essential in further verifying its practical usefulness.

Author Contributions

Amal S. Hassan: conceptualization, writing – original draft, writing – review and editing, methodology. Gaber Sallam Salem Abdalla: writing – original draft, writing – review and editing, conceptualization. Abdoulie Faal: writing – original draft, writing – review and editing, methodology. Omar A. Saudi: conceptualization, methodology, software, formal analysis, writing – original draft.

Acknowledgments

This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-DDRSP2501).

    Conflicts of Interest

    The authors declare no conflicts of interest.

    Appendix A: See Table A1.

    TABLE A1. Numerical values of the different entropy measures and their ABs and MSEs for set 1.
    n True value δ 1 $$ {\delta}_1 $$ δ 2 $$ {\delta}_2 $$ Ré (−0.40489) TS (−0.39680) H–C (−0.55285) AR (−0.39592)
    Estimate AB MSE AB MSE AB MSE AB MSE AB MSE AB MSE
    25 MLE 0.05340 0.02488 0.24693 0.40941 0.15783 0.04077 0.15059 0.03670 0.20981 0.07124 0.14981 0.03627
    KO 0.02500 0.02209 0.06776 0.19170 0.17053 0.04943 0.16258 0.04430 0.22652 0.08600 0.16172 0.04377
    LSE 0.01297 0.02684 0.06432 0.44842 0.17465 0.05201 0.16618 0.04642 0.23153 0.09011 0.16526 0.04584
    WLSE 0.01993 0.02510 0.09651 0.41082 0.16781 0.04780 0.15980 0.04274 0.22264 0.08297 0.15893 0.04222
    ADE 0.02725 0.02250 0.13136 0.37353 0.16513 0.04574 0.15736 0.04099 0.21924 0.07958 0.15652 0.04050
    50 MLE 0.02336 0.00971 0.11835 0.15239 0.10927 0.01931 0.10456 0.01758 0.14567 0.03412 0.10405 0.01739
    KO 0.00860 0.00936 0.03317 0.07818 0.12242 0.02458 0.11708 0.02231 0.16312 0.04332 0.11650 0.02208
    LSE 0.00551 0.01274 0.04028 0.19524 0.12285 0.02455 0.11739 0.02225 0.16355 0.04319 0.11680 0.02201
    WLSE 0.00983 0.01111 0.05896 0.16686 0.11667 0.02214 0.11154 0.02010 0.15541 0.03901 0.11099 0.01988
    ADE 0.01123 0.01005 0.06724 0.15494 0.11615 0.02180 0.11107 0.01980 0.15475 0.03844 0.11052 0.01959
    75 MLE 0.01429 0.00547 0.07256 0.08746 0.08907 0.01263 0.08533 0.01154 0.11889 0.02241 0.08493 0.01143
    KO 0.00672 0.00559 0.03038 0.05539 0.09982 0.01604 0.09559 0.01463 0.13319 0.02841 0.09514 0.01449
    LSE 0.00168 0.00698 0.02289 0.11871 0.10011 0.01626 0.09580 0.01481 0.13347 0.02875 0.09533 0.01466
    WLSE 0.00554 0.00602 0.03888 0.10034 0.09509 0.01463 0.09103 0.01334 0.12683 0.02590 0.09059 0.01321
    ADE 0.00579 0.00567 0.03997 0.09212 0.09449 0.01439 0.09047 0.01313 0.12605 0.02549 0.09003 0.01300
    100 MLE 0.01272 0.00425 0.05338 0.05952 0.07624 0.00906 0.07312 0.00831 0.10188 0.01614 0.07278 0.00823
    KO 0.00628 0.00415 0.02247 0.03687 0.08717 0.01182 0.08357 0.01082 0.11643 0.02101 0.08318 0.01072
    LSE 0.00249 0.00536 0.01372 0.08045 0.08703 0.01164 0.08339 0.01065 0.11618 0.02068 0.08299 0.01055
    WLSE 0.00588 0.00463 0.02734 0.06788 0.08217 0.01044 0.07877 0.00956 0.10974 0.01857 0.07840 0.00947
    ADE 0.00621 0.00448 0.02919 0.06465 0.08206 0.01039 0.07866 0.00953 0.10960 0.01849 0.07830 0.00943
    200 MLE 0.00549 0.00189 0.02550 0.02827 0.05363 0.00455 0.05146 0.00419 0.07170 0.00813 0.05122 0.00415
    KO 0.00347 0.00201 0.01300 0.01871 0.06076 0.00584 0.05830 0.00537 0.08122 0.01042 0.05803 0.00532
    LSE 0.00114 0.00256 0.00718 0.04065 0.06030 0.00575 0.05784 0.00528 0.08058 0.01024 0.05757 0.00523
    WLSE 0.00295 0.00213 0.01492 0.03314 0.05737 0.00518 0.05504 0.00476 0.07669 0.00923 0.05479 0.00471
    ADE 0.00261 0.00209 0.01358 0.03190 0.05724 0.00516 0.05492 0.00474 0.07651 0.00920 0.05466 0.00469

    See Table A2

    TABLE A2. Numerical values of the different entropy measures and their ABs and MSEs for set 2.
    n True value δ 1 $$ {\delta}_1 $$ δ 2 $$ {\delta}_2 $$ Ré (−0.61617) TS (−0.59757) H–C (−0.83257) AR (−0.59555)
    Estimate AB MSE AB MSE AB MSE AB MSE AB MSE AB MSE
    25 ML 0.36686 0.96741 0.05869 0.02876 0.16576 0.04412 0.15509 0.03828 0.21608 0.07431 0.15395 0.03768
    KO 0.02098 0.08897 0.01186 0.01179 0.16889 0.04534 0.15825 0.03947 0.22049 0.07661 0.15712 0.03887
    LS 0.13045 0.98354 0.00439 0.02990 0.17638 0.04983 0.16494 0.04315 0.22981 0.08375 0.16372 0.04246
    WLS 0.16587 0.91525 0.01468 0.02728 0.17148 0.04742 0.16041 0.04110 0.22350 0.07979 0.15923 0.04046
    AD 0.20623 0.79717 0.02624 0.02610 0.16935 0.04582 0.15846 0.03976 0.22078 0.07718 0.15730 0.03914
    50 ML 0.16187 0.30968 0.02955 0.01183 0.11537 0.02137 0.10824 0.01872 0.15081 0.03634 0.10748 0.01845
    KO 0.00556 0.05984 0.00748 0.00644 0.12120 0.02328 0.11378 0.02042 0.15853 0.03963 0.11299 0.02012
    LS 0.06454 0.41451 0.00531 0.01437 0.12417 0.02488 0.11644 0.02174 0.16224 0.04221 0.11562 0.02142
    WLS 0.08460 0.34898 0.01157 0.01253 0.11974 0.02320 0.11232 0.02029 0.15649 0.03940 0.11153 0.02000
    AD 0.09226 0.30718 0.01443 0.01182 0.11909 0.02271 0.11172 0.01989 0.15566 0.03860 0.11093 0.01960
    75 ML 0.09919 0.16256 0.01874 0.00707 0.09399 0.01397 0.08825 0.01227 0.12296 0.02383 0.08764 0.01210
    KO 0.00910 0.03891 0.00657 0.00417 0.09735 0.01496 0.09147 0.01318 0.12744 0.02559 0.09084 0.01300
    LS 0.02996 0.21567 0.00279 0.00886 0.09984 0.01579 0.09375 0.01388 0.13062 0.02695 0.09310 0.01368
    WLS 0.04932 0.17876 0.00802 0.00765 0.09659 0.01481 0.09071 0.01303 0.12638 0.02529 0.09008 0.01284
    AD 0.05078 0.16306 0.00869 0.00721 0.09636 0.01471 0.09048 0.01293 0.12607 0.02511 0.08985 0.01275
    100 ML 0.08186 0.11689 0.01402 0.00489 0.08161 0.01055 0.07662 0.00927 0.10676 0.01799 0.07609 0.00914
    KO 0.00421 0.02462 0.00322 0.00281 0.08661 0.01164 0.08137 0.01025 0.11337 0.01989 0.08081 0.01010
    LS 0.02614 0.15348 0.00144 0.00623 0.08829 0.01207 0.08291 0.01061 0.11552 0.02059 0.08233 0.01046
    WLS 0.04342 0.12828 0.00583 0.00533 0.08497 0.01129 0.07979 0.00992 0.11116 0.01926 0.07923 0.00978
    AD 0.04545 0.12290 0.00641 0.00516 0.08485 0.01123 0.07967 0.00987 0.11101 0.01917 0.07912 0.00973
    200 ML 0.03551 0.05016 0.00641 0.00237 0.05702 0.00515 0.05358 0.00454 0.07466 0.00882 0.05321 0.00448
    KO 0.00884 0.01463 0.00298 0.00158 0.06014 0.00577 0.05652 0.00509 0.07875 0.00988 0.05613 0.00502
    LS 0.01239 0.07289 0.00072 0.00323 0.06180 0.00607 0.05807 0.00535 0.08090 0.01038 0.05767 0.00527
    WLS 0.02141 0.05840 0.00316 0.00269 0.05944 0.00560 0.05585 0.00494 0.07782 0.00958 0.05547 0.00487
    AD 0.01959 0.05626 0.00281 0.00260 0.05931 0.00558 0.05573 0.00492 0.07765 0.00955 0.05535 0.00485

    See Table A3

    TABLE A3. Numerical values of the different entropy measures and their ABs and MSEs for set 3.
    n True value δ 1 $$ {\delta}_1 $$ δ 2 $$ {\delta}_2 $$ Ré (−0.38956) TS (−0.43008) H–C (−0.73420) AR (−0.41598)
    Estimate AB MSE AB MSE AB MSE AB MSE AB MSE AB MSE
    25 ML 0.10072 0.08191 0.27327 0.55313 0.15975 0.04703 0.20527 0.08657 0.35041 0.25227 0.18862 0.07026
    KO 0.04484 0.15533 0.05854 0.31544 0.17961 0.06759 0.23620 0.14103 0.40321 0.41099 0.21518 0.10913
    LS 0.02762 0.08723 0.04758 0.58054 0.20319 0.09479 0.27762 0.29193 0.47393 0.85074 0.24898 0.18696
    WLS 0.03971 0.08129 0.08888 0.53128 0.18559 0.07289 0.24644 0.16474 0.42069 0.48009 0.22368 0.12284
    AD 0.05335 0.07217 0.13611 0.50253 0.17570 0.06190 0.22998 0.12790 0.39259 0.37274 0.20988 0.09899
    50 ML 0.04444 0.03029 0.13392 0.21739 0.10739 0.01961 0.13417 0.03205 0.22903 0.09341 0.12453 0.02717
    KO 0.01335 0.02805 0.02924 0.11630 0.12149 0.02668 0.15312 0.04563 0.26139 0.13297 0.14167 0.03805
    LS 0.01277 0.04009 0.03541 0.26797 0.12805 0.03020 0.16262 0.05262 0.27760 0.15335 0.15007 0.04359
    WLS 0.02011 0.03457 0.06007 0.23212 0.11842 0.02488 0.14921 0.04199 0.25472 0.12236 0.13808 0.03519
    AD 0.02289 0.03100 0.07174 0.21825 0.11678 0.02378 0.14679 0.03978 0.25059 0.11592 0.13596 0.03344
    75 ML 0.02720 0.01667 0.08317 0.12749 0.08659 0.01260 0.10718 0.02002 0.18297 0.05834 0.09980 0.01714
    KO 0.00857 0.01645 0.02433 0.08268 0.09669 0.01633 0.12038 0.02647 0.20550 0.07713 0.11186 0.02250
    LS 0.00480 0.02152 0.01964 0.16432 0.10160 0.01860 0.12725 0.03132 0.21722 0.09129 0.11800 0.02624
    WLS 0.01150 0.01832 0.04042 0.14088 0.09438 0.01554 0.11753 0.02533 0.20063 0.07383 0.10920 0.02148
    AD 0.01215 0.01710 0.04288 0.13144 0.09335 0.01506 0.11611 0.02439 0.19821 0.07107 0.10793 0.02073
    100 ML 0.02360 0.01268 0.06163 0.08754 0.07291 0.00857 0.08964 0.01326 0.15302 0.03864 0.08366 0.01146
    KO 0.00749 0.01133 0.01555 0.05128 0.08339 0.01125 0.10288 0.01763 0.17562 0.05138 0.09590 0.01516
    LS 0.00547 0.01623 0.01125 0.11372 0.08569 0.01201 0.10611 0.01902 0.18114 0.05543 0.09879 0.01630
    WLS 0.01138 0.01386 0.02876 0.09699 0.07964 0.01023 0.09825 0.01599 0.16773 0.04661 0.09159 0.01377
    AD 0.01211 0.01337 0.03145 0.09329 0.07942 0.01014 0.09795 0.01583 0.16720 0.04613 0.09132 0.01363
    200 ML 0.01021 0.00558 0.02898 0.04206 0.05123 0.00424 0.06265 0.00643 0.10696 0.01873 0.05858 0.00559
    KO 0.00458 0.00586 0.00988 0.02975 0.05709 0.00541 0.06996 0.00828 0.11943 0.02412 0.06537 0.00718
    LS 0.00254 0.00775 0.00586 0.05821 0.05805 0.00549 0.07122 0.00841 0.12157 0.02452 0.06652 0.00730
    WLS 0.00566 0.00636 0.01571 0.04817 0.05489 0.00484 0.06722 0.00737 0.11475 0.02147 0.06282 0.00640
    AD 0.00513 0.00620 0.01432 0.04653 0.05476 0.00483 0.06705 0.00734 0.11447 0.02140 0.06267 0.00638

    See Table A4

    TABLE A4. Numerical values of the different entropy measures and their ABs and MSEs for set4.
    n True value δ 1 $$ {\delta}_1 $$ δ 2 $$ {\delta}_2 $$ Ré (−0.54937) TS (−0.63223) H–C (−1.07929) AR (−0.60289)
    Estimate AB MSE AB MSE AB MSE AB MSE AB MSE AB MSE
    25 ML 0.42082 1.26243 0.07633 0.04901 0.17225 0.05401 0.23837 0.11824 0.40692 0.34456 0.21362 0.09022
    KO 0.03616 0.16497 0.01603 0.02011 0.18521 0.06616 0.25917 0.19540 0.44244 0.56944 0.23095 0.12881
    LS 0.15341 1.27553 0.00520 0.05103 0.22446 0.12020 0.34359 0.93024 0.58654 0.71092 0.29423 0.37926
    WLS 0.19306 1.18734 0.01871 0.04652 0.20430 0.08595 0.29358 0.23877 0.50117 0.69584 0.25935 0.16526
    AD 0.23793 1.03226 0.03382 0.04448 0.19141 0.06930 0.26937 0.16560 0.45985 0.48258 0.23992 0.12209
    50 ML 0.18549 0.39709 0.03852 0.02021 0.11902 0.02370 0.15993 0.04506 0.27302 0.13131 0.14486 0.03628
    KO 0.01904 0.07098 0.01196 0.00960 0.12845 0.02741 0.17248 0.05241 0.29445 0.15272 0.15625 0.04210
    LS 0.07606 0.53152 0.00670 0.02455 0.13600 0.03243 0.18517 0.06463 0.31610 0.18833 0.16695 0.05119
    WLS 0.09825 0.44642 0.01492 0.02140 0.12802 0.02817 0.17322 0.05488 0.29570 0.15993 0.15652 0.04381
    AD 0.10661 0.39221 0.01866 0.02019 0.12549 0.02685 0.16942 0.05186 0.28921 0.15113 0.15320 0.04153
    75 ML 0.11350 0.20727 0.02445 0.01208 0.09577 0.01520 0.12779 0.02793 0.21815 0.08140 0.11604 0.02277
    KO 0.01381 0.04655 0.00882 0.00660 0.10290 0.01710 0.13695 0.03122 0.23379 0.09098 0.12446 0.02550
    LS 0.03578 0.27607 0.00349 0.01515 0.10624 0.01892 0.14257 0.03556 0.24339 0.10363 0.12921 0.02876
    WLS 0.05735 0.22807 0.01036 0.01308 0.10067 0.01690 0.13464 0.03130 0.22985 0.09121 0.12216 0.02545
    AD 0.05883 0.20742 0.01124 0.01232 0.10019 0.01668 0.13394 0.03086 0.22865 0.08993 0.12155 0.02510
    100 ML 0.09333 0.14814 0.01832 0.00836 0.08295 0.01104 0.11037 0.02007 0.18842 0.05848 0.10033 0.01642
    KO 0.01722 0.03820 0.00699 0.00507 0.09149 0.01325 0.12162 0.02402 0.20761 0.06999 0.11058 0.01967
    LS 0.03068 0.19483 0.00178 0.01066 0.09188 0.01348 0.12265 0.02469 0.20937 0.07195 0.11136 0.02016
    WLS 0.04998 0.16255 0.00755 0.00912 0.08726 0.01221 0.11627 0.02224 0.19848 0.06481 0.10564 0.01819
    AD 0.05219 0.15563 0.00830 0.00883 0.08682 0.01208 0.11564 0.02198 0.19741 0.06407 0.10508 0.01798
    200 ML 0.04052 0.06336 0.00836 0.00406 0.05820 0.00545 0.07701 0.00967 0.13146 0.02817 0.07014 0.00798
    KO 0.01201 0.02194 0.00399 0.00267 0.06348 0.00647 0.08399 0.01151 0.14338 0.03353 0.07650 0.00949
    LS 0.01457 0.09243 0.00088 0.00553 0.06417 0.00660 0.08510 0.01181 0.14527 0.03442 0.07745 0.00972
    WLS 0.02462 0.07390 0.00408 0.00461 0.06133 0.00600 0.08122 0.01067 0.13865 0.03109 0.07395 0.00880
    AD 0.02254 0.07112 0.00363 0.00445 0.06115 0.00597 0.08098 0.01063 0.13824 0.03098 0.07373 0.00877

    Appendix B:

    See Appendix B

    Coding in R of Lorenz and Bonferroni curves

    library(ineq)

    # Define parameter sets with distinct colors

    params < - list

    ( $$ \kern1em $$ list(delta1 = 0.5, delta2 = 2.4, color = “blue”),

    $$ \kern1em $$ list(delta1 = 1.4, delta2 = 0.8, color = “red”),

    $$ \kern1em $$ list(delta1 = 0.3, delta2 = 0.3, color = “green”),

    $$ \kern1em $$ list(delta1 = 2.5, delta2 = 2.5, color = “gold”),

    $$ \kern1em $$ list(delta1 = 1.5, delta2 = 2.3, color = “purple”)).

    # Basic Probability Distribution Functions (PDF, CDF, Quantile)

    fx < - function(x, delta1, delta2) {

    $$ \kern1em $$ delta1 * delta2 * (1 − x)^(delta2 − 1) * (1 − (1 − x)^delta2)^(delta1 − 1)

    }

    Fx < - function(x, delta1, delta2) {

    $$ \kern1em $$ (1 − (1 − x)^delta2)^delta1

    }

    Qx < - function(d, delta1, delta2) {

    $$ \kern1em $$ 1 − (1 − d^(1/delta1))^(1/delta2)

    }

    # Functions for Inequality Curves

    lorenz_curve < - function(samples) {

    $$ \kern1em $$ sorted_samples < - sort(samples)

    $$ \kern1em $$ cum_samples < - cumsum(sorted_samples)

    $$ \kern1em $$ total < - sum(sorted_samples)

    $$ \kern1em $$ L < - cum_samples/total

    $$ \kern1em $$ p < - seq(1/length(samples), 1, length.out = length(samples))

    $$ \kern1em $$ list(p = p, L = L)

    }

    bonferroni_curve < - function(lorenz_curve) {

    B < - lorenz_curve$L/lorenz_curve$p

    $$ \kern1em $$ list(p = lorenz_curve$p, B = B)}

    # Sample Generation

    generate_samples < - function(param) {

    $$ \kern1em $$ n < - 10,000

    $$ \kern1em $$ u < - runif(n)

    $$ \kern1em $$ Qx(u, param$delta1, param$delta2)

    }

    # Plotting Setup

    par(mfrow = c(1, 2), cex.main = 1.2, cex.lab = 1.5, cex.axis = 1.4,

    $$ \kern1em $$ mar = c(5, 5, 4, 2), mgp = c(3.5, 1, 0))

    # Plotting Lorenz Curves

    plot(NULL, type = “n”, xlim = c(0, 1), ylim = c(0, 1),

    $$ \kern2.00em $$ xlab = “t”, ylab = bquote({{L}}[F](t)), main = “Lorenz Curve”, lwd = 2)

    for (param in params) {

    $$ \kern1em $$ samples < - generate_samples(param)

    $$ \kern1em $$ lc < - lorenz_curve(samples)

    $$ \kern1em $$ lines(lc$p, lc$L, col = param$color, lwd = 3.5)}

    segments(0, 0, 1, 1, col = “black”, lty = 1, lwd = 3.5)

    text(0.3, 0.32, expression(L(t) == t), pos = 2, cex = 1.2)

    legend(“topleft”, legend = sapply(params, function(p) bquote(delta [1] == (p$delta1) ˜ delta [2] == (p$delta2))),

    $$ \kern1em $$ col = sapply(params, function(p) p$color), lwd = 4, bty = “n”, cex = 1.2)

    # Plotting Bonferroni Curves

    plot(NULL, type = “n”, xlim = c(0, 1), ylim = c(0, 1),

    $$ \kern2.00em $$ xlab = “t”, ylab = bquote({{B}}[F](t)), main = “Bonferroni Curve”, lwd = 2).

    for (param in params) {

    $$ \kern1em $$ samples < - generate_samples(param).

    $$ \kern1em $$ lc < - lorenz_curve(samples).

    $$ \kern1em $$ bc < - bonferroni_curve(lc).

    $$ \kern1em $$ lines(bc$p, bc$B, col = param$color, lwd = 3.5)}

    segments(0, 0, 1, 1, col = “black”, lty = 1, lwd = 3.5)

    text(0.3, 0.3, expression(B(t) == t), pos = 4, cex = 1.2)

    legend(“topleft”, legend = sapply(params, function(p) bquote(delta [1] == (p$delta1) ˜ delta [2] == (p$delta2))),

    $$ \kern2.00em $$ col = sapply(params, function(p) p$color), lwd = 4, bty = “n”, cex = 1.2)

    ########################## Goodness of Fit test ################################

    #################clean up everything###############

    remove(list = objects())

    options(warn = −1)

    #################Packages###############

    library(stats4)

    library(bbmle)

    library(MASS)

    library(AdequacyModel)

    library(ggplot2)

    ######################## PDF and CDF of Distribution

    ##############define pdf and cdf for Unit inverse Exponentiated Pareto (UIEP) Distribution################

    Pdf_UIEP < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ Pdf_UIEP < - delta1 * delta2 * (1 − x)^(delta2 − 1) * (1 − (1 − x)^delta2)^(delta1 − 1)}

    Cdf_UIEP < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ Cdf_UIEP < - (1 − (1 − x)^delta2)^delta1}

    #############define pdf and cdf for Unit Exponential Pareto (UEP) Distribution###############

    Pdf_UEP < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ delta3 < - parm[3]

    $$ \kern1em $$ Pdf_UEP < - (delta1 * delta3)/delta2*(x/(delta2 * (1 − x)))^(delta1 − 1)*exp(−delta3 * (x/(delta2 * (1 − x)))^delta1)}

    Cdf_UEP < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ delta3 < - parm[3]

    $$ \kern1em $$ Cdf_UEP < - 1 − exp(−delta3 * (x/(delta2 * (1 − x)))^delta1)}

    ########define pdf and cdf for unit exponentiated Lomax (UEL) Distribution

    Pdf_UEL < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ delta3 < - parm[3]

    $$ \kern1em $$ Pdf_UEL < - (delta1 * delta2 * delta3/x) * (1 − delta1 * log(x))^(−delta2 − 1) * (1 − (1 − delta1 * log(x))^(−delta2))^(delta3 − 1)}

    Cdf_UEL < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ delta3 < - parm[3]

    $$ \kern1em $$ Cdf_UEL < - (1-((1 − (1 − delta1 * log(x))^(−delta2))^(delta3)))}

    #############define pdf and cdf for Unit-Exponentiated Half-Logistic (UEHL) Distribution ##########

    Pdf_UEHL<- function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ Pdf_UEHL<- (2 * delta1 * delta2 * x^(delta2 − 1))/((1 + x^delta2)^2) * ((1 − x^delta2)/(1 + x^delta2))^(delta1 − 1)}

    Cdf_UEHL<- function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ Cdf_UEHL < - 1 − ((1 − x^delta2)/(1 + x^delta2))^(delta1)}

    ############define pdf and cdf for umaraswamy Distribution (KW) Distribution ################.

    Pdf_KW < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ Pdf_KW < - (delta1*delta2)*(x^(delta1 − 1))*((1 − (x^delta1))^(delta2 − 1))}

    Cdf_KW < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ Cdf_KW < - 1 − ((1 − (x^delta1))^delta2)}

    ############## define pdf and cdf of Exponentiated Topp-Leone (ETL) Distribution

    Pdf_ETL < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ Pdf_ETL < -2 * delta1 * delta2 * (1 − x) * (x * (2 − x))^(delta1 − 1) * (1 − x^delta1 * (2 − x)^delta1)^(delta2 − 1)}

    Cdf_ETL < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ Cdf_ETL < - 1 − (1 − x^delta1 * (2 − x)^delta1)^(delta2)}

    #############define pdf and cdf for unit log logistic (ULL) distribution ###############

    Pdf_ULL < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    Pdf_ULL < - (delta1/(x*delta2^delta1)) * (−log(x))^(delta1-1) * (1 + (−log(x)/delta2)^delta1)^(−2)}

    Cdf_ULL < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ Cdf_ULL < - (1 + (−log(x)/delta2)^delta1)^(−1)}

    #############define pdf and cdf for unit power Lomax (UPL) Distribution###############

    Pdf_UPL < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm [1]

    $$ \kern1em $$ delta2 < - parm [2]

    $$ \kern1em $$ delta3 < - parm [3]

    Pdf_UPL < - (delta1*delta2/(x*delta3))*((−log(x))^(delta1-1))*((1 + (1/delta3)*(−log(x))^delta1)^(−delta2 − 1))}

    Cdf_UPL < - function(parm,x){

    $$ \kern1em $$ delta1 < - parm[1]

    $$ \kern1em $$ delta2 < - parm[2]

    $$ \kern1em $$ delta3 < - parm[3]

    $$ \kern2.00em $$ Cdf_UPL < - (1 + (1/delta3)*(−log(x))^delta1)^(−delta2)}

    ######################## Loglikelihood function ################################

    LL_UIEP < - function(delta1,delta2){−sum(log(Pdf_UIEP(c(delta1,delta2),x)))}

    LL_UEP < - function(delta1,delta2,delta3){−sum(log(Pdf_UEP(c(delta1,delta2,delta3),x)))}

    LL_UEL < - function(delta1,delta2,delta3){−sum(log(Pdf_UEL(c(delta1,delta2,delta3),x)))}

    LL_UEHL < - function(delta1,delta2){−sum(log(Pdf_UEHL(c(delta1,delta2),x)))}

    LL_KW < - function(delta1,delta2){−sum(log(Pdf_KW(c(delta1,delta2),x)))}

    LL_ETL < - function(delta1,delta2){−sum(log(Pdf_ETL(c(delta1,delta2),x)))}

    LL_ULL < - function(delta1,delta2){−sum(log(Pdf_ULL(c(delta1,delta2),x)))}

    LL_UPL < - function(delta1,delta2,delta3){−sum(log(Pdf_UPL(c(delta1,delta2,delta3),x)))}

    ############################# Real data #############################

    ################################################################################

    x < - c(0.0903296, 0.2036540, 0.2043140, 0.2808870, 0.1976530, 0.3286410,

    $$ \kern2.00em $$ 0.1486220, 0.1623940, 0.2627270, 0.1794550, 0.3266350, 0.2300810,

    $$ \kern2.00em $$ 0.1833120, 0.1509440, 0.2000710, 0.1918020, 0.1541920, 0.4641250,

    $$ \kern2.00em $$ 0.1170630, 0.1481410, 0.1448100, 0.1330830, 0.2760160, 0.4204770,

    $$ \kern2.00em $$ 0.1224170, 0.2285950, 0.1138520, 0.2252140, 0.1769690, 0.2007440,

    $$ \kern2.00em $$ 0.1670450, 0.2316230, 0.2910290, 0.3412730, 0.4387120, 0.2626510,

    $$ \kern2.00em $$ 0.1896510, 0.1725670, 0.2400770, 0.3116460, 0.1635860, 0.1824530,

    $$ \kern2.00em $$ 0.1641270, 0.1534810, 0.1618650, 0.2760160, 0.2538320, 0.2004470)

    ######## Maximum likelihood estimation for many distributions ##############

    ################################################################################

    fit_UIEP < - mle2(minuslog = LL_UIEP,start = list(delta1 = 0.8,delta2 = 0.9),data = list(x), method = “BFGS”)

    fit_UEP < - mle2(minuslog = LL_UEP,start = list(delta1 = 0.8,delta2 = 0.5,delta3 = 0.1),data = list(x), method = “BFGS”)

    fit_UEL < - mle2(minuslog = LL_UEL,start = list(delta1 = 0.5,delta2 = 0.2,delta3 = 0.9),data = list(x), method = “BFGS”)

    fit_UEHL < - mle2(minuslog = LL_UEHL,start = list(delta1 = 0.08,delta2 = 0.01),data = list(x), method = “BFGS”)

    fit_KW < - mle2(minuslog = LL_KW,start = list(delta1 = 0.3,delta2 = 0.1),data = list(x), method = “BFGS”)

    fit_ETL < - mle2(minuslog = LL_ETL,start = list(delta1 = 0.2,delta2 = 0.4),data = list(x), method = “BFGS”)

    fit_ULL < - mle2(minuslog = LL_ULL,start = list(delta1 = 0.1,delta2 = 0.1),data = list(x), method = “BFGS”)

    fit_UPL < - mle2(minuslog = LL_UPL,start = list(delta1 = 0.8,delta2 = 0.9,delta3 = 0.1),data = list(x), method = “BFGS”)

    ############Goodness of fit test##############

    gof.test_UIEP < - goodness.fit(Pdf_UIEP,Cdf_UIEP,starts = c(coef(fit_UIEP)),data = x, method = “BFGS”, domain = c(0, 1))

    gof.test_UEP < - goodness. fit(Pdf_UEP,Cdf_UEP,starts = c(coef(fit_UEP)),data = x, method = “BFGS”, domain = c(0, 1))

    gof.test_UEL < - goodness. fit(Pdf_UEL,Cdf_UEL,starts = c(coef(fit_UEL)),data = x, method = “BFGS”, domain = c(0, 1))

    gof.test_UEHL < - goodness.fit(Pdf_UEHL,Cdf_UEHL,starts = c(coef(fit_UEHL)),data = x, method = “BFGS”, domain = c(0, 1))

    gof.test_KW < - goodness. fit(Pdf_KW,Cdf_KW,starts = c(coef(fit_KW)),data = x, method = “BFGS”, domain = c(0, 1))

    gof.test_ETL < - goodness. fit(Pdf_ETL,Cdf_ETL,starts = c(coef(fit_ETL)),data = x, method = “BFGS”, domain = c(0,1))

    gof.test_ULL < - goodness. fit(Pdf_ULL,Cdf_ULL,starts = c(coef(fit_ULL)),data = x, method = “BFGS”, domain = c(0, 1))

    gof.test_UPL < - goodness. fit(Pdf_UPL,Cdf_UPL,starts = c(coef(fit_UPL)),data = x, method = “BFGS”, domain = c(0, 1))

    ################# Results######################

    Name < - c(“UIEP”,”UEP”,”UEL”,”UEHL”,”KW”,”ETL”,”ULL”,”UPL”)

    ParmI < - c(gof.test_UIEP$mle[1],gof.test_UEP$mle[1]

    $$ \kern3.00em $$ ,gof.test_UEL$mle[1]

    $$ \kern3.00em $$ ,gof.test_UEHL$mle[1]

    $$ \kern3.00em $$ ,gof.test_KW$mle[1]

    $$ \kern3.00em $$ ,gof.test_ETL$mle[1]

    $$ \kern3.00em $$ ,gof.test_ULL$mle[1]

    $$ \kern3.00em $$ ,gof.test_UPL$mle[1])

    ParmII < - c(gof.test_UIEP$mle[2]

    $$ \kern3.00em $$ ,gof.test_UEP$mle[2]

    $$ \kern3.00em $$ ,gof.test_UEL$mle[2]

    $$ \kern3.00em $$ ,gof.test_UEHL$mle[2]

    $$ \kern3.00em $$ ,gof.test_KW$mle[2]

    $$ \kern3.00em $$ ,gof.test_ETL$mle[2]

    $$ \kern3.00em $$ ,gof.test_ULL$mle[2]

    $$ \kern3.00em $$ ,gof.test_UPL$mle[2])

    ParmIII < - c(gof.test_UIEP$mle[3]

    $$ \kern3.00em $$ ,gof.test_UEP$mle[3]

    $$ \kern3.00em $$ ,gof.test_UEL$mle[3]

    $$ \kern3.00em $$ ,gof.test_UEHL$mle[3]

    $$ \kern3.00em $$ ,gof.test_KW$mle[3]

    $$ \kern3.00em $$ ,gof.test_ETL$mle[3]

    $$ \kern3.00em $$ ,gof.test_ULL$mle[3]

    $$ \kern3.00em $$ ,gof.test_UPL$mle[3])

    St.Er_ParmI < - c(gof.test_UIEP$Erro[1]

    $$ \kern4.00em $$ ,gof.test_UEP$Erro[1]

    $$ \kern4.00em $$ ,gof.test_UEL$Erro[1]

    $$ \kern4.00em $$ ,gof.test_UEHL$Erro[1]

    $$ \kern4.00em $$ ,gof.test_KW$Erro[1]

    $$ \kern4.00em $$ ,gof.test_ETL$Erro[1]

    $$ \kern4.00em $$ ,gof.test_ULL$Erro[1]

    $$ \kern4.00em $$ ,gof.test_UPL$Erro[1])

    St.Er_ParmII < - c(gof.test_UIEP$Erro [2],gof.test_UEP$Erro[2]

    $$ \kern4.00em $$ ,gof.test_UEL$Erro[2]

    $$ \kern4.00em $$ ,gof.test_UEHL$Erro[2]

    $$ \kern4.00em $$ ,gof.test_KW$Erro[2]

    $$ \kern4.00em $$ ,gof.test_ETL$Erro[2]

    $$ \kern4.00em $$ ,gof.test_ULL$Erro[2]

    $$ \kern4.00em $$ ,gof.test_UPL$Erro[2])

    St.Er_ParmIII < - c(gof.test_UIEP$Erro[3],gof.test_UEP$Erro[3]

    $$ \kern4.00em $$ ,gof.test_UEL$Erro[3]

    $$ \kern4.00em $$ ,gof.test_UEHL$Erro[3]

    $$ \kern4.00em $$ ,gof.test_KW$Erro[3],gof.test_ETL$Erro[3]

    $$ \kern4.00em $$ ,gof.test_ULL$Erro[3]

    $$ \kern4.00em $$ ,gof.test_UPL$Erro[3])

    ML < - c(gof.test_UIEP$Value,gof.test_UEP$Value

    $$ \kern3.00em $$ ,gof.test_UEL$Value

    $$ \kern3.00em $$ ,gof.test_UEHL$Value

    $$ \kern3.00em $$ ,gof.test_KW$Value,gof.test_ETL$Value

    $$ \kern3.00em $$ ,gof.test_ULL$Value

    $$ \kern3.00em $$ ,gof.test_UPL$Value)

    AIC < - c(gof.test_UIEP$AIC,gof.test_UEP$AIC

    $$ \kern3.00em $$ ,gof.test_UEL$AIC

    $$ \kern3.00em $$ ,gof.test_UEHL$AIC

    $$ \kern3.00em $$ ,gof.test_KW$AIC,gof.test_ETL$AIC

    $$ \kern3.00em $$ ,gof.test_ULL$AIC

    $$ \kern3.00em $$ ,gof.test_UPL$AIC)

    BIC < - c(gof.test_UIEP$BIC,gof.test_UEP$BIC

    $$ \kern3.00em $$ ,gof.test_UEL$BIC

    $$ \kern3.00em $$ ,gof.test_UEHL$BIC

    $$ \kern3.00em $$ ,gof.test_KW$BIC,gof.test_ETL$BIC

    $$ \kern3.00em $$ ,gof.test_ULL$BIC

    $$ \kern3.00em $$ ,gof.test_UPL$BIC)

    CAIC < - c(gof.test_UIEP$CAIC,gof.test_UEP$CAIC

    $$ \kern3.00em $$ ,gof.test_UEL$CAIC

    $$ \kern3.00em $$ ,gof.test_UEHL$CAIC

    $$ \kern3.00em $$ ,gof.test_KW$CAIC,gof.test_ETL$CAIC

    $$ \kern3.00em $$ ,gof.test_ULL$CAIC

    $$ \kern3.00em $$ ,gof.test_UPL$CAIC)

    HQIC < - c(gof.test_UIEP$HQIC,gof.test_UEP$HQIC

    $$ \kern3.00em $$ ,gof.test_UEL$HQIC,gof.test_UEHL$HQIC

    $$ \kern3.00em $$ ,gof.test_KW$HQIC,gof.test_ETL$HQIC

    $$ \kern3.00em $$ ,gof.test_ULL$HQIC

    $$ \kern3.00em $$ ,gof.test_UPL$HQIC)

    KS < - c(gof.test_UIEP$KS$statistic,gof.test_UEP$KS$statistic

    $$ \kern3.00em $$ ,gof.test_UEL$KS$statistic,gof.test_UEHL$KS$statistic

    $$ \kern3.00em $$ ,gof.test_KW$KS$statistic,gof.test_ETL$KS$statistic

    $$ \kern3.00em $$ ,gof.test_ULL$KS$statistic

    $$ \kern3.00em $$ ,gof.test_UPL$KS$statistic)

    P_value < - c(gof.test_UIEP$KS$p. value,gof.test_UEP$KS$p. value

    $$ \kern3.00em $$ ,gof.test_UEL$KS$p. value,gof.test_UEHL$KS$p. value

    $$ \kern3.00em $$ ,gof.test_KW$KS$p. value,gof.test_ETL$KS$p. value

    $$ \kern3.00em $$ ,gof.test_ULL$KS$p. value

    $$ \kern3.00em $$ ,gof.test_UPL$KS$p. value)

    W < - c(gof.test_UIEP$W,gof.test_UEP$W

    $$ \kern2.00em $$ ,gof.test_UEL$W

    $$ \kern2.00em $$ ,gof.test_UEHL$W

    $$ \kern2.00em $$ ,gof.test_KW$W

    $$ \kern2.00em $$ ,gof.test_ETL$W

    $$ \kern2.00em $$ ,gof.test_ULL$W

    $$ \kern2.00em $$ ,gof.test_UPL$W)

    A < - c(gof.test_UIEP$A,gof.test_UEP$A

    $$ \kern2.00em $$ ,gof.test_UEL$A

    $$ \kern2.00em $$ ,gof.test_UEHL$A

    $$ \kern2.00em $$ ,gof.test_KW$A

    $$ \kern2.00em $$ ,gof.test_ETL$A

    $$ \kern2.00em $$ ,gof.test_ULL$A

    $$ \kern2.00em $$ ,gof.test_UPL$A)

    ResultsofMLE < - data.frame(Name,ParmI,ParmII,ParmIII,St.Er_ParmI,St.Er_ParmII,St.Er_ParmIII)

    Resultsofgof < - data. frame(Name,ML,AIC,BIC,CAIC,HQIC,W,A,KS,P_value)

    ##########Graph of Histogram##########

    data < - x

    # Set larger font sizes globally

    par(cex.axis = 1.2, cex.lab = 1.2, cex.main = 1.5, mfrow = c(1, 2), mar = c(5, 5, 4, 2),las = 1)

    y < - seq(0, max(x), length. out = 1000)

    hist(data, probability = TRUE,col = “skyblue”,ylim = c(0,7),xlim = c(min(x),max(x)), ylab = “h(y)”,xlab = “y”,main = “”)

    lines(y, Pdf_UIEP(par < - gof.test_UIEP$mle,y), col = c(2),lwd = 3.5)

    lines(y, Pdf_UEP(par < - gof.test_UEP$mle,y),col = c(3),lwd = 3.5)

    lines(y, Pdf_UEL(par < - gof.test_UEL$mle,y), col = c(4),lwd = 3.5)

    lines(y, Pdf_UEHL(par < - gof.test_UEHL$mle,y), col = c(5),lwd = 3.5)

    lines(y, Pdf_KW(par < - gof.test_KW$mle,y), col = c(6),lwd = 3.5)

    lines(y, Pdf_ETL(par < - gof.test_ETL$mle,y), col = c(7),lwd = 3.5)

    lines(y, Pdf_ULL(par < - gof.test_ULL$mle,y), col = c(8),lwd = 3.5)

    lines(y, Pdf_UPL(par < - gof.test_UPL$mle,y), col = “navy”,lwd = 3.5)

    legend(0.28,7,horiz = F, c(“UIEP”,”UEP”,”UEL”,”UEHL”,”KW”,”ETL”,”ULL”,”UPL”), cex = 0.85,lty = 1,col = c(2,3,4,5,6,7,8,”navy”),lwd = 3.5)

    #########Graph of Empirical cdf###########

    plot(ecdf(data),verticals = TRUE, main = ““,ylab = “H(y)”,xlab = “y”)

    lines(y,Cdf_UIEP(par < - gof.test_UIEP$mle,y), col = c(2),lwd = 3.5)

    lines(y, Cdf_UEP(par < - gof.test_UEP$mle,y),col = c(3),lwd = 3.5)

    lines(y, Cdf_UEL(par < - gof.test_UEL$mle,y), col = c(4),lwd = 3.5)

    lines(y, Cdf_UEHL(par < - gof.test_UEHL$mle,y), col = c(5),lwd = 3.5)

    lines(y, Cdf_KW(par < - gof.test_KW$mle,y), col = c(6),lwd = 3.5)

    lines(y, Cdf_ETL(par < - gof.test_ETL$mle,y), col = c(7),lwd = 3.5)

    lines(y, Cdf_ULL(par < - gof.test_ULL$mle,y), col = c(8),lwd = 3.5)

    lines(y, Cdf_UPL(par < - gof.test_UPL$mle,y), col = “navy”,lwd = 3.5)

    legend(0.25,0.58, c(“Empirical”,”UIEP”,”UEP”,”UEL”,”UEHL”,”KW”,”ETL”,”ULL”,”UPL”), cex = 0.85,lty = 1,col = c(1,2,3,4,5,6,7,8,”navy”),lwd = 3.5)

    ################# pp plot #################

    par(cex.axis = 1.3, cex.lab = 1.3, cex.main = 1.3, mfrow = c(2, 4), mar = c(5, 5, 4, 2))

    p < - (rank(x))/(length(x) + 1)

    plot(Cdf_UIEP(par < - gof.test_UIEP$mle,x),p,type = “p”,pch = 1,xlim = c(0,1),ylim = c(0,1),col = 2,xlab = “Obs”,ylab = “Exp”, lwd = 4, main = “UIEP”)

    par(new = TRUE)

    segments(0,0,1,1, lwd = 2)

     

    p < - (rank(x))/(length(x) + 1)

    plot(Cdf_UEP(par < - gof.test_UEP$mle,x),p,type = “p”,pch = 1,xlim = c(0,1),ylim = c(0,1),col = 3,xlab = “Obs”,ylab = “Exp”, lwd = 4, main = “UEP”)

    par(new = TRUE)

    segments(0,0,1,1, lwd = 2)

     

    p < - (rank(x))/(length(x) + 1)

    plot(Cdf_UEL(par < − gof.test_UEL$mle,x),p,type = “p”,pch = 1,xlim = c(0,1),ylim = c(0,1),col = 4,xlab = “Obs”,ylab = “Exp”, lwd = 4, main = “UEL”)

    par(new = TRUE)

    segments(0,0,1,1, lwd = 2)

     

    p < - (rank(x))/(length(x) + 1)

    plot(Cdf_UEHL(par < - gof.test_UEHL$mle,x),p,type = “p”,pch = 1,xlim = c(0,1),ylim = c(0,1),col = 5,xlab = “Obs”,ylab = “Exp”, lwd = 4, main = “UEHL”)

    par(new = TRUE)

    segments(0,0,1,1, lwd = 2)

     

    p < - (rank(x))/(length(x) + 1)

    plot(Cdf_KW(par < - gof.test_KW$mle,x),p,type = “p”,pch = 1,xlim = c(0,1),ylim = c(0,1),col = 6,xlab = “Obs”,ylab = “Exp”, lwd = 4, main = “KW”)

    par(new = TRUE)

    segments(0,0,1,1, lwd = 2)

     

    p < - (rank(x))/(length(x) + 1)

    plot(Cdf_ETL(par < - gof.test_ETL$mle,x),p,type = “p”,pch = 1,xlim = c(0,1),ylim = c(0,1),col = 7,xlab = “Obs”,ylab = “Exp”, lwd = 4, main = “ETL”)

    par(new = TRUE)

    segments(0,0,1,1, lwd = 2)

     

    p < - (rank(x))/(length(x) + 1)

    plot(Cdf_ULL(par < - gof.test_ULL$mle,x),p,type = “p”,pch = 1,xlim = c(0,1),ylim = c(0,1),col = 8,xlab = “Obs”,ylab = “Exp”, lwd = 4, main = “ULL”)

    par(new = TRUE)

    segments(0,0,1,1, lwd = 2)

    p < - (rank(x))/(length(x) + 1)

    plot(Cdf_UPL(par < - gof.test_UPL$mle,x),p,type = “p”,pch = 1,xlim = c(0,1),ylim = c(0,1),col = “navy”,xlab = “Obs”,ylab = “Exp”, lwd = 4, main = “UPL”)

    par(new = TRUE)

    segments(0,0,1,1, lwd = 2)

    ResultsofMLE

    Resultsofgof

    Data Availability Statement

    The data that support the findings of this study are available on request from the corresponding author. The data are not publicly available due to privacy or ethical restrictions.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.