Volume 7, Issue 5 e70169

REVIEW

Open Access

A Review of Lithium-Ion Battery Empirical and Semi-Empirical Aging Models for Off-Grid Renewable Energy Systems Application

Isaac Gwayi,

Corresponding Author

Isaac Gwayi

[email protected]

orcid.org/0009-0001-4165-4532

Department of Mechanical and Industrial Engineering, University of Dar es Salaam, Dar es Salaam, Tanzania

Correspondence: Isaac Gwayi ([email protected])

Contribution: Conceptualization, Investigation, Writing - original draft, Methodology, Validation, Visualization, Writing - review & editing, Data curation, Formal analysis

Search for more papers by this author

Sarah Paul Ayeng'o,

Sarah Paul Ayeng'o

Department of Mechanical and Industrial Engineering, University of Dar es Salaam, Dar es Salaam, Tanzania

Contribution: Conceptualization, Writing - review & editing, Supervision, Methodology

Search for more papers by this author

Cuthbert Z. M. Kimambo,

Cuthbert Z. M. Kimambo

Department of Mechanical and Industrial Engineering, University of Dar es Salaam, Dar es Salaam, Tanzania

Contribution: Conceptualization, Methodology, Writing - review & editing, Supervision

Search for more papers by this author

Isaac Gwayi,

Corresponding Author

Isaac Gwayi

[email protected]

orcid.org/0009-0001-4165-4532

Department of Mechanical and Industrial Engineering, University of Dar es Salaam, Dar es Salaam, Tanzania

Correspondence: Isaac Gwayi ([email protected])

Contribution: Conceptualization, Investigation, Writing - original draft, Methodology, Validation, Visualization, Writing - review & editing, Data curation, Formal analysis

Search for more papers by this author

Sarah Paul Ayeng'o,

Sarah Paul Ayeng'o

Department of Mechanical and Industrial Engineering, University of Dar es Salaam, Dar es Salaam, Tanzania

Contribution: Conceptualization, Writing - review & editing, Supervision, Methodology

Search for more papers by this author

Cuthbert Z. M. Kimambo,

Cuthbert Z. M. Kimambo

Department of Mechanical and Industrial Engineering, University of Dar es Salaam, Dar es Salaam, Tanzania

Contribution: Conceptualization, Methodology, Writing - review & editing, Supervision

Search for more papers by this author

First published: 09 May 2025

https://doi.org/10.1002/eng2.70169

Funding: The authors received no specific funding for this work.

Share a link

Email
Wechat
Bluesky

ABSTRACT

Aging of lithium-ion (Li-ion) batteries in off-grid renewable energy systems (RESs) can be monitored and controlled using battery management systems (BMSs) which utilize battery aging models. Empirical and semi-empirical models (EMs) of battery aging are preferred for BMSs due to their simplicity and intuitiveness. This study is unique as it aims at identifying appropriate empirical and semi-EMs, in terms of complexity and current fluctuation representation, for BMS for off-grid RESs. Different EMs of Li-ion battery calendar and cycle aging have been extracted from literature and compared mainly in terms of complexity, current fluctuation representation, and modeling of capacity fade and resistance increase. The extracted models have been put in groups which are based on modeling format used, namely: calendar aging (only) models (CAOM), cycle aging (only) models (CYAOM), calendar and cycle aging (separated) models (CCYAOM), and calendar and cycle aging (combined) models (CCYACM). Results show that three models meet requirements for BMS for off-grid RESs. The three models fall under CYAOM, CCYAOM, and CCYACM. The study further finds that 54% of EMs model current fluctuation as an aging factor, 92% model aging in terms of capacity fade, and 46% model aging as resistance increase. Furthermore, the study recommends comparison of EMs through simulations to further validate the different listed models. It also recommends evaluation of the models to establish an appropriate way of representing Li-ion battery aging, whether in terms of capacity fade or resistance increase.

1 Introduction

Electricity generation using fossil fuels (FFs) is the most substantial source of greenhouse gases, an example of such gases is carbon dioxide. These gases have adverse effects on the environment [1]. On the other side, FFs are inadequate and not fairly distributed in the earth's crust [2]. Furthermore, FF reserves continue to decrease. Therefore, generation of electrical energy by utilizing means that are independent of traditional fuels is the only option available to meet our daily life needs of electricity. Consequently, renewable energy (RE) sources have been regarded as a potential solution to generation of electricity. Examples of commonly available RE sources include wind, solar, hydro, and geothermal [3]. However, the availability of most RE sources is dependent on weather and climate conditions (e.g., solar and wind), which keep on changing. Due to the stochastic nature of these RE sources, they cannot be dispatched [4, 5]; this demands utilization of generated electrical energy as soon as it is generated [6], if not stored. However, deployment of energy storage systems (ESSs) has been recognized as a probable solution to the intermittency of RE sources [7].

Performance of these ESSs in renewable energy systems (RESs) has attracted the attention of researchers from both industry and academia. Among different ESSs that are deployed in RESs, it has been found that lithium-ion (Li-ion) batteries outperform other battery types in terms of energy density, cycle life, and memory effect [8, 9]. Furthermore, the price of Li-ion batteries continues to decline and in general it has been found that Li-ion batteries meet more RES requirements as compared to other battery technologies [10, 11]. Currently, two of the major factors that are hindering the full adoption of Li-ion batteries are cost and aging of the batteries [12]. In terms of aging, Li-ion battery performance reduces as a function of time, which is referred to as calendar aging, and as a function of use, which is referred to as cycle aging.

In general, calendar aging refers to capacity fade or resistance increase (power fade) during the time the battery is not functioning. Calendar aging is mainly a function of temperature and state of charge (SoC). In terms of temperature, the higher the temperature, the higher the aging rate of the Li-ion battery due to increased side reactions. For SoC, high SoC accelerates aging of the battery as well due to the imbalance of potential at the electrode and electrolyte interface [13-15]. Calendar aging can be divided into two groups, namely reversible aging and irreversible aging. Reversible aging can be reversed by charging the battery, while irreversible aging is permanent, that is, it cannot be reversed [16].

Cycle aging, on the other hand, is related to battery usage, that is, charge and discharge cycles. Cycling of the battery causes kinetically induced effects; for example, volume variations when charging and discharging, and concentrations gradients [17]. These effects also result into aging in addition to side reactions, which result from the thermodynamic instability of Li-ion battery construction materials. Cycle aging is mainly influenced by charge and discharge current rate (C_rate), initial SoC, and variation of SoC (also called depth of discharge [DoD]).

In off-grid RESs, there are pronounced current (power) fluctuations due to the intermittent nature of RE sources and variation of the load profile. Fluctuations caused by the load profile are due to loads that need high starting currents, for example, motors and welding machines. These fluctuations are intense in off-grid RESs due to the small inertia of the systems in comparison with on-grids [18]. These fluctuations result in spikes in C_rate, which then consequently accelerate Li-ion battery aging [19].

To minimize aging of Li-ion battery in off-grid RESs due to current fluctuations, an effective battery management system (BMS) must be deployed. The BMS can also be referred to as a battery storage control strategy, as explained in [20, 21]. The main function of the BMS is to monitor aging stress factors the battery is subjected to and the states of the battery system, such as SoC and state of health (SoH), and take appropriate action to reduce the battery aging rate. These BMSs also ensure safe, reliable, and optimized operations of the battery. Battery states, for example SoC and SoH, cannot be directly measured by any sensor; therefore, for the BMS to monitor them, they are usually inferred, commonly from estimation algorithms that are model-based [22-24].

For correct operation of the BMS, in terms of monitoring and control of the battery aging, accurate aging models are of utmost importance. However, in making sure the models are accurate, it should be noted that there is a need of striking a balance between accuracy and complexity. The balance should make sure that models are flexible for implementation in embedded microprocessors and are able to provide fairly accurate results in real time [25]. From off-grid RESs' economics point of view, BMS together with battery aging models can reduce systems' payback period and increase their profitability. This can be achieved by extending battery system lifetime due to reduced aging rate. Also, the development of aging models, specifically for BMS, is helpful to researchers in terms of identifying paths for improvement in Li-ion battery technology for off-grid RESs' implementation [26].

There are different models of Li-ion battery aging behavior. These models are normally grouped into four categories namely: physics-based models (PBMs), equivalent circuit models (ECMs), machine learning models (MLMs), and empirical and semi-empirical models (EMs). A summary of comparison of these models in terms of complexity, accuracy, amount of data, and application areas is given in Table 1. Among these models, PBMs, which are also known as electrochemical models, model the Li-ion battery's electrochemical and physical processes. The first PBM was based on a porous electrode model [27]; thereafter, a pseudo-2-D followed. The pseudo-2-D model extended the first model by including a thermal model [28]. Furthermore, solvent oxidation or layer growth, which are effects of parasitic side reactions, were added to account for aging of the battery. PBMs can achieve high accuracy; however, they are complex since they demand many differential equations to model the physical and chemical properties of the battery [14]. Due to the mentioned challenges, these PBMs are generally mainly used by chemical engineers [29].

TABLE 1. Comparison of aging models in terms of complexity, amount of data, and typical applications.

Model type	Complexity	Accuracy	Data amount	Typical applications
PBM	High	High	Low	Battery design
ECM	Medium	Medium	High	SoH estimation
MLM	Medium-high	Medium	High	SoH estimation
EM	Low	Low-medium	High	System design and optimization

ECMs model Li-ion battery by considering their transient response. The models achieve this by using passive circuit components; for example, inductances, resistances, and capacitances. These models can be made more complex and can achieve simulation of internal diffusion and charge transfer processes of the battery, whereby aging can be incorporated based on impedance data using variable components. ECMs are usually used in real-time applications simulation because of their mathematical simplicity [30], and they are combined with state estimators; for example, Kalman filters [14, 30-32].

Machine learning (ML) based models are also commonly used as SoC and SoH estimators. There are different approaches to this modeling technique. Some approaches utilize training algorithms which extract the battery's SoH information from the incremental capacity curve of the battery [33-36]. These models require parameters which can be easily extracted, such as temperature, voltage, and current, which makes the approach advantageous. There are also other techniques that combine ML with other models to train algorithms [37, 38]. For example, ML can be combined with empirical modeling techniques which utilize regression models to estimate SoH of the battery [39]. ML models require large datasets to train the algorithms, and they can achieve high accuracy [14, 33, 40].

EMs model the relationship of various battery aging stress factors using relatively simple analytical formulae. The EMs are used in a wide range of applications because of their simplicity. They are deployed, for example, in BMSs, systems-level design problems, and optimization problems. Due to their simplicity, these models are prone to missing out on some crucial data during battery modeling because of the complex relationship between battery aging stress factors.

In literature, various studies have focused on aging mechanisms and modeling of Li-ion batteries. Reference [41] reviewed factors that influence aging on a cell level as well as battery pack level. In [14, 28, 42], main aging mechanisms were reviewed and estimation techniques based on PBMs, ECMs, EMs, and statistical models were reviewed as well. Comparison of different EMs of battery aging based on a smart grid was done in [43]. Additionally, battery's SoH estimation techniques have been reviewed by many studies of which examples are as in [44-47]. Reference [46] discussed different types of self-adaptive SoH monitoring techniques. The techniques discussed include particle filter method, support vector regression, and neural networks. Furthermore, different types of remaining-useful-life estimation techniques and SoH estimation techniques were broadly reviewed in [44-46]. The techniques reviewed included direct measurement, model-based, and adaptive filtering.

All the studies mentioned focused on giving general reviews of different aging mechanisms or state estimation techniques. In most of these studies, EMs are partially mentioned without diving deep into them. Since EMs are not so complex in implementing in real-time BMS, and they strike a good balance between complexity and battery system representation, they are a better option when it comes to implementing in BMS for off-grid RESs. More complex models indirectly mean high implementation cost for BMS, hence raising the overall cost of off-grid RESs. It is, therefore, paramount to further study EMs to have a deeper understanding in terms of Li-ion battery aging representation and complexity for off-grid RESs. Furthermore, establishing which models best suit implementation in off-grid RESs considering power/current fluctuation representation (C_rate), in addition to complexity, is of great importance as well. This is because current fluctuations are eminent in off-grid RESs (as explained in previous paragraphs) leading to accelerated aging of Li-ion battery. In this study, therefore, the research question that is being addressed can be put as follows: what are appropriate EMs for BMS in off-grid RESs considering complexity and current fluctuation representation?

Considering the stated research question, the objective of this study, therefore, is to identify appropriate EMs for BMS in off-grid RESs. This objective is mainly achieved by analyzing EMs in terms of their complexity as well as current fluctuation representation. The research study is different from others and important because it brings out actual Li-ion aging models from the literature and compares them mainly in terms of current fluctuation representation and complexity. This is crucial for BMS implementation in off-grid RESs for a reduced Li-ion battery aging rate. In summary, the contributions of this study may, therefore, be stated as follows:

The study results in the identification of appropriate EMs for implementation in off-grid RESs. These models strike a good balance between complexity and current fluctuation representation for BMS for Li-ion battery aging monitoring and control.
The study acts as a quick reference material for academia and industry to quickly select Li-ion EMs for implementation during their research depending on their needs in terms of either calendar and cycle life representation or implementation complexity or variables to be measured.
The study provides an up-to-date research status on EMs' development, which gives insight into areas that need further research. This is helpful to new researchers to know important stress factors of Li-ion battery aging that are mostly considered in current research for informed decisions.

The rest sections of the paper are organized as follows: Section 2 details the methodology used in this study. Methods and materials used in this study are described in this section. Review of Li-ion battery aging mechanisms is done in Section 3, after which Section 4 compares different EMs mainly in terms of complexity as well as current fluctuations representation. After comparison of the different EMs, Section 5 provides a discussion of results by providing key findings and consequently identifying appropriate models for BMS implementation in off-grid RESs. Finally, the study is concluded in Section 6, where also recommendations are provided.

2 Methodology

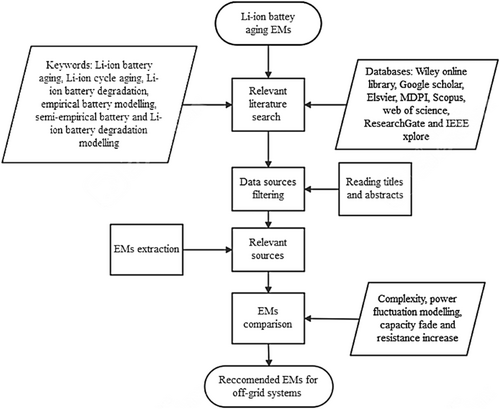
The aim of the study, as mentioned in the introduction section, is to identify appropriate EMs, based on their complexity and current fluctuation representation, for BMS implementation in off-grid RESs. Therefore, in this study, firstly, a review of Li-ion battery aging mechanisms is done to provide general information about battery aging. After which, different studies that have focused on empirical and semi-empirical aging modeling of Li-ion batteries are presented. These studies are split into two groups, that is, those that focused on calendar aging and those that focused on cycle aging (noting that some studies focused on both).

The studies have been extracted from literature using research publications (including journal and conference papers and reports from academic databases, for example Scopus and web of science), websites, and datasheets. Steps followed to find the studies were first to search for literature related to Li-ion battery aging using keywords. Examples of keywords used include Li-ion battery aging, Li-ion cycle aging, Li-ion battery degradation, empirical battery modeling, semi-empirical battery modeling, and Li-ion battery degradation modeling. Thereafter, to make a decision as to whether to read the whole article or not, the article's title, abstract, and date of publication (for published works) were read. This screening made sure relevant articles and information for the study are captured.

Second, extraction of models from the filtered studies followed; models were extracted from the studies which explicitly presented their models and validated them. After model extraction, the extracted models have been put into groups based on whether they capture calendar aging or cycle aging, or both, for clarity purposes. Thereafter, they are compared in terms of complexity and current fluctuations representation, because that is the main focus of this study. Model complexity has been evaluated based on the number of variables and parameters and the number of elementary operations the model has. Current fluctuation representation has been based on whether the model captures C_rate or not. Furthermore, the models are compared in terms of modeling of capacity fade or resistance increase, which is also referred to as power fade.

Finally, discussion of comparison results follows, which then culminates in recommending appropriate EMs for Li-ion battery aging for BMS in off-grid RESs. The methodology used in this study can be presented in a diagram as shown in Figure 1.

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Summary of methodology used in the study to identify appropriate empirical and semi-EMs for BMS implementation in off-grid RESs.

3 Review of Lithium-Ion Battery Aging Mechanism

Li-ion battery is mainly made up of four main components, namely: anode, cathode, electrolyte, and separator. On the anode, the most commonly used material is graphite [14, 48, 49]. Apart from graphite, other used materials include lithium-titanate-oxide (LTO) or silicon [50]. The cathode is made up of a mixture of materials that contains lithium. The most utilized materials are lithium-nickel-cobalt-aluminum (NCA), lithium-nickel-manganese-cobalt (NMC) oxide, lithium-iron-phosphate (LFP), and lithium-manganese oxide (LMO). On the other hand, the electrolyte composes lithium salts and organic solvents [43]. The transfer of ions between the cathode and the anode is achieved by utilizing the electrolyte. Finally, the separator, which is a porous plastic, is used to separate the anode and the cathode to prevent short-circuiting the electrodes. When the Li-ion battery is charging, Li-ions are released, a process called deintercalation, from the cathode and move through the electrolyte and separator and finally intercalate at the anode. An electrical current results from the flow of these ions from the cathode to the anode. During Li-ion battery charging, the cathode, which is the lithium-containing part of the cell, is the limiting factor as its maximum voltage determines the end of battery charge. On the other side, during discharge mode, the anode is the limiting factor because of its minimum discharge voltage limit [49].

Aging of Li-ion battery occurs during cycling (cycle aging) as well as during idle state (calendar aging) as highlighted in the introduction section of this study. Aging is caused by physical stresses and chemical side reactions [41]. There are many factors that influence Li-ion battery aging, including operating conditions, cell design, pack design, and cell chemistry. Li-ion battery aging is normally grouped into three different aging modes, as indicated in [41, 48, 49, 51, 52]. These aging modes are listed as follows:

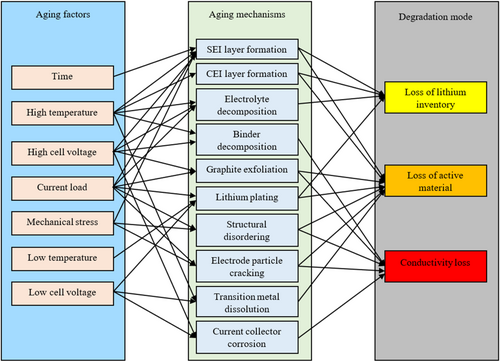
Loss of Active Material (LAM): this is anode or cathode material structural degradation. It is normally caused by electrode surface layer growth or cycling-induced cracks or exfoliation. The LAM can result in both capacity fade and resistance increase.
Loss of Lithium Inventory (LLI): this is the loss of active lithium ions. It makes the ions no longer available for cycling. LLI is mainly caused by parasitic side reactions which include lithium plating, decomposition reactions, and surface film formation. This LLI results in capacity fade, which is generally defined as the loss of effective milli-ampere-hour (mAh) of a cell.
Conductivity Loss (CL): This is the degradation of electrical parts, for example, corrosion of the current collector and decomposition of the binder [48]. CL results in resistance increase.

Another aging mode could be mentioned as loss of electrolytes, which results in LAM and CL after a certain point. These listed degradation modes interact, although they are mentioned separately in literature as listed. For example, a single degradation mode, such as surface layer formation, can trigger several degradation modes. Figure 2 shows aging factors, the corresponding aging mechanisms, and their effect on Li-ion battery aging. Aging occurs at the anode and cathode; therefore, aging is normally described as anode aging and cathode aging, which are detailed in the next subsections.

3.1 Anode Aging

This subsection focuses on anode aging of graphite-based Li-ion batteries. The focus is on graphite-based Li-ion batteries because the anode material that is used most is graphite [42, 48, 53]. Mainly, the aging of these anodes is grouped into five categories. These categories are listed as follows: solid electrolyte interphase (SEI) layer formation, lithium plating, mechanical stress at the anode, transition metal dissolution, and other aging mechanisms. These aging modes are detailed in the following subsections.

3.1.1 Solid Electrolyte Interphase Layer Formation

Organic electrolytes used in Li-ion batteries have a stability window in the range of 1–4.5 Volts (V). Various Li-ion batteries' electrode materials have different operating voltage ranges in relation to the stability window of the electrolytes. For graphite-based anodes, their voltage range is between 0.05 and 1 V [41, 54]. This range is outside the stability window of the electrolyte, making the batteries thermodynamically unstable, which then results in a reductive electrolyte decomposition reaction. This reaction causes a layer to form on the surface of the anode and consumes Li-ions as well, which then results in LLI and LAM [14, 41, 48]. During the initial few cycles of Li-ion batteries, the decomposition reaction rate is high, and a surface layer permeable to Li-ions but less permeable to electrolyte components is created. Due to this process, the decomposition rate decreases [48, 55, 56]. Regardless of the reduced decomposition rate, solvated lithium and other electrolyte components continue to pass through this semipermeable layer throughout the lifetime of the battery. This decomposition reaction occurs mainly at the electrolyte and anode interphase and is referred to as the solid SEI layer. The growth of the SEI layer is regarded as one of the main aging factors of graphite-based Li-ion batteries. The layer affects the capability of the battery in terms of energy as well as power capacities. In addition to this layer, there is also another layer that grows on the basal plane surface and is mostly referred to as the non-SEI layer [57]. This layer is impermeable to Li-ions. In general, both of these layers are commonly called the SEI layer [48]. The formation of the SEI layer continues throughout the lifetime of the battery during both cycling and idle states.

Growth rate of SEI layer is a function of operating conditions of the Li-ion cell [58]. During idle state, the rate is mainly dependent on temperature and SoC. On temperature, the higher the temperature, the higher the reaction rate, which then results in less stable organic SEI components to transform into more stable products, consequently decreasing the conductivity of the SEI layer. Moreover, the cell can catch fire or explode if temperatures go above 60°C due to thermal runaway. On SoC, at higher SoC, there is more intercalation of Li-ions into the anode material, which decreases the anode potential. Decreased anode potential results in increased reductive reaction rate [54]. In addition to temperature and SoC, there are also mechanical stresses on the electrodes during cycling, which result from volume changes as a result of (de) intercalation of Li-ions. These volume changes may result in the formation of cracks in the SEI layer, thereby allowing new reactions to take place, which then makes SEI grow further grow causing additional LLI and LAM [48]. Additionally, cycling Li-ion battery with high C_rates results in a more porous SEI layer compared to idle state [58]. This increased porosity creates room for more reductive reactions to occur as compared to a denser layer. Electrode balance and electrolyte composition are other factors that influence reaction rate [56].

3.1.2 Lithium Plating

Temperatures below 20°C cause the diffusion rate of Li-ions into the electrolyte or anode to reduce. This reduction in diffusion rate results in the intercalation potential of the anode material to approach that of a metallic lithium, causing lithium plating. In addition to low temperatures, low SoC and high C_rates also cause lithium plating. Lithium plating results in LLI and also causes dendrites to grow, which then reduces the safety of the cell since these dendrites can cause internal short circuits [48].

3.1.3 Mechanical Stress at Anode

During intercalation of Li-ions into the anode, there are rapid volume changes due to particles undergoing phase transition [48]. During this phase transition, different geometrical and electrical properties are realized because the orientation of molecules changes as a result of more molecules of Li-ion being inserted. The resulting geometrical and electrical property changes cause mechanical stress, which leads to surface layer cracking (LLI and LAM), anode structural damage (LAM), and contact loss with the composite electrode (CL). The changes in active material volume can also decrease electrode porosity, thereby blocking the electrolyte from reaching most of the electrode [48].

3.1.4 Transition Metal Dissolution

Cathodes and electrolytes of Li-ion batteries contain impurities. In cathodes, there are metals, for example, manganese, nickel, cobalt, iron, and vanadium, which are referred to as transition metals. Electrolytes, on the other hand, contain a salt called lithium hexafluorophosphate (LiPF₆). When lithium cells are cycled or stored at high voltages or temperatures, hydrogen fluoride is formed from the impurities in the electrolytes, which results in increased electrolyte acidity [59]. The formed hydrogen fluoride corrodes cathodes and also dissolves the transition metals. This phenomenon results in many degradation mechanisms at both the anode and cathode, which results in capacity fade or resistance increase of the battery. The dissolved metals can cause structural degradation of the cathode (LAM) which results in reduced insertion capability of the lithium ions [60]. Additionally, these dissolved metals move through the electrolyte to the anode, where they are deposited, and they influence the growth of the SEI layer by acting as catalyzers for the reductive decomposition reaction [61]. Also, when transition metals are deposited on the anode, they induce the formation of lithium dendrites (LLI and LAM), which can cause short circuits inside the battery.

3.1.5 Other Anode Aging Mechanisms

In addition to the described degradation mechanisms, there are also other mechanisms including graphite exfoliation, particle cracking, and binder decomposition. Graphite exfoliation (LAM) results from high current densities or solvent co-intercalation, and particle cracking (LAM) results from high current load or mechanical stress. Binder decomposition (CL) is mainly caused by high cell voltages and high temperatures. Other examples include loss of electrical contact (CL) and corrosion of current collectors (CL). More information about these can be found in literature including in [17, 48, 49].

3.2 Cathode Aging

There are different cathode materials for Li-ion batteries. These materials vary in terms of safety, cost, energy density, power density, toxicity, and natural abundance, to mention a few. Cathode materials that are commonly used are NMC, LFP, LCO, NCA, and LMO. Regarding the aging of Li-ion batteries, cathode aging is considered less significant [62] as compared to anode aging. Transition metal dissolution, surface film formation, and mechanical stress are the main aging mechanisms of the cathode materials. Furthermore, current collector corrosion, binder decomposition, and conducting agent oxidation are listed as other aging mechanisms of the inactive components [48].

3.2.1 Cathode Surface Layer Formation

Due to electrolyte oxidation and salt deposition at the cathode, surface layer films referred to as cathode electrolyte interphase (CEI) layer form [48, 63]. The CEI layer is similar to the SEI layer at the anode. The layer reduces the conductivity of the Li-ion, hence increasing cathode resistance. Furthermore, the organic products that result from the reduction process at the anode can also be transported through the electrolyte to the cathode. At the cathode, they can be oxidized and then get deposited on its surface, resulting in LAM and LLI [17].

3.2.2 Mechanical Stress at Cathode

During intercalation and deintercalation of Li-ions at the cathode, the cathode also goes through phase transitions, similar to that at the anode, resulting in CL and LAM. When transitions are taking place, the cathode material is the determining factor for volume changes. Some materials experience huge changes compared to others, resulting in different aging rates [48].

3.2.3 Transition Metal Dissolution

Similar to anode aging, structural degradation of the cathode (LAM) also takes place at the cathode due to transition metal in the cathode dissolution [59]. Transition metal dissolution effects are similar to the ones at the anode.

4 Comparison of Empirical and Semi-Empirical Aging Models

Several studies have been done on aging of Li-ion batteries. These studies either focus on calendar aging or cycle aging or both. In this review study, the studies which focused on calendar aging have been presented separately from the ones which focused on cycle aging. Even though some studies focused on both, they have been separately presented for clarity's sake under calendar aging studies and cycle aging studies, for example studies done in [64, 65].

4.1 Calendar and Cycle Aging Studies

Studies which focused on calendar aging of Li-ion battery using empirical and semi-EMs are shown in Table 2. Shown in the table are the chemistry of the battery, aging stress factors, aging conditions, capacity fade (cap. fade), resistance increase (res. increase), and the respective reference (ref.).

TABLE 2. Empirical and semi-empirical calendar aging model studies for Li-ion batteries.

Battery chemistry	Aging stress factors	Temp. (°C)	SoC (%)	Cap. fade	Res. increase	References
		Aging conditions
LFP	SoC, T, time	40–55	10–90	X	√	[66]
LFP	SoC, T, time	40–70	60–80	√	X	[67]
LFP	SoC, T, time	25–55	20–80	√	√	[68]
LFP	SoC, T, time	30–60	30–100	√	X	[69]
LFP	SoC, T, time	25–55	10–100	√	√	[70]
LFP	SoC, T, time	30–60	30–90	√	√	[71]
NMC	SoC, T, time	0–45	0–100	√	√	[15]
NMC	SoC, T, time	25–45	20–100	√	X	[72]
NMC-LMO	SoC, T, time	10–46	10–90	√	X	[64]
NMC-LMO & NCA	SoC, T, time	30–60	30–100	√	√	[73]
NMC	SoC, T, time	30–60	30–100	√	√	[74]
NMC	SoC, T, time	35–50	0–100	√	√	[29]
NMC	SoC, T, time	0–60	5–100	√	X	[75]
NMC	SoC, T, time	25–60	20–100	√	√	[76]
NMC	SoC, T, time	35–50	0–100	√	√	[77]
NMC	SoC, T, time	40–70	60–80	X	√	[78]
LFP	SoC, T, time	0–55	0–100	√	X	[65]
NMC	SoC, T, time	10–55	10–100	√	X	[79]
LFP	SoC, T, time	40–70	20–100	√	√	[80]

From the data presented in Table 2, it is noted that all the captured studies considered SoC, temperature (T) and time as calendar aging stress factors. Also, it has been noted that 17 out of the 19 studies (89.47%) presented considered capacity fade as a result of calendar aging. On the other hand, 12 out of the 19 studies (63.16%) presented considered resistance increase as a result of calendar aging. Furthermore, 10 out of the 19 studies (52.63%) considered both capacity fade and resistance increase as results of calendar aging of Li-ion batteries. Therefore, it can be concluded, based on the data in the table, that most studies about calendar aging of Li-ion battery consider capacity fade as a result of aging. In addition to that, capacity fade is a function of SoC, T, and time.

Studies that focused on cycle aging of Li-ion battery using empirical and semi-EMs are shown in Table 3. Shown in the table are the chemistry of the battery, aging stress factors, aging conditions, capacity fade, resistance increase, and respective reference.

TABLE 3. Empirical and semi-empirical cycle aging models studies for Li-ion batteries.

Battery chemistry	Aging stress factors	Temp. (°C)	SoC (%)	DoD (%)	C_rate (C)	Cap. fade	Res. increase	References
		Aging conditions
NMC	SoC, C, T	40–70	50–70	—	1–8	X	√	[78]
LFP	SoC, DoD, C, T	25	53.5–100	12.5–75	0.22–0.67	√	X	[81]
NMC	SoC, DoD, C, T	35	0–100	10–100	1	√	√	[77]
NMC	SoC, DoD, C, T	25–60	20–100	10–50	1	√	X	[76]
NMC	SoC, DoD, C, T	0–60	0–100	3–80	C/2	√	X	[75]
NMC-LMO	SoC, DoD, C, T	10–46	10–90	10–90	0.5–6.5	√	X	[64]
NMC/LMO & NCA	ΔSoC, C, T	40–50	20–40	—	C/20-C	√	√	[73]
LFP	SoC, DoD, C, T	40–70	60–80	10–60	C	√	√	[67]
LFP	SoC, C, T	25–55	20–80	—	4C	√	√	[68]
LFP	SoC, C, T	0–55	0–100		0.25–1	√	X	[65]
LFP	DoD, C, T	−30 to 60	—	10–90	C/2–10	√	√	[82]
NMC-LMO	SoC, C, T	10–45	25–45	—	C/3-3C/2	√	√	[83]
NMC	SoC, DoD, C, T	10–46	100 (start)	50	0.5–6.5	√	X	[79]
NMC	SoC, DoD, C, T	10–50	20–80	10–100	C/3-2C	√	X	[72]
LFP	DoD, C, T	30	—	20–80	1–6	√	√	[80]
NMC	SoC, DoD, C, T	35	10–95 (avg)	5–100	1	√	√	[29]
NMC	SoC, DoD, C, T	−10 to 50	20–80 (avg)	10–100	1/3–2	√	X	[75]
NCA	SoC, DoD, T, C	40–50	60–85 (avg)	20–65	18	√	X	[80]
LFP	SoC, DoD, T, C	30	50	5–100	1–3.5	√	X	[84]
LFP & NMC	DoD, T, C	23–45	—	25–100	1–8	√	√	[85]

From the data presented in Table 3, it is noted that all the captured studies (100%) considered temperature and C_rate as cycle aging stress factors. It is further noted that 17 out of the 20 studies (85.00%) capture SoC as an aging stress factor. Considering that the change of SoC (ΔSoC) is also referred to as DoD, as previously indicated in this study, it can be stated that all the studies capture SoC as a cycle aging stress factor. Also, it is noted that 19 out of the 20 studies (95.00%) presented considered capacity fade as a result of cycle aging. On the other hand, 10 out of the 20 studies (50.00%) presented considered resistance increase as a result of cycle aging. Furthermore, 9 out of the 20 studies (45.00%) considered both capacity fade and resistance increase as results of cycle aging of Li-ion batteries. Therefore, it can be concluded, based on the data in the table, that most studies about the cycle aging of Li-ion battery consider capacity fade as a result of aging. Furthermore, this aging is mainly influenced by temperature, C_rate, and SoC as stress factors.

4.2 Empirical and Semi-Empirical Aging Models

From the calendar and cycle aging studies presented in Tables 2 and 3 respectively, empirical and semi-EMs were extracted. Focus was mainly on those studies that presented model equations and validated their models. Note that most studies also identified fitting parameters for their models. For clarity and brevity's sake, this study has categorized the extracted models into four groups whose names and their abbreviations are as follows:

Calendar aging (only) models (CAOM).
Cycle aging (only) models (CYAOM).
Calendar and cycle aging (separated) models (CCYASM).
Calendar and cycle aging (combined) models (CCYACM).

The CAOM are models that capture calendar aging only in their formulae, while CYAOM are models that capture cycle aging only in their formulae. On the other hand, CCYASM are models that capture both calendar aging and cycle aging, but in separated formulae for each, while CCYACM are models that capture both calendar aging and cycle aging in a single formula.

Models under each group have been assigned codes to ease reference. These codes have a number at the end which represents the model number in the specific group, for example CAOM1 and CAOM2 meaning calendar aging (only) model numbers 1 and 2, respectively. The named and listed four groups of models and models falling under each group, including their codes, have been presented in Table 4.

TABLE 4. Extracted empirical and semi-empirical Li-ion battery aging models.

Aging models		Cap. fade	Res. increase	No. of vars. and pars.	No. of ele. opers.	C_rate	Model code	References
Calendar aging only models (CAOM)
${R}_i=\left(6.9656\cdotp {10}^{-8}\cdotp \exp \left(0.05022\cdotp {T}_K\right)\right)\cdotp \left(2.897\cdotp \exp \left(0.006614\cdotp SoC\right)\right)\cdotp {t_m}^{0.8},$ where ${R}_i$ is internal resistance increase (%), ${t}_m$ is time (months), ${T}_K$ is temperature (degrees kelvin) and $SoC$ is in percent (%).		X	√	9	9	X	CAOM1	[66]
Cycle aging only models (CYAOM)
${C}_{loss}\left(\%\right)\left(10\%\ge DoD\le 50\%\right)=\left(\gamma 1\cdotp {DoD}^2+\gamma 2\cdotp DoD+\gamma 3\right)\cdotp {Ah}^{0.87}$ , ${C}_{loss}\left(\%\right)\left( DoD<10\%\& DoD>\%0\%\right)=\left(\alpha 3\cdotp \exp \left(\beta 3\cdotp DoD\right)+\alpha 4\cdotp \exp \left(\beta 4\cdotp DoD\right)\right)\cdotp {Ah}^{0.65}$ , Where ${C}_{loss}$ is capacity loss, $DoD$ is depth of discharge (%), $Ah$ is ampere-hour (charge) throughput and $\gamma 1,\gamma 2,\gamma 3,\alpha 3,\alpha 4,$ $\beta 3$ , and $\beta 4$ are fitting parameters for the model.		√	X	10	16	X	CYAOM1	[84]
${C}_{loss}=B\cdotp \exp \left[\frac{-31,700+370.3\cdotp {C}_{rate}}{RT}\right]\cdotp \kern0.5em {Ah}^{0.55}$ , Where ${C}_{rate}$ is charge/discharge current value, $B$ is a constant and its optimal value for specific ${C}_{rate}$ was found to be as indicated in the following brackets against each current: C/2 (31,630); 2C (21,681); 6C (12,934), and 10C (15,512). $R$ is universal gas constant, $T$ is temperature in degrees Celsius (°C).		√	X	9	8	√	CYAOM2	[82]
${C}_{loss}={a}_c\left({SoC}_{min}, Ratio\right)\cdotp \exp \left(\frac{-{E}_a}{RT}\right)\cdotp A{h}^z$ , where ${a}_c(.)$ is capacity severity factor function given by the following equation: ${a}_c(.)={\alpha}_c+{\beta}_c\cdotp {(Ratio)}^b+{\gamma}_c\cdotp {\left({SoC}_{min}-{SoC}_0\right)}^c$ . ${R}_i={a}_R\left({SoC}_{min}, Ratio,{C}_{rate}\right)\cdotp \exp \left(\frac{-{E}_a}{RT}\right)\cdotp Ah$ where ${a}_R(.)$ is resistance severity factor function given by the following equation: ${a}_R(.)={\alpha}_R+{\beta}_R\cdotp {\left({SoC}_{min}-{SoC}_0\right)}^{c_R}+{\gamma}_R\cdotp e\cdotp \left[d\cdotp \left({C}_{rate,0}-{C}_{rate, eq}\right)+\exp\ \left({SoC}_{min}-{SoC}_0\right)\right]$ . Where $Ratio$ is ratio of discharging time to sum of discharging time and charge sustainability time. ${C}_{rate, eq}$ is a function of $Ratio$ , and is eqaul to 0 if $Ratio$ is 0, and is equal to ${C}_{rate, eq}$ if $Ratio$ is greater than 0. The constant coefficients for the model are as follows: ${\alpha}_c$ = 137, ${\beta}_c$ = 420, ${\gamma}_c$ = 9610, $b$ = 0.34, $c$ = 3, $z$ = 0.48, ${SoC}_0$ = 0.25, ${\alpha}_R$ = 3.2exp5, ${\beta}_R$ = 1.37exp9, ${\gamma}_R$ = 3.6exp3, ${c}_R$ = 5.45, $d$ = 0.9179, $e$ = 1.8277, ${C}_{rate,0}$ = 5, ${E}_a$ = 22,406 (J mol⁻¹) and $R$ = 8.314 (J K⁻¹ mol⁻¹).		√	√	23	33	√	CYAOM3	[83]
$C(n)={C}_{BoL}-\epsilon {(n)}^{\alpha_c}\cdotp \left({C}_{BoL}-{C}_{EoL}\right)$ , $R(n)={R}_{BoL}-\epsilon {(n)}^{\beta_r}\cdotp \left({R}_{EoL}-{R}_{BoL}\right)$ , Where $C(n)$ and $R(n)$ are battery capacity and internal resistance, respectively, at cycle number n, ${C}_{BoL}$ and ${C}_{EoL}$ are the battery capacity at beginning of life ( $BoL$ ) and end of life ( $EoL$ ) respectively, ${R}_{BoL}$ and ${R}_{EoL}$ are battery resistance at $BoL$ and $EoL$ respectively, ${\alpha}_c$ and ${\beta}_r$ are the aging exponents for the battery capacity and resistance respectively, and $\epsilon$ is aging index after each cycle. Aging index is given by the following equation: $\epsilon (n)=\epsilon \left(n-1\right)+\frac{N_{eq}(n)}{N_c\left(n-1\right)}$ , ${N}_{eq}(n)=0.5\left(2-\frac{DoD\left(n-2\right)+ DoD(n)}{DoD\left(n-1\right)}\right)$ , ${N}_c(n)=\frac{N_{c\_ ref}}{\theta (n)}={N}_{c\_ ref}{\left(\frac{DoD(n)}{DoD_{ref}}\right)}^{\frac{-1}{\varepsilon }}\cdotp {\left(\frac{\ {C}_{rate\_ dis\_ ave}(n)}{C_{rate\_ dis\_ ref}}\right)}^{\frac{-1}{\delta 1}}\cdotp {\left(\frac{C_{rate\_ ch\_ ave}(n)}{C_{rate\_ ch\_ ref}}\right)}^{\frac{-1}{\delta 2}}\cdotp \exp \left[-\varphi \left(\frac{1}{T_{ref}}-\frac{1}{T_{amb}(n)}\right)\right]$ . Where ${N}_c$ is number of cycles, ${N}_{eq}$ is equivalent number of cycles, ${N}_{c\_ ref}$ is reference number of cycles, $\theta (n)$ is total stress factor, ${DoD}_{ref}$ is reference depth of discharge, ${C}_{rate\_ dis\_ ave}$ and ${C}_{rate\_ ch\_ ave}$ are average charge and discharge currents with their references ${C}_{rate\_ dis\_ ref}$ and ${C}_{rate\_ ch\_ ref}$ respectively, ${T}_{ref}$ is reference temperature, ${T}_{amb}$ is ambient temperature, $\varphi$ is Arrhenius rate and $\varepsilon, \delta 1\ \mathrm{and}\ \delta 2$ are stress exponents for DoD, discharge and charge currents respectively. Estimated values for ${N}_{c\_ ref},\varepsilon, \varphi, \delta 1,\delta 2\ \mathrm{and}\ {\alpha}_c$ are 9175, 0.8, 3.7e3, 0.8, 2.34, and 0.9708, respectively.		√	√	33	34	√	CYAOM4	[85]
Calendar and cycle aging separated models (CCYASM)
Calendar model	Cycle model
${C}_{loss}=A(SoC)\cdotp \exp \frac{E_a(SoC)}{RT}\cdotp {t_d}^z$ . Where $A$ and $z$ are constant coefficients and ${t}_d$ is time in days.	${C}_{loss}=B\left({C}_{rate}\right)\cdotp \exp \frac{E_a\left({C}_{rate}\right)}{RT}\cdotp {Ah}^{z(T)}$ . Where B is a constant.	√	X	14	12	√	CCYASM1	[79]
${C}_{loss}=\left(0.019\cdotp {SoC}^{0.0823}+0.5195\right)\cdotp \left(3.258\cdotp {10}^{-9}\cdotp {T}^{5.087}+0.295\right)\cdotp {t_d}^{0.8}$ ${R}_i=\frac{0.000375\cdotp SoC+0.1363}{0.155}.\cdotp 0.003738\cdotp {e}^{0.78.T}$	${C}_{loss}=0.00024\cdotp \exp \left(0.02717\cdotp T\right).\mathrm{0.02982}.{cd}^{0.494}$ ${R}_i=\frac{1}{3}\left(5.78.{10}^{-4}.\exp (0.03.T).+1.22.{10}^{-7}\right).2.918.{10}^{-5}.\exp \left(0.08657. cd\right).{nc}^{\left(0.00434.T-0.008. cd-0.1504\right)}$ Where $cd$ and $nc$ are cycle depth and cycle number respectively.	√	√	32	38	X	CCYASM2	[68]
${L}_y=a.{t_d}^b.{SoC}^c+d.{t}_d. SoC$ With $\left\{\begin{array}{l}a(T)=-7.01.{T}^{-0.668}+0.5259\\ {}b(T)=3.5{E}^{-14}.{T}^{7.815}+0.0312\\ {}c(T)=0.0035.{T}^{1.395}\\ {}d(T)=-2.5{E}^{-6}.{T}^{-0.00013}+0.0019\end{array}\right.$ Where ${L}_y$ is life time in years.	${C}_{loss}=\left(a.{T}^2+b.T+c\right)\exp \left[\left(d.T+e\right).{C}_{rate}\right]. Ah+f.{t}_d^{0.5}.\exp \left[-{E}_a/ RT\right]$ Where the coefficients are given as follows: $a=$ 8.61E−6 1/Ah-K², $b=$ −5.13E−3 1/Ah-K, $c$ = 7.63E−1 1/Ah, $d=$ −6.7E−3 1/K, $e=$ 2.35 1/(C_rate), $f=$ 14,876 1/day^1/2 and ${E}_a=$ 24.5 kJ mol⁻¹.	√	X	26	35	√	CCYASM3	[64]
${C}_{loss}={k}_{c1}.\exp \left(-\frac{k_{c2}}{T}\right).\exp \left({k}_{c2}.V\right).\sqrt{t_d}$ ${R}_i={k}_{r1}.\exp \left(-\frac{k_{r2}}{T}\right).\left[{k}_{r3}.{V}^2+{k}_{r4}.V+{k}_{r5}\right].\sqrt{t_d}$ Where V is battery voltage (volts). Parameters of model are given as follows: ${k}_{c1}$ = 1.14e−3, ${k}_{c2}$ = 258, ${k}_{c3}$ = 2.01, ${k}_{r1}$ = −3.91e−3, ${k}_{r2}$ = 310.9, ${k}_{r3}$ = −124.36, ${k}_{r4}$ = 2.357e−14 and ${k}_{r5}$ = 4.471e−10.	${C}_{loss}=\frac{\Delta {C}_{EOL}}{NEFC}.\frac{DoD}{100}$ ${R}_i=\frac{\Delta {R}_{EOL}}{NEFC}.\frac{DoD}{100}$ ∆EOL is relative variation necessary to reach EOL criterion. $\Delta {C}_{EOL}$ = 0.2 and $\Delta {R}_{EOL}$ = 1. NEFC represents the number of equivalent full cycles and is given by the following relationship: $NEFC={x}_{c1,r1}.{DoD}^{x_{c2,r2}}$ , where ${x}_{c1}$ = 27453.96, ${x}_{c2}$ = −0.711, ${x}_{r1}$ = 16619.58 and ${x}_{r2}$ = −0.4898, are aging coefficients.	√	√	19	27	X	CCYASM4	[80]
${C}_{loss}={\alpha}_{cap}.{t_d}^{0.75}$ , ${R}_i={\alpha}_{res}.{t_d}^{0.75}$ , ${\alpha}_{cap}\left(T,V\right)=\left(7.543.V-23.75\right).{10}^6.\exp \left(\frac{-6976}{T}\right)$ ${\alpha}_{res}\left(T,V\right)=\left(5.270.V-16.32\right).{10}^5.\exp \left(\frac{-5986}{T}\right)$ Where ${\alpha}_{cap}$ and ${\alpha}_{res}$ are calendar aging factors for capacity and resistance respectively.	${C}_{loss}={\alpha}_{cap}.{t_d}^{0.75}+{\beta}_{cap}.\sqrt{Ah}$ , ${R}_i={\alpha}_{res}.{t_d}^{0.75}+{\beta}_{res}. Ah$ , ${\beta}_{cap}=7.348.{10}^{-3}.{\left(\varnothing V-3.667\right)}^2+7.600.{10}^{-4}+4.081.{10}^{-3}.\Delta DoD$ and ${\beta}_{res}=2.153.{10}^{-4}.{\left(\varnothing V-3.725\right)}^2-1.521.{10}^{-5}+2.798.{10}^{-4}.\Delta DoD.$ Where ${\beta}_{cap}$ and ${\beta}_{res}$ are cycle aging factors for capacity fade and resistance increase respectively, $\varnothing V$ is quadratic average voltage and $\Delta DOD$ is linear cycle depth.	√	√	34	35	X	CCYASM5	[29]
Calendar and cycle aging combined models (CCYACM)
${C}_{loss\_ rate}=\exp \left({p}_c.{C}_{rate}\right).\exp \left(\frac{q_c. SoC}{p_c}\right).\exp \left(\frac{s_c}{p_c}\right).\exp \left(\frac{-{m}_c}{p_c.T}\right)$ and ${R}_{i\_ rate}=\exp \left({p}_r.{C}_{rate}\right).\exp \left(\frac{q_r. SoC}{p_r}\right).\exp \left(\frac{s_r}{p_r}\right).\exp \left(\frac{-{m}_r}{p_r.T}\right)$ . where ${C}_{loss\_ rate}$ is capacity degradation rate, and values for ${p}_c,{q}_c,{s}_c\ \mathrm{and}\ {m}_c$ are 8.314, 72,580, 0.092 and 170.22 J mol⁻¹ K⁻¹ respectively for capacity degradation. ${R}_{i\_ rate}$ is resistor increase rate, and the values for ${p}_r,{q}_r,{s}_r\ \mathrm{and}\ {m}_r$ values are 8.314, 57,520, 0.35 and 112.92, respectively.		√	√	17	25	√	CCYACM1	[73]
${C}_{loss}=\sum \limits_i^E\left(\left({k}_1{SoC}_{dev,i}.\exp \left({k}_2.S{oC}_{avg,i}\right)+{k}_3.\exp \left({k}_4{SoC}_{dev,i}\right)\right).\exp \left(\frac{E_a}{R}\left(\frac{1}{T_i}-\frac{1}{T_{ref}}\right)\right)\right).A{h}_i$ Where $i$ is an event, $A{h}_i$ is charge processed during event $i$ , $E$ is total number of events, ${SoC}_{dev}$ is SoC standard deviation, $S{oC}_{avg,i}$ is average SoC, ${T}_i$ is temperature during event $i$ , ${T}_{ref}$ is reference temperature, ${k}_1=$ −4.092E−4, ${k}_2=$ −2.167, ${k}_3=$ 1.408E−5 and ${k}_4=$ 6.130.		√	X	12	16	X	CCYACM2	[81]
${C}_{loss}={k}_{Cal}\left(T, SoC\right).\sqrt{t_d}+{k}_{Cyc, High\ T}(T).\sqrt{Ah_{Tot}}+{k}_{Cyc, Low\ T}\left(T,{C}_{rate\_ Ch}\right).\sqrt{Ah_{Ch}}+{k}_{Cyc, Low\ T\ High\ SoC}\left(T,{C}_{rate\_ Ch}, SoC\right).{Ah}_{Ch}$ , where ${k}_{Cyc, Low\ T\ High\ SoC}\left(T,{I}_{Ch}, SoC\right)={k}_{Cyc, Low\ T\ High\ SoC, ref}.\exp \left[\frac{E_{a, Cyc, Low\ T\ High\ SoC}}{R}\left(\frac{1}{T}-\frac{1}{T_{Ref}}\right)\right].\exp \left[{\beta}_{Low\ T\ High\ SoC}\left(\frac{\ {C}_{rate\_ Ch}-{C}_{rate\_ Ch, Ref}}{\ {Ah}_o}\right)\right].\left(\frac{\mathit{\operatorname{sgn}}\ \left( SoC-{SoC}_{Ref}\right)+1\ }{2}\right)$ , ${k}_{Cyc, Low\ T}\left(T,{I}_{Ch}\right)={k}_{Cyc, Low\ T, Ref.}\ \exp \left[\frac{E_{a, Cyc, Low\ T}}{R}\left(\frac{1}{T}-\frac{1}{T_{Ref}}\right)\right].\exp \left[{\beta}_{Low\ T}\left(\frac{\ {C}_{rate\_ Ch}-{C}_{rate\_ Ch, Ref}}{\ {Ah}_o}\right)\right]$ , ${k}_{Cyc, High\ T}(T)={k}_{Cyc, High\ T, Ref.}\ \exp \left[\frac{-{E}_{a, Cyc, High\ T}}{R}\left(\frac{1}{T}-\frac{1}{T_{Ref}}\right)\right]$ , and ${k}_{Cal}\left(T, SoC\right)={k}_{Cal, Ref}.\exp \left[\frac{-{E}_{a, Cal}}{R}\left(\frac{1}{T}-\frac{1}{T_{Ref}}\right)\right].\left(\exp \left[\frac{\alpha .F}{R}\left(\frac{U_{a, Ref-}{U}_a\ (SoC)}{T_{Ref}}\right)\right]+{k}_0\ \right)$ . ${k}_{Cal}$ is calendar stress factor, ${k}_{Cal, Ref}$ is calendar reference stress factor, ${E}_{a, Cal}$ is parameter activation energy, ${T}_{Ref}$ is reference temperature, ${U}_a$ anode open circuit potential, ${U}_{a, Ref}$ anode open circuit reference, α = 0.384, ${k}_0$ = 0.142, $F$ is Faraday's constant, ${k}_{Cyc}$ is cycle stress factor, $High\ T$ is high temperature, $Low\ T$ is low temperature, ${C}_{rate\_ Ch}$ is charge current, ${C}_{rate\_ Ch, Ref}$ is charge current reference, ${Ah}_o$ is nominal cell capacity, ${\beta}_{Low\ T}$ is 2.64 h, ${t}_d$ is time in days, ${Ah}_{Tot}$ is total charge throughput, ${Ah}_{Ch}$ charge throughput in charge direction and ${\beta}_{Low\ T\ High\ SoC}$ is 7.8 h.		√	X	31	52	√	CCYACM3	[65]

Note: Shown in the table are aging models, that is, calendar aging (only) models (CAOM), cycle aging (only) models (CYAOM), calendar and cycle aging (separated) models (CCYASM), and calendar and cycle aging (combined) models (CCYACM).

As highlighted earlier that the study focuses mainly on models' complexity and their ability to capture current fluctuations (C_rate); these factors have been indicated against each extracted model as shown in the same Table 4. Model complexity has been presented using the total number of variables and parameters (no. of vars. and pars.) and the number of elementary operations (no. of ele. opers) for each model [86]. Furthermore, information regarding whether the model presents Li-ion battery aging as either capacity fade (cap. fade) or resistance increase (res. increase) or both has been presented in the same Table 4 as well.

5 Discussion of Results

Extracted data from the listed empirical and semi-EMs for Li-ion battery calendar aging and cycle aging presented in Table 4 has been summarized and presented in Table 5 to ease readability. Specifically, shown in Table 5 are assigned model code, number of variables and parameters (no. of vars. and pars.), number of elementary operations (no. of ele. opers.), current fluctuation modeling (C_rate), capacity fade (cap. fade), and resistance increase (res. increase). Additionally, the total number of variables, parameters, and operations has been calculated and included as well for analysis purposes.

TABLE 5. Summary of data for empirical and semi-EMs for Li-ion battery calendar and cycle aging presented in Table 4.

Assigned model code	No. of vars. and pars.	No. of ele. opers.	Total number of vars, pars. and opers.	C_rate	Cap. fade	Res. increase
CAOM1	9	9	18	X	X	√
CYAOM1	10	16	26	X	√	X
CYAOM2	9	8	17	√	√	X
CYAOM3	23	33	56	√	√	√
CYAOM4	33	34	67	√	√	√
CCYASM1	14	12	26	√	√	X
CCYASM2	32	38	70	X	√	√
CCYASM3	26	35	61	√	√	X
CCYASM4	19	27	46	X	√	√
CCYASM5	34	35	69	X	√	√
CCYACM1	17	25	42	√	√	√
CCYACM2	12	16	28	X	√	X
CCYACM3	31	52	83	√	√	X

From the summarized results presented in Table 5, the following points can be deduced:

Only one model was found under CAOM. Furthermore, it has been noted that most researchers model calendar aging using Arrhenius law [15, 76] for temperature dependency, power laws for time dependency, and exponential models for SoC dependency. An example of the model equation of which is presented under calendar aging of Table 4 (CAOM1).
Four models under CYAOM were extracted. Of these four, CYAOM1 does not consider current fluctuation in its model. Furthermore, CYAOM1 models capacity fade only, not resistance increase. Model CYAOM2 considers current fluctuations and models capacity fade as well; however, it does not model resistance increase. Models CYAOM3 and CYAOM4 model current fluctuation, capacity fade as well as resistance increase. In terms of model complexity, it is noted that model CYAOM4 has the highest total number of variables, parameters, and operations (67), making it more complex in that category. Model CYAOM2 has minimum complexity (17). Therefore, in general, it can be stated that models in this category which capture current fluctuations, capacity fade, and resistance increase are more complex than the ones which do not capture all three considered factors.
Five models under CCYASM were extracted as shown in the summary table (Table 5). It is noted that all these models model capacity fade of the batteries under consideration. However, out of these five models, two further capture current fluctuations (CCYASM1 and CCYASM3) but not resistance increase, and vice versa for the remaining three models (CCYASM2, CCYASM4, and CCYASM5). On complexity, it is noted that models which capture current fluctuations are less complex as compared to those which do not capture them, with the exception of model CCYASM4, which has 46 total number of variables, parameters, and operations. There is no model in this group that captures all three factors considered. Furthermore, it is also noted that models that capture both capacity fade and resistance increase are more complex, on average, as compared to those that capture current fluctuations and capacity fade only.
Three models under CCYACM were extracted. Out of these models, one model (CCYACM1) captures all three factors, namely current fluctuations, capacity fade, and resistance increase. For the remaining two models, CCYACM2 captures capacity fade only, while CCYACM3 captures capacity fade as well as current fluctuations. In terms of complexity, it is noted that model CCYACM3 is more complex (83) than the other two models, CCYACM1 (42) and CCYACM2 (28).

5.1 Key Findings

The extracted data regarding current fluctuation modeling, capacity fade, and resistance increase modeling of the models summarized in Table 5 has been further summed up for all the models considered. After which, a graph showing how current fluctuation, capacity fade, and resistance increase modeling have been represented in the considered models has been plotted as shown in Figure 3.

Therefore, from Figure 3 as well as Table 5, the following key findings are noted regarding all the extracted models:

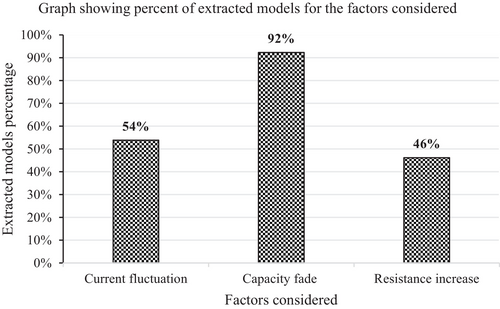
During modeling aging of Li-ion batteries, much focus is on capacity fade as compared to resistance increase (power fade). This is evidenced in Table 5 as almost all studies, 12 out of 13 (92.30%) considered capacity fade during aging modeling of the battery. Of these 12 studies, only 6 (50.00%) considered resistance increase as well during aging modeling. The remaining one study that did not consider capacity fade considered resistance increase only, and it focused on calendar aging only of the battery.
Of the 13 extracted cycle and calendar aging models, 7 models (53.85%) considered current fluctuations as one of the input variables to aging models. This shows that C_rate of Li-ion batteries is an important factor when it comes to the aging of the Li-ion battery.
There are 7 models (53.85%) that model capacity fade as a function of current fluctuation, while there are only 3 models (23.07%) that model resistance increase as a function of current fluctuation. This shows that current fluctuation is much more considered when modeling capacity fade of Li-ion battery as compared to when modeling resistance increase.

Based on these findings and the fact that the study focused on Li-ion battery aging modeling for BMS for off-grid RESs, mainly considering current fluctuation representation and complexity (considering minimum complexity), it is noted that there are three models that meet these requirements. These three models fall under CYAOM, CCYAOM, and CCYACM. The three model codes are CYAOM2, CCYASM1, and CCYACM1, and they have been extracted from Table 5 and presented in Table 6. Other extracted information is the total number of variables, parameters, and operations (renamed to complexity), current fluctuation modeling, capacity fade modeling, and resistance increase modeling.

TABLE 6. Extracted empirical and semi-EMs that meet BMS requirements for off-grid RESs.

Assigned model code	Complexity	C_rate	Cap. fade	Res. increase
CYAOM2	17	√	√	X
CCYASM1	26	√	√	X
CCYACM1	42	√	√	√

It is noted from Table 6 that CYAOM2 has minimum complexity among the three models; however, it only models cycle aging, disregarding calendar aging. Among the three, CCYACM1 has the highest complexity; this is due to the inclusion of resistance increase in the model. The other two models do not include resistance increase, as seen in the table. All these three models presented in Table 6 could be used depending on users' needs regarding aging monitoring and control of Li-ion batteries in off-grid RESs. However, if minimum complexity and current fluctuation representation are among the requirements for BMS for off-grid RESs, then the study recommends selecting either CYAOM2 or CCYASM1, as they have lower complexity compared to CCYACM1. Finally, the choice between CYAOM2 and CCYASM1 is dependent on whether the target is to capture cycle aging only or cycle and calendar. If cycle aging only is needed, then CYAOM2 is the option; otherwise, CCYASM1 is the option.

6 Conclusions and Recommendations

In this research paper, empirical and semi-empirical Li-ion battery aging models have been studied to identify appropriate models in terms of complexity and current fluctuation representation for BMS application in off-grid RESs. In this regard, different studies that focused on calendar aging and cycle aging of Li-ion battery and modeling of the same using empirical and semi-EMs were listed from the literature. After which, aging models were extracted and evaluated in terms of complexity, current fluctuation representation, capacity fade modeling, and resistance increase modeling. These evaluations eventually resulted in identifying appropriate Li-ion battery aging models for BMS application in off-grid RESs.

Based on the study conducted, the following conclusions have been arrived at:

When modeling aging of Li-ion batteries, capacity fade is mostly utilized compared to resistance increase. This capacity fade is influenced by SoC, T, and time during calendar aging, and mainly by temperature, C_rate, and SoC during cycle aging.
Empirical and semi-EMs of Li-ion battery aging that capture both capacity fade and resistance increase are more complex than those that capture only one of these parameters.
Three models meet BMS requirements for off-grid RESs considered in this study, which are current fluctuation representation and complexity. These three models fall under CYAOM, CCYAOM, and CCYACM. The three model codes are CYAOM2, CCYASM1, and CCYACM1. Any of these models can be implemented in Li-ion battery BMS for aging monitoring and control depending on the specific needs of the user.

Furthermore, the study recommends further research of the following in relation to empirical and semi-EMs for BMS in off-grid RESs:

Compare empirical and semi-EMs through both simulation and experimental studies using selected commonly available Li-ion battery chemistries. This would assist in validating the models using similar conditions, hence improving confidence levels for implementation in BMS for off-grid RESs. This would also make it possible to establish accuracy levels of the models when deployed for different Li-ion battery chemistries.
Evaluate the empirical and semi-EM using case studies to establish the appropriate way of representing Li-ion battery aging, whether in terms of capacity fade or resistance increase. This could be vital in further improving the models in terms of complexity and accuracy for different applications, including in off-grid RESs.
Characterize model-based BMS aiming at matching with appropriate empirical and semi-EMs for off-grid RESs implementation for reduced complexity and current fluctuation representation. This would facilitate deployment of efficient model-based BMS resulting in reduced overall Li-ion battery aging rate.

Nomenclature

Ah: Ampere-hour
BMS: battery management system
CAOM: calendar aging (only) models
CCYACM: calendar and cycle aging (combined) models
CCYASM: calendar and cycle aging (separated) models
CEI: cathode electrolyte interphase
CL: conductivity loss
C_loss: capacity loss
C_rate: current rate
CYAOM: cycle aging (only) models
DoD: depth of discharge
E_a: activation energy
ECM: equivalent circuit models
EM: empirical model
ESS: energy storage system
FF: fossil fuel
LAM: loss of active material
LCO: lithium cobalt oxide
LFP: lithium-iron-phosphate
Li-ion: lithium-ion
LLI: loss of lithium inventory
LMO: lithium-manganese oxide
LTO: lithium-titanate-oxide
ML: machine learning
MLM: machine learning model
NCA: nickel-cobalt-aluminum
NMC: nickel-manganese-cobalt
PBM: physics-based model
R: universal gas constant
RE: renewable energy
RES: renewable energy system
R_i: internal resistance increase
SEI: solid electrolyte interphase
SoC: state of charge
SoH: state of health
T: temperature in degrees Celsius
t_d: time in days
T_k: temperature in degrees Kelvins
t_m: time in months
ΔSoC: change of SoC

Author Contributions

Isaac Gwayi: conceptualization, investigation, writing – original draft, methodology, validation, visualization, writing – review and editing, data curation, formal analysis. Sarah Paul Ayeng'o: conceptualization, writing – review and editing, supervision, methodology. Cuthbert Z. M. Kimambo: conceptualization, methodology, writing – review and editing, supervision.

Acknowledgments

The authors acknowledge support from Malawi University of Business and Applied Sciences (MUBAS) and from the Department of Mechanical and Industrial Engineering, University of Dar es Salaam (UDSM).

Conflicts of Interest

The authors declare no conflicts of interest.

Open Research

Data Availability Statement

Data sharing is not applicable to this article as no new data were created or analyzed in this study.

References

1M. A. M. Ramli, A. Hiendro, and S. Twaha, “Economic Analysis of PV/Diesel Hybrid System With Flywheel Energy Storage,” Renewable Energy 78 (2015): 398–405, https://doi.org/10.1016/j.renene.2015.01.026.
10.1016/j.renene.2015.01.026
Web of Science® Google Scholar
2M. Ball, M. Wietschel, and O. Rentz, “Integration of a Hydrogen Economy Into the German Energy System: An Optimising Modelling Approach,” International Journal of Hydrogen Energy 32, no. 10–11 (2007): 1355–1368, https://doi.org/10.1016/j.ijhydene.2006.10.016.
10.1016/j.ijhydene.2006.10.016
CAS Web of Science® Google Scholar
3N. B. Mjami, C. Kimambo, S. Ayeng'o, and I. Orozova-Bekkevold, “Prospects and Challenges for Utilisation of Low-to Medium-Temperature Geothermal Resources in Tanzania,” Geothermics 129 (2025): 103288, https://doi.org/10.1016/j.geothermics.2025.103288.
10.1016/j.geothermics.2025.103288
Web of Science® Google Scholar
4R. Jiang, J. Wang, and Y. Guan, “Robust Unit Commitment With Wind Power and Pumped Storage Hydro,” IEEE Transactions on Power Systems 27, no. 2 (2012): 800–810, https://doi.org/10.1109/TPWRS.2011.2169817.
10.1109/TPWRS.2011.2169817
Web of Science® Google Scholar
5A. Panda, A. K. Dauda, H. Chua, R. R. Tan, and K. B. Aviso, “Recent Advances in the Integration of Renewable Energy Sources and Storage Facilities With Hybrid Power Systems,” Cleaner Engineering and Technology 12 (2023): 100598, https://doi.org/10.1016/j.clet.2023.100598.
10.1016/j.clet.2023.100598
Web of Science® Google Scholar
6A. Gabash and P. Li, “Active-Reactive Optimal Power Flow in Distribution Networks With Embedded Generation and Battery Storage,” IEEE Transactions on Power Systems 27, no. 4 (2012): 2026–2035, https://doi.org/10.1109/TPWRS.2012.2187315.
10.1109/TPWRS.2012.2187315
Web of Science® Google Scholar
7S. Tewari and N. Mohan, “Value of NAS Energy Storage Toward Integrating Wind: Results From the Wind to Battery Project,” IEEE Transactions on Power Systems 28, no. 1 (2013): 532–541, https://doi.org/10.1109/TPWRS.2012.2205278.
10.1109/TPWRS.2012.2205278
Web of Science® Google Scholar
8B. Scrosati and J. Garche, “Lithium Batteries: Status, Prospects and Future,” Journal of Power Sources 195, no. 9 (2010): 2419–2430, https://doi.org/10.1016/j.jpowsour.2009.11.048.
10.1016/j.jpowsour.2009.11.048
CAS Web of Science® Google Scholar
9C. Capasso and O. Veneri, “Experimental Analysis on the Performance of Lithium Based Batteries for Road Full Electric and Hybrid Vehicles,” Applied Energy 136 (2014): 921–930, https://doi.org/10.1016/j.apenergy.2014.04.013.
10.1016/j.apenergy.2014.04.013
CAS Web of Science® Google Scholar
10I. Gwayi, S. P. Ayeng'o, and C. Z. M. Kimambo, “Selection of Electrochemical and Electrical Energy Storage Systems for Off-Grid Renewable Energy Mini-Grids: A Review,” Cleaner Engineering and Technology 25 (2025): 100906, https://doi.org/10.1016/j.clet.2025.100906.
10.1016/j.clet.2025.100906
Web of Science® Google Scholar
11S. P. Ayeng'o, T. Schirmer, K. P. Kairies, H. Axelsen, and D. U. Sauer, “Comparison of Off-Grid Power Supply Systems Using Lead-Acid and Lithium-Ion Batteries,” Solar Energy 162 (2018): 140–152, https://doi.org/10.1016/j.solener.2017.12.049.
10.1016/j.solener.2017.12.049
Web of Science® Google Scholar
12N. Nitta, F. Wu, J. T. Lee, and G. Yushin, “Li-Ion Battery Materials: Present and Future,” Materials Today 18, no. 5 (2015): 252–264, https://doi.org/10.1016/j.mattod.2014.10.040.
10.1016/j.mattod.2014.10.040
CAS Web of Science® Google Scholar
13A. Eddahech, O. Briat, E. Woirgard, and J. M. Vinassa, “Remaining Useful Life Prediction of Lithium Batteries in Calendar Ageing for Automotive Applications,” Microelectronics Reliability 52, no. 9–10 (2012): 2438–2442, https://doi.org/10.1016/j.microrel.2012.06.085.
10.1016/j.microrel.2012.06.085
CAS Web of Science® Google Scholar
14A. Barré, B. Deguilhem, S. Grolleau, M. Gérard, F. Suard, and D. Riu, “A Review on Lithium-Ion Battery Ageing Mechanisms and Estimations for Automotive Applications,” Journal of Power Sources 241 (2013): 680–689, https://doi.org/10.1016/j.jpowsour.2013.05.040.
10.1016/j.jpowsour.2013.05.040
CAS Web of Science® Google Scholar
15J. Schmitt, A. Maheshwari, M. Heck, S. Lux, and M. Vetter, “Impedance Change and Capacity Fade of Lithium Nickel Manganese Cobalt Oxide-Based Batteries During Calendar Aging,” Journal of Power Sources 353 (2017): 183–194, https://doi.org/10.1016/j.jpowsour.2017.03.090.
10.1016/j.jpowsour.2017.03.090
CAS Web of Science® Google Scholar
16Y. Liu, K. Xie, Y. Pan, H. Wang, Y. Li, and C. Zheng, “Simplified Modeling and Parameter Estimation to Predict Calendar Life of Li-Ion Batteries,” Solid State Ionics 320 (2018): 126–131, https://doi.org/10.1016/j.ssi.2018.02.038.
10.1016/j.ssi.2018.02.038
CAS Web of Science® Google Scholar
17M. Broussely, P. Biensan, F. Bonhomme, P. Blanchard, S. Herreyre, and K. Nechev, “Main Aging Mechanisms in Li Ion Batteries,” Journal of Power Sources 146, no. 1–2 (2005): 90–96, https://doi.org/10.1016/j.jpowsour.2005.03.172.
10.1016/j.jpowsour.2005.03.172
CAS Web of Science® Google Scholar
18B. Schäfer, M. Matthiae, X. Zhang, M. Rohden, M. Timme, and D. Witthaut, “Escape Routes, Weak Links, and Desynchronization in Fluctuation-Driven Networks,” Physical Review E 95, no. 6 (2017): 060203, https://doi.org/10.1103/PhysRevE.95.060203.
10.1103/PhysRevE.95.060203
PubMed Web of Science® Google Scholar
19R. Sathishkumar, K. K. Sathish, and K. M. Mahesh, “ Dynamic Energy Management of Micro Grids Using Battery Super Capacitor Combined Storage,” in 2012 Annual IEEE India Conference: Kochi, Kerala, India (IEEE, 2012), 1078–1083, https://doi.org/10.1109/INDCON.2012.6420777.
10.1109/INDCON.2012.6420777
Google Scholar
20A. A. Raouf Mohamed, D. J. Morrow, R. J. Best, A. Cupples, I. Bailie, and J. Pollock, “Distributed Battery Energy Storage Systems Operation Framework for Grid Power Levelling in the Distribution Networks,” IET Smart Grid 4, no. 6 (2021): 582–598, https://doi.org/10.1049/stg2.12040.
10.1049/stg2.12040
Web of Science® Google Scholar
21S. A. Juma, S. P. Ayeng'o, and C. Z. M. Kimambo, “A Review of Control Strategies for Optimized Microgrid Operations,” IET Renewable Power Generation 18, no. 14 (2024): 2785–2818, https://doi.org/10.1049/rpg2.13056.
10.1049/rpg2.13056
Web of Science® Google Scholar
22I. S. Kim, “The Novel State of Charge Estimation Method for Lithium Battery Using Sliding Mode Observer,” Journal of Power Sources 163, no. 1 SPEC. ISS (2006): 584–590, https://doi.org/10.1016/j.jpowsour.2006.09.006.
10.1016/j.jpowsour.2006.09.006
CAS Google Scholar
23J. Han, D. Kim, and M. Sunwoo, “State-of-Charge Estimation of Lead-Acid Batteries Using an Adaptive Extended Kalman Filter,” Journal of Power Sources 188, no. 2 (2009): 606–612, https://doi.org/10.1016/j.jpowsour.2008.11.143.
10.1016/j.jpowsour.2008.11.143
CAS Web of Science® Google Scholar
24M. El-Dalahmeh, M. Al-Greer, M. El-Dalahmeh, and M. Short, “Smooth Particle Filter-Based Likelihood Approximations for Remaining Useful Life Prediction of Lithium-Ion Batteries,” IET Smart Grid 4, no. 2 (2021): 151–161, https://doi.org/10.1049/stg2.12013.
10.1049/stg2.12013
Web of Science® Google Scholar
25B. Pattipati, C. Sankavaram, and K. R. Pattipati, “System Identification and Estimation Framework for Pivotal Automotive Battery Management System Characteristics,” IEEE Transactions on Systems, Man and Cybernetics Part C: Applications and Reviews 41, no. 6 (2011): 869–884, https://doi.org/10.1109/TSMCC.2010.2089979.
10.1109/TSMCC.2010.2089979
Web of Science® Google Scholar
26A. I. Stan, M. Świerczyński, D. I. Stroe, R. Teodorescu, and S. J. Andreasen, “ Lithium-Ion Battery Chemistries From Renewable Energy Storage to Automotive and Back-Up Power Applications—An Overview,” in 2014 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM) (IEEE, 2014), 713–720, https://doi.org/10.1109/OPTIM.2014.6850936.
10.1109/OPTIM.2014.6850936
Google Scholar
27M. Doyle, F. Thomas, and N. John, “Modeling of Galvanostatic Charge and Discharge of the Lithium/Polymer/Insertion Cell,” Journal of the Electrochemical Society 140, no. 6 (1993): 1526, https://doi.org/10.1149/1.2221597.
10.1149/1.2221597
CAS Web of Science® Google Scholar
28M. Jafari, K. Khan, and L. Gauchia, “Deterministic Models of Li-Ion Battery Aging: It Is a Matter of Scale,” Journal of Energy Storage 20 (2018): 67–77, https://doi.org/10.1016/j.est.2018.09.002.
10.1016/j.est.2018.09.002
Web of Science® Google Scholar
29J. Schmalstieg, S. Käbitz, M. Ecker, and D. U. Sauer, “A Holistic Aging Model for Li(NiMnCo)O₂ Based 18650 Lithium-Ion Batteries,” Journal of Power Sources 257 (2014): 325–334, https://doi.org/10.1016/j.jpowsour.2014.02.012.
10.1016/j.jpowsour.2014.02.012
CAS Web of Science® Google Scholar
30S. Nejad, D. T. Gladwin, and D. A. Stone, “A Systematic Review of Lumped-Parameter Equivalent Circuit Models for Real-Time Estimation of Lithium-Ion Battery States,” Journal of Power Sources 316 (2016): 183–196, https://doi.org/10.1016/j.jpowsour.2016.03.042.
10.1016/j.jpowsour.2016.03.042
CAS Web of Science® Google Scholar
31S. Wang, P. Huang, C. Lian, and H. Liu, “Multi-Interest Adaptive Unscented Kalman Filter Based on Improved Matrix Decomposition Methods for Lithium-Ion Battery State of Charge Estimation,” Journal of Power Sources 606 (2024): 234547, https://doi.org/10.1016/J.JPOWSOUR.2024.234547.
10.1016/j.jpowsour.2024.234547
CAS Web of Science® Google Scholar
32J. Zhang, Y. Jiang, X. Li, M. Huo, H. Luo, and S. Yin, “An Adaptive Remaining Useful Life Prediction Approach for Single Battery With Unlabeled Small Sample Data and Parameter Uncertainty,” Reliability Engineering and System Safety 222 (2022): 108357, https://doi.org/10.1016/J.RESS.2022.108357.
10.1016/j.ress.2022.108357
Web of Science® Google Scholar
33S. Wang, R. Zhou, Y. Ren, M. Jiao, H. Liu, and C. Lian, “Advanced Data-Driven Techniques in AI for Predicting Lithium-Ion Battery Remaining Useful Life: A Comprehensive Review,” Green Chemical Engineering 6, no. 2 (2025): 139–153, https://doi.org/10.1016/j.gce.2024.09.001.
10.1016/j.gce.2024.09.001
Web of Science® Google Scholar
34Z. Wang, J. Ma, and L. Zhang, “State-of-Health Estimation for Lithium-Ion Batteries Based on the Multi-Island Genetic Algorithm and the Gaussian Process Regression,” IEEE Access 5 (2017): 21286–21295, https://doi.org/10.1109/ACCESS.2017.2759094.
10.1109/ACCESS.2017.2759094
Web of Science® Google Scholar
35M. Berecibar, F. Devriendt, M. Dubarry, I. Villarreal, N. Omar, and W. Verbeke, “Online State of Health Estimation on NMC Cells Based on Predictive Analytics,” Journal of Power Sources 320 (2016): 239–250, https://doi.org/10.1016/j.jpowsour.2016.04.109.
10.1016/j.jpowsour.2016.04.109
CAS Web of Science® Google Scholar
36S. Wang, M. Jiao, R. Zhou, Y. Ren, H. Liu, and C. Lian, “A Multi-Dimensional Machine Learning Framework for Accurate and Efficient Battery State of Charge Estimation,” Journal of Power Sources 623 (2024): 235417, https://doi.org/10.1016/J.JPOWSOUR.2024.235417.
10.1016/j.jpowsour.2024.235417
CAS Web of Science® Google Scholar
37H. Pan, Z. Lü, H. Wang, H. Wei, and L. Chen, “Novel Battery State-of-Health Online Estimation Method Using Multiple Health Indicators and an Extreme Learning Machine,” Energy 160 (2018): 466–477, https://doi.org/10.1016/j.energy.2018.06.220.
10.1016/j.energy.2018.06.220
Web of Science® Google Scholar
38D. Yang, Y. Wang, R. Pan, R. Chen, and Z. Chen, “State-of-Health Estimation for the Lithium-Ion Battery Based on Support Vector Regression,” Applied Energy 227 (2018): 273–283, https://doi.org/10.1016/j.apenergy.2017.08.096.
10.1016/j.apenergy.2017.08.096
Web of Science® Google Scholar
39K. Liu, X. Hu, Z. Wei, Y. Li, and Y. Jiang, “Modified Gaussian Process Regression Models for Cyclic Capacity Prediction of Lithium-Ion Batteries,” IEEE Transactions on Transportation Electrification 5, no. 4 (2019): 1225–1236, https://doi.org/10.1109/TTE.2019.2944802.
10.1109/TTE.2019.2944802
Web of Science® Google Scholar
40Y. Li, K. Liu, A. M. Foley, A. Zülke, M. Berecibar, and E. Nanini-Maury, “Data-Driven Health Estimation and Lifetime Prediction of Lithium-Ion Batteries: A Review,” Renewable and Sustainable Energy Reviews 113 (2019): 109254, https://doi.org/10.1016/j.rser.2019.109254.
10.1016/j.rser.2019.109254
Web of Science® Google Scholar
41X. Han, L. Lu, Y. Zheng, X. Feng, Z. Li, and J. Li, “A Review on the Key Issues of the Lithium Ion Battery Degradation Among the Whole Life Cycle,” eTransportation 1 (2019): 100005, https://doi.org/10.1016/j.etran.2019.100005.
10.1016/j.etran.2019.100005
Web of Science® Google Scholar
42M. Scarfogliero, S. Carmeli, F. Castelli-Dezza, M. Mauri, M. Rossi, and G. Marchegiani, “ Lithium-Ion Batteries for Electric Vehicles: A Review on Aging Models for Vehicle-to-Grid Services,” in 2018 International Conference of Electrical and Electronic Technologies for Automotive (IEEE, 2018), 1, https://doi.org/10.23919/EETA.2018.8493211.
10.23919/EETA.2018.8493211
Google Scholar
43A. Ahmadian, M. Sedghi, A. Elkamel, M. Fowler, and M. Aliakbar Golkar, “Plug-In Electric Vehicle Batteries Degradation Modeling for Smart Grid Studies: Review, Assessment and Conceptual Framework,” Renewable and Sustainable Energy Reviews 81 (2018): 2609–2624, https://doi.org/10.1016/j.rser.2017.06.067.
10.1016/j.rser.2017.06.067
Web of Science® Google Scholar
44R. Xiong, L. Li, and J. Tian, “Towards a Smarter Battery Management System: A Critical Review on Battery State of Health Monitoring Methods,” Journal of Power Sources 405 (2018): 18–29, https://doi.org/10.1016/j.jpowsour.2018.10.019.
10.1016/j.jpowsour.2018.10.019
CAS Web of Science® Google Scholar
45M. Berecibar, I. Gandiaga, I. Villarreal, N. Omar, J. Van Mierlo, and P. Van Den Bossche, “Critical Review of State of Health Estimation Methods of Li-Ion Batteries for Real Applications,” Renewable and Sustainable Energy Reviews 56 (2016): 572–587, https://doi.org/10.1016/j.rser.2015.11.042.
10.1016/j.rser.2015.11.042
CAS Web of Science® Google Scholar
46M. Lucu, E. Martinez-Laserna, I. Gandiaga, and H. Camblong, “A Critical Review on Self-Adaptive Li-Ion Battery Ageing Models,” Journal of Power Sources 401 (2018): 85–101, https://doi.org/10.1016/j.jpowsour.2018.08.064.
10.1016/j.jpowsour.2018.08.064
CAS Web of Science® Google Scholar
47M. S. H. Lipu, M. A. Hannan, A. Hussain, M. M. Hoque, P. J. Ker, and M. H. M. Saad, “A Review of State of Health and Remaining Useful Life Estimation Methods for Lithium-Ion Battery in Electric Vehicles: Challenges and Recommendations,” Journal of Cleaner Production 205, no. 2018 (2018): 115–133, https://doi.org/10.1016/j.jclepro.2018.09.065.
10.1016/j.jclepro.2018.09.065
Google Scholar
48J. Vetter, P. Novák, M. R. Wagner, C. Veit, K. C. Möller, and J. O. Besenhard, “Ageing Mechanisms in Lithium-Ion Batteries,” Journal of Power Sources 147, no. 1–2 (2005): 269–281, https://doi.org/10.1016/j.jpowsour.2005.01.006.
10.1016/j.jpowsour.2005.01.006
CAS Web of Science® Google Scholar
49C. R. Birkl, M. R. Roberts, E. McTurk, P. G. Bruce, and D. A. Howey, “Degradation Diagnostics for Lithium Ion Cells,” Journal of Power Sources 341 (2017): 373–386, https://doi.org/10.1016/j.jpowsour.2016.12.011.
10.1016/j.jpowsour.2016.12.011
CAS Web of Science® Google Scholar
50K. Kalaga, M. T. F. Rodrigues, S. E. Trask, I. A. Shkrob, and D. P. Abraham, “Calendar-Life Versus Cycle-Life Aging of Lithium-Ion Cells With Silicon-Graphite Composite Electrodes,” Electrochimica Acta 280 (2018): 221–228, https://doi.org/10.1016/j.electacta.2018.05.101.
10.1016/j.electacta.2018.05.101
CAS Web of Science® Google Scholar
51C. Pastor-Fernández, T. F. Yu, W. D. Widanage, and J. Marco, “Critical Review of Non-Invasive Diagnosis Techniques for Quantification of Degradation Modes in Lithium-Ion Batteries,” Renewable and Sustainable Energy Reviews 109 (2019): 138–159, https://doi.org/10.1016/j.rser.2019.03.060.
10.1016/j.rser.2019.03.060
CAS Web of Science® Google Scholar
52E. Sarasketa-Zabala, F. Aguesse, I. Villarreal, L. M. Rodriguez-Martinez, C. M. López, and P. Kubiak, “Understanding Lithium Inventory Loss and Sudden Performance Fade in Cylindrical Cells During Cycling With Deep-Discharge Steps,” Journal of Physical Chemistry C 119, no. 2 (2015): 896–906, https://doi.org/10.1021/jp510071d.
10.1021/jp510071d
CAS Web of Science® Google Scholar
53C. Delacourt and M. Safari, “ Mathematical Modeling of Aging of Li-Ion Batteries,” in Physical Multiscale Modeling and Numerical Simulation of Electrochemical Devices for Energy Conversion and Storage: From Theory to Engineering to Practice (IEEE, 2016), 151–190, https://doi.org/10.1007/978-1-4471-5677-2_5.
10.1007/978-1-4471-5677-2_5
Google Scholar
54P. Keil, S. F. Schuster, J. Wilhelm, J. Travi, A. Hauser, and R. C. Karl, “Calendar Aging of Lithium-Ion Batteries,” Journal of the Electrochemical Society 163, no. 9 (2016): A1872–A1880, https://doi.org/10.1149/2.0411609jes.
10.1149/2.0411609jes
CAS Web of Science® Google Scholar
55P. Arorat, R. E. White, and M. Doyle, “Capacity Fade Mechanisms and Side Reactions in Lithium-Ion Batteries,” Journal of the Electrochemical Society 145, no. 10 (1998): 3647, https://doi.org/10.1149/1.1838857.
10.1149/1.1838857
Google Scholar
56B. Xu, A. Oudalov, A. Ulbig, G. Andersson, and D. S. Kirschen, “Modeling of Lithium-Ion Battery Degradation for Cell Life Assessment,” IEEE Transactions on Smart Grid 9, no. 2 (2018): 1131–1140, https://doi.org/10.1109/TSG.2016.2578950.
10.1109/TSG.2016.2578950
Web of Science® Google Scholar
57E. Peled, D. B. Tow, A. Merson, A. Gladkich, L. Burstein, and D. Golodnitsky, “Composition, Depth Profiles and Lateral Distribution of Materials in the SEI Built on HOPG-TOF SIMS and XPS Studies,” Journal of Power Sources 97 (2001): 52–57, https://doi.org/10.1016/S0378-7753(01)00505-5.
10.1016/S0378-7753(01)00505-5
Web of Science® Google Scholar
58J. C. Hall, T. Lin, G. Brown, P. Biensan, F. Bonhomme, and S. Diego, “ Decay Processes and Life Predictions for Lithium Ion Satellite Cells,” in 4th International Energy Conversion Engineering Conference and Exhibit (IECEC) (American Institute of Aeronautics and Astronautics, 2006), 11, https://doi.org/10.2514/6.2006-4078.
10.2514/6.2006-4078
Google Scholar
59X. Liao, Q. Huang, S. Mai, X. Wang, M. Xu, and L. Xing, “Understanding Self-Discharge Mechanism of Layered Nickel Cobalt Manganese Oxide at High Potential,” Journal of Power Sources 286 (2015): 551–556, https://doi.org/10.1016/j.jpowsour.2015.04.032.
10.1016/j.jpowsour.2015.04.032
CAS Web of Science® Google Scholar
60T. Joshi, K. Eom, G. Yushin, and T. F. Fuller, “Effects of Dissolved Transition Metals on the Electrochemical Performance and SEI Growth in Lithium-Ion Batteries,” Journal of the Electrochemical Society 161, no. 12 (2014): A1915–A1921, https://doi.org/10.1149/2.0861412jes.
10.1149/2.0861412jes
Web of Science® Google Scholar
61W. Li, “Review—An Unpredictable Hazard in Lithium-Ion Batteries From Transition Metal Ions: Dissolution From Cathodes, Deposition on Anodes and Elimination Strategies,” Journal of the Electrochemical Society 167, no. 9 (2020): 090514, https://doi.org/10.1149/1945-7111/ab847f.
10.1149/1945-7111/ab847f
CAS Google Scholar
62S. Bourlot, P. Blanchard, and S. Robert, “Investigation of Aging Mechanisms of High Power Li-Ion Cells Used for Hybrid Electric Vehicles,” Journal of Power Sources 196, no. 16 (2011): 6841–6846, https://doi.org/10.1016/j.jpowsour.2010.09.103.
10.1016/j.jpowsour.2010.09.103
CAS Web of Science® Google Scholar
63K. Edström, T. Gustafsson, and J. O. Thomas, “The Cathode-Electrolyte Interface in the Li-Ion Battery,” Electrochimica Acta 50, no. 2-3 SPEC. ISS (2004): 397–403, https://doi.org/10.1016/j.electacta.2004.03.049.
10.1016/j.electacta.2004.03.049
Google Scholar
64J. Wang, J. Purewal, P. Liu, J. Hicks-Garner, S. Soukazian, and E. Sherman, “Degradation of Lithium Ion Batteries Employing Graphite Negatives and Nickel-Cobalt-Manganese Oxide + Spinel Manganese Oxide Positives: Part 1, Aging Mechanisms and Life Estimation,” Journal of Power Sources 269 (2014): 937–948, https://doi.org/10.1016/j.jpowsour.2014.07.030.
10.1016/j.jpowsour.2014.07.030
CAS Web of Science® Google Scholar
65M. Schimpe, M. E. von Kuepach, M. Naumann, H. C. Hesse, K. Smith, and A. Jossen, “Comprehensive Modeling of Temperature-Dependent Degradation Mechanisms in Lithium Iron Phosphate Batteries,” Journal of the Electrochemical Society 165, no. 2 (2018): A181–A193, https://doi.org/10.1149/2.1181714jes.
10.1149/2.1181714jes
CAS Web of Science® Google Scholar
66D. I. Stroe, M. Swierczynski, S. K. Kær, and R. Teodorescu, “Degradation Behavior of Lithium-Ion Batteries During Calendar Ageing—The Case of the Internal Resistance Increase,” IEEE Transactions on Industry Applications 54, no. 1 (2018): 517–525, https://doi.org/10.1109/TIA.2017.2756026.
10.1109/TIA.2017.2756026
CAS Web of Science® Google Scholar
67I. Bloom, B. W. Cole, J. J. Sohn, S. A. Jones, E. G. Polzin, and V. S. Battaglia, “An Accelerated Calendar and Cycle Life Study of Li-Ion Cells,” Journal of Power Sources 101 (2001): 238–247, https://doi.org/10.1016/S0378-7753(01)00783-2.
10.1016/S0378-7753(01)00783-2
CAS Web of Science® Google Scholar
68M. Swierczynski, D. I. Stroe, A. I. Stan, R. Teodorescu, and S. K. Kær, “Lifetime Estimation of the Nanophosphate LiFePO₄/C Battery Chemistry Used in Fully Electric Vehicles,” IEEE Transactions on Industry Applications 51, no. 4 (2015): 3453–3461, https://doi.org/10.1109/TIA.2015.2405500.
10.1109/TIA.2015.2405500
CAS Web of Science® Google Scholar
69A. Eddahech, O. Briat, and J. M. Vinassa, “Performance Comparison of Four Lithium-Ion Battery Technologies Under Calendar Aging,” Energy 84 (2015): 542–550, https://doi.org/10.1016/j.energy.2015.03.019.
10.1016/j.energy.2015.03.019
CAS Web of Science® Google Scholar
70P. Röder, B. Stiaszny, J. C. Ziegler, N. Baba, P. Lagaly, and H. D. Wiemhöfer, “The Impact of Calendar Aging on the Thermal Stability of a LiMn₂O₄-Li(Ni1/3Mn1/3Co 1/3)O₂/Graphite Lithium-Ion Cell,” Journal of Power Sources 268 (2014): 315–325, https://doi.org/10.1016/j.jpowsour.2014.06.040.
10.1016/j.jpowsour.2014.06.040
CAS Web of Science® Google Scholar
71J. Belt, V. Utgikar, and I. Bloom, “Calendar and PHEV Cycle Life Aging of High-Energy, Lithium-Ion Cells Containing Blended Spinel and Layered-Oxide Cathodes,” Journal of Power Sources 196, no. 23 (2011): 10213–10221, https://doi.org/10.1016/j.jpowsour.2011.08.067.
10.1016/j.jpowsour.2011.08.067
CAS Web of Science® Google Scholar
72J. de Hoog, J. M. Timmermans, D. Ioan-Stroe, M. Swierczynski, J. Jaguemont, and S. Goutam, “Combined Cycling and Calendar Capacity Fade Modeling of a Nickel-Manganese-Cobalt Oxide Cell With Real-Life Profile Validation,” Applied Energy 200 (2017): 47–61, https://doi.org/10.1016/j.apenergy.2017.05.018.
10.1016/j.apenergy.2017.05.018
Web of Science® Google Scholar
73I. Baghdadi, O. Briat, J. Y. Delétage, P. Gyan, and J. M. Vinassa, “Lithium Battery Aging Model Based on Dakin's Degradation Approach,” Journal of Power Sources 325 (2016): 273–285, https://doi.org/10.1016/j.jpowsour.2016.06.036.
10.1016/j.jpowsour.2016.06.036
CAS Web of Science® Google Scholar
74E. Redondo-Iglesias, P. Venet, and S. Pelissier, “ Influence of the Non-Conservation of SoC Value During Calendar Ageing Tests on Modelling the Capacity Loss of Batteries,” in 2015 Tenth International Conference on Ecological Vehicles and Renewable Energies (EVER) (IEEE, 2015), 1–5, https://doi.org/10.1109/EVER.2015.7112987.
10.1109/EVER.2015.7112987
Google Scholar
75H. Yoshida, N. Imamura, T. Inoue, K. Takeda, and H. Naito, “Verification of Life Estimation Model for Space Lithium-Ion Cells,” Electrochemistry 78, no. 5 (2010): 482–488, https://doi.org/10.5796/electrochemistry.78.482.
10.5796/electrochemistry.78.482
CAS Web of Science® Google Scholar
76S. Käbitz, J. B. Gerschler, M. Ecker, Y. Yurdagel, B. Emmermacher, and D. André, “Cycle and Calendar Life Study of a Graphite|LiNi1/3Mn 1/3Co1/3O2 Li-Ion High Energy System. Part A: Full Cell Characterization,” Journal of Power Sources 239 (2013): 572–583, https://doi.org/10.1016/j.jpowsour.2013.03.045.
10.1016/j.jpowsour.2013.03.045
Web of Science® Google Scholar
77M. Ecker, N. Nieto, S. Käbitz, J. Schmalstieg, H. Blanke, and D. U. Sauer, “Calendar and Cycle Life Study of Li(NiMnCo)O₂-Based 18650 Lithium-Ion Batteries,” Journal of Power Sources 248 (2014): 839–851, https://doi.org/10.1016/j.jpowsour.2013.09.143.
10.1016/j.jpowsour.2013.09.143
CAS Google Scholar
78R. B. Wright, C. G. Motloch, J. R. Belt, J. P. Christophersen, C. D. Ho, and R. A. Sutula, “Calendar-and Cycle-Life Studies of Advanced Technology Development Program Generation 1 Lithium-Ion Batteries,” Journal of Power Sources 110 (2002): 445–470, https://doi.org/10.1016/S0378-7753(02)00210-0.
10.1016/S0378-7753(02)00210-0
CAS Web of Science® Google Scholar
79M. Mauri, F. Castelli-Dezza, M. S. Carmeli, M. Scarforgliero, and G. Marchegiani, “ Electro-Thermal Aging Model of Li-Ion Batteries for Vehicle-to-Grid Services,” in 2019 AEIT International Conference of Electrical and Electronic Technologies for Automotive (AEIT AUTOMOTIVE) (IEEE, 2019), 1–6, https://doi.org/10.23919/EETA.2019.8804544.
10.23919/EETA.2019.8804544
Google Scholar
80A. Marongiu, M. Roscher, and D. U. Sauer, “Influence of the Vehicle-to-Grid Strategy on the Aging Behavior of Lithium Battery Electric Vehicles,” Applied Energy 137 (2015): 899–912, https://doi.org/10.1016/j.apenergy.2014.06.063.
10.1016/j.apenergy.2014.06.063
CAS Web of Science® Google Scholar
81L. Lam and P. Bauer, “Practical Capacity Fading Model for Li-Ion Battery Cells in Electric Vehicles,” IEEE Transactions on Power Electronics 28, no. 12 (2013): 5910–5918, https://doi.org/10.1109/TPEL.2012.2235083.
10.1109/TPEL.2012.2235083
Web of Science® Google Scholar
82J. Wang, P. Liu, J. Hicks-Garner, E. Sherman, S. Soukiazian, and M. Verbrugge, “Cycle-Life Model for Graphite-LiFePO₄ Cells,” Journal of Power Sources 196, no. 8 (2011): 3942–3948, https://doi.org/10.1016/j.jpowsour.2010.11.134.
10.1016/j.jpowsour.2010.11.134
CAS Web of Science® Google Scholar
83A. Cordoba-Arenas, S. Onori, Y. Guezennec, and G. Rizzoni, “Capacity and Power Fade Cycle-Life Model for Plug-In Hybrid Electric Vehicle Lithium-Ion Battery Cells Containing Blended Spinel and Layered-Oxide Positive Electrodes,” Journal of Power Sources 278 (2015): 473–483, https://doi.org/10.1016/j.jpowsour.2014.12.047.
10.1016/j.jpowsour.2014.12.047
CAS Web of Science® Google Scholar
84E. Sarasketa-Zabala, I. Gandiaga, E. Martinez-Laserna, L. M. Rodriguez-Martinez, and I. Villarreal, “Cycle Ageing Analysis of a LiFePO₄/Graphite Cell With Dynamic Model Validations: Towards Realistic Lifetime Predictions,” Journal of Power Sources 275 (2015): 573–587, https://doi.org/10.1016/j.jpowsour.2014.10.153.
10.1016/j.jpowsour.2014.10.153
CAS Web of Science® Google Scholar
85S. N. Motapon, E. Lachance, L. A. Dessaint, and K. Al-Haddad, “A Generic Cycle Life Model for Lithium-Ion Batteries Based on Fatigue Theory and Equivalent Cycle Counting,” IEEE Open Journal of the Industrial Electronics Society 1 (2020): 207–217, https://doi.org/10.1109/OJIES.2020.3015396.
10.1109/OJIES.2020.3015396
Web of Science® Google Scholar
86G. Papa, D. Ciuonzo, G. Romano, and P. Salvo Rossi, “A Dominance-Based Soft-Input Soft-Output MIMO Detector With Near-Optimal Performance,” IEEE Transactions on Communications 62, no. 12 (2014): 4320–4335, https://doi.org/10.1109/TCOMM.2014.2367013.
10.1109/TCOMM.2014.2367013
Web of Science® Google Scholar

Volume7, Issue5

May 2025

e70169

A Review of Lithium-Ion Battery Empirical and Semi-Empirical Aging Models for Off-Grid Renewable Energy Systems Application

ABSTRACT

1 Introduction

2 Methodology