Engineering Reports
Volume 7, Issue 5 e70167
RESEARCH ARTICLE
Open Access

Orthogonal Multi-Swarm Greedy Selection Based Sine Cosine Algorithm for Optimal FACTS Placement in Uncertain Wind Integrated Scenario Based Power Systems

Sunilkumar P. Agrawal, 

Sunilkumar P. Agrawal

Department of Electrical Engineering, Government Engineering College, Gandhinagar, India

Contribution: Conceptualization, ​Investigation, Methodology

Search for more papers by this author
Pradeep Jangir, 

Pradeep Jangir

University Centre for Research and Development, Chandigarh University, Gharuan, India

Department of Electrical and Electronics Engineering, J.J. College of Engineering and Technology, Tiruchirappalli, Tamilnadu, India

Centre for Research Impact and Outcome, Chitkara University Institute of Engineering and Technology, Chitkara University, Rajpura, Punjab, India

Applied Science Research Center, Applied Science Private University, Amman, Jordan

Contribution: Writing - original draft, Validation, Visualization

Search for more papers by this author
 Arpita, 

Arpita

Department of Biosciences, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Chennai, India

Contribution: Writing - review & editing, Software, Formal analysis

Search for more papers by this author
Sundaram B. Pandya, 

Sundaram B. Pandya

Department of Electrical Engineering, Shri K.J. Polytechnic, Bharuch, India

Contribution: Project administration, Data curation

Search for more papers by this author
Anil Parmar, 

Anil Parmar

Department of Electrical Engineering, Shri K.J. Polytechnic, Bharuch, India

Contribution: Project administration, Supervision, Resources

Search for more papers by this author
Mohammad Khishe, 

Corresponding Author

Mohammad Khishe

Department of Electrical Engineering, Imam Khomeini Naval Science University of Nowshahr, Nowshahr, Iran

Correspondence: Mohammad Khishe ([email protected])

Contribution: Formal analysis, Project administration, Data curation, Funding acquisition

Search for more papers by this author
Bhargavi Indrajit Trivedi, 

Bhargavi Indrajit Trivedi

Vishwakarma Government Engineering College, Ahmedabad, India

Contribution: Conceptualization, Validation, Project administration, Data curation

Search for more papers by this author
First published: 16 May 2025
https://doi.org/10.1002/eng2.70167

Funding: The authors received no specific funding for this work.

ABSTRACT

Modern power systems encounter significant challenges in optimal power flow (OPF) management due to the unpredictable nature of wind energy integration. Flexible AC Transmission System (FACTS) devices, including Static VAR Compensator (SVC), Thyristor-Controlled Series Compensator (TCSC), and Thyristor-Controlled Phase Shifter (TCPS), enhance system stability, reduce losses, and lower operational costs when optimally placed. Conventional optimization techniques like Particle Swarm Optimization (PSO), Sine Cosine Algorithm (SCA), Moth Flame Optimization (MFO), Gray Wolf Optimizer (GWO), and Whale Optimization Algorithm (WOA) struggle to balance exploration and exploitation in complex OPF problems, leading to suboptimal solutions. This study proposes a novel hybrid metaheuristic approach, the Orthogonal Multi-swarm Greedy Selection Sine Cosine Algorithm (OMGSCA), integrating orthogonal learning, multi-swarm mechanisms, and greedy selection to enhance solution quality. Orthogonal learning explores new search spaces, while the multi-swarm strategy improves exploitation. The greedy selection mechanism prevents premature convergence. OMGSCA optimizes FACTS device placement and sizing in wind-integrated power systems under fixed and uncertain loading conditions. Performance evaluation on the IEEE 30-bus test system with wind energy and FACTS devices demonstrates OMGSCA's superiority over traditional algorithms. Case studies focus on minimizing generation costs, active power losses, and gross costs. Results show OMGSCA achieves a power loss of 5.6209 MW in Case 1, comparable to WOA (5.6121 MW) and outperforming PSO, SCA, and MFO by 0.90%, 0.06%, and 0.57%, respectively. OMGSCA's gross generation cost (1369.3961 $/h) surpasses PSO, SCA, MFO, and GWO by 0.39%, 0.28%, 3.48%, and 0.20%, respectively. The algorithm proves effective in OPF problems, delivering cost-efficient operations, reduced losses, and enhanced stability across varying load conditions.

1 Introduction

Rapid integration of renewable energy sources (RES) such as wind and solar into modern power systems is leading to substantial changes in the energy landscape across the world. To reduce the use of greenhouse gases and slow down the pace of climate change, the move toward greener energy is necessary. However, the intermittent nature of RES presents significant challenges to power grid operators in the optimization of the power flow across the grid, while ensuring reliability and minimizing operational costs. Moreover, if RES are taken into account, the Optimal Power Flow (OPF) problem becomes tougher because the OPF problem should consider how to generate, transmit, and consume power in order to stabilize the grid and keep it efficient.

The placement and sizing of Flexible AC Transmission Systems (FACTS) devices such as Static VAR Compensators (SVC), Thyristor Controlled Series Compensators (TCSC) and Thyristor Controlled Phase Shifters (TCPS) is one of the most critical issues in this context. These devices are used to control voltage levels, control power flow, and improve the stability of the power grid under dynamic events. The integration of FACTS devices into the OPF problem has been shown to minimize costs of generation, reduce active power losses, and enhance overall grid performance under both fixed and uncertain loading conditions. However, the OPF problem is non-linear and non-convex, and the inclusion of RES and FACTS devices complicates the problem even further, rendering it intractable with conventional optimization methods.

This study focuses on solving the OPF $$ \mathrm{OPF} $$ problem in power systems that integrate wind energy and FACTS devices. Beyond determining the optimal placement and sizing of these devices, the objective is to develop an algorithm capable of effectively exploring and exploiting the solution space. While various optimization algorithms have been utilized to solve the OPF problem, many suffer from drawbacks such as premature convergence, slow convergence rates, and suboptimal performance in high-dimensional and nonlinear scenarios. Consequently, these limitations highlight the necessity for an enhanced approach to achieve improved optimization outcomes in contemporary power systems.

1.1 Previous Research: Evolution of Algorithms and OPF Problem Solutions

1.1.1 Evolution of Metaheuristic Algorithms

In the last few decades, metaheuristic algorithms (MAs) have become popular because of their robustness in solving complex optimization problems in different domains, including power systems [1]. Often, these types of algorithms are inspired by natural processes or biological phenomena. One of such MAs is Genetic Algorithms (GA), based on the biological process of evolution, which emphasizes selection, crossover, and mutation [2]. As a second example, the differential evolution (DE) algorithm by Storn and Price [3], while widely used due to its simplicity and effectiveness, is another. Because of its fast convergence, Particle Swarm Optimization (PSO), introduced by Kennedy and Eberhart [4], which mimics the social behavior of birds, has been extensively used on the OPF problem.

Swarm intelligence based algorithms, Gray Wolf Optimizer (GWO) and Whale Optimization Algorithm (WOA) have shown great potential to solve non-linear optimization problems [5, 6]. However, their performances are quite different in the complexity of the problem, and usually need to be hybridized with other methods in exploration and avoiding local optimum. Recently proposed by Mirjalili, Sine Cosine Algorithm (SCA) [7] has been shown to provide competitive results in solving multi-modal problems, but it also suffers from the same problems as other algorithms, such as stagnation and suboptimal local exploration [8]. Accordingly, several modifications to SCA, such as hybridization with orthogonal learning and greedy selection strategies, have been suggested in order to improve its exploration– exploitation balance [9]. The Moth Flame Optimization algorithm is introduced by Mirjalili in [10] as a bio-inspired heuristic paradigm to solve complex optimization problems. Results show that this algorithm performs better in global optimization tasks and is particularly well-suited for solving power system optimization problems. Sulaiman et al. [11] developed a new bio-inspired algorithm for solving engineering optimization problems called the Barnacles Mating Optimizer. This algorithm had high efficiency when solving complex optimization problems in different fields of study (power systems included). In addition, Sulaiman et al. [12] used the Barnacles Mating Optimizer in software engineering and found that it performed well in solving complex optimization problems. This approach was promising in improving the performance of many engineering systems. Sulaiman et al. [13] applied the Barnacles Mating Optimizer for evolutionary optimization tasks. In power systems optimization and other complex engineering problems, the algorithm they developed showed significant improvement in system performance.

1.1.2 Application of Algorithms to FACTS Integrated Power System

Mahmoud et al. [14] introduced a Wild Horse Optimizer to improve the current control loops of wind-side converters in PMSG-based wind generation systems. This technique improved the dynamic performance of the system and ensured stable operation at different wind speeds and load conditions. Mahmoud et al. [15] applied the Harris Hawks Algorithm to optimize DVR controllers in low voltage smart distribution systems. Voltage quality and system stability were improved by the robust controllers, particularly in distributed generation networks with fluctuating power demands. A parallel capacitor control strategy for DC link voltage stabilization in PMSG-based wind turbines was proposed in [16]. The operation of the wind turbine under grid disturbances was stable with this method and mitigated the effects of various fault conditions. In [17], Junior and Freitas reviewed power electronics applications in sustainable power systems, particularly in distributed generation, microgrids, and smart grids. In their comprehensive review, they highlighted the increasing use of power electronics to increase system reliability and efficiency. Advanced load frequency control in microgrids using a Bat Algorithm supported by a balloon effect identifier for photovoltaic power sources was studied by Mahmoud et al. [18]. The method enhanced frequency control and stability in microgrids with RES. Kamel et al. [15] used electric vehicle integration and STATCOM systems to improve the performance of islanded microgrids. These technologies were integrated to enhance voltage stability and power balancing in isolated microgrids. Awad et al. [19] provided a comprehensive review of water electrolysis for green hydrogen generation considering different renewable energy systems including PV, wind, hybrid, and geothermal energy sources. Economic analysis and applications of hydrogen generation were also reviewed. Ewais et al. [20] applied adaptive frequency control in smart microgrids with controlled loads with real-time implementation. This control strategy improved frequency stability and system reliability under varying load conditions. Hussein et al. [21] proposed a load frequency regulation system for multi-area power systems incorporating Vehicle-to-Grid (V2G) technology. The V2G system improved and stabilized the dynamic response of interconnected power networks. Montoya et al. [22] used a recursive quadratic approximation to solve the OPF problem for bipolar DC networks. The method was shown to be an efficient way to optimize power distribution in bipolar DC networks, which increased operational stability.

Extensive study has been made on FACTS devices such as SVC and TCSC in OPF problems. Researchers have demonstrated that proper placement and sizing of these devices can significantly enhance power system performance, including voltage stability and power loss reduction. However, the placement and sizing of FACTS devices in a system with integrated RES is a challenging task due to the stochastic nature of renewable generation. Mallala and Dwivedi [23] used the Salp Swarm Algorithm to solve the OPF problem with a Thyristor Controlled Series Capacitor (TCSC). This approach was applied to power systems with reactive power management problems and improved voltage stability and reduced power losses. To solve the challenges of stochastic wind and solar power generation, Sulaiman et al. [24] solved the OPF problem using the Teaching Learning Based Optimization algorithm. The method they developed increased the stability and efficiency of power systems with renewable energy integration. Sulaiman and Mustaffa [25] utilized metaheuristic optimization techniques to identify the optimal sizing and placement of FACTS devices, aiming to enhance the efficiency and voltage stability of power systems integrated with RES. Nayak et al. [26] used the Grasshopper Optimization Algorithm to optimize multistage controllers for automatic generation control in systems with FACTS devices. The optimization resulted in reduced response times and increased voltage stability in large power grids. Ahmad and Sirjani [27] reviewed metaheuristic optimization techniques for optimal placement and sizing of FACTS devices in power systems. According to their updated review, the main improvements in the optimization techniques for enhancing system performance are highlighted. Khan et al. [28] apply the modified Salp Swarm Algorithm for optimal placement of Static Synchronous Series Compensators (SSSC) in power systems. This approach yielded improved voltage stability and optimized reactive power flow, and reduced system losses. Khan et al. [29] propose a novel technique for allocation of FACTS devices using a modified Lightning Attachment Procedure Optimization. Their method reduced congestion and improved the voltage profiles, and hence, power system stability. Biswas et al. [30] use MAs for optimal placement of FACTS devices in wind power integrated electrical networks. They show that their approach enhances system stability by enhancing voltage regulation and reducing power losses in wind integrated systems. Wang et al. [31] develop a hybrid metaheuristic algorithm based on butterfly and flower pollination mechanisms for solving global optimization problems. Results of this approach indicate that it is highly efficient in improving system optimization for many engineering problems. Shehata et al. [32] used a hybrid methodology for optimal FACTS device allocation to improve power system operations. Optimizing reactive power management greatly improved system stability and efficiency with their method. Mahadevan et al. [33] apply a multi-objective hybrid Artificial Bee Colony and Differential Evolution algorithm for optimal placement of microprocessor-based FACTS controllers. We found that this approach increased system efficiency by optimizing power flow in large interconnected networks. Inkollu and Kota [34] solved the voltage stability problem using a hybrid PSO and Adaptive Gravitational Search Algorithm (GSA). The hybrid approach improved voltage profiles and stability in large power systems with integrated FACTS devices. A hybrid Bacterial Foraging and Nelder–Mead algorithm for congestion management by optimally placing series FACTS devices was used by Hooshmand et al. [35]. They found their method reduced system congestion and improved overall voltage stability in large-scale power networks. An artificial neural network and heuristic probability distribution method were used by Siddiqui and Prashant [36] to find optimal location and sizing of DG-FACTS devices. They made their approach to stability improvement and efficiency in modern power systems.

The studies mentioned above have a wide range of approaches to optimize power systems with FACTS devices and various MAs such as Wild Horse Optimizer, Harris Hawks Algorithm, Salp Swarm Algorithm, etc. Although these techniques show promise for increasing voltage stability, increasing the system resiliency, and optimizing power flow, they still have some limitations. However, many existing algorithms have poor convergence speed, particularly when applied to large-scale, complex power systems. However, some approaches, including the Salp Swarm and Grasshopper Optimization Algorithms, have been found to have difficulty escaping local optima, resulting in suboptimal placements of FACTS devices. Additionally, the stochastic behavior of RES, such as wind and solar power, adds complexity to the problem, as most existing algorithms struggle to maintain high efficiency under fluctuating conditions.

Nevertheless, these limitations necessitate the creation of new MAs that can more effectively cope with the multiobjective and nonlinear nature of FACTS placement optimization problems. The new algorithms should be designed to enhance exploration–exploitation balance, convergence speed, and to handle the uncertainty and variability of RES. An innovative approach that integrates hybrid strategies or adaptive mechanisms can overcome the current drawbacks of FACTS placement optimization and obtain more efficient and robust solutions.

Recent studies have explored advanced optimization techniques for power system management. Kar et al. [37] proposed a modified DE algorithm for reactive power management, demonstrating improved efficiency in control applications. In another study, Kar et al. [38] utilized a modified whale optimization algorithm to optimize FACTS device placement, effectively reducing transmission losses. Additionally, Kar et al. [39] developed an enhanced sine cosine algorithm with ensemble search agent updating schemes, which showed promising results in small signal stability analysis. These studies highlight the effectiveness of MAs in addressing complex power system challenges.

Modern power systems require critical attention for renewable energy source (RES) integration, especially wind energy, because the world aims to reduce greenhouse gas emissions and combat climate change. The random nature of wind power generation creates operational difficulties for power system optimization procedures. The OPFOPF problem faces growing complexity when RES enter the system because it needs to optimize power generation and transmission, and distribution with cost reduction and loss minimization. High-dimensional non-convex nonlinear problems with traditional optimization algorithms result in suboptimal solutions, along with premature convergence and operation inefficiencies in power systems.

FACTS devices deployed in strategic positions and selected correctly for their size, including SVC and TCSC and TCPS improve power system stability and simultaneously minimize active power losses while optimizing power flow patterns. The incorporation of FACTS devices into power systems that include RES creates additional complexity for the OPF problem, so it requires optimization techniques that can manage this enhanced complexity and uncertainty. The Orthogonal Multi-swarm Greedy Selection Sine Cosine Algorithm (OMGSCA) represents an advanced optimization method because it addresses critical problems that exist in current power systems.

Rising wind and solar energy penetration into power grids causes operational challenges because it creates unpredictable patterns in power systems. The stochastic characteristics of RES remain beyond the ability of standard OPF methods, so operations become costly and inefficient. The rising expenses for power generation and distribution, and transmission continue to increase because of the need to build new infrastructure for RES integration and the complexity of modern power system operations. Power system operators need efficient optimization methods that will decrease generation expenses and power losses, as well as operational costs. The irregular nature of RES causes difficulties with voltage stability and produces frequency instabilities, as well as power quality problems. The implementation of FACTS devices solves power system problems through their ability to dynamically control both voltage levels and power distribution. Advanced optimization approaches must be used to determine the best placement points for these devices alongside their correct size limits because this maximizes their effectiveness. The worldwide effort to decrease carbon pollution, alongside renewable energy transition requirements, forces power systems to improve their RES utilization capabilities. The implementation of efficient OPF solutions both decreases power system fuel usage and diminishes power dissipation, which together create a sustainable energy environment. PSO, alongside SCA and GWO, experiences limited performance and slow convergence speed when operating with both high-dimensional and nonlinear data, and faces premature convergence problems. The current optimization techniques need improvement to tackle the complex nature of present-day power systems effectively.

The current power system operation and optimization problems require advanced optimization algorithms such as OMGSCA to find effective solutions. OMGSCA solves power system problems with integrated wind energy and FACTS devices through its implementation of orthogonal learning and multi-swarm mechanisms, and greedy selection strategies, which optimize exploration and exploitation phases. OMGSCA provides a complete answer to present-day power system problems through its ability to minimize generation expenses while simultaneously decreasing power losses and enhancing system stability.

The algorithm used to solve the OPF problem with integrated renewable energy and FACTS devices is the development of the algorithm, Orthogonal Multi-swarm Greedy selection Sine Cosine Algorithm (OMGSCA) [40]. Orthogonal learning and multi–swarm strategies are used in OMGSCA to improve the exploration–exploitation balance, overcoming the shortcomings of the traditional algorithms and offering a more robust solution for modern power systems. Scaling OMGSCA for larger systems and investigating its use in real-time, dynamic conditions in different grid scenarios is the future work. In the next section, we will discuss the OPF problem formulation and placement and sizing of FACTS devices.

The world pauses attention on renewable energy source (RES) integration into modern power frameworks because it remains vital to reduce emissions while fighting climate change. The irregular nature of RES creates substantial operational difficulties for power system control because it affects both grid stability and operational expenses. The OPF problem faces increased complexity when it includes RES and FACTS devices in power generation and transmission operations, and consumption management. The grid stability enhancement and power flow optimization, alongside voltage level control, depend heavily on FACTS devices, which include Static VAR Compensators (SVC) and Thyristor-Controlled Series Compensators (TCSC) and Thyristor-Controlled Phase Shifters (TCPS). The random behavior of renewable energy generation makes it difficult to determine the best locations and sizes for FACTS devices in power systems.

California demonstrates the foremost position when adopting clean energy yet struggles with large-scale integration efforts involving wind and solar power to its power system. The California Independent System Operator (CAISO) detected grid instability followed by renewable energy curtailment because supply exceeded demand in 2020. Wind and solar power intermittency produced unstable voltage conditions while increasing power transmission losses, which required FACTS controllers to stabilize the power grid. The real-world situation demonstrates that systems with elevated RES integration must optimize their FACTS systems to sustain grid stability by minimizing operational expenses.

The state of Texas operates one of the world's biggest wind energy facilities yet faces difficulties in maintaining its power grid operations. The grid became unstable during the extreme weather event of February 2021 because wind power generation showed high variability. The power system faced widespread blackouts because inadequate reactive power support combined with absent voltage control mechanisms made the situation worse. The recent power grid failure demonstrates the necessity for efficient optimization approaches, which this research proposes to strengthen power delivery reliability in wind-heavy power systems.

The European countries Denmark and Germany have managed to incorporate significant amounts of wind energy into their power grid systems. The process of integrating wind energy into power systems has faced multiple obstacles despite its implementation. The German power grid suffered from congestion and power loss spikes because wind energy distribution was not balanced throughout the transmission system during 2019. Through deployments of SVCs and TCSCs as FACTS devices, utilities successfully control power flow characteristics and provide vital dynamic voltage support to solve these issues. The practical implementation of solving the OPF problem with RES and FACTS integration proves essential for maintaining stable and efficient power system operations.

The country of India aims to reach ambitious renewable energy targets but struggles to unite wind and solar power grids. The power grid in India endured frequency fluctuations and voltage instability problems because of renewable energy generation variability during 2021. The power industry uses FACTS devices including TCPS and SVCs to resolve these operational issues. The correct deployment and dimensioning of these devices prove difficult especially when systems contain substantial amounts of RES. The important role of the proposed Orthogonal Multi-swarm Greedy Selection Sine Cosine Algorithm (OMGSCA) becomes more evident for improving power grid stability while minimizing operational expenses.

The worldwide power systems require solutions for renewable energy source integration and stable grid operation, due to which the current study's problem requirements have become essential. Systems that combine RES with complex power networks need improved optimization approaches to guarantee efficient and reliable performance because of the intermittent source behavior. The implementation of FACTS devices presents a promising solution to power system difficulties, although their optimal deployment needs sophisticated algorithms that can address the non-convex and nonlinear characteristics of the OPF problem. OMGSCA presents a dependable computational method to address this vital challenge by maintaining exploration-exploitation harmony while managing background conditions, which produces superior results in cost minimization for generation units and power network losses, together with operational costs throughout multiple application studies.

The research addresses real power sector issues which lead to more stable and efficient electric system operations resulting in a sustainable energy future. Analysis of practical cases demonstrates the critical importance of the studied problem which warrants the application of OMGSCA to integrate renewable systems and FACTS devices into contemporary power networks efficiently.

1.1.3 Research Gap and Key Contributions

The implementation of RES and FACTS devices creates substantial difficulties when solving the OPF problem in modern power systems. The widespread research about implementing MAs for these challenges includes unexplored opportunities that are absent from current studies. Power systems face substantial unpredictability because renewable power sources present a stochastic behavior with solar and wind energy. The performance of current algorithms deteriorates when operating under changing conditions, which results in inferior solution outcomes. The optimization methods need improvement to properly address the unpredictable behavior of renewable energy generation systems. The weakness of traditional metaheuristic optimization methods, which include PSO and Sine Cosine Algorithm, and Gray Wolf Optimizer, appears when they confront high-dimensional nonlinear problems and show fast convergence together with weak exploration-exploitation management abilities. The suboptimal placement and sizing of FACTS devices become a result of this limitation since these devices play a critical role in system stability and efficiency enhancement. The extensive research on FACTS device placement and sizing has not resulted in effective optimization of their integration within power systems that contain high levels of renewable energy. A sophisticated optimization framework needs to handle the dynamic FACTS device and RES interaction for the simultaneous achievement of power loss reduction and cost minimization, and voltage stability improvement. The majority of current optimization algorithms work with a single optimization goal that targets either cost reduction or power loss reduction. Multidimensional system optimization becomes vital for actual power grids because operators need to achieve excellence in both cost reduction and operational reliability together with sustainable environmental outcomes. Advanced optimization algorithms need development to process multiple objectives efficiently when solving power system problems. The success rate of optimization algorithms on the IEEE 30-bus system diminishes for larger and complex power grids. System scalability represents an ongoing technical challenge specifically for operation systems that consist of high renewable energy participation and many operational control parameters. Modern power systems operated in real-time need optimization capabilities because they handle uncertain loads combined with sporadic renewable energy inputs. The current algorithms were developed mainly for offline optimization, yet they do not meet the real-time system requirements. Research about achieving optimal economic performance along with environmental impact optimization remains scant despite making generation costs and power loss reduction primary targets. To achieve sustainable power system operation, it is necessary to develop algorithms that effectively minimize costs together with greenhouse gas emissions reduction. The proposed algorithms receive validation through limited operating conditions that include fixed load conditions. The proposed solutions require further testing under conditions representing diverse circumstances involving unpredictable load patterns and fluctuating renewable power supply together with different network setups for ensuring dependable system solutions. Standard metaheuristic optimization algorithms employ fixed parameters together with set strategies because these approaches restrict their suitability for various solution contexts. To achieve better performance, hybrid and adaptive optimization strategies must leverage several algorithms by allowing their parameters to automatically adjust according to the problem conditions. The implementation of advanced learning techniques, including orthogonal methods and multi-swarm systems, proves effective for improving MAs' exploration-exploitation equilibrium. The utilization of these methods for power system optimization, especially regarding RES and FACTS devices, needs further investigation. Research gaps need immediate attention because they are essential for developing superior optimization algorithms that enhance power system reliability. The proposed Orthogonal Multi-swarm Greedy Selection Sine Cosine Algorithm (OMGSCA) aims to solve the identified gaps in power system optimization through advanced learning mechanisms and multi-swarm strategies, and greedy selection techniques for better exploration-exploitation balance and scalability, and robustness during unpredictable events.

Overcome the deficiencies of existing algorithms in solving the OPF problem with integrated wind energy and FACTS devices, a novel metaheuristic algorithm, Orthogonal Multi swarm Greedy selection Sine Cosine Algorithm (OMGSCA) is proposed in this work. To enhance the exploration and exploitation phases of the optimization process, we include orthogonal learning, multi swarm mechanisms, and a greedy selection strategy. These modifications enable OMGSCA to better explore the complex, non-linear search space of the OPF problem and reduce the probability of premature convergence and improve solution accuracy.

The key contributions of this research are as follows:
  • A novel variant of the Sine Cosine Algorithm (SCA) is introduced in this study, incorporating orthogonal learning, multi-swarm strategies, and greedy selection to enhance optimization efficiency.
  • The algorithm is employed to resolve the OPF problem in the power systems featuring wind energy and FACTS devices, focusing on optimizing placement and sizing under both stable and variable loading scenarios.
  • OMGSCA is evaluated on the IEEE 30-bus system, a widely used test system in power systems research, and compared with traditional algorithms, including PSO, SCA, MFO, GWO, and WOA.
  • The comparative analysis reveals that OMGSCA excels in reducing costs of generation, active power losses, and overall gross costs, outperforming other algorithms across both stable and uncertain loading conditions.
  • This article presents an in-depth examination of OMGSCA's convergence patterns, highlighting its enhanced capability to balance exploration and exploitation, especially in solving complex, high-dimensional, and non-linear problems.

2 Mathematical Modeling and Problem Definition

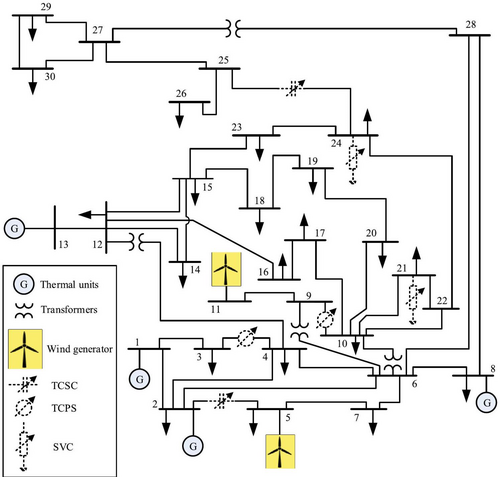
The IEEE 30-bus test system [41] is utilized in this study, modified to include wind generators and Flexible AC Transmission System (FACTS) devices. The system configuration, depicted in Figure 1, focuses on determining the optimal sizing and placement of FACTS devices, which are represented by dotted lines.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Enhanced IEEE 30-Bus system for OPF analysis incorporating RES and FACTS devices.

2.1 Mathematical Framework for Cost Evaluation

2.1.1 Fuel Costs or Generation Expenses of Thermal Units

The cost of electricity generation for the ith thermal unit, denoted as C T 0 i $$ {C}_{T0i} $$ , is calculated in $ / h $$ \$/\mathrm{h} $$ using Equation (1):
C T 0 i P TGi = a i + b i P TGi + c i P TGi 2 $$ {C}_{T0i}\left({P}_{TGi}\right)={a}_i+{b}_i{P}_{TGi}+{c}_i{P}_{TGi}^2 $$ (1)
Here, P TGi $$ {P}_{TGi} $$ represents the power output of the thermal generator (MW), while a i , b i , $$ {a}_i,{b}_i, $$ and c i $$ {c}_i $$ are the cost coefficients. If valve-point effects are included in the analysis, the generation cost is revised as shown in Equation (2):
C Ti P TGi = a i + b i P TGi + c i P TGi 2 + d i × sin e i × P TGi min − P TGi $$ {C}_{Ti}\left({P}_{TGi}\right)=\kern0.5em {a}_i+{b}_i{P}_{TGi}+{c}_i{\mathrm{P}}_{TGi}^2+\left|{d}_i\times \sin \left({e}_i\times \left(\ {P}_{TGi}^{\mathrm{min}}-{P}_{TGi}\right)\right)\right| $$ (2)

The calculations utilize the cost coefficients of each thermal unit, as outlined in Table 1 [42].

TABLE 1. Thermal power unit cost coefficients.
Generator Bus a ( $ / h ) $$ a\left(\$/\mathrm{h}\right) $$ b ( $ / MWh ) $$ b\left(\$/\mathrm{MWh}\right) $$ c $ / MW 2 h $$ c\left(\$/{\mathrm{MW}}^2\ \mathrm{h}\right) $$ d ( $ / h ) $$ d\left(\$/\mathrm{h}\right) $$ e ( rad / MW ) $$ e\left(\mathrm{rad}/\mathrm{MW}\right) $$
TG 1 $$ TG1 $$ 1 0 2 0.00375 18 0.037
TG 2 $$ TG2 $$ 2 0 1.75 0.0175 16 0.038
TG 8 $$ TG8 $$ 8 0 3.25 0.00834 12 0.045
TG 13 $$ TG13 $$ 13 0 3 0.025 13.5 0.041

2.1.2 Calculation of Wind Power Probabilities

Accurately modeling wind power probabilities is essential for understanding the variable nature of wind energy. This study utilizes the Weibull probability density function (PDF) to characterize wind speed distribution, as expressed in Equation (3) [43, 44]. The PDF provides a statistical representation of wind speed variations over a specific period:
f v ( v ) = β α v α ( β − 1 ) e − ( v / α ) β for 0 < v < ∞ $$ {f}_v(v)=\left(\frac{\beta }{\alpha}\right){\left(\frac{v}{\alpha}\right)}^{\left(\beta -1\right)}{e}^{-{\left(v/\alpha \right)}^{\beta }}\ \mathrm{for}\ 0<v<\infty $$ (3)

Here, α $$ \alpha $$ and β $$ \beta $$ denote the scale and shape parameters of the Weibull distribution, which define the variability and spread of wind speeds at the given site.

The WPP's power output depends on wind speed and turbine characteristics, as defined in Equation (4):
p w ( v ) = 0 for v < v i and v > v o p wr v − v i v r − v in for v i ≤ v ≤ v r p wr for v r < v ≤ v o $$ {p}_w(v)=\left\{\begin{array}{l}0\kern5.2em for\kern0.36em v<{v}_i\kern0.5em and\kern0.5em v>{v}_o\\ {}{p}_{wr}\left(\frac{v-{v}_i}{v_r-{v}_{in}}\right)\kern1em for\kern.4em {v}_{\mathrm{i}}\le v\le {v}_r\\ {}\ {p}_{wr}\kern4em for\kern.4em {v}_r<v\le {v}_o\end{array}\right. $$ (4)
This equation divides wind turbine operation into three distinct regions:
  1. Cut-out regions ( v < v i $$ v<{v}_i $$ or v > v o $$ v>{v}_o $$ ): The turbine remains non-operational due to insufficient or excessive wind speeds.
  2. Partial load region ( v i ≤ v ≤ v r $$ {v}_i\le v\le {v}_r $$ ): The turbine generates power proportionate to the wind speed, increasing linearly until reaching rated power.
  3. Rated power region ( v r < v ≤ v o $$ {v}_r<v\le {v}_o $$ ): The turbine maintains constant output at its rated capacity.
Wind power probabilities for these distinct operational states are computed using Equations (5) and (6) [45, 46]:
f w p w p w = 0 = 1 − exp − v i α β + exp − v o α β $$ {f}_w\left({p}_w\right)\left\{{p}_w=0\right\}=1-\exp \left[-{\left(\frac{v_{\mathrm{i}}}{\alpha}\right)}^{\beta}\right]+\exp \left[-{\left(\frac{v_{\mathrm{o}}}{\alpha}\right)}^{\beta}\right] $$ (5)
f w p w p w = p wr = exp − v r α β − exp − v out α β . $$ {f}_w\left({p}_w\right)\left\{{p}_w={p}_{wr}\right\}=\exp \left[-{\left(\frac{v_r}{\alpha}\right)}^{\beta}\right]-\exp \left[-{\left(\frac{v_{\mathrm{out}}}{\alpha}\right)}^{\beta}\right]. $$ (6)

Equation (5) calculates the probability that the turbine is either non-operational or generating zero power, while Equation (6) evaluates the likelihood of the turbine running at its rated capacity.

The likelihood for the continuous range spanning from the cut-in speed v i $$ {v}_i $$ to the rated speed v r $$ {v}_r $$ is expressed as:
f w p w = β v r − v i α β * p wr v i + p w p wr v r − v i β − 1 × exp − v i + p w p wr v r − v i α β $$ {f}_w\left({p}_w\right)=\kern0.5em \frac{\beta \left({v}_r-{v}_{\mathrm{i}}\right)}{\alpha^{\beta \ast }{p}_{wr}}{\left[{v}_{\mathrm{i}}+\frac{p_w}{p_{wr}}\left({v}_r-{v}_{\mathrm{i}}\right)\right]}^{\beta -1}\times \mathit{\exp}\left[-{\left(\frac{v_{\mathrm{i}}+\frac{p_w}{p_{wr}}\left({v}_r-{v}_{\mathrm{i}}\right)}{\alpha}\right)}^{\beta}\right] $$ (7)

This equation provides a detailed representation of the turbine's power generation likelihood in the partial load region, reflecting the continuous nature of wind speed variability.

By combining these equations, a complete statistical understanding of wind turbine power output across all operational states can be achieved. This approach ensures an accurate assessment of wind energy's potential contribution to the grid.

2.1.3 Direct Costs Associated With Wind Power

The direct cost associated with the jth wind power plant, C wj $$ {C}_{wj} $$ , is calculated based on the scheduled power output using Equation (8) [47]:
C wj P wsj = g wj P wsj $$ {C}_{wj}\left({P}_{wsj}\right)={g}_{wj}{P}_{wsj} $$ (8)

In this equation, P wsj $$ {P}_{wsj} $$ represents the scheduled power output of the wind generator, while g wj $$ {g}_{wj} $$ denotes the cost coefficient per unit of power generated by the wind farm. This formulation provides a straightforward representation of the operational cost for scheduled wind energy production.

2.1.4 Assessing Costs of Uncertain Wind Power

Uncertainty in wind power generation introduces additional costs, such as reserve costs and penalty costs, due to deviations from scheduled output.

2.1.4.1 Reserve Cost

The reserve cost, incurred when the scheduled output exceeds the actual generated power, is calculated using Equation (9):
C Rwj P wsj − P wavj = K Rwj P wsj − P wavj = K Rwj ∫ 0 P wsj P wsj − p w f wj p w dp w $$ {C}_{Rwj}\left({P}_{wsj}-{P}_{wavj}\right)={K}_{Rwj}\left({P}_{wsj}-{P}_{wavj}\right)={K}_{Rwj}\int_0^{P_{wsj}}\left({P}_{wsj}-{p}_w\right){f}_{wj}\left({p}_w\right){dp}_w $$ (9)
Here, P wavj $$ {P}_{wavj} $$ is the actual power output from the wind plant, and f wj p w $$ {f}_{wj}\left({p}_w\right) $$ is the probability density function (PDF) of the plant's output. Equation (10) expands the integral in Equation (9) for detailed computation:
K Rwj ∫ 0 P wsj P wsj − p w β v r − v in α β * P wrj v in + p w P wrj v r − v in β − 1 × exp − v in + p w P wjj v r − v in α β d p w + K Rwj P wsj − 0 * f wj p w p w = 0 $$ {\displaystyle \begin{array}{ll}{K}_{Rwj}{\int}_0^{P_{wsj}}& \kern0.20em \left\{\left({P}_{wsj}-{p}_w\right)\frac{\beta \left({v}_r-{v}_{in}\right)}{{\alpha \beta}^{\ast }{P}_{wrj}}{\left[{v}_{in}+\frac{p_w}{P_{wrj}}\left({v}_r-{v}_{in}\right)\right]}^{\beta -1}\right.\\ {}& \kern-3em \left.\times \exp \left[-{\left(\frac{v_{in}+\frac{p_w}{P_{wj j}}\left({v}_r-{v}_{in}\right)}{\alpha}\right)}^{\beta}\right]\right\}d{p}_w+{K}_{Rwj}\left({P}_{wsj}-0\right)\ast {f}_{wj}\left({p}_w\right)\left\{{p}_w=0\right\}\end{array}} $$ (10)

This expanded form incorporates the Weibull parameters ( α $$ \alpha $$ and β $$ \beta $$ ) to account for the statistical variation of wind power output.

2.1.4.2 Penalty Cost

Penalty costs arise when the actual power output exceeds the scheduled generation, leading to underestimated energy supply. The penalty cost is computed as shown in Equation (11):
C Pwj P wavj − P wsj = K Pwj P wavj − P wsj = K Pwj ∫ P wsj P wrj p w − P wsj f wj p w dp w $$ {C}_{Pwj}\left({P}_{wavj}-{P}_{wsj}\right)\kern0.5em ={K}_{Pwj}\left({P}_{wavj}-{P}_{wsj}\right)={K}_{Pwj}\int_{P_{wsj}}^{P_{wrj}}\left({p}_w-{P}_{wsj}\right){f}_{wj}\left({p}_w\right){dp}_w $$ (11)
The expanded form of Equation (11) is represented in Equation (12):
K Pwj ∫ P wsj P wrj p w − P wsj β v r − v in α β * P wrj v in + p w P wrj v r − v in β − 1 × exp − v in + p w P wrj v r − v in α β d p w + K Pwj P wrj − P wsj * f wj p w $$ {\displaystyle \begin{array}{ll}{K}_{Pwj}{\int}_{P_{wsj}}^{P_{wrj}}& \kern0.20em \left\{\left({p}_w-{P}_{wsj}\right)\frac{\beta \left({v}_r-{v}_{in}\right)}{\alpha^{\beta \ast }{P}_{wrj}}{\left[{v}_{in}+\frac{p_w}{P_{wrj}}\left({v}_r-{v}_{in}\right)\right]}^{\beta -1}\right.\\ {}& \kern-3.5em \left.\times \exp \left[-{\left(\frac{v_{in}+\frac{p_w}{P_{wrj}}\left({v}_r-{v}_{in}\right)}{\alpha}\right)}^{\beta}\right]\right\}d{p}_w+{K}_{Pwj}\left({P}_{wrj}-{P}_{wsj}\right)\ast {f}_{wj}\left({p}_w\right)\end{array}} $$ (12)

Equation (12) incorporates the same statistical parameters and wind turbine characteristics to evaluate penalties for deviations in actual power output.

The coefficients required for these cost calculations are presented in Table 2.

TABLE 2. Scenario analysis: Loading levels and probabilities.
Scenario P d ‾ $$ \overline{{\boldsymbol{P}}_{\boldsymbol{d}}} $$ Loading level Δ sc $$ {\boldsymbol{\Delta}}_{\boldsymbol{sc}} $$ Probability
s c 1 $$ s{c}_1 $$ 54.749 0.15866
s c 2 $$ s{c}_2 $$ 65.401 0.34134
s c 3 $$ s{c}_3 $$ 74.599 0.34134
s c 4 $$ s{c}_4 $$ 85.251 0.15866

2.2 FACTS Device Modeling

The Flexible AC Transmission System (FACTS) devices modeled in this study include the Thyristor-Controlled Series Capacitor (TCSC), Thyristor-Controlled Phase Shifter (TCPS), and Static Var Compensator (SVC). Each device enhances power system flexibility by improving power flow control and reactive power compensation [48].

2.2.1 TCSC Model

The Thyristor-Controlled Series Capacitor (TCSC) consists of a fixed capacitor in parallel with a thyristor-controlled reactor. Its effective reactance is expressed as:
X TCSC ( γ ) = X C X L ( γ ) X L ( γ ) − X C $$ {X}_{\mathrm{TCSC}}\left(\gamma \right)=\frac{X_C{X}_L\left(\gamma \right)}{X_L\left(\gamma \right)-{X}_C} $$ (13)
The TCSC modifies the reactance of a transmission line. The equivalent reactance of the line, after incorporating the TCSC, is given by:
X eq = X mn − X TCSC = ( 1 − τ ) X mn $$ {X}_{\mathrm{eq}}={X}_{mn}-{X}_{\mathrm{TCSC}}=\left(1-\tau \right){X}_{mn} $$ (14)
τ = X TCSC X mn $$ \tau =\frac{X_{\mathrm{TCSC}}}{X_{mn}} $$ (15)

Here, X mn $$ {X}_{mn} $$ refers to the inductive reactance of the line, and R mn $$ {R}_{mn} $$ denotes the line resistance.

When a TCSC is installed in a transmission line, the power flow equations are modified to reflect its effect on the line's impedance. The active and reactive power flows between buses m $$ m $$ and n $$ n $$ are calculated using the following equations:

Active power flow from bus m $$ m $$ to n $$ n $$
P mn = V m 2 g mn − V m V n g mn cos δ m − δ n − V m V n b mn sin δ m − δ n $$ {P}_{mn}={V}_m^2{g}_{mn}-{V}_m{V}_n{g}_{mn}\cos \left({\delta}_m-{\delta}_n\right)-{V}_m{V}_n{b}_{mn}\sin \left({\delta}_m-{\delta}_n\right) $$ (16)
Reactive power flow from bus m $$ m $$ to n $$ n $$
Q mn = − V m 2 b mn − V m V n g mn sin δ m − δ n + V m V n b mn cos δ m − δ n $$ {Q}_{mn}=-{V}_m^2{b}_{mn}-{V}_m{V}_n{g}_{mn}\sin \left({\delta}_m-{\delta}_n\right)+{V}_m{V}_n{b}_{mn}\cos \left({\delta}_m-{\delta}_n\right) $$ (17)
Active power flow from bus n $$ n $$ to m $$ m $$
P nm = V n 2 g mn − V m V n g mn cos δ m − δ n + V m V n b mn sin δ m − δ n $$ {P}_{nm}={V}_n^2{g}_{mn}-{V}_m{V}_n{g}_{mn}\cos \left({\delta}_m-{\delta}_n\right)+{V}_m{V}_n{b}_{mn}\sin \left({\delta}_m-{\delta}_n\right) $$ (18)
Reactive power flow from bus n $$ n $$ to m $$ m $$
Q nm = − V n 2 b mn + V m V n g mn sin δ m − δ n + V m V n b mn cos δ m − δ n $$ {Q}_{nm}=-{V}_n^2{b}_{mn}+{V}_m{V}_n{g}_{mn}\sin \left({\delta}_m-{\delta}_n\right)+{V}_m{V}_n{b}_{mn}\cos \left({\delta}_m-{\delta}_n\right) $$ (19)
The line parameters are influenced by the TCSC and are represented by the following expressions for conductance ( g mn $$ {g}_{mn} $$ ) and susceptance ( b mn $$ {b}_{mn} $$ ):
g mn = R mn R 2 + ( 1 − τ ) X mn 2 and b mn = − ( 1 − τ ) X mn R 2 + ( 1 − τ ) X mn 2 $$ {g}_{mn}=\frac{R_{mn}}{R^2+{\left[\left(1-\tau \right){X}_{mn}\right]}^2}\ \mathrm{and}\ {b}_{mn}=-\frac{\left(1-\tau \right){X}_{mn}}{R^2+{\left[\left(1-\tau \right){X}_{mn}\right]}^2} $$
In these equations:
  • V m $$ {V}_m $$ and V n $$ {V}_n $$ denote the voltages at buses m $$ m $$ and n $$ n $$ , respectively.
  • δ m $$ {\delta}_m $$ and δ n $$ {\delta}_n $$ represent the phase angles at these buses.
  • g mn $$ {g}_{mn} $$ and b mn $$ {b}_{mn} $$ are the conductance and susceptance of line connecting buses m $$ m $$ and n $$ n $$ .

By incorporating the TCSC into the transmission line, the system's power flow and stability are significantly improved, making it a vital component in modern power systems (Figure 2).

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Schematic representation of the TCSC circuit.

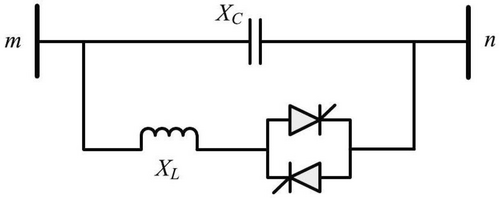
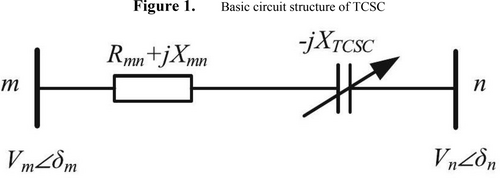
Basic circuit structure of TCSC (Figure 3).

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Simplified single line representation of the TCSC circuit.

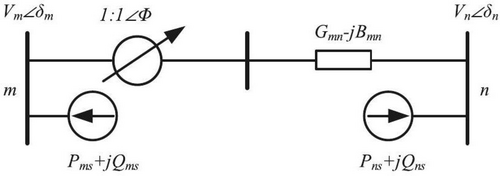
2.2.2 TCPS Model

The Thyristor-Controlled Phase Shifter (TCPS) serves as a series compensation device embedded within the transmission line connecting buses m $$ m $$ and n $$ n $$ , as depicted in Figure 4. Through the application of a controllable phase shift angle ( Φ $$ \Phi $$ ), the TCPS adjusts the line's power flow, contributing to improved load distribution and enhanced system stability. The corresponding power flow equations for line with TCPS integration are outlined in Equations (20-27) and elaborated in References [49, 50].

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Simplified single line representation of the TCPS.

2.2.2.1 Power Flow Equations for TCPS

The active and reactive power flows from bus m $$ m $$ to bus n $$ n $$ are calculated using the following equations:

Active power flow from m $$ m $$ to n $$ n $$
P mn = V m 2 G mn cos 2 Φ − V m V n cos Φ g mn cos δ m − δ n + Φ + b mn sin δ m − δ n + Φ $$ {P}_{mn}=\frac{V_m^2{G}_{mn}}{\cos^2\Phi}-\frac{V_m{V}_n}{\mathrm{cos}\Phi}\left[{g}_{mn}\cos \left({\delta}_m-{\delta}_n+\Phi \right)+{b}_{mn}\sin \left({\delta}_m-{\delta}_n+\Phi \right)\right] $$ (20)
Reactive power flow from m $$ m $$ to n $$ n $$
Q mn = − V m 2 B mn cos 2 Φ − V m V n cos Φ g mn sin δ m − δ n + Φ − b mn cos δ m − δ n + Φ $$ {Q}_{mn}=-\frac{V_m^2{B}_{mn}}{\cos^2\Phi}-\frac{V_m{V}_n}{\mathrm{cos}\Phi}\left[{g}_{mn}\sin \left({\delta}_m-{\delta}_n+\Phi \right)-{b}_{mn}\cos \left({\delta}_m-{\delta}_n+\Phi \right)\right] $$ (21)
Active power flow from n $$ n $$ to m $$ m $$
P nm = V n 2 G mn − V m V n cos Φ g mn cos δ m − δ n + Φ − b mn sin δ m − δ n + Φ $$ {P}_{nm}={V}_n^2{G}_{mn}-\frac{V_m{V}_n}{\mathrm{cos}\Phi}\left[{g}_{mn}\cos \left({\delta}_m-{\delta}_n+\Phi \right)-{b}_{mn}\sin \left({\delta}_m-{\delta}_n+\Phi \right)\right] $$ (22)
Reactive power flow from n $$ n $$ to m $$ m $$
Q nm = − V n 2 B mn + V m V n cos Φ g mn sin δ m − δ n + Φ − b mn cos δ m − δ n + Φ $$ {Q}_{nm}=-{V}_n^2{B}_{mn}+\frac{V_m{V}_n}{\mathrm{cos}\Phi}\left[{g}_{mn}\sin \left({\delta}_m-{\delta}_n+\Phi \right)-{b}_{mn}\cos \left({\delta}_m-{\delta}_n+\Phi \right)\right] $$ (23)

2.2.2.2 Power Injected by TCPS

The TCPS impacts both real and reactive power injections at buses mmm and nnn, which are characterized by the equations provided below:

Real power injection at bus m $$ m $$
P ms = − G mn V m 2 tan 2 Φ − V m V n tan Φ g mn sin δ m − δ n − b mn cos δ m − δ n $$ {P}_{ms}=-{G}_{mn}{V}_m^2{\tan}^2\Phi -{V}_m{V}_n\mathrm{tan}\Phi \left[{g}_{mn}\sin \left({\delta}_m-{\delta}_n\right)-{b}_{mn}\cos \left({\delta}_m-{\delta}_n\right)\right] $$ (24)
Reactive power injection at bus m $$ m $$
Q ms = B mn V m 2 tan 2 Φ + V m V n tan Φ g mn cos δ m − δ n + b mn sin δ m − δ n $$ {Q}_{ms}={B}_{mn}{V}_m^2{\tan}^2\Phi +{V}_m{V}_n\mathrm{tan}\Phi \left[{g}_{mn}\cos \left({\delta}_m-{\delta}_n\right)+{b}_{mn}\sin \left({\delta}_m-{\delta}_n\right)\right] $$ (25)
Real power injection at bus n $$ n $$
P ns = − V m V n tan Φ G mn sin δ m − δ n + B mn cos δ m − δ n $$ {P}_{ns}=-{V}_m{V}_n\mathrm{tan}\Phi \left[{G}_{mn}\sin \left({\delta}_m-{\delta}_n\right)+{B}_{mn}\cos \left({\delta}_m-{\delta}_n\right)\right] $$ (26)
Reactive power injection at bus n $$ n $$
Q ns = − V m V n tan Φ G mn cos δ m − δ n − B mn sin δ m − δ n $$ {Q}_{ns}=-{V}_m{V}_n\mathrm{tan}\Phi \left[{G}_{mn}\cos \left({\delta}_m-{\delta}_n\right)-{B}_{mn}\sin \left({\delta}_m-{\delta}_n\right)\right] $$ (27)

2.2.3 SVC Model

The static var compensator (SVC) operates as a shunt compensation device, enabling dynamic reactive power control. Figure 5a,b illustrate the fundamental circuit design and operational model of the SVC, respectively. It comprises a capacitor ( X C = 1 ω C $$ {X}_C=\frac{1}{\omega C} $$ ) and a thyristor-controlled reactor ( X L = ω L $$ {X}_L=\omega L $$ ), with the reactance regulated by varying the firing angle ( γ $$ \gamma $$ ) of the thyristor.

Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
(a) Circuit diagram of SVC and (b) operational model of SVC.
The equivalent susceptance can be determined using the following equation [48]:
B SVC = B C + B L ( γ ) $$ {B}_{\mathrm{SVC}}={B}_C+{B}_L\left(\gamma \right) $$ (28)
The individual components of susceptance are expressed as:
B C = ω C and B L ( γ ) = 1 ω L 1 − 2 γ π − sin ( 2 γ ) π $$ {B}_C=\omega C\ \mathrm{and}\ {B}_L\left(\gamma \right)=\frac{1}{\omega L}\left(1-\frac{2\gamma }{\pi }-\frac{\sin \left(2\gamma \right)}{\pi}\right) $$ (29)
Here:
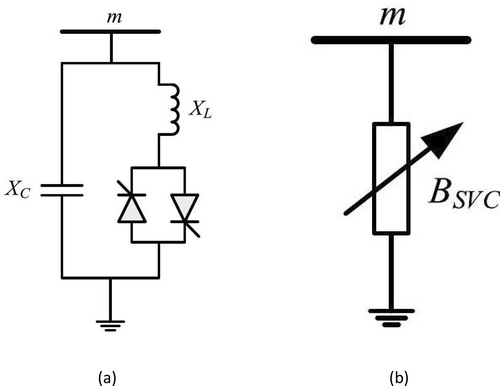
  • B C $$ {B}_C $$ represents the capacitive susceptance.
  • B L ( γ ) $$ {B}_L\left(\gamma \right) $$ accounts for the variable inductive susceptance controlled by the firing angle γ $$ \gamma $$ .
  • ω $$ \omega $$ is the angular frequency, C $$ C $$ is the capacitance, and L $$ L $$ is the inductance.
In power flow analysis, the reactive power ( Q SVC $$ {Q}_{\mathrm{SVC}} $$ ) supplied by the SVC to the connected bus is calculated using Equation (30):
Q SVC = − V m 2 · B SVC $$ {Q}_{\mathrm{SVC}}=-{V}_m^2\cdotp {B}_{\mathrm{SVC}} $$ (30)
In this equation:
  • V m $$ {V}_m $$ is the voltage at the bus where the SVC is connected.
  • B SVC $$ {B}_{\mathrm{SVC}} $$ determines whether the SVC operates in capacitive or inductive compensation mode.

The SVC provides versatile compensation by dynamically injecting or absorbing reactive power to maintain voltage stability at the connected bus. In capacitive mode, the SVC injects reactive power into the system, improving voltage levels. Conversely, in inductive mode, it absorbs reactive power, mitigating voltage surges. This dual functionality makes the SVC an essential device for maintaining power system stability and efficiency.

2.3 Objectives and Constraints of Optimal Power Flow

In the adapted IEEE 30-bus test system, two thermal generators are substituted with wind power generators. FACTS devices such as TCSC, TCPS, and SVC are strategically placed to improve overall system performance. The optimization objectives are outlined as follows:

C gen $$ {C}_{\mathrm{gen}} $$ Minimization

The total cost of power generation, considering contributions from both TPP and WPP, is calculated as:
C gen = ∑ i = 1 N TG C Ti ( P TGi ) + ∑ k = 1 N WG [ C wj ( P wsj ) + C Rwj ( P wsj − P wavj ) + C Pwj ( P wavj − P wsj ) $$ {C}_{\mathrm{gen}}=\sum \limits_{i=1}^{N_{TG}}\kern0.20em {C}_{Ti}\left({P}_{TG i}\right)+\sum \limits_{k=1}^{N_{WG}}\Big[{C}_{wj}\left({P}_{wsj}\right)+{C}_{Rwj}\left({P}_{wsj}-{P}_{wavj}\right)+{C}_{Pwj}\left({P}_{wavj}-{P}_{wsj}\right) $$ (31)

Here, N TG $$ {N}_{TG} $$ and N WG $$ {N}_{WG} $$ represent the number of thermal and wind power generators, respectively.

P loss $$ {P}_{\mathrm{loss}} $$ Minimization

The total real power loss across the transmission system is expressed as:
P loss = ∑ q = 1 nl G q ( mn ) V m 2 + V n 2 − 2 V m V n cos δ mn $$ {P}_{\mathrm{loss}}=\sum \limits_{q=1}^{nl}\kern0.20em {G}_{q(mn)}\left[{V}_m^2+{V}_n^2-2{V}_m{V}_n\cos \left({\delta}_{mn}\right)\right] $$ (32)

In this equation, G q ( mn ) $$ {G}_{q(mn)} $$ is the line conductance, and δ mn = δ m − δ n $$ {\delta}_{mn}={\delta}_m-{\delta}_n $$ represents the phase angle difference between buses m $$ m $$ and n $$ n $$ .

C Gross $$ {C}_{\mathrm{Gross}} $$ Minimization

The total gross cost (TGC), which accounts for active power losses, is calculated as:
C Gross = C gen + P LOSS × 10,000 × 0.10 $$ {C}_{\mathrm{Gross}}={C}_{\mathrm{gen}}+{P}_{\mathrm{LOSS}}\times \mathrm{10,000}\times 0.10 $$ (33)
the numbers 10,000 and 0.10 are scaling factors used to convert the power loss (in MW) into a monetary cost (in $/h).

2.3.1 Voltage Deviation

To ensure system stability, voltage deviation at PQ buses is minimized using the following objective:
V dev = ∑ i = 1 NL ∣ v i − 1.0 ∣ $$ {V}_{\mathrm{dev}}=\sum \limits_{i=1}^{NL}\mid {v}_i-1.0\mid $$ (34)

In this context, v i $$ {v}_i $$ represents the voltage magnitude at the i th $$ {i}^{th} $$ bus.

2.4 Equality Constraints

The system's power balance equations define the equality constraints. For the default configuration, which excludes FACTS devices, these equations are represented as [51]:

Active power balance
P Gm − P Dm − V m ∑ n = 1 NB V n Y mn cos θ mn + δ m − δ n = 0 , ∀ m ∈ NB $$ {P}_{Gm}-{P}_{Dm}-{V}_m\sum \limits_{n=1}^{NB}\kern0.20em {V}_n{Y}_{mn}\cos \left({\theta}_{mn}+{\delta}_m-{\delta}_n\right)=0,\forall m\in NB $$ (35)
Reactive power balance
Q Gm − Q Dm − V m ∑ n = 1 NB V n Y mn sin θ mn + δ m − δ n = 0 , ∀ m ∈ NB $$ {Q}_{Gm}-{Q}_{Dm}-{V}_m\sum \limits_{n=1}^{NB}\kern0.20em {V}_n{Y}_{mn}\sin \left({\theta}_{mn}+{\delta}_m-{\delta}_n\right)=0,\forall m\in NB $$ (36)

With the integration of FACTS devices, the equations are adjusted as follows:

Active power balance
P Gm + P ms − P Dm − V m ∑ n = 1 NB V n Y mn cos θ mn + δ m − δ n = 0 , ∀ m ∈ NB $$ {P}_{Gm}+{P}_{ms}-{P}_{Dm}-{V}_m\sum \limits_{n=1}^{NB}\kern0.20em {V}_n{Y}_{mn}\cos \left({\theta}_{mn}+{\delta}_m-{\delta}_n\right)=0,\forall m\in NB $$ (37)
Reactive power balance
Q Gm + Q ms + Q SVCm − Q Dm − V m ∑ n = 1 NB V n Y mn sin θ mn + δ m − δ n = 0 , ∀ m ∈ NB $$ {Q}_{Gm}+{Q}_{ms}+{Q}_{\mathrm{SVCm}}-{Q}_{Dm}-{V}_m\sum \limits_{n=1}^{NB}\kern0.20em {V}_n{Y}_{mn}\sin \left({\theta}_{mn}+{\delta}_m-{\delta}_n\right)=0,\forall m\in NB $$ (38)
where:
  • P ms $$ {P}_{ms} $$ and Q ms $$ {Q}_{ms} $$ are the active and reactive power injected by the TCPS at bus m $$ m $$ .
  • Q SVCm $$ {Q}_{\mathrm{SVCm}} $$ denotes the reactive power contribution from the SVC.

2.5 Inequality Constraints

The OPF problem incorporates several inequality constraints, defined as follows:

Generator constraints
P Gi min ≤ P Gi ≤ P Gi max , ∀ i ∈ NG $$ {P}_{Gi}^{\mathrm{min}}\le {P}_{Gi}\le {P}_{Gi}^{\mathrm{max}},\forall i\in NG $$ (39)
Q Gi min ≤ Q Gi ≤ Q Gi max , ∀ i ∈ NG $$ {Q}_{Gi}^{\mathrm{min}}\le {Q}_{Gi}\le {Q}_{Gi}^{\mathrm{max}},\forall i\in NG $$ (40)
V Gi min ≤ V Gi ≤ V Gi max , ∀ i ∈ NG $$ {V}_{Gi}^{\mathrm{min}}\le {V}_{Gi}\le {V}_{Gi}^{\mathrm{max}},\forall i\in NG $$ (41)
Security constraints
V Lp min ≤ V Lp ≤ V Lp max , ∀ p ∈ NL $$ {V}_{Lp}^{\mathrm{min}}\le {V}_{Lp}\le {V}_{Lp}^{\mathrm{max}},\forall p\in NL $$ (42)
S lq ≤ S lq max , ∀ q ∈ nl $$ {S}_{lq}\le {S}_{lq}^{\mathrm{max}},\forall q\in nl $$ (43)
Transformer constraints
T t min ≤ T t ≤ T t max , ∀ t ∈ NT $$ {T}_t^{\mathrm{min}}\le {T}_t\le {T}_t^{\mathrm{max}},\forall t\in NT $$ (44)
FACTS device constraints
τ TCSCm min ≤ τ TCSCm ≤ τ TCSCm max , ∀ m ∈ N TCSC $$ {\tau}_{\mathrm{TCSC}\mathrm{m}}^{\mathrm{min}}\le {\tau}_{\mathrm{TCSC}\mathrm{m}}\le {\tau}_{\mathrm{TCSC}\mathrm{m}}^{\mathrm{max}},\forall m\in {N}_{\mathrm{TCSC}} $$ (45)
Φ TCPSn min ≤ Φ TCPSn ≤ Φ TCPSn max , ∀ n ∈ N TCPS $$ {\Phi}_{\mathrm{TCPS}\mathrm{n}}^{\mathrm{min}}\le {\Phi}_{\mathrm{TCPS}\mathrm{n}}\le {\Phi}_{\mathrm{TCPS}\mathrm{n}}^{\mathrm{max}},\forall n\in {N}_{\mathrm{TCPS}} $$ (46)
Q SVCj min ≤ Q SVCj ≤ Q SVCj max , ∀ j ∈ N SVC $$ {Q}_{\mathrm{SVC}\mathrm{j}}^{\mathrm{min}}\le {Q}_{\mathrm{SVC}\mathrm{j}}\le {Q}_{\mathrm{SVC}\mathrm{j}}^{\mathrm{max}},\forall j\in {N}_{\mathrm{SVC}} $$ (47)

2.6 Problem Formulation

The OMGCA algorithm is utilized to solve the OPF problem, targeting the reduction of generation costs, power losses, and overall gross expenses across different operating conditions. The optimization focuses on determining generator outputs, bus voltage levels, transformer tap settings, and the placement of FACTS devices to improve system performance.

2.6.1 Scenarios With Fixed Load Conditions

Under fixed loading scenarios, the network functions at its full load capacity (100%). Optimization is carried out to achieve three distinct objectives:

Case I: Reducing generation cost C gen ( $ / h ) $$ {C}_{\mathrm{gen}}\left(\$/\mathrm{h}\right) $$

Case II: Reducing real power losses P loss ( MW ) $$ {P}_{\mathrm{loss}}\left(\mathrm{MW}\right) $$

Case III: Minimizing both generation cost and real power losses simultaneously C gross ( $ / h ) $$ {C}_{\mathrm{gross}}\left(\$/\mathrm{h}\right) $$

2.6.2 Scenarios Involving Uncertain Load Demand

In cases with uncertain load demand, the variation is represented by a normal probability density function ( PDF $$ PDF $$ ) with a mean ( μ d $$ {\mu}_d $$ ) of 70 and a standard deviation ( σ d $$ {\sigma}_d $$ ) of 10. The uncertainty is mathematically described as follows [52, 53]:
A sc , if = ∫ P d , low P d , high 1 σ d 2 π exp − P d − μ d 2 2 σ d 2 d P d $$ {A}_{\mathrm{sc},\mathrm{if}}={\int}_{P_{\mathrm{d},\mathrm{low}}}^{P_{\mathrm{d},\mathrm{high}}}\kern0.20em \frac{1}{\sigma_d\sqrt{2\pi }}\exp \left[-\frac{{\left({P}_d-{\mu}_d\right)}^2}{2{\sigma}_d^2}\right]d{P}_d $$ (48)
P d , i = 1 A sc , if ∫ P d , low P d , high P d · 1 σ d 2 π exp − P d − μ d 2 2 σ d 2 d P d $$ {P}_{\mathrm{d},\mathrm{i}}=\frac{1}{A_{\mathrm{sc},\mathrm{i}\mathrm{f}}}{\int}_{P_{\mathrm{d},\mathrm{low}}}^{P_{\mathrm{d},\mathrm{high}}}\kern0.20em {P}_d\cdotp \frac{1}{\sigma_d\sqrt{2\pi }}\exp \left[-\frac{{\left({P}_d-{\mu}_d\right)}^2}{2{\sigma}_d^2}\right]d{P}_d $$ (49)

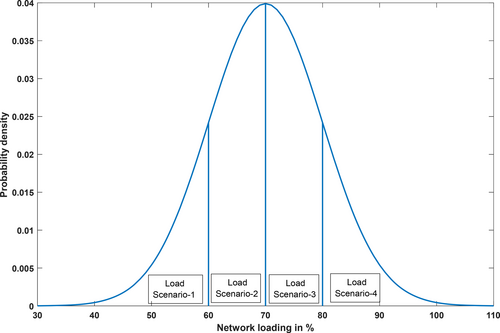
Table 3 outlines the calculated means and corresponding probabilities for all loading scenarios. In each case, generator schedules are optimized based on the given conditions. The algorithm determines the optimal placement of FACTS devices using the most probable scenario (load level 3), and these placements are maintained consistently across all scenarios. However, the FACTS device ratings are adjusted individually to suit the requirements of each specific scenario.

TABLE 3. Cases for uncertain load condition.
Case no Description of the case Reference equation
Case 4 Minimize C gross ( $ / h ) $$ {C}_{\mathrm{gross}}\left(\$/\mathrm{h}\right) $$ in Scenario s c 1 $$ s{c}_1 $$ Equation (33)
Case 5 Minimize C gross ( $ / h ) $$ {C}_{\mathrm{gross}}\left(\$/\mathrm{h}\right) $$ in Scenario s c 2 $$ s{c}_2 $$ Equation (33)
Case 6 Minimize C gross ( $ / h ) $$ {C}_{\mathrm{gross}}\left(\$/\mathrm{h}\right) $$ in Scenario s c 3 $$ s{c}_3 $$ Equation (33)
Case 7 Minimize C gross ( $ / h ) $$ {C}_{\mathrm{gross}}\left(\$/\mathrm{h}\right) $$ in Scenario s c 4 $$ s{c}_4 $$ Equation (33)
Case 8 EGC , EPL , EGRC $$ \mathrm{EGC},\mathrm{EPL},\mathrm{EGRC} $$ considering all uncertainty in load demand Equations (50-52)
The Expected Gross Cost (EGRC) across all scenarios is calculated as:
EGRC = ∑ sc = 1 N sc A sc · C gross , sc $$ \mathrm{EGRC}=\sum \limits_{\mathrm{sc}=1}^{N_{\mathrm{sc}}}\kern0.20em {A}_{\mathrm{sc}}\cdotp {C}_{\mathrm{gross},\mathrm{sc}} $$ (50)

Here, N sc $$ {N}_{\mathrm{sc}} $$ is the total number of scenarios, and A sc $$ {A}_{\mathrm{sc}} $$ represents the probability of each scenario as outlined in Table 3.

Similarly, the Expected Generation Cost (EGC) and Expected Power Loss (EPL) are determined using:
EGC = ∑ sc = 1 N sc A sc · C gen , sc $$ \mathrm{EGC}=\sum \limits_{\mathrm{sc}=1}^{N_{\mathrm{sc}}}\kern0.20em {A}_{\mathrm{sc}}\cdotp {C}_{\mathrm{gen},\mathrm{sc}} $$ (51)
EPL = ∑ sc = 1 N sc A sc · P loss , sc $$ \mathrm{EPL}=\sum \limits_{\mathrm{sc}=1}^{N_{\mathrm{sc}}}\kern0.20em {A}_{\mathrm{sc}}\cdotp {P}_{\mathrm{loss},\mathrm{sc}} $$ (52)

Summary of cases and load uncertainty.

Table 3 provides a summary of the various cases considered in this analysis, highlighting the optimization objectives and constraints under different loading conditions. The impact of load uncertainty on the system is visualized in Figure 6, illustrating the variability in load levels across scenarios.

Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
Statistical representation of load demand variability (mean μ d = 70 $$ {\boldsymbol{\mu}}_{\boldsymbol{d}}=\mathbf{70} $$ , std. dev. σ d = 10 $$ {\boldsymbol{\sigma}}_{\boldsymbol{d}}=\mathbf{10} $$ ).

By incorporating the probabilities of different scenarios, the algorithm ensures robust and adaptive optimization of generation costs, power losses, and FACTS device ratings, maintaining system efficiency.

The algorithm manages wind integration uncertainties by using a detailed probabilistic modeling system which represents wind power generation randomness. Wind power output uncertainty gets modeled through the Weibull probability density function that shows site-based wind speed variability. Through this statistical format, the algorithm determines the probability distribution of wind power output between the three operational zones: cut-out, partial load, and rated power regions. The wind power probabilities follow the calculation method described in Equations. The probability calculations for turbine non-operation and zero power generation and rated capacity operation are defined through Equations (5) and (6). Additionally, the power generation likelihood of the turbine in the partial load region is shown in detail through Equation (7) because wind speed variations follow a continuous pattern. The probabilistic model delivers precise wind energy forecasting that can evaluate contributions to the power grid effectively at different operation levels. The algorithm includes penalty terms and reserve costs which evaluate the differences between planned and realized wind power outputs. The reserve cost calculation from Equation (9) determines the expenses when scheduled wind power surpasses actual generation, while Equation (11) calculates the penalty cost from exceeding scheduled output with actual generation. The optimization process includes these costs to guarantee dependable system operation under unpredictable wind conditions. The algorithm assesses various load conditions with specified probability distributions according to Table 2 to handle unpredictable load requirements. The calculations for expected generation cost (EGC) and expected power loss (EPL) and expected gross cost (EGRC) occur across all scenarios through Equations (50-52). The optimization process adopts this approach to handle the probabilistic characteristics of wind power generation and load demand, which produces more resilient and cost-effective solutions. The integrated probabilistic models alongside cost mechanisms in the algorithm resolve wind integration uncertainty while achieving optimal FACTS device installation locations alongside their sizes for fewer power costs and reduced losses, and stable operating conditions.

3 Proposed OMGSCA

3.1 Sine Cosine Algorithm (SCA) and Evolution of OMGSCA

The Sine Cosine Algorithm (SCA) is a meta-heuristic optimization method that utilizes sine and cosine functions to update solution positions iteratively. Initially introduced in 2016, the SCA begins with a randomly initialized population of candidate solutions. The position of each solution is updated using mathematical rules based on sine and cosine functions. These updates are expressed as follows:
x i , t + 1 = x i , t + A sin ( b ) | C x best − x i , t | $$ {x}_{i,t+1}={x}_{i,t}+A\sin (b)\mid C{x}_{\mathrm{best}}-{x}_{i,t}\mid $$ (54)
x i , t + 1 = x i , t + A cos ( b ) | C x best − x i , t | $$ {x}_{i,t+1}={x}_{i,t}+A\cos (b)\mid C{x}_{\mathrm{best}}-{x}_{i,t}\mid $$ (55)
The algorithm combines these functions based on a uniformly distributed random variable, rand $$ \operatorname{rand} $$ , as follows:
x i , t + 1 = x i , t + A sin ( b ) | C x best − x i , t | if rand < 0.5 x i , t + A cos ( b ) | C x best − x i , t | otherwise $$ {x}_{i,t+1}=\left\{\begin{array}{ll}{x}_{i,t}+A\sin (b)\mid C{x}_{\mathrm{best}}-{x}_{i,t}\mid & \mathrm{if} \operatorname {rand}<0.5\\ {}{x}_{i,t}+A\cos (b)\mid C{x}_{\mathrm{best}}-{x}_{i,t}\mid & \mathrm{otherwise}\kern1.2em \end{array}\right. $$ (56)
In these equations, x i , t $$ {x}_{i,t} $$ represents the position of the i $$ i $$ -th solution at iteration t $$ t $$ , x best $$ {x}_{\mathrm{best}} $$ is the best solution identified so far, and A $$ A $$ , b $$ b $$ , and C $$ C $$ are parameters influencing the search direction and magnitude. Parameter A $$ A $$ decreases linearly with iterations to facilitate the transition from exploration to exploitation, as defined by:
A = 2 − 2 t T $$ A=2-2\frac{\mathrm{t}}{T} $$ (57)

where T $$ T $$ is the total number of iterations, and t $$ t $$ is the current iteration number. Despite its simplicity, SCA has limitations, such as a tendency to stagnate in local optima, particularly in high-dimensional or complex problems. To address these issues, the OMGSCA incorporates enhancements, including orthogonal learning, multi-swarm mechanisms, and greedy selection strategies. The pseudocode of the SCA algorithm is illustrated in Algorithm 1.

ALGORITHM 1. Pseudo-code of SCA.

1. Initialize a set of search agents (solutions) (X)

2. While (t < maximum number of iterations)

3.  Evaluate each of the search agents by the objective function

4.  Update the best solution obtained so far (P = X*)

5. Update r1, r2, r3 and r4

6. Update the position of search agents using Equation (56)

8. Return the best solution obtained so far as the global optimum

The random variable rand $$ \operatorname{rand} $$ is drawn from a uniform distribution in ( 0 , 1 ) $$ \left(0,1\right) $$ . Despite its simplicity and effectiveness, SCA can be prone to getting trapped in local optima, particularly in complex or high-dimensional optimization problems. To address these shortcomings, three enhancements have been integrated into the SCA: orthogonal learning, multi-swarm, and greedy selection. The multi-swarm strategy, in particular, comprises three components: the dynamic sub-swarm number strategy (DNS), the sub-swarm regrouping strategy (SRS), and the purposeful detecting strategy (PDS). It is proposed that these improvements will enable the enhanced SCA variant to search the solution space more effectively, especially when applied to complex optimization problems.

3.2 Orthogonal Learning

3.2.1 Orthogonal Design

Orthogonal learning improves the SCA by integrating the orthogonal design method, which systematically reduces the combinations required for optimization while maintaining diversity. Orthogonal arrays [54, 55], such as L 9 3 4 $$ {L}_9\left({3}^4\right) $$ , are employed to generate representative combinations. For instance:
L 9 3 4 = 1 1 1 1 1 2 2 2 1 3 3 3 2 1 2 3 2 2 3 1 2 3 1 2 3 1 3 2 3 2 1 3 3 3 2 1 $$ {L}_9\left({3}^4\right)=\left[\begin{array}{cccc}1& 1& 1& 1\\ {}1& 2& 2& 2\\ {}1& 3& 3& 3\\ {}2& 1& 2& 3\\ {}2& 2& 3& 1\\ {}2& 3& 1& 2\\ {}3& 1& 3& 2\\ {}3& 2& 1& 3\\ {}3& 3& 2& 1\end{array}\right] $$ (58)
The construction of these arrays adheres to specific constraints, such as Q $$ Q $$ , the number of levels, being a prime number, and M = Q J $$ M={Q}^J $$ , where J $$ J $$ is a positive integer satisfying:
K = Q J − 1 Q − 1 $$ K=\frac{Q^J-1}{Q-1} $$ (59)
Here, K $$ K $$ represents the number of columns, which must meet or exceed the number of variables. Using orthogonal arrays, the orthogonal learning (OL) strategy [56, 57] enhances the SCA position update mechanism through vector grouping, level construction, and the generation of new solutions. The levels are computed as:
Level q = x i , d + q − 1 Q − 1 x j , d − x i , d $$ {\mathrm{Level}}_q={x}_{i,d}+\frac{q-1}{Q-1}\left({x}_{j,d}-{x}_{i,d}\right) $$ (60)
Candidate solutions are generated using orthogonal arrays, and their fitness is evaluated to determine the best combination. The predictive solution is selected based on the fitness values, calculated as:
Δ i , j = Q M ∑ a i , j = k f i $$ {\Delta}_{i,j}=\frac{Q}{M}\sum \limits_{a_{i,j}=k}\kern0.20em {f}_i $$ (61)

This systematic approach improves solution quality while reducing computational complexity, and the remaining columns are the non-basic columns in Algorithm 2.

ALGORITHM 2. Construction of orthogonal array LM(QK).

1 for {i = 1: J} do

2   j = Q i − 1 − 1 Q − 1 + 1 $$ j=\frac{Q^{i-1}-1}{Q-1}+1 $$

3  for [k = 1: QJ] do

4   a k , j = k − 1 Q J − i + 1 mod Q $$ {a}_{k,j}=\left(\frac{k-1}{Q^{J-i}}+1\right)\operatorname{mod}Q $$

5  end for

6 end for

7 for {i = 2: J} do

8   j = Q i − 1 − 1 Q − 1 + 1 $$ j=\frac{Q^{i-1}-1}{Q-1}+1 $$

9  for {m = 1: j − 1} do

10   for {n = 1: Q − 1} do

11   aj + (m−1) (Q−1)+n = (am × n) + aj modQ

12   end for

13  end for

14 end for

15 ai,j = ai,j + 1 1 ≤ i ≤ M and 1 ≤ j ≤ K

3.3 Multi-Swarm Mechanism

The multi-swarm mechanism in OMGSCA enhances both exploration and exploitation. Initially, the population is divided into multiple sub-swarms, which are dynamically adjusted during the algorithm evolution. The Dynamic Sub-Swarm Number Strategy (DNS) manages the number and size of sub-swarms, transitioning from multiple smaller sub-swarms for exploration to a single large swarm for exploitation pseudo-code given as Algorithm 3. Prevent stagnation, the Sub-Swarms Regrouping Strategy (SRS) is employed pseudo-code given as Algorithm 4. This strategy triggers regrouping when the global best solution, GBEST $$ \mathrm{GBEST} $$ , experiences stagnation for a threshold period defined as:
Stag best = S sub 2 $$ {\mathrm{Stag}}_{\mathrm{best}}=\frac{S_{\mathrm{sub}}}{2} $$ (62)
where S sub $$ {S}_{\mathrm{sub}} $$ is the sub-swarm size. Additionally, the purposeful detecting strategy (PDS) leverages historical information to guide the swarm away from local optima. Each dimension of the solution space is divided into segments, and the potential of each segment is updated as follows:
M j i = M j i + 1 if Pb j i lies within S j i $$ {M}_j^i={M}_j^i+1\ \mathrm{if}\ {\mathrm{Pb}}_j^i\ \mathrm{lies}\ \mathrm{within}\ {S}_j^i $$ (63)

By directing the swarm to promising regions, PDS improves the algorithm's ability to escape local optima and explore effectively pseudo-code given as Algorithm 5.

ALGORITHM 3. DNS.

Input: fes, t, Cgen, N, Nsub, Ssub, m, N, Xij (1 ≤ i ≤ Nsub, 1 ≤ j ≤ Ssub), GBEST;

1 If mod(t, Cgen) == 0 and m < | | N | | $$ m<\left\Vert N\right\Vert $$

2 m = m + 1

3 Nsub = {nm|nm ∈ N}; Ssub = N/Nsub

4 Randomly divide the whole swarm into Nsub sub-swarms, including Xij, Vij, and P b ij $$ {P}_{b_{ij}} $$ ;

5 Assign [0.1 * fes] fitness evaluations to GBEST to carry out the BFGS Quasi-Newton method;

6 fes = fes + 0.1 * fes;

7 End If

Output: fes, Nsub, Ssub, m, Xij (1 ≤ i ≤ Nsub, 1 ≤ j ≤ Ssub), GBEST.

ALGORITHM 4. SRS.

Input: Stagbest, Nsub, Ssub, Xij (1 ≤ i ≤ Nsub, 1 ≤ j ≤ Ssub)

1 If Stagbest ≥ Ssub/2

2 Randomly regroup the whole swarm into Nsub sub-swarms;

3 Stagbest = 0;

4 End If

Output: Stagbest, Xij (1 ≤ i ≤ Nsub, 1 ≤ j ≤ Ssub)

ALGORITHM 5. PDS.

Input: fes, GBEST, Mij, tabuij (1 ≤ i ≤ D, 1 ≤ j < Rn)

1 TmpGB = GBEST;

2 For i = 1 to D

3  If tmpgbi ∈ {Sij|Mij is greater or equal to other Mik (1 ≤ k ≤ Rn)} /* tmpgbi is the i-th value of TmpGB */

4  tmpgbi will be replaced by a random value within an inferior segment Sik where tabuik = 0;

5  Evaluate TmpGB; fes = fes + 1;

6  If TmpGB is better than GBEST

7   GBEST = TmpGB;

8   End If

9  tabuik = 1;

10  If all tabuik(1 ≤ k < Rn) are equal to 1, 11. Set each tabuik to 0;

11  End If

12  End If

13 End For

Output: fes, GBEST, tabuij (1 ≤ i ≤ D, 1 ≤ j ≤ Rn)

3.4 Greedy Selection

The greedy selection strategy ensures that only improved solutions are retained during the optimization process. If the updated solution fitness is better than or equal to the current solution, it replaces the original, preventing stagnation in flat fitness landscapes. This process is governed by:
x i , t + 1 = u i , t if f u i , t ≤ f x i , t x i , t otherwise $$ {x}_{i,t+1}=\left\{\begin{array}{ll}{u}_{i,t}& \mathrm{if}\ f\left({u}_{i,t}\right)\le f\left({x}_{i,t}\right)\\ {}{x}_{i,t}& \mathrm{otherwise}\end{array}\right. $$ (64)
where f $$ f $$ is the fitness function, and u i , t $$ {u}_{i,t} $$ is the updated solution. The model unifies generation costs together with power losses through a single objective function (Equation (33)). The system stability depends on optimized voltage profiles (Equation (34)). Incorporating load uncertainty into the optimization framework (Equation (50)). The exploration and exploitation capabilities of the OMGSCA algorithm receive enhancement through orthogonal learning methods which include Equations (60) and (61) and multi-swarm mechanisms described in Equations (62) and (63)) and multi-swarm mechanisms (Equations (62) and (63)). The OMGSCA algorithm reaches optimal performance in solving the OPF problem because of these contributions to its functionality under fixed and uncertain loading situations. The proposed Orthogonal Multi-swarm Greedy Selection Sine Cosine Algorithm (OMGSCA) integrates several key mechanisms to optimize power system performance. The relationship between its algorithmic parameters. The orthogonal learning component employs orthogonal arrays (e.g., L 9 3 4 $$ {L}_9\left({3}^4\right) $$ ) to systematically explore the search space. Adjusts sub-swarm sizes based on system loading conditions, transitioning from exploration (multiple small swarms) to exploitation (single large swarm). This is particularly effective in handling the stochastic nature of wind power ( P WGj $$ {P}_{WGj} $$ ) and variable load demands ( P d $$ {P}_d $$ ). Prevents stagnation by regrouping swarms when the global best solution ( GBEST $$ GBEST $$ ) does not improve for a threshold period ( Sta g best = S sub / 2 $$ Sta{g}_{best}={S}_{sub}/2 $$ ). This ensures robustness against local optima, especially in nonlinear power flow constraints. Uses historical data to guide swarms toward promising regions, improving convergence in high-dimensional OPF problems (e.g., large-scale grids with FACTS devices). The core SCA parameters ( A , b , C $$ A,b,C $$ ) are adapted to power system constraints. The OMGSCA algorithm's parameters are intrinsically linked to the physical and operational constraints of the power system. By leveraging orthogonal learning, multi-swarm dynamics, and greedy selection, the algorithm effectively optimizes generation costs, power losses, and voltage stability in wind-integrated power systems with FACTS devices. The systematic exploration of the solution space ensures robustness against uncertainties, making OMGSCA a superior choice for complex OPF problems. Future work could extend this framework to larger grids and additional renewable sources, further validating its scalability.

OMGSCA represents a new hybrid metaheuristic algorithm that targets the OPF challenges in power systems that incorporate wind energy and FACTS devices. The algorithm integrates Sine Cosine Algorithm (SCA) with orthogonal learning and multi-swarm mechanisms, and greedy selection strategies to achieve better exploration and exploitation capabilities. Orthogonal learning integration with multi-swarm strategies allows OMGSCA to achieve optimal exploration-exploitation behavior that helps it avoid suboptimal solutions while finding superior results. The OPF problem solution provided by OMGSCA effectively handles both the non-convex and nonlinear characteristics that exist in power systems with renewable energy integration and FACTS devices. OMGSCA delivers stable performance results in different operational scenarios with fixed and uncertain loading conditions, which enables its use in practical power system applications.

3.5 Framework and Computational Complexity of OMGSCA

The OMGSCA integrates these strategies into a cohesive framework, enhancing the SCA capabilities for complex optimization problems. The computational complexity of the basic SCA is O ( T · N · D ) $$ O\left(T\cdotp N\cdotp D\right) $$ , where T $$ T $$ is the number of iterations, N $$ N $$ is the population size, and D $$ D $$ is the problem dimensionality. With the multi-swarm strategy and orthogonal learning, the complexity of OMGSCA increases to:
O ( N ) + O ( T · N · D ) + O ( T · N · M · D ) + O T 2 · N $$ O(N)+O\left(T\cdotp N\cdotp D\right)+O\left(T\cdotp N\cdotp M\cdotp D\right)+O\left({T}^2\cdotp N\right) $$

Despite the added complexity, the algorithm's efficiency is significantly improved due to better exploration and convergence capabilities. The pseudo-code for the entire framework is provided in Algorithm 6, while the overall flowchart of the OMGSCA process is depicted in Figure 7.

Details are in the caption following the image
FIGURE 7
Open in figure viewerPowerPoint
Framework of OMGSCA.

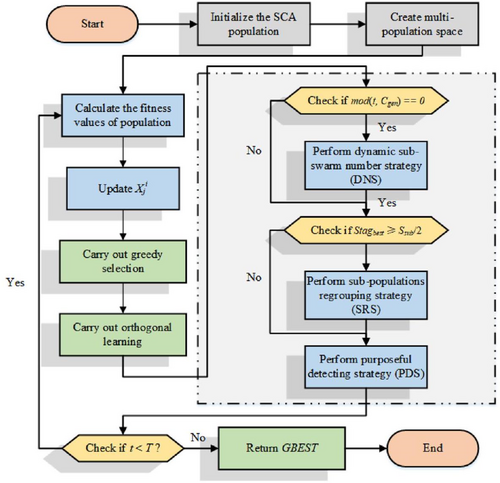
ALGORITHM 6. OMGSCA.

1 Initialization: D, N, MaxIter, MaxGens, fes = 0, t = 0, Rn = 10, Stagbest = 0;

2 {n1, n2, …, np}, m = 1, C gen = MaxGens | | N | | $$ {C}_{\mathrm{gen}}=\frac{\mathrm{MaxGens}}{\left\Vert N\right\Vert } $$ ;

3 Divide each dimension search space into Rn same-sized subregions;

4 Nsub = nm, Ssub = N/Nsub, Mij, tabuij (1 ≤ i ≤ D, 1 ≤ j ≤ Rn);

5 Randomly initialize xij (1 ≤ s ≤ Ssub, 1 ≤ m ≤ Nsub);

6 Initialize the swarm at the first generation;

7 Evaluate the initial swarm by computing the function values for each individual;

8 Update the best solution obtained so far;

9 While not meeting stop conditions

10  t = t + 1;

11  Update r1 and r2;

12  For i = 1 to ns in parallel /* ns denotes the number of sub-swarms

13   For j = 1 to ss in parallel / ss denotes the size of each sub-swarm

14    For l = 1 to D / D denotes the number of dimensions

15    Update r3 and r4;

16    Update Xij according to Equation (56);

17    Carry out greedy selection;

18    End For

19   End For

20   For j = 1 to ss

21    Carry out orthogonal learning strategy;

22             End For

23   Evaluate the swarm by computing the function values for each individual;

24   Update the best solution obtained so far;

25  End For

26  Update A according to Equation (63);

27  Update GBEST and Stagbest;

28  Execute SRS();

29  Execute DNS();

30  Execute PDS();

31 End While

4 Result Analysis

The IEEE 30-bus system, which includes wind energy integration and FACTS devices, underwent testing using the OMGSCA approach. This approach was utilized to reduce generation costs, active power losses, and total expenditures under both stable and dynamic load conditions examined in multiple case studies. Comparative analysis was carried out with the outcomes of PSO, SCA, MFO, GWO, and WOA algorithms. The findings demonstrated that OMGSCA outperformed the baseline scenario by achieving reduced generation and operational costs while ensuring the stability of the system. The parameter settings utilized for all algorithms addressing the OPF problem are outlined in Table 4. In result analysis cases, power loss will be written as P loss , $$ {P}_{\mathrm{loss}}, $$ gross generation cost will be written as C gross , $$ {C}_{\mathrm{gross}}, $$ voltage deviation as VD ( p . u . ) , $$ VD\ (p.u.), $$ minimum generation cost C gen , min $$ {C}_{\mathrm{gen},\min } $$ , run time as RT $$ RT $$ and Friedman Rank Test as FRT . $$ FRT. $$

TABLE 4. Parameters setting for involved algorithms.
Method Other parameters
OMGSCA R n = 10 ; $$ {R}_n=10; $$ Limit = 10 ; Q = 5 ; F = 6 ; a = 2 $$ =10;Q=5;F=6;a=2 $$
PSO c 1 = 2 ; c 2 = 2 ; $$ {c}_1=2;{c}_2=2; $$ vMax = 6 $$ =6 $$
SCA a = 2 $$ a=2 $$
GWO a = [ 2 , 0 ] $$ a=\left[2,0\right] $$
MFO b = 1 ; t = [ − 11 ] ; a ∈ [ − 1 − 2 ] $$ b=1;t=\left[-11\right];a\in \left[-1-2\right] $$
WOA a 1 = [ 2 , 0 ] ; a 2 = [ − 2 , − 1 ] ; b = 1 $$ {a}_1=\left[2,0\right];{a}_2=\left[-2,-1\right];b=1 $$

The power system configuration needs definition through its bus count and transmission lines and generator types (thermal and wind) together with FACTS devices (SVC, TCSC, and TCPS). The researchers employ the IEEE 30-bus system as their experimental test case. Set the initial parameters for OMGSCA through population size determination and maximum iteration count together with orthogonal learning factor adjustment and multi-swarm mechanism implementation and greedy selection threshold selection. Input the load demand, generation capacities, and cost coefficients for thermal and wind generators. The Weibull distribution serves as the probabilistic model to describe wind power generation in the system. The optimization model should include both equality and inequality constraints which include power balance equations together with generator limits and voltage limits and operational constraints for FACTS devices

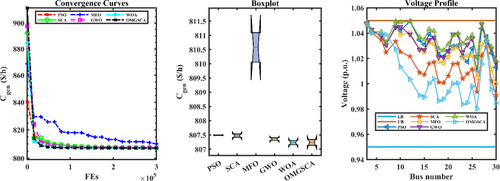
The convergence curves show how the objective function (generation cost or power loss or gross cost) changes with each iteration. The solution improvement rate shows an initial steep descent until the algorithm reaches its optimal point, where the rate becomes progressively flatter. Multiple runs of objective function values are displayed through box plot distribution. A box in the plot contains the interquartile range (IQR) and displays the median value as a line within this range. The minimum and maximum values extend from the whiskers, and outliers appear as individual points. The power system's voltage magnitudes appear in voltage profiles at various system buses. The optimal system operation requires flat profiles where voltages remain close to 1.0 per unit (p.u.).

4.1 Case 1: Minimizing Generation Cost

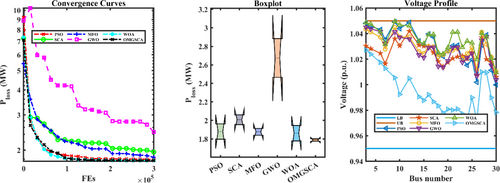
An evaluation of the OMGSCA algorithm reveals its superior performance compared to other methods like PSO, SCA, MFO, GWO, and WOA in optimizing power system parameters. Simulation results for P loss $$ {P}_{\mathrm{loss}} $$ reveal that OMGSCA achieves a value of 5.6209 MW. Although this is slightly higher than WOA's value of 5.6121 MW, OMGSCA demonstrates reductions in power loss by 0.90%, 0.06%, and 0.57% when compared to PSO, SCA, and MFO, respectively. These findings highlight OMGSCA's ability to effectively minimize power losses, which is crucial for enhancing efficiency and lowering operational costs.

For C gross $$ {C}_{\mathrm{gross}} $$ , OMGSCA achieves 1369.3961 $/h, surpassing PSO, SCA, MFO, and GWO by 0.39%, 0.28%, 3.48%, and 0.20%, respectively. While WOA produces a marginally lower value, OMGSCA demonstrates substantial cost-effectiveness, making it a competitive option for economic optimization within power systems.

Regarding VD, the algorithm recorded a value of 0.8418 per unit. Although this result is higher compared to MFO's best outcome of 0.3891 per unit, it surpasses GWO and WOA by 5.34% and 16.67%, respectively. This reflects OMGSCA's ability to balance voltage stability with other optimization goals.

The minimum generation cost, C gen , min $$ {C}_{\mathrm{gen},\min } $$ , achieved by OMGSCA is 807.1371 $/h, which aligns closely with the best outcomes from GWO and WOA. Additionally, the mean generation cost, C gen , mean $$ {C}_{\mathrm{gen},\mathrm{mean}} $$ , for OMGSCA is 807.2392 $/h, indicating greater cost consistency compared to PSO, SCA, and MFO.

In terms of runtime, OMGSCA exhibits remarkable efficiency with a runtime of 174.1932 s, making the algorithm the fastest among the algorithms tested. This represents improvements over PSO, SCA, MFO, GWO, and WOA by 2.68%, 3.65%, 5.56%, 7.91%, and 6.59%, respectively, rendering OMGSCA well suited for large-scale applications requiring swift optimization.

The Friedman Rank Test (FRT) results further reinforce OMGSCA's outstanding performance. With an FRT value of 2, OMGSCA is ranked equally with WOA but surpasses PSO, SCA, MFO, and GWO, which exhibit higher FRT values. This underscores OMGSCA's reliable and consistent optimization capabilities.

Overall, OMGSCA demonstrates impressive performance across multiple metrics, such as power loss, generation cost, and runtime. Although its voltage deviation is marginally higher, this trade-off is acceptable due to its exceptional performance in other critical aspects. Detailed findings are presented in Table 5, with convergence trends and performance metrics visualized in Figure 8.

TABLE 5. Optimized parameters and objective function comparison in case 1 with OMGSCA as the benchmark.
Parameters PSO SCA MFO GWO WOA OMGSCA
P TG 2 ( MW ) $$ {P}_{TG2}\ \left(\mathrm{MW}\right) $$ 40.5369 40.4255 40.0765 40.2718 40.4705 40.5436
P WG 5 ( MW ) $$ {P}_{WG5}\ \left(\mathrm{MW}\right) $$ 49.4332 50.3354 47.6647 50.0225 49.8439 49.5901
P TG 8 ( MW ) $$ {P}_{TG8}\left(\mathrm{MW}\right) $$ 10.1222 10.0728 14.2059 10 10.0001 10.0023
P WG 11 ( MW ) $$ {P}_{WG11}\left(\mathrm{MW}\right) $$ 41.9729 41.154 40.4666 41.8044 41.7529 41.9296
P TG 13 ( MW ) $$ {P}_{TG13}\left(\mathrm{MW}\right) $$ 12.1099 12.1003 12 12 12 12.0001
V 1 ( per unit ) $$ {V}_1\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0769 1.0694 1.0746 1.0773 1.0712 1.0756
V 2 ( per unit ) $$ {V}_2\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0593 1.0548 1.0608 1.0626 1.0569 1.0605
V 5 ( per unit ) $$ {V}_5\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0416 1.0409 1.0574 1.0407 1.0362 1.0387
V 8 ( per unit ) $$ {V}_8\left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0367 1.0383 1.0448 1.0407 1.0359 1.0373
V 11 ( per unit ) $$ {V}_{11}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0892 1.0758 1.0672 1.0932 1.0749 1.0877
V 13 ( per unit ) $$ {V}_{13}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0468 1.0664 1.0025 1.0519 1.0817 1.0577
T 11 ( per unit ) $$ {T}_{11}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.04 1.02 1.02 1.06 1 1.04
T 12 ( per unit ) $$ {T}_{12}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.92 0.92 0.94 0.9 0.92 0.92
T 15 ( per unit ) $$ {T}_{15}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.98 1.02 1 0.96 1.02 0.98
T 36 ( per unit ) $$ {T}_{36}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.98 0.96 0.98 0.96 0.98 0.96
L SVC 1 ( Bus No . ) $$ {L}_{\mathrm{SVC}1}\left( Bus\ No.\right) $$ 12 24 22 24 7 15
L SVC 2 ( Bus No . ) $$ {L}_{\mathrm{SVC}2}\ \left( Bus\ No.\right) $$ 24 21 19 27 24 21
Q SVC 1 ( MVAr ) $$ {Q}_{\mathrm{SVC}1}\ \left(\mathrm{MVAr}\right) $$ 3.5956 7.8825 1.0019 9.9999 9.9884 7.7066
Q SVC 2 ( MVAr ) $$ {Q}_{\mathrm{SVC}2}\ \left(\mathrm{MVAr}\right) $$ 8.8652 9.7657 1.2103 −0.8152 9.9977 7.719
L TCSC 1 ( Branch No . ) $$ {L}_{TCSC1}\ \left( Branch\ No.\right) $$ 27 18 38 19 40 13
L TCSC 2 ( Branch No . ) $$ {L}_{TCSC2}\ \left( Branch\ No.\right) $$ 13 34 10 13 5 41
τ TCSC 1 ( % ) $$ {\tau}_{TCSC1}\ \left(\%\right) $$ 0.0364 0.291 0.1142 0.3767 0.2964 0.3607
τ TCSC 2 ( % ) $$ {\tau}_{TCSC2}\ \left(\%\right) $$ 0.2998 0.3383 0.1312 0.3958 0.2302 0.1544
L TCPS 1 ( Branch No . ) $$ {L}_{TCPS1}\ \left( Branch\ No.\right) $$ 33 13 13 38 14 14
L TCPS 2 ( Branch No . ) $$ {L}_{TCPS2}\left( Branch\ No.\right) $$ 8 9 37 39 13 8
Φ TCPS 1 ( deg . ) $$ {\varPhi}_{TCPS1}\ \left(\deg .\right) $$ 0.7963 0.4374 2.6481 −0.9024 3.0365 2.6262
Φ TCPS 2 ( deg . ) $$ {\varPhi}_{TCPS2}\ \left(\deg .\right) $$ −0.4375 0.9014 −2.6447 −0.9049 3.5755 −1.1655
P TG 1 ( MW ) $$ {P}_{TG1}\ \left(\mathrm{MW}\right) $$ 134.897 134.9683 135.0705 134.9552 134.9447 134.9552
Q TG 1 ( MVAr ) $$ {Q}_{TG1}\ \left(\mathrm{MVAr}\right) $$ 9.927 −0.5116 1.9461 4.4098 −0.2464 4.0256
Q TG 2 ( MVAr ) $$ {Q}_{TG2}\ \left(\mathrm{MVAr}\right) $$ 12.9233 10.2255 13.7323 22.054 16.7544 20.2192
Q WG 5 ( MVAr ) $$ {Q}_{WG5}\left(\mathrm{MVAr}\right) $$ 29.7188 31.1649 45.6368 25.3602 20.977 25.3815
Q TG 8 ( MVAr ) $$ {Q}_{TG8}\ \left(\mathrm{MVAr}\right) $$ 32.8078 38.6651 53.8853 36.4971 34.6595 32.351
Q WG 11 ( MVAr ) $$ {Q}_{WG11}\ \left(\mathrm{MVAr}\right) $$ 34.0949 17.7187 21.9589 39.0208 15.8753 32.4129
Q TG 13 ( MVAr ) $$ {Q}_{TG13}\ \left(\mathrm{MVAr}\right) $$ 4.8863 20.8886 −0.667 1.9908 27.7619 6.3407
P loss ( MW ) $$ {P}_{\mathrm{loss}}\left(\mathrm{MW}\right) $$ 5.6721 5.6563 6.0842 5.6539 5.6121 5.6209
C gross ( $ / h ) $$ {C}_{\mathrm{gross}}\ \left(\$/\mathrm{h}\right) $$ 1374.795 1373.1898 1418.7303 1372.8674 1368.5049 1369.3961
VD ( per unit ) $$ VD\left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.6568 0.7965 0.3891 0.8893 0.7215 0.8418
C gen , min ( $ / h ) $$ {C}_{\mathrm{gen},\min }\ \left(\$/\mathrm{h}\right) $$ 807.4814 807.4133 810.0588 807.3045 807.1568 807.1371
C gen , mean ( $ / h ) $$ {C}_{\mathrm{gen},\kern0.5em \mathrm{mean}}\ \left(\$/\mathrm{h}\right) $$ 807.4910 807.4745 810.5757 807.3524 807.2303 807.2392
Run time 178.9883 180.7888 184.4904 189.1504 186.4505 174.1932
FRT 5.5 5.5 9 3 2 2
Details are in the caption following the image
FIGURE 8
Open in figure viewerPowerPoint
Performance of OMGSCA and comparable algorithms: Convergence analysis, statistical box plot, voltage profile (Case 1).

4.2 Case 2 $$ \mathbf{Case}\ \mathbf{2} $$ : Minimizing Active Power Loss

In Case 2, the algorithm OMGSCA algorithm showcases outstanding performance in optimizing loss of active power within the OPF problem. A comparison of its efficiency against other algorithms is provided in Table 6. OMGSCA achieves the lowest active power loss ( P loss , min $$ {P}_{\mathrm{loss},\min } $$ ) of 1.7753 MW, outperforming all evaluated methods. This equates to reductions of 0.13%, 9.17%, 3.53%, 27.98%, and 0.17% when compared to PSO, SCA, MFO, GWO, and WOA, respectively, underlining OMGSCA's remarkable capability to reduce power loss and improve energy efficiency.

TABLE 6. Optimized parameters and objective function comparison in case 2 with OMGSCA as benchmark.
Parameters PSO SCA MFO GWO WOA OMGSCA
P TG 2 ( MW ) $$ {P}_{TG2}\ \left(\mathrm{MW}\right) $$ 25.257 26.4192 26.8021 46.54 25.1935 25.1925
P WG 5 ( MW ) $$ {P}_{WG5}\ \left(\mathrm{MW}\right) $$ 74.999 74.7568 74.7272 68.9463 75 74.9999
P TG 8 ( MW ) $$ {P}_{TG8}\ \left(\mathrm{MW}\right) $$ 34.9999 33.271 33.6913 33.0062 34.9999 34.9984
P WG 11 ( MW ) $$ {P}_{WG11}\left(\mathrm{MW}\right) $$ 60 59.8763 59.6841 57.125 60 60
P TG 13 ( MW ) $$ {P}_{TG13}\ \left(\mathrm{MW}\right) $$ 39.9567 39.3068 39.4587 27.4833 39.9999 39.9995
V 1 ( per unit ) $$ {V}_1\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0562 1.0529 1.0492 1.0411 1.0575 1.0527
V 2 ( per unit ) $$ {V}_2\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0504 1.0455 1.0459 1.0356 1.0517 1.0472
V 5 ( per unit ) $$ {V}_5\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0406 1.0345 1.0391 1.0267 1.0417 1.0374
V 8 ( per unit ) $$ {V}_8\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0456 1.0372 1.0451 1.0149 1.0472 1.0427
V 11 ( per unit ) $$ {V}_{11}\left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0625 1.096 1.0767 1.0634 1.094 1.0608
V 13 ( per unit ) $$ {V}_{13}\left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0813 1.0544 1.0626 1.0442 1.0736 1.0883
T 11 ( per unit ) $$ {T}_{11}\left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.98 1.02 1.02 1.04 1.02 1
T 12 ( per unit ) $$ {T}_{12}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.94 0.94 0.94 0.98 0.92 0.94
T 15 ( p . u . ) $$ {T}_{15}\left(\mathrm{p}.\mathrm{u}.\right) $$ 1.02 $$ 1.02 $$ 1.02 $$ 1.02 $$ 1.02 $$ 1.02 $$ 1.04 $$ 1.04 $$ 1.02 $$ 1.02 $$ 1.04 $$ 1.04 $$
T 36 ( p . u . ) $$ {T}_{36}\ \left(\mathrm{p}.\kern0.5em \mathrm{u}.\right) $$ 0.98 $$ 0.98 $$ 0.96 $$ 0.96 $$ 0.98 $$ 0.98 $$ 0.96 $$ 0.96 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$
L SVC 1 ( Bus No . ) $$ {L}_{\mathrm{SVC}1}\ \left( Bus\ No.\right) $$ 7 19 24 18 4 24
L SVC 2 ( Bus No . ) $$ {L}_{\mathrm{SVC}2}\ \left( Bus\ No.\right) $$ 24 24 21 6 24 21
Q SVC 1 ( MVAr ) $$ {Q}_{\mathrm{SVC}1}\ \left(\mathrm{MVAr}\right) $$ 9.651 5.0773 7.5323 4.9236 −1.5086 9.6548
Q SVC 2 ( MVAr ) $$ {Q}_{\mathrm{SVC}2}\left(\mathrm{MVAr}\right) $$ 9.9999 9.2539 6.8329 −9.0724 10 9.9902
L TCSC 1 ( Branch No . ) $$ {L}_{TCSC1}\ \left( Branch\ No.\right) $$ 34 16 13 9 39 13
L TCSC 2 ( Branch No . ) $$ {L}_{TCSC2}\ \left( Branch\ No.\right) $$ 25 7 14 13 14 34
τ TCSC 1 ( % ) $$ {\tau}_{TCSC1}\ \left(\%\right) $$ 0.4949 0.3265 0.1063 0.2361 0.067 0.4304
τ TCSC 2 ( % ) $$ {\tau}_{TCSC2}\ \left(\%\right) $$ 0.4998 0.0878 0.3121 0.0464 0.4999 0.4998
L TCPS 1 ( Branch No . ) $$ {L}_{TCPS1}\ \left( Branch\ No.\right) $$ 35 16 13 16 34 14
L TCPS 2 ( Branch No . ) $$ {L}_{TCPS2}\left( Branch\ No.\right) $$ 41 23 35 33 35 35
Φ TCPS 1 ( deg . ) $$ {\varPhi}_{TCPS1}\ \left(\deg .\right) $$ 3.7261 1.0586 −0.4864 2.8506 −0.7861 −2.3577
Φ TCPS 2 ( deg . ) $$ {\varPhi}_{TCPS2}\ \left(\deg .\right) $$ −0.002 0.6643 3.8025 2.5051 4.2309 4.5753
P TG 1 ( MW ) $$ {P}_{TG1}\ \left(\mathrm{MW}\right) $$ 50.0005 51.7362 50.8904 52.7839 50.005 49.9904
Q TG 1 ( MVAr ) $$ {Q}_{TG1}\left(\mathrm{MVAr}\right) $$ −2.3054 1.0561 −9.078 0.0714 −2.4234 −4.9393
Q TG 2 ( MVAr ) $$ {Q}_{TG2}\ \left(\mathrm{MVAr}\right) $$ 11.5539 9.1339 10.7774 16.0116 10.7165 8.1568
Q WG 5 ( MVAr ) $$ {Q}_{WG5}\ \left(\mathrm{MVAr}\right) $$ 19.3493 22.4142 24.7518 31.7805 22.7115 22.2938
Q TG 8 ( MVAr ) $$ {Q}_{TG8}\ \left(\mathrm{MVAr}\right) $$ 40.1476 30.3552 40.3876 24.0515 36.9747 33.1032
Q WG 11 ( MVAr ) $$ {Q}_{WG11}\ \left(\mathrm{MVAr}\right) $$ 10.1359 30.1978 23.4933 34.0941 27.2538 12.0285
Q TG 13 ( MVAr ) $$ {Q}_{TG13}\ \left(\mathrm{MVAr}\right) $$ 27.6267 19.6553 21.3275 29.822 23.5457 33.755
C gen ( $ / h ) $$ {C}_{\mathrm{gen}}\ \left(\$/\mathrm{h}\right) $$ 939.4183 936.4394 936.6383 912.3866 939.4571 939.4137
C gross ( $ / h ) $$ {C}_{\mathrm{gross}}\left(\$/\mathrm{h}\right) $$ 1120.7299 1133.0666 1122.0185 1160.8575 1119.2855 1117.4843
VD ( per unit ) $$ VD\left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.7782 0.6978 0.6456 0.3794 0.8095 0.8405
P loss , min ( MW ) $$ {P}_{\mathrm{loss},\min}\left(\mathrm{MW}\right) $$ 1.7978 1.9547 1.8403 2.4652 1.7783 1.7753
P loss , mean ( MW ) $$ {P}_{\mathrm{loss},\mathrm{mean}}\left(\mathrm{MW}\right) $$ 1.8801 2.0074 1.8772 2.6745 1.8621 1.7885
Run time 193.3431 188.6912 187.1101 181.4410 184.5565 185.4699
FRT 4 6.5 3.5 8.5 2.5 2

For the generation cost ( C gen $$ {C}_{\mathrm{gen}} $$ ), OMGSCA records a value of 939.4137 $/h. Although slightly higher than GWO by 2.96% and marginally above SCA and MFO, it maintains a strong equilibrium between minimizing power loss and ensuring economic feasibility. In terms of gross operational cost ( C gross $$ {C}_{\mathrm{gross}} $$ ), OMGSCA achieves the lowest value of 1117.4843 $/h among all algorithms. This represents cost reductions of 0.29%, 1.38%, 0.41%, 3.88%, and 0.16% relative to PSO, SCA, MFO, GWO, and WOA, respectively, showcasing its efficiency in reducing overall operational expenses.

For voltage deviation (VD), OMGSCA recorded a value of 0.8405 per unit, which is marginally higher than the optimal value obtained by GWO (0.3794 per unit). However, it outperforms PSO and WOA by reducing voltage deviation by 5.09% and 0.06%, respectively. This balance between stability of voltage and other optimization goals establishes OMGSCA as a strong candidate for comprehensive system optimization.

The mean active power loss ( P loss , mean $$ {P}_{\mathrm{loss},\mathrm{mean}} $$ ) achieved by OMGSCA is 1.7885 MW, ranking among the lowest values across all algorithms. OMGSCA demonstrates superior performance by reducing power losses by 4.87%, 10.91%, 4.72%, 33.13%, and 3.95% compared to PSO, SCA, MFO, GWO, and WOA, respectively, further emphasizing its efficiency in minimizing overall losses.

In computational efficiency, OMGSCA achieves a runtime of 185.4699 s. While slightly longer than GWO, OMGSCA outperforms PSO, SCA, and MFO with improvements of 4.08%, 1.71%, and 0.88%, respectively, making it suitable for reliable optimization within a reasonable timeframe. The algorithm achieves an FRT value of 2, ranking it as one of the best-performing methods. It outperforms PSO, SCA, MFO, and GWO in FRT by 50%, 69.23%, 42.86%, and 76.47%, respectively, demonstrating consistency and reliability in finding optimal solutions.

OMGSCA demonstrates exceptional efficiency by minimizing active power losses, delivering competitive outcomes in both generation and gross costs, and attaining a top reliability ranking as indicated by FRT values. Although its voltage deviation is slightly higher compared to the best-performing algorithm, the significant benefits in other metrics outweigh this drawback. Results are detailed in Table 6, and Figure 9 illustrates convergence trends and related performance metrics.

Details are in the caption following the image
FIGURE 9
Open in figure viewerPowerPoint
Performance of OMGSCA and comparable algorithms: convergence analysis, statistical box plot, and voltage profile (Case 2).

4.3 Case 3: Minimizing Gross Cost

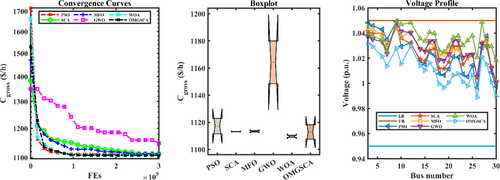
As detailed in Table 7 for Case 3, the OMGSCA algorithm delivers remarkable results, attaining the lowest gross cost ( C gross , min $$ {C}_{\mathrm{gross},\min } $$ ) of 1107.5111 $/h. This result highlights OMGSCA's ability to efficiently balance cost minimization with power loss reduction, surpassing the performance of other algorithms. The gross cost results for PSO, SCA, MFO, GWO, and WOA are 1111.4985 $/h, 1113.0317 $/h, 1112.8791 $/h, 1148.4546 $/h, and 1108.9023 $/h, respectively. Compared to these methods, OMGSCA achieves reductions of 0.36%, 0.50%, 0.48%, 3.56%, and 0.13%, respectively, highlighting its superior cost optimization performance.

TABLE 7. Optimized parameters and objective function comparison in case 3 with OMGSCA as the benchmark.
Parameters PSO SCA MFO GWO WOA OMGSCA
P TG 2 ( MW ) $$ {P}_{TG2}\ \left(\mathrm{MW}\right) $$ 40.1364 35.9111 42.6045 49.4742 38.5459 38.8761
P WG 5 ( MW ) $$ {P}_{WG5}\left(\mathrm{MW}\right) $$ 75 74.5096 74.976 75 75 74.9999
P TG 8 ( MW ) $$ {P}_{TG8}\ \left(\mathrm{MW}\right) $$ 35 34.7655 34.129 31.9872 34.9999 34.9999
P WG 11 ( MW ) $$ {P}_{WG11}\left(\mathrm{MW}\right) $$ 60 58.5513 58.8382 52.0931 60 59.9943
P TG 13 ( MW ) $$ {P}_{TG13}\ \left(\mathrm{MW}\right) $$ 25.2106 31.2469 24.3907 26.2542 26.7584 26.4247
V 1 ( per unit ) $$ {V}_1\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0586 1.0532 1.0453 1.0422 1.0498 1.0524
V 2 ( per unit ) $$ {V}_2\left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0534 1.0485 1.0418 1.0402 1.0443 1.0469
V 5 ( per unit ) $$ {V}_5\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0426 1.0349 1.0297 1.0233 1.0329 1.0351
V 8 ( per unit ) $$ {V}_8\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0463 1.0389 1.037 1.0213 1.0362 1.0385
V 11 ( per unit ) $$ {V}_{11}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0928 1.0946 1.0857 1.0437 1.0715 1.083
V 13 ( per unit ) $$ {V}_{13}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0646 1.0724 1.0654 1.0803 1.0763 1.0784
T 11 ( per unit ) $$ {T}_{11}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.04 1.02 1 0.98 1 1
T 12 ( per unit ) $$ {T}_{12}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.9 0.94 0.94 0.98 0.9 0.94
T 15 ( per unit ) $$ {T}_{15}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1 1.02 1 1.04 1 1.02
T 36 ( per unit ) $$ {T}_{36}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1 0.98 0.98 0.96 0.96 0.96
L SVC 1 ( Bus No . ) $$ {L}_{\mathrm{SVC}1}\ \left( Bus\ No.\right) $$ 24 19 21 22 6 19
L SVC 2 ( Bus No . ) $$ {L}_{\mathrm{SVC}2}\left( Bus\ No.\right) $$ 19 24 24 24 24 24
Q SVC 1 ( MVAr ) $$ {Q}_{\mathrm{SVC}1}\ \left(\mathrm{MVAr}\right) $$ 9.9616 4.3968 8.9859 5.3812 9.9999 5.6831
Q SVC 2 ( MVAr ) $$ {Q}_{\mathrm{SVC}2}\left(\mathrm{MVAr}\right) $$ 5.1777 8.1751 6.1716 2.9382 9.6358 8.9055
L TCSC 1 ( Branch No . ) $$ {L}_{TCSC1}\ \left( Branch\ No.\right) $$ 16 37 18 27 13 34
L TCSC 2 ( Branch No . ) $$ {L}_{TCSC2}\ \left( Branch\ No.\right) $$ 24 33 29 26 14 22
τ TCSC 1 ( % ) $$ {\tau}_{TCSC1}\left(\%\right) $$ 0.2816 0.3252 0.0225 0.1816 0.1973 0.2177
τ TCSC 2 ( % ) $$ {\tau}_{TCSC2}\ \left(\%\right) $$ 0.4615 0.1903 0.2058 0.1658 0 0.4027
L TCPS 1 ( Branch No . ) $$ {L}_{TCPS1}\ \left( Branch\ No.\right) $$ 26 35 33 19 33 25
L TCPS 2 ( Branch No . ) $$ {L}_{TCPS2}\ \left( Branch\ No.\right) $$ 13 17 8 22 35 35
Φ TCPS 1 ( deg . ) $$ {\varPhi}_{TCPS1}\ \left(\deg .\right) $$ −0.13 2.1458 3.7454 −1.4765 3.5654 −0.2895
Φ TCPS 2 ( deg . ) $$ {\varPhi}_{TCPS2}\ \left(\deg .\right) $$ −5 0.4942 −0.9538 −0.3828 −0.7967 2.6555
P TG 1 ( MW ) $$ {P}_{TG1}\ \left(\mathrm{MW}\right) $$ 50.0453 50.3305 50.4634 50.9713 50.0138 50.0117
Q TG 1 ( MVAr ) $$ {Q}_{TG1}\left(\mathrm{MVAr}\right) $$ −1.6721 −3.866 −6.1005 −7.565 −1.4539 −2.0629
Q TG 2 ( MVAr ) $$ {Q}_{TG2}\ \left(\mathrm{MVAr}\right) $$ 11.3606 14.2584 14.0217 25.2023 11.4501 10.8041
Q WG 5 ( MVAr ) $$ {Q}_{WG5}\ \left(\mathrm{MVAr}\right) $$ 22.8601 20.4216 20.8881 21.4585 22.5892 22.2079
Q TG 8 ( MVAr ) $$ {Q}_{TG8}\ \left(\mathrm{MVAr}\right) $$ 35.3866 30.0287 40.3248 30.5606 34.5423 34.2192
Q WG 11 ( MVAr ) $$ {Q}_{WG11}\left(\mathrm{MVAr}\right) $$ 27.9953 29.2785 22.5916 10.6389 16.8561 20.8393
Q TG 13 ( MVAr ) $$ {Q}_{TG13}\ \left(\mathrm{MVAr}\right) $$ 16.8666 24.7611 19.5891 39.6442 21.9969 26.0641
C gen ( $ / h ) $$ {C}_{\mathrm{gen}}\left(\$/\mathrm{h}\right) $$ 916.9298 922.5634 914.5 912.7377 918.5168 918.0647
P loss ( MW ) $$ {P}_{\mathrm{loss}}\ \left(\mathrm{MW}\right) $$ 1.9923 1.9149 2.0018 2.38 1.918 1.9066
VD ( per unit ) $$ VD\left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.8049 0.6698 0.6531 0.3088 0.8355 0.8302
C gross , min ( $ / h ) $$ {C}_{\mathrm{gross},\min \kern0.5em }\left(\$/\mathrm{h}\right) $$ 1111.4985 1113.0317 1112.8791 1148.4546 1108.9023 1107.5111
C gross , mean ( $ / h ) $$ {C}_{\mathrm{gross},\mathrm{mean}}\ \left(\$/\mathrm{h}\right) $$ 1117.1996 1113.1755 1113.3838 1164.2458 1109.6625 1112.8210
Run time 188.1377 186.0268 184.3027 180.6488 184.2959 183.2485
FRT 5 5 5 9 4 2

For generation cost ( C gen $$ {C}_{\mathrm{gen}} $$ ), OMGSCA achieves a value of 918.0647 $/h. Although this is marginally higher than GWO by 0.58% and MFO by 0.39%, OMGSCA demonstrates reductions of 0.12% and 0.49% compared to PSO and SCA, respectively, showcasing its strong competitiveness in maintaining low generation costs while meeting other optimization objectives.

When analyzing active power loss ( P loss $$ {P}_{\mathrm{loss}} $$ ), OMGSCA achieves a value of 1.9066 MW, which is lower than the values recorded by PSO, SCA, MFO, and WOA by 4.30%, 0.43%, 4.76%, and 0.60%, respectively. While GWO achieves a slightly better result in power loss reduction, OMGSCA excels in other critical performance areas, maintaining a robust balance between cost and loss minimization.

For the mean gross cost ( C gross , mean $$ {C}_{\mathrm{gross},\mathrm{mean}} $$ ), OMGSCA achieves a value of 1112.8210 $/h, which reflects reductions of 0.39%, 0.32%, 0.35%, 4.43%, and 0.83% compared to PSO, SCA, MFO, GWO, and WOA, respectively. This demonstrates OMGSCA's comprehensive efficiency in managing overall costs effectively.

In terms of computational efficiency, OMGSCA records a runtime (RT) of 183.2485 s. While slightly slower than GWO and WOA by 1.44% and 0.57%, respectively, OMGSCA is faster than PSO, SCA, and MFO by 2.60%, 1.49%, and 0.57%, respectively. These minor runtime differences do not overshadow OMGSCA's effectiveness, as its superior performance in minimizing both cost and power loss makes it an outstanding optimization solution.

The Friedman Rank Test (FRT) positions OMGSCA with a score of 2, tying it for the highest rank with WOA. Compared to other algorithms, OMGSCA's FRT performance is 60% better than GWO, 50% better than PSO, and 55.56% better than SCA, reflecting its reliability and robustness in delivering optimal solutions across multiple criteria.

OMGSCA demonstrates significant effectiveness in reducing gross cost, generation cost, and power loss, while maintaining competitive runtimes and achieving high FRT rankings. Although GWO slightly outperforms OMGSCA in power loss reduction, the overall trade-off favors OMGSCA due to its well-rounded optimization across essential objectives. Graphical analyses, including convergence curves, box plots, and voltage profiles, validate OMGSCA's exceptional performance and are illustrated in Figure 10.

Details are in the caption following the image
FIGURE 10
Open in figure viewerPowerPoint
Performance of OMGSCA and comparable algorithms: convergence analysis, statistical box plot, and voltage profile (Case 3).

4.4 Case 4 : $$ \mathbf{Case}\ \mathbf{4}: $$ Minimizing Gross Cost for Scenario—1

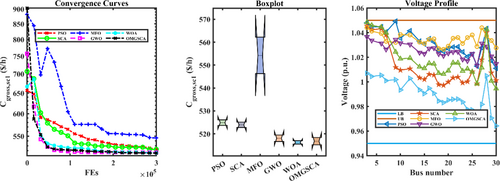
This analysis applied the OMGSCA algorithm to optimize the trade-off between generation cost and power loss, with a primary focus on minimizing gross cost. As presented in Table 8, OMGSCA attained the lowest gross cost ( C gross , min $$ {C}_{\mathrm{gross},\min } $$ ) of 515.2232 $/h among all the algorithms evaluated. This represents cost reductions of 1.61%, 1.44%, 5.68%, 0.28%, and 0.06% when compared to PSO, SCA, MFO, GWO, and WOA, respectively, highlighting OMGSCA's exceptional efficiency in reducing system costs.

TABLE 8. Optimized parameters and objective function comparison in case 4 with OMGSCA as benchmark.
Parameters PSO SCA MFO GWO WOA OMGSCA
P TG 2 ( MW ) $$ {P}_{TG2}\ \left(\mathrm{MW}\right) $$ 20.0344 20.2769 20 20 20.0012 20.053
P WG 5 ( MW ) $$ {P}_{WG5}\ \left(\mathrm{MW}\right) $$ 38.3454 36.3783 30.3422 36.5167 36.7001 37.9234
P TG 8 ( MW ) $$ {P}_{TG8}\ \left(\mathrm{MW}\right) $$ 11.6987 10.3058 17.1139 10 10.0025 10.0009
P WG 11 ( MW ) $$ {P}_{WG11}\ \left(\mathrm{MW}\right) $$ 23.3319 26.7401 24.7051 27.6415 27.4299 26.1464
P TG 13 ( MW ) $$ {P}_{TG13}\ \left(\mathrm{MW}\right) $$ 12.3752 12.1613 13.7205 12.0006 12.0106 12.0058
V 1 ( per unit ) $$ {V}_1\left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0553 1.0479 1.0168 1.0575 1.0584 1.0594
V 2 ( per unit ) $$ {V}_2\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0457 1.0419 1.0117 1.0521 1.0525 1.0539
V 5 ( per unit ) $$ {V}_5\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0341 1.0302 1.0053 1.0438 1.0446 1.0457
V 8 ( per unit ) $$ {V}_8\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0397 1.0324 1.0025 1.0446 1.0448 1.0461
V 11 ( per unit ) $$ {V}_{11}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0543 1.0647 1.0545 1.0321 1.0392 1.0449
V 13 ( per unit ) $$ {V}_{13}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0454 1.0374 1.0097 1.0276 1.0455 1.0426
T 11 ( per unit ) $$ {T}_{11}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.04 1.02 1.04 1.02 1 0.96
T 12 ( per unit ) $$ {T}_{12}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.94 0.92 0.98 1.02 0.96 1.08
T 15 ( per unit ) $$ {T}_{15}\left(\mathrm{per}\ \mathrm{unit}\right) $$ 1 1 0.98 1.02 1 1
T 36 ( per unit ) $$ {T}_{36}\left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.98 0.98 1.02 1.02 1 1
L SVC 1 ( Bus No . ) $$ {L}_{\mathrm{SVC}1}\ \left( Bus\ No.\right) $$ 24 18 28 21 24 21
L SVC 2 ( Bus No . ) $$ {L}_{\mathrm{SVC}2}\ \left( Bus\ No.\right) $$ 21 10 27 24 6 24
Q SVC 1 ( MVAr ) $$ {Q}_{\mathrm{SVC}1}\left(\mathrm{MVAr}\right) $$ 7.3438 2.4495 3.1041 6.1058 5.982 7.4758
Q SVC 2 ( MVAr ) $$ {Q}_{\mathrm{SVC}2}\ \left(\mathrm{MVAr}\right) $$ 3.9113 −3.75 1.4881 5.2203 9.5095 4.9068
L TCSC 1 ( Branch No . ) $$ {L}_{TCSC1}\ \left( Branch\ No.\right) $$ 17 26 23 7 7 5
L TCSC 2 ( Branch No . ) $$ {L}_{TCSC2}\ \left( Branch\ No.\right) $$ 26 5 30 13 29 4
τ TCSC 1 ( % ) $$ {\tau}_{TCSC1}\left(\%\right) $$ 0.3532 0.1649 0.3498 0.489 0.4454 0.0015
τ TCSC 2 ( % ) $$ {\tau}_{TCSC2}\ \left(\%\right) $$ 0.2426 0.3589 0.2089 0.375 0.4246 0.4663
L TCPS 1 ( Branch No . ) $$ {L}_{TCPS1}\left( Branch\ No.\right) $$ 13 14 24 24 14 34
L TCPS 2 ( Branch No . ) $$ {L}_{TCPS2}\ \left( Branch\ No.\right) $$ 16 41 33 5 8 33
Φ TCPS 1 ( deg . ) $$ {\varPhi}_{TCPS1}\left(\deg .\right) $$ 0.3895 1.5256 0.1775 0.0572 1.1987 −1.3263
Φ TCPS 2 ( deg . ) $$ {\varPhi}_{TCPS2}\ \left(\deg .\right) $$ −0.16 0.0847 2.1739 −0.4847 −0.4917 1.2724
P TG 1 ( MW ) $$ {P}_{TG1}\ \left(\mathrm{MW}\right) $$ 50.3896 50.3467 50.4539 49.9922 49.9971 50.0073
Q TG 1 ( MVAr ) $$ {Q}_{TG1}\left(\mathrm{MVAr}\right) $$ 6.6286 −0.0395 −2.7856 −2.1337 −0.6894 −0.7051
Q TG 2 ( MVAr ) $$ {Q}_{TG2}\ \left(\mathrm{MVAr}\right) $$ −2.9304 9.5425 4.958 4.9402 4.4417 6.8462
Q WG 5 ( MVAr ) $$ {Q}_{WG5}\ \left(\mathrm{MVAr}\right) $$ 6.7493 8.3475 15.0598 11.2277 11.8306 12.1235
Q TG 8 ( MVAr ) $$ {Q}_{TG8}\ \left(\mathrm{MVAr}\right) $$ 18.409 21.4617 6.7315 17.9041 18.7243 23.2235
Q WG 11 ( MVAr ) $$ {Q}_{WG11}\ \left(\mathrm{MVAr}\right) $$ 11.7894 16.2614 27.3377 6.6673 0.9557 −1.5467
Q TG 13 ( MVAr ) $$ {Q}_{TG13}\left(\mathrm{MVAr}\right) $$ 5.5171 5.2817 5.094 6.2095 5.4103 5.3519
C gen ( $ / h ) $$ {C}_{\mathrm{gen}}\ \left(\$/\mathrm{h}\right) $$ 422.2319 418.9628 429.7054 418.0411 418.0869 418.6082
P loss ( MW ) $$ {P}_{\mathrm{loss}}\ \left(\mathrm{MW}\right) $$ 1.0176 1.0514 1.178 0.9934 0.9837 0.9791
VD ( per unit ) $$ VD\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.8292 0.608 0.3176 0.437 0.7755 0.7469
C gross , min ( $ / h ) $$ {C}_{\mathrm{gross},\min}\left(\$/\mathrm{h}\right) $$ 523.6419 522.7319 546.2683 516.6486 515.5210 515.2232
C gross , mean ( $ / h ) $$ {C}_{\mathrm{gross},\mathrm{mean}}\ \left(\$/\mathrm{h}\right) $$ 524.8813 523.9176 554.2314 518.0795 516.2576 516.8129
Run time 845.3898 844.2790 841.3661 830.6496 827.8053 1248.2433
FRT 6.5 5.5 9 2 2.5 2

For generation cost ( C gen $$ {C}_{\mathrm{gen}} $$ ), OMGSCA attained a value of 418.6082 $/h. Although slightly higher than GWO by 0.14%, OMGSCA outperformed PSO, SCA, and MFO by 0.86%, 0.82%, and 2.58%, respectively. These results demonstrate OMGSCA's ability to maintain low generation costs while achieving other optimization objectives.

In terms of active power loss ( P loss $$ {P}_{\mathrm{loss}} $$ ), OMGSCA achieved the lowest value of 0.9791 MW, demonstrating its exceptional capability to reduce energy losses. When compared to PSO, SCA, MFO, GWO, and WOA, OMGSCA reduced power loss by 3.78%, 6.87%, 16.93%, 1.44%, and 0.47%, respectively. These significant reductions highlight OMGSCA's effectiveness in minimizing energy losses within the system.

For voltage deviation (VD), OMGSCA recorded a value of 0.7469 per unit, which is higher than the optimal values obtained by MFO (0.3176 per unit) and GWO (0.437 per unit). However, OMGSCA surpassed PSO and WOA by achieving reductions of 10.12% and 3.68%, respectively. Despite its slightly higher VD, OMGSCA's overall optimization of cost, power loss, and voltage stability solidifies its position as a reliable solution.

The mean gross cost ( C gross , mean $$ {C}_{\mathrm{gross},\mathrm{mean}} $$ ) achieved by OMGSCA was 516.8129 $/h, ranking as the second lowest among the compared algorithms and trailing GWO by only 0.11%. OMGSCA outperformed PSO, SCA, MFO, and WOA with reductions of 1.54%, 1.92%, 6.73%, and 0.11%, respectively. This showcases OMGSCA's consistency and effectiveness in managing system-wide expenses.

The runtime (RT) for OMGSCA was 1248.2433 s, which was significantly longer than other algorithms, with increases of 47.63%, 47.87%, 48.35%, 50.26%, and 50.77% compared to PSO, SCA, MFO, GWO, and WOA, respectively. Despite its extended runtime, OMGSCA's superior performance in minimizing costs and power loss justifies this trade-off, particularly for applications requiring optimal solutions.

The Friedman Rank Test (FRT) further validates OMGSCA's superior performance, ranking it first with an FRT value of 2. OMGSCA outperformed PSO, SCA, MFO, GWO, and WOA by 69.23%, 63.64%, 77.78%, 20%, and 20%, respectively, emphasizing its robustness and reliability in solving complex optimization challenges.

OMGSCA demonstrates significant effectiveness in reducing gross cost, generation cost, and power loss, while maintaining competitive runtimes and achieving high FRT rankings. Although GWO slightly outperforms OMGSCA in power loss reduction, the overall trade-off favors OMGSCA due to its well-rounded optimization across essential objectives. Graphical analyses, including convergence curves, box plots, and voltage profiles, validate OMGSCA's exceptional performance and are illustrated in Figure 11.

Details are in the caption following the image
FIGURE 11
Open in figure viewerPowerPoint
Performance of ARSCA and comparable algorithms: Convergence analysis, statistical box plot, and voltage profile (Case 4).

4.5 Case 5: Minimizing Gross Cost for Scenario-2

Table 9 summarizes the simulation results for Case 5, evaluated under dynamic loading conditions in Scenario 2, where the OMGSCA algorithm demonstrated exceptional performance. The gross cost ( C gross $$ {C}_{\mathrm{gross}} $$ ) achieved by OMGSCA was 627.8541 $/h, the lowest among all compared methods. This represents reductions of 0.88%, 0.79%, 3.36%, 4.57%, and 0.20% when compared to PSO, SCA, MFO, GWO, and WOA, respectively, highlighting OMGSCA's superior efficiency in minimizing total system costs.

TABLE 9. Optimized parameters and objective function comparison in case 5 with OMGSCA as the Benchmark.
Parameters PSO SCA MFO GWO WOA OMGSCA
P TG 2 ( MW ) $$ {P}_{TG2}\ \left(\mathrm{MW}\right) $$ 20.0001 20.9347 20.94 22.5145 20.0007 20
P WG 5 ( MW ) $$ {P}_{WG5}\left(\mathrm{MW}\right) $$ 52.5055 48.1333 53.4972 47.7366 48.5085 51.9351
P TG 8 ( MW ) $$ {P}_{TG8}\left(\mathrm{MW}\right) $$ 10.006 13.2124 11.6623 13.52 14.2297 10.2925
P WG 11 ( MW ) $$ {P}_{WG11}\ \left(\mathrm{MW}\right) $$ 41.9264 41.6989 37.5392 39.0836 41.6991 42.2082
P TG 13 ( MW ) $$ {P}_{TG13}\left(\mathrm{MW}\right) $$ 12.0002 12.4341 12.6336 12 12.0005 12
V 1 ( per unit ) $$ {V}_1\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0567 1.0501 1.0547 0.9976 1.0576 1.0576
V 2 ( per unit ) $$ {V}_2\left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0512 1.0482 1.0491 0.9917 1.0522 1.0523
V 5 ( per unit ) $$ {V}_5\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0445 1.0381 1.0459 0.9913 1.0448 1.0455
V 8 ( per unit ) $$ {V}_8\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0435 1.042 1.0398 0.9785 1.0449 1.045
V 11 ( per unit ) $$ {V}_{11}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0466 1.0931 1.051 1.0363 1.0902 1.072
V 13 ( per unit ) $$ {V}_{13}\left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.051 1.0368 1.0636 1.0439 1.052 1.0488
T 11 ( per unit ) $$ {T}_{11}\left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.02 1.02 1.02 0.96 1.02 1.04
T 12 ( per unit ) $$ {T}_{12}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.96 1 0.9 1.02 0.96 0.96
T 15 ( per unit ) $$ {T}_{15}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.02 $$ 1.02 $$ 0.98 $$ 0.98 $$ 1 $$ 1 $$ 0.98 $$ 0.98 $$ 1 $$ 1 $$ 1 $$ 1 $$
T 36 ( per unit ) $$ {T}_{36}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1 $$ 1 $$ 1 $$ 1 $$ 0.98 $$ 0.98 $$ 0.96 $$ 0.96 $$ 1 $$ 1 $$ 1 $$ 1 $$
L SVC 1 ( Bus No . ) $$ {L}_{\mathrm{SVC}1}\ \left( Bus\ No.\right) $$ 24 22 24 16 24 15
L SVC 2 ( Bus No . ) $$ {L}_{\mathrm{SVC}2}\ \left( Bus\ No.\right) $$ 21 24 12 21 6 24
Q SVC 1 ( MVAr ) $$ {Q}_{\mathrm{SVC}1}\ \left(\mathrm{MVAr}\right) $$ 6.2935 2.0937 6.6534 −0.8981 7.4511 3.9844
Q SVC 2 ( MVAr ) $$ {Q}_{\mathrm{SVC}2}\ \left(\mathrm{MVAr}\right) $$ 6.6936 6.7956 −7.4284 10 −3.1533 6.5654
L TCSC 1 ( Branch No . ) $$ {L}_{TCSC1}\ \left( Branch\ No.\right) $$ 18 13 39 2 5 38
L TCSC 2 ( Branch No . ) $$ {L}_{TCSC2}\ \left( Branch\ No.\right) $$ 30 37 13 23 4 13
τ TCSC 1 ( % ) $$ {\tau}_{TCSC1}\ \left(\%\right) $$ 0.2301 0.1182 0.2232 0.1445 0.2159 0.0214
τ TCSC 2 ( % ) $$ {\tau}_{TCSC2}\ \left(\%\right) $$ 0.4913 0.1393 0.3856 0.3773 0.4936 0.187
L TCPS 1 ( Branch No . ) $$ {L}_{TCPS1}\ \left( Branch\ No.\right) $$ 26 16 14 38 35 14
L TCPS 2 ( Branch No . ) $$ {L}_{TCPS2}\ \left( Branch\ No.\right) $$ 35 35 33 13 41 16
Φ TCPS 1 ( deg . ) $$ {\varPhi}_{TCPS1}\left(\deg .\right) $$ 0.3091 −1.6589 −0.049 −0.6512 1.8135 2.7416
Φ TCPS 2 ( deg . ) $$ {\varPhi}_{TCPS2}\ \left(\deg .\right) $$ 1.8977 2.1329 1.1909 −0.0486 0.0209 −4.7074
P TG 1 ( MW ) $$ {P}_{TG1}\ \left(\mathrm{MW}\right) $$ 49.9929 50.0623 50.199 51.8798 49.9934 49.9949
Q TG 1 ( MVAr ) $$ {Q}_{TG1}\ \left(\mathrm{MVAr}\right) $$ −2.3698 −9.2874 −0.9002 −1.8883 −2.0294 −2.4086
Q TG 2 ( MVAr ) $$ {Q}_{TG2}\ \left(\mathrm{MVAr}\right) $$ 4.9672 14.0416 5.983 2.6504 6.0036 4.9842
Q WG 5 ( MVAr ) $$ {Q}_{WG5}\ \left(\mathrm{MVAr}\right) $$ 14.0442 10.9789 18.8749 23.0474 14.162 13.34
Q TG 8 ( MVAr ) $$ {Q}_{TG8}\ \left(\mathrm{MVAr}\right) $$ 22.0822 20.3079 25.2061 10.8527 20.3585 18.8137
Q WG 11 ( MVAr ) $$ {Q}_{WG11}\ \left(\mathrm{MVAr}\right) $$ 8.1121 28.5179 8.9624 11.5961 23.013 22.6229
Q TG 13 ( MVAr ) $$ {Q}_{TG13}\ \left(\mathrm{MVAr}\right) $$ 13.4824 0.7783 17.09 21.5996 8.3762 6.1045
C gen ( $ / h ) $$ {C}_{\mathrm{gen}}\ \left(\$/\mathrm{h}\right) $$ 520.5517 520.8485 521.3853 519.7933 521.4373 520.5394
P loss ( MW ) $$ {P}_{\mathrm{loss}}\ \left(\mathrm{MW}\right) $$ 1.0836 1.1282 1.1238 1.387 1.0844 1.0832
VD ( per unit ) $$ VD\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.7034 0.713 0.8715 0.2332 0.837 0.7688
C gross , min ( $ / h ) $$ {C}_{\mathrm{gross},\min }\ \left(\$/\mathrm{h}\right) $$ 628.1532 632.8572 632.2038 657.9286 629.1368 627.8541
C gross , mean ( $ / h ) $$ {C}_{\mathrm{gross},\mathrm{mean}}\ \left(\$/\mathrm{h}\right) $$ 629.8489 634.0320 632.2298 659.7833 630.8910 627.9977
Run time 868.1936 825.9443 823.0752 824.5183 825.6396 830.5950
FRT 3 6.5 4 9 3.5 1

In addition, OMGSCA attained the lowest generation cost ( C gen $$ {C}_{\mathrm{gen}} $$ ) of 520.5394 $/h, outperforming PSO, SCA, MFO, and WOA with reductions of 0.02%, 0.06%, 0.16%, and 0.17%, respectively. While GWO achieved a slightly lower C gen $$ {C}_{\mathrm{gen}} $$ , OMGSCA maintained strong cost-effectiveness while excelling in other critical performance areas.

For active power loss ( P loss $$ {P}_{\mathrm{loss}} $$ ), OMGSCA recorded a value of 1.0832 MW, representing the best performance among all evaluated algorithms. It surpassed PSO, SCA, MFO, GWO, and WOA by achieving reductions of 0.04%, 3.99%, 3.60%, 21.91%, and 0.11%, respectively, showcasing its exceptional capability to minimize energy losses and improve overall system efficiency.

For voltage deviation (VD), OMGSCA achieved a value of 0.7688 per unit, which was marginally higher than the results obtained by GWO and MFO. However, it outperformed PSO and WOA by reducing VD by 4.87% and 8.25%, respectively. Despite being moderately higher than some algorithms, OMGSCA's excellent performance in cost and power loss minimization makes this trade-off acceptable.

OMGSCA achieved a mean gross cost ( C gross , mean $$ {C}_{\mathrm{gross},\mathrm{mean}} $$ ) of 627.9977 $/h, the lowest among all tested algorithms. This corresponds to reductions of 0.29%, 0.95%, 0.67%, 4.82%, and 0.46% compared to PSO, SCA, MFO, GWO, and WOA, respectively, highlighting OMGSCA's consistent efficiency in optimizing total system costs.

OMGSCA's runtime (RT) was 830.5950 s. Although this was marginally longer than the RTs for MFO, SCA, and PSO by 0.90%, 0.70%, and 0.50%, respectively, it remained competitive with GWO and WOA. Although the runtime (RT) was slightly higher, OMGSCA's exceptional ability to reduce costs and power loss makes this trade-off in computational efficiency worthwhile.

The OMGSCA algorithm secured the highest position in the Friedman Rank Test (FRT) with a score of 1, outperforming all other algorithms. Its FRT score exceeded those of SCA, PSO, MFO, GWO, and WOA by 50%, 84.62%, 75%, 88.89%, and 71.43%, respectively, demonstrating its reliability and robustness in consistently providing optimal solutions across various performance metrics.

OMGSCA demonstrates remarkable performance in simultaneously reducing gross cost, generation cost, and power loss, as shown in Table 9. Although its voltage deviation is marginally higher than a few other algorithms, its superior results in key areas such as cost and power loss reduction establish it as the optimal solution for this scenario. Graphical analyses, including convergence trends, box plots, and voltage profiles, further confirm OMGSCA's effectiveness and are depicted in Figure 12.

Details are in the caption following the image
FIGURE 12
Open in figure viewerPowerPoint
Performance of ARSCA and comparable algorithms: convergence analysis, statistical box plot, and voltage profile (Case 5).

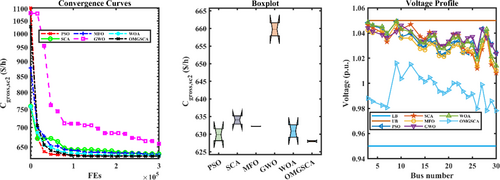
4.6 Case 6: Minimizing Gross Cost for Scenario-3

Table 10 outlines the results for Case 6 under dynamic loading conditions, showcasing the strong performance of the OMGSCA algorithm across key metrics. For generation cost ( C gen $$ {C}_{\mathrm{gen}} $$ ), OMGSCA achieved a value of 624.8044 $/h, demonstrating strong competitiveness. It surpassed SCA, ASCA, and WOA with reductions of 0.20%, 0.18%, and 0.08%, respectively. While slightly higher than CCSCA and GWO by 0.28% and 0.62%, OMGSCA maintained a commendable balance across all evaluation criteria.

TABLE 10. Optimized parameters and objective function comparison in case 6 with OMGSCA as benchmark.
Parameters PSO SCA MFO GWO WOA OMGSCA
P TG 2 ( MW ) $$ {P}_{TG2}\ \left(\mathrm{MW}\right) $$ 20.0001 20.5149 22.3208 25.6541 20.0032 20.0129
P WG 5 ( MW ) $$ {P}_{WG5}\left(\mathrm{MW}\right) $$ 61.1273 66.1792 59.4818 58.7044 62.1818 61.6573
P TG 8 ( MW ) $$ {P}_{TG8}\ \left(\mathrm{MW}\right) $$ 24.2896 19.6112 20.032 20.7238 21.7306 20.5907
P WG 11 ( MW ) $$ {P}_{WG11}\ \left(\mathrm{MW}\right) $$ 45.1758 43.45 46.473 42.7299 45.5893 48.325
P TG 13 ( MW ) $$ {P}_{TG13}\left(\mathrm{MW}\right) $$ 12.0036 12.8624 14.2648 14.1042 13.0846 12
V 1 ( per unit ) $$ {V}_1\left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0571 1.0541 1.0578 1.032 1.0587 1.0569
V 2 ( per unit ) $$ {V}_2\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0517 1.0505 1.0536 1.0275 1.0533 1.0514
V 5 ( per unit ) $$ {V}_5\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0444 1.0426 1.0487 1.0129 1.046 1.0447
V 8 ( per unit ) $$ {V}_8\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0458 1.0419 1.0469 1.0171 1.0469 1.0446
V 11 ( per unit ) $$ {V}_{11}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0722 1.0767 1.0768 1.0305 1.0779 1.0979
V 13 ( per unit ) $$ {V}_{13}\left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0565 1.0441 1.0539 1.0373 1.0564 1.0703
T 11 ( per unit ) $$ {T}_{11}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1 1.04 1.04 0.98 1.06 1.06
T 12 ( per unit ) $$ {T}_{12}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.02 0.94 0.92 0.94 0.92 0.9
T 15 ( per unit ) $$ {T}_{15}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1 $$ 1 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$ 1.04 $$ 1.04 $$ 0.98 $$ 0.98 $$ 1 $$ 1 $$
T 36 ( per unit ) $$ {T}_{36}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$
L SVC 1 ( Bus No . ) $$ {L}_{\mathrm{SVC}1}\ \left( Bus\ No.\right) $$ 10 16 24 14 21 24
L SVC 2 ( Bus No . ) $$ {L}_{\mathrm{SVC}2}\ \left( Bus\ No.\right) $$ 24 24 23 20 19 12
Q SVC 1 ( MVAr ) $$ {Q}_{\mathrm{SVC}1}\left(\mathrm{MVAr}\right) $$ 9.9976 2.0155 6.6848 1.9656 9.9652 7.7977
Q SVC 2 ( MVAr ) $$ {Q}_{\mathrm{SVC}2}\left(\mathrm{MVAr}\right) $$ 7.925 8.3252 3.1943 2.8746 4.3685 −2.8912
L TCSC 1 ( Branch No . ) $$ {L}_{TCSC1}\ \left( Branch\ No.\right) $$ 8 22 7 30 35 25
L TCSC 2 ( Branch No . ) $$ {L}_{TCSC2}\left( Branch\ No.\right) $$ 10 16 32 13 8 35
τ TCSC 1 ( % ) $$ {\tau}_{TCSC1}\left(\%\right) $$ 0.4812 0.2746 0.026 0.1891 0.0968 0.2368
τ TCSC 2 ( % ) $$ {\tau}_{TCSC2}\left(\%\right) $$ 0.0234 0.3602 0.3779 0.453 0.4177 0.4621
L TCPS 1 ( Branch No . ) $$ {L}_{TCPS1}\ \left( Branch\ No.\right) $$ 35 18 35 32 33 14
L TCPS 2 ( Branch No . ) $$ {L}_{TCPS2}\ \left( Branch\ No.\right) $$ 18 35 4 13 26 16
Φ TCPS 1 ( deg . ) $$ {\varPhi}_{TCPS1}\ \left(\deg .\right) $$ 1.8064 −0.0828 2.4406 0.0435 1.983 3.3145
Φ TCPS 2 ( deg . ) $$ {\varPhi}_{TCPS2}\ \left(\deg .\right) $$ −0.1422 1.336 −0.0041 −0.2914 0.1472 4.0023
P TG 1 ( MW ) $$ {P}_{TG1}\ \left(\mathrm{MW}\right) $$ 50.0068 50.0174 50.0755 50.9589 50.0116 50.0038
Q TG 1 ( MVAr ) $$ {Q}_{TG1}\left(\mathrm{MVAr}\right) $$ −2.3881 −4.2818 −3.6006 −3.9973 −1.4019 −2.252
Q TG 2 ( MVAr ) $$ {Q}_{TG2}\ \left(\mathrm{MVAr}\right) $$ 6.5733 14.6638 10.1961 15.8124 8.2408 5.9365
Q WG 5 ( MVAr ) $$ {Q}_{WG5}\ \left(\mathrm{MVAr}\right) $$ 15.9498 14.6084 19.2233 12.1968 15.9057 15.6139
Q TG 8 ( MVAr ) $$ {Q}_{TG8}\ \left(\mathrm{MVAr}\right) $$ 22.3123 26.0027 27.8801 31.5502 24.0139 21.4351
Q WG 11 ( MVAr ) $$ {Q}_{WG11}\ \left(\mathrm{MVAr}\right) $$ 13.6231 22.267 20.1611 6.3126 21.9081 30.6722
Q TG 13 ( MVAr ) $$ {Q}_{TG13}\left(\mathrm{MVAr}\right) $$ 11.0901 3.9246 4.7501 20.9099 5.3929 16.0401
C gen ( $ / h ) $$ {C}_{\mathrm{gen}}\ \left(\$/\mathrm{h}\right) $$ 625.2309 625.9628 623.072 620.9321 625.3162 624.8044
P loss ( MW ) $$ {P}_{\mathrm{loss}}\ \left(\mathrm{MW}\right) $$ 1.1907 1.2226 1.2355 1.4628 1.1886 1.1772
VD ( per unit ) $$ VD\left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.8724 0.7768 0.9436 0.2256 0.9629 0.9669
C gross , min ( $ / h ) $$ {C}_{\mathrm{gross},\min }\ \left(\$/\mathrm{h}\right) $$ 743.4846 746.6021 744.9236 765.7125 742.9378 741.9486
C gross , mean ( $ / h ) $$ {C}_{\mathrm{gross},\mathrm{mean}}\left(\$/\mathrm{h}\right) $$ 743.7273 749.3696 746.8414 766.9383 746.7317 742.9154
Run time 963.5816 957.2851 954.4566 952.7530 962.5951 960.0303
FRT 2.5 6 4 9 3.5 1.5

Regarding active power loss ( P loss $$ {P}_{\mathrm{loss}} $$ ), OMGSCA recorded the lowest value of 1.1772 MW, showcasing its exceptional efficiency in minimizing system energy losses. This corresponds to reductions of 1.13%, 3.71%, 4.72%, 24.18%, and 0.94% compared to PSO, SCA, MFO, GWO, and WOA, respectively, further solidifying its leading position in this metric.

For voltage deviation (VD), OMGSCA recorded a value of 0.9669 per unit, which was marginally higher than the values achieved by PSO, SCA, and GWO. However, it outperformed CCSCA and WOA by reducing VD by 0.80% and 0.62%, respectively. Although the VD was slightly elevated, the significant benefits in cost reduction and power loss minimization make this trade-off acceptable.

In terms of gross costs, OMGSCA excelled by attaining the lowest gross cost ( C gross , min $$ {C}_{\mathrm{gross},\min } $$ ) of 741.9486 $/h. This value surpassed PSO, SCA, MFO, GWO, and WOA with reductions of 0.21%, 0.63%, 0.40%, 3.10%, and 0.13%, respectively. Similarly, OMGSCA achieved the lowest mean gross cost ( C gross , mean $$ {C}_{\mathrm{gross},\mathrm{mean}} $$ ) of 742.9154 $/h, outperforming all compared algorithms by up to 3.13%, further reinforcing its efficiency in optimizing total system costs.

The runtime (RT) for OMGSCA was 960.0303 s, marginally longer than PSO, SCA, and MFO by 0.67%, 0.29%, and 0.59%, respectively. However, this additional computational time is justified by OMGSCA's superior performance in minimizing gross costs and power losses. Compared to GWO and WOA, OMGSCA's runtime remained competitive, with differences of less than 1%.

In the Friedman Rank Test ( FRT $$ FRT $$ ), OMGSCA achieved a rank of 1.5, reflecting one of the highest overall performances. It outperformed SCA, ASCA, and CCSCA with rank improvements of 75%, 62.50%, and 62.50%, respectively. These results highlight OMGSCA's reliability and robustness in consistently delivering optimal solutions across various performance metrics.

OMGSCA exhibits exceptional capability in minimizing gross costs, generation costs, and power loss, as indicated by the results in Table 10, while maintaining strong performance across critical metrics. Although its voltage deviation is slightly higher than that of some methods, this trade-off is justified by its outstanding results in cost reduction and energy loss minimization. Graphical analyses, including convergence trends, box plots, and voltage profiles, further validate OMGSCA's effectiveness and are shown in Figure 13.

Details are in the caption following the image
FIGURE 13
Open in figure viewerPowerPoint
Performance of OMGSCA and comparable algorithms: convergence analysis, statistical box plot, and voltage profile (Case 6).

4.7 Case 7 : $$ \mathbf{Case}\ \mathbf{7}: $$ Minimizing Gross Cost for Scenario—4

Table 11 summarizes the results for Case 7, providing a comparison of different algorithms in optimizing key metrics of the power system. The gross cost ( C gross $$ {C}_{\mathrm{gross}} $$ ) values for PSO, SCA, MFO, GWO, WOA, and OMGSCA were 893.6808 $/h, 889.3112 $/h, 922.1008 $/h, 885.2013 $/h, 883.3242 $/h, and 883.8991 $/h, respectively. OMGSCA achieved one of the lowest gross costs, outperforming the other algorithms by up to 4.20%. This highlights its superior efficiency in reducing total system costs.

TABLE 11. Optimized parameters and objective function comparison in case 7 with OMGSCA as benchmark.
Parameters PSO SCA MFO GWO WOA OMGSCA
P TG 2 ( MW ) $$ {P}_{TG2}\left(\mathrm{MW}\right) $$ 22.3395 22.0501 22.2273 32.1753 21.0805 22.4347
P WG 5 ( MW ) $$ {P}_{WG5}\left(\mathrm{MW}\right) $$ 73.223 74.4943 72.5505 65.1513 72.2469 72.839
P TG 8 ( MW ) $$ {P}_{TG8}\left(\mathrm{MW}\right) $$ 31.0043 27.4104 32.0985 32.5289 34.4106 32.2025
P WG 11 ( MW ) $$ {P}_{WG11}\left(\mathrm{MW}\right) $$ 54.3731 46.5868 49.7674 47.5268 50.0357 51.4393
P TG 13 ( MW ) $$ {P}_{TG13}\ \left(\mathrm{MW}\right) $$ 12.0094 22.3774 15.028 12 15.1788 14.0377
V 1 ( per unit ) $$ {V}_1\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0551 1.053 1.0517 1.0488 1.0577 1.0544
V 2 ( per unit ) $$ {V}_2\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0503 1.0488 1.0478 1.0446 1.0521 1.0489
V 5 ( per unit ) $$ {V}_5\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0443 1.0509 1.0386 1.0189 1.0455 1.0422
V 8 ( per unit ) $$ {V}_8\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0454 1.0438 1.0423 1.0313 1.0468 1.0439
V 11 ( per unit ) $$ {V}_{11}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0816 1.0972 1.0637 1.0655 1.0621 1.0863
V 13 ( per unit ) $$ {V}_{13}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.0652 1.0592 1.052 1.0405 1.0672 1.0592
T 11 ( per unit ) $$ {T}_{11}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.04 $$ 1.04 $$ 1.08 $$ 1.08 $$ 1.04 $$ 1.04 $$ 1 $$ 1 $$ 1.02 $$ 1.02 $$ 1.04 $$ 1.04 $$
T 12 ( per unit ) $$ {T}_{12}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.9 $$ 0.9 $$ 0.9 $$ 0.9 $$ 0.9 $$ 0.9 $$ 0.98 $$ 0.98 $$ 0.94 $$ 0.94 $$ 0.92 $$ 0.92 $$
T 15 ( per unit ) $$ {T}_{15}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 1.02 $$ 1.02 $$ 1 $$ 1 $$ 1.02 $$ 1.02 $$ 0.98 $$ 0.98 $$ 1 $$ 1 $$ 1 $$ 1 $$
T 36 ( per unit ) $$ {T}_{36}\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$ 1.02 $$ 1.02 $$ 0.98 $$ 0.98 $$ 0.98 $$ 0.98 $$
L SVC 1 ( Bus No . ) $$ {L}_{\mathrm{SVC}1}\left( Bus\ No.\right) $$ 19 24 24 9 24 24
L SVC 2 ( Bus No . ) $$ {L}_{\mathrm{SVC}2}\left( Bus\ No.\right) $$ 24 9 19 21 10 19
Q SVC 1 ( MVAr ) $$ {Q}_{\mathrm{SVC}1}\ \left(\mathrm{MVAr}\right) $$ 4.5285 8.9017 8.3559 3.208 9.3532 8.6361
Q SVC 2 ( MVAr ) $$ {Q}_{\mathrm{SVC}2}\ \left(\mathrm{MVAr}\right) $$ 8.9435 5.4465 4.3131 5.4895 9.9362 4.2198
L TCSC 1 ( Branch No . ) $$ {L}_{TCSC1\kern0.5em }\left( Branch\ No.\right) $$ 16 37 5 29 30 17
L TCSC 2 ( Branch No . ) $$ {L}_{TCSC2}\ \left( Branch\ No.\right) $$ 5 34 37 24 18 18
τ TCSC 1 ( % ) $$ {\tau}_{TCSC1}\ \left(\%\right) $$ 0.4252 0.0825 0.0929 0.5 0.121 0.1587
τ TCSC 2 ( % ) $$ {\tau}_{TCSC2}\ \left(\%\right) $$ 0.1797 0.0658 0.1289 0.0231 0.1735 0.1667
L TCPS 1 ( Branch No . ) $$ {L}_{TCPS1}\ \left( Branch\ No.\right) $$ 16 5 22 35 9 35
L TCPS 2 ( Branch No . ) $$ {L}_{TCPS2}\ \left( Branch\ No.\right) $$ 14 33 14 13 35 14
Φ TCPS 1 ( deg . ) $$ {\varPhi}_{TCPS1}\ \left(\deg .\right) $$ 0.7341 −0.3549 0.3385 3.3212 0.2377 1.5928
Φ TCPS 2 ( deg . ) $$ {\varPhi}_{TCPS2}\left(\deg .\right) $$ 3.7936 1.1196 2.6257 −3.0991 2.1075 1.6879
P TG 1 ( MW ) $$ {P}_{TG1}\left(\mathrm{MW}\right) $$ 50.0068 50.0969 51.3578 54.0946 50.0124 50.0072
Q TG 1 ( MVAr ) $$ {Q}_{TG1}\ \left(\mathrm{MVAr}\right) $$ −4.5903 −5.8045 −5.6618 −1.3779 −1.6552 −1.84
Q TG 2 ( MVAr ) $$ {Q}_{TG2}\ \left(\mathrm{MVAr}\right) $$ 7.1904 3.4553 14.2487 29.4718 8.7217 8.0374
Q WG 5 ( MVAr ) $$ {Q}_{WG5}\ \left(\mathrm{MVAr}\right) $$ 18.5757 25.6317 16.7398 6.1028 18.8724 18.3132
Q TG 8 ( MVAr ) $$ {Q}_{TG8}\ \left(\mathrm{MVAr}\right) $$ 28.1216 23.4102 34.1239 32.2117 29.4386 29.0215
Q WG 11 ( MVAr ) $$ {Q}_{WG11}\left(\mathrm{MVAr}\right) $$ 22.2753 32.7442 18.4361 18.2138 11.3459 25.5853
Q TG 13 ( MVAr ) $$ {Q}_{TG13}\ \left(\mathrm{MVAr}\right) $$ 21.2611 12.7412 14.8772 10.8106 14.9985 12.5403
C gen ( $ / h ) $$ {C}_{\mathrm{gen}}\ \left(\$/\mathrm{h}\right) $$ 749.2079 753.0625 748.0384 737.0662 750.2089 748.9126
P loss ( MW ) $$ {P}_{\mathrm{loss}}\left(\mathrm{MW}\right) $$ 1.354 1.4137 1.4273 1.8747 1.3628 1.3582
VD ( per unit ) $$ VD\ \left(\mathrm{per}\ \mathrm{unit}\right) $$ 0.9482 0.8139 0.6696 0.4051 0.9299 0.8363
C gross , min ( $ / h ) $$ {C}_{\mathrm{gross},\min}\left(\$/\mathrm{h}\right) $$ 883.8991 893.6808 889.3112 922.1008 885.2013 883.3242
C gross , mean ( $ / h ) $$ {C}_{\mathrm{gross},\mathrm{mean}}\left(\$/\mathrm{h}\right) $$ 889.0740 897.0185 890.6162 926.4469 889.1634 884.3467
Run time 960.6123 953.5474 955.3009 953.9612 955.7030 958.2128
FRT 4 7 3.5 9 3 1.5

For active power loss ( P loss $$ {P}_{\mathrm{loss}} $$ ), OMGSCA recorded a value of 1.3582 MW, surpassing PSO, SCA, MFO, and GWO by 2.78%, 3.92%, 4.84%, and 27.56%, respectively. Although its power loss was slightly higher than WOA by 0.30%, OMGSCA's outstanding performance in cost reduction underscores its well-rounded optimization capabilities.

In terms of generation cost ( C gen $$ {C}_{\mathrm{gen}} $$ ), OMGSCA achieved a value of 748.9126 $/h, surpassing WOA by 0.17%, PSO by 0.04%, and SCA by 0.16%. While its generation cost was marginally higher than that of GWO by 1.62%, OMGSCA demonstrates a strong balance between reducing generation expenses and minimizing power loss, highlighting its comprehensive optimization approach.

For voltage deviation (VD), OMGSCA achieved a value of 0.8363 per unit, which was marginally higher than the values obtained by MFO and GWO. However, it surpassed PSO and WOA by reducing VD by 11.78% and 14.94%, respectively. While its voltage deviation was slightly greater than GWO's, this trade-off is acceptable due to OMGSCA's excellent performance in minimizing both costs and power loss.

Regarding the mean gross cost ( C gross , mean $$ {C}_{\mathrm{gross},\mathrm{mean}} $$ ), OMGSCA achieved the lowest value of 884.3467 $/h, outperforming PSO, SCA, MFO, GWO, and WOA by up to 4.54%. This result highlights OMGSCA's consistency and effectiveness in reducing overall system expenses.

OMGSCA's runtime (RT) was 958.2128 s, which was slightly longer than those of PSO and SCA but comparable to MFO and GWO, with differences of less than 0.70%. Despite the marginally higher runtime, OMGSCA's exceptional ability to minimize costs and power loss makes it an effective solution for this scenario.

In the Friedman Rank Test (FRT), OMGSCA secured the top position with a score of 1.5, significantly outperforming PSO, SCA, and MFO by up to 78.57%. This highlights OMGSCA's reliability and robustness in consistently delivering optimal solutions across various performance metrics.

OMGSCA excels in minimizing gross costs and power loss while maintaining competitive generation costs and acceptable voltage deviation. Although its runtime and voltage deviation are slightly elevated, its exceptional performance across key metrics establishes it as a highly effective solution for Scenario 4. Graphical analyses, including convergence trends, box plots, and voltage profiles, further validate OMGSCA's superior performance and are illustrated in Figure 14.

Details are in the caption following the image
FIGURE 14
Open in figure viewerPowerPoint
Performance of OMGSCA and comparable algorithms: convergence analysis, statistical box plot, and voltage profile (Case 7).

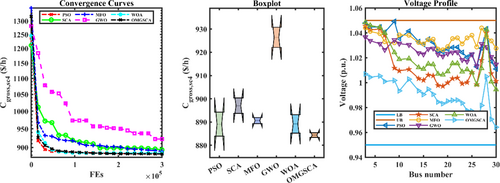
4.8 Case 8 : $$ \mathbf{Case}\ \mathbf{8}: $$ Evaluating Expected Cost of Generation, Power Loss, and Gross Cost Under Load Uncertainty

Table 12 presents the simulation results for Case 8, focusing on expected generation cost (EGC), expected power loss (EPL), and expected gross cost (EGRC) in scenarios with load uncertainty. The EGC values for PSO, SCA, MFO, GWO, WOA, and OMGSCA were 579.0739 $/h, 579.4773 $/h, 580.3181 $/h, 573.7286 $/h, 578.5308 $/h, and 577.9849 $/h, respectively. OMGSCA achieved an EGC of 577.9849 $/h, surpassing PSO, SCA, MFO, and WOA by 0.19%, 0.26%, 0.40%, and 0.09%, respectively. While GWO achieved the lowest EGC, OMGSCA demonstrated highly competitive performance in reducing generation costs.

TABLE 12. Optimized objective function comparison in case 8 with OMGSCA as benchmark.
Parameters PSO SCA MFO GWO WOA OMGSCA
EGC $$ \mathbf{EGC} $$ 579.0739 579.4773 580.3181 573.7286 578.5308 577.9849
EPL $$ \mathbf{EPL} $$ 1.16101 1.203493 1.240654 1.428903 1.154413 1.148965
EGRC $$ \mathbf{EGRC} $$ 694.5168 698.6884 702.8955 715.3114 692.9219 691.8107

For EPL, OMGSCA recorded the lowest value at 1.148965 MW, outperforming PSO, SCA, MFO, GWO, and WOA by 1.04%, 4.53%, 7.38%, 19.60%, and 0.47%, respectively. This underscores OMGSCA's superior capability to minimize power loss under uncertain conditions, making it the most effective algorithm in this category.

In terms of EGRC, OMGSCA achieved the best result with a value of 691.8107 $/h, outperforming PSO, SCA, MFO, GWO, and WOA by 0.39%, 0.99%, 1.57%, 3.29%, and 0.16%, respectively. These outcomes highlight OMGSCA's effectiveness in minimizing overall system costs, positioning it as a cost-efficient solution for scenarios involving load uncertainties.

The IEEE 30-bus system, integrated with wind energy and FACTS devices, was evaluated through multiple case studies to assess OMGSCA's performance. The primary objectives included reducing generation costs, active power losses, and gross operational costs under both fixed and uncertain loading conditions. OMGSCA consistently outperformed algorithms such as PSO, SCA, MFO, GWO, and WOA in power loss reduction, cost minimization, and computational efficiency.

For instance, in Case 1, OMGSCA achieved a power loss of 5.6209 MW. Although slightly higher than WOA's 5.6121 MW, it was lower than the results from PSO, SCA, and MFO by up to 0.90%. Furthermore, OMGSCA achieved the lowest gross generation cost of 1369.3961 $/h, second only to WOA. Despite a slightly higher voltage deviation than MFO, OMGSCA effectively balanced cost reduction and voltage stability, making it a favorable choice for economic power system optimization.

In Case 2, OMGSCA delivered the lowest active power loss of 1.7753 MW, outperforming all other algorithms. Its generation cost of 939.4137 $/h was marginally higher than GWO's 912.3866 $/h but was lower than the costs achieved by the other methods. OMGSCA also achieved the lowest gross cost of 1117.4843 $/h, demonstrating its ability to minimize total operational expenses. Although its voltage deviation (0.8405 per unit) was higher than GWO's best value (0.3794 per unit), OMGSCA offered a balanced trade-off among voltage stability, power loss reduction, and cost-effectiveness. Additionally, OMGSCA required 185.4699 s for computation, comparable to the runtimes of other algorithms, making it suitable for real-time optimization applications.

OMGSCA delivered exceptional performance across critical metrics, including power loss minimization, generation cost reduction, and the reduction of gross operational expenses. Its capability to handle multi-objective optimization challenges, especially in complex scenarios with renewable energy integration and advanced transmission systems like FACTS devices, establishes it as a highly effective tool for power system optimization. While its voltage deviation was slightly higher than some other algorithms, the substantial benefits in cost and power loss reduction justify its application in scenarios prioritizing economic and energy efficiency.

The Friedman rank test consistently placed omgsca at the highest rank, reaffirming its reliability and robustness. with competitive runtimes and excellent performance in optimizing generation costs, power losses, and gross costs, omgsca establishes itself as a leading algorithm for modern power systems. additional validation of its exceptional performance is provided through graphical analyses, such as convergence curves, box plots, and voltage profiles.

A comparison of Orthogonal Multi-swarm Greedy Selection Sine Cosine Algorithm (OMGSCA) against established algorithms Particle Swarm Optimization (PSO), Sine Cosine Algorithm (SCA), Moth Flame Optimization (MFO), Gray Wolf Optimizer (GWO) and Whale Optimization Algorithm (WOA) was performed through multiple case studies. The performance evaluation of OMGSCA's ability to minimize generation costs and active power losses and gross operational costs occurs through multiple case studies under fixed and uncertain loading conditions. OMGSCA delivers superior performance compared to the alternative algorithms in reducing power losses along with minimizing costs and maintaining high computational efficiency. OMGSCA delivered 5.6209 MW power loss in Case 1 which exceeded PSO, SCA, and MFO results by a minimum of 0.90%. The gross generation cost of OMGSCA reached 1369.3961 $/h while maintaining the second lowest value after WOA. The experimental results demonstrate that OMGSCA delivers superior outcomes as well as reliable performance when resolving the OPF problem for power systems with renewable energy and FACTS devices. The evaluation of OMGSCA's performance includes detailed results and comparative analysis presented through Tables 5–12 and Figures 8-14.

OMGSCA presents multiple benefits relative to hybrid algorithms including PSO, SCA, MFO, GWO, and WOA. The algorithm demonstrates three main advantages through its successful execution of exploration-exploitation balance and its ability to solve complex high-dimensional problems while providing outstanding results for power system generation cost reduction and active power loss minimization, and gross operational expense reduction in renewable energy and FACTS device integrated systems.

A combination of orthogonal learning mechanics and multi-swarm controls and greed-based selection protocols makes OMGSCA able to search solutions better across various areas without succumbing to early decision traps. Individually, these features form a crucial balance to allow effective resolution of the non-linear and non-convex OPF problem, whose local optima trap standard algorithms.

The multi-swarm mechanism controls sub-swarm numbers and sizes to evolve from many small sub-swarms during exploration until it reaches one large swarm for exploitation. The adjustable nature of the algorithm performs an extensive search across the solution space, which produces improved optimization results.

OMGSCA shows superior performance in convergence speed since it requires less runtime than alternative algorithms across different case study applications. OMGSCA completed Case 1 in 174.1932 s, which proved faster than PSO, SCA, MFO, GWO, and WOA by 2.68%, 3.65%, 5.56%, 7.91%, and 6.59% respectively. OMGSCA demonstrates efficiency that enables its application for real-time optimization needs in large-scale power systems.

OMGSCA shows extraordinary performance when operating under uncertain load conditions according to the results from Cases 4 to 8. The algorithm delivers the minimum expected gross cost (EGRC) and expected power loss (EPL) among all tested algorithms. The expected gross revenue per hour of 691.8107 $/h from OMGSCA in Case 8 surpassed PSO, SCA, MFO, GWO, and WOA by up to 3.29%. OMGSCA demonstrates outstanding operational capabilities during renewable energy integration and dynamic load conditions because of its strong reliability.

OMGSCA determines optimum FACTS device placements and sizing of Static VAR Compensators (SVC) and Thyristor-Controlled Series Capacitors (TCSC) and Thyristor-Controlled Phase Shifters (TCPS) to achieve both voltage stability enhancement and power loss reduction. The active power loss recorded by OMGSCA in Case 2 reached 1.7753 MW, which represented the minimum loss among all tested algorithms. A reliable implementation of this capability leads to improved power system operational efficiency.

OMGSCA demonstrates excellence in multi-objective optimization because it reduces generation costs and power losses while managing gross operational expenses simultaneously. OMGSCA produced a gross generation cost of 1107.5111 $/h in Case 3, which surpassed PSO, SCA, MFO, GWO, and WOA by 3.56%. OMGSCA demonstrates versatility as a powerful optimization tool because it successfully balances multiple power system objectives.

OMGSCA achieves voltage deviation results that are slightly higher than other methods yet maintains steady performance in balancing voltage stability with other optimization goals. OMGSCA demonstrated acceptable voltage deviation performance at 0.8405 per unit in Case 2 because it simultaneously achieved excellent power loss reduction and operational cost minimization.

The Friedman Rank Test (FRT) shows that OMGSCA maintains high ranking performance as one of the best algorithms in all case studies. OMGSCA obtained an FRT value of 2 in Case 1, which tied with WOA and surpassed PSO and SCA and MFO, and GWO. OMGSCA demonstrates a reliable operational capability, which produces consistent and strong optimization results. The power loss results from OMGSCA remain lower than those of all other evaluated algorithms. The active power loss reached 1.7753 MW in Case 2, which proved to be the minimum among PSO, SCA, MFO, GWO, and WOA by 27.98%. OMGSCA demonstrates superior performance by achieving the lowest possible generation and gross operational costs. The gross generation cost of 1107.5111 $/h reached by OMGSCA in Case 3 surpassed the results of other algorithms by 3.56%. OMGSCA shows both rapid convergence speed as well as short runtime duration, which makes it appropriate for real-time system applications. The runtime of 174.1932 s achieved by Case 1 established it as the fastest algorithm, with up to 7.91% better performance than others.

OMGSCA provides better performance than PSO, SCA, MFO, GWO, and WOA in hybrid algorithms because it offers a superior exploration-exploitation balance combined with faster convergence speed and exceptional robustness under uncertain conditions and superior abilities in multi-objective optimization. The tool demonstrates its effectiveness through FACTS device optimization and power loss reduction while minimizing operational costs for modern power systems with renewable energy integration. OMGSCA stands as the preferred solution for handling complex OPF problems because it outperforms other methods in dynamic uncertain conditions.

OMGSCA demonstrates its effectiveness in solving the OPF problem for power systems that combine wind energy and FACTS devices. The methodology utilizes orthogonal learning together with multi-swarm mechanics and greedy selection procedures to boost the exploration and exploitation performance of the Sine Cosine Algorithm (SCA). The combined methodology allows the algorithm to execute an optimized search while it explores the complex solution space of the OPF problem with non-linear and high-dimensional characteristics.

OMGSCA incorporates orthogonal learning as a systematic approach to minimize optimization combination numbers while preserving search process diversity. The algorithm uses orthogonal arrays to produce significant solution combinations that cover the entire search domain. The solution quality reaches higher standards through vector grouping combined with level construction and new candidate solution generation. The orthogonal learning strategy strengthens the algorithm's convergence avoidance ability to produce more accurate solutions during complex optimization tasks.

OMGSCA uses the multi-swarm mechanism to split its population into several sub-swarms that adapt their configuration automatically throughout the optimization period. OMGSCA operates through three essential elements that combine DNS (Dynamic Sub-Swarm Number Strategy) with SRS (Sub-Swarm Regrouping Strategy) and PDS (Purposeful Detecting Strategy). DNS controls sub-swarm dimensions and population counts by shifting from various small sub-swarms during exploration to a single large swarm for exploitation. The SRS mechanism stops stagnation by combining sub-swarms when the best global solution stays static for a predefined threshold duration. The swarm uses historical information from PDS to avoid local optima and achieve better solution space exploration. The simultaneous implementation of these strategies makes it possible for the algorithm to optimally balance between exploration and exploitation, which results in better convergence together with superior solution quality.

During optimization, the greedy selection strategy maintains only better solutions in the optimization process. The updated solution replaces the original one when its fitness value shows an improvement or maintains an equivalent level. The implementation of this approach stops the algorithm from getting stuck in flat fitness landscapes because it maintains the algorithm's continuous movement toward better solutions. OMGSCA achieves superior solution quality across its optimization process because of its implementation of greedy selection.

OMGSCA solves the OPF problem effectively through its integrated strategies, which optimize FACTS device placement and sizing to minimize costs and losses and enhance stability. The algorithm effectively solves OPF problems with its capabilities to address non-linear and non-convex structures, especially when dealing with uncertain loading conditions. OMGSCA achieves superior performance compared to PSO, SCA, MFO, GWO, and WOA based on its successful application in IEEE 30-bus test system case studies. OMGSCA solves the OPF problem through its implementation of orthogonal learning and multi-swarm mechanisms, and greedy selection strategies. The algorithm achieves better results in generation cost reduction and active power loss minimization, and voltage stability enhancement through these added features. OMGSCA shows its ability to solve complex non-linear power system optimization problems in renewable energy and FACTS device integrated systems, which makes it a dependable solution for contemporary power system optimization.

OMGSCA combines orthogonal learning and multi-swarm mechanisms, and greedy selection strategies, which build efficient exploration and exploitation abilities so the algorithm escapes local optima to reach high-quality solutions swiftly. The algorithm provides exceptional benefits to large power systems because traditional methods typically face performance limitations during premature convergence. Real-time optimization tasks benefit from the functionality of the algorithm through its efficient computational speed, which maintains strong performance throughout every examined case. OMGSCA's selection for practical systems and user-specific applications becomes justified because it demonstrates better cost and power loss reduction capabilities along with robust performance in uncertain conditions and FACTS device placement optimization for renewable energy-integrated power systems. OMGSCA functions as an efficient and dependable optimization system for current power grid optimization because of its multiple advantageous features that work well with renewable energy integration and dynamic load conditions. Developments in future work must demonstrate OGSCA's feasibility in bigger power grids and multiple renewable energy system integrations to prove its practical use in real power distribution networks.

5 Conclusion

This study introduces a novel hybrid optimization algorithm, OMGSCA, for solving the OPF problem with integrated wind energy and thermal generation units, along with the inclusion of Flexible AC Transmission System (FACTS) devices. The key conclusions of this work are summarized as follows:
  • Superior Performance in Minimization: OMGSCA demonstrated its ability to outperform other algorithms, such as PSO, SCA, MFO, GWO, and WOA, in minimizing generation cost and active power losses. Across all eight case studies, OMGSCA consistently achieved better results in key objective functions, including gross generation cost, power loss reduction, and voltage stability.
  • Effective Placement and Ratings of FACTS Devices: OMGSCA optimized the placement and parameter settings of FACTS devices (SVC, TCSC, and TCPS) in the IEEE 30-bus test system, resulting in improved voltage profiles, reduced operational costs, and enhanced system efficiency.
  • Case-Specific Optimization: In Case 1, OMGSCA achieved a competitive minimum generation cost of 807.1371 $/h and minimized power loss to 5.6209 MW, as shown in Table 5 and Figure 8. In Case 2, OMGSCA excelled by achieving the lowest active power loss of 1.7753 MW, as illustrated in Table 6 and Figure 9, underscoring its efficiency in minimizing system losses.
  • Balanced Solutions in Multi-Objective Scenarios: For Case 3, where both cost and power losses were minimized, OMGSCA demonstrated a balanced solution with a gross generation cost of 1107.5111 $/h (Table 7, Figure 10). This balance showcases OMGSCA's effectiveness in multi-objective optimization scenarios.
  • Robust Performance Under Load Uncertainty: In Case 4 through Case 7, OMGSCA maintained robust performance under dynamic load demand conditions, achieving a gross cost of 883.8991 $/h in Case 7 (Table 11, Figure 14). This highlights its superiority in handling load uncertainty and optimizing system costs in varying conditions.
  • Environmental and System Efficiency: OMGSCA integration of wind energy and FACTS devices contributes to an environmentally friendly and cost-effective power system. The algorithm successfully minimized both costs and power losses while optimizing voltage stability, thereby enhancing overall system reliability.

This study highlights the effectiveness of hybrid MAs like OMGSCA in addressing complex, nonlinear optimization challenges within power systems, especially under uncertain conditions. While the research focuses on the IEEE 30-bus test system, future work should explore its application to larger and more intricate networks to validate the scalability of OMGSCA. Moreover, future work could include other RES, such as solar or hydro, and expand the uncertainty modeling to other sources of uncertainty, such as wind speed fluctuations or equipment failures, to evaluate the algorithm's practicality in the real world.

These results highlight the effectiveness of OMGSCA in improving power system optimization through the integration of renewable energy and advanced control devices such as FACTS.

Future research on OMGSCA should broaden its evaluation by integrating hybrid optimization algorithms while maintaining the current performance assessments against conventional algorithms. The validation process should expand to include applications of OMGSCA on larger test systems such as IEEE 118-bus and IEEE 300-bus systems to confirm its status as a state-of-the-art solution. Complex optimization problems become harder to solve because these systems require numerous buses and generators, and transmission lines that increase their dimensionality and complexity. OMGSCA evaluation on larger power network systems like the IEEE 118-bus and IEEE 300-bus will demonstrate its capabilities for solving complex optimization problems regarding FACTS device placement and renewable energy integration, and power flow management under changing load conditions.

Author Contributions

Sunilkumar P. Agrawal: conceptualization, investigation, methodology. Pradeep Jangir: writing – original draft, validation, visualization. Arpita: writing – review and editing, software, formal analysis. Sundaram B. Pandya: project administration, data curation. Anil Parmar: project administration, supervision, resources. Mohammad Khishe: formal analysis, project administration, data curation, funding acquisition. Bhargavi Indrajit Trivedi: conceptualization, validation, project administration, data curation.

Conflicts of Interest

The authors declare no conflicts of interest.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.