The three-dimensional model of Darcy-Forchheimer flow in a convection system consisting of Ti-alloy nanoparticles (TiO₂) suspended in paraffin oil is mathematically constructed using fluid mechanics and partial differential equations (PDEs). A novel aspect of this study is the application of similarity transformation techniques to convert complex PDEs into a system of ordinary differential equations (ODEs), which are then solved using the Runge–Kutta 4th order method with the shooting technique. This unique approach provides deeper insights into the effects of magnetohydrodynamics (MHD), porosity, heat source, stretching surface, and radiation on bi-directional velocity and temperature profiles. The results demonstrate that Ti-alloy nanoparticles significantly enhance the thermal conductivity of the base fluid, leading to a 34.7% increase in temperature profiles compared to conventional fluids. The presence of a magnetic field induces a Lorentz force, reducing the bi-directional velocity by 18.5% while increasing fluid temperature by 22.9%. An increase in the porosity parameter results in a 15.3% reduction in velocity due to higher resistance, whereas the temperature profile shows a corresponding rise of 26.1%. Furthermore, an increase in the Forchheimer parameter reduces velocity by 21.6%, while the radiation parameter enhances heat transfer by 29.4%. These findings highlight the superior heat transfer efficiency of Ti-alloy-based nanofluids, making them highly suitable for applications in thermal energy storage, solar energy systems, and industrial cooling technologies.

1 Introduction

Fluid dynamics plays a crucial role in the advancement of engineering and technology, impacting a wide range of fields. In mechanical engineering, for instance, it is essential for the design and optimization of systems such as pumps, turbines, and heat exchangers. By applying principles of fluid dynamics, engineers can enhance the efficiency and performance of these devices, leading to reduced energy consumption and improved functionality. In addition to these applications, fluid dynamics is vital for understanding the behavior of lubricants, which is key for reducing friction and wear in machinery. It also aids in the analysis of hydraulic systems, allowing for more effective control and transmission of power in various applications, from heavy machinery to automotive systems. Furthermore, fluid dynamics is fundamental in the study of combustion processes, influencing the design of engines and burners for optimal performance and emissions reduction. As highlighted by Qin [1], these applications demonstrate how fluid dynamics not only contributes to current engineering practices but also drives innovation and technological advancements. The heat transfer augmentation methods that assist large particle suspensions, porous media, flexible seals, fins, and micro fins in enhancing heat transfer are reviewed by Wang et al. [2]. Si and xi [3] explained that one can focus on the fluid forces acting on structures without any complexity of density variations consisting of incompressible fluid that has constant density over the boundary region. Nanotechnology is revolutionizing fluid dynamics, opening up exciting avenues for research and practical applications. At the nanoscale, unique physical phenomena emerge that significantly differ from classical fluid dynamics. This shift leads to a deeper understanding of nanoscale transport mechanisms, which are crucial for the development of advanced devices. One of the key areas impacted by nanotechnology is high-frequency nanofluidics, where fluids behave differently at such small scales, allowing for faster and more efficient transport of materials. This has applications in fields like microelectronics and biomedical devices, where rapid fluid movement can enhance performance and efficiency. Additionally, investigating molecular momentum transport at fluid–solid interfaces is crucial for optimizing various applications, such as sensors and actuators. Understanding how molecules interact at these boundaries enables more precise control over fluid behavior, which is essential in nanotechnology. Titanium alloy nanoparticles are gaining significant attention in various fields due to their unique properties and applications. These nanoparticles, derived from titanium alloys, exhibit exceptional strength, lightweight characteristics, and excellent corrosion resistance, making them ideal for applications in aerospace, biomedical engineering, and advanced manufacturing. The incorporation of titanium alloy nanoparticles into materials can lead to enhanced mechanical properties, such as improved tensile strength and hardness, while maintaining a low weight. This makes them particularly valuable in aerospace and automotive industries, where reducing weight without compromising performance is crucial. Additionally, their biocompatibility and ability to promote osseointegration make titanium alloy nanoparticles highly sought after in biomedical applications, such as in bone implants and drug delivery systems. Moreover, the unique physical and chemical behavior of titanium alloy nanoparticles at the nanoscale enables advancements in nanotechnology and fluid dynamics. As the properties of materials can differ significantly at this scale, titanium alloy nanoparticles contribute to a better understanding of nanoscale transport phenomena, high-frequency nanofluidics, and molecular momentum transport at fluid–solid interfaces. This understanding not only improves device performance but also drives innovative applications in sensor technology and advanced manufacturing, as established by Veiga et al. [4]. Nisar et al. [5] fixed nanoparticles AA7075 and Ti6AI4V in secondary flow directions in a streamwise configuration, where results indicated an increase in temperature and concentration, with initial velocity reduced due to the volume fraction of particles in streamwise, and cross-flow directions. Further research by Shahzad et al. [6] concluded that hybrid nanofluids outperform basic nanofluids in heat transfer efficiency due to higher thermal conductivity. Theoretical analysis by Li et al. [7] focused on hybrid titanium alloys, with enhanced thermomechanical properties developed through mixture theory and differential quadrature methods. The Paraffin oil consists of various components, including normal alkanes, naphthenic acids, polypropylene glycol, and additives. It is used as a low-temperature phase change material to recover and store heat in a thermal utilization system. Moreover, it is used in a heat exchanger system for ventilation heat recovery with Sensible and Latent Heat Transfer (SLHT), Parallel Plate Direct Contact Air-to-Liquid Heat Exchanger (PPHE) and other Prototype Heat Exchanger (PHE) can be seen in References [8-10]. In the solar thermal sector, the employment of magnetic fields, porous media, and nanofluids in various heat transfer applications is primarily studied. It has been established that by using these strategies, especially when combined, convective heat transfer is significantly improved. A comprehensive review was conducted by Scott et al. [11] on hybrid nanofluid flow and heat transfer in cavities, focusing on advancements in technology and applications. Enhanced thermal properties of hybrid nanofluids were examined for their potential to improve heat transfer efficiency in confined spaces. Gholinia et al. [12] investigated a convection system utilizing a hybrid nanofluid blend of carbon nanotubes, ethylene glycol, and water, highlighting the enhanced heat transfer properties achieved with this composition. Dero et al. [13] further analyzed the flow characteristics of a stable, two-dimensional Hiemenz nanofluid, incorporating carbon nanotubes within an ethylene glycol and water based fluid. The study focused on fluid behavior over a linearly shrinking/stretching surface, offering insights into the impact of CNTs on flow stability and efficiency in varied thermal applications. Ahmed et al. [14] employed the CBS finite element technique to analyze heat transport, Lorentz force effects, and thermal radiation while studying free convection in wavy porous triangular enclosures with Al₂O₃-CuO/water hybrid nanosuspension. The entropy generation and MHD stagnation point flow in hybrid nanofluids across porous and stretchy sheets with generated magnetic fields were examined by Jakeer et al. [15, 16]. The study investigated heat transmission, thermal radiation, velocity, entropy production, and fluid stability using MATLAB's bvp4c and the homotopy perturbation approach. The findings emphasize the impacts of electric fields, thermal relaxation, and nanoparticle volume fraction, as well as boundary-layer separation and fluid friction irreversibility. While thermal radiation and viscous dissipation affected stability and heat transfer efficiency, especially in applications like airplane wings and biomedical systems, Maxwell fluid showed more friction than Eyring-Powell fluid, which affected velocity and heat transmission. In fluid dynamics, three-dimensional (3D) flow analysis examines fluid movement across all spatial dimensions (x, y, and z), which is essential in fields like aerodynamics, chemical processing, and environmental modeling due to the complex interactions across dimensions. Khan et al. [17] investigated such 3D flow over a plane surface, which was stretched nonlinearly along two lateral directions. This study contributed to understanding how nonlinear stretching affects fluid behavior in multidimensional flow systems, with applications in optimizing engineering processes involving complex fluid dynamics. Mohd et al. [18] conducted a study on unsteady three-dimensional flow in a rotating hybrid nanofluid over a stretching sheet, exploring how rotation and stretching influence flow stability and heat transfer. This work contributes to the understanding of hybrid nanofluid dynamics in rotating systems, with potential applications in advanced heat transfer technologies and rotating machinery. Mohanty et al. [19] analyzed the irreversibility of 3D Darcy–Forchheimer Casson hybrid nanofluid flow caused by a rotating disk, incorporating Cattaneo–Christov heat flux, Joule heating, and nonlinear thermal radiation. Results showed that increased Brinkman and Reynolds numbers elevate entropy generation, while various parameters enhance surface heat transfer, contributing to industrial applications and solar panel efficiency. Abderrahmane et al. [20] studied water-Fe₂O₄ nanofluids for enhancing 3D natural convection and entropy generation in permeable wavy-walled enclosures. Increasing Rayleigh and Darcy numbers improved convection significantly, while Lorentz force reduced flow dynamics, decreasing irreversibility by 15% at a Hartmann number of 100. Ali et al. [21] simulated Darcy-Forchheimer hybrid nanofluid (HNF) flow over a permeable rotating disc using aluminum alloy nanoparticles (AA7072 and AA7075) in water. Results showed that increased porosity and aluminum concentrations reduced both radial and axial velocities and temperature fields. Upreti et al. [22] analyzed a 3D fluid flow with the Darcy-Forchheimer model and with CNTs incorporated nanofluids: This study resulted in an improved thermal boundary layer with SWCNT and MWCNT. Bafe et al. [23] examined the heat and mass transfer in 3D thermo-bioconvective flow of rotating Williamson nanofluid over an exponentially stretching vertical sheet. Factors such as thermal radiation, Joule heating, and diffusion effects were analyzed. Results indicated significant changes in velocity, temperature, and mass transfer rates, with broad applications in biotechnology and polymer production. Wang et al. [24] studied the 3D flow of Maxwell nanoliquid, made by mixing graphene nanoparticles with engine oil, over a stretched sheet in a porous medium. The study explored the effects of thermal radiation, Darcy-Forchheimer conditions, and magnetic fields on flow behavior, highlighting significant findings regarding velocity, thermal profiles, and Nusselt number. Followed by Zhang et al. [25] looked into the flow of three-dimensional upper-convected Darcy-Forchheimer Maxwell nanofluids over a stretching surface. They explored how activation energy, thermodiffusion, and MHD affect heat and mass transfer. The findings reveal the influence of different parameters on the velocity, temperature, and concentration profiles. The research conducted by [26-30] examined the dynamics of several nanofluids and their applications. The study involved 3D numerical assessments of thermal systems, the behavior of gyrotactic microorganisms, and the impacts of heat production and radiative fluxes in chemically reactive settings, providing significant insights into thermofluids and nanofluid dynamics. Tarakaramu's et al. [31] study analyzes the impact of activation energy on 3D nanofluid motion over a stretching surface with nonlinear thermal radiation. The governing equations are transformed into nonlinear ODEs, solved numerically using the Runge–Kutta–Fehlberg method. The results demonstrate a strong correlation with previous studies, focusing on various activation energy values. Rahman et al. [32] used the Cattaneo-Christov theory to analyze non-linear mixed convection and chemical reactions over a stretching sheet with Sutterby nanofluid. The model was solved numerically and sensitivity analysis showed that Forchheimer and Deborah numbers affected velocity similarly, while heat transport rate was more sensitive to Brownian motion. In a related study, Thenmozhi et al. [33, 34] analyzed 3D Darcy-Forchheimer flow of paraffin oil with carbon nanotubes, emphasizing magnetized thermal radiation on Williamson hybrid ferrofluids. Transforming equations into ODEs, they highlighted porosity, radiation, and thermophoresis effects, enhancing thermal conductivity and temperature profiles for industrial applications.

The present work introduces a novel mathematical model for the convection system of Darcy-Forchheimer flow, incorporating titanium alloy nanoparticles suspended in paraffin oil as the base fluid. The study uniquely applies similarity transformations to convert complex PDEs into ODEs, allowing for numerical solutions. The findings reveal significant influences of key factors such as porosity, MHD radiation, thermophoresis, and Brownian motion on the flow dynamics and heat transfer characteristics of the system. Moreover, the detailed exploration of how these physical parameters affect bi-directional velocity and fluid temperature highlights the intricate interplay between the various mechanisms at work.

2 Mathematical Formulation

It is significant to form few assumptions while formulating the relevant equations before taking into account the governing equations for this investigation. Initially, consider the steady incompressible laminar flow of the base fluid is paraffin oil which is under the 3D hydromagnetic flow along a bidirectional stretchable surface with Ti-alloy nanoparticles. The magnitude of the magnetic field

{B}_0

is applied perpendicular to the x and y-plane of such a 3D coordinate system which is also normal to the z-axis. The MHD flow of a surface temperature

{T}_w

is fixed at constant temperature and the velocities of an incompressible laminar flow at

t=0

on the x-axis and y-axis can be expressed as

{u}_w=c{\left(x+y\right)}^n

and

{v}_w=d{\left(x+y\right)}^n

(Figure 1). Considering the Buongiorno model, the Arrhenius activation energy and 3D MHD Darcy-Forchheimer flow of fluid, which consists of three base fluids paraffin oil, the effect of porosity and radiation on a bidirectional stretched surface and an additional Ti-alloy nanomaterials are incorporated as described in the PDE equation as follows [17, 22, 33].

\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}+\frac{\partial w}{\partial z}=0

(1)

u\frac{\partial u}{\partial x}+v\frac{\partial u}{\partial y}+w\frac{\partial u}{\partial z}={\upsilon}_{nf}\frac{\partial^2u}{\partial {z}^2}-\frac{\sigma_c{B}_0^2u}{\rho_{nf}}-\frac{\upsilon_{nf}u}{\kappa_{nf}}-{F}_c{u}^2

(2)

u\frac{\partial v}{\partial x}+v\frac{\partial v}{\partial y}+w\frac{\partial v}{\partial z}={\upsilon}_{nf}\frac{\partial^2v}{\partial {z}^2}-\frac{\sigma_c{B}_0^2v}{\rho_{nf}}-\frac{\upsilon_{nf}v}{\kappa_{nf}}-{F}_c{v}^2

(3)

u\frac{\partial T}{\partial x}+v\frac{\partial T}{\partial y}+w\frac{\partial T}{\partial z}={\alpha}_{nf}\frac{\partial^2T}{\partial {z}^2}-\frac{1}{{\left(\rho {C}_p\right)}_{nf}}\frac{\partial {q}_r}{\partial z}+\frac{Q_o\left(T-{T}_{\infty}\right)}{{\left(\rho {C}_p\right)}_{nf}}

(4)

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

Graphical representation of mathematically modeled system.

The boundary conditions are

u={u}_w,\kern0.6em v={v}_w,\kern0.6em w=0,\kern0.48em T={T}_w,\kern0.49em \mathrm{at}\ z=0

u=0,\kern0.6em v=0,\kern0.6em w=0,\kern0.48em T\to {T}_{\infty}\kern0.48em \mathrm{when}\ z\to \infty

(5)

where

T

is the temperature of the fluid, respectively and

\left(u,v,w\right)

are the velocity components of the x, y and z-axis respectively.

The Rosseland approximation [35] for the radiative heat flux is defined as follows

{q}_r=\frac{-16{\sigma}^{\ast \ast }{T}_{\infty}^3}{3{K}^{\ast }}\frac{\partial T}{\partial z}

(6)

Here ${\sigma}^{\ast \ast }$ defines the mean absorption coefficient and ${K}^{\ast }$ represents the Boltzmann coefficient.

2.1 Thermophysical Properties of the Nanofluids

Let define the effective dynamic viscosity, thermal conductivity, density, thermal diffusivity, specific heat, and kinematic viscosity of nanofluid as described [36-38] as follows (Table 1).

{\mu}_{nf}={\mu}_f\left(1+7.3\Phi +123{\Phi}^2\right)

(7)

\frac{\Upsilon_{nf}}{\Upsilon_f}=\frac{\Upsilon_{np}+\left(\omega -1\right){\Upsilon}_f-\left(\omega -1\right)\Phi \left({\Upsilon}_f-{\Upsilon}_{np}\right)}{\Upsilon_{np}+\left(\omega -1\right){\Upsilon}_f+\Phi \left({\Upsilon}_f-{\Upsilon}_{np}\right)}

(8)

{\rho}_{nf}=\left({\rho}_f\left(1-\Phi \right)+{\rho}_{np}\Phi \right),\kern1.08em {\alpha}_{nf}=\frac{\Upsilon_{nf}}{{\left(\rho {C}_p\right)}_{nf}}

(9)

{\left(\rho {C}_p\right)}_{nf}=\left({\left(\rho {C}_p\right)}_f\left(1-\Phi \right)+\Phi {\left(\rho {C}_p\right)}_{np}\right),\kern0.84em {\upsilon}_{nf}=\frac{\mu_{nf}}{\rho_{nf}}

(10)

where the subscript

nf

f

, and

np

are nanofluid, base fluid, and nanoparticle, respectively.

TABLE 1. The thermophysical properties of paraffin oil and Ti-alloy nanoparticle

\mathit{\Pr}=6.72

Properties	Density $\rho \left( Kg/{m}^3\right)$	Thermal conductivity $\Upsilon \left(W/ mK\right)$	Specific heat ${C}_p\left(J/ kgK\right)$
Paraffin oil	840	0.2	2100
Ti-alloy	4420	6.7	526.3

Let us non-linearize the determining PDEs (2-5) into ODEs by using the following similarity transformation (11)

\left.\begin{array}{l}u=c{\left(x+y\right)}^n{g}^{\prime },\kern0.48em v=c{\left(x+y\right)}^n{h}^{\prime}\kern0.48em \eta ={\left(\frac{c}{\upsilon_f}\right)}^{\frac{1}{2}}z{\left(x+y\right)}^{\frac{\left(n-1\right)}{2}}\\ {}w=-{\left(c{\upsilon}_f\right)}^{0.5}{\left(x+y\right)}^{n-1}\left[0.5\left(n+1\right)\left(g+h\right)+0.5\left(n-1\right)\eta \left({g}^{\prime }+{h}^{\prime}\right)\right],\kern0.72em \theta \left(\eta \right)=\frac{T-{T}_{\infty }}{T_w-{T}_{\infty }}\end{array}\right\}

(11)

{A}_c{g}^{\prime \prime \prime }-{B}_c\left(\left(n+{F}_0\right){g}^{\prime 2}+{ng}^{\prime }{h}^{\prime }+0.5\left(n+1\right){g}^{\prime \prime}\left(h+g\right)\right)-{M}_d{g}^{\prime }-{A}_c{K}_p{g}^{\prime }=0

(12)

{A}_c{h}^{\prime \prime \prime }-{B}_c\left[\left(n+{F}_0\right){h}^{\prime 2}+{ng}^{\prime }{h}^{\prime }+0.5\left(n+1\right){h}^{\prime \prime}\left(h+g\right)\right]-{M}_d{h}^{\prime }-{A}_c{K}_p{h}^{\prime }=0

(13)

\left(\frac{4}{3}{R}_d+{D}_c\right){\theta}^{\prime \prime }+{C}_c\mathit{\Pr}\left[0.5\left(n+1\right)\left(g+h\right){\theta}^{\prime }+{Q}_{\ast}\theta \right]=0

(14)

The boundary conditions are

\left.\begin{array}{l}g=h=0,\kern0.48em {g}^{\prime }=0,\kern0.48em {h}^{\prime }={\lambda}_s,\kern0.48em \theta =1\kern0.48em at\kern0.72em \eta =0\\ {}{g}^{\prime}\to 0,\kern0.48em {h}^{\prime}\to 0,\kern0.48em {\theta}^{\prime}\to 0,\kern0.72em as\kern0.96em \eta \to \infty \end{array}\right\}

(15)

where

{M}_d=\frac{\sigma {B}_0^2}{c{\rho}_f{\left(x+y\right)}^{n-1}}

represents the magnetic field,

{A}_c=1+7.3\Phi +123{\Phi}^2,

{B}_c=\left(\frac{\left(1-\Phi \right){\rho}_f+\Phi {\rho}_{CNT}}{\rho_f}\right)

{C}_c=\left(\frac{{\left(\rho {C}_p\right)}_{CNT}}{{\left(\rho {C}_p\right)}_f}\right)\Phi +\left(1-\Phi \right)

{D}_c=\frac{\Upsilon_{nf}}{\Upsilon_f}

, are constants,

\mathit{\Pr}=\frac{{\left(\rho {C}_p\right)}_f}{\Upsilon_f}

denotes the Prandtl number,

{R}_d=\frac{4{\sigma}^{\ast }{T}_{\infty}^3}{K^{\ast }{\upsilon}_f}

Represents the Radiation parameter,

{K}_p=\frac{\upsilon_f}{c{\kappa}_{nf}}

denotes the porosity parameter,

{F}_0=\left(x+y\right){F}_c

represents the Forchheimer parameter and

{Q}_{\ast }=\frac{Q_0}{c{\left(\rho {C}_p\right)}_f}

represents the heat source parameter.

The physical importance of the quantities are the local Nusselt number and surface friction coefficients at

z=0

as follows

Nu=\frac{\left({q}_r+{q}_w\right)\left(x+y\right)}{\Upsilon_f\left({T}_w-{T}_{\infty}\right)},\kern0.72em {C}_{fx}=\frac{\tau_{zx}}{u_w^2{\rho}_f},\kern0.72em {C}_{fy}=\frac{\tau_{zy}}{v_w^2{\rho}_f}

(16)

where

\left({q}_r,{q}_w\right)

denote the radiative heat flux and wall heat flux, respectively and

\left({\tau}_{xy},{\tau}_{zy}\right)

represents the wall shear stresses respectively

\left.\begin{array}{l}{\left.{q}_w=-{\Upsilon}_{nf}\frac{\partial T}{\partial z}\right|}_{z=0},\kern0.6em {\left.{q}_r=-\frac{4{\sigma}^{\ast }}{3{K}^{\ast }}\left[\frac{\partial }{\partial z}\left({T}_{\infty}^3\left(4T-3{T}_{\infty}\right)\right)\right]\right|}_{z=0}\\ {}\kern0.24em {\left.{\tau}_{zx}={\mu}_{nf}\left(\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}\right)\right|}_{z=0},\kern0.72em {\tau}_{zy}={\left.{\mu}_{nf}\left(\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}\right)\right|}_{z=0}\end{array}\right\}

(17)

Substituting the above Equation (17) into (16) hence the Equation (18) becomes

\begin{array}{cc}& {\left.{\operatorname{Re}}_x^{1/2}{C}_{fx}={A}_c{g}^{\prime \prime }(0)\right|}_{z=0},\kern0.48em {\left.{\operatorname{Re}}_y^{1/2}{C}_{fy}=\frac{A_c}{\lambda^{3/2}}{h}^{\prime \prime }(0)\right|}_{z=0},\kern0.36em \\ {}& \kern1em {\left.{\operatorname{Re}}_x^{-1/2} Nu=-\left(\frac{4}{3}{R}_d+\frac{\Upsilon_{nf}}{\Upsilon_f}\right){\theta}^{\prime }(0)\right|}_{z=0}\end{array}

(18)

where

{\operatorname{Re}}_x=\frac{\left(x+y\right){u}_w}{\upsilon_f}

represents the Reynolds number in the x-direction and

{\operatorname{Re}}_y=\frac{\left(x+y\right){v}_w}{\upsilon_f}

denotes the Reynolds number in the y-direction.

3 Numerical Solution

The resultant nonlinear ODES must first be transformed into BVPs by applying proper boundary conditions in order to be solved. The shooting technique is then employed to solve the BVPs by converting into IVPs and guessing the missing initial conditions. The fourth-order Runge–Kutta method is used to solve the IVPs, and the guessed initial conditions are iteratively adjusted until the solution satisfies the boundary conditions. We check our solution for different finite values of the infinite boundary condition

{\eta}_{\infty}\to \infty

until we achieve an asymptotically convergent solution. In our complete analysis, we take

{\eta}_{\infty }=4

. The following are the steps to convert the nonlinear ODE into BVP

g={f}_1,{g}^{\prime }={f}_2,{g}^{{\prime\prime} }={f}_3,h={f}_4,{h}^{\prime }={f}_5,{h}^{{\prime\prime} }={f}_6,\theta ={f}_7,{\theta}^{\prime }={f}_8

\left.\begin{array}{l}{f_1}^{\prime }={f}_2\\ {}{f_2}^{\prime }={f}_3\\ {}{f_3}^{\prime }=\frac{1}{A_c}\left[{B}_c\left(\left(n+{F}_0\right){f}_2^2+{nf}_2{f}_5+0.5\left(n+1\right){f}_3\left({f}_4+{f}_1\right)\right)+{M}_d{f}_2+{A}_c{K}_p{f}_2\right]\\ {}{f_4}^{\prime }={f}_5\\ {}{f_5}^{\prime }={f}_6\\ {}{f_6}^{\prime }=\frac{1}{A_c}\left[{B}_c\left(\left(n+{F}_0\right){f}_5^2+{nf}_2{f}_5+0.5\left(n+1\right){f}_6\left({f}_4+{f}_1\right)\right)+{M}_d{f}_5+{A}_c{K}_p{f}_5\right]\\ {}{f_7}^{\prime }={f}_8\\ {}{f_8}^{\prime }=\frac{-3{C}_c\mathit{\Pr}}{4{R}_d+3{D}_c}\left[0.5\left(n+1\right)\left({f}_1+{f}_4\right){f}_8\right]\end{array}\right\}

(19)

with respect to boundary conditions

{\left[{f}_1\kern0.24em {f}_2\kern0.24em {f}_3\kern0.24em {f}_4\kern0.24em {f}_5\kern0.24em {f}_6\kern0.24em {f}_7\kern0.24em {f}_8\right]}^t={\left[0\kern0.24em 1\kern0.24em {r}_1\kern0.24em 0\kern0.24em {\lambda}_s\kern0.24em {r}_2\kern0.24em 1\kern0.24em {r}_3\right]}^t

where

{r}_1,{r}_2

and

{r}_3

are unknown initial conditions, that are chosen to maintain free stream conditions

{g}^{\prime}\left(\infty \right)={h}^{\prime}\left(\infty \right)=\theta \left(\infty \right)

4 Results and Discussion

A three-dimensional model of Darcy-Forchheimer flow in a convective system with Ti-alloy nanoparticles suspended in paraffin oil as the base fluid is formulated using partial differential equations. These equations are transformed into a system of ordinary differential equations and solved numerically using MATLAB RK-4th order along with the shooting technique. Results are displayed through graphs and tables for various parameter values.

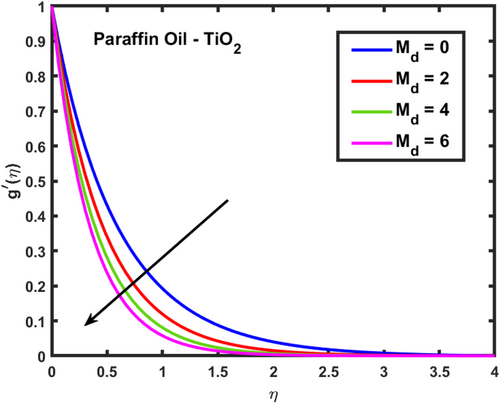
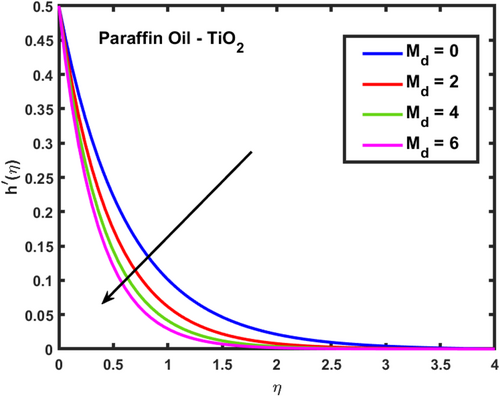
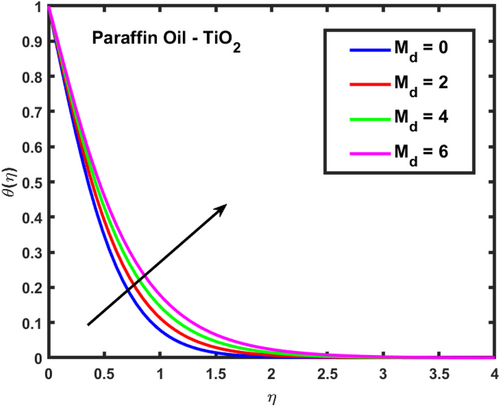
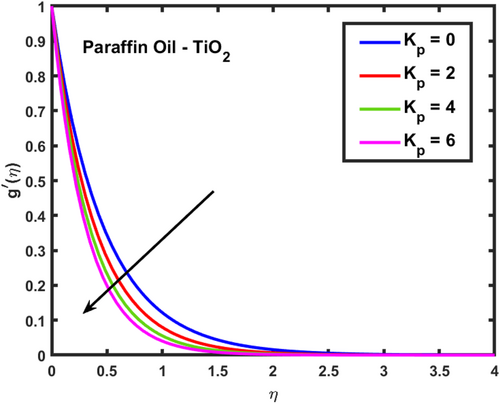
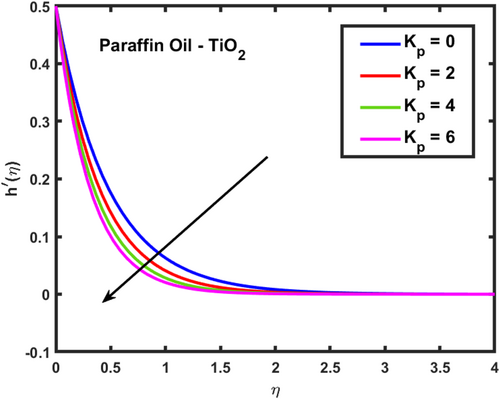
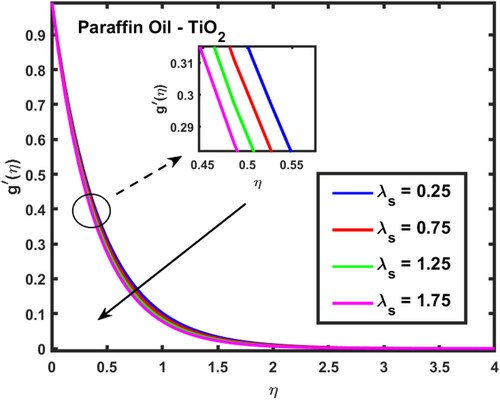
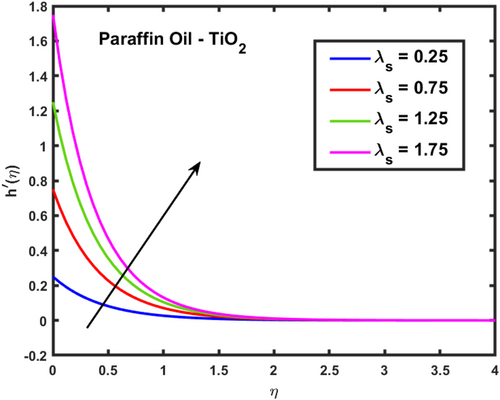
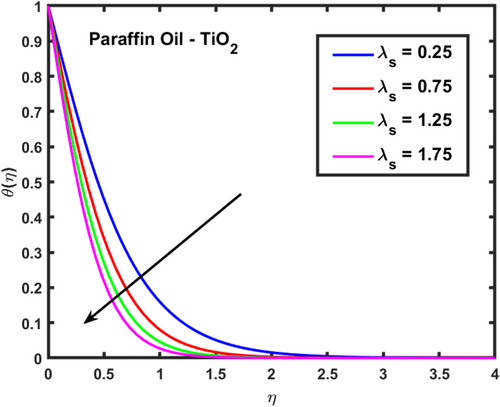
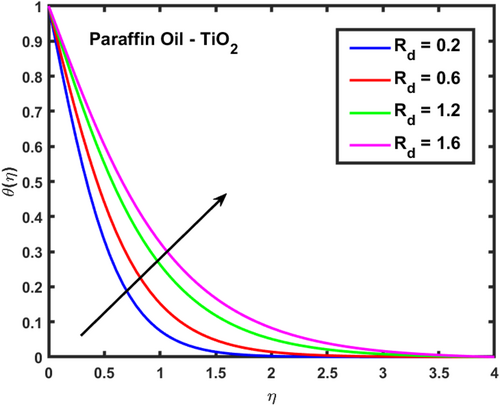
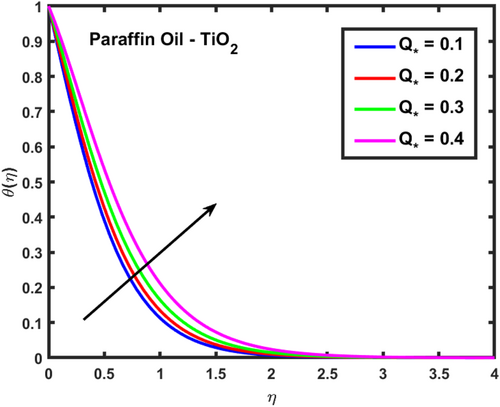
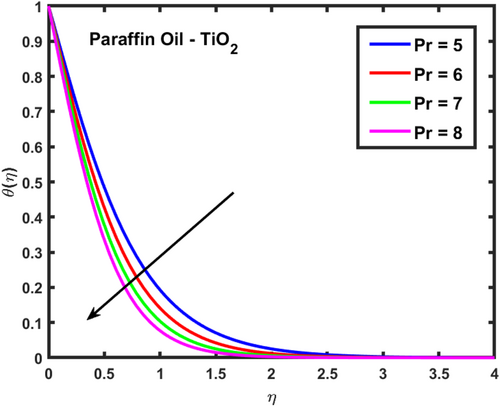
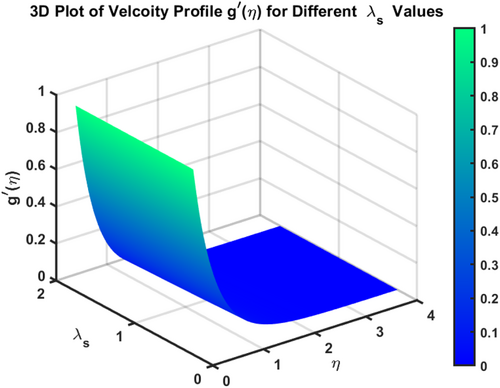
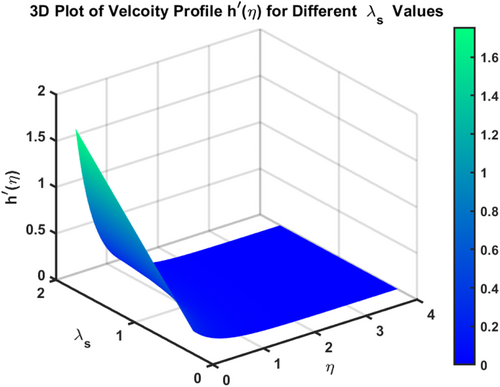
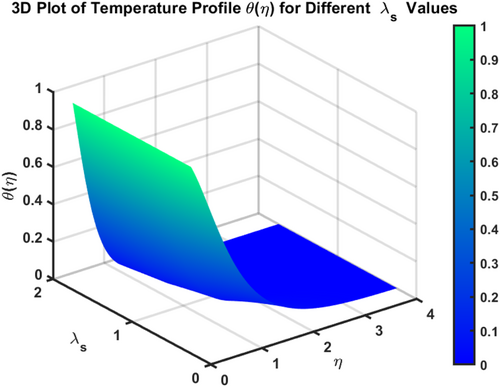
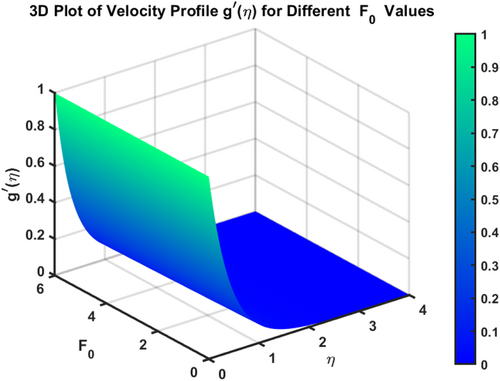
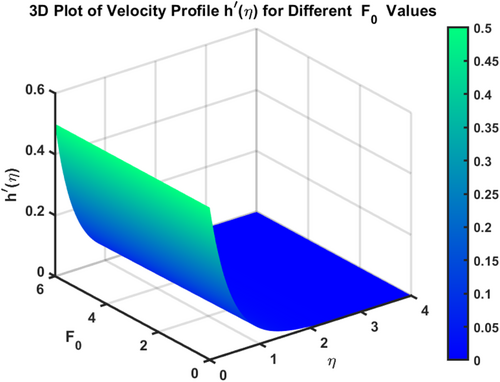
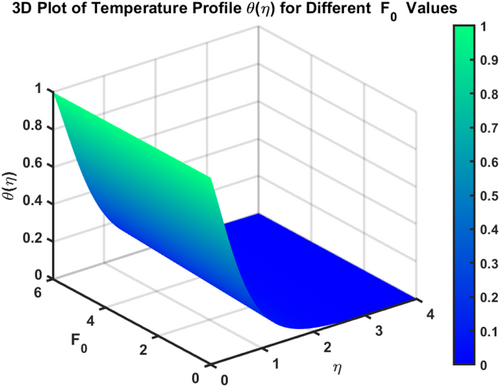
The velocity profiles ${g}^{\prime}\left(\eta \right)$ and ${h}^{\prime}\left(\eta \right)$ demonstrate the influence of the magnetic parameter ${M}_d$ on fluid flow in a boundary layer over a stretching sheet as show in Figures 2 and 3. As ${M}_d$ both velocity profiles decrease significantly across the boundary layer. Without the magnetic field $\left({M}_d=0\right)$ , the fluid velocity is highest, but as the magnetic field strength increases, the velocity profiles for ${M}_d=2,4,6$ shift downward, indicating a reduction in fluid flow. This is due to the Lorentz force generated by the interaction between the magnetic field and the conducting fluid, which resists the flow and acts as a damping mechanism. Physically, this behavior reflects the characteristics of MHD flows, where the magnetic field exerts a retarding effect on the fluid motion. The increasing magnetic parameter ${M}_d$ results in stronger resistance to the flow, leading to reduced velocity and a thicker boundary layer. The temperature profile $\theta \left(\eta \right)$ depicted in Figure 4 illustrates the influence of the magnetic parameter ${M}_d$ and other thermal-related parameters on the fluid's temperature distribution within the boundary layer. As observed, the temperature increases as the parameter ${M}_d$ rises, showing that stronger magnetic fields generate more heat within the fluid due to the resistive effects caused by Lorentz forces. This enhanced temperature rise can be attributed to the suppression of fluid flow, which in turn leads to higher energy dissipation and heat accumulation. As the porosity parameter ${K}_p$ increases, the velocity components ${g}^{\prime}\left(\eta \right)$ and ${h}^{\prime}\left(\eta \right)$ exhibit a decreasing trend, as shown in the 2D plots Figures 5 and 6. This reduction in velocity can be attributed to the increased resistance offered by the porous medium. The porous structure impedes the flow, thereby reducing the momentum of the fluid as it traverses through the medium. On the other hand, the temperature profile $\theta \left(\eta \right)$ shows an increasing trend, as observed in Figure 7. The rise in temperature is due to the fact that a more porous medium allows heat to be trapped more effectively, leading to an increase in thermal energy within the fluid. As the bi-directional stretching surface parameter ${\lambda}_s$ increases, the velocity components show differing trends. Specifically, ${g}^{\prime}\left(\eta \right)$ exhibits a slight decrease, while ${h}^{\prime}\left(\eta \right)$ experiences a significant increase. This behavior is clearly depicted in the Figures 8 and 9. The decrease in ${g}^{\prime}\left(\eta \right)$ may be due to the fact that the stretching in one direction tends to reduce the flow velocity along that axis. In contrast, the sharp increase in ${h}^{\prime}\left(\eta \right)$ suggests that the stretching surface amplifies velocity along the orthogonal direction, potentially due to enhanced shear effects. As observed in Figure 10, the reduction in temperature can be attributed to enhanced stretching,which causes more heat dissipation as the fluid layersare pulled apart. As the Darcy-Forchheimer parameter ${F}_0$ the velocity components ${g}^{\prime}\left(\eta \right)$ and ${h}^{\prime}\left(\eta \right)$ exhibit a decreasing trend, as shown in the Figures 11 and 12. This reduction in velocity is due to the enhanced resistance created by the porous medium combined with inertial effects represented by the Darcy-Forchheimer model. The flow experiences more drag, causing a significant slowdown in both velocity components. Regarding the thermal field, the temperature distribution increases with rising ${F}_0$ , as shown in Figure 13. The increase in temperature can be attributed to the greater energy dissipation due to the reduced fluid motion and higher resistive forces in the porous medium, which traps more heat. As the radiation parameter ${R}_d$ increases, the effects on the temperature distribution become evident in Figure 14. This is because greater radiation leads to enhanced heat transfer within the fluid, resulting in a more pronounced rise in temperature. In Figure 15, the plot illustrates that the temperature of the nanofluid rises with increasing values of ${Q}_{\ast }$ . This can be attributed to the fact that a larger heat source parameter intensifies the internal energy generation within the fluid, thereby raising the temperature throughout the boundary layer. The increased heat generation creates a more substantial thermal gradient, promoting heat transfer within the system. In Figure 16, the plot reveals that the temperature distribution increases with higher values of the Prandtl number. This trend can be explained by the fact that a higher Prandtl number indicates a fluid with higher momentum diffusivity compared to thermal diffusivity, which causes heat to be retained longer within the boundary layer. The 3D plots Figures 17 and 18 give a more detailed spatial understanding of how this bidirectional stretching impacts the velocity components, showing a strong influence in the flow behavior, particularly along the stretching direction. In contrast, the temperature profile decreases with increasing ${\lambda}_s$ as shown in Figure 19. The 3D plot in Figure 19 provides further insights, highlighting the spatial evolution of temperature reduction, critical for applications that involve manipulating fields through mechanical stretching, such as in polymer processing or coating techniques. The corresponding 3D plots Figures 20 and 21 further illustrate this decrease in velocity across the boundary layer, providing a detailed spatial representation of how the fluid motion is impeded with higher ${F}_0$ . The 3D plot Figure 22 provide a more comprehensive spatial view of these trends, highlighting the growing temperature distribution with increasing ${F}_0$ . These findings are particularly relevant in systems where controlling fluid flow through porous media with additional inertial effects is necessary, such as in packed bed reactors or filtration processes, balancing temperature gradients is critical for system efficiency. Table 2 shows how different parameters affect the velocity and temperature gradients, as well as heat transfer and skin friction in Ti-alloy-Paraffin oil. As the magnetic field strength ${M}_d$ increases, the velocity gradient decreases, showing that the magnetic field slows the fluid down. Porosity ${K}_p$ and Forchheimer ${F}_0$ also reduce velocity, with less porous media and higher resistance leading to slower fluid motion. The heat source parameter $Q$ increases the temperature gradient, meaning more heat is retained in the fluid, improving heat transfer. Table 3 represents the comparison analysis of calculated values of ${g}^{{\prime\prime} }(0)$ and ${h}^{{\prime\prime} }(0)$ for the regular viscous fluids. The present results exploring the good qualitative results with the reference studies, particularly in capturing the enhanced values of ${g}^{{\prime\prime} }(0)$ and ${h}^{{\prime\prime} }(0)$ as ${\lambda}_s$ increases. Slight deviations in the results can be observed, which are likely due to differences in numerical techniques, grid independence studies, or convergence criteria. Nevertheless, this study offers reliable insights into the behavior of the regular viscous.

TABLE 2. Variations of

{g}^{\prime \prime }(0)

{h}^{\prime \prime }(0)

{\theta}^{\prime }(0)

{\phi}^{\prime }(0)

{\operatorname{Re}}_x^{1/2}{C}_{fx}

{\operatorname{Re}}_y^{1/2}{C}_{fy}

, and

{\operatorname{Re}}_x^{-1/2} Nu

for Ti-alloy-paraffin oil when

n=1

${M}_d$	${\lambda}_s$	${K}_p$	${F}_0$	${R}_d$	${Q}_{\ast }$	$\mathit{\Pr}$	${g}^{{\prime\prime} }(0)$	${h}^{{\prime\prime} }(0)$	$-{\theta}^{\prime }(0)$	${\operatorname{Re}}_x^{1/2}{C}_{fx}$	${\operatorname{Re}}_y^{1/2}{C}_{fy}$	${\operatorname{Re}}_x^{-1/2} Nu$
0		1	1	0.4	0.1	6.72	−1.7534	−0.8274	1.5179	−1.9029	−2.5399	2.4050
2							−2.2181	−1.0713	1.3961	−2.4073	−3.2886	2.2120
4							−2.6008	−1.2686	1.2951	−2.8226	−3.8943	2.0519
6							−2.9339	−1.4390	1.2070	−3.1841	−4.4172	1.9124
2	0.25						−2.1633	−0.5116	1.2095	−2.3479	−4.4419	1.9163
	0.75						−2.2711	−1.6758	1.5603	−2.4648	−2.8002	2.4721
	1.25						−2.3725	−3.0090	1.8449	−2.5749	−2.3367	2.9230
	1.75						−2.4687	−4.4937	2.0908	−2.6793	−2.1067	3.3127
	0.5	0					−1.9796	−0.9469	1.4588	−2.1484	−2.9068	2.3113
		2					−2.4333	−1.1825	1.3394	−2.6408	−2.6408	2.1221
		4					−2.8145	−1.3781	1.2385	−3.0546	−4.2302	1.9624
		6					−3.1500	−1.5490	1.1501	−3.4187	−4.7550	1.8222
		1	0				−2.0697	−1.0349	1.4170	−2.2463	−3.1767	2.2451
			2				−2.3573	−1.1068	1.3767	−2.5584	−3.3974	2.1812
			4				−2.6138	−1.1749	1.3412	−2.8367	−2.8368	2.1249
			6				−2.8475	−1.2397	1.3093	−3.0904	−3.8055	2.0744
			1	0.2			−2.2181	−1.0713	1.5835	2.4073	−3.2886	2.0867
				0.6			−2.2181	−1.0713	1.2507	−2.4073	−3.2886	2.3152
				1.2			−2.2181	−1.0713	0.9573	−2.4073	−3.2886	2.5379
				1.6			−2.2181	−1.0713	0.8304	−2.4073	−3.2886	2.6444
				0.4	0.1		−2.2181	−1.0713	1.2232	−2.4073	−3.2886	2.2120
					0.2		−2.2181	−1.0713	1.2232	−2.4073	−3.2886	1.9381
					0.3		−2.2181	−1.0713	1.0194	−2.4073	−3.2886	1.6151
					0.4		−2.2181	−1.0713	0.7606	−2.4073	−3.2886	1.2050
					0.1	5	−2.2181	−1.0713	1.1294	−2.4073	−3.2886	1.7894
						6	−2.2181	−1.0713	1.2891	−2.4073	−3.2886	2.0424
						7	−2.2181	−1.0713	1.4362	−2.4073	−3.2886	2.2755
						8	−2.2181	−1.0713	1.5730	−2.4073	−3.2886	2.4923

TABLE 3. The results of

{g}^{{\prime\prime} }(0)

and

{h}^{{\prime\prime} }(0)

for the regular viscous fluids with various of values of

{\lambda}_s

when

n=1

${\lambda}_s$	Khan et al. [17]		Upreti et al. [22]		Present values
${\lambda}_s$	${g}^{{\prime\prime} }(0)$	${h}^{{\prime\prime} }(0)$	${g}^{{\prime\prime} }(0)$	${h}^{{\prime\prime} }(0)$	${g}^{{\prime\prime} }(0)$	${h}^{{\prime\prime} }(0)$
0.0	−1.000000	0.000000	−1.00000	0.00000	−0.957942	0.0000000
0.5	−1.224745	−0.612372	−1.22474	−0.6123719	−1.169386	−0.584693
1.0	−1.414214	−1.414214	−1.414214	−1.4142135	−1.348826	−1.348826

5 Conclusion

The study offers a comprehensive analysis of the Darcy-Forchheimer flow in a convective system with a Ti-alloy nanoparticle suspension in paraffin oil. The Buongiorno model is mathematically described in the form of PDE, and it is converted into a nonlinear ODE by using a similarity transformation, which is solved through the BVP4C technique to obtain better solutions. Graphs generated through MATLAB simulations analyze various parameters of the heat transfer system, focusing on factors impacting fluid dynamics and temperature profiles. The influence of the magnetic field, porosity, bi-directional stretching, and Darcy-Forchheimer effects reveals notable changes in the flow characteristics, indicating how each parameter either enhances or resists fluid movement through the boundary layer. Based on the changes in the current study, we conclude the following observation.

The study highlights that magnetic fields induce a Lorentz force that slows fluid velocity and impacts temperature by generating resistive heat, which increases with magnetic strength. Similarly, a porous medium reduces velocity due to increased resistance, while amplifying temperature as visualized in figure representations.
The bi-directional stretching parameter has a directional impact on velocity and temperature, while the Darcy-Forchheimer parameter further impedes flow and promotes temperature rise, aligning with applications in industrial processes where fluid manipulation is necessary.
Radiation, heat sources, and Prandtl number exhibit distinct effects on temperature distributions, with radiation and heat sources contributing to thermal gradients.

Overall, the work highlights the potential of paraffin oil-based Ti-alloy nanoparticle suspensions for energy-related applications. This nanofluid's improved heat transfer properties, together with its capacity to regulate fluid flow across porous media and magnetic fields, make it ideal for: Enhancing energy efficiency in solar thermal energy systems by optimizing heat absorption and transmission in solar collectors; improving thermal control in power plant cooling systems, such as condensers and cooling towers, which is essential for energy generation; and Facilitating effective heat dissipation in thermal energy storage units utilized in renewable energy systems, which is part of energy storage systems.

Nomenclature

${A}_c,{B}_c,{C}_c,{D}_c$: constants
$\upsilon$: kinematic viscosity
${M}_d$: magnetic field parameter
${B}_0$: applied magnetic field
$c,d,n$: stretching constants
${K}^{\ast }$: mean absorption coefficient
$\Phi$: volume fraction
${M}_d$: magnetic field
$Nu$: Nusselt number
$\mathit{\Pr}$: Prandtl number
${C}_{fx},{C}_{fy}$: surface friction coefficient
${R}_d$: radiation parameter
${\operatorname{Re}}_x,{\operatorname{Re}}_y$: reynolds number
$T,{T}_{\infty }$: temperature and ambient temperature
${\sigma}_c$: electrical conductivity
${\sigma}^{\ast \ast }$: Stefan-Boltzmann constant
$\rho$: fluid density
$\eta$: similarity variable
$\mu$: dynamic viscosity
${\lambda}_s$: stretching parameter
$\Upsilon$: electrical conductivity

Author Contributions

D. Thenmozhi: conceptualization. M. Eswara Rao: validation, software. Kalyan Kumar Challa: writing – original draft. Muhammad Jawad: formal analysis, conceptualization. Liaqat Hamdard: validation, methodology. Walid Abdelfattah: writing – review and editing, software.

Acknowledgments

The authors extend their appreciation to the Deanship of Scientific Research at Northern Border University, Arar, KSA, for funding this research work through the project number NBU-FFR-2025-2230-04.

Conflicts of Interest

The authors declare no conflicts of interest.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1G. Qin, Computational Fluid Dynamics for Mechanical Engineering (CRC Press, 2021).
10.1201/9781003138822
Google Scholar
2C. Wang, Q. Lu, Y. Liu, H. Huang, and J. Sun, “Progressive Review of Heat Transfer Enhancement Technologies in 2010–2020,” Sustainable Energy Technologies and Assessments 56 (2023): 103121.
10.1016/j.seta.2023.103121
CAS Web of Science® Google Scholar
3X. A. Si and J. Xi, “ Modeling Nasal Spray Droplet Deposition and Translocation in Nasal Airway for Olfactory Delivery,” in Modeling of Mass Transport Processes in Biological Media, ed. X. A. Si and J. Xi (Academic Press, 2022), 311–333.
10.1016/B978-0-323-85740-6.00007-8
Google Scholar
4C. Veiga, J. P. Davim, and A. J. R. Loureiro, “Properties and Applications of Titanium Alloys: A Brief Review,” Reviews on Advanced Materials Science 32, no. 2 (2012): 133–148.
CAS Web of Science® Google Scholar
5K. S. Nisar, U. Khan, A. Zaib, I. Khan, and D. Baleanu, “Exploration of Aluminum and Titanium Alloys in the Stream-Wise and Secondary Flow Directions Comprising the Significant Impacts of Magnetohydrodynamic and Hybrid Nanofluid,” Crystals 10, no. 8 (2020): 679.
10.3390/cryst10080679
CAS Web of Science® Google Scholar
6F. Shahzad, W. Jamshed, M. R. Eid, et al., “Thermal Cooling Efficacy of a Solar Water Pump Using Oldroyd-B (Aluminium Alloy-Titanium Alloy/Engine Oil) Hybrid Nanofluid by Applying New Version for the Model of Buongiorno,” Scientific Reports 12, no. 1 (2022): 19817.
10.1038/s41598-022-24294-3
CAS PubMed Web of Science® Google Scholar
7Z. J. Li, Z. H. Xiao, H. L. Zhang, et al., “3D Numerical Modeling for Thermo-Mechanical Behavior of Additively Manufactured Titanium Alloy Parts With Process-Induced Defects,” International Journal of Heat and Mass Transfer 209 (2023): 124112, https://doi.org/10.1016/j.ijheatmasstransfer.2023.124112.
10.1016/j.ijheatmasstransfer.2023.124112
CAS Web of Science® Google Scholar
8N. C. Bergstrom and P. N. Walker, “Air-To-Liquid Heat Exchanger System for Ventilation Heat Recovery,” Transactions of ASAE 30, no. 6 (1987): 1751–1757.
10.13031/2013.30632
Google Scholar
9A. Palou, J. Cruz, M. Blanco, et al., “Characterization of the Composition of Paraffin Waxes on Industrial Applications,” Energy & Fuels 28, no. 2 (2014): 956–963.
10.1021/ef4021813
CAS Web of Science® Google Scholar
10F. Mebarek-Oudina and I. Chabani, “Review on Nano-Fluids Applications and Heat Transfer Enhancement Techniques in Different Enclosures,” Journal of Nanofluids 11, no. 2 (2022): 155–168.
10.1166/jon.2022.1834
Web of Science® Google Scholar
11T. O. Scott, D. R. Ewim, and A. C. Eloka-Eboka, “Hybrid Nanofluids Flow and Heat Transfer in Cavities: A Technological Review,” InternationalJournal of Low Carbon Technologies 17 (2022): 1104–1123, https://doi.org/10.1093/ijlct/ctac093.
10.1093/ijlct/ctac093
CAS Web of Science® Google Scholar
12M. Gholinia, M. Armin, A. A. Ranjbar, and D. D. Ganji, “Numerical Thermal Study on CNTs/C₂H₆O₂+ H₂O Hybrid Base Nanofluid Upon a Porous Stretching Cylinder Under Impact of Magnetic Source,” Case Studies in Thermal Engineering 14 (2019): 100490.
10.1016/j.csite.2019.100490
Web of Science® Google Scholar
13S. Dero, M. A. Fadhel, Z. Shah, et al., “Multiple Solutions of Hiemenz Flow of CNTs Hybrid Base C₂H₆O₂+ H₂O Nanofluid and Heat Transfer Over Stretching/Shrinking Surface: Stability Analysis,” Case Studies in Thermal Engineering 49 (2023): 103190.
10.1016/j.csite.2023.103190
Web of Science® Google Scholar
14S. E. Ahmed, P. B. A. Reddy, S. Jakeer, A. M. Rashad, and T. Salah, “Magnetic Convection-Radiation Interaction in Wavy Porous Triangular Containers Using Hybrid Nanofluids: Entropy Analysis,” Journal of Porous Media 26, no. 5 (2023): 3523.
10.1615/JPorMedia.2022043523
Web of Science® Google Scholar
15S. Jakeer and P. B. A. Reddy, “Stability Analysis of Electrical Magneto Hydrodynamic Stagnation Point Flow of ag-Cu/Water Hybrid Nanofluid Over a Permeable Stretching/Shrinking Slendering Sheet: Entropy Generation,” Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering 238, no. 3 (2024): 1172–1184.
10.1177/09544089231153356
CAS Web of Science® Google Scholar
16S. Jakeer, P. B. A. Reddy, H. T. Basha, and S. R. R. Reddy, “Entropy Minimization of the Non-Newtonian Bio-Hybrid (Fe₃O₄-CuO/Blood) Nanofluid Flow Over a Linear Extending Sheet by Means of Induced Magnetic Field,” International Journal of Modern Physics B 38, no. 10 (2024): 2450142, https://doi.org/10.1142/S021797922450142X.
10.1142/S021797922450142X
CAS Web of Science® Google Scholar
17J. A. Khan, M. Mustafa, T. Hayat, and A. Alsaedi, “Three-Dimensional Flow of Nanofluid Over a Non-Linearly Stretching Sheet: An Application to Solar Energy,” International Journal of Heat and Mass Transfer 86 (2015): 158–164.
10.1016/j.ijheatmasstransfer.2015.02.078
Web of Science® Google Scholar
18N. F. H. Mohd Sohut, S. K. Soid, S. Abu Bakar, and A. Ishak, “Unsteady Three-Dimensional Flow in a Rotating Hybrid Nanofluid Over a Stretching Sheet,” Mathematics 2022, no. 10 (2022): 348.
10.3390/math10030348
Google Scholar
19D. Mohanty, G. Mahanta, and S. Shaw, “Analysis of Irreversibility for 3-D MHD Convective Darcy–Forchheimer Casson Hybrid Nanofluid Flow due to a Rotating Disk With Cattaneo–Christov Heat Flux, Joule Heating, and Nonlinear Thermal Radiation,” Numerical Heat Transfer, Part B: Fundamentals 84, no. 2 (2023): 115–142.
10.1080/10407790.2023.2189644
Web of Science® Google Scholar
20A. Abderrahmane, Y. Khetib, P. Ghodratallah, et al., “Thermal Performance of 3D Darcy-Forchheimer Porous Rectangular Wavy Enclosures Containing a Water-Fe3O4 Ferro-Nanofluid Under Magnetic Fields,” Case Studies in Thermal Engineering 53 (2024): 103790, https://doi.org/10.1016/j.csite.2023.103790.
10.1016/j.csite.2023.103790
Web of Science® Google Scholar
21B. Ali, S. Jubair, and M. I. H. Siddiqui, “Numerical Simulation of 3D Darcy-Forchheimer Hybrid Nanofluid Flow With Heat Source/Sink and Partial Slip Effect Across a Spinning Disc,” Journal of Porous Media 27, no. 10 (2024): 97–111, https://doi.org/10.1615/JPorMedia.2024051759.
10.1615/JPorMedia.2024051759
Web of Science® Google Scholar
22H. Upreti, A. K. Pandey, S. K. Rawat, and M. Kumar, “Modified Arrhenius and Thermal Radiation Effects on Three-Dimensional Magnetohydrodynamic Flow of Carbon Nanotubes Nanofluids Over Bi-Directional Stretchable Surface,” Journal of Nanofluids 10, no. 4 (2021): 538–551.
10.1166/jon.2021.1804
Web of Science® Google Scholar
23E. E. Bafe, M. D. Firdi, and L. G. Enyadene, “Magnetohydrodynamic Thermo-Bioconvective Flow of 3D Rotating Williamson Nanofluid With Arrhenius Activation Energy in a Darcy–Forchheimer Medium Over an Exponentially Stretching Surface,” International Journal of Thermofluids 21 (2024): 100585.
10.1016/j.ijft.2024.100585
CAS Google Scholar
24F. Wang, M. Awais, R. Parveen, M. K. Alam, S. Rehman, and N. A. Shah, “Melting Rheology of Three-Dimensional Maxwell Nanofluid (Graphene-Engine-Oil) Flow With Slip Condition Past a Stretching Surface Through Darcy-Forchheimer Medium,” Results in Physics 51 (2023): 106647.
10.1016/j.rinp.2023.106647
Web of Science® Google Scholar
25L. Zhang, R. R. Vaddemani, A. Ganjikunta, S. Bingi, and R. Kodi, “3D-MHD Mixed Convection in a Darcy-Forchheimer Maxwell Fluid: Thermo Diffusion, Diffusion-Thermo Effects, and Activation Energy Influence,” Case Studies in Thermal Engineering 61 (2024): 104916.
10.1016/j.csite.2024.104916
Web of Science® Google Scholar
26A. Khelifa, M. E. H. Attia, M. Abdelgaied, M. Arıcı, and M. M. Abdel-Aziz, “3D Numerical Analysis of a Photovoltaic Thermal Using Bi-Fluid: Al2O3–Water Nanofluid at Various Concentrations,” International Journal of Thermofluids 20 (2023): 100523.
10.1016/j.ijft.2023.100523
CAS Google Scholar
27Z. Hussain, W. A. Khan, T. Muhammad, H. A. Alghamdi, M. Ali, and M. Waqas, “Dynamics of Gyrotactic Microorganisms for Chemically Reactive Magnetized 3D Sutterby Nanofluid Flow Comprising Non-Uniform Heat Sink-Source Aspects,” Journal of Magnetism and Magnetic Materials 578 (2023): 170798.
10.1016/j.jmmm.2023.170798
CAS Web of Science® Google Scholar
28I. Ullah, W. A. Khan, W. Jamshed, et al., “Heat Generation (Absorption) in 3D Bioconvection Flow of Casson Nanofluid via a Convective Heated Stretchable Surface,” Journal of Molecular Liquids 392 (2023): 123503.
10.1016/j.molliq.2023.123503
CAS Web of Science® Google Scholar
29A. A. Pasha, Z. Hussain, M. M. Alam, et al., “Impact of Magnetized Non-Linear Radiative Flow on 3D Chemically Reactive Sutterby Nanofluid Capturing Heat Sink/Source Aspects,” Case Studies in Thermal Engineering 41 (2023): 102610, https://doi.org/10.1016/j.csite.2022.102610.
10.1016/j.csite.2022.102610
Web of Science® Google Scholar
30Z. Hussain, M. M. Alam, A. A. Pasha, W. A. Khan, M. Ali, and A. I. Khan, “Gyrotatic Microorganisms Analysis for Radiative 3D Carreau Nanofluid Flow Configured by Activation Energy and Viscous Dissipation,” Thermal Science and Engineering Progress 42 (2023): 101898.
10.1016/j.tsep.2023.101898
CAS Web of Science® Google Scholar
31N. Tarakaramu, N. Sivakumar, N. Tamam, P. V. Satya Narayana, and S. Ramalingam, “Theoretical Analysis of Arrhenius Activation Energy on 3D MHD Nanofluid Flow With Convective Boundary Condition,” Modern Physics Letters B 38, no. 16 (2024): 2341009.
10.1142/S0217984923410099
CAS Web of Science® Google Scholar
32M. I. U. Rehman, H. Chen, and A. Hamid, “Numerical Investigation of Cattaneo–Christov Double Diffusion and Mixed Convection Effects in Non-Darcian Sutterby Nanofluid Using Multi Objective Optimization Through RSM,” International Journal of Hydrogen Energy 100 (2025): 1219–1230.
10.1016/j.ijhydene.2024.12.422
Web of Science® Google Scholar
33D. Thenmozhi, E. M. Rao, K. Vajravelu, and P. Lakshminarayana, “Analysis of Carbon Nanotubes-Based Nanofluid With Paraffin Oil in 3D MHD Darcy-Forchheimer Flow Through a Bi-Directional Stretchable Surface: Application to Heat Exchanger Systems,” Proceedings of the Institution of Mechanical Engineers, Part E: Journal of Process Mechanical Engineering 238 (2024): 09544089241259446.
Google Scholar
34D. Thenmozhi, M. Eswara Rao, P. D. Selvi, R. R. Devi, S. Kiranmaiye, and C. Nagalakshmi, “The Significance of Magnetized Thermal Radiation on the Magnetohydrodynamic (MHD) Behavior of Williamson Hybrid Ferrofluids Over a Stretching Sheet,” International Journal of Thermofluids 25 (2025): 100997.
10.1016/j.ijft.2024.100997
CAS Google Scholar
35S. Rosseland, Astrophysik und Atom-Theoretische Grundlagen (Springer Verlag, 1931), 41–44.
10.1007/978-3-662-26679-3
Google Scholar
36R. L. Hamilton and O. K. Crosser, “Thermal Conductivity of Heterogeneous Two-Component Systems,” Industrial & Engineering Chemistry Fundamentals 1, no. 3 (1962): 187–191.
10.1021/i160003a005
CAS Web of Science® Google Scholar
37X. Wang, X. Xu, and S. U. Choi, “Thermal Conductivity of Nanoparticle-Fluid Mixture,” Journal of Thermophysics and Heat Transfer 13, no. 4 (1999): 474–480.
10.2514/2.6486
CAS Web of Science® Google Scholar
38H. Upreti, A. K. Pandey, and M. Kumar, “MHD Flow of Ag-Water Nanofluid Over a Flat Porous Plate With Viscous-Ohmic Dissipation, Suction/Injection and Heat Generation/Absorption,” Alexandria Engineering Journal 57, no. 3 (2018): 1839–1847.
10.1016/j.aej.2017.03.018
Web of Science® Google Scholar

Volume7, Issue5

May 2025

e70136

Analysis of Ti-Alloy Nanoparticles in Paraffin Oil for 3D MHD Darcy-Forchheimer Flow Over a Bi-Directional Stretching Surface

ABSTRACT

1 Introduction

2 Mathematical Formulation

2.1 Thermophysical Properties of the Nanofluids

3 Numerical Solution

4 Results and Discussion

5 Conclusion

Nomenclature

Author Contributions

Acknowledgments

Conflicts of Interest

Open Research

Data Availability Statement

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Analysis of Ti-Alloy Nanoparticles in Paraffin Oil for 3D MHD Darcy-Forchheimer Flow Over a Bi-Directional Stretching Surface

ABSTRACT

1 Introduction

2 Mathematical Formulation

2.1 Thermophysical Properties of the Nanofluids

3 Numerical Solution

4 Results and Discussion

5 Conclusion

Nomenclature

Author Contributions

Acknowledgments

Conflicts of Interest

Open Research

Data Availability Statement

References

Figures

References

Related

Information