Engineering Reports
Volume 7, Issue 4 e70100
RESEARCH ARTICLE
Open Access

Water-to-Air Imaging: A Recovery Method for the Instantaneous Distorted Image Based on Structured Light and Local Approximate Registration

Bijian Jian, 

Bijian Jian

College of Artificial Intelligence, Hezhou University, Guangxi, China

Contribution: Conceptualization, Methodology, Software, Validation, Writing - original draft

Search for more papers by this author
Ting Peng, 

Corresponding Author

Ting Peng

School of Electronic Information Engineering, China West Normal University, Sichuan, China

Correspondence:

Ting Peng ([email protected])

Contribution: Project administration, Funding acquisition, Writing - review & editing

Search for more papers by this author
Xuebo Zhang, 

Xuebo Zhang

College of Artificial Intelligence, Hezhou University, Guangxi, China

Contribution: Data curation

Search for more papers by this author
Changyong Lin, 

Changyong Lin

College of Artificial Intelligence, Hezhou University, Guangxi, China

Contribution: Validation

Search for more papers by this author
First published: 30 March 2025
https://doi.org/10.1002/eng2.70100

Funding: This work was supported by Guangxi Natural Science Foundation projects (Grant Number: 2024JJA170158 and 2025GXNSFAA069222), Hezhou University Doctoral Research Start-up Fund Project (Grant Number: 2024BSQD10), Hezhou University Interdisciplinary and Collaborative Research Project (Grant Number: XKJC202404), and Guangxi Young and Middle-Aged Teachers' Basic Research Ability Improvement Project (Grant Number: 2024KY0715).

ABSTRACT

Imaging through a continuously fluctuating water–air interface (WAI) is challenging. The image obtained in this way will suffer from complex refraction distortions that hinder the observer's accurate identification of the object. Reversing these distortions is an ill-posed problem, and the current restoration methods using high-resolution video streams are difficult to adapt to real-time observation scenarios. This paper proposes a method for restoring instantaneous distorted images based on structured light and local approximate registration. The scheme first uses structured light measurement technology to obtain the fluctuation information of the water surface. Then, the displacement information of the feature points on the distorted structured light image and the standard structured light image is obtained through the feature extraction algorithm and is used to estimate the distortion vector field of the corresponding sampling points in the distorted scene image. On this basis, the local approximate algorithm is used to reconstruct the distortion-free scene image. Experimental results show that the proposed algorithm can not only reduce image distortion and improve image visualization, but also has significantly better computational efficiency than other methods, achieving an “end-to-end” processing effect.

1 Introduction

Cross-media imaging has the ability to perceive targets above water and has important application value in military and civil fields, such as seabed exploration, airborne warning, and marine life research [1-5]. However, images obtained in this way will have complex refraction distortion and motion blur problems, which may lead to image fragmentation in severe cases. Since the shape of the seawater interface is unknown, it is difficult to remove these distortions from a single distorted image, and it must be estimated synchronously with the real scene image.

Research on this complex problem has been going on for decades. Currently, there are two main types of methods. One is the method based on image sequence [6-13]. This scheme assumes that the real scene is hidden in the image sequence of the distorted scene observed through the water surface multiple times, so the time–space correlation of the distorted image sequence can be used to restore a clear, distortion-free image. The image sequence-based method adopts the idea of multi-image fusion, which can obtain more complete image information and perform better in image reconstruction, but it needs to obtain a certain length of data frames before processing, so there is a time delay in the recovery result.

Another approach is to estimate the shape of the water surface in real time. Milder et al. [14] first proposed reconstructing distorted scenes by estimating the water surface shape. Levin et al. [15] designed a dual-band underwater imaging device and elaborated on the restoration process of distorted images. First, different illumination sources were used to illuminate the water surface and underwater target scene respectively (red light source illuminates the water surface, and green light source illuminates the object under test). a camera was employed to concurrently acquire the warped scene image as well as the reflected image of water–air interface (WAI). Subsequently, the slope of the flashing point was extracted from the reflection image and used to retrieve the scene image fragment. Finally, by accumulating multiple short-exposure images, a complete distortion-free image was obtained. Alterman et al. [16, 17] combined a refraction imaging sensor with an underwater camera to construct a new underwater–air imaging system. The system utilizes the sun as a reference point and applies the pinhole imaging concept to sample the wave surface via a pinhole array, thus obtaining a sparse representation of the water ripples' slope. The configuration of the water ripple is assessed on the premise that it is smooth and integrable, ultimately restoring the undistorted image by ray tracing. Gardashov et al. [18] proposed a real-time distortion correction method. They first used the characteristics of sunlight scintillation to reconstruct the geometric shape of WAI, and then corrected the geometrically distorted image by back-projection. The aforementioned method seeks to recover the undistorted image by measuring the slope distribution of the water surface. However, current approaches have strict prerequisites on application settings, necessitating either specialized lighting conditions or particular lighting apparatus, and the precision of water surface estimation often fails to satisfy application standards.

The three-dimensional (3D) measurement technology based on structured light has the advantages of high accuracy, fast speed, and strong adaptability, and is widely used in various fields [19-21]. Considering the restoration problem of instantaneous distorted images, this paper presents an image restoration method based on structured light and local approximate registration. This scheme first constructs a cross-media imaging model based on structured light and uses this model to simultaneously capture the distorted structured light image and the distorted scene image. On this basis, a method based on local approximate registration is proposed to restore the distortion-free image. Compared with previous methods, the proposed method only needs a simple projection device and one frame of distorted scene image to reconstruct a distortion-free scene, which can better meet the needs of real-time processing.

2 Materials and Methods

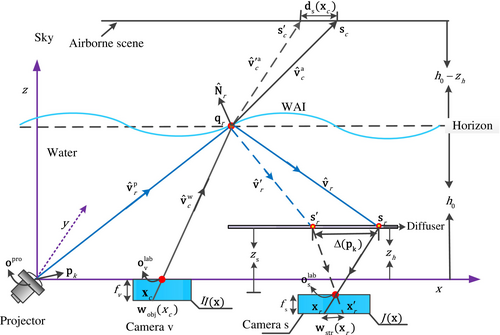
2.1 Image Formation Through Wavy WAI

When an underwater camera is used to view the scene above water through a wavy WAI, the oscillation of the water ripple will alter the transmission pathway of the imaging light ray, resulting in a deviation in the pixel position of the scene image, ultimately causing image distortion. Therefore, the relationship between a warped target scene image I t ( x ) $$ {I}_t\left(\mathbf{x}\right) $$ and the ground-truth image I g ( x ) $$ {I}_g\left(\mathbf{x}\right) $$ can be described as follows:
I t ( x ) = I g x + w t ( x ) , t $$ {I}_t\left(\mathbf{x}\right)={I}_g\left(\left(\mathbf{x}+{\mathbf{w}}_t\left(\mathbf{x}\right)\right),t\right) $$ (1)
where x ∈ R 2 $$ \mathbf{x}\in {R}^2 $$ is a two-dimensional (2D) pixel coordinate, w t ( x ) $$ {\mathbf{w}}_t\left(\mathbf{x}\right) $$ represents a 2D-variable vector field corresponding to the image distortion caused by the water wave at the time t $$ t $$ .

As shown in Figure 1, when the water surface is calm, the scene point captured by pixel x $$ \mathbf{x} $$ is A 1 $$ {\mathrm{A}}_1 $$ . But, as WAI is fluctuating, the intersection angle between the back-projected ray (which originates from point x $$ \mathbf{x} $$ and passes through the optical center o lab $$ {\mathbf{o}}_{\mathrm{lab}} $$ ) and the wave surface changes. This results in the deflection of the back-projected light above the sea surface, at this time, pixel x $$ \mathbf{x} $$ will image scene point A 2 $$ {\mathrm{A}}_2 $$ instead of A 1 $$ {\mathrm{A}}_1 $$ . As a result, variations in the sea surface cause changes in the pixel location of the visual scene.

Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Illustration of refractive distortion.
According to the first order approximation of Snell's law [22], the amount of the position offset experienced by the reverse projected light of the pixel x $$ \mathbf{x} $$ can be calculated, and its expression is a function related to the height distribution of the water surface, that is,
d t ( x ) = α ∇ h t ( x ) $$ {\mathbf{d}}_t\left(\mathbf{x}\right)=\alpha \nabla {h}_t\left(\mathbf{x}\right) $$ (2)
where α = h 0 1 − n water / n air $$ \alpha ={h}_0\left(1-{n}_{\mathrm{water}}/{n}_{\mathrm{air}}\right) $$ is a constant associated with the mean water depth h 0 $$ {h}_0 $$ , ∇ h t ( x ) $$ \nabla {h}_t\left(\mathbf{x}\right) $$ Indicates the water surface slope distribution at the moment t $$ t $$ .
According to the perspective projection transformation [22], the relationship between the displacement vector of the pixel x $$ \mathbf{x} $$ and the position offset w t ( x ) $$ {\mathbf{w}}_t\left(\mathbf{x}\right) $$ of the imaging light can be further obtained:
w t ( x ) = − pd t ( x ) $$ {\mathbf{w}}_t\left(\mathbf{x}\right)=-{\mathbf{pd}}_t\left(\mathbf{x}\right) $$ (3)
where d t ( x ) $$ {\mathbf{d}}_t\left(\mathbf{x}\right) $$ is the displacement of target scene point. w t ( x ) $$ {\mathbf{w}}_t\left(\mathbf{x}\right) $$ and d t ( x ) $$ {\mathbf{d}}_t\left(\mathbf{x}\right) $$ are both expressed in homogeneous coordinates, while p $$ \mathbf{p} $$ represents the projection matrix, that is,
P = 1 z 1 / dx 0 0 0 1 / dy 0 0 0 1 f 0 0 0 f 0 0 0 1 $$ \mathbf{P}=\frac{1}{z}\left[\begin{array}{ccc}1/ dx& 0& 0\\ {}0& 1/ dy& 0\\ {}0& 0& 1\end{array}\right]\left[\begin{array}{ccc}f& 0& 0\\ {}0& f& 0\\ {}0& 0& 1\end{array}\right] $$ (4)
where z $$ z $$ represents the distance from o lab $$ {\mathbf{o}}_{\mathrm{lab}} $$ to the planar scene above the water, f $$ f $$ denotes the focal length, dx $$ dx $$ and dy $$ dy $$ denote the image pixel's physical size.

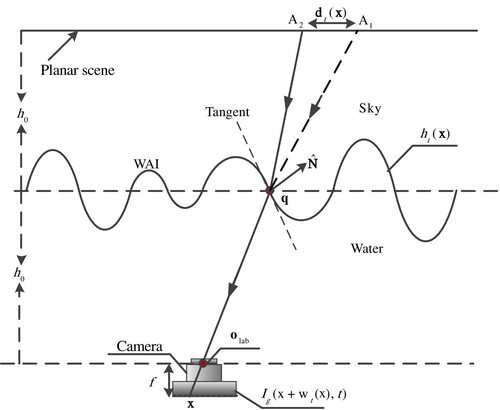
Equation (3) shows that, due to the spatial difference in the height distribution of the WAI, different pixels may experience different displacements. This explains why the image exhibits complex geometric distortion.

2.2 Cross-Media Imaging Model Based on Structured Light

To quickly restore images distorted by surface waves, This paper first constructs a cross-media imaging a model based on structured light, which takes into account the underwater optical transmission characteristics of blue–green light and uses the characteristic point information of structured light to realize the sampling of instantaneous wavefront. As shown in Figure 2, the system model includes a structured light projection system S and a passive imaging system V, wherein component S is composed of a projector, a diffuser, and a camera s, and component V is composed of an underwater observation camera v. Consistent with our previous research [23], the system first obtains the distorted structured light image through the structured light projection system and obtains the aerial scene image passing through the same sampling area in real time through the passive imaging system. The specific process is as follows.

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Schematic diagram of the underwater-air imaging based on structured light.

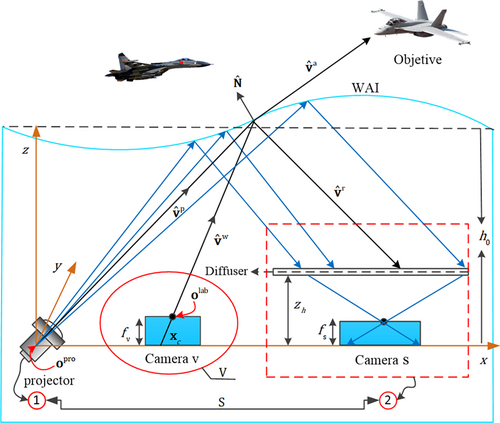
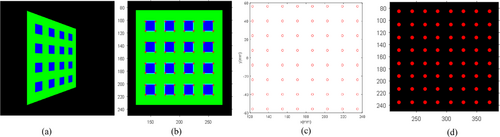
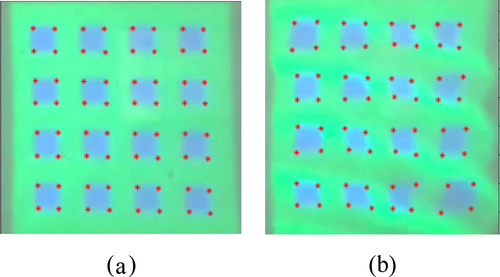
As shown in Figure 3, an adaptive and adjustable structured light pattern is projected onto the water surface to sample the instantaneous wave surface. When the water surface is calm, the WAI sampling point distribution, the corresponding control point distribution in the scene image, and the distribution information of the corresponding feature points in the reference structured light image can be easily obtained by perspective projection transformation from the feature point information of the structured light pattern. The above information is generally implemented through a full computer simulation process and used as the system initialization parameter. The simulation example of WAI sampling is shown in Figure 3, where Figure 3a is the preset structured light pattern, Figure 3b is the WAI sampling point distribution, Figure 3c is the corresponding control point distribution in the scene image, and Figure 3d is the corresponding feature point distribution in the reference structured light image, where the control points correspond to the feature points one by one, and their corresponding light rays all pass through the same sampling point on the wave surface.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Example of WAI sampling simulation when the water surface is calm. IEEE, (a) Structural-light pattern. (b) Virtual image generated on the WAI. (c) Sample points Distribution. (d) Control points distribution on the scene image.

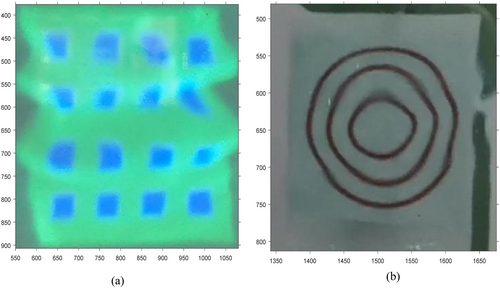
In actual scenes, the random fluctuation of the water surface will cause the structured light image on the diffusion plane and the aerial target scene image to be distorted. At this time, the distorted structured light image and the distorted scene image are simultaneously acquired through the camera, where the camera s acquires the distorted structured light image from the diffusion plane, and the camera v acquires the distorted scene image through the same sampling area. The instantaneous distorted image acquired by the underwater air imaging platform described in Section 3.3.1 is shown in Figure 4, where Figure 4a is the distorted structured light image on the diffusion plate, and Figure 4b is the aerial scene image through the same sampling area. As can be seen from the figure, the random fluctuation of the water surface causes serious geometric distortion of the structured light image and the scene image.

Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Images collected by the cross-medium system based on structured light. (a) Distorted structured light image.(b) Distorted scene image.

2.3 Image Restoration Using Local Approximate Registration

Based on the above model, this paper further proposes an image restoration method based on local approximate registration, and the algorithm flow is shown in Figure 5. The core idea of the algorithm is to use the feature point information on the reference structured light image and the distorted structured light image, estimate the spatial transformation model of the scene image in real time through the local approximate registration algorithm, and finally reconstruct the distortion-free scene image through the bi-linear interpolation algorithm.

Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
Processing flow of local approximate registration algorithm.

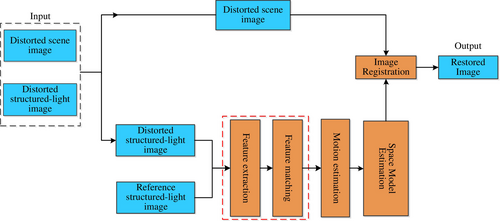
2.3.1 Feature Extraction and Matching

The random fluctuation of the water surface will cause the structured light and the target scene to be distorted. At this time, the camera can be used to collect the distorted structured light image and the distorted scene image at the same time. After acquiring the data, the reference structured light image J g ( x ) $$ {J}_g\left(\mathbf{x}\right) $$ and the distorted structured light image J ( x ) $$ J\left(\mathbf{x}\right) $$ are firstly extracted and matched with feature points to obtain the 2D distorted vector field of the feature points on the structured light image, as follows:
w str x r = x r − x r ′ = ω x , r , ω y , r , 0 T $$ {\mathbf{w}}_{\mathrm{str}}\left({\mathbf{x}}_r\right)={\mathbf{x}}_r-{\mathbf{x}}_r^{\prime }={\left[{\omega}_{x,r},{\omega}_{y,r},0\right]}^{\mathrm{T}} $$ (5)
where r = 1 , 2 , … , m s × n s $$ r=1,2,\dots, \left({m}_{\mathrm{s}}\times {n}_{\mathrm{s}}\right) $$ is the subscript of the feature matrix. x r $$ {\mathbf{x}}_r $$ , x r ′ $$ {\mathbf{x}}_r^{\prime } $$ are the corresponding feature point pairs on the reference image J g ( x ) $$ {J}_g\left(\mathbf{x}\right) $$ and the structured light image J ( x ) $$ J\left(\mathbf{x}\right) $$ . Next, we will briefly introduce the feature point extraction and matching process.
Affected by the fluctuations of the water surface, the structured light image reflected from the wave surface to the diffusion plate will have serious geometric distortion. At this time, the image edges are mostly jagged and no longer regular and smooth. If the traditional corner point detection algorithm [24-26] is used, it is easy to have problems such as false detection, missed detection, and multiple detections, and the feature information of the image cannot be correctly extracted. Therefore, this paper adopts the centroid-based corner detection algorithm we proposed earlier to extract the feature points of the structured light image. The specific steps of the algorithm are as follows [27]:
  1. Target image extraction and binarization. First, use the Sobel edge detection algorithm to obtain the contour information of the original image; then search for the largest connected domain in the image as the target image, and finally binarize the target image.
  2. Region segmentation. The connected domain algorithm (eight-connected) is used to segment the image into regions to obtain multiple locally connected domains and mark them.
  3. Centroid extraction. Based on region segmentation, use the spatial torch function to calculate the centroid coordinates of each connected domain.
  4. Sub-region segmentation. Traverse the pixel points of each connected domain, and then divide the connected domain into n sub-regions according to the centroid coordinate position and standard structured light shape features, where n is the number of sides of the polygon.
  5. Corner point extraction. According to the Euclidean distance formula, search for the pixel point with the farthest distance from the sub-contour set of each connected domain to the centroid, which is the corner point.

The image processed by the corner detection algorithm is shown in Figure 6, where Figure 6a shows the feature point distribution of the reference image and Figure 6b shows the feature point distribution of the distorted image. Subsequently, the bubble sort method is used to match the feature points of the two images respectively. Assuming that the size of the feature point matrix D $$ D $$ is m s × n s $$ {m}_{\mathrm{s}}\times {n}_{\mathrm{s}} $$ , the feature point matrix is updated column by column through bubble sorting. The specific process is as follows: First, a candidate matrix D c k $$ {D}_{\mathrm{c}k} $$ of size m s × 2 $$ {m}_{\mathrm{s}}\times 2 $$ is constructed to update the feature point coordinates of the k th $$ k\mathrm{th} $$ column in the matrix D $$ D $$ , where D c k $$ {D}_{\mathrm{c}k} $$ is composed of the feature points of the k $$ k $$ and k + 1 $$ k+1 $$ columns of the matrix. Then, the feature points of the matrix D c k $$ {D}_{\mathrm{c}k} $$ are arranged in ascending order according to the row values of the feature points to obtain a vector D m k $$ {D}_{\mathrm{m}k} $$ of size 2 m s × 1 $$ 2{m}_{\mathrm{s}}\times 1 $$ . Subsequently, the vector is divided into m s $$ {m}_{\mathrm{s}} $$ subsets D m k , j j = 1 m s $$ {\left\{{D}_{\mathrm{m}k,j}\right\}}_{j=1}^{m_{\mathrm{s}}} $$ from smallest to largest. Finally, the feature point with the smallest column value is selected from each subset D m k , j j = 1 m s $$ {\left\{{D}_{\mathrm{m}k,j}\right\}}_{j=1}^{m_{\mathrm{s}}} $$ as the sorting result of the k th $$ k\mathrm{th} $$ column, and the matrix D $$ D $$ is updated.

Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
Processing examples. (a) Characteristic extraction of reference image. (b) Characteristic extraction of distorted image.

2.3.2 Distortion Estimation of Scene Images

It is widely recognized that light radiation traversing the sea surface undergoes angular deflection due to the impact of surface undulations. As a result, the deviation between any two arbitrary light rays intersecting at the same location on the WAI is interrelated. Inspired by this, this section analyzes the displacement relationship between the corresponding points of the structured light image and the scene image from the perspective of geometric optics.

As illustrated in Figure 7, the z-axis is directed vertically upwards, and the projection center o pro $$ {\mathbf{o}}^{\mathrm{pro}} $$ is used to build the universal coordinate system. Let p r $$ {\mathbf{p}}_r $$ be the 3D coordinates of the rth characteristic point of the structural light template to be emitted. The projected ray is as follows:
R r p ≡ o pro + v ^ r p l p ∀ l p > 0 $$ {R}_r^{\mathrm{p}}\equiv {\left\{{\mathbf{o}}^{\mathrm{p}\mathrm{ro}}+{\hat{\mathbf{v}}}_r^{\mathrm{p}}{l}_p\right\}}_{\forall {l}_p>0} $$ (6)
where v ^ r p $$ {\hat{\mathbf{v}}}_r^{\mathrm{p}} $$ denotes the direction vector, and l p $$ {l}_p $$ indicates the length of the spread along v ^ r p $$ {\hat{\mathbf{v}}}_r^{\mathrm{p}} $$ . The projection light ray R r p $$ {R}_r^{\mathrm{p}} $$ is reflected at the WAI, where the intersection point is q r $$ {\mathbf{q}}_r $$ , which is the interface sampling point,
q r = WAI ∩ R r $$ {\mathbf{q}}_r=\mathrm{WAI}\cap {R}_r $$ (7)
Details are in the caption following the image
FIGURE 7
Open in figure viewerPowerPoint
Optical schematic diagram of distortion estimation of scene images.
The corresponding reflected light is
R r ≡ q r + v ^ r l r ∀ l r > 0 $$ {R}_r\equiv {\left\{{\mathbf{q}}_r+{\hat{\mathbf{v}}}_r{l}_r\right\}}_{\forall {l}_r>0} $$ (8)
Among them, v ^ r $$ {\hat{\mathbf{v}}}_r $$ is the direction vector, l r $$ {l}_r $$ indicates the propagation length along v ^ r $$ {\hat{\mathbf{v}}}_r $$ . The reflected beam creates a light spot at point s r $$ {\mathbf{s}}_r $$ on the diffusion plane. At this time, the normal of WAI is N ^ r $$ {\hat{\mathbf{N}}}_r $$ , and s r ′ $$ {\mathbf{s}}_r^{\prime } $$ represents the point coordinate on the diffusion plane as the WAI is flat. Consequently, the displacement Δ p r $$ \varDelta \left({\mathbf{p}}_r\right) $$ at the diffusion plane can be calculated as:
Δ p k = Δ x , Δ y , 0 T = s r − s r ′ = P s ′ w r str $$ \varDelta \left({\mathbf{p}}_k\right)={\left[{\varDelta}_x,{\varDelta}_y,0\right]}^{\mathrm{T}}={\mathbf{s}}_r-{\mathbf{s}}_r^{\prime }={{\mathbf{P}}_{\mathrm{s}}}^{\prime }{\mathbf{w}}_r^{\mathrm{s}\mathrm{tr}} $$ (9)
in which w r str $$ {\mathbf{w}}_r^{\mathrm{str}} $$ represents the pixel displacement of the corresponding pixel x r $$ {\mathbf{x}}_r $$ of the structural light image, P s ′ $$ {\mathbf{P}}_{\mathrm{s}}^{\prime } $$ represents camera's inverse projection matrix, which is expressed as follows:
P s ′ = z s 1 / f s 0 0 0 1 / f s 0 0 0 1 dx 0 0 0 dy 0 0 0 1 $$ {{\mathbf{P}}_{\mathrm{s}}}^{\prime }={z}_{\mathrm{s}}\left[\begin{array}{ccc}1/{f}_{\mathrm{s}}& 0& 0\\ {}0& 1/{f}_{\mathrm{s}}& 0\\ {}0& 0& 1\end{array}\right]\left[\begin{array}{ccc} dx& 0& 0\\ {}0& dy& 0\\ {}0& 0& 1\end{array}\right] $$ (10)
where f s $$ {f}_{\mathrm{s}} $$ and z s $$ {z}_{\mathbf{s}} $$ represent the focal distance and the distance from camera s to diffusion plate Π diffuser $$ {\Pi}^{\mathrm{diffuser}} $$ , respectively.
The optical location of camera s as o s lab = − R s T t s $$ {\mathbf{o}}_{\mathrm{s}}^{\mathrm{lab}}=-{R_{\mathrm{s}}}^{\mathrm{T}}{t}_{\mathrm{s}} $$ , where R s T $$ {R_{\mathrm{s}}}^{\mathrm{T}} $$ is the rotation matrix, t s $$ {t}_{\mathrm{s}} $$ is translation vector. Similarly, the optical center of camera v is denoted as o v lab = − R v T t v $$ {\mathbf{o}}_{\mathrm{v}}^{\mathrm{lab}}=-{R_{\mathrm{v}}}^{\mathrm{T}}{t}_{\mathrm{v}} $$ . When imaging through water, the reverse-projected light in the water corresponding to pixel x c $$ {\mathbf{x}}_c $$ and the feature point x r $$ {\mathbf{x}}_r $$ passes through the optical center o v lab $$ {\mathbf{o}}_{\mathrm{v}}^{\mathrm{lab}} $$ , as
R c w x c ≡ o v lab + v ^ c w l w ∀ l w > 0 $$ {R}_c^{\mathrm{w}}\left({\mathbf{x}}_c\right)\equiv {\left\{{\mathbf{o}}_{\mathrm{v}}^{\mathrm{lab}}+{\hat{\mathbf{v}}}_c^{\mathrm{w}}{l}_{\mathrm{w}}\right\}}_{\forall {l}_{\mathrm{w}}>0} $$ (11)
where v ^ c w $$ {\hat{\mathbf{v}}}_c^{\mathrm{w}} $$ denotes the direction vector of the reverse-projected ray corresponding to pixel x c $$ {\mathbf{x}}_c $$ , and l w $$ {l}_{\mathrm{w}} $$ is the length of the spread along v ^ c w $$ {\hat{\mathbf{v}}}_c^{\mathrm{w}} $$ . And then the reverse-projection ray R c w x c $$ {R}_c^{\mathrm{w}}\left({\mathbf{x}}_c\right) $$ intersects WAI at
q r = WAI ∩ R c w x c $$ {\mathbf{q}}_r=\mathrm{WAI}\cap {R}_c^{\mathrm{w}}\left({\mathbf{x}}_c\right) $$ (12)
The reverse-projection ray above water can be expressed as follows:
R c a x c ≡ q r + v ^ c a l a ∀ l a > 0 $$ {R}_c^{\mathrm{a}}\left({\mathbf{x}}_c\right)\equiv {\left\{{\mathbf{q}}_r+{\hat{\mathbf{v}}}_c^{\mathrm{a}}{l}_{\mathrm{a}}\right\}}_{\forall {l}_{\mathrm{a}}>0} $$ (13)
where v ^ c a $$ {\hat{\mathbf{v}}}_c^{\mathrm{a}} $$ represents the orientation vector of the air observation ray associated with pixel x c $$ {\mathbf{x}}_c $$ , while l a $$ {l}_{\mathrm{a}} $$ denotes its spread distance along v ^ c a $$ {\hat{\mathbf{v}}}_c^{\mathrm{a}} $$ . The reverse-projection ray R c a x c $$ {R}_c^{\mathrm{a}}\left({\mathbf{x}}_c\right) $$ above water is directed toward the actual scene and crosses the scene planar Π object $$ {\Pi}^{\mathrm{object}} $$ at point s c $$ {\mathbf{s}}_c $$ . Let s c ′ $$ {\mathbf{s}}_c^{\prime } $$ denote the scene point corresponding to the calm water surface. Therefore, the displacement on the scene plane is given by:
d s x c = s c − s c ′ $$ {\mathbf{d}}_{\mathrm{s}}\left({\mathbf{x}}_c\right)={\mathbf{s}}_c-{\mathbf{s}}_c^{\prime } $$ (14)
At this point, the displacement w obj x c $$ {\mathbf{w}}_{\mathrm{obj}}\left({\mathbf{x}}_c\right) $$ of pixel x c $$ {\mathbf{x}}_c $$ can be calculated as follows:
w obj x c = − P v d s x c , c = 1 , 2 , … , m s × n s $$ {\mathbf{w}}_{\mathrm{obj}}\left({\mathbf{x}}_c\right)=-{\mathbf{P}}_{\mathrm{v}}{\mathbf{d}}_{\mathrm{s}}\left({\mathbf{x}}_c\right),\kern1em c=1,2,\dots, \left({m}_{\mathbf{s}}\times {n}_{\mathrm{s}}\right) $$ (15)
where c $$ c $$ represents the subscript of the control point matrix, and P v $$ {\mathbf{P}}_{\mathrm{v}} $$ denotes the camera's projection matrix,
P v = 1 z v 1 dx 0 0 0 1 dy 0 0 0 1 f v 0 0 0 f v 0 0 0 1 $$ {\mathbf{P}}_{\mathrm{v}}=\frac{1}{z_{\mathrm{v}}}\left[\begin{array}{ccc}\frac{1}{dx}& 0& 0\\ {}0& \frac{1}{dy}& 0\\ {}0& 0& 1\end{array}\right]\left[\begin{array}{ccc}{f}_{\mathrm{v}}& 0& 0\\ {}0& {f}_v& 0\\ {}0& 0& 1\end{array}\right] $$ (16)
where f v $$ {f}_{\mathrm{v}} $$ and z v $$ {z}_{\mathrm{v}} $$ are the focal length and the distance from camera v to scene planar Π object $$ {\Pi}^{\mathrm{object}} $$ , and
z v = h q r + h q r − z h $$ {z}_{\mathrm{v}}=h\left({\mathbf{q}}_r\right)+\left(h\left({\mathbf{q}}_r\right)-{z}_h\right) $$ (17)
where h q r $$ h\left({\mathbf{q}}_r\right) $$ is the altitude of q r $$ {\mathbf{q}}_r $$ , and z h $$ {z}_h $$ represents the water depth of Π diffuser $$ {\Pi}^{\mathrm{diffuser}} $$ . The WAI is the point where the pixel projection beam R r p $$ {R}_r^{\mathrm{p}} $$ and the inverse-projected beam R c w x c $$ {R}_c^{\mathrm{w}}\left({\mathbf{x}}_c\right) $$ converge. Consequently, the displacements Δ p r $$ \varDelta \left({\mathbf{p}}_r\right) $$ and d s x c $$ {\mathbf{d}}_{\mathrm{s}}\left({\mathbf{x}}_c\right) $$ are proportional to the slope and height of q r $$ {\mathbf{q}}_r $$ and the height z h $$ {z}_h $$ of Π diffuser $$ {\Pi}^{\mathrm{diffuser}} $$ .
Typically, WAI's height variation is significantly less than the operational depth of the system. Therefore, the 3D position of the wave surface intersection point can be approximated as
q r ≈ q x , q y , h 0 = p r + v ^ r p h 0 / γ r $$ {\mathbf{q}}_r\approx \left({q}_x,{q}_y,{h}_0\right)={\mathbf{p}}_r+{\hat{\mathbf{v}}}_r^{\mathrm{p}}\left({h}_0/{\gamma}_r\right) $$ (18)
where h 0 $$ {h}_0 $$ represents the system depth. γ r $$ {\gamma}_r $$ marks the component of the z-axis. Hence, the moving amount Δ p r $$ \varDelta \left({\mathbf{p}}_r\right) $$ and d s x c $$ {\mathbf{d}}_{\mathrm{s}}\left({\mathbf{x}}_c\right) $$ are equivalent to:
Δ p r = s r − s r ′ = v ^ r h 0 − z h / γ r − v ^ r ′ h 0 − z h / γ r ′ , d x c = s c − s c ′ = v ^ c a ( h 0 − z h / γ c a − v ^ c ′ a h 0 − z h / γ c ′ a $$ {\displaystyle \begin{array}{l}\varDelta \left({\mathbf{p}}_r\right)={\mathbf{s}}_r-{\mathbf{s}}_r^{\prime }={\hat{\mathbf{v}}}_r\left({h}_0-{z}_h\right)/{\gamma}_r-\left({\hat{\mathbf{v}}}_r^{\prime}\left({h}_0-{z}_h\right)/{\gamma}_r^{\prime}\right),\\ {}\mathbf{d}\left({\mathbf{x}}_c\right)={\mathbf{s}}_c-{\mathbf{s}}_c^{\prime }={\hat{\mathbf{v}}}_c^{\mathrm{a}}\Big(\left({h}_0-{z}_h\right)/{\gamma}_c^{\mathrm{a}}-\left({\hat{\mathbf{v}}}_c^{\prime \mathrm{a}}\left({h}_0-{z}_h\right)/{\gamma}_c^{\prime \mathrm{a}}\right)\end{array}} $$ (19)
Among them γ r $$ {\gamma}_r $$ , γ r ′ $$ {\gamma}_r^{\prime } $$ , γ c a $$ {\gamma}_c^{\mathrm{a}} $$ , and γ c ′ a $$ {\gamma}_c^{\prime \mathrm{a}} $$ denote z-axis component of their respective vector directions. v ^ r ′ $$ {\hat{\mathbf{v}}}_r^{\prime } $$ and v ^ c ′ a $$ {\hat{\mathbf{v}}}_c^{\prime \mathrm{a}} $$ represent the direction vector of the reflection light ray and the direction vector of the airborne viewing light ray of the corresponding pixel as WAI is calm, respectively. In terms of Snell's Law, v ^ r $$ {\hat{\mathbf{v}}}_r $$ , v ^ r ′ $$ {\hat{\mathbf{v}}}_r^{\prime } $$ , v ^ c a $$ {\hat{\mathbf{v}}}_c^{\mathrm{a}} $$ , and v ^ c ′ a $$ {\hat{\mathbf{v}}}_c^{\prime \mathrm{a}} $$ are also represented as:
v ^ r = v ^ r p + 2 N ^ r − N ^ r · v ^ r p , v ^ r ′ = v ^ r p + 2 N ^ 0 − N ^ 0 · v ^ r p , v ^ c a = v ^ c w + N ^ r 1 − n w 2 + n w 2 v ^ c w · N ^ r 2 − n w v ^ c w · N ^ r , v ^ c ′ a = v ^ c w + N ^ 0 1 − n w 2 + n w 2 v ^ c w · N ^ 0 2 − n w v ^ c w · N ^ 0 $$ {\displaystyle \begin{array}{ll}{\hat{\mathbf{v}}}_r& ={\hat{\mathbf{v}}}_r^{\mathrm{p}}+2{\hat{\mathbf{N}}}_r\left(-{\hat{\mathbf{N}}}_r\cdotp {\hat{\mathbf{v}}}_r^{\mathrm{p}}\right),\\ {}{\hat{\mathbf{v}}}_r^{\prime }& ={\hat{\mathbf{v}}}_r^{\mathrm{p}}+2{\hat{\mathbf{N}}}_0\left(-{\hat{\mathbf{N}}}_0\cdotp {\hat{\mathbf{v}}}_r^{\mathrm{p}}\right),\\ {}{\hat{\mathbf{v}}}_c^{\mathrm{a}}& ={\hat{\mathbf{v}}}_c^{\mathrm{w}}+{\hat{\mathbf{N}}}_r\left[\sqrt{1-{n_{\mathrm{w}}}^2+{n_{\mathrm{w}}}^2{\left({\hat{\mathbf{v}}}_c^{\mathrm{w}}\cdotp {\hat{\mathbf{N}}}_r\right)}^2}-{n}_{\mathrm{w}}{\hat{\mathbf{v}}}_c^{\mathrm{w}}\cdotp {\hat{\mathbf{N}}}_r\right],\\ {}{\hat{\mathbf{v}}}_c^{\prime \mathrm{a}}& ={\hat{\mathbf{v}}}_c^{\mathrm{w}}+{\hat{\mathbf{N}}}_0\left[\sqrt{1-{n_{\mathrm{w}}}^2+{n_{\mathrm{w}}}^2{\left({\hat{\mathbf{v}}}_c^{\mathrm{w}}\cdotp {\hat{\mathbf{N}}}_0\right)}^2}-{n}_{\mathrm{w}}{\hat{\mathbf{v}}}_c^{\mathrm{w}}\cdotp {\hat{\mathbf{N}}}_0\right]\end{array}} $$ (20)
where N ^ 0 $$ {\hat{\mathbf{N}}}_0 $$ represents the normal of the water-air interface while the water waves seems calm, namely is denoted by N ^ 0 = [ 0 , 0 , 1 ] T $$ {\hat{\mathbf{N}}}_0={\left[0,0,1\right]}^{\mathrm{T}} $$ , and N ^ r $$ {\hat{\mathbf{N}}}_r $$ represents the normal of q r $$ {\mathbf{q}}_r $$ given that the WAI is wavy, and n w $$ {n}_{\mathrm{w}} $$ represents water's refractive index, that is, n w = 4 / 3 $$ {n}_{\mathrm{w}}=4/3 $$ .
From Equations (19) and (20), it can be seen that the displacements Δ p r $$ \varDelta \left({\mathbf{p}}_r\right) $$ and d s x c $$ {\mathbf{d}}_{\mathrm{s}}\left({\mathbf{x}}_c\right) $$ are related only to the slope of the sampling point q r $$ {\mathbf{q}}_r $$ once the system parameters h 0 $$ {h}_0 $$ and z h $$ {z}_h $$ given. Consequently, the ray-tracing approach can be utilized to ascertain the mapping relationship between Δ p r $$ \varDelta \left({\mathbf{p}}_r\right) $$ and d s x c $$ {\mathbf{d}}_{\mathrm{s}}\left({\mathbf{x}}_c\right) $$ , assuming the normal vector is known,
d s x c = F Δ p r $$ {\mathbf{d}}_{\mathrm{s}}\left({\mathbf{x}}_c\right)=\mathrm{F}\left[\varDelta \left({\mathbf{p}}_r\right)\right] $$ (21)
where F represents a mapping function relating Δ p r $$ \varDelta \left({\mathbf{p}}_r\right) $$ and d s x c $$ {\mathbf{d}}_{\mathrm{s}}\left({\mathbf{x}}_c\right) $$ .

Specifically, the displacement transformation relationship can be constructed using a polynomial representation method. First, based on the displacement model from Equation (19), the normal vectors N ^ r $$ {\hat{\mathbf{N}}}_r $$ of the wavefront sampling points under different slopes are computed, and the mapping values of multiple sets of displacement vectors Δ p r $$ \varDelta \left({\mathbf{p}}_r\right) $$ and d s x c $$ {\mathbf{d}}_{\mathrm{s}}\left({\mathbf{x}}_c\right) $$ are determined. Then, the transformation function F can be constructed using polynomial fitting.

Furthermore, the perturbation can be partitioned into two components due to the fact that the normal vectors of the WAI fluctuate around the z-axis: (1) the xoy component and (2) the yoz component, with their respective components as follows:
N ^ r xoz = sin θ r , 0 , − cos θ r T N ^ r yoz = 0 , sin θ r , − cos θ r T $$ {\displaystyle \begin{array}{l}{\hat{\mathbf{N}}}_r^{\mathrm{xoz}}={\left(\sin {\theta}_r,0,-\cos {\theta}_r\right)}^{\mathrm{T}}\\ {}{\hat{\mathbf{N}}}_r^{\mathrm{yoz}}={\left(0,\sin {\theta}_r,-\cos {\theta}_r\right)}^{\mathrm{T}}\end{array}} $$ (22)
where θ r $$ {\theta}_r $$ represents the waterfront's inclination angle.
In summary, according to Equations (9), (19), (20), and (22), and employing the least squares method, Equation (21) can be written as:
d s x c = ∑ i = 0 η 1 a i Δ x η 1 , ∑ j = 0 η 2 b j Δ y η 2 , 0 T $$ {\mathbf{d}}_{\mathrm{s}}\left({\mathbf{x}}_c\right)={\left[\sum \limits_{i=0}^{\eta_1}{a}_i{\varDelta_x}^{\eta_1},\sum \limits_{j=0}^{\eta_2}{\mathrm{b}}_j{\varDelta_y}^{\eta_2},0\right]}^{\mathrm{T}} $$ (23)

Among then η 1 $$ {\eta}_1 $$ and η 2 $$ {\eta}_2 $$ represent the fit's order. a i $$ {a}_i $$ and b j $$ {b}_j $$ denote the relative coefficients.

Finally, combining Equations (5), (9), (15), and (23), the displacement field w obj $$ {\mathbf{w}}_{\mathrm{obj}} $$ of any objective image can be obtained employing the distortion field w str $$ {\mathbf{w}}_{\mathrm{str}} $$ of the structured-light image which is be captured at the same moment.

2.3.3 Image Restoration

Given the 2D distortion vector field w obj $$ {\mathbf{w}}_{\mathrm{obj}} $$ on both the warped and ground-truth images or the spatial transformation model between the two images, it is easy to obtain the desired image by interpolating for the instantaneous distorted image [28].

Considering the non-rigid deformation properties of image distortion, This research provides a local surface fitting approach utilizing a weighted average to develop the spatial conversion model comparing the warped frame I ( x ) $$ I\left(\mathrm{x}\right) $$ and the undeformed frame I g ( x ) $$ {I}_g\left(\mathrm{x}\right) $$ . The spatial transformation function between I ( x ) $$ I\left(\mathrm{x}\right) $$ and I g ( x ) $$ {I}_g\left(\mathrm{x}\right) $$ are given by:
u ^ = f ( u , v ) v ^ = g ( u , v ) $$ {\displaystyle \begin{array}{l}\hat{u}=f\left(u,v\right)\\ {}\hat{v}=g\left(u,v\right)\end{array}} $$ (24)
in which ( u , v ) $$ \left(u,v\right) $$ represents pixel coordinate of the image that is free of distortion and ( u ^ , v ^ ) $$ \left(\hat{u},\hat{v}\right) $$ represents the position of the image that corresponds to something that is deformed. Our goal is to estimate the optimal spatial transformation functions f ( · ) $$ f\left(\cdotp \right) $$ and g ( · ) $$ g\left(\cdotp \right) $$ to describe the refraction distortion information caused by the wavy water surface.
Assuming that any pixel point ( u , v ) $$ \left(u,v\right) $$ in the distortion-free image is close to a control point u k , v k $$ \left({u}_k,{v}_k\right) $$ , then the corresponding point ( u ^ , v ^ ) $$ \left(\hat{u},\hat{v}\right) $$ in the distorted image is also close to the corresponding control point u ^ k , v ^ k $$ \left({\hat{u}}_k,{\hat{v}}_k\right) $$ , where u k , v k $$ \left({u}_k,{v}_k\right) $$ and u ^ k , v ^ k $$ \left({\hat{u}}_k,{\hat{v}}_k\right) $$ are the corresponding control point pairs in I g ( x ) $$ {I}_g\left(\mathrm{x}\right) $$ and I ( x ) $$ I\left(\mathrm{x}\right) $$ , and the corresponding distortion vector filed w x k $$ \mathbf{w}\left({\mathbf{x}}_k\right) $$ is equal to:
w x k = u ^ k − u k , v ^ k − v k , 0 T $$ \mathbf{w}\left({\mathbf{x}}_k\right)={\left[\left({\hat{u}}_k-{u}_k\right),\left({\hat{v}}_k-{v}_k\right),0\right]}^{\mathrm{T}} $$ (25)
where w x k $$ \mathbf{w}\left({\mathbf{x}}_k\right) $$ can be obtained from Section 2.3.2. The above description shows that the coordinate ( u , v ) $$ \left(u,v\right) $$ of any given pixel in the distortion-free image and its corresponding pixel ( u ^ , v ^ ) $$ \left(\hat{u},\hat{v}\right) $$ can be determined by weighted fusion of adjacent control points [29, 30]. The specific description is as follows.
The algorithm starts with the control point u k , v k $$ \left({u}_k,{v}_k\right) $$ of the distortion-free image, and finds the adjacent M - 1 control point pairs, and fits each control point with a K-order polynomial to obtain the spatial transformation function of m × n $$ m\times n $$ group of control point pairs.
u ^ k = P k u k , v k = ∑ i = 0 K ∑ j = 0 i a ij u k i v k i − j , k = 1 , 2 , … , m × n v ^ k = Q k u k , v k = ∑ i = 0 K ∑ j = 0 i b ij u k i v k i − j $$ {\displaystyle \begin{array}{ll}{\hat{u}}_k& ={P}_k\left({u}_k,{v}_k\right)=\sum \limits_{i=0}^K\sum \limits_{j=0}^i{a}_{ij}{u_k}^i{v_k}^{i-j},\\ {}& \kern0em k=1,2,\dots, m\times n\\ {}& {\hat{v}}_k={Q}_k\left({u}_k,{v}_k\right)=\sum \limits_{i=0}^K\sum \limits_{j=0}^i{b}_{ij}{u_k}^i{v_k}^{i-j}\end{array}} $$ (26)
where u ^ k , v ^ k $$ \left({\hat{u}}_k,{\hat{v}}_k\right) $$ is the control point of the distorted image, u k , v k $$ \left({u}_k,{v}_k\right) $$ is the control point of the distortion-free image, k represents the kth control point pair. P k $$ {P}_k $$ and Q k $$ {Q}_k $$ are the polynomial functions of the kth control point pair. M represents the size of the data set for polynomial fitting, M ≥ ( K + 1 ) ( K + 2 ) / 2 $$ M\ge \left(K+1\right)\left(K+2\right)/2 $$ . And m × n $$ m\times n $$ represents the number of feature point pairs. Second, based on the least square method, the minimum mean square errors E P $$ {E}_{\mathrm{P}} $$ and E Q $$ {E}_{\mathrm{Q}} $$ are minimized to obtain the fitting coefficients a ij $$ {a}_{ij} $$ and b ij $$ {b}_{ij} $$ .
E P = ∑ i = 1 τ P k u k , v k − u ^ k 2 , E Q = ∑ i = 1 τ Q k u k , v k − v ^ k 2 $$ {\displaystyle \begin{array}{l}{E}_{\mathrm{P}}=\sum \limits_{i=1}^{\tau }{\left[{P}_k\left({u}_k,{v}_k\right)-{\hat{u}}_k\right]}^2,\\ {}{E}_{\mathrm{Q}}=\sum \limits_{i=1}^{\tau }{\left[{Q}_k\left({u}_k,{v}_k\right)-{\hat{v}}_k\right]}^2\end{array}} $$ (27)
Then, according to the bi-cubic interpolation theory [28], the weight function of the control point is defined as
ω k ( R ) = ( a + 2 ) R 3 − ( a + 3 ) R 2 + 1 , 0 ≤ R ≤ 1 aR 3 − 5 aR 2 + 8 aR − 4 a , 1 < R < 2 0 , otherwise $$ {\omega}_k(R)=\left\{\begin{array}{l}\left(a+2\right){R}^3-\left(a+3\right){R}^2+1,\kern1.1em 0\le R\le 1\\ {}\kern0.0em {aR}^3-5{aR}^2+8 aR-4a,\kern2em 1<R<2\\ {}\kern0.0em 0,\kern11.2em \mathrm{otherwise}\end{array}\right. $$ (28)
where
R = u − u k 2 + v − v k 2 1 2 / R τ $$ R={\left[{\left(u-{u}_k\right)}^2+{\left(v-{v}_k\right)}^2\right]}^{\frac{1}{2}}/{R}_{\tau } $$ (29)
where R τ $$ {R}_{\tau } $$ is the maximum distance between control point u k , v k $$ \left({u}_k,{v}_k\right) $$ and the M nearest control points in the distortion-free image. As the distance is greater than R τ $$ {R}_{\tau } $$ , it indicates that the control point u k , v k $$ \left({u}_k,{v}_k\right) $$ has no effect on the pixel ( u , v ) $$ \left(u,v\right) $$ on the image. Therefore, let the weight coefficient a = 0 $$ a=0 $$ , then Equation (28) can be further written as
ω k ( R ) = 2 R 3 − 3 R 2 + 1 , 0 ≤ R ≤ 1 0 , otherwise $$ {\omega}_k(R)=\left\{\begin{array}{l}2{R}^3-3{R}^2+1,\kern1em 0\le R\le 1\\ {}\kern0.0em 0,\kern6.7em \mathrm{otherwise}\end{array}\right. $$ (30)
Subsequently, the spatial transformation model of the distorted scene image and the distortion-free scene image can be derived from Equations (26) and (30),
u ^ = f ( u , v ) = ∑ k m air × n air ω k u − u k 2 + v − v k 2 1 2 / R τ ∑ i = 0 K ∑ j = 0 i a ij u k i v k i − j ∑ k m air × n air ω k u − u k 2 + v − v k 2 1 2 / R τ , v ^ = g ( u , v ) = ∑ k m air × n air ω k u − u k 2 + v − v k 2 1 2 / R τ ∑ i = 0 K ∑ j = 0 i b ij u k i v k i − j ∑ k m air × n air ω k u − u k 2 + v − v k 2 1 2 / R τ $$ {\displaystyle \begin{array}{l}\hat{u}=f\left(u,v\right)=\frac{\sum_k^{m_{air}\times {n}_{air}}\left\{{\omega}_k\left({\left[{\left(u-{u}_k\right)}^2+{\left(v-{v}_k\right)}^2\right]}^{\frac{1}{2}}/{R}_{\tau}\right){\sum}_{i=0}^K{\sum}_{j=0}^i{a}_{ij}{u_k}^i{v_k}^{i-j}\right\}}{\sum_k^{m_{air}\times {n}_{air}}{\omega}_k\left({\left[{\left(u-{u}_k\right)}^2+{\left(v-{v}_k\right)}^2\right]}^{\frac{1}{2}}/{R}_{\tau}\right)},\\ {}\\ {}\\ {}\hat{v}=g\left(u,v\right)=\frac{\sum_k^{m_{air}\times {n}_{air}}\left\{{\omega}_k\left({\left[{\left(u-{u}_k\right)}^2+{\left(v-{v}_k\right)}^2\right]}^{\frac{1}{2}}/{R}_{\tau}\right){\sum}_{i=0}^K{\sum}_{j=0}^i{b}_{ij}{u_k}^i{v_k}^{i-j}\right\}}{\sum_k^{m_{air}\times {n}_{air}}{\omega}_k\left({\left[{\left(u-{u}_k\right)}^2+{\left(v-{v}_k\right)}^2\right]}^{\frac{1}{2}}/{R}_{\tau}\right)}\end{array}} $$ (31)

Finally, according to the spatial model shown in formula (31), the undistorted scene image is restored using the bi-linear interpolation method. The complete process of the local approximate registration method is described in Algorithm 1.

ALGORITHM 1. Image Restoration Algorithm Based on Local Approximate Registration.

Input: Reference structured light image J g ( x ) ∈ ℝ M s × N s $$ {J}_{\mathrm{g}}\left(\mathbf{x}\right)\in {\mathrm{\mathbb{R}}}^{M_{\mathrm{s}}\times {N}_{\mathrm{s}}} $$ .

Distorted structured light image J ( x ) ∈ ℝ M s × N s $$ J\left(\mathbf{x}\right)\in {\mathrm{\mathbb{R}}}^{M_{\mathrm{s}}\times {N}_{\mathrm{s}}} $$ .

Distorted scene image I ( x ) ∈ ℝ M a × N a $$ I\left(\mathbf{x}\right)\in {\mathrm{\mathbb{R}}}^{M_{\mathrm{a}}\times {N}_{\mathrm{a}}} $$ .

Output: No-distortion scene image I g ( x ) ∈ ℝ M a × N a $$ {I}_{\mathrm{g}}\left(\mathbf{x}\right)\in {\mathrm{\mathbb{R}}}^{M_{\mathrm{a}}\times {N}_{\mathrm{a}}} $$ .

1. Feature extraction and matching

   D ⇐ FeatureExtractSort ( J ( x ) ) , D ∈ ℝ m s × n s $$ D\Leftarrow FeatureExtractSort\left(J\left(\mathbf{x}\right)\right),D\in {\mathrm{\mathbb{R}}}^{m_{\mathrm{s}}\times {n}_{\mathrm{s}}} $$

   D g ⇐ FeatureExtractSort J g ( x ) , D g ∈ ℝ m s × n s $$ {D}_{\mathrm{g}}\Leftarrow FeatureExtractSort\left({J}_{\mathrm{g}}\left(\mathbf{x}\right)\right),{D}_{\mathrm{g}}\in {\mathrm{\mathbb{R}}}^{m_{\mathrm{s}}\times {n}_{\mathrm{s}}} $$

   w str ⇐ DisplacementCalculate D , D g , w str ∈ ℝ m s × n s $$ {\mathbf{w}}_{\mathrm{s}\mathrm{tr}}\Leftarrow \mathrm{DisplacementCalculate}\left(D,{D}_{\mathrm{g}}\right),{\mathbf{w}}_{\mathrm{s}\mathrm{tr}}\in {\mathrm{\mathbb{R}}}^{m_{\mathrm{s}}\times {n}_{\mathrm{s}}} $$

2. Distortion estimation of the control points

   w obj ⇐ DisplacementConvert w str , w obj ∈ ℝ m s × n s $$ {\mathbf{w}}_{\mathrm{obj}}\Leftarrow \mathrm{DisplacementConvert}\left({\mathbf{w}}_{str}\right),{\mathbf{w}}_{\mathrm{obj}}\in {\mathrm{\mathbb{R}}}^{m_{\mathrm{s}}\times {n}_{\mathrm{s}}} $$

3. Local approximation registration

   Γ lwm ( x ) ⇐ LocalApproximateRegistration w obj $$ {\Gamma}_{\mathrm{lwm}}\left(\mathbf{x}\right)\Leftarrow LocalApproximateRegistration\left({\mathbf{w}}_{\mathrm{obj}}\right) $$

4. Bilinear interpolation

   I g ( x ) ⇐ BilinearInterpolation I ( x ) , Γ lwm ( x ) $$ {I}_{\mathrm{g}}\left(\mathbf{x}\right)\Leftarrow BilinearInterpolation\left(I\left(\mathbf{x}\right),{\Gamma}_{\mathrm{lwm}}\left(\mathbf{x}\right)\right) $$

3 Results and Discussion

In order to verify the performance of the algorithm, this paper first conducted a simulation test on MATLAB and compared it with similar algorithms. Second, a simplified cross-media imaging platform was built in the laboratory, and a camera was used to collect aerial target scene images and distorted structured light images through the fluctuating water surface in real time. Then, the real data collected by the experimental platform was used to test it on MATLAB. The data can be obtained from [31]. Finally, a real image sequence of a certain length was used to test and analyze the stability of the algorithm. In addition, this section also conducted a real-time processing test on the algorithm in OpenCV and gave the test results.

3.1 Image Quality Metrics

In order to objectively evaluate the distortion correction capability of the algorithm, this chapter uses four standard image quality evaluation indicators to quantitatively analyze the correction results of the algorithm, namely, peak signal-to-noise ratio (PSNR) [32], mean square error (MSE) [21], gradient magnitude similarity deviation (GMSD) [33], and structural similarity (SSIM) [34]. Among them, the larger the PSNR, the richer the real information of the restored image and the better the image quality. The smaller the MSE, the better the image quality. GMSD indicates the degree of difference in structural information between images. The smaller the value, the higher the similarity of edge details between the two images. The larger the SSIM value, the higher the similarity between the two images in brightness, contrast, and structure.

3.2 Algorithm Simulation Analysis

The simulation model is shown in Figure 2. Simulation parameters includes: h 0 = 150 mm $$ {h}_0=150\kern0.5em \mathrm{mm} $$ , θ pro = 40 ∘ $$ {\theta}_{\mathrm{pro}}={40}^{\circ } $$ , z h = 60 mm $$ {z}_h=60\kern0.5em \mathrm{mm} $$ , the relevant attributes of the projector, cameras, and camera v are given in [23]. Furthermore, in order to simulate the movement of ocean waves, this paper uses spectral theory to numerically simulate the wavy water surface with a wind speed of 1.0 m/s. Research shows that using spectra to describe ocean waves is one of the most effective methods.

Assuming a checkerboard is placed at the height z a = 1.15 m $$ {z}_a=1.15\mathrm{m} $$ , the underwater camera images the checkerboard through the WAI. Subsequently, a local approximate registration method is adopted to reconstruct the distortion-free scene image using the 2D distortion field of the distorted scene image.

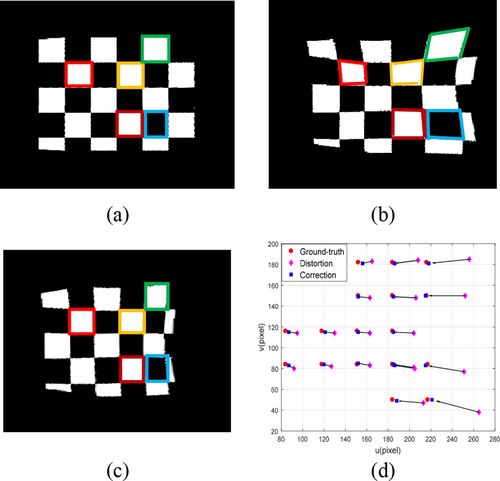
The restoration results of the sampled image at any time are shown in Figure 8, where the image size is 300 × 250 $$ 300\times 250 $$ . Figure 8a is the ground-truth scene image, Figure 8b is the distorted scene image, and Figure 8c is the restored image. Furthermore, the corner point position distribution of the color-coded checkerboard in Figure 8a–c is depicted in Figure 8d. Among them, the corner point locations in the distorted image have a standard deviation (STD) of 24.3311 pixels, whereas the STD of the recovered image, which was obtained using the proposed method, is 2.4698 pixels. The error elimination rate reached 89.84%. Simulation results show that the algorithm proposed in this paper can significantly eliminate image distortion in cross-media imaging scenes and improve the visual effect of the image.

Details are in the caption following the image
FIGURE 8
Open in figure viewerPowerPoint
Analysis of restoration results of instantaneous sampling image. (a) Distortion-free image. (b) Deformed image. (c) Recovered image. (d) Scatter plot.

First, the correction results of the proposed algorithm are compared with those of a similar algorithm, namely, the Alterman's method [16]. For the sake of fairness, the two methods are tested using the same simulation data. As can be seen from Figure 9, both methods have the ability to correct the distortion of cross-medium images. Compared with the original images, the distortion of the images processed by the two algorithms is significantly reduced, and their edge details are closer to the real scene. From the perspective of the distortion correction effect, the Alterman's method still has a large deviation in the correction of local details, while the proposed method has a better correction effect, as shown in the red box. From the data in the Table 1, it can be seen that compared with the Alterman's method, the images processed by the proposed algorithm perform better in terms of performance indicators such as PSNR, SSIM, and MSE, indicating that the proposed method has a stronger ability to correct underwater image distortion.

Details are in the caption following the image
FIGURE 9
Open in figure viewerPowerPoint
Recovery results of the two methods.
TABLE 1. Comparison of image quality metrics (Bold font is good).
Distorted image Alterman's [16] Our method
Data 1
MSE (L) 0.1393 0.0520 0.0409
PSNR (H) 8.5597 12.8389 14.1328
SSIM(H) 0.5584 0.6814 0.7004
Data 2
MSE (L) 0.1215 0.0441 0.0394
PSNR (H) 9.1535 13.5571 14.2596
SSIM(H) 0.5660 0.6784 0.7066
Data 3
MSE (L) 0.0910 0.0514 0.0429
PSNR (H) 10.4074 12.8878 14.6756
SSIM(H) 0.6127 0.6270 0.7070

3.3 Test Using Real Through-Water Scenes

3.3.1 Experiment Setup

In order to further test the effectiveness of the algorithm in real imaging scenarios, we first established a cross-media imaging system platform in the laboratory, as shown in Figure 10. Figure 10a is the real experimental scene, and Figure 10 is a schematic diagram of the experimental setup. The setup includes an acrylic water tank (dimensions: 100 × 70 × 60 $$ 100\times 70\times 60 $$ cm), with a projector positioned to the left at a height of zero from the tank's base, accompanied by a diffuser plate and a camera. The system is engineered to photograph both the diffusion plane and the airborne scene, utilizing a single camera to simultaneously capture both areas for operating efficiency. In the experiment, Zhang's calibration technique [35] was utilized to calibrate the parameters of both the projector and the camera. The system's relevant parameters are as follows: the projection angle of the projector is θ pro = 40 ∘ $$ {\theta}_{\mathrm{pro}}={40}^{\circ } $$ , the average water depth of the system is h 0 = 42 cm $$ {h}_0=42\mathrm{cm} $$ the system height of the diffusion plate is z h = 30 cm $$ {z}_h=30\mathrm{cm} $$ , and the target scene is located 1.6 m above the water surface.

Details are in the caption following the image
FIGURE 10
Open in figure viewerPowerPoint
Experimental platform. (a) Experimental environment. (b) Geometry diagram of the Experimental platform.

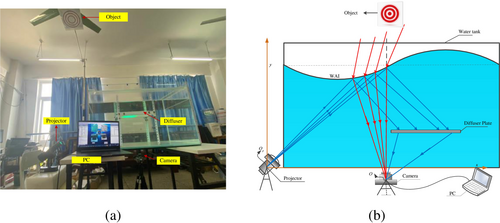
In the experiment, artificial waves were used to simulate real water surface movement; that is, the water surface was stirred vigorously to generate surface waves and then left to stand for 1 min, thus forming a natural oscillation phenomenon. Then, a camera was used to simultaneously capture structural-light images on the diffusion plate and the airborne scene image.

Figure 11 displays a randomly sampled image consisting of two parts: structured light on diffuser and distorted landscape above water. Both navigate the identical expanse at the water's surface. Figure 11 illustrates that water surface oscillations induce significant refraction distortion, adversely impacting the underwater observer's ability to track and identify airborne subjects.

Details are in the caption following the image
FIGURE 11
Open in figure viewerPowerPoint
Random sampled image.

3.3.2 Image Processing

The image processing process is shown in Figure 12, which is divided into three stages: system initialization stage, data acquisition stage and data processing stage. The task of the system initialization phase is to complete the sampling of the wave surface (as shown in Figure 12a) and obtain the reference structured light image (as shown in Figure 12b).During the data acquisition stage, the camera collects distorted scene images and distorted structured light images in real time, as shown in Figure 12c and Figure 12d. In the data processing stage, the characteristics of the structured light image are first extracted and matched. The distortion field of the control points on the target picture can be computed using the displacement transformation relationship. Ultimately, the local surface fitting method is employed to rectify the picture distortion, resulting in the generation and output of the processed image, as illustrated in Figure 12f.

Details are in the caption following the image
FIGURE 12
Open in figure viewerPowerPoint
Processing flow. (a) Sampling image of WAI. (b) Reference structural-light. (c) Warped structural- light. (d) Distortion-free image. (e) Distorted image. (f) Recovered image.

3.3.3 Image Quality Analysis

In order to test the effectiveness of the algorithm, we first use real scene data for analysis. The data is collected by the underwater air imaging platform described in Section 3.3.1. The target scene is “concentric circles”. The data is stored in the form of video sequences and has been shared in the literature [31]. Sampled images at different times are randomly selected from the real scene sequence for testing, where the target scene image size is 256 × 256 $$ 256\times 256 $$ .

As can be seen from Figure 13, the proposed method can effectively compensate for the random distortion of the cross-media imaging scene, the distortion of the target image is significantly reduced, and the contour details are closer to the real scene. As shown in the red box in the figure, the distortion of the concentric circles is effectively reduced after processing, and the real shape of the target image is closer to the real scene, which improves the visualization of the image. Table 2 gives the numerical results of the distorted image and the restored image. Compared with the distorted image, the restored image has significant improvements in performance indicators such as PSNR, MSE, and SSIM, which prove the effectiveness of the algorithm in the distortion compensation process of instantaneous distorted images.

Details are in the caption following the image
FIGURE 13
Open in figure viewerPowerPoint
The recovery results of the proposed method.
TABLE 2. Image quality metrics (Bold font is good).
SSIM MSE PSNR
Samples Ours Samples Ours Samples Ours
Time 1 0.7702 0.8749 0.0051 0.0022 22.8897 26.8138
Time 2 0.6978 0.8878 0.0076 0.0018 21.2091 27.4072
Time 3 0.7606 0.8772 0.0055 0.0020 22.6351 27.0769

In order to more comprehensively evaluate the performance of the algorithm and its application scenarios the restoration results are compared with other advanced methods, including Oreifej's method [6], James' method [9] and T. Sun's method [10]. Unlike the proposed method, the above methods all require a video sequence of a specific length to complete the reconstruction of the distorted scene, while the method in this paper only requires a single frame input image. For the sake of fairness, considering the restoration results of the sampled images at the same time, first, with the sampled frame at a specific time as the center, a certain length of image sequence is selected forward or backward as the input parameter of the other three methods, and then the restoration results of the corresponding frames are compared with the proposed method.

All methods were tested using the same source data [31]. The maximum number of iterations for Oreifej's method and T.Sun's method was set to 3 (after three iterations of the source data [31], the results have stabilized). The block size in the corresponding sequence of T. Sun's method is 74 × 74 $$ 74\times 74 $$ . In addition, in order to statistically compare the real-time processing efficiency of different methods, all methods were executed on the same computer, where the system operating environment is: CPU (i7-6700HQ), RAM (8 GB), MATLAB2018b.

Figure 14 shows the recovery results of the proposed method and the state-of-the-art methods. Oreifej's method, T. Sun's method and James' method use image sequences of 10 and 20 frames, respectively, to reconstruct the sampling frames, while the proposed method only processes the distorted image at the current moment. Table 3 shows the numerical comparison results of the restored images under different methods.

Details are in the caption following the image
FIGURE 14
Open in figure viewerPowerPoint
Recovery results of different methods.
TABLE 3. Numerical comparison.
Methods GMSD SSIM PSNR Time (s)
Time 1
1 fps $$ 1 fps $$ Ours 0.1568 0.8749 26.8138 1.4370
10 fps $$ 10 fps $$ Oreifej's 0.1419 0.8890 27.5162 141.1623
T. Sun's 0.1607 0.8677 26.1908 167.5526
James's 0.1674 0.8596 25.9702 9.0383
20 fps $$ 20 fps $$ Oreifej's 0.1274 0.9028 28.3086 349.6122
T. Sun's 0.1397 0.8898 27.2052 341.5579
James's 0.1545 0.8739 26.5241 11.0007
Time 2
1 fps $$ 1 fps $$ Ours 0.1492 0.8878 27.4072 1.4382
10 fps $$ 10 fps $$ Oreifej's 0.1430 0.8883 27.3552 177.2077
T. Sun's 0.1514 0.8779 26.5544 168.7399
James's 0.1711 0.8591 25.5864 3.4897
20 fps $$ 20 fps $$ Oreifej's 0.1658 0.8690 26.1154 350.2627
T. Sun's 0.1694 0.8582 25.5472 339.0449
James's 0.2017 0.8271 24.2426 6.4821
Time 3
1 fps $$ 1 fps $$ Ours 0.1570 0.8771 27.0769 1.4363
10 fps $$ 10 fps $$ Oreifej's 0.1710 0.8549 25.4536 177.7958
T. Sun's 0.1911 0.8262 24.3011 182.5569
James's 0.1761 0.8543 26.2393 3.5057
20 fps $$ 20 fps $$ Oreifej's 0.1395 0.8904 27.9088 351.2541
T. Sun's 0.1661 0.8615 26.1695 362.3698
James's 0.1620 0.8738 26.8630 4.9811

As can be seen from the figure, all methods can effectively suppress the refraction distortion caused by water waves, reduce the degree of image distortion, and improve the visual effect of the image, which shows the effectiveness of the above algorithms. Intuitively, the visual effects of Oreifej's method and Sun's method are the best, but in numerical analysis, it is found that their correction accuracy is not optimal. The main reasons are: (1) the image sequence is not long enough; (2) the inter-frame difference of the test sequence is large. The above reasons will affect the reconstruction quality of the reference frame, thereby affecting the image registration accuracy. The correction result of James's method is closer to the real image in terms of graphic contour, but there are still a lot of local distortions in the image and it is accompanied by motion blur. This is related to the fact that this method only considers image distortion caused by periodic waves. In addition, the periodic assumption of James's method requires that the length of the image sequence is long enough to fully guarantee the periodic characteristics of the water surface fluctuations, which means that the algorithm cannot reconstruct high-quality results through short video sequences (e.g., the restoration effect of 10- and 20-frame image sequences is not ideal). Unlike the above methods, the algorithm in this chapter can restore a distortion-free image through a single frame image. From the correction results and data, we can see that the algorithm in this chapter not only significantly reduces image distortion but also has better stability. The reason is that the local approximate registration and interpolation method can better estimate the local changes of the scene image, thus obtaining a stable output result.

From the perspective of distortion correction efficiency, the processing speed of the proposed method is significantly better than other methods. Taking random sampling time 1 as an example, in order to reconstruct the distortion-free scene, Oreifej's method takes a total of 141.1623 s using 10 frames of data. T. Sun's method takes 167.5526 s using 10 frames. James' method takes 9.0383 s using 10 frames. Our method only takes 1.4370 s, which effectively reduces the image processing delay and improves the image processing efficiency.

In summary, compared with other methods, the proposed method can not only reduce image distortion and improve the visualization of the image, but also is significantly better than other methods in terms of computational efficiency, realizing an “end-to-end” processing process.

3.3.4 Robustness Analysis

In order to test the stability of the algorithm, 120 frames of sampled images were randomly selected from the test scene sequence [31] and processed on MATLAB, and the measurement indicators (including SSIM, MSE, PSNR, and Times) were statistically averaged. Then, the real-time processing process of the algorithm was implemented on OpenCV, which included three stages: data acquisition, data processing, and result display, and the real-time processing time was calculated. The robustness analysis results of the algorithm are shown in Table 4.

TABLE 4. Robustness analysis.
SSIM (H) GMSD (L) PSNR (H) Time (L)/s (MATLAB) Time (L)/s (OpenCV)
Sampled frames 0.7903 0.2148 23.3990 — —
Proposed method 0.9028 0.1314 28.5695 0.8978 0.6000

As can be seen from Table 4, compared with the distorted image, the results of the proposed method have obvious improvements in performance indicators such as SSIM, GMSD, and PSNR. The image is closer to the real image in terms of brightness, contrast and similarity, with richer edge detail information, less image noise, and significantly improved image quality. From the perspective of real-time processing performance, the image processing time of the proposed method is 0.6 s, realizing the “end-to-end” processing process of a single frame image, which can be better applied to dynamic target monitoring scenarios.

4 Conclusions

This work introduces an innovative model that employs structured light projection technology for real-time water surface measurement and proposes a distortion-free image reconstruction and restoration method based on local approximate registration. The method begins by using structured light to capture the real-time water surface. It then employs feature points from the structured light image to calculate the deformation vector field of the corresponding sampling points of the distorted scene. Finally, a local approximate registration is employed to reconstruct an image free from distortion. Experimental results show that the proposed method can not only reduce image distortion and improve image visualization, but also has significantly better computational efficiency than the state-of-the-art methods.

As can be seen from Section 2.3.3, the restoration accuracy of the image is directly related to the wavefront sampling interval; that is, the smaller the sampling interval, the higher the image restoration accuracy. However, when the water surface fluctuation increases, a small sampling interval is prone to cause sampling point aliasing problems, which will reduce the image restoration effect. Therefore, in the future, we will further carry out research on adaptive and adjustable structured light projection technology.

Author Contributions

Bijian Jian: conceptualization, methodology, software, validation, writing – original draft. Ting Peng: project administration, funding acquisition, writing – review and editing. Xuebo Zhang: data curation. Changyong Lin: validation.

Acknowledgments

This research was funded by Guangxi Natural Science Foundation projects (2024JJA170158) and (2025GXNSFAA069222), Hezhou University Doctoral Research Start-up Fund Project (2024BSQD10), Guangxi Young and Middle-Aged Teachers' Basic Research Ability Improvement Project (2024KY0715) and Hezhou University Interdisciplinary and Collaborative Research Project (XKJC202404).

    Conflicts of Interest

    The authors declare no conflicts of interest.

    Data Availability Statement

    The data that support the findings of this study are openly available in (repository “figshare”) at https://doi.org/10.6084/m9.figshare.28091540.v2, reference number [31].

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.