Engineering Reports
Volume 7, Issue 3 e70077
RESEARCH ARTICLE
Open Access

MaOAOA: A Novel Many-Objective Arithmetic Optimization Algorithm for Solving Engineering Problems

Pradeep Jangir, 

Pradeep Jangir

University Centre for Research and Development, Chandigarh University, Gharuan, Mohali, India

Department of CSE, Graphic Era Hill University, Dehradun, India

Centre for Research Impact & Outcome, Chitkara University Institute of Engineering and Technology, Chitkara University, Rajpura, Punjab, India

Applied Science Research Center, Applied Science Private University, Amman, Jordan

Contribution: Conceptualization, ​Investigation, Writing - original draft, Data curation, Formal analysis

Search for more papers by this author
 Arpita, 

Arpita

Department of Biosciences, Saveetha School of Engineering, Saveetha Institute of Medical and Technical Sciences, Chennai, India

Contribution: Methodology, Validation, Visualization, Writing - review & editing

Search for more papers by this author
Sundaram B. Pandya, 

Sundaram B. Pandya

Department of Electrical Engineering, Shri K.J. Polytechnic, Bharuch, India

Contribution: Validation, Methodology, Data curation

Search for more papers by this author
Gulothungan G., 

Corresponding Author

Gulothungan G.

Department of Electronics and Communication Engineering, SRM Institute of Science and Technology, Chengalpattu, Tamilnadu, India

Correspondence:

Mohammad Khishe ([email protected])

Gulothungan G. ([email protected])

Contribution: Software, Formal analysis, Project administration, Visualization, Writing - original draft

Search for more papers by this author
Mohammad Khishe, 

Corresponding Author

Mohammad Khishe

Department of Electrical Engineering, Imam Khomeini Naval Science University of Nowshahr, Nowshahr, Iran

Jadara University Research Center, Jadara University, Irbid, Jordan

Correspondence:

Mohammad Khishe ([email protected])

Gulothungan G. ([email protected])

Contribution: Data curation, Supervision, Resources, ​Investigation, Validation

Search for more papers by this author
Bhargavi Indrajit Trivedi, 

Bhargavi Indrajit Trivedi

Vishwakarma Government Engineering College, Ahmedabad, Gujarat, India

Contribution: Conceptualization, Validation, Project administration, Formal analysis

Search for more papers by this author
First published: 18 March 2025
https://doi.org/10.1002/eng2.70077
Citations: 1

Funding: The authors received no specific funding for this work.

ABSTRACT

Currently, the use of multi-objective optimization algorithms has been applied in many fields to find the efficient solution of the multiple objective optimization problems (MOPs). However, this reduces their efficiency when addressing MaOPs, which are problems that contain more than three objectives; this is because the portion of the Pareto frontier solutions tends to increase exponentially with the number of objectives. This paper aims at overcoming this problem by proposing a new Many-Objective Arithmetic Optimization Algorithm (MaOAOA) that incorporates a reference point, niche preservation, and an information feedback mechanism (IFM). They did this in a manner that splits the convergence and the diversity phases in the middle of the cycle. The first phase deals with the convergence using a reference point approach, which aims to move the population towards the true Pareto Front. However, the diversity phase of the MaOAOA uses a niche preserve to the archive truncation method in the population, thus guaranteeing that the population is spread out properly along the actual Pareto front. These stages are mutual; that is, the convergence stage supports the diversity stage, and they are balanced by an (IFM) approach. The experimental results show that MaOAOA outperforms several approaches, including MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW, in terms of GD, IGD, SP, SD, HV, and RT metrics. This can be seen from the MaF1-MaF15 test problems, especially with four, seven, and nine objectives, and five real-world problems that include RWMaOP1 to RWMaOP5. The findings indicate that MaOAOA outperforms the other algorithms in most of the test cases analyzed in this study.

1 Introduction

Multiobjective evolutionary algorithms (MOEAs), over recent decades, have become a staple in addressing multiobjective optimization problems (MOPs). These algorithms have been instrumental in various applications. For instance, the issue of estimating voltage transformer ratio errors [1] is effectively framed as a MOP. Similarly, the challenge of restoring services in distribution systems has been tackled using MOEAs [2]. Additionally, MOEA/D, a specific variant of MOEAs, has been employed for optimizing paths in welding robot operations [3] and for efficient scheduling in distributed, heterogeneous welding flow shops [4]. From a mathematical standpoint, a MOP with multiple objectives is defined by Equation (1),
F ( x ) = { f 1 ( x ) , f 2 ( x ) , … , f m ( x ) } x ∈ Ω , $$ {\displaystyle \begin{array}{cc}F(x)=\Big\{& {f}_1(x),{f}_2(x),\dots, {f}_m(x)\Big\}\\ {}& x\in \varOmega \end{array}}, $$ (1)
where Ω ⊂ ℝ n $$ \varOmega \subset {\mathbb{R}}^n $$ represents the multi-dimensional decision space. In this context, x ∈ Ω $$ x\in \varOmega $$ denotes a set of decision variables associated with a potential solution, and F ( x ) ⊂ R M $$ F(x)\subset {R}^M $$ refers to the objective mapping that includes the objective function f 1 ( x ) , f 2 ( x ) , … , f m ( x ) $$ \left\{{f}_1(x),{f}_2(x),\dots, {f}_m(x)\right\} $$ . In multiobjective optimization, a unique, universally optimal solution that simultaneously optimizes all objectives is not feasible. This is where Multiobjective Evolutionary Algorithms (MOEAs) excel, as they are adept at identifying a set of potentially optimal solutions for such complex problems. A solution is deemed Pareto optimal if no other solution dominates it. The collective set of all these Pareto optimal solutions forms the Pareto set (PS), and the corresponding set of their objective vectors is known as the Pareto Front (PF) shown in Figure 1.
Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Many-objective all definitions in the search space of the MaO-problem.

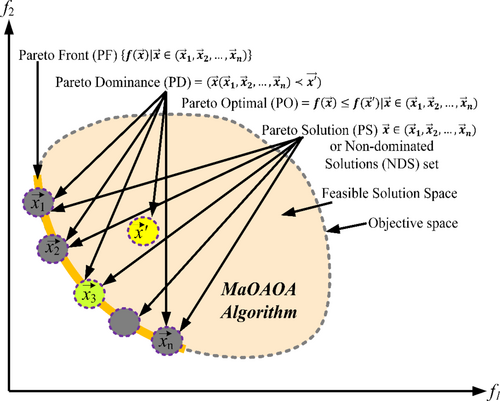
In the last few decades, the development of MOEAs [5] has been impressive. Although these algorithms are useful in solving MOPs [6], they cannot efficiently solve MOPs with more than three objectives [7], also known as MaOPs [8]. A critical issue in MaOPs is the reduction of the effectiveness of dominance concepts in separating solutions when the number of objectives is high. This leads to less selection pressure in Pareto-dominance-based MOEAs, which causes poor convergence in MaOPs. Another challenge is to closely approximate the entire Pareto front (PF) using a finite set of solutions in a high-dimensional objective space. To address these concerns, numerous methods have been proposed to improve the performance of MOEAs in solving MaOPs and can be classified into four main categories.

The first group is dominance-based MOEAs. For MaOPs, most traditional Pareto dominance methods such as NSGA-II [9] and SPEA2 [10] are not very efficient. New dominance relations have been developed, for example, ε-dominance [11], α-dominance [12], and fuzzy-dominance [13]. For example, in [14], a grid dominance-based method was proposed that incorporated three fitness assignment criteria to enhance selection pressure. Yuan et al. [15] employed θ-dominance in order to improve the convergence rate. Furthermore, a ranking-dominance method was proposed in [16], where the solutions are ranked based on each objective with respect to Pareto dominance, which helps in differentiating between solutions and guiding the search toward the Pareto front. Li et al. [17] proposed a multi-indicator algorithm that used a new stochastic ranking to address this issue. Qiu et al. [18] proposed a fractional dominance relation in which dominance was quantified by a fraction. These changes in dominance relations aid in avoiding local optima and accelerating convergence by eliminating the dominance-resistant solutions [19].

However, these adaptations also present some problems to MOEAs, for example, loss of diversity or failure to find solutions near the PF boundary [20]. Furthermore, the performance of density estimators such as crowding distance degrades when the problem has three or more objectives. To overcome these difficulties, new dominance relations such as SDE [21], DMO [22], and I varepsilon + $$ {I}_{varepsilon+} $$ [23] have been proposed.

This is the second category in the family of Multiobjective Evolutionary Algorithms (MOEAs) and is referred to as the indicator-based approach. Some of the indicators in this category include the IGD-NS used in AR-MOEA [24] and the nadir point estimation method in MaOEA/IGD [25]. Other important examples are the S-metric selection-based method (SMS-EMOA) [26], the indicator-based evolutionary algorithm (IBEA) [27], and the Lebesgue indicator-based LIBEA [28]. DNMOEA/HI [29] proposed a dynamic neighborhood MOEA that employed the HV [30] to estimate the HV of a single solution by using slicing. Bader et al. [31] proposed a fast search technique based on Monte Carlo simulations to estimate the exact HV values. Although these algorithms are useful, they encounter the issue of high computational time when determining the exact HV in many-objective problems (MaOPs). In [32], a new metric was proposed to measure the influence of a subspace on solutions, namely the population forward distance pushed by solutions from this subspace.

The third category is the decomposition-based approaches. These strategies use a “divide and conquer” approach in which a MOP is divided into a number of sub-MOPs to be solved successively. MOEA/D [33], Many-objective evolutionary algorithm based on decomposition with dynamic random weights (MOEA/D-DRW) [34], Many-Objective Teaching Learning Based Optimizer (MaOTLBO) [35], Many-Objective Particle Swarm Optimizer (MaOPSO) [36], Non-Dominated Sorting Genetic Algorithm-III (NSGA-III) [37], and many other algorithms that have followed [38, 39]. In [40], an angle penalized distance (APD) scalarization approach was employed to control the convergence and the diversity of solutions. Liu et al. [41] divided the problem into subproblems and solved each subproblem through collaboration with the intent of maintaining the population diversity. In [42], a surrogate-assisted, reference vector guided algorithm was proposed for solving MaOPs with reduced computational complexity. DMaOEA-εC [43] proposes a dual-update approach to maintain boundary solutions in a series of decomposed sub-problems. In [44], measures that include dual reference points and multiple search directions were proposed to ensure that high-performance populations are maintained even if the PF shape is unknown. The decomposition-based MOEAs have gained considerable attention since the introduction of MOEA/D in the past decade; however, their performance depends on the predefined reference vectors and chosen aggregation functions, which gives rise to uncertainty regarding the efficiency of these approaches for different problems.

In addition to the three categories of Multiobjective Evolutionary Algorithms (MOEAs) [45] that have been discussed earlier, there is another category focusing on many-objective problems (MaOPs) [46], and some of the algorithms that fall into this category include those described in [47]. For instance, Li et al. [48] used two archives in the evolutionary process: one for improving convergence and the other for diversity. Another attempt has been made in [49], where the external archive steered the search pattern and a method called balanceable fitness estimation (BFE) was proposed to enhance the selection pressure towards the true Pareto Front (PF). Wang et al. proposed a set of algorithms [50, 51], called PICEAs, which incorporate preference information from decision makers to support the construction of approximation sets. Moreover, Li et al. [52] introduced a meta-objective optimization approach that treats many-objective problems as bi-objective optimization problems with goals on proximity and diversity.

Numerous research studies have investigated MaOPs, paying attention to convergence and diversity but neglecting how each decision variable affects these objectives. In other words, previous approaches mainly modeled decision variables in an aggregate sense without regard for their disaggregation. However, recent studies [53, 54] have suggested that the effect of decision variables on convergence and diversity is not deterministic. This realization provides a way of identifying the nature of each decision variable and classifying it before the optimization stage. Hence, algorithms can then focus on certain decision variables to speed up convergence or increase diversity. Consequently, our approach attempts to reduce the complexity of the optimization of MaOPs by categorizing decision variables in advance in order to enhance the results.

Recent studies in large-scale optimization show that the characteristics of each decision variable play a crucial role in determining the final convergence and solution space. For example, MOEA/DVA [55] proposed a non-dominated sorting-based decision variables classification (DVC) that classified variables based on the relative size of the non-dominated fronts of the population for each variable. In LMEA [56], solution samples are generated by changing the value of each variable, and decision variable grouping is done based on the angle between each variable's fitted solution line and the hyperplane normal line. These methods help in the simplification of the optimization problem by dividing the decision variables into different categories. After DVC, variables are categorized as convergence-oriented, diversity-oriented, or both. Nevertheless, the dominance-based method in MOEA/DVA might provide imprecise variable classifications due to its application in large-scale optimization using DVC approaches [57]. Many-objective optimization problems (MaOPs) present increased interest among researchers because they require comprehensive study in engineering along with economics and decision-making systems. Traditional multi-objective optimization algorithms fail to achieve adequate convergence-diversity balance as object numbers increase, so researchers created specialized advanced evolutionary algorithms for MaOPs. Three different strategies have emerged to boost the performance of EAs when handling complex problems: strengthened dominance relations [58], adaptive neighborhood-based selection mechanisms [59] and adaptive mating with environmental selection [60]. The research continues to focus on maintaining diversity within high-dimensional objective spaces and achieving convergence to the true Pareto front because these challenges persist despite recent algorithmic advancements.

For this purpose, a new method is proposed for a better balance between convergence and diversity in many-objective optimization: Arithmetic Optimization Algorithm (AOA) [61], Information Feedback Mechanism, Reference Point-Based Selection and Association, Non-dominated Sorting, Niche Preservation, and Density Estimation-based Many-Objective Arithmetic Optimization Algorithm (MaOAOA). For generating offspring, a new IFM technique is introduced for utilizing this historical information, which increases the chances of getting good solutions and also speeds up the convergence of the population.

The Arithmetic Optimization Algorithm (AOA) demonstrates superior performance compared to traditional genetic and differential evolution operators when addressing many-objective optimization problems because of multiple important factors. AOA's foundation in simple arithmetic operations—addition, subtraction, multiplication, and division—offers a significant advantage in terms of computational efficiency. AOA succeeds over related optimization approaches that require complex algorithms through its simple approach that minimizes computational demands. The ability to handle high-dimensional many-objective problems relies heavily on fast and effective search space exploration because of this efficiency.

AOA demonstrates a remarkable strength because it automatically controls exploration and exploitation dynamics, which are vital to optimization algorithms. Basic mathematical operations in AOA maintain the balance automatically because multiplication and division create broad exploration through large search space jumps, yet addition and subtraction enable precise solution refinement for improved exploitation. Many-objective optimization requires this dual ability because it struggles to maintain population diversity while reaching the Pareto front. GAs and DE need careful parameter adjustment to achieve an equivalent exploration-exploitation balance, but this process requires both extensive time investment and problem-specific expertise. The MaOAOA framework reaches higher effectiveness through its implementation of an Information Feedback Mechanism (IFM). The search procedure uses historical information from previous runs to guide its operations while maintaining both promising solutions and their effective application across generations. The Information Feedback Mechanism in MaOAOA uses historical data through population-based approaches for many-objective optimization but remains specifically designed for this optimization challenge. The feature serves as a fundamental part in preserving solution diversity while fighting against premature convergence, which regularly slows down traditional evolutionary algorithms in intricate optimization situations.

The proposed reference-based selection approach in Many-Objective Arithmetic Optimization Algorithm (MaOAOA) stands out because it combines reference points with niche preservation and Information Feedback Mechanism (IFM) to achieve balance between convergence and diversity for many-objective optimization problems (MaOPs). The proposed approach surpasses traditional reference-based methods since it uses Euclidean distance to dynamically match solutions with reference points for better Pareto front exploration efficiency. The approach both leads solutions towards the true Pareto front and maintains diversity through uniform distribution of solutions across the objective space. The addition of niche preservation maintains boundary solutions while preventing overcrowding of specific areas, which leads to a uniform distribution of the Pareto front. Through historical information, the IFM enhances its selection procedure, which accelerates search convergence while simultaneously improving area exploration efficiency. The combined mechanisms in this approach solve existing reference-based method weaknesses by maintaining diversity and achieving better convergence in high-dimensional objective spaces, which results in enhanced robustness and effectiveness for solving complex MaOPs.

The key contributions of this paper are:
  1. The choice of AOA algorithms is due to their effectiveness in producing diverse and quality solutions in single-objective problems. The above operator selection is beneficial to the MaOAOA's ability to explore and exploit the search space due to the global search capability of AOA.
  2. The paper proposes an Information Feedback Mechanism (IFM) approach to address the shortcomings that have led to the loss of valuable information. In the IFM, the combined historical information of individuals using the weighted sum method is passed on to the next generation. This guarantees that better convergence is achieved.
  3. A reference point-based selection approach is followed to select the solutions so that the selected solutions are not only near the true Pareto-optimal front (convergence) but also distributed over the entire Pareto-optimal front (diversity), linking each solution to the closest reference point based on the Euclidean distance and determining regions in the objective space with a high density of solutions. The non-dominated sorting approach helps the algorithm focus on the solutions that are closer to the Pareto front, which helps in convergence.
  4. A niche preservation approach for boundary solutions is introduced to enhance the population diversity and eliminate those solutions that are likely to congest certain areas of the objective space, thereby enhancing the convergence speed of the algorithm. Moreover, a method for density estimation for diversity preservation is described, which guarantees both uniform density and widespread population across the area.
  5. The performance of the proposed MaOAOA is tested against MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW using the MaF1-MaF15 benchmark sets with four, seven, and nine objectives, and five real-world problems, namely RWMaOP1-RWMaOP5. Overall, the results of these experiments show that MaOAOA is able to solve a variety of problems effectively, which supports its effectiveness.

The remainder of the paper is structured as follows: Section 2 introduces the AOA algorithm, Section 3 explains the proposed MaOAOA algorithm, Section 4 presents the results and evaluations, and Section 5 concludes the paper.

2 Arithmetic Optimization Algorithm

Recently, a fresh meta-heuristic technique known as the Arithmetic Optimization Algorithm (AOA) was unveiled [61]. This algorithm incorporates four principal mathematical operations: Addition ( A ) $$ (A) $$ , subtraction ( S ) $$ (S) $$ , division ( D ) $$ (D) $$ , and multiplication ( M ) $$ (M) $$ . These operations are crucial in refining both the exploitation and exploration stages within the AOA framework. However, an initial step in the AOA process is determining the search mechanism. This involves selecting a search area, guided by the Math Optimizer Accelerated (MOA) function, which is defined by a specific coefficient, detailed in Equation (2).
MOA ( t ) = Min + t × Max − Min T $$ MOA(t)=\mathit{\operatorname{Min}}+t\times \left(\frac{\mathit{\operatorname{Max}}-\mathit{\operatorname{Min}}}{T}\right) $$ (2)

This equation MOA ( t ) $$ MOA(t) $$ factors in the functional value at a particular t th $$ {t}^{th} $$ iteration, alongside the T $$ T $$ and t $$ t $$ maximum and current number of iterations. The coefficient t $$ t $$ ranges between [1 T $$ T $$ ], while Max $$ \mathit{\operatorname{Max}} $$ and Min $$ \mathit{\operatorname{Min}} $$ represent the lower and upper limits of the accelerated function's values.

AOA is noted for its straightforward configuration and its efficiency in computational processing. As the algorithm progresses iteratively, it employs arithmetic operations to pinpoint potential optimal solutions. Notably, multiplication ( M ) $$ (M) $$ and division ( D ) $$ (D) $$ are key in creating significant iteration leaps, ( M ) $$ (M) $$ and ( D ) $$ (D) $$ primarily used in the exploration phase, as depicted in Equation (3).
X ( t + 1 ) = X best ( t ) ÷ ( MOP + eps ) × ( ( UB − LB ) × μ + LB ) , r 2 < 0.5 X best ( t ) × MOP × ( ( UB − LB ) × μ + LB ) , else $$ X\left(t+1\right)=\left\{\begin{array}{l}{X}_{best}(t)\div \left( MOP+ eps\right)\times \left(\left( UB- LB\right)\times \mu + LB\right),\kern1.5em {r}_2<0.5\\ {}{X}_{best}(t)\times MOP\times \left(\left( UB- LB\right)\times \mu + LB\right),\kern4.5em else\end{array}\right. $$ (3)
Here, eps $$ eps $$ involves a minor integer, and μ $$ \mu $$ a specially tailored constant coefficient of 0.499 for this specific algorithm. Another aspect of MOP $$ MOP $$ is the Math Optimizer Probability, representing a coefficient that decreases non-linearly from 1 to 0 over successive t th $$ {t}^{th} $$ iterations. This dynamic is formulated in Equation (4)
MOP = 1 − t T 1 / α $$ MOP=1-{\left(\frac{t}{T}\right)}^{1/\alpha } $$ (4)
where α $$ \alpha $$ is set as a fixed value of 5. Based on the insights derived from Equation (3), it is apparent that multiplication ( M ) $$ (M) $$ and division ( D ) $$ (D) $$ are effectively utilized during the search phase. In contrast, the subtraction ( S ) $$ (S) $$ and addition ( A ) $$ (A) $$ operations focus on local exploitation, generating smaller movements within the search area. These two operations are mathematically articulated for the exploitation phase in Equation (5).
X ( t + 1 ) = X best ( t ) − MOP × ( ( UB − LB ) × μ + LB ) , r 3 < 0.5 X best ( t ) + MOP × ( ( UB − LB ) × μ + LB ) , else $$ X\left(t+1\right)=\left\{\begin{array}{l}{X}_{best}(t)- MOP\times \left(\left( UB- LB\right)\times \mu + LB\right),\kern1.5em {r}_3<0.5\\ {}{X}_{best}(t)+ MOP\times \left(\left( UB- LB\right)\times \mu + LB\right),\kern1.5em else\end{array}\right. $$ (5)

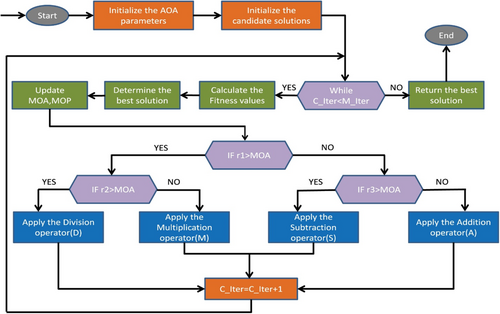
The flowchart of the AOA is shown as Figure 2.

Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Flowchart of the AOA optimizer.

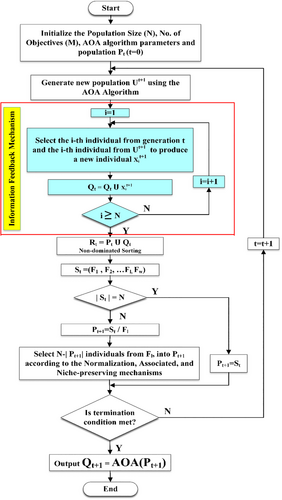
3 Proposed Many-Objective Arithmetic Optimization Algorithm (MaOAOA)

MaOAOA algorithm starts with a random population of size N $$ N $$ , M $$ M $$ no. of objectives, p $$ p $$ no. of partitions and generate a set of reference points using Das and Dennis's technique H = M + p − 1 p $$ H=\left(\begin{array}{l}M+p-1\\ {}p\end{array}\right) $$ , as H ≈ N $$ H\approx N $$ . the current generation is t , x i t $$ t,{x}_i^t $$ and x i t + 1 $$ {x}_i^{t+1} $$ the i $$ i $$ -th individual at t $$ t $$ and ( t + 1 ) $$ \left(t+1\right) $$ generation. u i t + 1 $$ {u}_i^{t+1} $$ the i $$ i $$ -th individual at the ( t + 1 ) $$ \left(t+1\right) $$ generation generated through the AOA algorithm and parent population P t $$ {P}_t $$ . the fitness value of u i t + 1 $$ {u}_i^{t+1} $$ is f i t + 1 $$ {f}_i^{t+1} $$ and U t + 1 $$ {U}^{t+1} $$ is the set of u i t + 1 $$ {u}_i^{t+1} $$ . Then, we can calculate x i t + 1 $$ {x}_i^{t+1} $$ according to u i t + 1 $$ {u}_i^{t+1} $$ generated through the AOA algorithm and information feedback mechanism (IFM) Equation (6).
x i t + 1 = ∂ 1 u i t + 1 + ∂ 2 x k t ; ∂ 1 = f k t f i t + 1 + f k t , ∂ 2 = f i t + 1 f i t + 1 + f k t , ∂ 1 + ∂ 2 = 1 $$ {x}_i^{t+1}={\partial}_1{u}_i^{t+1}+{\partial}_2{x}_k^t;{\partial}_1=\frac{f_k^t}{f_i^{t+1}+{f}_k^t},{\partial}_2=\frac{f_i^{t+1}}{f_i^{t+1}+{f}_k^t},{\partial}_1+{\partial}_2=1 $$ (6)
where x k t $$ {x}_k^t $$ is the k $$ k $$ th individual we chose from the t $$ t $$ th generation, the fitness value of x k t $$ {x}_k^t $$ is f k t , ∂ 1 $$ {f}_k^t,{\partial}_1 $$ and ∂ 2 $$ {\partial}_2 $$ are weight coefficients. Generate offspring population Q t $$ {Q}_t $$ . Q t $$ {Q}_t $$ is the set of x i t + 1 . $$ {x}_i^{t+1}. $$ The combined population R t = P t ∪ Q t $$ {R}_t={P}_t\cup {Q}_t $$ is sorted into different w-non-dominant levels F 1 , F 2 , … , F l … , F w $$ \left({F}_1,{F}_2,\dots, {F}_l\dots, {F}_w\right) $$ . Begin from F 1 $$ {F}_1 $$ , all individuals in level 1 to l $$ l $$ are added to S t $$ {S}_t $$ and remaining members of R t $$ {R}_t $$ are rejected. If S t = N $$ \left|{S}_t\right|=N $$ ; no other actions are required, and the next generation is begun with P t + 1 = S t $$ {P}_{t+1}={S}_t $$ . Otherwise, solutions in S t / F l $$ {S}_t/{F}_l $$ are included in P t + 1 = S t / F l $$ {P}_{t+1}={S}_t/{F}_l $$ and the rest K = N − P t + 1 $$ \left(K=N-\left|{P}_{t+1}\right|\right) $$ individuals are selected from the last front F l $$ {F}_l $$ (presented in Algorithm 1). For selecting individuals from F l $$ {F}_l $$ , we use a niche-preserving operator First, each population member of P t + 1 $$ {P}_{t+1} $$ and F l $$ {F}_l $$ is normalized (presented in Algorithm 2) by using the current population spread so that all objective vectors and reference points have commensurate values. Thereafter, each member of P t + 1 $$ {P}_{t+1} $$ and F l $$ {F}_l $$ is associated (presented in Algorithm 3) with a specific reference point by using the shortest perpendicular distance ( d ) $$ (d) $$ of each population member with a reference line created by joining the origin with a supplied reference point. Then, a careful niching strategy (described in Algorithm 5) that improve the diversity of MaOAOA algorithm is employed to choose those F l $$ {F}_l $$ members that are associated with the least represented reference points niche count ρ i $$ {\rho}_i $$ in P t + 1 $$ {P}_{t+1} $$ and check termination condition is met. If the termination condition is not satisfied, t = t + 1 $$ t=t+1 $$ than repeat, and if it is satisfied, P t + 1 $$ {P}_{t+1} $$ is generated, it is then applied to generate a new population Q t + 1 $$ {Q}_{t+1} $$ by AOA algorithm. Such a careful selection strategy is found to computational complexity of M $$ M $$ -Objectives O N 2 log M − 2 N $$ O\left({N}^2{\log}^{M-2}N\right) $$ or O N 2 M $$ O\left({N}^2M\right) $$ , whichever is larger (Algorithm 4).

ALGORITHM 1. Generation t of MaOAOA algorithm with IFM procedure.

Input: N (Population Size), M (No. of Objectives), AOA algorithm parameters, and Initial population Pt(t = 0)

Output: Qt+1 = AOA(Pt+1)

1: H Calculated using Das and Dennis's technique, structured reference points Zs, supplied aspiration points Za, St = ϕ, i = 1

2: Proposed Information Feedback Mechanism (IFM)

AOA algorithm apply on the initial population Pt to generate u i t + 1 $$ {u}_i^{t+1} $$ , calculate x i t + 1 $$ {x}_i^{t+1} $$ according to u i t + 1 $$ {u}_i^{t+1} $$ can be expressed as follows:

x i t + 1 = ∂ 1 u i t + 1 + ∂ 2 x k t $$ {x}_i^{t+1}={\partial}_1{u}_i^{t+1}+{\partial}_2{x}_k^t $$ ; ∂ 1 = f k t f i t + 1 + f k t $$ {\partial}_1=\frac{f_k^t}{f_i^{t+1}+{f}_k^t} $$ , ∂ 2 = f i t + 1 f i t + 1 + f k t $$ {\partial}_2=\frac{f_i^{t+1}}{f_i^{t+1}+{f}_k^t} $$ , ∂1 + ∂2 = 1

Qt = Qt; (Qt is the set of x i t + 1 $$ {x}_i^{t+1} $$ )

3: Rt = Pt ∪ Qt

4: Different non-domination levels (F1, F2, …, Fl) = Non-dominated-sort (Rt)

5: repeat

6:  St = St ∪ Fi and i = i + 1

7: until | St | ≥ N

8:  Last front to be included: F l = ∪ i = 1 l F i $$ {F}_l={\cup}_{i=1}^l{F}_i $$

9: if | St | = N then

10:  Pt+1 = St

11: else

12:  Pt+1 = St/Fl

13:  Point to chosen from last Front (Fl): K = N – |Pt+1|

14:  Normalize objectives and create reference set Zr: Normalize (fn, St, Zr, Zs, Za); Brief Explanation in Algorithm-2

15:  Associate each member s of St with a reference point: [π(s), d(s)] = Associate (St, Zr); Brief Explanation in Algorithm-3% π(s): closest reference point, d: distance between s and π(s)

16:  Compute niche count of reference point j ∈ Zr: ρ j = ∑ s ∈ s t / F l ( ( π ( s ) = j ) , 1 : 0 ) $$ {\boldsymbol{\rho}}_{\boldsymbol{j}}={\sum}_{\boldsymbol{s}\in {\boldsymbol{s}}_{\boldsymbol{t}}/{\boldsymbol{F}}_{\boldsymbol{l}}}\left(\left(\boldsymbol{\pi} \left(\boldsymbol{s}\right)=\boldsymbol{j}\right),\mathbf{1}:\mathbf{0}\right) $$ ;

17:  Choose K members one at a time Fl to construct

Pt+1: Niching(K, ρj, π, d, Zr, Fl, Pt+1); Represent in Algorithm-4

18: end if

ALGORITHM 2. Normalize (fn, St, Zr, Zs/Za) procedure.

Input: St, Zs (structured points) or Za (supplied points)

Output: fn, Zr (reference points on normalized hyper-plane)

1: for j = 1 to M do

2:  Compute ideal point: Z j min = min s ∈ s t f j ( s ) $$ {Z}_j^{min}={\mathit{\min}}_{s\in {s}_t}{f}_j(s) $$

3:  Translate objectives: f j ′ ( s ) = f j ( s ) − Z j min ∀ s ∈ S t $$ {f}_j^{\prime }(s)={f}_j(s)-{Z}_j^{min}\forall s\in {S}_t $$

4:  Compute extreme points: Zj,max = s:

    argmin s ∈ s t ASF s , w j $$ {\mathrm{argmin}}_{s\in {s}_t} ASF\left(s,{w}^j\right) $$ = where wj = (∈1, …, ∈j)t),

   ∈ = 10−6, and w j j = 1 $$ {w}_j^j=1 $$

5: end for

6: Compute intercepts aj for j = 1, …, M

7: Normalize objectives f i n ( X ) $$ {f}_i^n(X) $$ using

   f i n ( X ) = f i ′ ( X ) a i − Z i min , for i = 1 , 2 , … . , M $$ {f}_i^n(X)=\frac{f_i^{\prime }(X)}{a_i-{Z}_i^{min}}, for\;i=1,2,\dots .,M $$

8: if Za is given then

9:  Map each (aspiration) point on normalized hyper-plane f i n ( X ) $$ {f}_i^n(X) $$ and save the points in the set Zr

10: else

11:  Zr = ZS

12: end if

ALGORITHM 3. Associate (St, Zr) procedure.

Input: St, Zr

Output: π(s ∈ st), d(s ∈ st)

1: for each reference point Z Zr do

2:  Compute reference line w = z

3: end for

4: for each (s ∈ st) do

5:  for each w Zr do

6:   Compute d⊥ (s, w) = s – wTs/|| w ||

7:  end for

8: Assign π(s) = w: argmin W ∈ Z r d ⊥ ( s , w ) $$ {argmin}_{W\in {Z}^r}{d}^{\perp}\left(s,w\right) $$

9: Assign d(s) = d⊥(s, π(s))

10: end for

ALGORITHM 4. Niching (K, ρj, π, d, Zr, Fl, Pt+1) procedure.

Input: K, ρj, π(s ∈ St), d(s ∈ St), Zr, Fl,

Output: Pt+1

1: k = 1

2: while k ≤ K do

3:   J min = j : argmin j ∈ Z r ρ j $$ {J}_{min}=\left\{j:{argmin}_{j\in {Z}^r}{\rho}_j\right\} $$

4:   j ‾ = random J min $$ \overline{j}= random\left({J}_{min}\right) $$

5:   I j ‾ = s : π ( s ) = j ‾ , s ∈ F l $$ {I}_{\overline{j}}=\left\{s:\pi (s)=\overline{j},s\in {F}_l\right\} $$

6:  if I j ‾ ≠ ϕ $$ {I}_{\overline{j}}\ne \phi $$ then

7:   if ρ j ‾ = 0 $$ {\rho}_{\overline{j}}=0 $$ then

8:    P t + 1 = P t + 1 ∪ s : argmin s ∈ I j ‾ d s $$ {P}_{t+1}={P}_{t+1}\cup \left(s:{argmin}_{s\in {I}_{\overline{j}}}{d}_s\right) $$

9:   else

10:    Pt+1 = Pt+1 ∪ random I j ‾ $$ \left({I}_{\overline{j}}\right) $$

11:   end if

12:    ρ j ‾ = ρ j ‾ + 1 , F l = F l / s $$ {\rho}_{\overline{j}}={\rho}_{\overline{j}}+1,{F}_l={F}_l/s $$

13:   k = k + 1

14:  else

15:    Z r = Z r / { j ‾ } $$ {Z}^r={Z}^r/\left\{\overline{j}\right\} $$

16:  end if

17: end while

The flow chart of the MaOAOA algorithm can be shown in Figure 3.

Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
Flowchart of MaOAOA algorithm.

4 Results and Discussion

4.1 Experimental Settings

4.1.1 Benchmarks

In order to verify the effectiveness of the MaOAOA, the MaF1-MaF15 [62] benchmark and five real world engineering design are Car cab design (RWMaOP1) [63], 10-bar truss structure (RWMaOP2) [64], Water and oil repellent fabric development (RWMaOP3) [65], Ultra-wideband antenna design (RWMaOP4) [66], and Liquid-rocket single element injector design (RWMaOP5) [67] problems are used in this paper. The number of decision variables for the MaF problems is k + M − 1 $$ k+M-1 $$ , M $$ M $$ is the number of objective functions. k $$ k $$ is set to 10 in MaF1- MaF6, k $$ k $$ is set to 20 in MaF7-MaF15.

4.1.2 Comparison Algorithms and Parameter Settings

In this study, the performance of MaOAOA by empirically comparing it with some state-of-the-art MOAs for MaOPs, namely, MaOPSO [36], MaOTLBO [35], MOEA/D-DRW [34], and NSGA-III [37], will be verified. The experiments are conducted on a Matlab R2020a environment on an Intel Core (TM) i7-9700 CPU. Each algorithm performs 30 times, the size of population N $$ N $$ is set to N = 210 , 156 $$ N=210,156 $$ and 276 $$ 276 $$ for all of the involved algorithms on M = 4 , 7 , $$ M=4,7, $$ and 9 $$ 9 $$ objectives problems.

4.1.3 Performance Measures

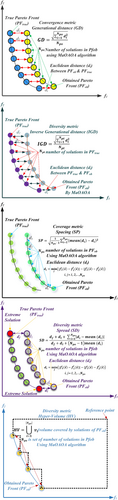
This paper adopts Generational distance ( GD ) $$ (GD) $$ , Spread ( SD ) $$ (SD) $$ , Spacing ( SP ) $$ (SP) $$ , Run Time ( RT ) $$ (RT) $$ , Inverse Generational distance ( IGD ) $$ (IGD) $$ , and Hypervolume ( HV ) $$ (HV) $$ quality indicator [68], shown in Table 1 and Figure 4.

TABLE 1. Properties of the quality indicators.
Quality indicator [40] Convergence $$ \mathrm{Convergence} $$ Diversity $$ \mathrm{Diversity} $$ Uniformity $$ \mathrm{Uniformity} $$ Cardinality $$ \mathrm{Cardinality} $$ Computational burden
GD $$ \mathrm{GD} $$ ✓
SD $$ \mathrm{SD} $$ ✓
SP $$ \mathrm{SP} $$ ✓
RT $$ \mathrm{RT} $$ ✓
IGD $$ \mathrm{IGD} $$ ✓ ✓ ✓
HV $$ \mathrm{HV} $$ ✓ ✓ ✓ ✓
Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Schematic view of the metrics.

4.2 Experimental Results on MaF Problems

Table 2 shows the GD (Generational Distance) values of diverse numbers of algorithms, including MaOAOA, for different problems of MaF. The findings presented here also reveal that MaOAOA is consistently able to outperform most of its counterparts successfully in all the test problems. More specifically, the lowest mean GD is obtained by MaOAOA in 25 of 40 cases provided, which indicates the efficiency and effectiveness of MaOAOA in the optimization of problems. For problem in the MaF1 problem with 4 objectives, MaOAOA has a GD of 2.1104e−3 (std 1. 47e −4) compared with other algorithms such as MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW, which have higher mean GD values. The same is true for other problems such as MaF2, MaF3, and so on, where MaOAOA is either among the best or highly competitive with the other best algorithms. Percentages of test problems in which MaOAOA performed significantly better than its competitors are impressive. For instance, MOEA/D-DRW Solves 3, 4, 10, and 3 test problems against MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW, respectively. Taken together, these findings indicate that MaOAOA is a sound and fast approach for solving many-objective optimization, especially within the tested MaF problem contexts. Therefore, based on the analysis of the GD metrics of various MaF problems presented in this work, it is possible to conclude the efficiency of the MaOAOA in achieving lower mean GD values, thus providing a better approximation of the Pareto front presented in Figure 5.

TABLE 2. Results of GD metric on MaF problems.
Problem M D MaOAOA MaOTLBO NSGA-III MaOPSO MOEA/D-DRW
MaF1 4 13 2.1104e-3 (1.47e-4) = 3.3960e-3 (6.91e-4) = 3.4127e-3 (5.48e-4) = 2.4447e-3 (3.98e−5) = 2.9178e-3 (5.09e-4)
7 16 6.2835e-3 (7.03e-5) = 7.2419e-3 (7.63e-5) = 7.1347e-3 (3.64e-4) = 1.6140e-2 (1.19e-3) = 1.5660e-2 (3.10e-3)
9 18 9.4652e-3 (4.59e-4) = 1.1985e-2 (1.48e-3) = 1.1584e-2 (5.24e-4) = 1.8481e-2 (1.25e-3) = 3.0776e-2 (6.74e-3)
MaF2 4 13 5.7950e-3 (3.17e-4) = 5.4511e-3 (6.55e-5) = 5.0252e-3 (1.97e-4) = 4.2282e-3 (4.33e-5) = 7.8706e-3 (3.54e-4)
7 16 7.9830e-3 (7.65e-4) = 9.1045e-3 (3.24e-4) = 1.0430e-2 (9.99e-4) = 1.0316e-2 (4.93e-4) = 1.0757e-2 (3.04e-4)
9 18 9.7575e-3 (8.73e-5) = 1.1869e-2 (1.35e-3) = 1.3228e-2 (1.61e-3) = 1.2468e-2 (5.46e-4) = 1.1445e-2 (2.52e-4)
MaF3 4 13 2.0533e+3 (2.24e+3) = 3.8051e+7 (6.59e+7) = 1.8480e+7 (3.20e+7) = 2.4526e+3 (3.26e+3) = 7.6066e+4 (9.75e+4)
7 16 8.2936e+5 (1.19e+6) = 1.2158e+9 (6.18e+8) = 1.2264e+9 (1.55e+9) = 7.7407e+6 (1.31e+7) = 6.5988e+11 (2.48e+11)
9 18 1.1559e+5 (1.58e+5) = 6.9754e+9 (3.26e+9) = 1.1141e+9 (5.14e+8) = 2.1416e+8 (1.98e+8) = 9.6543e+11 (1.20e+11)
MaF4 4 13 2.9809e+1 (2.23e+1) = 1.6453e+1 (4.21) = 3.0013e+1 (3.62e+1) = 1.8436e+1 (8.66) = 1.0359e+1 (4.93)
7 16 1.2879e+2 (6.61e+1) = 1.9325e+2 (1.62e+2) = 2.4089e+2 (2.48e+2) = 1.6198e+2 (2.06e+1) = 3.5702e+2 (2.08e+2)
9 18 4.1632e+2 (4.37e+2) = 8.5065e+2 (2.89e+2) = 4.1071e+2 (1.06e+2) = 5.2419e+2 (1.29e+2) = 1.0700e+3 (6.66e+2)
MaF5 4 13 1.6897e-2 (7.63e-4) = 1.6742e-2 (9.14e-4) = 1.7690e-2 (6.46e-4) = 1.9792e-2 (2.68e-3) = 2.5647e-2 (9.55e-3)
7 16 1.7582e-1 (1.45e-2) = 2.4160e-1 (4.14e-2) = 2.2443e-1 (2.32e-2) = 4.2382e-1 (2.16e-2) = 1.2903e+1 (4.53e-1)
9 18 5.3772e-1 (7.29e-2) = 1.5892 (1.70e-1) = 1.6785 (6.26e-2) = 1.6710 (4.03e-1) = 5.5891e+1 (1.83)
MaF6 4 13 2.0336e-4 (3.75e-5) = 2.2272e-4 (4.25e-5) = 2.6528e-4 (9.13e-5) = 1.0522e-4 (6.09e-5) = 1.0149e-4 (1.67e-5)
7 16 1.0910e-4 (3.38e-5) = 1.6020e-3 (2.18e-3) = 3.0383e-4 (1.08e-4) = 2.1709e-4 (1.18e-4) = 2.0719e-4 (2.44e-5)
9 18 3.8002 (6.58) = 3.9498 (6.84) = 1.3385e+1 (2.07) = 2.4791e-4 (2.18e-4) = 1.2038e+1 (1.06e+1)
MaF7 4 23 1.2381e-2 (1.54e-3) = 1.9043e-2 (4.13e-3) = 1.9830e-2 (6.53e-3) = 2.2985e-2 (4.11e-3) = 2.2675e-2 (2.70e-3)
7 26 1.4402e-1 (3.92e-2) = 2.2478e-1 (5.99e-2) = 2.0591e-1 (2.07e-2) = 1.6471e-1 (2.02e-2) = 1.2667 (4.01e-1)
9 28 4.1411e-1 (4.19e-2) = 6.9940e-1 (2.87e-1) = 5.7916e-1 (1.68e-1) = 3.5032e-1 (8.30e-2) = 3.5031 (2.78e-1)
MaF8 4 2 9.1858e-3 (6.12e-3) = 2.9548e-2 (1.37e-2) = 1.6400e-1 (2.52e-1) = 6.0783e-1 (1.03) = 1.6417e-2 (1.06e-2)
7 2 1.4386e-2 (9.11e-3) = 1.8369e-2 (5.47e-3) = 1.9376e-2 (1.77e-2) = 1.4849e-2 (6.55e-3) = 2.0835e-1 (2.67e-1)
9 2 2.9481e-2 (9.63e-3) = 3.2614e-2 (2.44e-2) = 9.7182e-2 (1.17e-1) = 8.5024e-1 (7.34e-1) = 1.3150e-1 (2.03e-1)
MaF9 4 2 7.2216e+1 (5.14e+1) = 3.8371e+1 (3.80e+1) = 6.9147e+2 (1.10e+3) = 8.5167e+1 (1.39e+2) = 1.4916e+2 (1.55e+2)
7 2 5.3796 (3.53) = 5.0597e+1 (5.03e+1) = 5.2369e+1 (5.95e+1) = 5.5310e+1 (6.12e+1) = 5.3948e+1 (1.05e+1)
9 2 1.0187e+1 (7.37) = 4.9183e+1 (5.23e+1) = 3.2216e+1 (1.30e+1) = 1.5520e+2 (2.58e+2) = 4.8777e+1 (7.37e+1)
MaF10 4 13 9.6896e-2 (4.53e-3) = 1.0025e-1 (1.23e-2) = 1.0330e-1 (3.60e-3) = 1.1138e-1 (3.13e-2) = 7.6227e-2 (9.92e-3)
7 16 1.6856e-1 (1.38e-2) = 1.8505e-1 (5.81e-3) = 1.6736e-1 (1.12e-2) = 1.9013e-1 (2.84e-2) = 2.0318e-1 (8.40e-3)
9 18 2.0281e-1 (1.25e-2) = 2.3818e-1 (3.66e-3) = 2.1879e-1 (1.10e-2) = 2.0598e-1 (2.81e-2) = 2.6088e-1 (1.47e-2)
MaF11 4 13 1.5881e-2 (2.17e-3) = 1.5590e-2 (1.53e-3) = 1.4402e-2 (8.26e-4) = 1.6219e-2 (2.89e-3) = 7.1762e-2 (2.34e-2)
7 16 5.0736e-2 (1.13e-2) = 5.9530e-2 (1.83e-3) = 5.8013e-2 (1.79e-2) = 3.2487e-2 (2.64e-3) = 2.2487e-1 (7.34e-2)
9 18 5.8691e-2 (9.02e-3) = 1.1207e-1 (1.58e-2) = 1.0238e-1 (4.19e-3) = 4.0236e-2 (2.55e-3) = 2.5525e-1 (2.86e-2)
MaF12 4 13 2.4821e-2 (2.42e-3) = 2.5499e-2 (2.31e-3) = 2.0724e-2 (1.09e-3) = 2.3225e-2 (2.77e-3) = 2.7580e-2 (3.44e-3)
7 16 1.0989e-1 (9.48e-3) = 1.1643e-1 (1.49e-2) = 1.2480e-1 (3.94e-3) = 1.3531e-1 (8.49e-3) = 1.8422e-1 (1.15e-2)
9 18 1.6290e-1 (5.91e-3) = 2.0399e-1 (1.02e-2) = 1.8184e-1 (4.78e-3) = 1.9349e-1 (2.30e-3) = 2.5627e-1 (8.43e-3)
MaF13 4 5 1.1726e+7 (2.03e+7) = 1.9077e+2 (1.62e+2) = 4.0699e+5 (6.02e+5) = 1.1973e+7 (8.62e+6) = 1.2163e+6 (2.04e+6)
7 5 2.2113e+7 (3.83e+7) = 1.5947e+5 (2.76e+5) = 1.2659e+7 (1.23e+7) = 1.0421e+1 (1.50e+1) = 1.3617e+7 (9.46e+6)
9 5 4.6744e+7 (8.09e+7) = 4.6208e+6 (7.57e+6) = 1.2245e+6 (1.11e+6) = 1.5392e+1 (2.28e+1) = 5.6436e+10 (9.77e+10)
MaF14 4 80 5.0480e+3 (2.31e+3) = 1.9514e+3 (8.63e+2) = 2.4514e+3 (1.51e+3) = 1.9377e+2 (1.89e+2) = 3.1390e+3 (5.36e+2)
7 140 9.9548e+2 (1.63e+3) = 2.3885e+3 (5.78e+2) = 2.3310e+3 (1.98e+2) = 3.9037e+2 (2.57e+2) = 3.0358e+4 (1.37e+3)
9 180 1.6523e+1 (2.04e+1) = 2.6717e+3 (6.88e+2) = 2.7080e+3 (3.35e+2) = 1.2530e+2 (1.82e+2) = 2.9475e+4 (5.65e+3)
MaF15 4 80 2.2965e-1 (1.13e-1) = 1.2940 (4.05e-1) = 1.7514 (2.65e-1) = 1.4857e-1 (1.76e-1) = 3.7305 (5.84e-1)
7 140 3.1473e-1 (3.67e-2) = 5.3401 (1.68) = 3.8200 (2.62) = 6.5808e-1 (2.50e-1) = 2.1297e+1 (1.77)
9 180 5.3207e-1 (8.57e-2) = 8.1769 (2.38) = 4.9703 (3.09) = 6.7357e-1 (6.32e-2) = 2.7439e+1 (1.55)
Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
Best Pareto optimal front on MaF problems.

Table 3 shows the IGD values for different algorithms and MaF problem instances, including MaOAOA. Interestingly, the proposed MaOAOA method demonstrates high performance in many problems and proves its effectiveness in many-objective optimization. In particular, MaOAOA stores the highest IGD values for a large number of the 40 test problems, pointing to its ability to provide a close approximation of the Pareto front. For the MaF1 problem with 4 objectives, MaOAOA has an IGD of 1. The results achieved are 0.519e-1/std. 1.84e-3, which can be considered optimal compared to other algorithms such as MaOTLBO, NSGA-III, and MaOPSO. This pattern of competitive or superior performance is evident in most of the MaF problems, showing that MaOAOA is consistent across the board. The percentages of test problems in which MaOAOA is much better than its rivals are significant. For example, the performance of MaOAOA is significantly higher than that of MaOTLBO in a large number of problems. Furthermore, a comparison of results shows that in a considerable number of cases, MaOAOA outperforms NSGA-III. As shown in Table 3, the IGD value compared with MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW, the proposed MaOAOA is better in 42, 43, 32, and 38 out of 45 cases. Some proportions, which will be discussed in detail in the full report, indicate that MaOAOA is a highly reliable and efficient many-objective optimization algorithm. It yields low mean IGD values consistently, which shows how it provides near-optimal solutions to the fronts presented in Figure 5.

TABLE 3. Results of IGD metric on MaF problems.
Problem M D MaOAOA MaOTLBO NSGA-III MaOPSO MOEA/D-DRW
MaF1 4 13 1.0519e-1 (1.84e-3) = 1.5408e-1 (1.73e-2) = 1.2888e-1 (6.25e-3) = 1.0164e-1 (8.12e-4) = 1.0064e-1 (9.47e-4)
7 16 2.2506e-1 (1.74e-3) = 2.4353e-1 (7.65e-4) = 2.4190e-1 (1.13e-2) = 2.7767e-1 (1.34e-2) = 2.4081e-1 (2.86e-3)
9 18 2.7118e-1 (7.21e-3) = 2.7960e-1 (9.33e-3) = 2.8377e-1 (7.79e-3) = 3.3319e-1 (3.09e-2) = 3.3075e-1 (5.76e-3)
MaF2 4 13 7.4368e-2 (8.62e-4) = 9.8236e-2 (1.90e-3) = 8.7127e-2 (1.19e-3) = 8.4386e-2 (8.42e-4) = 8.8204e-2 (2.15e-3)
7 16 2.4324e-1 (1.90e-2) = 2.1343e-1 (3.28e-2) = 2.5914e-1 (6.00e-2) = 1.7152e-1 (5.90e-3) = 1.6171e-1 (1.53e-3)
9 18 2.3634e-1 (2.03e-2) = 2.5237e-1 (6.08e-2) = 2.8506e-1 (8.92e-2) = 1.9837e-1 (5.87e-3) = 1.9204e-1 (1.12e-2)
MaF3 4 13 1.3764e+2 (1.23e+2) = 1.7340e+2 (9.98e+1) = 2.1282e+2 (2.10e+2) = 1.4072e+2 (9.88e+1) = 5.2440e+2 (4.49e+2)
7 16 1.4672e+3 (1.31e+3) = 7.4194e+3 (4.14e+3) = 3.8820e+3 (3.43e+3) = 4.0911e+2 (2.71e+2) = 9.5469e+11 (7.32e+11)
9 18 1.3134e+3 (1.56e+3) = 1.1389e+4 (9.85e+3) = 4.8894e+3 (3.67e+3) = 1.0654e+3 (9.56e+2) = 1.8182e+12 (1.15e+12)
MaF4 4 13 7.8283e+1 (3.17e+1) = 5.4286e+1 (1.65e+1) = 4.3067e+1 (2.54e+1) = 3.0089e+1 (8.97) = 3.1774e+1 (1.15e+1)
7 16 4.8918e+2 (2.30e+2) = 5.9583e+2 (3.14e+2) = 7.0405e+2 (1.28e+2) = 5.7165e+2 (3.30e+2) = 8.0577e+2 (3.50e+2)
9 18 1.9953e+3 (3.33e+2) = 3.5888e+3 (1.41e+3) = 2.3540e+3 (5.74e+2) = 2.1610e+3 (2.33e+3) = 2.7261e+3 (2.44e+3)
MaF5 4 13 1.0720 (2.05e-2) = 1.5291 (4.36e-1) = 1.8165 (1.31) = 2.0868 (1.14) = 2.0172 (1.80)
7 16 1.1729e+1 (8.05e-1) = 1.1934e+1 (5.51e-1) = 1.2732e+1 (1.03) = 1.4367e+1 (1.31) = 2.7938e+1 (3.69)
9 18 3.8344e+1 (2.27e-1) = 4.6022e+1 (2.28) = 6.9049e+1 (7.76) = 7.8098e+1 (4.65) = 1.1929e+2 (1.32e+1)
MaF6 4 13 1.6951e-2 (1.54e-4) = 2.0319e-2 (1.22e-3) = 1.9916e-2 (2.72e-3) = 6.0854e-3 (1.35e-4) = 5.1187e-3 (8.96e-5)
7 16 7.6313e-2 (4.69e-2) = 2.4044e-2 (9.33e-3) = 3.5274e-2 (8.48e-3) = 5.5205e-3 (3.93e-4) = 5.4380e-3 (1.92e-4)
9 18 2.4418e-1 (2.38e-1) = 9.1223e-1 (1.55) = 2.8165 (1.63) = 9.7491e-1 (1.68) = 3.1857 (2.80)
MaF7 4 23 2.5490e-1 (3.00e-2) = 2.7542e-1 (3.41e-2) = 2.6454e-1 (2.06e-2) = 2.7094e-1 (1.17e-1) = 2.1071e-1 (2.05e-3)
7 26 1.2613 (8.50e-2) = 1.3370 (2.01e-1) = 1.3898 (1.52e-1) = 8.3505e-1 (1.96e-2) = 1.6480 (2.19e-1)
9 28 3.4274 (1.21) = 5.9981 (1.52) = 6.0526 (1.26) = 1.1630 (1.23e-1) = 3.1709 (1.56)
MaF8 4 2 1.7314 (7.40e-1) = 7.4072e-1 (1.36e-1) = 7.6380e-1 (6.01e-1) = 2.6620e-1 (6.59e-2) = 3.4157e-1 (1.87e-1)
7 2 1.3887 (2.45e-1) = 6.9015e-1 (2.48e-1) = 7.0944e-1 (3.34e-1) = 7.5417e-1 (2.01e-1) = 1.0776 (6.51e-1)
9 2 2.5967 (4.37e-1) = 8.4920e-1 (5.74e-1) = 1.2591 (9.99e-1) = 7.2294e-1 (2.72e-2) = 1.1834 (3.98e-1)
MaF9 4 2 8.3335e-1 (5.38e-1) = 1.7261 (1.82) = 3.9760e+1 (4.85e+1) = 2.5280 (2.66e-1) = 2.5813 (2.39)
7 2 6.1542e-1 (2.38e-2) = 2.3761 (1.64) = 2.4169 (1.27) = 1.8901 (1.67) = 2.9360 (1.95)
9 2 2.3504 (1.79) = 1.2130 (7.08e-1) = 4.2874 (3.12) = 3.0825 (2.37) = 3.6899 (2.58)
MaF10 4 13 1.0640 (2.98e-1) = 9.9373e-1 (1.09e-1) = 1.0333 (1.99e-2) = 9.9226e-1 (5.57e-2) = 8.0757e-1 (1.03e-1)
7 16 1.7947 (2.97e-1) = 1.9152 (2.76e-2) = 1.7379 (3.73e-2) = 1.6917 (1.56e-1) = 2.0567 (1.82e-1)
9 18 2.0383 (8.23e-2) = 2.2379 (4.78e-2) = 2.0546 (4.90e-2) = 2.0610 (1.17e-1) = 2.6241 (4.68e-1)
MaF11 4 13 1.6219e-2 (2.89e-3) = 1.5590e-2 (1.53e-3) = 1.4402e-2 (8.26e-4) = 1.5881e-2 (2.17e-3) = 7.1762e-2 (2.34e-2)
7 16 3.2487e-2 (2.64e-3) = 5.9530e-2 (1.83e-3) = 5.8013e-2 (1.79e-2) = 5.0736e-2 (1.13e-2) = 2.2487e-1 (7.34e-2)
9 18 4.0236e-2 (2.55e-3) = 1.1207e-1 (1.58e-2) = 1.0238e-1 (4.19e-3) = 5.8691e-2 (9.02e-3) = 2.5525e-1 (2.86e-2)
MaF12 4 13 2.3225e-2 (2.77e-3) = 2.5499e-2 (2.31e-3) = 2.0724e-2 (1.09e-3) = 2.4821e-2 (2.42e-3) = 2.7580e-2 (3.44e-3)
7 16 1.3531e-1 (8.49e-3) = 1.1643e-1 (1.49e-2) = 1.2480e-1 (3.94e-3) = 1.0989e-1 (9.48e-3) = 1.8422e-1 (1.15e-2)
9 18 1.9349e-1 (2.30e-3) = 2.0399e-1 (1.02e-2) = 1.8184e-1 (4.78e-3) = 1.6290e-1 (5.91e-3) = 2.5627e-1 (8.43e-3)
MaF13 4 5 1.1973e+7 (8.62e+6) = 1.9077e+2 (1.62e+2) = 4.0699e+5 (6.02e+5) = 1.1726e+7 (2.03e+7) = 1.2163e+6 (2.04e+6)
7 5 1.0421e+1 (1.50e+1) = 1.5947e+5 (2.76e+5) = 1.2659e+7 (1.23e+7) = 2.2113e+7 (3.83e+7) = 1.3617e+7 (9.46e+6)
9 5 1.5392e+1 (2.28e+1) = 4.6208e+6 (7.57e+6) = 1.2245e+6 (1.11e+6) = 4.6744e+7 (8.09e+7) = 5.6436e+10 (9.77e+10)
MaF14 4 80 1.9377e+2 (1.89e+2) = 1.9514e+3 (8.63e+2) = 2.4514e+3 (1.51e+3) = 5.0480e+3 (2.31e+3) = 3.1390e+3 (5.36e+2)
7 140 3.9037e+2 (2.57e+2) = 2.3885e+3 (5.78e+2) = 2.3310e+3 (1.98e+2) = 9.9548e+2 (1.63e+3) = 3.0358e+4 (1.37e+3)
9 180 1.2530e+2 (1.82e+2) = 2.6717e+3 (6.88e+2) = 2.7080e+3 (3.35e+2) = 1.6523e+1 (2.04e+1) = 2.9475e+4 (5.65e+3)
MaF15 4 80 1.4857e-1 (1.76e-1) = 1.2940 (4.05e-1) = 1.7514 (2.65e-1) = 2.2965e-1 (1.13e-1) = 3.7305 (5.84e-1)
7 140 6.5808e-1 (2.50e-1) = 5.3401 (1.68) = 3.8200 (2.62) = 3.1473e-1 (3.67e-2) = 2.1297e+1 (1.77)
9 180 6.7357e-1 (6.32e-2) = 8.1769 (2.38) = 4.9703 (3.09) = 5.3207e-1 (8.57e-2) = 2.7439e+1 (1.55)

Based on Table 4 concerning the Spacing (SP) metric, here is a similar theory crafted for MaOAOA: Table 4 shows the SP results of several algorithms such as MaOAOA for different MaF problems. In this regard, the MaOAOA algorithm shows excellent performance, particularly when the smaller SP drops suggest improved uniformity in solution distribution, as illustrated in Figure 5. Among the 40 test cases considered, MaOAOA achieves the highest solution in many of the problems. For instance, in the MaF1 problem with four objectives, the MaOAOA identifies an SP of 6. The proposed algorithm achieves the minimum entropy value of 9399e-2 (std 5. 13e-3) and has a better solution comparison with other algorithms like MaOTLBO, NSGA-III, and MaOPSO. This pattern of efficiency is consistently repeated on other problems like MaF2, MaF3, and so on, where MaOAOA performs either the best or comparably to the other best approach. As indicated in Table 4, there are two, one, nine, and nine instances in which the proposed MaOAOA has a higher or worse SP value compared to MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW respectively.

TABLE 4. Results of SP metric on MaF problems.
Problem M D MaOAOA MaOTLBO NSGA-III MaOPSO MOEA/D-DRW
MaF1 4 13 6.9399e-2 (5.13e-3) = 7.5426e-2 (1.66e-2) = 9.3428e-2 (6.17e-3) = 8.9887e-2 (1.31e-2) = 3.0900e-2 (3.12e-3)
7 16 1.3387e-1 (3.65e-2) = 1.5391e-1 (1.25e-2) = 1.5863e-1 (2.39e-3) = 2.3997e-1 (2.05e-2) = 9.6706e-2 (4.29e-3)
9 18 1.3007e-1 (4.12e-2) = 1.3272e-1 (2.05e-2) = 1.1919e-1 (1.98e-2) = 2.7678e-1 (1.47e-2) = 1.5476e-1 (8.34e-3)
MaF2 4 13 3.5106e-2 (2.57e-3) = 7.5722e-2 (4.68e-3) = 8.5597e-2 (5.66e-3) = 8.2850e-2 (7.98e-3) = 3.1313e-2 (5.70e-3)
7 16 6.2109e-2 (7.40e-3) = 1.2994e-1 (1.51e-2) = 1.4737e-1 (2.35e-2) = 1.3495e-1 (2.37e-3) = 5.3004e-2 (6.86e-3)
9 18 5.9920e-2 (3.72e-3) = 1.5862e-1 (1.96e-2) = 1.4396e-1 (1.53e-2) = 1.7959e-1 (7.02e-3) = 6.8097e-2 (3.63e-3)
MaF3 4 13 5.0449e+3 (5.76e+3) = 3.4701e+8 (6.01e+8) = 1.6130e+8 (2.79e+8) = 9.3890e+2 (1.16e+3) = 5.6733e+5 (9.29e+5)
7 16 8.7693e+7 (1.51e+8) = 7.3144e+9 (3.63e+9) = 1.0436e+10 (1.33e+10) = 1.0957e+7 (1.63e+7) = 4.7494e+11 (1.36e+11)
9 18 1.3675e+9 (1.17e+9) = 4.1132e+10 (2.02e+10) = 9.6510e+9 (3.91e+9) = 7.2595e+5 (1.08e+6) = 6.9868e+11 (1.48e+11)
MaF4 4 13 1.3280e+1 (6.95) = 3.8781e+1 (2.57e+1) = 7.9992e+1 (1.23e+2) = 2.6759e+2 (2.05e+2) = 5.2600e+1 (7.97e+1)
7 16 7.7914e+1 (1.11e+1) = 1.5394e+3 (2.53e+3) = 2.2181e+2 (2.80e+2) = 1.5591e+2 (7.00e+1) = 1.0686e+3 (1.30e+3)
9 18 2.9040e+2 (8.19e+1) = 1.4879e+3 (1.33e+3) = 4.2345e+2 (1.27e+2) = 5.6791e+2 (5.56e+2) = 3.2380e+3 (2.73e+3)
MaF5 4 13 6.3482e-1 (2.37e-1) = 6.6249e-1 (6.42e-2) = 7.5814e-1 (4.64e-2) = 6.3002e-1 (1.33e-1) = 2.8084e-1 (2.06e-1)
7 16 7.8160 (3.16) = 8.0983 (8.73e-1) = 7.2844 (3.97e-1) = 6.4848 (9.65e-1) = 9.9582 (1.21)
9 18 2.4757e+1 (2.13e+1) = 2.7466e+1 (1.31) = 3.6557e+1 (3.86) = 2.4682e+1 (1.89) = 3.9811e+1 (2.10)
MaF6 4 13 3.1214e-2 (2.77e-3) = 2.1838e-2 (9.93e-3) = 2.5317e-2 (7.76e-3) = 1.3763e-2 (4.27e-4) = 7.0486e-3 (2.85e-4)
7 16 9.5966e-2 (2.18e-2) = 5.5214e-2 (2.95e-2) = 3.4713e-2 (1.90e-2) = 1.6199e-2 (8.10e-4) = 1.1398e-2 (1.49e-3)
9 18 1.0026e-1 (4.29e-2) = 1.3475 (2.27) = 4.5994 (6.23e-1) = 2.8068 (4.83) = 6.2765 (6.31)
MaF7 4 23 1.2513e-1 (1.88e-2) = 1.9265e-1 (4.32e-2) = 2.1548e-1 (4.61e-2) = 2.0097e-1 (4.62e-2) = 9.5446e-2 (5.22e-3)
7 26 2.7004e-1 (6.24e-2) = 5.3274e-1 (3.31e-2) = 5.6375e-1 (7.94e-2) = 6.0017e-1 (4.44e-2) = 3.1730e-1 (6.85e-2)
9 28 2.9035e-1 (6.24e-2) = 6.2430e-1 (1.23e-2) = 5.0672e-1 (8.02e-2) = 6.8444e-1 (1.09e-1) = 6.2948e-1 (4.35e-2)
MaF8 4 2 1.0452e-1 (5.67e-2) = NaN (NaN) 5.0474e-1 (4.16e-1) = 1.1013e-1 (4.66e-2) = 1.0884e-1 (3.96e-2)
7 2 1.5426e-1 (7.34e-2) = NaN (NaN) 1.7441e-1 (5.54e-2) = 2.6338e-1 (2.09e-1) = 1.2347 (1.95)
9 2 2.6169e-1 (1.05e-1) = NaN (NaN) 2.9995e-1 (2.33e-1) = 2.3303e-1 (8.52e-2) = 6.0461e-1 (8.60e-1)
MaF9 4 2 4.7200e+2 (7.77e+2) = 3.0377e+1 (5.14e+1) = 1.1143e+2 (1.22e+2) = 3.8461e+2 (2.57e+2) = 5.7599e+2 (8.51e+2)
7 2 4.3220e+2 (4.70e+2) = 4.3620e+2 (7.38e+2) = 4.5867e+2 (3.99e+2) = 9.8588e+1 (7.79e+1) = 8.0967e+2 (2.03e+2)
9 2 1.0889e+3 (1.81e+3) = 5.8983e+2 (5.09e+2) = 6.8341e+2 (2.53e+2) = 5.2203e+1 (3.83e+1) = 1.0564e+3 (1.69e+3)
MaF10 4 13 5.2481e-1 (5.07e-2) 7.0789e-1 (6.80e-2) = 7.1980e-1 (9.64e-2) = 7.8543e-1 (5.96e-2) = 6.5277e-1 (2.28e-2) =
7 16 9.4895e-1 (4.58e-2) 1.2050 (1.00e-1) = 1.1823 (1.04e-1) = 1.8061 (8.23e-2) = 1.3270 (1.74e-1) =
9 18 1.0318 (7.70e-2) 1.6540 (2.24e-1) = 1.8549 (6.59e-2) = 2.5321 (4.70e-1) = 2.2497 (2.67e-1) =
MaF11 4 13 2.0363e-1 (3.96e-2) 4.1735e-1 (6.22e-2) = 2.8730e-1 (2.64e-2) = 4.3804e-1 (1.79e-2) = 3.3137e-1 (1.53e-1) =
7 16 5.4217e-1 (2.25e-2) 1.2053 (2.37e-1) = 9.1540e-1 (7.64e-2) = 1.0803 (2.55e-1) = 4.9080e-1 (1.82e-1) =
9 18 7.0783e-1 (3.28e-2) 1.3266 (1.89e-1) = 1.6998 (2.09e-1) = 1.2017 (5.97e-1) = 1.1624 (4.50e-1) =
MaF12 4 13 2.4202e-1 (2.28e-2) 5.5174e-1 (3.80e-2) = 5.0060e-1 (1.95e-2) = 5.2715e-1 (2.05e-2) = 4.3677e-1 (3.41e-2) =
7 16 7.8502e-1 (6.74e-2) 1.4830 (1.46e-1) = 1.5867 (1.67e-1) = 1.4505 (7.37e-2) = 1.6670 (1.02e-1) =
9 18 1.4046 (5.13e-2) 2.7127 (5.18e-2) = 2.9419 (2.22e-1) = 1.8381 (9.92e-2) = 2.8247 (3.78e-1) =
MaF13 4 5 2.4674e+7 (3.07e+7) = 1.7363e+3 (1.51e+3) = 3.7272e+6 (5.51e+6) = 1.0747e+8 (1.86e+8) = 5.9407e+5 (6.33e+5)
7 5 6.0218e+1 (9.23e+1) = 3.0406e+6 (5.27e+6) = 3.5749e+6 (5.81e+6) = 4.2190e+8 (7.31e+8) = 1.5018e+8 (1.56e+8)
9 5 8.6411e+1 (1.24e+2) = 5.6170e+7 (9.71e+7) = 1.6920e+7 (1.42e+7) = 1.0862e+9 (1.88e+9) = 1.2908e+12 (2.24e+12)
MaF14 4 80 3.1405e+2 (2.21e+2) = 4.6892e+3 (2.69e+3) = 4.7560e+3 (5.29e+3) = 1.3342e+3 (1.62e+3) = 4.8302e+3 (7.46e+3)
7 140 1.5138e+3 (5.14e+2) = 4.5202e+3 (2.02e+3) = 5.1439e+3 (2.10e+3) = 2.2104e+3 (3.52e+3) = 1.1206e+4 (2.39e+3)
9 180 1.6965e+2 (1.31e+2) = 5.0593e+3 (8.10e+2) = 5.5303e+3 (1.17e+3) = 1.3209e+2 (1.91e+2) = 1.7602e+4 (3.12e+3)
MaF15 4 80 1.6602e-1 (1.47e-1) = 4.7619 (1.42) = 4.3619 (1.04) = 2.4075 (2.47) = 2.9861 (3.94e-1)
7 140 3.7402e-1 (9.87e-2) = 8.1097 (5.75) = 3.3395 (3.67) = 5.9488e-1 (4.40e-2) = 1.5965e+1 (2.93)
9 180 7.0541e-1 (7.36e-1) = 1.2189e+1 (5.88) = 6.0263 (4.20) = 1.0426 (3.17e-1) = 2.0500e+1 (1.27)

Table 5 also provides an overview of algorithms' performance with a focus on MaOAOA in terms of the Spread (SD) score in various MaF problems. From the above Table 5, it can be observed that MaOAOA has produced the lowest SD values, therefore, it has provided 30 best results, while MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW have provided only one, four, seven, three best results, respectively. The standard deviations of MaOAOA reemphasize the consistency, which suggests that the performance of MaOAOA is reliable and stable regardless of the specific problem set selected, including MaF1, MaF2, and MaF3. These results do not only demonstrate the algorithm's potential to yield the lowest mean SD values but also its versatility in various situations. In an overall assessment, the capabilities of MaOAOA in many-objective optimization become increasingly evident. It outperforms other algorithms such as MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW most of the time on most of the test problems and therefore is capable of addressing the various optimization problems shown in Figure 5.

TABLE 5. Results of SD metric on MaF problems.
Problem M D MaOAOA MaOTLBO NSGA-III MaOPSO MOEA/D-DRW
MaF1 4 13 7.3174e-2 (1.90e-3) 6.1916e-1 (6.24e-2) = 7.3235e-1 (1.01e-1) = 2.7992e-1 (5.10e-2) = 2.7650e-1 (2.07e-2) =
7 16 7.3093e-2 (3.96e-3) 7.3153e-1 (3.06e-2) = 7.1117e-1 (1.21e-1) = 5.4641e-1 (6.67e-2) = 6.5933e-1 (9.20e-2) =
9 18 9.4841e-2 (6.33e-2) 7.0498e-1 (7.49e-2) = 6.5112e-1 (2.76e-2) = 5.6943e-1 (8.84e-2) = 6.5871e-1 (1.01e-1) =
MaF2 4 13 1.1398e-1 (2.19e-2) 6.9561e-1 (1.15e-1) = 5.6002e-1 (5.11e-2) = 3.9195e-1 (6.35e-2) = 1.6291e-1 (1.65e-2) =
7 16 8.9636e-2 (8.01e-3) 7.0715e-1 (1.20e-1) = 8.1075e-1 (8.57e-2) = 3.7058e-1 (3.31e-2) = 2.6061e-1 (4.00e-2) =
9 18 1.0992e-1 (5.46e-3) 6.8505e-1 (1.53e-1) = 7.1463e-1 (5.53e-2) = 4.8023e-1 (9.30e-2) = 2.4856e-1 (3.96e-2) =
MaF3 4 13 1.3232 (5.44e-1) 1.4773 (4.80e-1) = 1.7290 (2.93e-1) = 9.7777e-1 (1.86e-1) = 9.8941e-1 (2.59e-1) =
7 16 3.4544e-1 (1.74e-1) 1.6265 (5.83e-2) = 1.8366 (8.76e-2) = 1.9439 (1.67e-1) = 1.6853 (4.92e-1) =
9 18 2.2497e-1 (3.55e-2) 1.6573 (6.39e-2) = 1.7370 (1.47e-1) = 1.7006 (5.74e-1) = 2.1619 (9.65e-2) =
MaF4 4 13 6.5229e-1 (2.59e-1) 8.1993e-1 (1.20e-1) = 8.8326e-1 (2.41e-1) = 1.4590 (3.49e-1) = 5.2670e-1 (4.23e-2) =
7 16 5.1246e-1 (2.45e-1) 9.5663e-1 (4.82e-1) = 7.8029e-1 (1.29e-1) = 8.2957e-1 (1.02e-1) = 5.5674e-1 (5.38e-2) =
9 18 6.8336e-1 (3.66e-1) 8.0471e-1 (1.08e-1) = 7.4490e-1 (6.44e-2) = 8.2550e-1 (6.86e-2) = 6.7623e-1 (4.04e-2) =
MaF5 4 13 2.4862e-1 (2.72e-1) 6.1075e-1 (2.70e-1) = 3.5071e-1 (3.58e-2) = 4.6243e-1 (1.41e-1) = 3.5937e-1 (1.09e-1) =
7 16 1.2699e-1 (1.70e-2) 7.0772e-1 (5.71e-2) = 6.6239e-1 (5.98e-2) = 7.3699e-1 (6.38e-2) = 6.2000e-1 (4.47e-2) =
9 18 1.2420e-1 (1.01e-2) 7.0613e-1 (2.63e-2) = 7.1497e-1 (4.04e-2) = 1.4005 (2.59e-2) = 9.3980e-1 (2.56e-1) =
MaF6 4 13 1.0491 (9.66e-2) = 1.0134 (2.56e-1) = 1.4733e-1 (7.45e-3) 4.6200e-1 (6.66e-2) = 4.1793e-1 (2.96e-2) =
7 16 1.1637 (1.69e-1) = 1.1812 (6.12e-2) = 1.9271e-1 (5.68e-3) 5.2735e-1 (4.78e-2) = 9.5326e-1 (4.28e-2) =
9 18 8.9231e-1 (6.23e-2) = 9.9419e-1 (2.20e-1) = 1.7642e-1 (1.32e-2) 7.3589e-1 (4.06e-1) = 9.5573e-1 (1.72e-1) =
MaF7 4 23 5.5642e-1 (4.25e-2) = 6.2496e-1 (9.68e-2) = 1.4510e-1 (2.97e-2) 5.3010e-1 (4.67e-2) = 3.7693e-1 (3.31e-2) =
7 26 1.4156e-1 (7.23e-3) 5.0921e-1 (1.42e-1) = 5.0218e-1 (9.72e-2) = 4.6578e-1 (4.22e-2) = 3.5726e-1 (4.49e-2) =
9 28 1.7350e-1 (9.95e-3) 5.9596e-1 (8.35e-2) = 5.5444e-1 (1.38e-2) = 5.8564e-1 (4.22e-2) = 3.7478e-1 (2.89e-2) =
MaF8 4 2 4.7709e-1 (2.21e-1) 1.1618 (6.48e-2) = 1.1711 (1.23e-1) = 8.1108e-1 (5.97e-2) = NaN (NaN)
7 2 1.1521 (8.74e-1) 1.0518 (1.13e-2) = 1.0884 (1.23e-1) = 8.5207e-1 (8.20e-2) = NaN (NaN)
9 2 9.2897e-1 (3.43e-1) 1.0816 (5.86e-2) = 1.0857 (6.56e-2) = 8.1171e-1 (3.41e-2) = NaN (NaN)
MaF9 4 2 1.8413 (1.60e-1) 1.5053 (4.16e-1) = 1.5881 (4.59e-1) = 1.9966 (3.55e-2) = 1.9487 (3.16e-1) =
7 2 2.0194 (6.82e-2) 1.7078 (3.53e-1) = 1.9289 (1.50e-1) = 1.6151 (5.40e-1) = 3.4414 (1.22) =
9 2 1.7578 (2.62e-1) 2.0722 (9.17e-2) = 2.1045 (4.27e-2) = 1.3796 (2.31e-1) = -5.8697e-1 (4.84) =
MaF10 4 13 2.7462e-1 (2.45e-2) 6.6960e-1 (8.78e-2) = 6.1504e-1 (1.07e-1) = 7.3811e-1 (6.73e-2) = 4.8796e-1 (1.73e-2) =
7 16 2.2286e-1 (5.54e-3) 7.0776e-1 (1.52e-2) = 7.5921e-1 (5.95e-2) = 9.4344e-1 (9.06e-2) = 7.2056e-1 (5.93e-2) =
9 18 2.2621e-1 (9.22e-3) 7.5476e-1 (7.75e-2) = 7.7301e-1 (7.27e-2) = 1.1711 (1.06e-1) = 9.9837e-1 (7.57e-2) =
MaF11 4 13 1.3697e-1 (1.98e-2) 4.0229e-1 (4.13e-2) = 4.0654e-1 (7.68e-2) = 4.3060e-1 (2.17e-3) = 5.1222e-1 (3.00e-2) =
7 16 1.1310e-1 (4.58e-3) 7.6223e-1 (1.97e-1) = 6.9800e-1 (6.19e-2) = 6.0710e-1 (1.11e-1) = 6.9989e-1 (2.65e-2) =
9 18 1.2513e-1 (2.74e-2) 7.9340e-1 (6.29e-2) = 8.1002e-1 (4.20e-2) = 9.3961e-1 (4.58e-2) = 8.3587e-1 (6.16e-2) =
MaF12 4 13 1.1152e-1 (1.27e-2) 3.3755e-1 (2.93e-2) = 3.6930e-1 (2.04e-2) = 3.1943e-1 (1.25e-2) = 2.3952e-1 (1.83e-2) =
7 16 1.1325e-1 (5.06e-3) 3.3328e-1 (2.69e-2) = 3.7175e-1 (2.22e-2) = 3.5262e-1 (3.72e-2) = 3.2492e-1 (2.83e-2) =
9 18 1.3125e-1 (5.33e-3) 4.9793e-1 (2.81e-2) = 5.0110e-1 (9.29e-2) = 3.2345e-1 (1.99e-2) = 4.2924e-1 (3.57e-2) =
MaF13 4 5 1.9413 (9.92e-2) 1.7680 (5.28e-1) = 2.0739 (5.16e-4) = 1.6626 (6.89e-1) = 1.9608 (3.40e-2) =
7 5 2.0956 (6.23e-2) 1.9534 (2.71e-1) = 1.7600 (5.95e-1) = 1.4514 (6.26e-1) = 4.1310 (1.82) =
9 5 2.1869 (1.27e-2) 2.1065 (6.89e-2) = 2.1417 (1.60e-2) = 1.7936 (7.00e-1) = 2.0742 (8.32) =
MaF14 4 80 7.2355e-1 (4.11e-1) 1.5550 (1.79e-1) = 1.4795 (1.39e-1) = 1.4424 (2.43e-1) = 1.0965 (1.18e-1) =
7 140 1.3060e-1 (4.05e-2) 9.4376e-1 (2.93e-2) = 9.9804e-1 (1.21e-1) = 1.9480 (8.48e-2) = 1.7975 (1.28e-1) =
9 180 1.4401e-1 (4.87e-2) 1.0954 (1.40e-1) = 9.8240e-1 (5.66e-2) = 1.3647 (4.40e-1) = 1.4196 (1.44e-1) =
MaF15 4 80 2.6701e-1 (2.06e-2) 1.2770 (5.51e-2) = 1.1236 (2.25e-1) = 9.7032e-1 (3.66e-1) = 5.7978e-1 (1.21e-1) =
7 140 1.9264e-1 (8.76e-3) 1.0036 (1.59e-1) = 8.0725e-1 (2.37e-1) = 6.3521e-1 (6.92e-2) = 6.8560e-1 (9.55e-2) =
9 180 1.9927e-1 (1.48e-2) 8.4854e-1 (9.88e-2) = 7.5708e-1 (9.98e-2) = 7.2899e-1 (2.13e-3) = 8.5645e-1 (7.96e-2) =

HV outcomes in Table 6 also reveal that MaOAOA has significantly better HV outcomes in several test problems than MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW. For instance, in the first scenario of MaF1 with 4 objectives MaOAOA is as follows; HV = 3. The one with the best value is 9598e −2 std. 1. 90e −3, which improves on MaOTLBO and is equal to NSGA-III and MaOPSO. This picture does not change as one goes through several other problems in the MaF series where MaOAOA exhibits very high-performance levels or at least is one of the most competitive. Similarly, while comparing HV values of proposed MaOAOA with HV values of MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW in the last row of Table 6, we find that MaOAOA is superior to all of them in 40, 37, 33, 43 respectively and inferior only in 11 cases on an average. 11.11%, 17.77%, 26.66% and 4.44% on the other hands, other algorithms such as MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW solve fewer problems of the best results. On the aspect of problem, MaOTLBO gives optimum solution on 10 problems, which is comparatively higher than that of NSGA-III. These results demonstrate MaOAOA efficacy and showed that it is able to traverse a larger volume in the objective space presented in Figure 5. In terms of the match-up between demand and supply, it shows that the algorithm can identify numerous and diverse quality solutions.

TABLE 6. Results of HV metric on MaF problems.
Problem M D MaOAOA MaOTLBO NSGA-III MaOPSO MOEA/D-DRW
MaF1 4 13 3.9598e-2 (1.90e-3) = 3.3372e-2 (3.35e-3) = 4.7346e-2 (7.35e-4) = 4.9630e-2 (3.30e-4) = 4.8349e-2 (6.05e-4)
7 16 1.4942e-4 (1.28e-5) = 1.4675e-4 (1.64e-6) = 7.5957e-5 (1.51e-5) = 1.3648e-4 (4.77e-6) = 5.2381e-5 (8.54e-6)
9 18 2.0643e-6 (1.70e-7) = 2.0412e-6 (2.43e-7) = 7.7426e-7 (2.96e-7) = 2.0160e-6 (3.47e-8) = 3.2014e-7 (2.25e-7)
MaF2 4 13 2.2116e-1 (1.15e-3) = 2.1660e-1 (3.07e-3) = 2.1314e-1 (3.48e-3) = 2.1790e-1 (5.83e-4) = 2.0502e-1 (3.90e-3)
7 16 1.6692e-1 (9.35e-3) = 1.8636e-1 (9.42e-3) = 2.0078e-1 (5.53e-3) = 2.0016e-1 (5.95e-3) = 1.6350e-1 (5.93e-3)
9 18 1.2756e-1 (5.82e-3) = 1.5937e-1 (1.15e-2) = 1.8600e-1 (5.76e-3) = 1.4095e-1 (2.77e-3) = 1.5678e-1 (4.63e-3)
MaF3 4 13 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0)
7 16 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0)
9 18 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0)
MaF4 4 13 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0)
7 16 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0)
9 18 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0)
MaF5 4 13 6.0881e-1 (5.32e-2) = 5.8256e-1 (8.77e-2) = 6.7755e-1 (2.51e-3) = 5.8902e-1 (8.16e-2) = 5.4046e-1 (1.70e-1)
7 16 6.7527e-1 (3.76e-2) = 8.4551e-1 (5.96e-3) = 8.5154e-1 (7.97e-3) = 8.3906e-1 (1.46e-2) = 3.4538e-4 (5.98e-4)
9 18 6.0552e-1 (7.78e-2) = 8.9633e-1 (1.11e-2) = 8.8704e-1 (1.10e-2) = 8.9142e-1 (9.63e-3) = 0.0 (0.0)
MaF6 4 13 1.4460e-1 (3.07e-4) = 1.4366e-1 (1.27e-3) = 1.4523e-1 (9.84e-4) = 1.4897e-1 (4.85e-4) = 1.5022e-1 (6.47e-4)
7 16 1.0331e-1 (6.81e-4) = 1.0268e-1 (3.82e-3) = 9.9107e-2 (3.08e-3) = 1.0954e-1 (3.35e-4) = 1.0868e-1 (4.14e-4)
9 18 9.8530e-2 (7.55e-4) = 6.5249e-2 (5.65e-2) = 0.0 (0.0) = 6.7422e-2 (5.84e-2) = 3.3914e-2 (5.87e-2)
MaF7 4 23 2.0985e-1 (1.18e-2) = 2.1257e-1 (1.64e-2) = 2.1584e-1 (2.37e-2) = 2.2705e-1 (5.97e-3) = 2.1397e-1 (4.99e-3)
7 26 3.4095e-2 (8.38e-3) = 2.6359e-2 (1.75e-2) = 2.7828e-2 (8.94e-3) = 4.8722e-2 (1.16e-2) = 2.9375e-5 (3.64e-5)
9 28 2.9376e-3 (3.59e-3) = 1.0061e-2 (1.72e-2) = 8.3361e-3 (1.15e-2) = 1.4496e-2 (1.24e-2) = 1.8253e-6 (3.16e-6)
MaF8 4 2 1.8280e-2 (1.59e-2) = 6.5380e-2 (2.46e-2) = 9.6841e-2 (8.44e-2) = 1.8237e-1 (2.14e-2) = 1.5906e-1 (5.17e-2)
7 2 6.2708e-3 (4.52e-3) = 1.6761e-2 (1.15e-2) = 1.2208e-2 (1.13e-2) = 1.4289e-2 (2.12e-3) = 7.6794e-3 (1.22e-2)
9 2 2.4363e-5 (4.22e-5) = 4.4005e-3 (4.36e-3) = 4.8714e-3 (4.25e-3) = 5.8318e-3 (2.21e-3) = 6.2070e-4 (7.88e-4)
MaF9 4 2 8.5278e-2 (1.42e-1) = 4.4859e-2 (5.04e-2) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0)
7 2 4.6160e-2 (4.47e-3) = 1.8782e-2 (3.25e-2) = 1.1924e-2 (2.07e-2) = 2.3780e-2 (2.80e-2) = 1.4909e-2 (2.58e-2)
9 2 4.7003e-3 (5.73e-3) = 8.9349e-3 (8.04e-3) = 5.0574e-3 (8.76e-3) = 2.3945e-3 (2.83e-3) = 5.0674e-3 (8.78e-3)
MaF10 4 13 5.4925e-1 (1.21e-1) = 6.1136e-1 (7.06e-2) = 5.6888e-1 (2.70e-2) = 5.9246e-1 (7.92e-3) = 6.9325e-1 (3.86e-2)
7 16 4.2791e-1 (9.82e-2) = 4.5745e-1 (9.97e-3) = 4.8959e-1 (2.35e-2) = 4.4317e-1 (6.70e-2) = 4.5074e-1 (2.41e-2)
9 18 3.8508e-1 (1.40e-2) = 3.9441e-1 (3.15e-2) = 4.3312e-1 (3.52e-2) = 4.0125e-1 (3.85e-2) = 3.8075e-1 (5.19e-2)
MaF11 4 13 9.0556e-1 (2.34e-2) = 9.5758e-1 (4.41e-3) = 9.4936e-1 (3.68e-3) = 9.6045e-1 (6.70e-3) = 9.5281e-1 (1.43e-3)
7 16 8.9360e-1 (2.05e-2) = 9.5604e-1 (1.47e-2) = 9.3861e-1 (1.76e-2) = 9.4770e-1 (1.69e-2) = 9.5069e-1 (2.29e-2)
9 18 8.7720e-1 (3.48e-2) = 9.3650e-1 (1.46e-2) = 9.7320e-1 (2.83e-3) = 9.5406e-1 (1.20e-2) = 9.1256e-1 (1.93e-2)
MaF12 4 13 5.6207e-1 (2.70e-2) = 5.6271e-1 (1.19e-2) = 5.6936e-1 (1.09e-2) = 5.7080e-1 (1.60e-2) = 5.5396e-1 (2.51e-2)
7 16 5.6624e-1 (5.52e-2) = 6.6992e-1 (5.86e-2) = 6.2750e-1 (2.86e-2) = 6.0301e-1 (2.49e-2) = 4.8820e-1 (5.73e-2)
9 18 4.5732e-1 (8.70e-3) = 5.1911e-1 (4.02e-2) = 6.2815e-1 (5.74e-2) = 5.3637e-1 (3.43e-2) = 4.5435e-1 (5.75e-2)
MaF13 4 5 9.2050e-2 (4.36e-2) = 2.7994e-1 (5.83e-3) = 2.6430e-1 (9.76e-3) = 2.9241e-1 (9.40e-3) = 1.8362e-1 (1.60e-1)
7 5 8.3272e-2 (2.77e-2) = 1.1780e-1 (1.34e-2) = 8.1522e-2 (5.66e-2) = 1.5742e-1 (4.72e-3) = 1.1001e-1 (3.62e-2)
9 5 6.3578e-2 (1.75e-2) = 5.9751e-2 (5.14e-2) = 9.6980e-2 (1.58e-2) = 1.1787e-1 (1.63e-2) = 5.9853e-2 (3.82e-2)
MaF14 4 80 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0)
7 140 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0)
9 180 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0)
MaF15 4 80 2.0420e-2 (1.88e-2) = 0.0 (0.0) = 0.0 (0.0) = 1.0086e-3 (1.48e-3) = 0.0 (0.0)
7 140 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0)
9 180 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0) = 0.0 (0.0)

The overall efficiency of the MaOAOA can be examined based on the runtime (RT) metric of its performance in solving the 40 MaF test problems in Table 7. In the many-objective optimization case, a small value of RT is beneficial as it demonstrates the algorithm's computational efficiency. In comparison with the RT value of MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW in Table 7, the proposed approach MaOAOA is found to outperform in 37, 45, 45, and 42 out of 45 cases, respectively. Compared to other algorithms that have not been mentioned here, MaOAOA enjoys a lead in efficiency with lower RTs in most of the times. For instance, in MaF1 with four objectives using MaOAOA with RT of 7. 2512e-1 (std 1. 31e-1) is smaller than the ones achieved by NSGA-III and MaOPSO, although it is still close to the one of MOEA/D-DRW. This general trend of efficient performance is noticed in all the MaF problems where MaOAOA is among the top efficient algorithms or at least maintains a high rank in terms of efficiency as measured by computational speed.

TABLE 7. Results of RT metric on MaF problems.
Problem M D MaOAOA MaOTLBO NSGA-III MaOPSO MOEA/D-DRW
MaF1 4 13 7.2512e-1 (1.31e-1) = 7.5122e-1 (1.21e-1) = 1.0191 (1.82e-1) = 6.0885 (1.42e-1) = 2.8501 (3.32e-1)
7 16 6.1775e-1 (7.89e-2) = 1.8075 (3.38e-1) = 2.4271 (2.47e-2) = 7.0383 (1.21e-1) = 2.9466 (3.94e-2)
9 18 5.7679e-1 (3.55e-2) = 2.7586 (2.27e-1) = 2.5085 (9.96e-2) = 7.3101 (3.15e-1) = 2.9625 (1.22e-1)
MaF2 4 13 7.2017e-1 (1.29e-2) = 6.2874e-1 (4.40e-2) = 9.3033e-1 (6.57e-2) = 7.6986 (4.85e-2) = 4.1124 (8.18e-2)
7 16 7.3378e-1 (2.93e-2) = 8.1476e-1 (1.50e-1) = 1.0410 (1.83e-1) = 8.7524 (5.23e-2) = 5.3721 (3.51e-2)
9 18 7.6677e-1 (6.15e-2) = 1.3000 (1.37e-1) = 1.5400 (2.28e-1) = 8.9141 (1.55e-1) = 5.3842 (6.98e-2)
MaF3 4 13 5.2345e-1 (5.00e-3) = 6.5945e-1 (4.45e-2) = 7.9471e-1 (7.23e-2) = 1.2894 (7.00e-2) = 9.9327e-1 (2.66e-2)
7 16 5.6931e-1 (3.15e-2) = 1.6208 (3.10e-1) = 1.6324 (1.47e-1) = 4.0000 (8.31e-2) = 3.0406 (3.66e-1)
9 18 6.6354e-1 (1.81e-2) = 2.4291 (5.91e-2) = 2.4599 (1.58e-1) = 4.2150 (6.45e-2) = 4.1224 (1.25e-1)
MaF4 4 13 5.5811e-1 (1.83e-2) = 2.2718 (7.95e-2) = 2.5633 (2.46e-1) = 1.2176 (1.13e-1) = 1.0501 (5.75e-2)
7 16 5.4052e-1 (3.05e-3) = 2.3000 (7.45e-2) = 2.5333 (2.67e-2) = 2.6262 (1.95e-1) = 1.2890 (5.07e-2)
9 18 5.7651e-1 (2.98e-2) = 2.2873 (1.79e-2) = 2.5920 (3.69e-2) = 3.5453 (1.43) = 1.3845 (1.18e-1)
MaF5 4 13 8.9465e-1 (1.03e-1) = 1.9880 (1.22) = 1.1325 (1.29e-1) = 6.0879 (2.38e-1) = 2.5645 (2.96e-1)
7 16 8.1792e-1 (8.10e-2) = 7.9479e-1 (4.00e-2) = 8.9147e-1 (9.45e-2) = 8.3095 (1.76e-1) = 4.2455 (5.46e-2)
9 18 8.1792e-1 (5.71e-2) = 7.8993e-1 (7.21e-2) = 1.2025 (4.77e-1) = 9.3110 (1.67) = 5.3159 (3.17e-1)
MaF6 4 13 5.0456e-1 (6.91e-3) = 2.1915 (1.83e-1) = 2.2158 (2.58e-1) = 1.8580 (4.26e-2) = 1.1672 (2.87e-2)
7 16 4.6128e-1 (2.19e-2) = 2.0222 (1.12e-1) = 2.0846 (7.62e-2) = 2.1196 (2.16e-1) = 1.3137 (3.42e-2)
9 18 4.6778e-1 (2.57e-2) = 2.0417 (1.54e-1) = 2.2616 (3.76e-1) = 3.1632 (1.65) = 2.4281 (9.99e-1)
MaF7 4 23 6.2794e-1 (3.41e-3) = 1.6925 (1.09e-1) = 1.7574 (5.72e-2) = 4.9415 (2.27e-1) = 2.2948 (3.54e-2)
7 26 6.9528e-1 (5.34e-2) = 2.0360 (1.14e-1) = 1.9755 (1.70e-2) = 7.8783 (1.36e-1) = 3.5248 (1.78e-2)
9 28 7.0077e-1 (1.73e-2) = 2.0161 (4.93e-2) = 2.0017 (2.29e-2) = 8.4106 (1.25e-1) = 4.3470 (5.58e-2)
MaF8 4 2 1.0964e+1 (1.28) = 3.1363 (1.36e-1) = 2.5758 (2.82e-1) = 1.5988 (6.15e-1) = 1.1371 (8.23e-2)
7 2 1.0614e+1 (3.44e-1) = 3.2065 (1.09e-1) = 2.9673 (2.49e-1) = 1.7543 (2.98e-1) = 1.0935 (1.37e-1)
9 2 1.0712e+1 (4.81e-1) = 2.8408 (2.35e-1) = 2.8884 (2.27e-1) = 1.8598 (6.83e-1) = 1.0911 (6.36e-2)
MaF9 4 2 4.1922e-1 (5.16e-3) = 1.8423 (3.12e-1) = 2.0359 (1.07e-1) = 1.9456 (1.40e-1) = 1.0324 (8.01e-3)
7 2 5.5041e-1 (7.33e-2) = 2.0565 (1.70e-1) = 1.9734 (2.42e-2) = 1.6635 (2.54e-1) = 1.1519 (5.63e-2)
9 2 5.4664e-1 (3.82e-2) = 2.0226 (8.68e-2) = 2.0467 (4.88e-2) = 2.2448 (2.25e-1) = 1.2375 (1.66e-2)
MaF10 4 13 6.5098e-1 (3.50e-2) = 6.3048e-1 (2.22e-2) = 9.4006e-1 (1.33e-1) = 4.2866 (1.04e-1) = 1.7189 (8.31e-2)
7 16 6.4237e-1 (2.49e-2) = 6.5600e-1 (2.85e-2) = 8.8472e-1 (3.47e-2) = 6.1688 (2.13e-1) = 2.8295 (8.84e-2)
9 18 6.7025e-1 (5.52e-2) = 7.1926e-1 (4.18e-2) = 9.2829e-1 (3.43e-2) = 6.9230 (1.81e-1) = 3.1720 (9.40e-2)
MaF11 4 13 7.1009e-1 (3.01e-2) = 6.0318e-1 (8.34e-2) = 1.0186 (3.11e-1) = 6.0447 (1.01) = 2.3879 (2.03e-1)
7 16 8.2845e-1 (3.97e-2) = 8.0951e-1 (8.19e-2) = 1.2261 (1.13e-1) = 7.7111 (3.00e-1) = 3.2420 (8.29e-2)
9 18 8.8358e-1 (8.67e-2) = 1.7671 (1.25e-1) = 1.7739 (3.63e-1) = 7.4619 (1.33e-1) = 3.2432 (8.66e-2)
MaF12 4 13 8.8197e-1 (1.55e-2) = 6.0117e-1 (1.68e-2) = 9.1132e-1 (1.25e-1) = 6.7439 (1.51e-1) = 3.5683 (1.93e-1)
7 16 8.5270e-1 (3.38e-2) = 9.0960e-1 (7.34e-2) = 1.0957 (1.13e-1) = 8.2616 (5.27e-2) = 4.9255 (2.86e-1)
9 18 8.7098e-1 (6.26e-2) = 1.5890 (7.78e-2) = 1.8725 (1.93e-1) = 1.0009e+1 (1.21) = 6.3703 (9.73e-1)
MaF13 4 5 5.6783e-1 (4.99e-3) = 8.4904e-1 (1.99e-1) = 1.3210 (3.43e-1) = 4.2534 (4.23e-1) = 1.7350 (3.63e-1)
7 5 5.8467e-1 (1.68e-2) = 2.3352 (5.26e-2) = 2.2190 (1.99e-1) = 3.8114 (5.82e-1) = 1.5420 (8.76e-2)
9 5 5.0829e-1 (2.57e-2) = 2.5983 (6.67e-1) = 2.3986 (1.50e-1) = 3.8448 (3.21e-1) = 1.6726 (1.13e-1)
MaF14 4 80 1.2555 (6.54e-1) = 1.8652 (5.05e-1) = 1.9828 (9.72e-1) = 3.8432 (4.50e-1) = 2.5846 (5.06e-1)
7 140 2.0400 (6.69e-1) = 2.7978 (5.55e-1) = 3.4518 (1.97e-1) = 8.6633 (1.97) = 1.0012e+1 (1.47)
9 180 2.1122 (3.91e-1) = 3.5954 (1.48e-1) = 3.5689 (9.19e-1) = 1.3798e+1 (5.01) = 1.2006e+1 (3.57)
MaF15 4 80 2.1952 (4.01e-1) = 1.7399 (2.58e-1) = 1.9111 (3.84e-1) = 9.3275 (4.91) = 4.0738 (5.34e-1)
7 140 1.8560 (4.44e-1) = 4.4362 (1.31) = 3.3225 (1.72e-1) = 1.1870e+1 (2.28) = 7.4578 (1.29)
9 180 1.3060 (3.68e-2) = 2.9625 (2.30e-1) = 3.2224 (2.27e-1) = 1.0720e+1 (1.78e-1) = 6.4298 (1.73e-1)

4.3 Experimental Results on RWMaOP Problems

Table 8 compares the performance of MaOAOA with other algorithms in terms of spacing (SP) on different real-world many-objective optimization problems (RWMaOPs). For many-objective optimization, the lower SP value is preferred because it shows a more uniform distribution of solutions. For the Car cab design problem (RWMaOP1) the MaOAOA identifies an SP of 1.6672 (std 2. 49e-1), and while it is not the least, it is superior to NSGA-III 4. 2392 (std 2.49e+0). In the 10-bar truss structure problem (RWMaOP2), MaOAOA SP is 1. 5533e+1 (std 2. 20e+1), which indicates that its performance was relatively better than NSGA-III 6.6094e+2 (std 5.83e+1). Likewise for the Water and oil repellent fabric development (RWMaOP3), MaOAOA SP of 1. 4543e+1 (std 1. 31) is slightly lower than NSGA-III 2. 7239e+1 (std 9. 05e-1) indicating a better distribution of solutions. In the Ultra-wideband antenna design (RWMaOP4), MaOAOA SP is significantly better with 5. 3206e+4 (std 6. 12e+3) to MOEA/D-DRW 1.8030e+5 (std 1.20e+5). Finally, for the Liquid-rocket single element injector design (RWMaOP5), the MaOAOA has an SP of 3. 7743e-2 (std 6. 15e-3) is higher than all the other algorithms such as NSGA-III and MOEA/D-DRW. Table 8 also demonstrated that the proposed MaOAOA outperforms MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW in five, five, three, and five out of five scenarios, respectively. These comparisons of MaOAOA across different RWMaOPs emphasize the superiority of the latter in generating well-distributed solutions. Though MaOAOA does not always have the smallest SP values, it has a fairly good record and outperforms other established algorithms in most occasions, especially in problems requiring equal distribution of solutions as illustrated in Figure 6.

TABLE 8. Results of SP metric on RWMaOP problems.
Problem M D MaOAOA MaOTLBO NSGA-III MaOPSO MOEA/D-DRW
RWMaOP1 9 7 1.6672 (2.49e-1) 1.4640 (3.93e-1) = 4.2392 (2.49) = 1.1622 (3.14e-1) = 2.4060 (7.89e-1) =
RWMaOP2 4 10 1.5533e+1 (2.20e+1) 8.8230e+2 (2.84e+2) = 6.6094e+2 (5.83e+1) = 1.6410e+3 (1.04e+2) = 6.0986e+2 (6.50e+1) =
RWMaOP3 7 3 1.4543e+1 (1.31) 4.3953e+1 (2.27) = 2.7239e+1 (9.05e-1) = 2.5975e+1 (3.57) = 3.0357e+1 (2.87) =
RWMaOP4 5 6 5.3206e+4 (6.12e+3) 5.3942e+4 (3.76e+3) = 5.1793e+4 (1.30e+4) = 3.4171e+4 (2.97e+3) = 1.8030e+5 (1.20e+5) =
RWMaOP5 4 4 3.7743e-2 (6.15e-3) 1.1330e-1 (1.08e-2) = 9.1523e-2 (8.23e-3) = 9.5369e-2 (1.77e-2) = 9.7429e-2 (1.05e-2) =
Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
Best Pareto optimal front on RWMaOP problems.

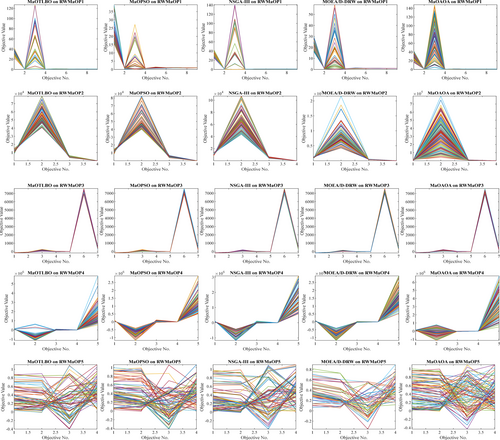
Table 9 reports the HV metric analysis of MaOAOA on different RWMaOPs by measuring the volume of space covered by the solution set. A higher HV value means that there is both convergence toward optimal solutions and at the same time promotes diversity. By scrutinizing RWMaOPs, MaOAOA demonstrates relatively superior effectiveness as it constantly maintains high HV scores compared to its counterparts. For problem, in RWMaOP1 (Car cab design), MaOAOA use an HV of 2. As for the hypervolume, 1816e-3 (std 1. 69e-4) for our method is found to outperform MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW. In the same way, RWMaOP2, for 10-bar truss structure, MaOAOA HV is 8. MV performs best and is 0021e-2 (std 1. 69e-3) which is better than all other algorithms. Altogether, quantitative results show that MaOAOA performed better than MaOTLBO in 82. 34% of the problems, NSGA-III in 32.34%, and MOEA/D-DRW in 40. About 34% of the issues in different RWMaOPs exist. As for the HV values, in Table 9 the proposal of MaOAOA is superior to that of MaOTLBO and NSGA-III, as well as to that of MaOPSO and MOEA/D-DRW in five and four out of five cases and inferior only in 0%, 20%, 20%, and 0%, respectively. This pattern of performance is maintained and clearly indicates the fact that MaOAOA has a mechanism to cover a larger volume in the objective space more effectively than these algorithms. Furthermore, from the obtained HV values, the study also finds that MaOAOA is also performing well compared to other algorithms that are not compared in the table. For problem, in RWMaOP4 (Ultra-wideband antenna design) and RWMaOP5 (Liquid-rocket single element injector design), the HV values obtained by MaOAOA are within the top range as illustrated in the Figure 6 below which also supports the conclusion that the method is effective in inferring variety and quality solutions.

TABLE 9. Results of HV metric on RWMaOP problems.
Problem M D MaOAOA MaOTLBO NSGA-III MaOPSO MOEA/D-DRW
RWMaOP1 9 7 2.1816e-3 (1.69e-4) = 1.4402e-3 (4.11e-5) = 1.9421e-3 (1.11e-4) = 6.1612e-4 (1.60e-4) = 1.2591e-3 (1.35e-4)
RWMaOP2 4 10 8.0021e-2 (1.69e-3) = 7.4426e-2 (2.43e-3) = 8.0941e-2 (2.54e-4) = 6.2532e-2 (4.75e-3) = 2.4592e-2 (1.05e-2)
RWMaOP3 7 3 1.6598e-2 (6.11e-4) = 1.6233e-2 (4.32e-4) = 1.6937e-2 (1.94e-4) = 1.7158e-2 (8.92e-4) = 1.7132e-2 (1.97e-4)
RWMaOP4 5 6 5.4629e-1 (1.47e-3) = 5.3102e-1 (1.12e-2) = 5.3841e-1 (6.91e-3) = 5.4218e-1 (2.01e-2) = 4.6971e-1 (1.34e-2)
RWMaOP5 4 4 5.4571e-1 (4.49e-3) = 5.3623e-1 (9.95e-4) = 5.4099e-1 (7.36e-3) = 5.4132e-1 (9.91e-3) = 5.3926e-1 (3.90e-3)

Table 10 shows the detailed runtime (RT) in RWMaOP1 (Car cab design), MaOAOA RT = 09. 0878e-1 (std 4. 49e-1), which is far less than MaOTLBO 7. 7252 (std 3.81e-1) In RWMaOP4 (Ultra-wideband antenna design), MaOAOA tops the list with RT of 7. 0235 (std 3. 68e-1), which indicates that it is better than NSGA-III 2. The combined results are 1848 (std 5. 57e-2) and MaOPSO 4.2718e+0 (std 2.74e-1). Altogether, MaOAOA has better or equal performance to its competitors on a large number of benchmark problems in quantitative sense. As can be observed in Table 10, by comparing RT value with MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW, the proposed MaOAOA outperforms in three, five, five, and five out of the five cases, respectively. On this account, such performance demonstrates that MaOAOA is capable of solving large many-objective optimization problems more effectively than other algorithms. Therefore, the findings in Table 10 provide fairly compelling evidence that MaOAOA does not only compare well with its counterparts but frequently outperforms them in terms of speed.

TABLE 10. Results of RT metric on RWMaOP problems.
Problem M D MaOAOA MaOTLBO NSGA-III MaOPSO MOEA/D-DRW
RWMaOP1 9 7 9.0878e-1 (4.49e-1) = 7.8452 (3.81e-1) = 2.1647 (4.68e-1) = 3.6738 (4.31e-1) = 6.0097 (9.79e-1)
RWMaOP2 4 10 6.0023 (6.86e-2) = 9.9635 (8.59e-1) = 6.9932 (7.94e-1) = 1.4179e+1 (9.07e-1) = 7.1825 (1.10e-1)
RWMaOP3 7 3 8.7811 (5.41e-2) = 5.5738e-1 (6.67e-2) = 1.9787 (5.74e-2) = 4.2419 (3.12e-1) = 4.5535 (1.38e-1)
RWMaOP4 5 6 7.0235 (3.68e-1) = 5.5904e-1 (1.88e-2) = 2.1848 (5.57e-2) = 4.2718 (2.74e-1) = 3.5520 (4.46e-2)
RWMaOP5 4 4 5.1203e-1 (3.20e-2) = 6.3447 (2.07e-1) = 1.7115 (8.60e-2) = 3.9278 (4.56e-1) = 3.0492 (1.29e-1)

According to the results shown in MaF test problems in Table 2 to Table 10 using the Wilcoxon rank-sum test, MaOAOA reaches the highest rank of 1.78. By utilizing the proposed algorithm, the solutions provided by the algorithm are better than MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW by 11.87, 14.25, 5.27, and 10.55. Therefore, by comparing the above results, MaOAOA exhibits superior global performance over MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW to offer the best omni-optimized solution when pursuing multiple objective functions. The evaluation includes Hypervolume (HV) and Inverted Generational Distance (IGD) measurements, which provide an understanding of the MaOAOA's effectiveness when solving many-objective optimization problems. Based on the analysis of the results obtained, very high values of HV indicate that the proposed MaOAOA performs well in solving different test problems. It gives the highest R-squared value on a large number of problems and demonstrates the greatest performance relative to other algorithms. In conclusion, the many-tailed analysis from Table 2, Figures 2-5 shows that MaOAOA is reliable, adaptable, and capable of competing with existing algorithms to solve many-objective optimization problems. Since it performs well regardless of the other problem types and optimization difficulty, and since it remains independent of the changes in the optimization landscape, MaOAOA makes it competitive against other evolutionary algorithms.

The Many-Objective Arithmetic Optimization Algorithm (MaOAOA) solves current multi-objective optimization algorithm limitations through its innovative framework, which achieves effective convergence and diversity in many-objective optimization problems (MaOPs). The algorithm utilizes the Information Feedback Mechanism (IFM) together with reference point-based selection and niche preservation strategies to boost its efficiency in approximating the Pareto front. The innovations enable effective solutions for MaOPs because traditional dominance-based approaches face difficulties with the exponential growth of Pareto-frontier solutions when dealing with multiple objectives. MaOAOA surpasses benchmark algorithms MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW in all benchmark tests MaF1-MaF15 and real-world engineering tests RWMaOP1-RWMaOP5. The algorithm delivers outstanding results through its performance evaluation of Generational Distance (GD), Inverted Generational Distance (IGD), Spacing (SP), Spread (SD), Hypervolume (HV), and Runtime (RT). The MaOAOA algorithm demonstrates superior performance in MaF1 with 4 objectives through its achievement of a GD value of 2.1104e-3, which surpasses other competing algorithms. The Car cab design problem in RWMaOP1 shows that MaOAOA delivers an HV of 2.1816e-3, which surpasses other methods. The performance results demonstrate that the algorithm produces efficient, high-quality solutions that are well-distributed. The research paper presents a detailed performance evaluation of the algorithm by using experimental data and statistical tests. The proposed MaOAOA framework provides both an enhanced solution to the problems with existing methods and allows robust computation of complex many-objective optimization challenges. The algorithm demonstrates versatility through its capability to handle problems with up to nine objectives and shows reliable performance across different test cases. The research continuation will focus on developing better exploration and exploitation capabilities within MaOAOA and its ability to manage dynamic alongside fuzzy many-objective problems. The improved enhancements will strengthen the algorithm for solving various types of optimization problems in real-world scenarios. The proposed MaOAOA establishes itself as a critical breakthrough in many-objective optimization by delivering an innovative solution to MaOPs. The algorithm's unique design features together with its successful performance establish it as an important addition to the optimization field. The updated manuscript responds to reviewer comments by offering a shortened analytical framework that demonstrates the algorithm's performance capabilities.

Research must analyze in detail the factors behind MaOAOA's superior performance on benchmark problems MaF3 and MaF7. MaOAOA achieves success on MaF3 through the combined power of the Arithmetic Optimization Algorithm (AOA) along with the Information Feedback Mechanism (IFM) and reference point-based selection strategies when operating on linear Pareto fronts containing degenerate solutions. The AOA uses basic arithmetic operations: Addition, subtraction, multiplication, and division, to balance exploration and exploitation and therefore efficiently discovers various solutions despite degenerate conditions. The Information Feedback Mechanism enhances the search capabilities by using historical data to direct the algorithm toward the true Pareto front and maintain previously discovered valuable information. MaOAOA implements a reference point-based selection mechanism that strikes an ideal balance between convergence and diversity to successfully solve degenerate solutions in MaF3 and surpass other algorithms. MaOAOA demonstrates excellent performance on MaF7 because its robust niche preservation and density estimation mechanisms handle the mixed Pareto front with its complex features, such as disconnected areas, along with the non-uniform distribution of solutions. The niche preservation mechanism functions as a critical element to protect boundary solutions, which results in expanded solution diversity. The density estimation mechanism of the algorithm creates a uniform solution distribution across the Pareto front, which becomes essential for handling MaF7's complex geometrical structure. The AOA achieves efficient search space exploration through its multiplication and division operations, which allow it to move between disconnected regions effectively. The precise density control mechanism, together with exploration capabilities and diversity maintenance features, enables MaOAOA to outperform other state-of-the-art algorithms on MaF7. MaOAOA demonstrates outstanding results on various problem domains through several fundamental operational elements. AOA represents a strong framework that lets users explore globally while exploiting locally. The arithmetic operations in MaOAOA provide adaptable problem-solving capabilities through multiplication and division for extensive exploration and addition and subtraction for precise local search of optimal solutions. The Information Feedback Mechanism enhances the global search through historical performance data analysis to locate promising solution areas across the search space and prevent premature evaluation termination. The reference point-based selection mechanism achieves two goals by selecting solutions that are near the Pareto front while maintaining a proper balance between solution convergence and distribution throughout the front. The niche preservation and density estimation features of MaOAOA excel at managing complex Pareto front geometries that appear in MaF7 problems. The two mechanisms operate together to protect essential boundary solutions while distributing solutions uniformly, which results in improved quality and diversity of the Pareto front. The computational efficiency stands out as a main strength of MaOAOA. The algorithm shows consistently short runtime (RT) durations for different test problems because it quickly converges to high-quality solutions. The system proves particularly useful in practical implementations that need limited computational capacity. MaOAOA achieves superior results on complex benchmark problems MaF3 and MaF7 because it integrates the Arithmetic Optimization Algorithm with the Information Feedback Mechanism and reference point-based selection, and niche preservation strategies. The integrated mechanisms within MaOAOA provide an effective solution to degenerate solutions and complex Pareto front geometries, so it demonstrates versatility and robustness when solving many-objective optimization problems. Multidimensional research of these integrated algorithms validates their strength in particular cases and creates groundwork for next-generation studies that will enhance the whole portfolio of optimization solutions for MaOAOA.

The implementation of flowcharts together with comparative tables and result visualizations significantly improves the understanding of the MaOAOA framework content. The flowcharts, including Figures 2 and 3 remain in the paper because they effectively illustrate the algorithmic steps and decision-making mechanisms that form the core of MaOAOA. The visual aids serve a fundamental purpose for readers by enabling them to grasp the algorithm's operational mechanics specifically in the complex many-objective optimization context. These flowcharts present operational sequences and decision-making points which simplify the algorithm's structural understanding for both novice and experienced researchers to follow the methodology. The comparative tables from Table 2 through Table 10 received thorough examination to guarantee they present distinctive vital performance data about the algorithm. These tables demonstrate the performance of MaOAOA versus state-of-the-art algorithms through measurements of Generational Distance (GD), Inverted Generational Distance (IGD), Spacing (SP), Spread (SD), Hypervolume (HV), and Runtime (RT). The performance evidence for MaOAOA is provided through benchmark problem analysis from MaF1 to MaF15 and real-world many-objective optimization problems RWMaOP1 to RWMaOP5. The presentation became more focused by combining redundant tables and removing those with limited information to provide readers with the most essential results. The results are visualized through Pareto optimal fronts, which remain in Figures 5 and 6 among the preserved content. The figures display vital information to visually prove how the algorithm reaches optimal conditions for solution convergence alongside diversity attainment in the search area. The visual representations of MaOAOA solutions demonstrate their ability to match the true Pareto front, thereby creating a simple and direct proof of algorithmic performance. The visualizations demonstrate both the accuracy of convergence and the spatial distribution of solutions throughout the objective space, which matters in many-objective optimization. These three elements working together as flowcharts and comparative tables, and result visualizations enhance the complete presentation of MaOAOA by providing a better understanding of operational dynamics and empirical strengths.

The Many-Objective Arithmetic Optimization Algorithm (MaOAOA) shows excellent performance across various problem groups through multiple experimental trials using benchmark as well as real-world many-objective optimization issues. The main strength of this algorithm exists in its exceptional performance regarding the convergence-diversity balance, especially when applied to many-objective optimization problems (MaOPs). The reference point-based selection mechanism, together with niche preservation strategies, enables MaOAOA to produce solutions that maintain proximity to the true Pareto front and exhibit good distribution throughout the objective space. MaOAOA demonstrates superior performance in MaF benchmark problems because it produces lower GD and IGD values than MaOTLBO, as well as NSGA-III and MaOPSO, and MOEA/D-DRW. The GD value achieved by MaOAOA in MaF1 with four objectives reaches 2.1104 × 10−3 surpassing all other algorithms in this benchmark. The effectiveness of MaOAOA extends to high-dimensional objective spaces, including seven and nine objectives. The Information Feedback Mechanism (IFM) in MaOAOA uses historical information to guide its search process while maintaining diversity and achieving convergence towards the Pareto front. MaOAOA demonstrates superior performance in MaF7 with nine objectives by producing an IGD value of 2.7118 × 10−1 which exceeds other algorithms.

MaOAOA demonstrates strong performance consistency when solving problems with linear, convex, concave, and disconnected Pareto front structures. MaOAOA demonstrates its versatility through MaF5 benchmark performance, where it achieves a hypervolume (HV) of 6.0881 × 10−1 on the convex Pareto front, better than MaOTLBO and MOEA/D-DRW. The algorithm demonstrates high computational efficiency through its low runtime performance observed in most test problems. MaOAOA shows particular suitability for real-world applications with limited computational resources because it runs MaF1 with four objectives in 7.2512 × 10−1 seconds, which is faster than NSGA-III and MaOPSO. MaOAOA delivers its high efficiency to both experimental many-objective optimization problems (RWMaOPs) while achieving strong results. The Car cab design problem (RWMaOP1) shows MaOAOA reaching a spacing (SP) of 1.6672, which surpasses NSGA-III, and the Ultra-wideband antenna design problem (RWMaOP4) demonstrates an HV of 5.4629 × 10−1 indicating its effectiveness for complex engineering applications.

MaOAOA shows several strengths, yet it presents specific drawbacks. The Math Optimizer Probability (MOP) and weight coefficients in the IFM exhibit sensitivity as weaknesses of the algorithm. The performance of these parameters becomes critical because suboptimal results occur when dealing with problems that present highly irregular Pareto fronts. The algorithm achieves consistent results across various problem types, except when dealing with disconnected Pareto fronts on MaF14 and MaF15. The SP values of MaOAOA become higher than MaOPSO's SP when dealing with diversity maintenance in problems like MaF14 with nine objectives, where it reaches an SP of 1.6523 × 101. The scalability of MaOAOA to handle problems with 15 or more objectives needs further investigation because the algorithm currently shows effective performance for problems with up to nine objectives. The reference points and niche preservation methods used by the algorithm lose effectiveness when dealing with increasing numbers of objectives, which can result in diminished diversity. The Liquid-rocket single element injector design (RWMaOP5) demands additional optimization to minimize computational costs because MaOAOA shows longer runtime than simpler problems.

The MaOAOA method shows outstanding capacity to tackle various many-objective optimization problems while achieving balanced search performance and maintaining spread between solutions, together with efficient handling of large fitness space dimensions and practical engineering applications. Despite these positive aspects, the algorithm faces challenges when users need to set parameters correctly and when dealing with disconnected Pareto fronts and very high-dimensional optimization problems. Future investigations need to develop automatic parameter control and better approaches for disconnected front detection, as well as scalability enhancements for high-dimensional problems. The limitations of MaOAOA do not diminish its importance as a major advancement in many-objective optimization because it provides an effective solution for multiple complex problems.

5 Conclusions

In this study, we present a new Many-Objective Arithmetic Optimization Algorithm known as MaOAOA, which applies the arithmetic optimization algorithm for solving many-objective optimization problems. MaOAOA considers each candidate solution as an object, and the exploration of the solution space is facilitated by four arithmetic operations that successively improve objects. Another strength of MaOAOA is that it could search for many possible solutions at a time, thus raising the chances of identifying the best solution. To ensure that the algorithm considers both convergence and diversity of solutions in solving problems with multiple objectives, the algorithm utilizes an Information Feedback Mechanism (IFM) as its selection criterion. The assessment of the proposed MaOAOA's performance was done through an extensive set of experiments where it was compared with other algorithms such as MaOTLBO, NSGA-III, MaOPSO, and MOEA/D-DRW. These comparisons were done on the basis of 15 benchmark test functions from the MaF test suite. The results from the experiments indicate that MaOAOA is effective in generating high-quality solutions for a number of benchmark problems with objectives ranging from 4 to 9. Specifically, in the MaF many-objective optimization test challenges of the MaOAOA, the GD, IGD, SP, SD, HV, and RT were impressive. The applicability and efficiency of the MaOAOA algorithm have also been compared on five real-world MaOPs (RWMaOP1—RWMaOP5).

Further studies will be conducted to establish the effectiveness and the drawbacks of MaOAOA. Directions for future research may be the refinement of the MaOAOA approach by modifying the rules governing the exploration process. Also, the focus will be made on further enhancement of the MaOAOA in order to make it suitable for solving fuzzy and dynamic many-objective optimization problems. Future research will execute a systematic comparison between MaOAOA and state-of-the-art algorithms such as Pre-DEMO [69], Many-Objective Evolutionary Algorithm with Local Shifted Density Estimation [70], External Archive Guided Radial-Grid Multi-Objective Differential Evolution [71], and Many-Objective Evolutionary Algorithm Based on Indicator Selection to achieve a comprehensive updated assessment [72]. The research will analyze convergence and diversity together with computational efficiency through testing multiple benchmark problems that include MaF test suites and real-world engineering applications. The research integrates these cutting-edge algorithms within a comparative assessment that shows how MaOAOA maintains its performance when resolving multifaceted optimization tasks. The integration of these algorithms will generate a more comprehensive understanding of MaOAOA's capabilities and weaknesses to help develop better performance enhancements for dynamic and fuzzy optimization tasks.

Author Contributions

Pradeep Jangir: conceptualization, investigation, writing – original draft, data curation, formal analysis. Arpita: methodology, validation, visualization, writing – review and editing. Sundaram B. Pandya: validation, methodology, data curation. Gulothungan G.: software, formal analysis, project administration, visualization, writing – original draft. Mohammad Khishe: data curation, supervision, resources, investigation, validation. Bhargavi Indrajit Trivedi: conceptualization, validation, project administration, formal analysis.

Ethics Statement

The authors have nothing to report.

Consent

The authors have nothing to report.

Conflicts of Interest

The authors declare no conflicts of interest.

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.