Engineering Reports
Volume 7, Issue 2 e70019
RESEARCH ARTICLE
Open Access

Improved Conjugate Gradient Methods for Unconstrained Minimization Problems and Training Recurrent Neural Network

Bassim A. Hassan, 

Bassim A. Hassan

College of Computer Science and Mathematics, University of Mosul, Mosul, Iraq

Contribution: Conceptualization, ​Investigation

Search for more papers by this author
Issam A. R. Moghrabi, 

Corresponding Author

Issam A. R. Moghrabi

Department of Computer Science, University of Central Asia, Naryn, Kyrgyzstan

Department of Information Systems and Technology, Kuwait Technical College, Kuwait City, Kuwait

Correspondence: Issam A. R. Moghrabi ([email protected])

Contribution: ​Investigation, Funding acquisition, Methodology

Search for more papers by this author
Alaa Luqman Ibrahim, 

Alaa Luqman Ibrahim

Department of Mathematics, College of Science, University of Zakho, Zakho, Iraq

Contribution: Data curation, Writing - review & editing

Search for more papers by this author
Hawraz N. Jabbar, 

Hawraz N. Jabbar

College of Sciences, University of Kirkuk, Kirkuk, Iraq

Contribution: Software

Search for more papers by this author
First published: 09 February 2025
https://doi.org/10.1002/eng2.70019
Citations: 1

ABSTRACT

This research introduces two conjugate gradient methods, BIV1 and BIV2, designed to enhance the efficiency and performance of unconstrained optimization problems with only first derivative vectors. The study explores the derivation of new conjugate gradient parameters and investigates their practical performance. The proposed BIV1 and BIV2 methods are compared with the traditional Hestenes-Stiefel (HS) method through a series of numerical experiments. These experiments evaluate the methods on various test problems sourced from the CUTE library and other unconstrained problem collections. Key performance metrics, including the number of iterations, function evaluations, and CPU time, demonstrate that both BIV1 and BIV2 methods offer superior efficiency and effectiveness compared to the HS method. Furthermore, the effectiveness of these methods is illustrated in the context of training artificial neural networks. Experimental results show that the new methods achieve competitive performance in terms of convergence rate and accuracy.

1 Introduction

Optimization is a fundamental process in various scientific and engineering fields, involving the implementation of a systematic approach to determine the minimum or maximum of an objective function. Unconstrained optimization, a key branch within this domain, focuses on minimizing an objective function that is dependent on real-valued variables, with no restrictions placed on those variables. This problem can be mathematically formulated as follows:
Min f ( x ) : x ∈ R n $$ \mathit{\operatorname{Min}}\left\{f(x):x\in {R}^n\right\} $$ (1)
where f $$ f $$ represents a smooth and differentiable function, with its gradient readily available [1]. Unconstrained optimization plays a pivotal role in various scientific and engineering disciplines. Its applications span from parameter estimation in mathematical modeling to advanced machine learning algorithms used in artificial intelligence (AI). The ability to minimize objective functions effectively and efficiently is essential for solving complex real-world problems, including resource allocation, predictive analytics, and design optimization. Numerous numerical methods have been developed to solve such problems, including the Steepest Descent (SD) method, Newton's method, Conjugate Gradient (CG) methods, and Quasi-Newton (QN) methods. Among these, the CG method stands out due to its simplicity, efficient memory usage, and effectiveness in handling large-scale optimization problems. Despite the existence of more advanced and robust algorithms for nonlinear optimization, CG methods continue to be widely utilized by engineers and mathematicians, particularly for solving high-dimensional problems where computational efficiency is crucial [2].
The origins of the CG method can be traced back to 1952 when Hestenes and Stiefel [3] introduced it as a technique for solving unconstrained linear optimization problems, particularly those involving quadratic functions. This method was later extended to nonlinear unconstrained minimization problems by Fletcher and Reeves in 1964 [4]. The fundamental principle underlying all CG methods is the generation of a sequence x k $$ \left\{{x}_k\right\} $$ starting from an initial guess x 0 ∈ R n $$ {x}_0\in {R}^n $$ , and iteratively updating this sequence using the recurrence relation:
x k + 1 = x k + α k d k $$ {x}_{k+1}={x}_k+{\alpha}_k{d}_k $$ (2)
Here, α k $$ {\alpha}_k $$ denotes the step size, which is typically determined through a line search procedure [5]. In practice, an exact line search is often computationally prohibitive and time-consuming, thus an inexact line search is generally preferred [6, 7]. The search direction d k $$ {d}_k $$ is computed using the rule:
d k + 1 = − g k + 1 , k = 0 − g k + 1 + β k d k , k > 0 $$ {d}_{k+1}=\left\{\begin{array}{l}-{g}_{k+1},\kern4em k=0\\ {}-{g}_{k+1}+{\beta}_k{d}_k,\kern0.9em k>0\end{array}\right. $$ (3)
where g k $$ {g}_k $$ represents the gradient of the function f $$ f $$ at the point x k $$ {x}_k $$ , and β k $$ {\beta}_k $$ is a scalar known as the conjugacy or CG parameter. The selection of β k $$ {\beta}_k $$ directly influences the type of conjugate gradient method employed, with different values corresponding to various CG algorithms. Table 1 summarizes some of the most widely used formulas for computing β k $$ {\beta}_k $$ in different CG methods.
TABLE 1. The beta formulas.
No. Formula Author
1 β k HS = g k + 1 T y k d k T y k $$ {\beta}_k^{HS}=\frac{g_{k+1}^T{y}_k}{d_k^T{y}_k} $$ Hestenes-Stiefel [3] and Stiefel [8].
2 β k FR = g k + 1 T g k + 1 g k T g k $$ {\beta}_k^{FR}=\frac{g_{k+1}^T{g}_{k+1}}{g_k^T{g}_k} $$ Fletcher-Reeves [4]
3 β k PR = g k + 1 T y k g k T g k $$ {\beta}_k^{PR}=\frac{g_{k+1}^T{y}_k}{g_k^T{g}_k} $$ Polak-Ribiere [9]
4 β k Perry = g k + 1 T y k − v k d k T y k $$ {\beta}_k^{\mathrm{Perry}}=\frac{g_{k+1}^T\left({y}_k-{v}_k\right)}{d_k^T{y}_k} $$ Perry [10].

The CG method has garnered significant attention in recent years due to its wide applicability in solving unconstrained optimization problems. Its favorable properties, such as global convergence and low memory requirements, have made it a key tool in many fields. Many of the advanced CG methods proposed in the literature are modifications or enhancements of the classical CG methods, aiming to improve their efficiency and robustness in practical applications [11-13]. The scope of CG methods has expanded to encompass applications in diverse areas such as data estimation [14], image restoration [15-18], and signal processing [19, 20].

In recent years, with the increasing demand for AI in various fields, CG methods have become an essential tool in training artificial neural networks. The gradient-based optimization techniques employed in these networks are crucial for achieving accurate and efficient learning ([12, 21-23]).

Recent studies have further advanced the CG method in the context of machine learning. For instance, a stochastic three-term conjugate gradient method with variance reduction for non-convex learning was proposed by [24]. This method aims to improve the efficiency of stochastic gradient descent in machine learning applications, where the slow convergence of traditional methods can be a limitation. By integrating variance reduction techniques with the CG method, the authors achieved linear convergence under less stringent assumptions, thereby enhancing both theoretical and practical performance for non-convex machine learning models.

Similarly, Huang [25] introduced a biased stochastic conjugate gradient algorithm with an adaptive step size for non-convex problems. This algorithm combines the stochastic recursive gradient method with the Barzilai–Borwein (BB) technique to improve step size selection, avoiding issues associated with fixed step sizes. The BSCG algorithm has demonstrated strong competitiveness, offering global optimal convergence and linear convergence rates for non-convex functions, with promising numerical results across machine learning applications.

Beyond machine learning, optimization techniques have been applied to various engineering fields. For example, studies by [26] utilized advanced metaheuristic algorithms, such as Depth Information-Based Differential Evolution (Di-DE), to enhance the precision of Proton Exchange Membrane Fuel Cell (PEMFC) parameter estimation. Their algorithm demonstrated excellent performance in optimizing parameters for multiple PEMFC models, offering substantial improvements in both runtime and accuracy compared to conventional methods. This work underscores the significance of optimization techniques in enhancing the design and operation of clean energy systems.

Additionally, the integration of machine learning and finite element methods has proven effective in investigating the axial compressive behavior of elliptical FRP-confined concrete columns. Yue [27] utilized machine learning models, such as XGBoost, to predict the compressive strength of concrete columns, achieving high predictive accuracy. Their work highlights the power of combining computational methods with machine learning to optimize engineering analysis.

Optimization techniques have also found applications in environmental research. For instance, [28] proposed a novel approach for analyzing marine life in the polar regions using advanced machine learning techniques. Their model achieved impressive accuracy and precision, underscoring the potential of combining environmental monitoring with machine learning to ensure sustainable food security in fragile ecosystems.

These studies collectively demonstrate the transformative role of optimization methods and machine learning in solving complex, real-world problems across a wide range of domains. From machine learning and energy systems to environmental analysis, the continued development of these techniques promises to drive innovation and improve efficiency in various industries.

The increasing demand for advanced optimization methods in machine learning and engineering has highlighted the limitations of classical techniques, such as the HS and FR methods. These methods often face challenges like slow convergence and inefficiency in handling large-scale problems. To address these limitations, this paper introduces two novel conjugate gradient methods, BIV1 and BIV2, that enhance convergence speed and robustness while maintaining computational efficiency. These methods are validated through extensive numerical experiments and real-world applications, demonstrating their potential in training artificial neural networks and solving complex optimization problems with higher precision.

The structure of this paper is as follows: Section 2 presents the proposed method in detail. Section 3 establishes the global convergence properties of the method. Finally, Section 4 provides numerical results to illustrate the performance and practical benefits of the method.

2 The Derivation of the Algorithm

An essential concept in iterative methods is Taylor's series expansion. In the context of conjugate gradient methods, we begin by utilizing Taylor's series expansion to approximate the objective function at the point x k $$ {x}_k $$ . The general form of this expansion is expressed as:
f k = f k + 1 − g k + 1 T s k + 1 2 s k T G k + 1 s k + 1 6 s k T T k + 1 s k s k $$ {f}_k={f}_{k+1}-{g}_{k+1}^T{s}_k+\frac{1}{2}{s}_k^T{G}_{k+1}{s}_k+\frac{1}{6}{s}_k^T\left({T}_{k+1}{s}_k\right){s}_k $$ (4a)
The gradient of (4a), is, thus,
g k + 1 = − g k + G k + 1 s k + 1 2 s k T T k + 1 s k $$ {g}_{k+1}=-{g}_k+{G}_{k+1}{s}_k+\frac{1}{2}{s}_k^T\left({T}_{k+1}\right){s}_k $$ (4b)
This leads to:
s k T Q x k s k = 5 / 6 s k T y k + f k − f k + 1 − 1 / 3 g k T s k $$ {s}_k^TQ\left({x}_k\right){s}_k=5/6{s}_k^T{y}_k+\left({f}_k-{f}_{k+1}\right)-1/3{g}_k^T{s}_k $$ (5a)
and
s k T Q x k s k = 6 / 5 s k T y k + 6 / 5 f k − f k + 1 + 2 / 5 g k T s k $$ {s}_k^TQ\left({x}_k\right){s}_k=6/5{s}_k^T{y}_k+6/5\left({f}_k-{f}_{k+1}\right)+2/5{g}_k^T{s}_k $$ (5b)

The terms in (5a) and (5b), illustrate how the conjugate gradient method adjusts its search direction based on the gradient differences, the function values, and additional properties of the objective function.

The vector y k $$ {y}_k $$ represents the difference in gradients between two consecutive iterations and is defined as:
y k = g k + 1 − g k = Q x k s k $$ {y}_k={g}_{k+1}-{g}_k=Q\left({x}_k\right){s}_k $$ (6)
Pre-multiplying Equation (6) by an appropriate vector s k T $$ {s}_k^T $$ , yields:
s k T Q x k s k = s k T g k + 1 − s k T g k $$ {s}_k^TQ\left({x}_k\right){s}_k={s}_k^T{g}_{k+1}-{s}_k^T{g}_k $$ (7)
In [10], the conjugacy condition takes the form:
d k + 1 T y k = − s k T g k + 1 $$ {d}_{k+1}^T{y}_k=-{s}_k^T{g}_{k+1} $$ (8)
Therefore, from (7), (8), and search direction (3), we obtain:
β k s k T y k = g k + 1 T y k − s k T Q x k s k − s k T g k $$ {\beta}_k{s}_k^T{y}_k={g}_{k+1}^T{y}_k-{s}_k^TQ\left({x}_k\right){s}_k-{s}_k^T{g}_k $$ (9)
Or, equivalently,
β k = g k + 1 T y k s k T y k − s k T Q x k s k s k T y k − s k T g k s k T y k $$ {\beta}_k=\frac{g_{k+1}^T{y}_k}{s_k^T{y}_k}-\frac{s_k^TQ\left({x}_k\right){s}_k}{s_k^T{y}_k}-\frac{s_k^T{g}_k}{s_k^T{y}_k} $$ (10)
By substituting Equations (5a) and (5b) into (10), the following equation is obtained
β k BBV 1 = g k + 1 T y k s k T y k − 5 / 6 s k T y k + f k − f k + 1 − 1 / 3 g k T s k s k T y k − s k T g k s k T y k . $$ {\beta}_k^{BBV1}=\frac{g_{k+1}^T{y}_k}{s_k^T{y}_k}-\frac{\left[5/6{s}_k^T{y}_k+\left({f}_k-{f}_{k+1}\right)-1/3{g}_k^T{s}_k\right]}{s_k^T{y}_k}-\frac{s_k^T{g}_k}{s_k^T{y}_k}. $$ (11)
additionally, the following expression is derived:
β k BBV 2 = g k + 1 T y k s k T y k − 6 / 5 s k T y k + 6 / 5 f k − f k + 1 + 2 / 5 g k T s k s k T y k − s k T g k s k T y k $$ {\beta}_k^{BBV2}=\frac{g_{k+1}^T{y}_k}{s_k^T{y}_k}-\frac{\left[6/5{s}_k^T{y}_k+6/5\left({f}_k-{f}_{k+1}\right)+2/5{g}_k^T{s}_k\right]}{s_k^T{y}_k}-\frac{s_k^T{g}_k}{s_k^T{y}_k} $$ (12)

The newly developed conjugate gradient methods, termed BIV1 and BIV2, aim to improve the efficiency and convergence characteristics of traditional conjugate gradient approaches, particularly in high-dimensional optimization scenarios. The algorithm outline is presented next (Algorithm 1).

ALGORITHM 1.  

  • Step 1:

    (Initialization) Given an initial point x 0 ∈ R n $$ {x}_0\in {R}^n $$ , parameters, 0 < ρ < σ < 1 , $$ 0<\rho <\sigma <1, $$ and ε > 0 $$ \varepsilon >0 $$ . Set d 0 = − g 0 $$ {d}_0=-{g}_0 $$ , and k = 0 $$ k=0 $$ .

  • Step 2:

    If g k ≤ ε $$ \left\Vert {g}_k\right\Vert \le \varepsilon $$ then stop.

  • Step 3:

    Compute the step size α k $$ {\alpha}_k $$ by the weak Wolfe line search [29, 30],

    f x k + α k d k ≤ f x k + ρ α k g k T d k g x k + α k d k T d k ≥ σ g k T d k . $$ \left\{\begin{array}{l}f\left({x}_k+{\alpha}_k{d}_k\right)\le f\left({x}_k\right)+\rho\ {\alpha}_k{g}_k^T{d}_k\\ {}g{\left({x}_k+{\alpha}_k{d}_k\right)}^T{d}_k\ge \sigma {g}_k^T{d}_k.\end{array}\right. $$

  • Step 4:

    Generate the next iteration by (2).

  • Step 5:

    Compute d k + 1 $$ {d}_{k+1} $$ by (3) and choose an appropriate conjugate parameter β k $$ {\beta}_k $$ by (11) or (12).

  • Step 6:

    Set k ≔ k + 1 $$ k:= k+1 $$ and go to Step 1.

3 Algorithm Convergence Characteristics

This section outlines the key properties of the new algorithm, including its descent property, and global convergence. The following necessary assumptions about the objective function f $$ f $$ are considered as essential for the analysis to follow.

Assumption 1.

  1. Bounded Level Set: The level set δ = x | f ( x ) ≤ f x k $$ \delta =\left\{x \mid f(x)\le f\left({x}_k\right)\right\} $$ at x k $$ {x}_k $$ is bounded. There exists a constant a > 0 $$ a>0 $$ such that:
    ‖ x ‖ ≤ a , ∀ x ∈ δ . $$ \left\Vert x\right\Vert \le a,\forall x\in \delta . $$ (13)

  1. Lipschitz Continuity of the Gradient: In some neighborhood N $$ N $$ of δ $$ \delta $$ , the function f $$ f $$ is continuously differentiable, and its gradient is Lipschitz continuous with Lipschitz constant L > 0 $$ L>0 $$ , This implies:
    ‖ g ( x ) − g ( y ) ‖ ≤ L ‖ x − y ‖ ∀ x , y ∈ δ $$ \left\Vert g(x)-g(y)\right\Vert \le L\left\Vert x-y\right\Vert \forall x,y\in \delta $$ (14)

  1. Bounded Gradient: There exists a positive constant b $$ b $$ such that:
    ‖ g ( b ) ‖ ≤ b ∀ x ∈ δ $$ \left\Vert g(b)\right\Vert \le b\kern0.5em \forall x\in \delta $$ (15)

  1. Strong Convexity: If f $$ f $$ is strongly convex, then there exists a constant μ > 0 $$ \mu >0 $$ , such that:
    μ ‖ x − y ‖ 2 ≤ ( ∇ f ( x ) − ∇ f ( y ) ) T ( x − y ) , for all x , y ∈ δ $$ \mu\ {\left\Vert x-y\right\Vert}^2\le {\left(\nabla f\ (x)-\nabla f\ (y)\right)}^T\ \left(x-y\right),\mathrm{for}\ \mathrm{all}\ x,y\in \delta $$ (16)

These assumptions are fundamental for establishing the global convergence of optimization algorithms, ensuring that the level sets are manageable, the gradient does not oscillate excessively, and the function exhibits desirable convexity properties.

We start with the analysis of the descent property of the methods to ensure a reduction in the objective function value. This property is fundamental for the convergence of optimization methods, ensuring that the algorithm consistently moves toward a minimum.

Theorem 1.Suppose that assumption (1) holds, then the sequence of search directions yielded by BIV1 and BIV2 satisfies:

d k + 1 T g k + 1 < 0 $$ {d}_{k+1}^T{g}_{k+1}<0 $$ (17)

Proof: If k = 0 $$ k=0 $$ then g 0 T d 0 = − g 0 2 $$ {g}_0^T{d}_0=-{\left\Vert {g}_0\right\Vert}^2 $$ , Let d k T g k < 0 $$ {d}_k^T{g}_k<0 $$ for all k $$ k $$ . Multiplying ( 3 ) $$ (3) $$ by g k + 1 , $$ {g}_{k+1}, $$ we have
d k + 1 T g k + 1 = − g k + 1 T g k + 1 + β k s k T g k + 1 . $$ {d}_{k+1}^T{g}_{k+1}=-{g}_{k+1}^T{g}_{k+1}+{\beta}_k{s}_k^T{g}_{k+1}. $$
Thus, we obtain:
d k + 1 T g k + 1 = − g k + 1 2 + g k + 1 T y k s k T y k − s k T g k + 1 s k T y k s k T g k + 1 $$ {d}_{k+1}^T{g}_{k+1}=-{\left\Vert {g}_{k+1}\right\Vert}^2+\left(\frac{g_{k+1}^T{y}_k}{s_k^T{y}_k}-\frac{s_k^T{g}_{k+1}}{s_k^T{y}_k}\right){s}_k^T{g}_{k+1} $$ (18)
Implies:
d k + 1 T g k + 1 = − g k + 1 2 + g k + 1 T y k s k T g k + 1 s k T y k − s k T g k + 1 2 s k T y k $$ {d}_{k+1}^T{g}_{k+1}=-{\left\Vert {g}_{k+1}\right\Vert}^2+\frac{g_{k+1}^T{y}_k{s}_k^T{g}_{k+1}}{s_k^T{y}_k}-\frac{{\left({s}_k^T{g}_{k+1}\right)}^2}{s_k^T{y}_k} $$ (19)
Let w = y k T s k g k + 1 $$ w=\left({y}_k^T{s}_k\right){g}_{k+1} $$ and v = s k T g k + 1 y k $$ v=\left({s}_k^T{g}_{k+1}\right){y}_k $$ , then by the inequality w T v ≤ 1 2 ( ‖ w ‖ 2 + ‖ v ‖ 2 $$ {w}^Tv\le \frac{1}{2}\Big({\left\Vert w\right\Vert}^2+{\left\Vert v\right\Vert}^2 $$ , we get:
g k + 1 T y k s k T g k + 1 s k T y k ≤ 1 2 g k + 1 2 y k T s k 2 + s k T g k + 1 2 y k 2 s k T y k 2 $$ \frac{g_{k+1}^T{y}_k{s}_k^T{g}_{k+1}}{s_k^T{y}_k}\le \frac{\frac{1}{2}\left[{\left\Vert {g}_{k+1}\right\Vert}^2{\left({y}_k^T{s}_k\right)}^2+{\left({s}_k^T{g}_{k+1}\right)}^2{\left\Vert {y}_k\right\Vert}^2\right]}{{\left({s}_k^T{y}_k\right)}^2} $$ (20)
Plugging (20) in (19) we get:
d k + 1 T g k + 1 ≤ − g k + 1 2 + 1 / 2 g k + 1 2 y k T s k 2 + s k T g k + 1 2 y k 2 s k T y k 2 − s k T g k + 1 2 s k T y k $$ {d}_{k+1}^T{g}_{k+1}\le -{\left\Vert {g}_{k+1}\right\Vert}^2+\frac{1/2\left[{\left\Vert {g}_{k+1}\right\Vert}^2{\left({y}_k^T{s}_k\right)}^2+{\left({s}_k^T{g}_{k+1}\right)}^2{\left\Vert {y}_k\right\Vert}^2\right]}{{\left({s}_k^T{y}_k\right)}^2}-\frac{{\left({s}_k^T{g}_{k+1}\right)}^2}{s_k^T{y}_k} $$ (21)
Using y k T y k ≤ L s k T y k $$ {y}_k^T{y}_k\le L{s}_k^T{y}_k $$ in Equation (21), we obtain:
d k + 1 T g k + 1 ≤ − 1 2 g k + 1 2 + 1 2 L − 1 s k T g k + 1 2 s k T y k $$ {d}_{k+1}^T{g}_{k+1}\le -\frac{1}{2}{\left\Vert {g}_{k+1}\right\Vert}^2+\left[\frac{1}{2}L-1\right]\frac{{\left({s}_k^T{g}_{k+1}\right)}^2}{s_k^T{y}_k} $$ (22)

Therefore if L < 1 $$ L<1 $$ , the search direction satisfies d k + 1 T g k + 1 < 0 $$ {d}_{k+1}^T{g}_{k+1}<0 $$ . A BIV1 method's similar descending feature is demonstrated.

Now, the global convergence of the algorithm is established by demonstrating that, under appropriate conditions, the sequence generated by the algorithm converges to a stationary point of the objective function. This characteristic is vital for ensuring the reliability of the algorithm in solving a wide range of unconstrained optimization problems.

It may be inferred that Dai et al. [31] established the necessary condition for CG techniques to converge while using Wolfe line search conditions mentioned in Step 3 of the algorithm outline.

Lemma: Let Assumption (1), hold. Consider methods (2) and (3), where α k $$ {\alpha}_k $$ is obtained while satisfying the Wolfe conditions and d k $$ {d}_k $$ is a descent direction. If:
∑ k ≥ 0 1 d k + 1 2 = ∞ $$ {\sum}_{k\ge 0}\frac{1}{{\left\Vert {d}_{k+1}\right\Vert}^2}=\infty $$ (23)
then:
lim k → ∞ inf g k + 1 = 0 $$ \underset{k\to \infty }{\mathit{\lim}}\mathit{\operatorname{inf}}\ \left\Vert {g}_{k+1}\right\Vert =0 $$ (24)

Theorem 2.Suppose that assumption (1) holds and the sequences g k + 1 $$ \left\{{g}_{k+1}\right\} $$ and d k + 1 $$ \left\{{d}_{k+1}\right\} $$ are generated by BIV1 and BIV2 Algorithms. Also, let f $$ f $$ be strongly convex then:

lim k → ∞ inf g k = 0 $$ \underset{k\to \infty }{\mathit{\lim}}\mathit{\operatorname{inf}}\kern0.35em \left\Vert {g}_k\right\Vert =0 $$ (25)

Proof: From the search direction given by (3), we have:
d k + 1 = − g k + 1 + β k BIV 1 s k $$ \left\Vert {d}_{k+1}\right\Vert =\left\Vert -{g}_{k+1}+{\beta}_k^{\mathrm{BIV}1}{s}_k\right\Vert $$ (26)
After manipulation of the new β k BIV 1 $$ {\beta}_k^{\mathrm{BIV}1} $$ in (11) to facilitate the convergence proof, we obtain:
d k + 1 = − g k + 1 + g k + 1 T y k d k T y k s k − s k T g k + 1 d k T y k s k $$ \kern-1.8em \left\Vert {d}_{k+1}\right\Vert =\left\Vert -{g}_{k+1}+\frac{g_{k+1}^T{y}_k}{d_k^T{y}_k}{s}_k-\frac{s_k^T{g}_{k+1}}{d_k^T{y}_k}{s}_k\right\Vert $$
≤ g k + 1 + g k + 1 L s k 2 μ s k 2 + g k + 1 s k 2 μ s k 2 $$ \le \left\Vert {g}_{k+1}\right\Vert +\frac{\left\Vert {g}_{k+1}\right\Vert L{\left\Vert {s}_k\right\Vert}^2}{\mu {\left\Vert {s}_k\right\Vert}^2}+\frac{\left\Vert {g}_{k+1}\right\Vert {\left\Vert {s}_k\right\Vert}^2}{\mu {\left\Vert {s}_k\right\Vert}^2} $$
≤ 1 + L μ + 1 μ g k + 1 ≤ μ + L + 1 μ g k + 1 $$ \kern3.5em \le \left(1+\frac{L}{\mu }+\frac{1}{\mu}\right)\left\Vert {g}_{k+1}\right\Vert \le \left[\frac{\mu +L+1}{\mu}\right]\left\Vert {g}_{k+1}\right\Vert $$ (27)
This leads to:
∑ k ≥ 1 1 d k 2 ≥ μ μ + L + 1 1 Γ ∑ k ≥ 1 1 = ∞ $$ {\sum}_{k\ge 1}\frac{1}{{\left\Vert {d}_k\right\Vert}^2}\ge \left(\frac{\mu }{\mu +L+1}\right)\frac{1}{\varGamma }{\sum}_{k\ge 1}1=\infty $$

Therefore, we get lim k → ∞ inf g k = 0 $$ \underset{k\to \infty }{\mathit{\lim}}\mathit{\operatorname{inf}}\ \left\Vert {g}_k\right\Vert =0 $$ . Also, the same can be similarly shown for BIV2 method.

4 Numerical Results

This section presents the numerical results to assess the performance of the proposed BIV1 and BIV2 methods for solving unconstrained optimization problems and training neural networks.

4.1 Unconstrained Optimization Problems

In this subsection, a series of experiments is conducted to evaluate the effectiveness of the BIV1 and BIV2 methods. The performance of these methods is compared with that of the original HS method [27]. The test problems are sourced from the CUTE library [32], in addition to other unconstrained problem collections [33, 34]. The problems vary in dimensionality. To ensure a fair comparison, all methods utilize the weak Wolfe line search for computing the step length α k $$ {\alpha}_k $$ , with the parameters set to ρ = 0.01 , and σ = 0.3 $$ \rho =0.01, and\ \sigma =0.3 $$ in Step 3 of the algorithmic outline. Instances where a method fails to converge are denoted by “F”. The implementations are coded in MATLAB 2013b and executed on an HP i5 CPU. The results are summarized in Table 2, which includes the number of iterations (NOI), number of function evaluations (NOF), and CPU time (CPUT) for each method. Additionally, performance profiles proposed by Dolan and Moré e [35] are used to visually represent the performance of the algorithms in terms of CPUT, NOI, and NOF. In these profiles, the top curve indicates the superior performance of the corresponding method. For a detailed interpretation of the performance profiles (see [35]). Figures 1-3 graphically demonstrate the effectiveness of the proposed methods.

TABLE 2. Numerical result.
HS BIV1 BIV2
Test function Dimension NOI NOF CPUT NOI NOF CPUT NOI NOF CPUT
dixmaana 1500 29 110 0.316537 18 71 0.180405 28 98 0.259175
3000 29 111 0.706153 24 85 0.543393 33 106 0.68775
15,000 30 102 2.23231 25 106 1.968824 31 96 1.79831
30,000 30 108 7.998396 23 112 3.737099 24 89 2.492262
dixmaanb 1500 24 109 0.201828 25 95 0.134428 25 91 0.135213
3000 21 120 0.343729 28 99 0.361824 32 135 0.449273
15,000 32 150 2.061474 31 134 1.849407 29 113 1.494153
30,000 29 158 4.226191 58 202 5.354701 25 105 2.796302
dixmaanc 1500 29 119 0.203829 25 101 0.146666 25 114 0.148214
3000 31 170 0.55656 29 114 0.36507 27 108 0.359118
3500 31 170 0.569967 29 114 0.408739 27 108 0.340748
dixmaanh 150 73 159 0.074138 84 289 0.060672 100 162 0.043974
300 110 211 0.075646 123 369 0.115186 118 176 0.068489
1500 220 359 0.489699 399 991 1.249954 184 252 0.318739
3000 279 450 1.47394 450 1186 3.742389 263 342 1.068857
dixmaani 150 914 1324 0.317954 509 1524 0.350794 699 761 0.174667
300 1835 2688 0.912329 1690 4365 1.488733 1610 1701 0.594278
dixmaank 30,000 523 770 30.0027 263 720 28.09845 560 649 25.53606
dixmaanl 1500 361 542 1.081864 270 825 1.623452 274 344 0.713821
3000 324 503 2.067315 243 702 3.027228 833 906 3.862978
dixon3dq 4 36 84 0.012875 34 80 0.00452 42 92 0.005674
10 95 173 0.011285 67 112 0.009195 79 139 0.009589
50 500 742 0.052055 488 722 0.048882 431 580 0.036346
150 F F F 1543 2200 0.152255 1791 2396 0.184449
dqdrtic 500 63 215 0.039847 62 215 0.014765 58 189 0.012824
1000 57 200 0.022139 57 212 0.023357 85 309 0.034885
5000 87 225 0.112033 81 253 0.127161 83 287 0.146353
10,000 80 276 0.245279 85 254 0.242468 68 228 0.218394
edensch 500 41 120 0.052105 47 135 0.049649 43 115 0.041321
1000 38 129 0.076774 37 104 0.057072 45 115 0.062021
5000 59 209 0.628168 43 155 0.470628 33 108 0.330272
10,000 66 366 2.209617 42 127 0.752922 63 338 1.995954
eg2 4 62 269 0.0258 53 149 0.011001 28 90 0.005776
10 170 527 0.02691 40 113 0.00783 72 261 0.012004
freuroth 4 118 332 0.028455 110 313 0.022637 95 287 0.013671
10 143 581 0.026425 131 315 0.020824 104 266 0.023772
50 276 1852 0.106111 135 505 0.03218 204 1095 0.058964
genrose 5 136 301 0.01805 128 280 0.014683 151 320 0.017226
10 231 396 0.02025 212 390 0.020666 195 362 0.01679
50 518 851 0.040162 556 859 0.056088 588 904 0.054324
100 1040 1532 0.084112 1043 1469 0.100657 1038 1489 0.103955
himmelbg 500 2 9 0.007709 2 19 0.003734 2 9 0.001225
1000 2 9 0.002726 2 19 0.004869 2 9 0.002142
5000 4 24 0.029593 2 20 0.02599 3 21 0.019761
10,000 2 11 0.026899 2 21 0.050476 2 11 0.027043
liarwhd 500 33 193 0.032243 37 190 0.025924 38 198 0.022408
1000 35 194 0.03873 35 173 0.026811 31 178 0.024539
5000 33 197 0.154518 31 190 0.148918 42 231 0.177914
10,000 36 202 0.27832 40 246 0.349674 38 212 0.296326
tridia 100 399 601 0.047609 340 501 0.047107 352 537 0.046237
500 919 1323 0.12928 806 1185 0.136477 810 1217 0.137777
1000 1318 1896 0.283023 1324 1914 0.318049 1259 1797 0.305579
woods 500 143 373 0.052992 180 516 0.062388 157 418 0.042886
1000 145 340 0.059803 155 384 0.057868 145 366 0.054964
5000 185 436 0.336435 182 510 0.399586 152 425 0.331176
10,000 180 485 0.665108 131 379 0.537269 201 525 0.771983
bdexp 500 F F F 2 17 0.005497 2 7 0.002079
1000 F F F 2 17 0.007379 2 7 0.004119
5000 F F F 2 18 0.047326 3 19 0.042788
10,000 F F F 2 19 0.122673 2 9 0.05276
exdenschnf 500 35 140 0.029804 33 135 0.023352 30 128 0.019169
1000 33 171 0.045795 31 157 0.035075 37 149 0.033175
5000 37 156 0.187795 33 143 0.177363 35 184 0.221485
10,000 32 143 0.31959 22 114 0.255317 36 153 0.355844
exdenschnb 500 19 81 0.013092 27 90 0.008818 25 89 0.007233
1000 30 128 0.019187 28 88 0.013373 26 113 0.014828
5000 30 144 0.079273 23 95 0.053415 31 111 0.06545
10,000 24 116 0.118173 25 92 0.09615 22 89 0.091395
genquartic 500 22 103 0.014983 30 90 0.010116 31 96 0.011146
1000 34 106 0.017846 30 94 0.013895 39 112 0.015938
5000 83 296 0.200322 22 82 0.05613 32 125 0.090893
10,000 80 344 0.405754 33 102 0.129429 38 124 0.153277
sine 500 F F F 41 121 0.017884 79 181 0.028588
1000 F F F 179 430 0.120689 30 127 0.032797
3000 F F F 46 156 0.165628 F F F
4000 F F F 148 279 0.36614 32 103 0.13183
nonscomp 500 69 173 0.019018 58 135 0.012412 59 139 0.012658
1000 64 164 0.02137 80 176 0.022737 56 135 0.016616
5000 84 234 0.133352 113 239 0.163906 60 149 0.096034
8000 96 335 0.279778 92 206 0.203052 52 155 0.137261
power1 4 36 115 0.010565 34 84 0.004088 39 92 0.006248
10 80 152 0.007042 99 181 0.014148 93 167 0.012801
50 525 770 0.039481 424 601 0.041841 480 699 0.047738
100 1507 2212 0.115852 950 1373 0.093585 1213 1761 0.122915
raydan2 500 13 104 0.017271 13 72 0.008234 13 79 0.009178
1000 14 109 0.023428 13 67 0.013571 13 88 0.016172
5000 13 113 0.089322 16 67 0.057177 15 106 0.079644
10,000 18 119 0.169038 16 77 0.120475 15 90 0.136587
diagonal1 4 28 85 0.027115 15 60 0.002191 23 83 0.002858
10 35 96 0.007381 34 94 0.0043 34 86 0.004209
50 60 134 0.009285 66 141 0.009415 60 128 0.009754
100 86 207 0.015374 85 155 0.015413 85 174 0.015016
diagonal3 4 24 79 0.009064 25 62 0.002967 28 72 0.003306
10 44 100 0.00573 30 82 0.005306 29 69 0.003596
50 64 123 0.010683 62 117 0.009367 68 151 0.011549
100 77 148 0.011931 79 142 0.013774 86 147 0.015354
bv 500 34 197 0.313009 15 55 0.082684 16 60 0.095251
500 34 197 0.323984 15 55 0.092808 16 60 0.093831
ie 100 24 108 0.627906 19 52 0.291691 21 64 0.359395
10 17 77 0.013197 16 48 0.010059 20 63 0.009969
100 24 108 0.607525 19 52 0.292058 21 64 0.357973
500 20 79 10.36819 18 61 8.168849 22 78 10.92053
singx 10 138 423 0.057436 150 468 0.045229 161 478 0.03211
100 163 482 0.058416 83 276 0.034068 202 596 0.080094
500 176 495 1.114685 84 249 0.558046 182 573 1.317241
1000 327 1034 8.013881 131 433 3.387001 181 634 4.925833
lin 10 20 100 0.40033 8 40 0.171426 15 85 0.330003
100 22 105 0.927588 12 61 0.568424 17 80 0.755016
500 19 88 1.472771 17 76 1.239389 7 38 0.604436
1000 25 145 101.473 16 80 55.37229 17 103 71.63816
osb2 11 515 915 0.142208 520 923 0.120573 584 1002 0.133202
pen1 5 F F F 305 996 0.077507 109 420 0.031771
10 F F F 286 941 0.10827 32 139 0.014378
100 89 525 0.543558 118 395 0.543039 89 460 0.481589
rosex 50 39 187 0.041484 41 198 0.011787 33 153 0.011307
100 55 271 0.029444 49 297 0.029552 42 187 0.0207
500 44 195 0.409298 39 195 0.407273 38 170 0.352088
1000 45 232 1.655528 46 234 1.689615 47 203 1.427371
trid 500 83 160 0.314366 43 108 0.194168 47 112 0.206705
1000 44 115 0.583352 43 121 0.60428 47 113 0.576777
5000 54 138 13.26894 45 118 11.16649 46 110 10.52469
Details are in the caption following the image
FIGURE 1
Open in figure viewerPowerPoint
Number of iterations.
Details are in the caption following the image
FIGURE 2
Open in figure viewerPowerPoint
Number of function evaluations.
Details are in the caption following the image
FIGURE 3
Open in figure viewerPowerPoint
CUP time.

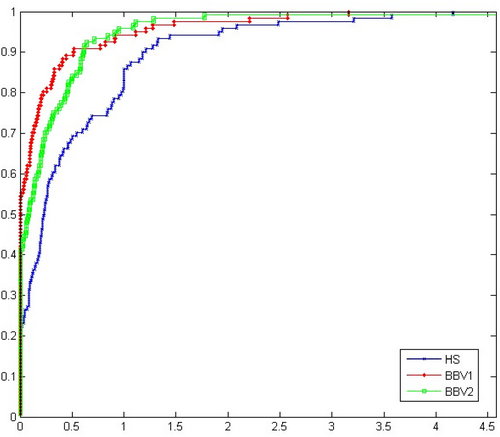
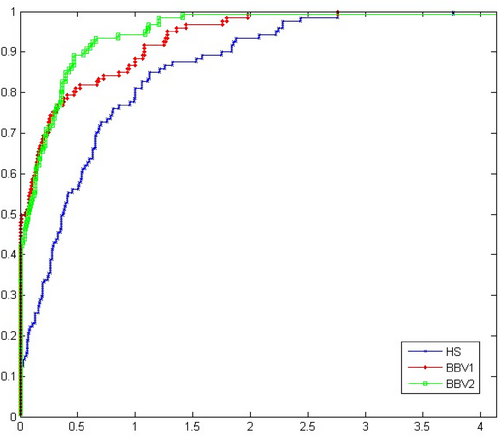
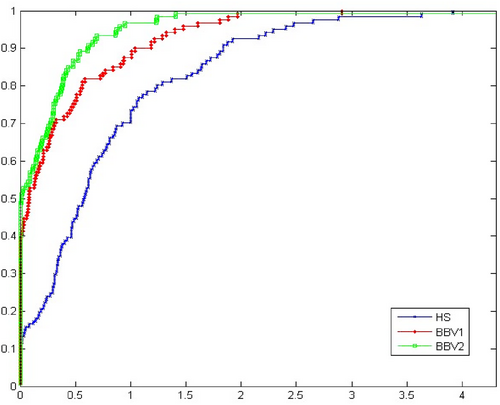
In this subsection, we present a series of experiments to evaluate the performance of the proposed BIV1 and BIV2 methods for unconstrained optimization problems. These methods are compared to the traditional (HS) method [8], using a diverse set of test problems sourced from the CUTE library [32] and other unconstrained problem collections [33, 34]. These test problems are selected to cover a range of dimensions, providing a comprehensive analysis of the methods' performance in different scenarios.

To ensure fairness in comparison, all methods employed the weak Wolfe line search for computing the step length α k $$ {\alpha}_k $$ , with parameters set to ρ = 0.01 , and σ = 0.3 $$ \rho =0.01, and\ \sigma =0.3 $$ as per the algorithm outline. The methods are tested on a variety of problems, and instances where a method fails to converge are denoted as “F”. The algorithms are implemented in MATLAB 2013b and run on an HP i5 CPU.

We evaluate the performance of the methods using three key metrics: the number of iterations (NOI), the number of function evaluations (NOF), and CPU time (CPUT). The results are summarized in Table 2, which presents the performance of each method across these metrics.
  • (NOI): BIV1 and BIV2 methods consistently outperform the HS method in terms of the number of iterations. On average, BIV2 requires fewer iterations to converge to an optimal solution, with BIV2 showing similar but slightly improved performance in higher-dimensional problems.
  • (NOF): The number of function evaluations required by the BIV1 and BIV2 methods is lower than that of the HS method, particularly for larger problem sizes. This suggests that the proposed methods are more efficient in terms of evaluating the objective function during the optimization process.
  • CPU Time (CPUT): The BIV1 and BIV2 methods demonstrate a significant reduction in CPU time compared to the HS method, especially when solving large-scale problems. This reduction in computational time is especially notable for the higher-dimensional test cases, where the BIV methods exhibit faster convergence.
To further illustrate the performance of the methods, we use performance profiles as proposed by [35]. These profiles provide a visual representation of the relative performance of the algorithms with respect to CPUT, NOI, and NOF. The top curve in each profile indicates the superior performance of the corresponding method.
  • Figure 1 demonstrates the comparison of the methods in terms of the number of iterations, where the BIV1 and BIV2 methods show a clear advantage.
  • Figure 2 compares the methods based on the number of function evaluations, where the BIV1 and BIV2 methods again outperform the HS method in most test cases.
  • Figure 2 shows the performance profile for CPUT, highlighting the superiority of the BIV1 and BIV2 methods over the HS method, particularly in high-dimensional cases.

4.2 The Conjugate Gradient Algorithm in Neural Network Training Applications

Artificial Neural Networks (ANNs) are parallel computational models consisting of densely interconnected processing units, inherently capable of learning from tests and discovering new knowledge. Due to their exceptional ability to self-learn and adapt, ANNs have been successfully applied in many areas of AI see, [36, 37]. This adaptability allows ANNs to handle complex tasks where traditional methods may fall short. They often demonstrate superior accuracy and efficiency compared to other classification techniques [38], making them a preferred choice in various applications. Among the different architectures of ANNs, feedforward neural networks (FNNs) stand out as the most widely recognized and utilized across diverse applications. Their straightforward structure and effectiveness in handling numerous tasks contribute to their popularity. However, despite their strengths, the training of FNNs presents several challenges, especially when using the Backpropagation (BP) algorithm.

Backpropagation (BP) [39] of error gradients has proven effective in training feedforward neural networks, enabling them to address numerous classification and function interpolation challenges. The success of BP lies in its ability to iteratively adjust the weights within the network, thereby minimizing the error between the predicted and actual outputs. However, BP suffers from several significant drawbacks. It requires selecting three arbitrary parameters: learning rate, momentum, and the number of hidden nodes, where poor choices can lead to slow convergence. Additionally, the network may become trapped in a local minimum of the error function, resulting in suboptimal solutions. This issue is particularly problematic in complex or high-dimensional data sets, where finding the global minimum is essential for optimal performance. Moreover, BP demands many iterations to optimally adjust network weights, which can be impractical in certain applications due to time and computational resource constraints.

To address these limitations, numerical optimization theory (“Basic Optimisation Methods/by B.D. Bunday,” 1984) provides a robust set of techniques for training neural networks. These advanced methods offer an alternative to BP by focusing not only on the local gradient of the error function but also its second derivative. The first derivative measures the slope of the error surface at a given point, providing direction for the weight updates, while the second derivative assesses the curvature of the error surface, offering insights into the landscape of the optimization problem. This dual approach is crucial for determining the optimal update direction, thereby enhancing the efficiency of the training process. As these methods make use of the second derivatives of the function to be optimized, they are typically referred to as second-order methods.

Over the years, several second-order methods have been proposed (“Basic Optimisation Methods/by B.D. Bunday,” 1984), demonstrating substantial improvements in training efficiency and effectiveness. In particular, the conjugate gradient method has gained popularity in training BP networks due to its speed and simplicity. Unlike basic gradient descent, which may oscillate or converge slowly, the conjugate gradient method leverages past gradient information to determine search directions, leading to faster convergence. Studies [13, 22, 40, 41] have shown that training time can be significantly reduced when feedforward networks are trained using these second-order methods, making them highly suitable for large-scale and complex problems.

Training of neural networks (NNs) can be formulated as a problem of nonlinear unconstrained optimization. Therefore, the training procedure can be achieved by minimizing the error function E $$ E $$ , defined by the sum of squared differences between the actual output of the FNN, denoted by o j h $$ {o}_j^h $$ , and the desired output, denoted by t j h $$ {t}_j^h $$ , across all output patterns. Mathematically, this can be expressed as:
E ( w ) = 1 2 ∑ h = 1 n . h ∑ j = 1 N o j h − t j h 2 $$ E(w)=\frac{1}{2}\sum \limits_{h=1}^{n.h}\sum \limits_{j=1}^N{\left({o}_j^h-{t}_j^h\right)}^2 $$ (28)
where w ∈ R n $$ w\in {R}^n $$ represents the vector of network weights, and h $$ h $$ is the number of patterns used in the training set. This error function serves as the objective to be minimized during the training process.

This section details the experimental results aiming at evaluating the effectiveness of both the standard and new CG methods in training neural networks. The study compares the performance of the HS method with that of the new CG BIV1 and BIV2 methods through four separate program runs. The implementation was carried out using MATLAB (2013a) and the MATLAB Neural Network Toolbox version 8.1 for conjugate gradient computations. The experiments were designed to rigorously assess the training efficiency and accuracy of the methods under consideration.

During the experiments, the network training continued until the mean squared error (MSE) fell below a designated error target, effectively minimizing the error function. Consistent initial weights were used across all tested algorithms, with weights randomly initialized within the range (0, 1). This consistency ensured that differences in performance were attributable to the optimization methods rather than variations in initial conditions. The tested problems included:
  • Input P = [−1,−1,2,2;0,5,0,5] and the target T = [−1,−1,1,1], with the target error set to 1 x 10 − 10 $$ 1x{10}^{-10} $$ and the maximum epochs to 1000.

This configuration allowed for a thorough evaluation of the methods' capabilities in optimizing neural network performance, providing valuable insights into their practical application.

The results of these training methods are summarized in Table 3 and illustrated in Figures 4-6. These visual representations not only highlight the comparative performance of the different methods but also provide a clear understanding of their effectiveness in optimizing neural network training. By examining these figures and the corresponding table, one can observe the nuances of how each method influences the convergence rate, accuracy, and overall efficiency, thereby offering valuable insights into their practical applications in neural network training.

TABLE 3. Performance comparison of different training methods: epochs and mean squared error (MSE).
Method No. running Epochs MSE
HS 1 1000 8.74e-06
2 34 6.07e-09
3 41 4.40e-09
4 21 5.46e-09
BIV1 1 30 1.18e-08
2 30 1.08e-08
3 32 2.23e-09
4 11 9.10e-06
BIV2 1 31 2.08e-08
2 33 1.08e-08
3 32 4.55e-08
4 22 9.73e-09
Details are in the caption following the image
FIGURE 4
Open in figure viewerPowerPoint
Training and performance of HS.
Details are in the caption following the image
FIGURE 5
Open in figure viewerPowerPoint
Training and performance of BIV1.
Details are in the caption following the image
FIGURE 6
Open in figure viewerPowerPoint
Training and performance of BIV2.
Table 3 presents the results of different methods (HS, BIV1 and BIV2) used to train a neural network. The comparison is based on the number of epochs (iterations) required to train the network and the resulting Mean Squared Error (MSE), which measures the accuracy of the training.
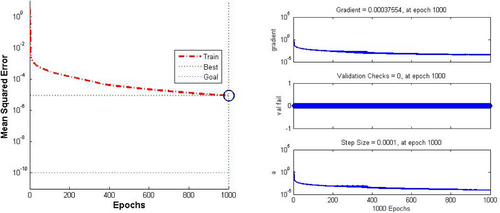
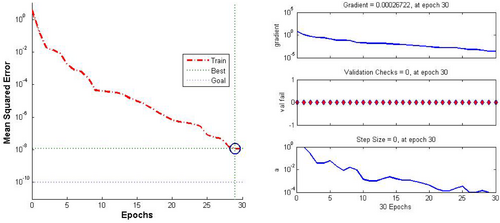
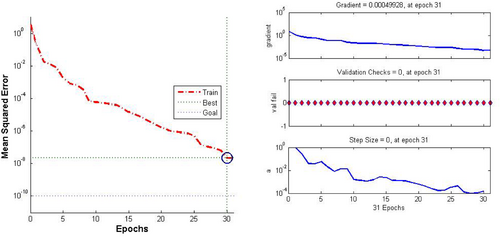
  • HS Method: This method shows a wide range of epochs (from 21 to 1000) and varying MSE values, with the lowest being 4.40e-09. However, the high number of epochs in one of the runs (1000 epochs) suggests that this method might not be the most efficient in terms of convergence speed.
  • BIV1 Method: The BIV1 method generally requires fewer epochs (between 11 and 32) and produces MSE values that are consistently low. This indicates better efficiency in terms of speed and accuracy compared to the HS method.
  • BIV2 Method: The BIV2 method shows a balanced performance, with the number of epochs ranging from 22 to 33 and producing low MSE values. This suggests that the BIV2 method offers a good compromise between speed and accuracy, making it potentially the best overall option for training neural networks in this context.

In summary, while the BIV1 method is faster with fewer epochs, the BIV2 method provides a combination of speed and accuracy, making it a reliable choice for training neural networks.

5 Conclusions

This study presents innovative gradient-based methods, BIV1 and BIV2, designed to improve unconstrained optimization and enhance neural network training. Through rigorous evaluation, the proposed methods demonstrate significant advantages over the traditional Hestenes-Stiefel method. The experimental results reveal that BIV1 and BIV2 achieve superior performance in terms of reduced computational time, fewer iterations, and lower mean squared error during neural network training. The methods' effectiveness is evident across various unconstrained optimization problems, highlighting their efficiency and robustness in high-dimensional scenarios. The BIV1 and BIV2 methods incorporate advanced conjugate gradient techniques that enhance convergence properties and computational efficiency. These improvements are particularly beneficial in training feedforward neural networks, where the optimization process is crucial for achieving accurate and reliable results. The findings underscore the potential of these methods to address complex optimization challenges and contribute to the development of more effective training algorithms for neural networks.

Author Contributions

Bassim A. Hassan: conceptualization, investigation. Issam A. R. Moghrabi: investigation, funding acquisition, methodology. Alaa Luqman Ibrahim: data curation, writing – review and editing. Hawraz N. Jabbar: software.

Conflicts of Interest

The authors declare no conflicts of interest.

Data Availability Statement

Data sharing not applicable to this article as no datasets were generated or analysed during the current study.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.