Intensity-duration-frequency (IDF) models are considered one of the most important tools used in water resources projects, as well as the design and planning of hydraulic structures such as sewerage channels, bridges, culverts, and road networks. This study aims to generate IDF curves for the Iraqi city of Babylon based on the Indian Meteorological Department (IMD) empirical reduction formula and to choose the optimal distribution that gives the greatest rainfall intensity among the three distributions used in this research (generalized extreme value, Log-Pearson type III, and Gumbel). This study examined daily rainfall data collected from the Iraqi Authority of Meteorology and Seismic Monitoring for a period of 32 years, from 1991 to 2022. The IMD reduction formula was used to calculate rainfall intensity for shorter durations (5, 10, 20, 30, 60, 120, 360, 720, and 1440 min) and custom return periods (2, 5, 10, 25, 50, and 100 years). To determine the goodness of fit for the data distributions, the Easy Fit 5.6 program was applied with three tests (the χ² test, the Anderson–Darling test, and the Kolmogorov–Smirnov test). The results showed that all distributions were acceptable for both tests and all storm durations and that the rainfall intensity decreased with increasing duration of the rainstorm. It also showed that rainfall increases rainfall intensity during large return periods. Based on the criteria of AIC and BIC, the LP-3 distribution was chosen as the best distribution to simulate rainfall in Babylon City using the IDM reduction formula.

1 Introduction

Rainfall is one of the basic components of the hydrological cycle. The variability and patterns of rainfall are crucial for agriculture as well as for the economy, as rainfall is a natural factor that greatly determines agricultural production [1, 2]. The Iraqi climate is marked by volatility and extreme characteristics. Iraq's geographical location in the Middle East, in a transitional zone between the moderate and desert climates, influences these characteristics. The most important factors in Iraq's weather are the high temperatures, particularly in the summer, where they reach record levels, especially in the central and southern regions of the country. In addition, there are climate fluctuations, where some areas experience heavy rains, while others experience drought, leading to negative impacts on agriculture and water sources [3].

For designing storm and sewer systems, determining the necessary discharge capacity of channels, and determining the capacity of pumping stations, statistics and evaluation of extreme rainfall data are crucial in water resources planning and management. Thus, their significance lies in mitigating flooding, which in turn lowers the loss of life and property, as well as insuring against water damage and assessing the likelihood of hazardous weather [4, 5].

Evaluating the relationship between rainfall intensity, duration, and frequency (IDF) curves is a fundamental component of designing a city's stormwater drainage system. Hydrologists use this mathematical relationship to study the impact of climate change on rainfall patterns. Engineers can create affordable and safe flood control solutions using IDF curves [6]. In the last few decades, research on the relationship between rainfall and IDF has drawn a lot of attention. The IDF curves were constructed for Krishna District, India, and the results showed that the rainfall data adhered to Gumbel's distribution [7]. In the Kingdom of Saudi Arabia, specifically in the Najran and Hafr Albatin regions, the frequency between rainfall depth and rainfall duration was estimated using two distribution methods (the Log Pearson type III [LPT III] and Gumbel) [8]. The IDF relationship is a mathematical equation that relates rainfall intensity, duration, and return period. IDF curves are used to estimate the return period of a recorded rainfall event or, conversely, the rainfall amount associated with a specific return period for different time intervals [8, 9].

The IDF curve for short-term rainfall in Sylhet City, Bangladesh, was developed for return periods of 2, 5, 10, 20, 50, and 100 years based on the empirical reduction formula from the Indian Meteorological Department (IMD), which has been proven to be suitable in this study and shows that the short-term data adhere to the Extreme Value Type-I distribution [10]. In Slovakia, the assessment of extreme rainfall IDF curves using basic scaling theory was expanded upon and applied to the short-duration rainfall IDF characteristics [11]. Generalized least squares and L-moments regression techniques were used to estimate short-duration design rainfall depths and create IDF relationships in Australia [12]. Also, the rainfall intensity was calculated, and the IDF curves were drawn in Riyadh City using the empirical formula. It was found that the Gumbel and LPT III distributions did not significantly change the IDF curves rainfall analysis results [13].

IDF curves are derived based on the IMD reduction formula for different cities in Iraq, like Karbala, Najaf, Kut, and so on. Following the derivation of Karbala City's IDF empirical formula and evaluation of various statistical distributions, it was determined that the Log Pearson type III (LP-3) approach was the most efficient compared to other methods ([14]). In the city of Najaf, IDF curves were estimated and the best distribution that gave the highest rainfall intensity was determined. The Gumbel distribution was selected as the optimal distribution for determining rainfall intensity for various return periods and periods [15]. In Kut City, IDF curves were generated using the lognormal probability distribution that was considered the best choice for analyzing and predicting rainfall intensity [16].

This study aims to obtain IDF curves for daily rainfall data for Babylon City (1991–2022) based on the IMD reduction formula for different return periods of 2, 5, 10, 25, 50, and 100 years. Three statistical distributions were tested: Gumbel (EV-1), Generalized Extreme Value (GEV), and LP-3 to determine the best IDF curve. Three tests, namely the χ² test, Anderson–Darling (AD) test, and Kolmogorov–Smirnov (KS) test, were conducted on the maximum daily rainfall data's probability distributions using Easy Fit 5.6 software at a 5% significance level to assess their fit to the study area's data. Urban planning and drainage projects rely on these curves and equations for designing storm sewers, canals, and other hydraulic structures.

2 Methodology

2.1 Description of Study Area

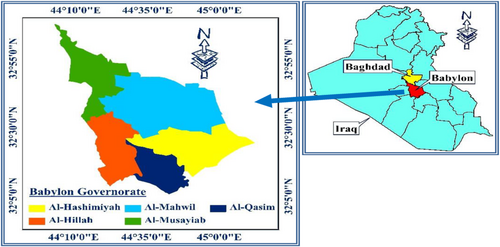
The Babylon Governorate covers approximately 1.2% of Iraq's total land area, spanning 5315 km² in central Iraq. It is situated between latitudes 32°5′41′′ N and 33°7′36′′ N and longitudes 44°2′43′′ E and 45°12′11′′ E and is bordered by Baghdad to the south. It has a population of 2,200,000. Figure 1 illustrates the local division of the Babylon Governorate into five regions: Al-Mahawil, Al-Hillah, Al-Musayyab, Al-Qasim, and Al-Hashimiyah. In general, its winters are cold and rainy, with some periods of drought, and its summers are hot because it is located in the interior region between the Euphrates and Tigris rivers [12].

Details are in the caption following the image — **FIGURE 1**
Open in figure viewer PowerPoint

The geographical location of Babylon City, located in Iraq.

2.2 Collection Rainfall Data

The data (from 1991 to 2022) utilized was sourced from the Iraqi Meteorological Organization, and Seismology. This information was utilized to create the IDF curve for Babylon City and determine the equation for the intensity duration frequency relationship is shown in Table 1.

TABLE 1. The highest daily rainfall amount recorded by the Iraqi Meteorological Organization and Seismology in Babylon Governorate between 1991 and 2022.

No.	Year	Maximum daily rainfall (mm/year)	No.	Year	Maximum daily rainfall (mm/year)
1	1991	16.60	17	2007	7.80
2	1992	32.60	18	2008	10.60
3	1993	26.95	19	2009	7.80
4	1994	23.60	20	2010	11.00
5	1995	31.50	21	2011	24.00
6	1996	29.90	22	2012	73.30
7	1997	17.70	23	2013	98.60
8	1998	13.90	24	2014	25.20
9	1999	16.10	25	2015	38.00
10	2000	19.80	26	2016	46.90
11	2001	12.10	27	2017	9.90
12	2002	40.40	28	2018	21.40
13	2003	43.20	29	2019	51.30
14	2004	22.00	30	2020	24.20
15	2005	24.20	31	2021	16.50
16	2006	24.10	32	2022	23.00

2.3 Analysis Rainfall Data

To perform a careful examination of IDF curves with constant duration precipitation amounts, it is necessary to determine the probability of best fit between theory distributions. The following procedures must be followed to generate any IDF curve ([16, 17]):

Examining the rainfall information and choosing the highest amount of rainfall in a single day each year.
Develop probability density functions (PDFs) and identify the most suitable distribution for the data sets provided in the study area.
The distribution of best-fit yields a mean for calculating the intensity of rainfall over a given duration and for certain return periods.

2.4 Short Duration Rainfall Calculation

The rainfall data consists of the maximum daily rainfall values from 1991 to 2022. Rainfall values can be obtained from maximum daily rainfall corresponding values of (5, 10, 15, 20, 30, 60, 120, 360, 720, and 1440 min) using the Indian Meteorological Department's (IMD) empirical reduction formula [18], which is:

{P}_t={P}_{24}\times {\left(\ \frac{t}{24}\right)}^{\frac{1}{\ 3}}

(1)

where P_t is the required rainfall depth in millimeters (mm) for the given duration of t hours, the constant value of 24 indicates the number of day hours, t is the required rainfall depth in hours, and P₂₄ is the maximum depth of daily rainfall in millimeters.

2.5 Theory of Distributions

2.5.1 Gumbel Distribution Theory

The Gumbel distribution, also known as EV-1 or GEV Distribution Type-I, is employed to characterize the distribution of the largest (or smallest) sample sizes across various distributions. This distribution is commonly used for IDF analysis because it can accommodate various modeling techniques. The Gumbel distribution is rather straightforward and just makes use of extreme events (the peak rainfalls or the maximum values) [19]. The maximal intensity, as well as the statistical variables (average and standard deviation), should be calculated for any duration given by the following equation is the Gumbel extreme value distribution [20]:

{P}_T={P}_{\mathrm{avg}}+\left(K\times S\right)

(2)

where P_T is the rainfall amount (mm) during various time intervals for a certain return period T (year), P_avg is the average maximum precipitation for certain time intervals can be calculated using the equation provided:

{P}_{\mathrm{avg}}=\frac{1}{n}\ \sum \limits_{i=1}^n{P}_i

(3)

P_i is an individual rainfall extremist amount, n is the record years, and K is the Gumbel frequency factor that depends on both the sample size and the return period, which can be calculated using this equation:

K=-\frac{\sqrt{6}}{\pi}\times \left[0.5772+\ln \left(\ \ln \frac{T}{T-1}\right)\right]

(4)

S is the data (P_i) standard deviation can be computed using the following equation:

S={\left[\frac{1}{n-1}\times \sum \limits_{i=1}^n{\left({P}_i-{P}_{\mathrm{avg}}\right)}^2\right]}^{\frac{1}{2}}

(5)

By multiplying the frequency factor K with S, the rainfall intensities for a specific return period from the average data mentioned earlier can be calculated. The equation below can be used to find the intensity I (mm/h) for the return period T:

{I}_t=\frac{P_t}{\ {T}_d}

(6)

where T_d is the duration (h).

2.5.2 LPT III Distribution Theory

It is a type of Pearson distribution. This type of log distribution transforms the water volume before being analyzed by the LPT III for hydrologic frequency in the year 1967, according to a review by the USA Weather Resources Council. Computers use it with the frequency factors in a frequency analysis because it is quick to calculate. LPT III is therefore important and helpful [19]. Using historical IDF curves, this probability model was used to determine the rainfall durations for each station as well as the intensity of the precipitation for various return periods. Logarithms of the measured values are used. Using the data that have been logarithmically transformed, the mean and standard deviation are calculated. The LPT's straightforward provided by the following equations [8]:

P=\log \left({P}_i\right)

(7)

{P}_T={P}_{\mathrm{avg}}+{K}_T\times S

(8)

{P}_{\mathrm{avg}}=\frac{1}{n}\times \sum \limits_{i=1}^1P

(9)

S={\left[\frac{1}{n-1} \times \sum \limits_{i=1}^n{\left({P}_i-{P}_{\mathrm{avg}}\right)}^2\right]}^{\frac{1}{2}}

(10)

where P_T, S, and P_avg are defined the same way as in Gumbel theory, except they are calculated based on the logarithmically transformed numbers of P, rather than P_i values. The symbol K_T is used to calculate the frequency factor distribution based on the return period (T) and the skewness coefficient (C_s). C_s is necessary for determining the frequency factor and is calculated by the following equation [8]:

{C}_{\mathrm{s}}=\frac{n\sum \limits_{i=1}^n{\left(\ {P}_i-{P}_{\mathrm{avg}}\ \right)}^3}{\left(n-1\right)\ \left(n-2\right)\ {(s)}^3}

(11)

Hydrology references, such as [21], contain tables of K_T values. K_T distribution for LPT III can be determined by knowing C_s and T. The estimated maximum value for the return period will be provided to the solution in Equation (8).

2.5.3 GEV Distribution Theory

The GEV distribution, a set of continuous probability distributions in probability theory and statistics was developed in extreme value theory by merging the Gumbel, Fréchet, and Weibull families, also referred to as type I, II, and III extreme value distributions. According to the extreme value theorem, among a set of randomly distributed variables with the same distribution that are independently distributed, the GEV distribution is the only possible limit distribution for suitably normalized maxima. It can be stated as [22]:

F(y)=\exp\ \left\{-{\left[1+\theta\ \left(\frac{y}{\sigma }-\psi \right)\right]}^{\frac{-1}{\theta }}\right\}\kern2em \mathrm{for}\kern1.25em y\ge \sigma\ \left(\ \frac{\psi -1\ }{\theta}\right)

(12)

where the parameters for shape, scale, and location are ψ > 0, σ > 0, and ψ, respectively. When θ = 0, the GEV distribution is replaced by the Gumbel distribution (EV-1). When θ < 0, the Extreme Value Type II distribution suggests an upper bound for the variable; however, this is not the case when considering the maximum intensity of precipitation. Next, the value of y_T is given as.

{y}_T=\sigma\ \left\{\psi +\frac{{\left[-\mathrm{lnln}\left(1-\frac{1}{T}\right)\right]}^{-\theta }-1}{\theta}\right\}

(13)

2.6 The Goodness of Fit Test

The goal of the goodness-of-fit test is to assess the extent to which the observed frequency of occurrence in the sample aligns with the expected frequencies based on the proposed distribution. Three tests were used (the χ², AD, and KS) to transform goodness tests using (Easy Fit 5.6) software https://easyfit.informer.com. The lower value of the three tests is considered the best for the chosen distributions.

2.6.1 AD Test

An observed CDF and an expected CDF are compared using the AD test. The AD test is stronger and has more weight than the KS test because this method gives the tail of the distribution more weight than the KS test. If the statistic is greater than a critical value at a given significance level (α), the test rejects the hypothesis about the distribution level. The most often utilized significance level is α = 0.05. After that, the test distribution statistic is compared with this number to see if it can be rejected or not [21]. A² is the AD test statistic.

{A}^2=-n-\frac{1}{n}\ {\sum}_{i=1}^n\left(2i-1\right).\kern0.5em \left[\ln F\left({X}_i\right)+\ln \left(1-F\left({X}_n-i+1\right)\right)\right]

(14)

2.6.2 KS Test

The largest vertical distance between the empirical and theoretical CDFs is the basis for the KS test statistic. If the test statistic at a selected significance level is greater than the critical value, a hypothesis is rejected, just like with the AD test statistic [21]. At the α = 0.05 level of significance. It is assumed that the samples come from a CDF F(x). The test statistic (D) is:

D=\max \left[F\left({x}_i\right)-\frac{i-1}{n},\frac{i}{n}-F\left({x}_i\right)\ \right]

(15)

2.6.3 χ² Test

Finding out if a sample is representative of a given distribution is done with the χ² test. Please take note that this statistical test is not very useful and is not thought to have high power [21]. The data used for the test is binned, and the number of bins (k) is established by:

k=1+{\log}_2N

(16)

The χ² statistic is defined as:

{\chi}^2=\sum \limits_{i=1}^k\frac{{\left({O}_i-{E}_i\ \right)}^2}{E_i}

(17)

where O_i represents the frequency observed in bin i, while E_i signifies the frequency expected in bin i as calculated by:

{E}_i=F\left({x}_2\right)-F\left({x}_1\right)

F represents the CDF for the given probability distribution, with x₁ and x₂ serving as the boundaries for bin i. If the test statistic χ² exceeds the critical value, the distributional form hypothesis is rejected at the selected significance level (0.05).

2.7 Derivation of IDF Equations

The IDF application creates empirical equations utilizing existing rainfall data to relate maximum rainfall intensity, frequency, and duration. These empirical equations represent the connection between the parameters of rainfall duration. The maximum rainfall is regarded as a dependent variable and the frequencies as independent variables. The literature contains several frequently used equations for hydrology applications. The following outlines the typical formats of the four commonly used equations that depict the correlation between rainfall intensity and duration [21]:

Sherman's equation:
$i=\frac{a}{{\left(T+b\right)}^c}$ (18)
Bernard's equation:
$i=\frac{C^{\ast }{T}^m}{d^e}$ (19)
Talbot's equation:
$i=\frac{C^{\ast }{T}^m}{d+b}$ (20)
Kimijima's equation:
$i=\frac{C^{\ast }{T}^m}{d^e+b}$ (21)

where the i (mm/h) is used for precipitation intensity, D (min) stands for duration, T (years) symbolizes the return period, while a, b, c, e, and m stand for the constant parameters linked to meteorological circumstances. The empirical equations mentioned earlier show that as the duration of rainfall increases for a specific return period, the intensity of rainfall decreases. These empirical equations have been widely used in practical hydrology applications. The Sherman equation is employed in the present study to determine the intensity of rainfall for certain return periods.

3 Results and Discussion

Five different steps were adopted for the generation of IDF curves and selection of best distributions, the steps continuously discussed in the following sections.

3.1 The Application of IMD Empirical Reduction Formula

The IDF curves are generated based on the IMD reduction formula according to Steps 1 and 2.

Step 1: Examining the precipitation records and choosing the highest amount of daily rainfall from the compiled daily rainfall data over the course of the year, as presented in Table 1.

Step 2: Using the IMD reduction formula, Equation (1), and the daily rainfall depth (mm) calculated over a period of 5, 10, 15, 20, 30, 60, 120, 360, 720, and 1440 min from the maximum daily rainfall during the year. Table 2 describes how shorter-duration rainfalls are calculated from the annual maximum daily rainfall.

TABLE 2. The generated rainfall P_t depth (mm) for the duration (5–1440 min).

Year	P₂₄	P_t
Year	P₂₄	5	10	15	20	30	60	120	360	720	1440
1991	16.60	2.51	3.17	3.63	3.99	4.57	5.76	7.25	10.46	13.18	16.60
1992	32.60	4.94	6.22	7.12	7.84	8.97	11.30	14.24	20.54	25.87	32.60
1993	26.95	4.08	5.14	5.89	6.48	7.42	9.34	11.77	16.98	21.39	26.95
1994	23.60	3.57	4.50	5.15	5.67	6.49	8.18	10.31	14.87	18.73	23.60
1995	31.50	4.77	6.01	6.88	7.57	8.67	10.92	13.76	19.84	25.00	31.50
1996	29.90	4.53	5.70	6.53	7.19	8.23	10.37	13.06	18.84	23.73	29.90
1997	17.70	2.68	3.38	3.87	4.25	4.87	6.14	7.73	11.15	14.05	17.70
1998	13.90	2.10	2.65	3.04	3.34	3.82	4.82	6.07	8.76	11.03	13.90
1999	16.10	2.44	3.07	3.52	3.87	4.43	5.58	7.03	10.14	12.78	16.10
2000	19.80	3.00	3.78	4.32	4.76	5.45	6.86	8.65	12.47	15.72	19.80
2001	12.10	1.83	2.31	2.64	2.91	3.33	4.19	5.29	7.62	9.60	12.10
2002	40.40	6.12	7.71	8.82	9.71	11.12	14.01	17.65	25.45	32.07	40.40
2003	43.20	6.54	8.24	9.43	10.38	11.89	14.98	18.87	27.21	34.29	43.20
2004	22.00	3.33	4.20	4.80	5.29	6.05	7.63	9.61	13.86	17.46	22.00
2005	24.20	3.66	4.62	5.29	5.82	6.66	8.39	10.57	15.25	19.21	24.20
2006	24.10	3.65	4.60	5.26	5.79	6.63	8.36	10.53	15.18	19.13	24.10
2007	7.80	1.18	1.49	1.70	1.87	2.15	2.70	3.41	4.91	6.19	7.80
2008	10.60	1.61	2.02	2.31	2.55	2.92	3.67	4.63	6.68	8.41	10.60
2009	7.80	1.18	1.49	1.70	1.87	2.15	2.70	3.41	4.91	6.19	7.80
2010	11.00	1.67	2.10	2.40	2.64	3.03	3.81	4.80	6.93	8.73	11.00
2011	24.00	3.63	4.58	5.24	5.77	6.60	8.32	10.48	15.12	19.05	24.00
2012	73.30	11.10	13.98	16.01	17.62	20.17	25.41	32.02	46.18	58.18	73.30
2013	98.60	14.93	18.81	21.53	23.70	27.13	34.18	43.07	62.11	78.26	98.60
2014	25.20	3.82	4.81	5.50	6.06	6.93	8.74	11.01	15.88	20.00	25.20
2015	38.00	5.75	7.25	8.30	9.13	10.46	13.17	16.60	23.94	30.16	38.00
2016	46.90	7.10	8.95	10.24	11.27	12.91	16.26	20.49	29.55	37.22	46.90
2017	9.90	1.50	1.89	2.16	2.38	2.72	3.43	4.32	6.24	7.86	9.90
2018	21.40	3.24	4.08	4.67	5.14	5.89	7.42	9.35	13.48	16.99	21.40
2019	51.30	7.77	9.79	11.20	12.33	14.12	17.78	22.41	32.32	40.72	51.30
2020	24.20	3.66	4.62	5.29	5.82	6.66	8.39	10.57	15.25	19.21	24.20
2021	16.50	2.50	3.15	3.60	3.97	4.54	5.72	7.21	10.39	13.10	16.50
2022	23.00	3.48	4.39	5.02	5.53	6.33	7.97	10.05	14.49	18.26	23.00

In this study, the IMD reduction formula was used to separate the maximum daily rainfall depth into rainfall depths shorter than 1 day (5, 10, 20, 30, 60, 120, 360, 720, and 1440 min). The highest value was in 2013, at all rainstorm durations (Table 2). As shown in Table 1, the rainfall rate over a period of 16 years (1991–2006) was 24.7 mm. The rainfall rate in the recent period (2007–2022) was 30.6 mm, indicating an increase in the rainfall rate. The Kingdom of Saudi Arabia, specifically in the Riyadh region, has previously applied the IMD to separate the maximum daily rainfall depth into shorter depths (10, 20, 30, 60, 120, and 1440 min). The equation predicts the rainfall amounts in the city of Riyadh for any return period and storm duration [13].

This method (IMD) was also used to separate the daily rainfall depth into periods shorter than a day (1, 2, 3, 6, and 12 h), and it was noted that the Gumbel distribution was the best distribution used [7]. As for Iraq, the reduction equation (IMD) was used, specifically in the city of Baghdad [19], to separate the daily rainfall data into short depths (15, 30, 60, 120, 360, and 720 min) and during limited return periods (2–100 years) used in creating IDF curves, and all distribution results were acceptable at a significance level of 10%.

3.2 Selection of Best Distribution

The best statistical distributions among the Gumbel (EV-1), GEV, and LP-3 were selected according to Step 3, in addition to finding the rainfall intensity (mm/h) (Step 4) based on Sherman's equation (Equation 18).

Step 3: The short-duration rainfall dataset (5, 10, 15, 20, 30, 60, 120, 360, 720, and 1440 min) from Table 2 is used in Easy-Fit 5.6 to determine the goodness of fit of the three distributions used in this study (EV-1, GEV, and LP-3) to these datasets. Three tests were conducted for these distributions (the χ² test, the AD test, and the KS test) at a 5% significance level. The results showed absolute acceptance and non-rejection of any distribution for the three tests for each storm duration.

Step 4: The latest version of the Hydrognomon program used Sherman's equation (Equation 18) to turn rainfall depth data (Table 2) for each storm duration and specific return periods (2, 5, 10, 25, 50, and 100) into rainfall intensity (mm/ h). Tables 3, 4, and 5 display the rainfall intensity data for the LP-3, GEV, and the Gumbel (EV-1) distributions, respectively, over a specific period (min).

TABLE 3. The rainfall intensity (in millimeters per hour) for a specific period (min) utilizing the Log-Pearson type III (LP-3) distribution.

Storm duration (min)	Return period (years)
Storm duration (min)	2	5	10	25	50	100
5	40.34	67.53	89.65	122.58	150.94	182.76
10	25.88	43.32	57.51	78.63	96.83	117.24
20	16.39	27.44	36.43	49.81	61.34	74.26
30	12.51	20.94	27.80	38.01	46.81	56.67
60	7.86	13.15	17.45	23.87	29.39	35.58
120	4.92	8.24	10.93	14.95	18.41	22.29
360	2.34	3.92	5.20	7.11	8.76	10.60
720	1.46	2.45	3.25	4.45	5.48	6.63
1440	0.91	1.53	2.03	2.78	3.42	4.14

TABLE 4. The rainfall intensity (in millimeters per hour) for a specific period (min) utilizing Generalized Extreme Value (GEV) distribution.

Storm duration (min)	Return period (years)
Storm duration (min)	2	5	10	25	50	100
5	42.37	70.46	91.11	119.81	143.15	168.21
10	27.18	45.20	58.45	76.86	91.83	107.90
20	17.22	28.63	37.02	48.69	58.17	68.35
30	13.14	21.85	28.25	37.15	44.39	52.16
60	8.25	13.72	17.74	23.33	27.87	32.75
120	5.17	8.59	11.11	14.61	17.46	20.52
360	2.46	4.09	5.29	6.95	8.30	9.76
720	1.54	2.56	3.30	4.35	5.19	6.10
1440	0.96	1.60	2.07	2.72	3.25	3.81

TABLE 5. The rainfall intensity (in millimeters per hour) for a specific period (min) utilizing the Gumbel (EV-1) distribution.

Storm duration (min)	Return period (years)
Storm duration (min)	2	5	10	25	50	100
5	44.06	74.12	94.01	119.16	137.81	156.32
10	28.27	47.54	60.31	76.44	88.40	100.28
20	17.91	30.12	38.20	48.42	56.00	63.52
30	13.66	22.98	29.15	36.95	42.73	48.47
60	8.58	14.43	18.30	23.20	26.83	30.44
120	5.37	9.04	11.47	14.53	16.81	19.07
360	2.56	4.30	5.45	6.91	7.99	9.07
720	1.60	2.69	3.41	4.32	5.00	5.67
1440	1.00	1.68	2.13	2.70	3.12	3.54

Empirical equations based on different return periods and durations have been formulated using Equation (18). The parameters for Sherman's IDF empirical formula were determined using the least squares method (LSM). Table 6 presents the parameters (a, b, and c) of the equations created for each return period for the three distributions.

TABLE 6. The IDF curves parameters values derived from the three distributions in Babylon City.

Distribution	Parameter	Return period (years)
Distribution	Parameter	2	5	10	25	50	100
LP-3	a	7.881	13.191	17.509	23.943	29.487	35.696
	b	0.010	0.010	0.010	0.010	0.010	0.010
	c	0.688	0.688	0.688	0.688	0.688	0.688
GEV	a	8.278	13.763	17.769	23.404	27.961	32.856
	b	0.010	0.010	0.010	0.010	0.010	0.010
	c	0.688	0.688	0.688	0.688	0.688	0.688
EV-1	a	8.607	14.476	18.362	23.274	26.917	30.535
	b	0.010	0.010	0.010	0.010	0.010	0.010
	c	0.688	0.688	0.688	0.688	0.688	0.688

When comparing the results of this study with the results of previous studies for most Iraqi cities, the same method (IMD) was applied, and similar values were obtained for the maximum values of rainfall intensity as well as for choosing the best suitable distribution. The LP-3 distribution was chosen as the best distribution suitable for the Iraqi cities (Nasiriyah, Karbala, and Mosul) in different studies [14, 23, 24], respectively. As for the city of Najaf, the Gumbel distribution was the best for the region [15], and in the city of Dohuk, the LPIII and Gumbel distributions obtained the best results [25].

3.3 The IDF Curves Generation

The generation of the IDF curve is a result of the previous four steps (use of IMD equation and selection of best distribution) and is highlighted in Step 5.

Step 5: Generation of IDF curves for the three distributions selected in this study based on the rainfall intensity dataset calculated in Tables 3, 4, and 5 as well as the coefficient values calculated in Table 6 for the specified return periods of 2, 5, 10, 25, 50, and 100 years and time (5, 10, 15, 20, 30, 60, 120, 360, 720, and 1440 min). The IDF curves for Babylon City's six return periods (2, 5, 10, 25, 50, and 100 years) are shown in Figures 2, 3, and 4. They were made using the LP-3, GEV, and Gumbel (EV-1) distributions, respectively. Based on the results, the figures for the three distributions showed that the longer the period, the lower the rainfall intensity, and that the rainfall intensity is high at long return periods and gradually decreases at short return periods. The maximum values of rainfall intensity in the long return periods (100 years) and during a period of 5 min are high for the LP-3 distribution, reaching 183 mm/h, while they reached 169 mm/h for the GEV distribution, and finally, the Gumbel distribution, reaching 157 mm/h. As for the short return periods (2 years) and during the same period (5 min), the maximum values of rainfall intensity exceeded 40 mm/h for all distributions, which is considered very high.

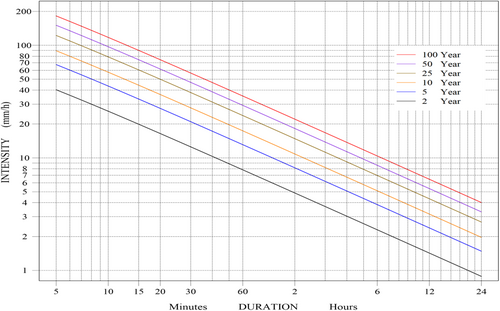
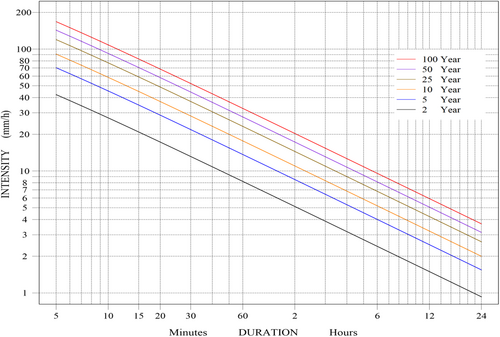
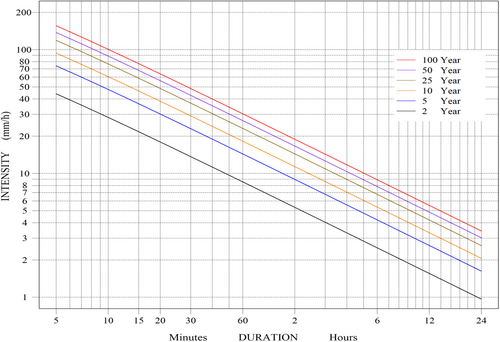
Table 7 shows the characteristics of the three tests selected in this study, the KS, AD, and χ² tests, and their estimated coefficient values, using a 5% significance level to determine the acceptance or rejection of the distributions. The results showed that all distributions were accepted for all tests. The LP-3 distribution was rated as the top choice by the KS test for all time periods, with the GEV distribution coming in second place for the same periods. As for the AD and χ² tests, in both tests, the GEV distribution ranked first, and the LP-3 distribution ranked second for all rainfall periods. The Gumbel distribution was the least efficient and not suitable for these data for the three tests mentioned.

TABLE 7. The features of Kolmogorov–Smirnov, Anderson-Darling, and χ² tests, along with their calculated coefficient values, at a 5% significance level to decide whether to accept or reject the distributions and assess the goodness-of-fit criteria (AIC and BIC) for model selection.

Rainfall duration (min)	Distribution	Shape	Scale	Location	KS		AD		χ²		Best fit statistic results of AIC and BIC
Rainfall duration (min)	Distribution	Shape	Scale	Location	Statistic	Rank	Statistic	Rank	Statistic	Rank	AIC	Rank	BIC	Rank
5	GEV	0.2622	1.5191	2.7814	0.0984	2	0.2379	1	0.1047	1	143.083	2	147.480	2
	Gumbel	—	2.2652	2.8759	0.1390	3	0.8233	3	7.6198	3	145.308	3	148.239	3
	LP-3	59.4730	0.0780	−3.3900	0.0940	1	0.2470	2	0.1099	2	142.743	1	147.140	1
10	GEV	0.2618	1.9148	3.5059	0.0977	2	0.2384	1	0.1051	1	157.877	2	162.274	2
	Gumbel		2.8535	3.6248	0.1395	3	0.8219	3	7.6226	3	160.093	3	163.025	3
	LP-3	59.5420	0.0779	−3.1601	0.0934	1	0.2477	2	0.1100	2	157.534	1	161.931	1
15	GEV	0.2616	2.1931	4.0114	0.0979	2	0.2377	1	0.1048	1	166.532	2	170.929	2
	Gumbel	—	3.2668	4.1475	0.1399	3	0.8204	3	7.6172	3	168.746	3	171.677	3
	LP-3	61.021	0.0770	−3.0869	0.0935	1	0.2472	2	0.1098	2	166.188	1	170.585	1
20	GEV	0.2616	2.4139	4.4158	0.0978	2	0.2381	1	0.1046	1	172.699	2	177.096	2
	Gumbel	—	3.5958	4.5654	0.1394	3	0.8207	3	7.6149	3	174.899	3	177.831	3
	LP-3	61.033	0.0770	−2.9910	0.0934	1	0.2475	2	0.1098	2	172.360	1	176.757	1
30	GEV	0.2621	2.7613	5.0555	0.0985	2	0.2382	1	0.1052	1	181.316	2	185.713	2
	Gumbel	—	4.1164	5.2274	0.1401	3	0.8227	3	7.6257	3	183.543	3	186.474	3
	LP-3	59.051	0.0783	−2.7753	0.0941	1	0.2474	2	0.1101	2	180.971	1	185.368	1
60	GEV	0.2615	3.4818	6.3687	0.0984	2	0.2389	1	0.1049	1	196.123	2	200.520	2
	Gumbel	—	5.1861	6.5846	0.1394	3	0.8210	3	7.6179	3	198.333	3	201.265	3
	LP-3	60.867	0.0771	−2.6185	0.0941	1	0.2483	2	0.1099	2	195.779	1	200.176	1
120	GEV	0.2619	4.3844	8.0252	0.0985	2	0.2391	1	0.1051	1	210.903	2	215.301	2
	Gumbel	—	6.5347	8.2974	0.1395	3	0.8227	3	7.6238	3	213.122	3	216.053	3
	LP-3	59.6110	0.0779	−2.3361	0.0941	1	0.2483	2	0.1100	2	210.560	1	214.957	1
360	GEV	0.262	6.324	11.574	0.0982	2	0.2382	1	0.1049	1	234.347	2	238.744	2
	Gumbel	—	9.424	11.967	0.1395	3	0.8217	3	7.6191	3	236.558	3	239.489	3
	LP-3	60.129	0.078	−1.991	0.0939	1	0.2475	2	0.1099	2	234.006	1	238.403	1
720	GEV	0.262	7.967	14.582	0.0985	2	0.2392	1	0.1049	1	249.130	2	253.527	2
	Gumbel	—	11.873	15.077	0.1397	3	0.8227	3	7.6209	3	251.342	3	254.273	3
	LP-3	59.964	0.078	−1.7529	0.0941	1	0.2485	2	0.1099	2	248.788	1	253.185	1
1440	GEV	0.262	10.037	18.372	0.0983	2	0.2387	1	0.1049	1	263.906	2	268.303	2
	Gumbel	—	14.959	18.995	0.1396	3	0.8226	3	7.6214	3	266.124	3	269.055	3
	LP-3	59.802	0.078	−1.5150	0.0940	1	0.2480	2	0.1099	2	263.563	1	267.960	1

The Akaike information criterion (AIC) and Bayesian information criterion (BIC) criteria, as displayed in Table 7, were utilized to select the best distribution. To find the final classification for choosing the optimal distribution, a ranking was conducted for both tests and each storm duration separately, where the value of 1 was given as a rank for the lowest value and the value of 3 as a rank for the highest value. As shown in Columns 13 and 15 of Table 7, the total weight of the AIC test ranking values for the distributions (EV-1, GEV, and LP-3) was 30, 20, and 10, respectively. As for the BIC test, its results were similar to the AIC test values. The LP-3 distribution, having the lowest value in both AIC and BIC tests, was found to be the most appropriate choice for modeling rainfall in Babylon, Iraq, considering the combined classification weights in the AIC and BIC tests.

Previous studies in Iraq created IDF curves for various locations, particularly the city of Kut, using three distributions (Gumbel, lognormal, and LP-3). Based on the results, the intensity of rainfall decreased with increasing storm duration and increased with long return periods. In addition, the lognormal distribution was the most appropriate among the distributions used [16]. IDF curves were also generated in the city of Sulaimani during different periods (10, 20, 30, 60, 120, 360, 720, and 1440 min) and return periods (2–100 years). During this, a general empirical equation was obtained to predict rainfall intensity during any return period and any duration [26].

4 Conclusion

Using rainfall data collected from Iraq's Meteorology and Seismic Monitoring Authority in Babylon rain gauge station over 32 years, IDF curves and their corresponding equations were created for various durations and return periods. The IMD reduction formula was used to estimate rainfall intensity for periods of less than 24 h (5, 10, 20, 30, 60, 120, 360, 720, and 1440 min). The LP-3 distribution was selected as the best distribution because it has the highest rainfall intensity for the specified return periods based on the AIC and BIC criteria, thus providing a safer and more secure criterion for designing and analyzing water management projects. It was also concluded that the lowest rainfall intensity occurred in the 2-year return period and the highest intensity occurred in the 100-year return period. The rainfall intensity calculated in this research is important and can be used in water management projects and in analyzing sewage and stormwater networks to prevent flood risks.

Author Contributions

Sajad Khalil Al-Jalili: writing – original draft, investigation, formal analysis. Haider M. Zwain: writing – review and editing, supervision, project administration, data curation. Ali Mohsen Hayder: methodology, conceptualization, validation.

Conflicts of Interest

The authors declare no conflicts of interest.

Open Research

Data Availability Statement

The data that support the findings of this study are available from the corresponding author upon reasonable request.

References

1M. W. Boota, H. M. Zwain, X. Shi, et al., “How Effective Is Twitter (X) Social Media Data for Urban Flood Management?,” Journal of Hydrology 634 (2024): 131129.
10.1016/j.jhydrol.2024.131129
Google Scholar
2S. Shahid, “Rainfall Variability and the Trends of Wet and Dry Periods in Bangladesh,” International Journal of Climatology 30, no. 15 (2010): 2299–2313.
10.1002/joc.2053
Web of Science® Google Scholar
3H. I. Z. Al-Sudani, “Rainfall Returns Periods in Iraq,” Journal of University of Babylon for Engineering Sciences 27, no. 2 (2019): 1–9, https://doi.org/10.29196/jubes.v27i2.2288.
10.29196/jubes.v27i2.2288
Google Scholar
4S. N. H. S. Alamri, B. K. Nile, and H. M. Zwain, “Topographic Effects on Stormwater Drainage Under Different Rainfall Intensities Case Study of Al-Najaf City,” Kerbala Journal for Engineering Science 1, no. 2 (2021): 191–201.
Google Scholar
5A. Mohammed, S. Dan'Azumi, A. A. Modibbo, and A. A. Adamu, “Development of Rainfall Intensity Duration Frequency (IDF) Curves for Design of Hydraulic Structures in Kano State, Nigeria,” PLATFORM—A Journal of Engineering 5, no. 2 (2021): 10–22.
10.61762/pajevol5iss2art12706
Google Scholar
6S. N. Hussain, H. M. Zwain, and B. K. Nile, “Modeling the Effects of Land-Use and Climate Change on the Performance of Stormwater Sewer System Using SWMM Simulation: Case Study,” Journal of Water and Climate Change 13, no. 1 (2022): 125–138, https://doi.org/10.2166/wcc.2021.180.
10.2166/wcc.2021.180
Web of Science® Google Scholar
7S. Agarwal and A. S. Suchithra, “ IDF Curve Generation for Historical Rainfall Events,” in Proceeding of National Conference on Emerging Trends in Civil Engineering, September (Coimbatore Tamil Nadu, India: Karpagam Academy of Higher Education, 2020), 898–907, https://www.researchgate.net/publication/344071719.
Google Scholar
8I. H. Elsebaie, “Developing Rainfall Intensity–Duration–Frequency Relationship for Two Regions in Saudi Arabia,” Journal of King Saud University, Engineering Sciences 24, no. 2 (2012): 131–140.
10.1016/j.jksues.2011.06.001
Google Scholar
9D. N. Hussein, S. H. D. AL-Zakar, and A. M. Yonis, “Estimating the Intensity Equations for Rain Intensity Frequency Curves (Mosul /Iraq),” Tikrit Journal of Engineering Sciences 30, no. 3 (2023): 38–48, https://doi.org/10.25130/tjes.30.3.5.
10.25130/tjes.30.3.5
Google Scholar
10R. K. Chowdhury, M. J. B. Alam, P. Das, and M. A. Alam, “Short Duration Rainfall Estimation of Sylhet: IMD and USWB Method,” Journal of the Indian Water Works Association 39, no. 4 (2007): 285–292.
Google Scholar
11B. Marta, S. Kohnová, G. Ladislav, J. Szolgay, and K. Hlavčová, “Estimation of IDF Curves of Extreme Rainfall by Simple Scaling in Slovakia,” Contributions to Geophysics & Geodesy 39, no. 3 (2009): 187–206.
Google Scholar
12K. Haddad, A. Rahman, J. Green, and G. Kuczera, “Design Rainfall Estimation for Short Storm Durations Using L-Moments and Generalised Least Squares Regression-Application to Australian Data,” International Journal of Water Resources & Arid Environments 1 (2011): 210–218.
Google Scholar
13S. A. AlHassoun, “Developing an Empirical Formulae to Estimate Rainfall Intensity in Riyadh Region,” Journal of King Saud University, Engineering Sciences 23, no. 2 (2011): 81–88.
10.1016/j.jksues.2011.03.003
Google Scholar
14A. K. Hussein, “Deriving Rainfall Intensity-Duration-Frequency Relationships for Kerbala City,” AL Muthana Journal for Engineering Sciences 3, no. 1 (2014): 25–37.
Google Scholar
15A. R. Majeed, B. K. Nile, and J. H. Al-Baidhani, “Selection of Suitable PDF Model and Build of IDF Curves for Rainfall in Najaf City, Iraq,” Journal of Physics: Conference Series 1973, no. 1 (2021): 012184, https://doi.org/10.1088/1742-6596/1973/1/012184.
10.1088/1742-6596/1973/1/012184
Google Scholar
16M. S. Shamkhi, M. K. Azeez, and Z. H. Obeid, “Deriving Rainfall Intensity-Duration-Frequency (IDF) Curves and Testing the Best Distribution Using EasyFit Software 5.5 for Kut City, Iraq,” Open Engineering 12, no. 1 (2022): 834–843, https://doi.org/10.1515/eng-2022-0330.
10.1515/eng-2022-0330
Web of Science® Google Scholar
17M. H. Mohammed, W. H. Hassan, and H. M. Zwain, “Overflow Sanitary Sewer Systems During the Rainy Season: A Case Study in Al-Samawah City,” AIP Conference Proceedings 2631, no. 1 (2023): 020012.
Google Scholar
18M. H. Mohammed, H. M. Zwain, and W. H. Hassan, “Modeling the Impacts of Climate Change and Flooding on Sanitary Sewage System Using SWMM Simulation: A Case Study,” Results in Engineering 12, no. September (2021): 100307, https://doi.org/10.1016/j.rineng.2021.100307.
10.1016/j.rineng.2021.100307
Google Scholar
19E. S. Mahdi and M. Z. Mohamedmeki, “Analysis of Rainfall Intensity-Duration-Frequency (IDF) Curves of Baghdad City,” IOP Conference Series: Materials Science and Engineering 888, no. 1 (2020): 012066, https://doi.org/10.1088/1757-899X/888/1/012066.
10.1088/1757-899X/888/1/012066
Google Scholar
20Z. Ahmed, D. Rao, K. Reddy, and E. Raj, “Rainfall Intensity Variation for Observed Data and Derived Data—A Case Study of Imphal,” Arpn Journal of Engineering and Applied Sciences 7, no. 11 (2012): 1506–1513.
Google Scholar
21V. T. Chow, D. R. Maidment, and L. W. Mays, Applied Hydrology; International Edition (New York, NY: MacGraw-Hill. Inc., 1988), 149.
Google Scholar
22A. M. Hayder and M. Al-Mukhtar, “Modelling the IDF Curves Using the Temporal Stochastic Disaggregation BLRP Model for Precipitation Data in Najaf City,” Arabian Journal of Geosciences 14, no. 19 (2021): 1957, https://doi.org/10.1007/s12517-021-08314-6.
10.1007/s12517-021-08314-6
Google Scholar
23A. A. Dakheel, “Drawing Curves of the Rainfall Intensity Duration Frequency (IDF) and Assessment Equation Intensity Rainfall for Nasiriyah City, Iraq,” University of Thi-Qar Journal 12, no. 2 (2017): 63–82.
Google Scholar
24S. N. Hussein, B. K. Nile, and H. M. Zwain, “Evaluation and Determination of Flood Areas Using SWMM and the Creation of a Mathematical Model Using Dimensional Analysis: A Case Study of the City of Najaf,” AIP Conference Proceedings 2631, no. 1 (2023): 020023.
Google Scholar
25A. R. M. Amen, D. A. Kareem, A. A. Mirza, and A. M. Salih, “Development of Intensity-Duration-Frequency Curves “IDF” for Dohuk City in Kurdistan Region of Iraq,” Journal of Duhok University 25, no. 2 (2022): 366–379.
Google Scholar
26Y. A. H. Hamaamin, “Developing of Rainfall Intensity-Duration-Frequency Model for Sulaimani City,” Journal of Zankoy Sulaimani—Part A 19, no. 3&4 (2016): 93–102, https://doi.org/10.17656/jzs.10634.
10.17656/jzs.10634
Google Scholar

Citing Literature

Volume7, Issue1

January 2025

e13053

Generating Rainfall IDF Curves Using IMD Reduction Formula and Choosing the Best Distribution for Babylon City, Iraq

ABSTRACT

1 Introduction