Application of the Filippov Method to PV-fed DC-DC converters modeled as hybrid-DAEs

1 INTRODUCTION

A large-scale redesign process is currently under way in power systems across the globe. Conventional sources of energy based on fossil fuels are being replaced by renewable sources of energy such as photovoltaic (PV) solar panels, wind turbines, and batteries. This redesign is primarily motivated by growing environmental concerns as well as the economic aspects of nations maximizing their available energy resources.¹

PV solar panels have gained an increase in market share due to falling prices, the free availability of sunlight, and their low rate of emissions.^{2, 3} PV panels have a nonlinear I-V characteristic curve. Hence, as the solar irradiance varies, the output voltage of the PV panel will vary according to the I-V curve. The output voltage of the PV panel is nonlinear with a maximum power point (MPP) voltage in the range of 15 to 40 V.⁴ The output voltage of each PV panel must be stepped up to meet the demands of the interconnecting device. Such applications include connecting to the AC grid through a DC-AC inverter, charging a storage battery or electric vehicle, or contributing to the 380 V DC distribution system.⁵

The conventional method for stepping up the output voltage of multiple PV panels is to connect several PV panels together in series. As the combined output of the array of panels is variable, some form of power electronics is used to condition and regulate the output voltage. However, shading and other unideal operating conditions can drastically reduce the efficiency of series connected PV devices.⁶

The approach under study in this article is to connect a DC-DC converter in series with each PV panel. Each PV module operates independently from one another and can be connected to the load, battery, AC-grid, or DC-link separately. The control algorithm for each DC-DC converter can be optimized as environmental conditions vary in order to operate at the MPP.

The desired behavior of DC-DC converters is a stable periodic motion around a predefined value with a frequency that is equal to the external clock. However, as parameters vary, such systems exhibit a wide range of nonlinear behaviors such as subharmonic oscillations.^7-10 These oscillations can manifest themselves through a series of bifurcations, which can increase the current/voltage ripple, add extra harmonics, and increase the switching losses.¹⁰ Thus, bifurcations can greatly impact on the efficiency of the system. This bifurcation behavior can lead to high ripples in the state variables or control variables and high stress in the switches. For example, a period-doubling bifurcation can double the current ripple, which can damage the DC-DC converter, the PV source, or the load.¹¹ Hence, accurate techniques to predict and avoid their occurrence in PV applications is essential in order to maximize the efficiency of the overall system. A variety of different control algorithms for DC-DC converters have been proposed in the literature to avoid such undesirable behavior.^12-15

2 LITERATURE SURVEY

The research relating to PV-fed DC-DC converters is sparse and limited. In this section, we provide a brief overview of the available literature and identify how it differs from the novelty and results of this research.

There exists a variety of methods to predict bifurcations in DC-DC converters. These include trajectory sensitivity analysis,¹⁹ an auxiliary vector method,²⁰ among others. However, they have not found widespread acceptance or application in power electronics design. This may be due to the mathematical complexity in their application. In recent years, the Filippov method has gained the most traction for studying the nonlinear dynamics of DC-DC converters most probably due to the mathematical simplicity of its application. However, little research has been conducted into quantitative analysis of PV-fed DC-DC converters or DC-DC converters modeled as a set of hybrid DAEs. Hence, the focus of this research is on the extension of the Filippov method to PV-fed DC-DC converters modeled as a set of hybrid DAEs.

This is not the first article to study the nonlinear dynamics of PV-fed DC-DC converters, a new method for studying the nonlinear dynamics of DC-DC converters and predicting unstable modes of operation was proposed in References 21 and 22. In References 4, 22, 23, this new method is applied to a PV-fed boost converter and quadratic boost converter. However, the system differs slightly from that studied in this research as the output of the PV panel does not feed directly into the DC-DC converter. Instead, there is an input capacitor in order to smooth the input voltage and avoid the injection of high current ripples. This enables an additional state variable to be created and the system can be modeled as a hybrid ODE.

In this work, the PV panel is connected directly to the DC-DC converter and the DC-link capacitor is omitted. The resulting mathematical model is a hybrid DAE. The rationale for this can be found in Section 5. The results of References 4, 22, 23 are only applicable to hybrid-ODEs. Hence, the results of this work are more general as they can be applied to DAEs and ODEs with no adaptation to the equations to model the system.

The application of the Filippov method to PV-fed DC-DC converters is not a novel concept. In Reference 11, stability analysis of a PV-fed boost converter operating under different control algorithms is performed. The authors identify over what range of values of R, I_ref, and I_ph give a stable period-1 output through simulations and bifurcation diagrams. The results are experimentally verified. For peak current mode control (CMC) and average CMC, the eigenvalues of the system are found using the conventional Filippov method. As outlined in this research, the conventional method is applicable as the algebraic variable is not present in the switching manifold, that is, $n_y^T=0$ for these control strategies. However, only qualitative results are presented when the maximum power point tracking (MPPT) control algorithm is considered. There is no quantitative analysis performed. The stability of the system is determined through bifurcation diagrams, time-domain simulations, and experimental waveforms. The eigenvalues of the system are not found. This is because the standard Filippov method cannot be employed as the algebraic constraint is present in the switching condition for MPPT control.

The approach taken in this research is to extend the work of References 11 and 18. Both of these works consider quantitative analysis of hybrid ODEs and the derived formulas only have a mathematical foundation in such systems. This work considers hybrid-DAEs and extends the mathematical foundation developed in Reference 18 to such systems. A new formula to calculate the saltation matrix is derived to include the effect of the algebraic term on the calculation of the stability of the system. This enables the Filippov method to be applied to hybrid DAEs, as well as, hybrid ODEs.

By considering the same circuit, parameters, and operating conditions, the experimental results of Reference 11 can be extended to verify the validity of proposed method developed in this work.

The main author in References 4, 23 contributed to References 24-26 where they study the bifurcation behavior of a PV-fed boost converter. In a similar manner to Reference 11, the conventional Filippov method is applied in order to find the eigenvalues of the monodromy matrix. However, there is an input capacitor filtering the output of the PV-panel. Hence, the approach taken in References 24-26 is not as general as that developed in this research.

In Reference 27, an MPPT controlled boost converter fed by a PV-panel is studied. In all the articles discussed in this literature survey, the temperature and solar irradiance is fixed when studying the effect of other parameters on the nonlinear dynamics of the system or the solar irradiance is the bifurcation parameter with all other parameters fixed. However, in Reference 27, the authors calculate the maximum power point for each value of solar irradiance and fix v_in at the MPP. For this reason, the results of Reference 27 are for a specific converter, at a specific temperature, and operating under specific conditions. The algorithm presented in this article is generalized and can be applied to any DC-DC converter with a PV source with any operating conditions.

In all the research articles discussed here, the system is modeled and analyzed as an ODE. Hence, it is important to consider the work carried out in the field of hybrid DAE analysis. The work of Federico Bizarri and Angelo Brambilla in Reference 28 studies mixed analog/digital circuits that are modeled as hybrid DAEs. In a similar manner that is undertaken in this research, they derive a generalized version of the saltation matrix that is applicable to hybrid DAEs. However, the systems that they study undergo an impact event, that is, G₁ ≠ G₂ unlike this work where G₁ = G₂. Furthermore, the application of the derived saltation matrix is to analog mixed signal circuits and not PV-fed DC-DC converters or similar.

The proposed algorithmic approach offers a powerful technique that can be applied to any DC-DC converter modeled as a set of hybrid DAEs, a set of piecewise-linear ODEs, or a set of hybrid ODEs. The approach can be applied regardless of the index of the DAE, the number of algebraic constraints present in the DAE, or the topology of the DC-DC converter. The boost converter is studied in this work as experimental results are presented in Reference 11. Hence, the same system model and parameters are used. The approach is valid if isolated DC-DC converters are considered, such as the forward converter or other transformerless high-gain DC-DC converters such as the quadratic boost converter.

3 OVERVIEW OF FILIPPOV THEORY

In this section, a brief overview of the Filippov method is presented. The differences between studying a hybrid-DAE and piecewise-linear ODE are highlighted along with the relevant notation used throughout this work.

The desirable behavior of a DC-DC converter is a stable periodic motion around a predefined value with a frequency that is equal to the external clock. As parameters vary, the system may undergo a bifurcation and the stability of the periodic motion may be lost. This can greatly increase the current ripple and therefore damage the DC-DC converter itself, the PV-source, or the interconnecting load.¹¹ Operating in the unstable region may lead to a degradation in the efficiency of PV array or reduce the lifespan of the PV module. Hence, the prediction of these stability bounds is imperative for PV arrays.

Furthermore, the transition matrix is not given by the exponential matrix as the system is not LTI. Instead, it must be calculated numerically. Section 4.2 provides a mathematical reasoning as to why $\mathrm{\Gamma }(t,t_0)$ is constructed in this form and presents a method for numerically calculating $\mathrm{\Phi }(t,t_0)$, $\mathrm{\Psi }(t,t_0)$, and $\mathrm{\Gamma }(t,t_0)$.

If the orbit is periodic, the stability can be quantitatively determined by assessing the eigenvalues of the fundamental solution matrix evaluated at t = t₀ + T, where T is period of the orbit under study. The fundamental solution matrix obtained at t = T is termed the monodromy matrix.

When a PV-fed DC-DC converter is considered, the system is modeled as a nonlinear hybrid DAE. As a result, the formula for the calculation of the saltation matrix must be adapted accordingly. This adaptation is presented in the next section.

4 MONODROMY MATRIX FOR DAEs

In this section we will outline a method to calculate the monodromy matrix for a hybrid-DAE. First we will derive the method used to calculate the saltation matrix before briefly describing the method to find the transition matrices.

5 PV-FED BOOST CONVERTER

The output voltage of a PV panel is in the range of 15 to 40 V. However, applications at grid level require a much higher voltage, such as the 380 V DC-link voltage. Hence, the output voltage of the PV panel must be stepped up. For some applications, the required high-voltage gain could be as high as 20.⁴ Conventional DC-DC converter topologies, such as the boost converter, cannot achieve this due to parasitic resistances in the switching devices and reactive components.⁴ However, the purpose and novelty of this article lies in the development of an algorithm to determine the monodromy matrix for PV solar panels operating with DC-DC converters in series where the system is modeled as a set of hybrid DAEs. Hence, the topology of the converter is not important as all relevant DC-DC converters can be modeled as a set of ODEs. The PV panel supplying the input to the boost converter is what introduces the algebraic term and hence is the reason we model the system as a hybrid DAE. For this reason, for simplicity but without loss of generality, the boost converter is chosen.

All simulations are obtained using Matlab 2017b using the ode15s solver with the tolerance set to 1 × 10⁻¹⁰ with a maximum step size, $\mathrm{\Delta }t$, of T/100, where T is the switching period of the boost converter. All simulations were executed on a 64-bit Windows 10 operating system running on an 4 core 1.90 GHz Intel Core with 16 GB of RAM.

It is important to note that there is no experimental verification presented in this research. However, in Reference 11, a PV-fed boost converter is considered. The results of Reference 11 are verified experimentally. For this reason, we have chosen the same parameter values for the circuit and control system. Hence, by extension, the experimental results of Reference 11 verify the approach undertaken in the proceeding analysis.

5.1 Mathematical models for simulation

The circuit diagram for the PV-fed boost converter, using the single diode model,³¹ is shown in Figure 1. The diode equation is:

$$i_{\text{pv}}=I_0(e^{A{v}_{\text{pv}}}-1)$$ (20)

where $A=q/(\gamma k{T}_e)$ and I₀ is the saturation current of the diode, q is the charge of an electron =1.6 × 10⁻¹⁹ C, k is the Boltzmann's constant =1.38 × 10⁻²³ J/K, T_e is the absolute temperature, and $\gamma$ is the diode ideality factor. Applying Kirchhoff's current law:

$$I_{\text{ph}}-i_{\text{pv}}-i_{\text{sh}}=i_L$$

Since v_pv = v_in + i_LR_s and substituting in (20), we can derive:

$$I_{\text{ph}}-I_0(e^{A(v_{\text{in}}+i_L{R}_s)}-1)-\frac{v_{\text{in}}+i_L{R}_s}{R_{\text{sh}}}=i_L.$$ (21)

PV devices have a nonlinear I-V characteristic.³¹ Hence, the resulting equation to find the input voltage to the boost converter, v_in, is nonlinear. Equation (21) is an algebraic constraint that causes the overall system to be modeled as a hybrid-DAE.

It is important to note that in Figure 1, and the resulting mathematical model, there is no DC-link capacitor between the PV panel and the boost converter. A real-world system would include this capacitor and the resulting system would be modeled as a set of hybrid ODEs as in References 24-26 and not a set of hybrid DAEs. The reason for not including the DC-link capacitor is 2-fold:

1. Power systems and microgrids are often modeled as a set of DAEs.³² The inclusion of a switched mode power supply changes the system model to a set of hybrid-DAEs. An example of this is Reference 33 where a PV panel is connected to a battery. The battery is modeled as a DAE and hence the resulting system is a set of hybrid-DAEs. There are a variety of different applications and loads where the resulting mathematical model for the entire system is a set of hybrid-DAEs. Hence, for simplicity without loss of generality, an resistive load is considered and the DC-link capacitor removed in order to model the system as a set of hybrid-DAEs.

2. The work carried out in this article extends that of Reference 11. The experimental work in Reference 11 serves to verify the proposed approach, where the DC-link capacitor is not included. Hence, it is not included in this work.

For the boost converter, the switch is closed at the start of the switching period (ON) for a time dT and then opens and remains open (OFF) for the rest of the switching period, that is, (1 − d)T. The control signal, v_con, is compared against a ramp signal, v_ramp. When v_con = v_ramp, the converter switches from ON to OFF. Hence, the switching manifold is given by h(x,y,t) = v_con − v_ramp = 0, which determines when switching occurs. The state equations for the boost converter are expressed as:

$$\dot{\left[\begin{array}{c}{i}_L\\ v_o\end{array}\right]}=\left\{\begin{array}{cc}{f}_{\text{ON}}(x,y)& \text{switch is closed}\\ f_{\text{OFF}}(x,y)& \text{switch is open}\end{array}\right.,$$ (22)

where

$$\begin{array}{ll}{f}_{\text{ON}}=\left[\begin{array}{c}\frac{1}{L}{v}_{\text{in}}\\ -\frac{1}{RC}{v}_0\end{array}\right]f_{\text{OFF}}=\left[\begin{array}{c}\frac{1}{L}{v}_{\text{in}}-\frac{v_o}{L}\\ \frac{1}{C}{i}_L-\frac{1}{RC}{v}_0\end{array}\right].& \end{array}$$

Hence, combining (21) and (22), the equations to model the system illustrated in Figure 1 gives a nonlinear hybrid DAE:

$$\dot{\left[\begin{array}{c}{i}_L\\ v_o\\ 0\end{array}\right]}=\left\{\begin{array}{cc}\left[\begin{array}{c}{f}_{\text{ON}}(x,y)\\ g_{\text{ON}}(x,y)\end{array}\right]& \text{switch is closed}\\ \left[\begin{array}{c}{f}_{\text{OFF}}(x,y)\\ g_{\text{OFF}}(x,y)\end{array}\right]& \text{switch is open}\end{array}\right.,$$

where

$$g_{\text{ON}}=g_{\text{OFF}}=i_L-I_{\text{ph}}+I_0(e^{A(v_{\text{in}}+i_L{R}_s)}-1)+\frac{v_{\text{in}}+i_L{R}_s}{R_{\text{sh}}}.$$

Hence, the differential variables, x, are i_L and v_o and the algebraic variable, y is v_in.

Unless otherwise stated, the parameters used in this work are as follows (Table 1):

TABLE 1. Parameters of the PV-fed boost converter

Parameter	Value	Parameter	Value
q	1.6 × 10−19 C	L	3.125 × 10−3 H
k	1.38 × 10−23 J/K	C	20 × 10−6 F
Te	300 K	T	1/10 000 s
$\gamma$	10	VL	0
Iph	1.0 A	VU	1
I0	1 × 10−11 A	Kp	2
Rs	0.1 $\mathrm{\Omega }$	vref	5.1 V
Rsh	100 $\mathrm{\Omega }$

5.2 Average current mode control

CMC algorithms for switching power devices can give rise to many issues such as poor noise immunity and peak-to-average current errors which the low current loop gain cannot correct.³⁴ Average CMC is a popular method employed to overcome the limitations of other current sensing techniques. In average CMC, the inductor current is compared against a reference current to create an error signal. The error signal is then adjusted by a proportional integral (PI) control algorithm to produce a control voltage:

$$v_{\text{con}}=K_p(I_{\text{ref}}-i_L)+K_i\int (I_{\text{ref}}-i_L)dt.$$

The control signal is compared against a ramp voltage:

$$v_{\text{ramp}}=V_L+(V_U-V_L)t\text{mod}T,$$

where V_L is the lower value of the ramp signal and V_U is the upper value. Using this control strategy, at the start of the switching period the switch is open. When the ramp signal is equal to the control signal, the switch is closed and remains closed for the rest of the switching period.

Figure 2 shows a bifurcation diagram with R as the bifurcation parameter ranging from 40 to 46 $\mathrm{\Omega }$. The system is simulated for 100 switching cycles for each value of R and the output sampled at the end of each switching cycle. It is clear, that for values of $R\le 43.5\mathrm{\Omega }$, the system operates with a stable period-1 orbit. When $R=44\mathrm{\Omega }$, the system has exceeded the critical load value and undergoes a period-doubling bifurcation. The system operates in this unstable region for all values of $R\ge 44\mathrm{\Omega }$.

Bifurcation diagrams are qualitative tools for assessing the stability of systems. The Filippov method is a quantitative tool that can achieve the same results. As the system is a nonlinear hybrid DAE, we must apply the adapted Filippov method given by (10) and (12) to find the relevant saltation matrices. It is important to note that no adaptation to the DAE needs to be made. The equations derived in (10) and (12) can be applied directly to the DAE model of the system.

$$\begin{array}{ll}{f}_1& =\left[\begin{array}{c}\frac{1}{L}{v}_{in}-\frac{v_o}{L}\\ \frac{1}{C}{i}_L-\frac{1}{RC}{v}_0\end{array}\right]f_2=\left[\begin{array}{c}\frac{1}{L}{v}_{in}\\ -\frac{1}{RC}{v}_0\end{array}\right]\begin{array}{cc}{n}_x^T& =\left[\begin{array}{cc}-K_p& 0\end{array}\right]\\ n_y^T& =\left[\begin{array}{c}0\end{array}\right]\\ \frac{\partial h}{\partial t}& =\left[\begin{array}{c}-1/T\end{array}\right]\end{array},\\ g_{1x}& =g_{2x}=\left[\begin{array}{cc}1-R_s{I}_{0}A{e}^{A(v_{in}+i_L{R}_s)}+\frac{R_s}{R_{sh}}& 0\end{array}\right],\\ g_{1y}& =g_{2y}=\left[\begin{array}{c}A{I}_0{e}^{A(v_{in}+i_L{R}_s)}+\frac{1}{R_{sh}}\end{array}\right],\\ g_{1t}& =g_{2t}=\left[\begin{array}{c}0\end{array}\right].\end{array}$$

As has been shown in the literature, the integrator is effectively isolated from the rest of the system dynamics. It introduces an eigenvalue very close to +1 and it does not contribute to the systems stability. It must be ignored when estimating the stability margin.¹⁸ For these reasons, it has been omitted from the calculation of the saltation matrix and transition matrix. It has been included in the simulation as it plays a role in deciding the switching condition.

5.2.1 Modeling as a DAE

Since $n_y^T=0$, (10) and (12) reduce to

$$\begin{array}{ll}{S}_{\mathrm{\Phi }}& =I_{N_{\mathrm{D}}}+\frac{(f_2-f_1)n_x^T}{n_x^T{f}_1+{\frac{\partial h}{\partial t}|}_{(x_1,y_1,t_1)}},\end{array}$$ (23)

$$\begin{array}{ll}{S}_{\mathrm{\Psi }}& =-g_{2y}^{-1}{g}_{2x}+\frac{(g_{2y}^{-1}{g}_{2x}{f}_1-g_{2y}^{-1}{g}_{2x}{f}_2)n_x^T}{n_x^T{f}_1+{\frac{\partial h}{\partial t}|}_{(x_1,y_1,t_1)}}.\end{array}$$ (24)

The saltation matrix is found using the above reduced formulas and the transition matrix is numerically calculated by solving (18) and (19). Since the formulation of the transition matrix and the saltation matrix are:

$${\mathrm{\Gamma }}_{\text{ON/OFF}}=\left[\begin{array}{cc}{\mathrm{\Phi }}_{\text{ON/OFF}}& 0_{N_{\mathrm{D}}\times N_{\mathrm{A}}}\\ {\mathrm{\Psi }}_{\text{ON/OFF}}& 0_{N_{\mathrm{A}}\times N_{\mathrm{A}}}\end{array}\right]$$

and

$$S=\left[\begin{array}{cc}{S}_{\mathrm{\Phi }}& 0_{N_{\mathrm{D}}\times N_{\mathrm{A}}}\\ S_{\mathrm{\Psi }}& 0_{N_{\mathrm{A}}\times N_{\mathrm{A}}}\end{array}\right].$$ (25)

The monodromy matrix will take the form:

$${\mathrm{\Gamma }}_{\mathrm{M}}=\left[\begin{array}{cc}{\mathrm{\Phi }}_{\text{ON}}{S}_{\mathrm{\Phi }}{\mathrm{\Phi }}_{\text{OFF}}& 0_{N_{\mathrm{D}}\times N_{\mathrm{A}}}\\ {\mathrm{\Psi }}_{\text{ON}}{S}_{\mathrm{\Psi }}{\mathrm{\Psi }}_{\text{OFF}}& 0_{N_{\mathrm{A}}\times N_{\mathrm{A}}}\end{array}\right].$$

There are N_D + N_A eigenvalues of this matrix. However, since the last N_A columns are zero, there are N_A zero eigenvalues. The ${\mathrm{\Psi }}_{\text{ON}}{S}_{\mathrm{\Psi }}{\mathrm{\Psi }}_{\text{OFF}}$ block of the monodromy matrix does not factor into the calculation of the eigenvalues. Hence, it is sufficient to only consider the following reduced monodromy matrix for stability analysis:

$${\mathrm{\Gamma }}_{\mathrm{R}}={\mathrm{\Phi }}_{\text{ON}}{S}_{\mathrm{\Phi }}{\mathrm{\Phi }}_{\text{OFF}}.$$ (26)

Using (23) and (26), the eigenvalues of the monodromy matrix are determined to be: $\left[\begin{array}{cc}-0.9979& 0.7914\end{array}\right]$ for $R=43.5\mathrm{\Omega }$ and $\left[\begin{array}{cc}-1.0060& 0.7772\end{array}\right]$ for $R=44\mathrm{\Omega }$. It is clear that the eigenvalues of the system move outside the unit circle across $\lambda =-1$, which indicates a period-doubling bifurcation. This matches Figure 2 and serves to verify the derived equations.

We will compare the results obtained if the system is assumed to be a two-dimensional piecewise-linear ODE as opposed to the hybrid DAE approach proposed in this article.

5.2.2 Conventional method

DC-DC converters are systems typically described by:

$$\dot{x}=A_{j}x+B_j{v}_{\text{in}},$$ (27)

where j denotes the different topologies of the DC-DC converter, and A_ON/OFF are given by the respective f_x. The state transition matrix is given by $\mathrm{\Phi }(t,t_0)=e^{A(t-t_0)}$ if the system is LTI. It is important to note that v_in does not appear in the state transition matrix as, for a LTI system, the input will affect both the perturbed orbit and unperturbed orbit equally as Bv_in does not depend on the state variables. As shown in Section 5.2.1${\mathrm{\Psi }}_{\text{ON/OFF}}$ and $S_{\mathrm{\Psi }}$ do not have an effect on the eigenvalues of the monodromy matrix. It is sufficient to consider ${\mathrm{\Gamma }}_{\mathrm{R}}={\mathrm{\Phi }}_{\text{ON}}{S}_{\mathrm{\Phi }}{\mathrm{\Phi }}_{\text{OFF}}$.

For these reasons, it would be natural to assume that the fluctuations of v_in do not need to be taken into account for the state transition matrix and, hence, the monodromy matrix of a PV-fed boost converter would be given by:

$${\mathrm{\Gamma }}_{\mathrm{M}}=e^{A_{\text{OFF}}(1-d)T}{S}_{\mathrm{\Phi }}{e}^{A_{\text{ON}}dT}$$ (28)

where d is the duty cycle and $S_{\mathrm{\Phi }}$ calculated according to (23). However, for $R=43.5\mathrm{\Omega }$, (28) yields eigenvalues at ${\lambda }_{1,2}=\left[\begin{array}{cc}-1.5393& 0.7865\end{array}\right]$. This indicates that the system is unstable. However, according to Figure 2, it is clear that the system operates with the desired stable period-1 orbit.

The reason these assumptions are not valid is because the system is modeled as a set of DAEs. It is a nonlinear system and cannot be described by (27). The algebraic constraint can cause the perturbation to shrink or grow over time. Hence, it can have an effect on the stability of the system and this must be taken into account over the entire switching period. Hence, $\mathrm{\Phi }(t,t_0)$ is not given by $e^{(f_x(t-t_0))}$. A far better estimation is given by $\mathrm{\Phi }(t,t_0)=e^{(f_x-f_y{g}_y^{-1}{g}_x)(t-t_0)}$.

5.2.3 Conclusions: CMC control

Table 2 summarizes the results of the CMC case study. From this table it is clear that when the transition matrix is calculated according to (18), the eigenvalues correctly predict the bifurcation point. Calculating the state transition matrix according to $\mathrm{\Phi }(t,t_0)=e^{(f_x(t-t_0))}$ gives incorrect eigenvalues of the system and the bifurcation point is not correctly calculated.

TABLE 2. Eigenvalues of the system for $R=43.5\mathrm{\Omega }$ and R = 34 for two methods of calculating the transition matrix

R ($\mathrm{\Omega }$)	Orbit	$\mathrm{\Phi }(t,t_0)$	Eigenvalues, $\lambda$
43.5	Stable	Numerically from (18)	−0.9979, 0.7914
		$e^{(f_x(t-t_0))}$	−1.5393, 0.7865
44.0	Unstable	Numerically from (18)	−1.0060, 0.7772
		$e^{(f_x(t-t_0))}$	−1.7843 0.7725

The conclusions drawn from this case study are:

• Conventional ODE-based algorithms to calculate the state-transition matrix, and hence the monodromy matrix, are not applicable for PV-fed DC-DC converters. As the system is not LTI, the algebraic constraint must be taken into account.
• While it is important to include the algebraic terms when calculating the transition matrix, the perturbation of the algebraic variables does not need to be calculated when considering the stability of the system. Hence, $S_{\mathrm{\Psi }}$ does not need to be calculated, only $S_{\mathrm{\Phi }}$ does. For very large simulations, this will reduce the computational burden as calculating the transition matrix is not trivial and computationally expensive.³⁰
• If $n_y^T=0$, then the reduced form of the saltation matrix which closely resembles that widely found in literature (such as in Reference 18) can be used.

In the next section, we will find the eigenvalues of the monodromy matrix for a PV-fed boost converter with MPPT.

5.3 Maximum power point tracking

MPPT is a technique used to maximize the power extraction of PV panels regardless of the environmental conditions. As shown in Reference 11, the MPPT algorithm is far more efficient compared with conventional control techniques. Unlike these conventional techniques, MPPT aims to maximize the output of the PV panel. In this algorithm, the input to the boost converter, that is, the output of the PV cell, is compared against a suitable reference voltage, v_ref. The resulting signal, v_con, is then amplified by a proportional controller, K_p, to create the control signal v_con:

$$v_{\text{con}}=K_p(v_{\text{in}}-v_{\text{ref}}).$$

The control signal is then compared with a ramp signal. Thus, the switching surface is given by:

$$h(x,y,t)=K_p(v_{\text{in}}-v_{\text{ref}})-(V_L+(V_U-V_L)t\text{mod}T).$$ (29)

At the start of the switching period, the switch is closed (ON). When v_con = v_ramp, the switch opens (OFF) and remains open for the rest of the switching period.

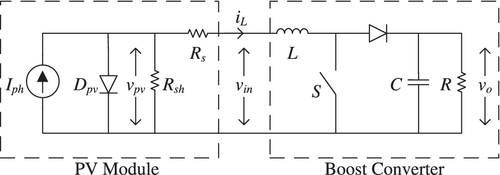
Figure 3 illustrates a bifurcation diagram of the PV-fed boost converter with MPPT. It follows a similar pattern to Figure 2. For low values of R, the system operates with a stable period-1 orbit. The critical load value is at $R\approx 37\mathrm{\Omega }$ as the system undergoes a period-doubling bifurcation for values greater than this. A further bifurcation point can be seen at $R=41.95\mathrm{\Omega }$.

In order to analytically determine the bifurcation point, we find $S_{\mathrm{\Phi }}$, ${\mathrm{\Phi }}_{\text{ON}}$, and ${\mathrm{\Phi }}_{\text{OFF}}$ and determine the eigenvalues of (26).

$$\begin{array}{ll}{f}_1& =\left[\begin{array}{c}\frac{1}{L}{v}_{in}-\frac{v_o}{L}\\ \frac{1}{C}{i}_L-\frac{1}{RC}{v}_0\end{array}\right]f_2=\left[\begin{array}{c}\frac{1}{L}{v}_{in}\\ -\frac{1}{RC}{v}_0\end{array}\right]\begin{array}{c}{n}_x^T\\ n_y^T\\ \frac{\partial h}{\partial t}\end{array}\begin{array}{c}=\left[\begin{array}{cc}0& 0\end{array}\right]\\ =\left[\begin{array}{c}{k}_p\end{array}\right]\\ =\left[\begin{array}{c}-1/T\end{array}\right]\end{array},\\ g_x& =\left[\begin{array}{cc}1-R_s{I}_{0}A{e}^{A(v_{in}+i_L{R}_s)}+\frac{R_s}{R_{sh}}& 0\end{array}\right],\\ g_y& =\left[\begin{array}{c}A{I}_0{e}^{A(v_{in}+i_L{R}_s)}+\frac{1}{R_{sh}}\end{array}\right],\\ g_t& =\left[\begin{array}{c}0\end{array}\right].\end{array}$$

The MPPT control algorithm differs from CMC in that the algebraic variable, v_in, is compared against a reference voltage as opposed to a state variable. Hence, the algebraic variable forms part of the switching manifold in (29) and $n_y^T\ne 0$. For this reason, the conventional formulation of the Filippov method, shown in (23), cannot be applied. The resulting eigenvalues of the monodromy matrix will be incorrect and this may lead to an inaccurate prediction of the bifurcation points of the system. This case study highlights the relevance and requirement of this work for maximizing the power output of PV solar panels.

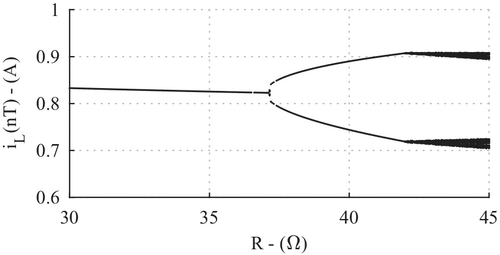
Figure 4 shows the time-domain response for the inductor current, i_L, with $R=37\mathrm{\Omega }$ and $R=37.1\mathrm{\Omega }$. It is clear, that the system operates with the desired period-1 orbit for $R=37\mathrm{\Omega }$ hence, we determine that the system is stable. An undesirable period-2 orbit can be seen for $R=37.1\mathrm{\Omega }$ hence, the system is deemed to be unstable. The system loses stability at $R\approx 37.1\mathrm{\Omega }$. We will now find the eigenvalues for both cases.

In order to find the reduced monodromy matrix given in (26), we find ${\mathrm{\Phi }}_{\text{ON}}$ and ${\mathrm{\Phi }}_{\text{OFF}}$ by solving the variational equation for $R=37\mathrm{\Omega }$ and $R=37.1\mathrm{\Omega }$.

$$\begin{array}{ll}R& =37\mathrm{\Omega }:{\mathrm{\Phi }}_{\text{OFF}}=\left[\begin{array}{cc}0.9221& -0.0120\\ 1.9426& 0.9316\end{array}\right]R=37.1\mathrm{\Omega }:{\mathrm{\Phi }}_{\text{OFF}}=\left[\begin{array}{cc}0.9322& -0.0110\\ 1.6972& 0.9423\end{array}\right],\\ & \\ {\mathrm{\Phi }}_{\text{ON}}& =\left[\begin{array}{cc}0.9107& 0\\ 0& 0.9246\end{array}\right]{\mathrm{\Phi }}_{\text{ON}}=\left[\begin{array}{cc}0.9112& 0\\ 0& 0.9177\end{array}\right].\end{array}$$

The saltation matrix is calculated in two manners. The first uses the adapted method to find $S_{\mathrm{\Phi }}$ given by (10). The second method uses the conventional formula to find $S_{\mathrm{\Phi }}$ that is widely given in literature such as Reference 18. This method is equivalent to setting $n_y^T=0$ of (10) as this ignores the effect of the algebraic constraint. The eigenvalues for the system with $R=37\mathrm{\Omega }$ and $R=37.1\mathrm{\Omega }$ are presented in Table 3.

TABLE 3. Eigenvalues of the system for $R=37\mathrm{\Omega }$ and R = 37.1 calculated using both the adapted formula to find the saltation matrix and the conventional formula

R ($\mathrm{\Omega }$)	Saltation matrix	Eigenvalues, $\lambda$	$|\lambda |$
37.0	Adapted method	0.7533, −0.993	0.7533, 0.993
	Conventional method	0.8505 ± 0.1436i	0.8624
37.1	Adapted method	0.7390, −1.0514	0.7390, 1.0514
	Conventional method	0.8571 ± 0.1249i	0.8662

When $R=37\mathrm{\Omega }$, using both the adapted method and the conventional method for finding $S_{\mathrm{\Phi }}$ results in both sets of eigenvalues being placed inside the unit circle. Both methods indicate that the system is stable and operating with a period-1 orbit as shown in Figure 4A. However, it is important to note that the adapted method shows that one of the eigenvalues is very close to $\lambda =-1$. Hence, the system is on the cusp of instability, which may result in a period-doubling bifurcation if any of the system parameters vary. The conventional method places the eigenvalues further away from the edge of the unit circle. The distance an eigenvalue is from the edge of the unit circle can be used as a metric to determine the relative stability of a system. This concept is similar to gain and phase margin and can be used to indicate how far away from the instability the system is. If a control engineer was to interpret the results using the conventional method, they may believe that the system is robust to noise or parameter variations. However, R shifting from 37 to 37.1 $\mathrm{\Omega }$ causes the system to undergo a period-doubling bifurcation. These types of bifurcations can greatly increase the current ripple and damage the DC-DC converter, the solar panel, or the interconnecting devices. Hence, the incorrect calculation of $\lambda$ may lead to designs that damage devices. For this reason, it is imperative that we employ the correct method for finding the eigenvalues of the monodromy matrix.

When $R=37.1\mathrm{\Omega }$, the adapted method for finding $S_{\mathrm{\Phi }}$ correctly shows that the eigenvalues now lie outside the unit circle and that the system is unstable. However, the conventional method no longer gives the correct indication of stability, instead it indicates that the eigenvalues lie inside the unit circle. Figure 4B clearly shows that the system is operating with a period-2 orbit and hence, is unstable.

This case study has served to show the importance of considering the effect of the algebraic terms in the calculation of the saltation matrix and, hence, the monodromy matrix. If $n_y^T\ne 0$, the algebraic terms have a significant effect on the stability of the system. This is due to the fact that they feature in the switching manifold. Furthermore, this section has also served to show the simplicity of the proposed approach. While the derivation of the new formulas to calculate the saltation matrix is mathematically complicated, its application does not greatly differ from the approach of applying the standard Filippov method. Hence, the mathematical burden is not greatly increased and the approach retains the main benefit of the Filippov method, which is the simplicity of its application. However, it is important to note that the transition matrix must be calculated numerically as part of the simulation and cannot be calculated in isolation unlike the state transition matrix for equivalent linear time-invariant ODEs.

6 CONCLUSION

This study, and the available literature discussed in Section 2, has shown that PV-fed DC-DC converters may undergo bifurcations, leading to unstable and undesired outputs. Traditionally, these systems have been modeled as a set of ODEs where the effect of the algebraic constraint imposed by the PV panel has been neglected during the stability analysis or an additional state variable has been created through the inclusion of additional input capacitors allowing the algebraic constraint to be expressed in the form of an ODE.

In this work, we propose modeling the system as a set of DAEs. However, the typical methods for studying DC-DC converters have been developed around modeling such systems as ODEs. Hence, in order to study PV-fed DC-DC converters modeled as a set of DAEs, we demonstrate how the Filippov method can be adapted accordingly. The main advantage of the proposed approach is that it is a general method as, regardless of the converter topology or the number of algebraic constraints, the derived formulas to perform stability analysis can be applied while maintaining the main benefit of the Filippov method which is the simplicity of its application. This reformulation of the Filippov method simplifies the analysis as no additional reformulation of the system equations needs to be performed.

We consider two case studies with the purpose of demonstrating two separate scenarios. In the first, we consider CMC. In CMC, there is no algebraic term in the switching manifold. Hence, the reformulated formulas to find the saltation matrix reduces to the conventional formula for the Filippov method found in the literature. The calculation of the saltation matrix can be treated as if it were an ODE. However, since the system is a DAE, it is shown that the calculation of the transition matrix differs and must be done so numerically.

In the second case study, we study a PV-fed boost converter with MPPT. It is shown in Section 5.3, since the algebraic term is present in the switching manifold, the equation to find the saltation matrix differs to that when the system is an ODE. It is shown that the application of the derived formula, presented in Section 4.1, retains the main benefit of the Filippov method, which is the simplicity of its application compared with other available methods outlined in Section 2. The approach was verified through brute-force simulations and experimental results can be seen in Reference 11.

The derived formula for the saltation matrix can be applied to any PV-fed DC-DC converter modeled as a hybrid DAE of any index with any number of algebraic constraints nor is it limited to the boost converter. The approach can be applied to any DC-DC converter, such as the isolated forward converter or the transformerless quadratic boost converter among many others, once the system model is a set of hybrid DAEs.

CONFLICTS OF INTEREST

The authors declare no potential conflict of interest.

PEER REVIEW INFORMATION

Engineering Reports thanks Abdelmajid Abouloifa, Abdelali El Aroudi, and Meng Huang for their contribution to the peer review of this work.