Engineering Reports
Volume 1, Issue 5 e12070
RESEARCH ARTICLE
Open Access

An ANFIS-based model for solar energy forecasting and its smart grid application

Gulnar Perveen, 

Corresponding Author

Gulnar Perveen

Department of Electronics and Communication Engineering, Delhi Technological University, Delhi, India

Correspondence

Gulnar Perveen, Department of Electronics and Communication Engineering, Delhi Technological University, Delhi 110042, India.

Email: [email protected]

Search for more papers by this author
Mohammad Rizwan, 

Mohammad Rizwan

Department of Electrical Engineering, Delhi Technological University, Delhi, India

Search for more papers by this author
Nidhi Goel, 

Nidhi Goel

Department of Electronics and Communication Engineering, Indira Gandhi Delhi Technical University for Women, Delhi, India

Search for more papers by this author
First published: 04 December 2019
https://doi.org/10.1002/eng2.12070
Citations: 22

Abstract

In the present work, a model underlying the principle of adaptive neural-fuzzy inference system (ANFIS) architecture is proposed. This research investigates the ANFIS-based model performance to forecast global solar energy under different weather conditions, namely, clear sky, hazy sky, hazy and cloudy sky, and cloudy sky; and for distinct climate zones using salient meteorological parameters. Power generation from solar photovoltaic (PV) may be affected by different factors, such as cloud cover, topographical locations, time, and seasonal variations. Therefore, accurate forecasting of PV power is an important factor for system reliability and robustness. In this work, the proposed model is implemented for smart grid applications in forecasting short-term PV power in a composite climate zone. Finally, the accuracy of the model is compared with other approaches, namely, support vector machine, feedforward neural network, multivariate adaptive regression splines, generalized regression neural network, linear neural network, fuzzy logic-based model, and empirical models based on multiple regression analysis using statistical performance indicators. The overall analysis reveals that the ANFIS-based model outperforms the other models in terms of accuracy.

Abbreviations

  • fi
  • ith forecasted data (dimensionless)
  • Hg
  • measured global solar energy (MJ/m2)
  • Ipmax
  • solar PV module current at MPP (A)
  • Isc
  • solar PV module short circuit current (A)
  • MAPE
  • mean absolute percentage error (%)
  • mi
  • ith measured value (dimensionless)
  • NMAE
  • normalized mean absolute error (%)
  • NPVP
  • number of solar PV module arranged in parallel (number)
  • NPVS
  • number of solar PV module arranged in series (number)
  • nRMSE
  • normalized root mean square error (%)
  • Pmax
  • solar PV module power at MPP (W)
  • PPV
  • PV array output (W)
  • PPV, STC
  • PV array output at STC (W)
  • ST
  • solar irradiance at STC (W/m2)
  • Tamb
  • ambient temperature (°C)
  • Tj
  • junction temperature of solar PV module (°C)
  • Voc
  • solar PV module open circuit voltage (V)
  • Vpmax
  • solar PV module voltage at MPP (V)
  • x
  • number of observation (dimensionless)
  • γ
  • temperature parameter at MPP

    • 1 INTRODUCTION

    Solar energy has played an important role in achieving the goal of replacing fossil fuels and reducing greenhouse gas emissions. Accurate information on solar energy has been essential for designing, development, sizing, and optimization of solar photovoltaic (PV) systems. Unfortunately, the data based on solar energy resource are unavailable because of the high cost of the instrument, maintenance, sufficient length of the record, and calibration of the measuring equipment. Due to nonavailability of the measured data, forecasting solar energy has been important at the surface of the earth. Therefore, a need has arisen for developing the model based on readily available data to forecast global solar energy. Furthermore, the power prediction has been a new concept and gained economic importance and it has been known that, solar energy changes with time, topographical locations, and seasonal variations. Therefore, if investors know the prediction of power in short-term duration, it would be easy for the investor to market and make a decision about energy planning for them. Therefore, in this research, the model being proposed has been further implemented for application in smart grid system for short-term PV power forecasting.

    Many previous types of research have been carried out that employ artificial intelligence techniques for global solar energy forecasting using large datasets. Artificial neural network (ANN) models have been used in a broad series of applications which include optimum estimation and forecasting; least-square optimization of numerical weather prediction.1-4 In one of the recent research by Nespoli et al wherein 24 hour ahead solar power forecasting has been performed in a solar PV system. In this research, two methods based on the ANN have been used, one in which training and testing have been done on the same dataset and the other based on the daily weather forecast. It has been concluded that for cloudy days, the performance of both of these methods has reduced; however, the performance has been noticed stable for the method, which uses the same dataset for training and testing and does not use weather forecasts.5 Researches carried out shows that for estimating complex functions, accurately analyzing the number of neurons, and hidden layers using ANN has been difficult as they are large in number. In addition to this, the training time involved has been large which resulted in slower system response. Therefore, adaptive neural-fuzzy inference system (ANFIS)-based model has been introduced focusing onto the theoretical aspects, design, and methodology to forecast global solar energy.

    Many researches have been carried out based on the integrated features of ANFIS to forecast global solar energy.6-8 Zheng et al proposed a hybrid approach based on ANFIS for a day-ahead PV power estimation in microgrids. It has been concluded from this research that the proposed method outperforms the ANN model and persistence based forecasting methods with favorable accuracy and reliability.9 Olatomiwa et al proposed ANFIS model for simulating solar radiation based on meteorological parameters, namely, sunshine hours and ambient temperature. It has been concluded from this research that the proposed ANFIS-based model provides an efficient method to estimate global solar energy.10 Yadav et al proposed an ANFIS-based model to forecast short-term PV power and it has been concluded in this research that the ANFIS model provides more accuracy as compared with other models such as fuzzy logic model and regression model.11-13 Many researches have been carried out that employs ANFIS-based model for wind power forecasting.14-17 In one of the recent research, Diaz et al proposed an ANFIS-based model for obtaining the best electrical power estimation from the solar PV system. It has been concluded from this research that the ANFIS-based model overcomes both multiple linear regression and gradient descent optimization methods.18 For real-time applications, a comprehensive survey has been carried out based on neuro-fuzzy rule generation algorithm for delivering maximum power to the load based on the maximum power point (MPP) as it gives a faster response with precision and accuracy. Many grid-connected solar PV plants have been based on PV technology, but variation in weather condition makes the system output nondeterministic and stochastic.19-21 Therefore, accurately forecasting global solar energy under variation in weather conditions has been essential as the uncertainty in weather condition greatly affects the PV power output in smart grid systems.

    In recent years, for modeling nonlinear complex processes, soft computing approaches have been used to define as support vector machines (SVMs) and multivariate adaptive regression splines (MARS) widely used in a variant branch of engineering. Vapnik proposed SVM model based on statistical learning theory and used for classification and regression analysis.22, 23 MARS has been modeled using a set of coefficients and functions based on the nonparametric regression approach. Its ability includes the estimation of the contribution of basis functions in a manner that the additive and interactive effects of predictors have been allowed to determine the response variable.24, 25 A lot of researches have been carried out based on a linear neural network (LNN) which can be trained to model static and dynamic linear systems, given a low learning rate to be stable and generalized regression neural network (GRNN) which has been designed and used for function approximation. Many kinds of research have been carried out using these soft computing approaches for estimating mean reference evapotranspiration.26, 27 Wen et al proposed SVM and ANN models for estimating evapotranspiration using meteorological parameters in China. It has been concluded that the SVM model gives better performance as compared with the ANN model.28 Feng et al proposed different methods for estimating evapotranspiration using temperature parameter for six stations located in south-west China. It has been concluded in this research that the GRNN model has been observed to perform better than other methods available in the literature.29

    Detailed literature analysis reveals that the ANFIS-based model available in the literature has been based on using meteorological parameters such as ambient temperature, relative humidity, and others; however, very few literatures have focused on forecasting solar energy using dew point, the addition of which has significantly increased the model accuracy. Furthermore, most of the models have been defined for the clear weather condition; however, very few literatures have discussed varying weather condition such as clear/sunny sky, hazy sky, hazy and cloudy sky, and cloudy weather forecast and for different climate zone.

    Therefore, the novelty of the work lies in establishing an ANFIS-based model to forecast global solar energy for different weather condition classified as clear sky, hazy sky, hazy and cloudy sky, and cloudy sky condition and for five different climate zones. Furthermore, the proposed model has been implemented in a smart grid system for estimation of short-term PV power and for the composite climate zone. A comparative analysis has been done in evaluating the performance of SVM, feedforward neural network (FFNN), MARS, GRNN, LNN, fuzzy logic-based model, and empirical models based on multiple regression analysis using statistical performance indicators for validation of the results.

    The work has been arranged in the following fashion. The methods and methodology have been presented in Section 2. Section 3 presents ANFIS-based model to forecast global solar energy. Section 4 presents the implementation of an ANFIS-based model for smart grid application. Statistical performance indicators have been made in Section 5. Section 6 carries out the results and discussions. The comparison of ANFIS-based model with other models has been carried out in Section 7. The conclusion has been shown in Section 8 followed by references.

    2 METHODS AND METHODOLOGY

    2.1 Data

    In the present work, the recorded data on an hourly basis averaged of 15 years have been obtained from IMD, NISE, and NIWE.30, 31 The measured data have been considered for the duration of 24 hour at the meteorological stations for five distinct climate zones. Furthermore, the scaling/normalization has been done and defined in 0.1 to 0.9 range for avoiding any convergence issues and have been shown in Tables 1-5, respectively.

    2.2 Climate zone

    The climate of India possesses a wide range of weather conditions with varied topography ranging from glaciers in the north, arid desert in the west, tropical in the south, and the island territories. The factors affect the Indian climatic conditions include location and latitudinal extent, the northern mountain ranges, monsoon winds, upper air circulation, physiography, tropical cyclones, and the southern oscillation. One of the main criteria for assigning a site to climatic zone depends on weather condition which exists for 6 months or more. Bansal and Minke32 have divided the entire country in a different climate zone after averaging the climate data of 233 meteorological stations/sites as shown in Figure 1.

    Table 1. Measured and normalized data for composite climate zone
    Sunshine hours (h) Hg (MJ/m2) Relative humidity (%) Ambient temperature (°C) Wind speed (m/s) Dew-point (°C)
    Months Measured Scaled Measured Scaled Measured Scaled Measured Scaled Measured Scaled Measured Scaled
    January 7.719 0.650 13.985 0.428 65.487 0.381 14.119 0.475 5.153 0.420 4.600 0.446
    February 7.936 0.594 16.788 0.449 59.643 0.496 18.581 0.557 7.848 0.280 4.900 0.448
    March 7.406 0.722 21.118 0.682 53.297 0.409 22.730 0.361 7.344 0.422 5.620 0.479
    April 9.220 0.718 25.214 0.609 36.188 0.456 30.027 0.538 8.417 0.350 5.720 0.433
    May 8.848 0.645 24.227 0.561 34.297 0.355 34.138 0.656 9.516 0.409 8.559 0.539
    June 7.133 0.599 20.912 0.638 52.560 0.383 33.399 0.530 10.589 0.458 16.14 0.491
    July 4.587 0.431 19.381 0.414 70.637 0.610 30.480 0.422 10.395 0.508 24.60 0.629
    August 5.552 0.531 18.802 0.538 79.359 0.429 29.140 0.599 9.570 0.379 26.06 0.609
    September 6.683 0.550 13.851 0.534 69.278 0.377 29.728 0.516 9.428 0.562 24.49 0.654
    October 9.329 0.713 18.334 0.542 64.519 0.534 26.179 0.492 6.339 0.371 12.43 0.629
    November 7.197 0.547 14.562 0.341 49.800 0.437 20.921 0.622 6.531 0.484 7.060 0.553
    December 5.261 0.595 12.124 0.574 65.683 0.484 15.995 0.468 5.933 0.444 3.330 0.366
    Table 2. Measured and scaled data for warm and humid climate zone
    Sunshine hours (h) Hg (MJ/m2) Relative humidity (%) Ambient temperature (°C) Wind speed (m/s) Dew-point (°C)
    Months Measured Scaled Measured Scaled Measured Scaled Measured Scaled Measured Scaled Measured Scaled
    January 8.94 0.701 17.64 0.524 71.32 0.515 25.46 0.223 8.22 0.432 20.33 0.467
    February 9.75 0.866 21.07 0.899 76.29 0.549 26.61 0.788 9.06 0.451 21.13 0.519
    March 9.05 0.882 23.53 0.594 73.75 0.318 27.84 0.799 6.98 0.503 20.77 0.540
    April 9.37 0.610 23.86 0.472 71.26 0.412 30.53 0.475 8.78 0.420 23.07 0.468
    May 8.83 0.626 22.87 0.753 67.14 0.452 31.71 0.506 7.49 0.583 24.49 0.498
    June 7.35 0.64 21.51 0.683 64.04 0.532 30.73 0.539 8.48 0.569 24.65 0.433
    July 6.18 0.534 18.87 0.661 62.25 0.465 30.53 0.649 10.04 0.455 22.74 0.501
    August 4.78 0.511 19.04 0.583 71.30 0.504 29.07 0.554 8.85 0.491 24.52 0.490
    September 6.16 0.582 19.66 0.596 79.09 0.542 29.10 0.216 8.41 0.442 24.63 0.436
    October 6.52 0.622 17.28 0.633 80.06 0.461 27.75 0.595 6.25 0.415 24.20 0.694
    November 5.81 0.547 15.13 0.566 83.73 0.467 25.64 0.519 11.58 0.461 22.71 0.577
    December 7.07 0.638 13.89 0.527 78.13 0.527 26.09 0.272 9.49 0.50 21.16 0.482
    Table 3. Measured and scaled data for hot and dry climate zone
    Sunshine hours (h) Hg (MJ/m2) Relative humidity (%) Ambient temperature (°C) Wind speed (m/s) Dew-point (°C)
    Months Measured Scaled Measured Scaled Measured Scaled Measured Scaled Measured Scaled Measured Scaled
    January 9.226 0.683 16.244 0.598 45.327 0.396 18.095 0.462 6.371 0.504 2.230 0.523
    February 9.714 0.694 19.311 0.485 41.857 0.41 19.867 0.535 6.116 0.376 4.370 0.48
    March 9.142 0.653 22.059 0.490 30.913 0.442 26.115 0.463 7.742 0.408 4.680 0.485
    April 9.867 0.633 23.554 0.656 23.975 0.379 32.910 0.618 5.696 0.349 6.710 0.435
    May 10.219 0.759 26.062 0.644 35.823 0.428 34.877 0.479 8.653 0.461 9.640 0.521
    June 8.937 0.682 23.354 0.587 45.914 0.573 33.520 0.553 14.038 0.555 19.38 0.678
    July 8.039 0.645 19.055 0.618 60.780 0.426 31.518 0.533 13.996 0.540 25.07 0.511
    August 8.097 0.675 20.157 0.716 62.331 0.422 31.445 0.471 5.988 0.462 25.39 0.499
    September 9.727 0.669 23.084 0.534 59.593 0.474 29.702 0.515 6.746 0.470 23.34 0.512
    October 9.790 0.794 19.978 0.522 42.026 0.503 28.457 0.511 4.375 0.414 15.29 0.626
    November 9.323 0.774 17.342 0.474 42.008 0.474 22.078 0.475 3.30 0.351 9.560 0.451
    December 8.503 0.809 14.671 0.317 48.582 0.554 18.639 0.570 3.214 0.362 7.820 0.538
    Table 4. Measured and scaled data for moderate climate zone
    Sunshine hours (h) Hg (MJ/m2) Relative humidity (%) Ambient temperature (°C) Wind speed (m/s) Dew-point (°C)
    Months Measured Scaled Measured Scaled Measured Scaled Measured Scaled Measured Scaled Measured Scaled
    January 9.497 0.529 16.998 0.607 59.887 0.49 19.781 0.464 1.493 0.504 11.58 0.494
    February 10.214 0.730 20.640 0.588 48.815 0.437 23.179 0.423 5.343 0.201 12.59 0.496
    March 9.900 0.695 22.667 0.600 41.278 0.459 26.277 0.492 3.234 0.344 5.080 0.303
    April 9.970 0.650 24.342 0.641 44.469 0.588 29.192 0.598 6.066 0.486 10.73 0.571
    May 10.832 0.720 25.393 0.612 55.212 0.608 29.138 0.406 11.756 0.521 18.39 0.525
    June 4.753 0.484 18.937 0.600 76.922 0.407 25.889 0.643 10.475 0.469 22.38 0.482
    July 4.271 0.283 15.119 0.503 86.028 0.523 23.913 0.544 7.931 0.304 21.78 0.546
    August 4.003 0.437 16.453 0.433 85.245 0.522 23.298 0.555 7.734 0.523 21.87 0.533
    September 5.567 0.530 18.404 0.535 84.233 0.555 24.07 0.388 4.675 0.518 21.58 0.575
    October 7.668 0.590 18.785 0.534 75.960 0.615 24.237 0.552 2.274 0.304 20.06 0.60
    November 8.460 0.607 17.527 0.469 71.969 0.404 22.401 0.484 2.000 0.450 18.12 0.418
    December 8.739 0.734 17.109 0.721 63.012 0.405 19.274 0.502 2.407 0.503 16.33 0.653
    Table 5. Measured and scaled data for cold and cloudy climate zone
    Sunshine hours (h) Hg (MJ/m2) Relative humidity (%) Ambient temperature (°C) Wind speed (m/s) Dew-point (°C)
    Months Measured Scaled Measured Scaled Measured Scaled Measured Scaled Measured Scaled Measured Scaled
    January 7.055 0.720 14.437 0.637 75.581 0.426 9.948 0.635 3.613 0.363 6.420 0.475
    February 6.264 0.606 16.575 0.511 71.839 0.529 10.242 0.551 3.804 0.404 6.360 0.495
    March 7.216 0.635 21.004 0.588 59.645 0.470 15.544 0.450 5.645 0.386 9.380 0.523
    April 3.79 0.352 19.967 0.541 63.533 0.523 18.258 0.501 7.633 0.476 15.24 0.646
    May 4.842 0.483 18.429 0.428 80.290 0.523 20.694 0.576 4.290 0.363 18.19 0.658
    June 3.487 0.453 16.416 0.593 85.500 0.568 21.04 0.600 3.633 0.351 20.80 0.536
    July 2.706 0.358 16.064 0.611 87.516 0.535 21.206 0.599 3.145 0.380 21.58 0.458
    August 2.158 0.414 14.253 0.520 89.226 0.560 20.642 0.519 1.226 0.189 21.23 0.49
    September 2.747 0.356 13.982 0.432 85.917 0.483 20.002 0.471 0.867 0.331 20.05 0.64
    October 5.871 0.557 15.004 0.464 80.742 0.654 18.39 0.603 2.290 0.466 17.79 0.467
    November 7.057 0.632 15.643 0.546 75.600 0.525 15.273 0.393 2.650 0.336 12.53 0.441
    December 7.597 0.638 15.632 0.634 74.403 0.593 11.889 0.344 0.839 0.268 10.04 0.527
    Details are in the caption following the image
    Figure 1
    Open in figure viewerPowerPoint
    Meteorological stations for resource assessment across India

    2.3 Classification of weather condition

    The variation in weather condition can be classified in the following fashion33:

    2.3.1 Clear sky (blue sky)

    If the sunshine hours are equal and more than 9 hour. In addition, the diffuse solar energy is lower or equal to 25% of global solar energy.

    2.3.2 Hazy sky (fully)

    If the sunshine hours lies in the range of 7 to 9 hour. In addition, diffuse solar energy is less than 50% or more than 25% of global solar energy.

    2.3.3 Hazy and cloudy sky (partially)

    If the sunshine hour lies between 5 and 7 hour. In addition, diffuse solar energy is less than 75% or more than 50% of global solar energy.

    2.3.4 Cloudy sky (fully)

    If diffuse solar energy is more than 75% of global solar energy and the sunshine hour is less than 5 hour.

    3 ANFIS-BASED MODEL TO FORECAST GLOBAL SOLAR ENERGY

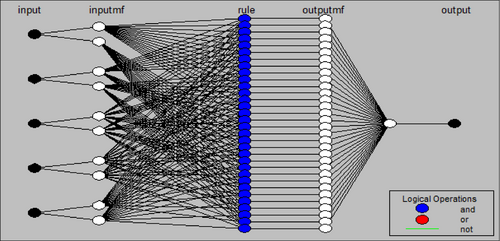
    ANFIS is a hybrid-learning rule for system optimization, which involves Fuzzy-Sugeno system lying within the adaptive-network frameworks and is surrounded by neural learning capabilities. The main factor influencing this model is that the rate of convergence is faster as search space dimensions are reduced for the neural network method. The architecture is a multilayered feedforward network, which contains five layers wherein the first and the fourth layer comprises an adaptive node while others have a fixed node. The first layer consists of adaptive neurons wherein the fuzzification is performed and the second layer comprises fixed nodes the output of which signifies the incoming signal products. The third layer comprises fixed nodes where each node is fixed and labeled as “N,” indicating firing strength normalization from the previous layer and simulates precondition fuzzy rules matching. The fourth layer comprises adaptive nodes, which result from the rule inference and the output layer is the fifth layer labeled as “∑.” It does the summation of signals coming from previous layers and converts fuzzy classification outcomes into crisp values.34

    4 IMPLEMENTATION OF AN ANFIS-BASED MODEL FOR SMART GRID APPLICATION

    The power generation in a solar PV system is sensitive to fluctuation and varying weather condition; so, to forecast accurately the power output can enhance the system robustness, reliability, and lessen the impact of solar PV output uncertainty on the grid. In the present work, 250 Wp multicrystalline solar PV modules are considered wherein the module efficiency obtained is 15.30% for the short-term PV forecast. The input parameters include solar irradiance and cell temperature while PV power is the output. The data have been collected on a daily basis, which depends on sunshine hours availability from sunrise to sunset. The implementation of an ANFIS-based model for smart grid application has been carried out to predict the behavior of a PV system under composite climatic conditions. The PV power generation can be given by Equation (1) as Reference 35:
    P PV = P PV , STC * S T 1000 * 1 − γ * T j − 25 * N PVS * N PVP , (1)
    and
    T j = T amb + S T 800 * N OCT − 20 , (2)
    where PPV is the PV system output at MPP, ST is solar irradiance in W/m2 at STC, PPV, STC denotes rated PV system output at MPP, NPVS is the series-connected PV modules, γ is MPP temperature parameter, NPVP is the parallel-connected PV modules, Tamb is ambient/air temperature in °C, Tj is the junction temperature of the module in °C, and NOCT is a constant.

    5 STATISTICAL PERFORMANCE INDICATORS

    For model evaluation, statistical performance indicators have been used and defined as follows Reference 36:

    5.1 Mean absolute percentage error

    It reflects the amount of error present in comparing the measured and forecasted data. It is defined as the summation or addition of the absolute error which is divided by the measured data and then averaging the fixed percentages. The relationship is expressed by Equation (3) as follows:
    NMAE % = 1 x ∑ i = 1 x E m i × 100 , (3)
    where E = (mi − fi) is the absolute error, x represents the number of observations, fi and mi are the ith forecasted and measured value, respectively.

    5.2 Normalized mean absolute error

    The hourly measured power significantly changes during the entire day from sunrise to sunset, so normalized mean absolute error (NMAE) has been preferred for comparing the forecasted and measured data. The relationship is expressed by Equation (4) as follows:
    NMAE % = 1 x ∑ i = 1 x E max m i × 100 , (4)
    where E = (mi − fi) is the absolute error, x represents the number of observations, fi and mi are the ith forecasted and measured value, respectively.

    5.3 Normalized root mean square error

    It measures the absolute hourly errors mean and is normalized over the maximum power output in the considered time range. The relationship is given by Equation (5) as follows:
    nRMS E % = 1 x ∑ i = 1 x E 2 max m i × 100 , (5)
    where E = (mi − fi) is the absolute error, x represents the number of observations, fi and mi are the ith forecasted and measured value, respectively.

    6 RESULTS AND DISCUSSION

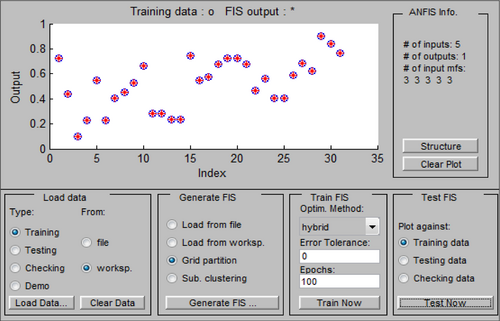
    The proposed model has been employed in forecasting global solar energy with the aid of meteorological parameters. For training and testing of the data, MATLAB software has been used with function “anfisedit” and evaluating the output using the function “evalfis (input, tra)” where “input” contains the input data and “tra” represents the training data. The recorded hourly data, night hours included, are used as the data for the comparison between forecasting methods.

    In the present research, the recorded hourly data has been employed for forecasting global solar energy. The required data were gathered from the National Institute of Solar Energy and the Indian Meteorological Department. The dataset covers the monthly mean meteorological parameters between the period 2002 and 2016. The mentioned data include input parameters such as ambient temperature, sunshine duration, relative humidity, wind speed, and dew point whereas clearness index is the output parameter. The data have been segregated in two parts: wherein the data for the year 2002 to 2011 have been used for training, whereas the data for the year 2012 to 2016 have been used for testing and are shown in Tables A1-A5 of Appendix A, respectively. In the proposed model, membership function has been assigned for every input, so that the rules were formed. After effective training of the proposed model based on ANFIS modeling, the model has been tested with data samples which were not present in the training datasets. For validation of the proposed model, statistical performance indicators have been used for comparing the measured and forecasted data values for varying weather condition such as sunny sky (blue sky), hazy sky (fully), hazy and cloudy sky (partially), and cloudy sky (fully), respectively, and applied for distinct climate zone and are shown in Table 6.

    Table 6. ANFIS-based model to forecast global solar energy for different weather condition and for distinct climate zone across India
    Hg (MJ/m2)
    Stations covered Weather condition Measured ANFIS MAPE (%) NMAE (%) nRMSE (%)
    Warm and humid (Chennai) Sunny 23.60 23.60 0.00012 0.00012 0.11429
    Hazy 21.11 21.11 0.00924 0.00852 0.19315
    Hazy and cloudy 17.58 17.58 0.00750 0.00610 0.19967
    Cloudy 12.30 12.20 0.00008 0.41493 0.49918
    Hot and dry (Jodhpur) Sunny 21.758 21.758 0.00010 0.00013 0.12458
    Hazy 19.986 19.986 0.00006 0.00005 0.11210
    Hazy and cloudy 18.075 18.075 0.00905 0.00007 0.13261
    Cloudy 16.628 16.752 0.00544 0.00442 0.09626
    Composite (Delhi) Sunny 20.60 20.60 0.00013 0.00012 0.13798
    Hazy 18.10 18.10 0.00005 0.00008 0.13700
    Hazy and cloudy 12.52 12.52 0.00089 0.00006 0.19377
    Cloudy 7.48 7.48 0.00004 0.00000 0.00000
    Moderate (Pune) Sunny 21.49 21.52 0.10504 0.09868 0.28673
    Hazy 20.42 20.43 0.03890 0.03146 0.21360
    Hazy and cloudy 18.71 18.71 0.00180 0.00013 0.10925
    Cloudy 13.73 13.83 0.00012 0.00006 0.13132
    Cold and cloudy (Shillong) Sunny 22.83 22.83 0.00966 0.00889 0.14512
    Hazy 19.25 19.25 0.00662 0.00509 0.20678
    Hazy and cloudy 16.09 16.09 0.00421 0.00267 0.24032
    Cloudy 11.22 11.22 0.00001 0.00054 0.20333
    • Abbreviations: ANFIS, adaptive neural-fuzzy inference system; MAPE, mean absolute percentage error; NMAE, normalized mean absolute error; nRMSE, normalized root mean square error.

    Furthermore, the training details generated in MATLAB with input, hidden, and output parameters are shown in Figures 2 and 3 wherein the input layer has five inputs and the clearness index is the output parameter.

    Details are in the caption following the image
    Figure 2
    Open in figure viewerPowerPoint
    ANFIS training data simulated in MATLAB with five inputs and one output. ANFIS, adaptive neural-fuzzy inference system
    Details are in the caption following the image
    Figure 3
    Open in figure viewerPowerPoint
    Schematic of ANFIS architecture with five inputs to forecast global solar energy. ANFIS, adaptive neural-fuzzy inference system

    From Table 6, a significant difference has been noticed between the measured and forecasted data with respect to statistical performance indicators for distinct climate zone.

    6.1 Clear sky (blue sky)

    For clear/sunny sky, the computed error has been observed to be less for the Jodhpur station in comparison to other station with a mean absolute percentage error (MAPE) of 0.00010%. The reason behind is that Jodhpur enjoys hot and dry climatic conditions wherein prevails sunny weather all through the year.

    6.2 Hazy sky (fully)

    For hazy sky condition, the computed error has been observed to be less for the composite climate in comparison to other stations with a MAPE of 0.00005%. This is due to the presence of high value of relative humidity which varies about 60% to 90% in wet periods and 25% to 35% in dry periods that places Delhi under composite climatic conditions.

    6.3 Hazy and cloudy sky (partially)

    For this sky condition, the computed error has been observed to be less for a warm and humid climate in comparison to other station with MAPE of 0.0075%. This is due to high diffuse solar radiation owing to the cloudy weather condition, which results in the marginal dissipation of heat during the night.

    6.4 Cloudy sky (fully)

    In this weather condition, the computed error has been observed to be less for a Shillong station in comparison to other station with MAPE of 0.00001%. The main contributing factor is that in winter the solar radiation intensity is comparatively low with a high percentage of diffuse solar radiation that makes winters very cold.

    Furthermore, the comparison of the measured and forecasted data obtained by employing ANFIS model for different weather condition has been shown in Figures 4-8 and further simulated for five meteorological stations across India.

    Details are in the caption following the image
    Figure 4
    Open in figure viewerPowerPoint
    Measured and forecasted Hg by employing ANFIS methodology for warm and humid climate zone. ANFIS, adaptive neural-fuzzy inference system
    Details are in the caption following the image
    Figure 5
    Open in figure viewerPowerPoint
    Measured and forecasted Hg by employing ANFIS methodology for hot and dry climate zone. ANFIS, adaptive neural-fuzzy inference system
    Details are in the caption following the image
    Figure 6
    Open in figure viewerPowerPoint
    Measured and forecasted Hg by employing ANFIS methodology for composite climate zone. ANFIS, adaptive neural-fuzzy inference system
    Details are in the caption following the image
    Figure 7
    Open in figure viewerPowerPoint
    Measured and forecasted Hg by employing ANFIS methodology for moderate climate zone. ANFIS, adaptive neural-fuzzy inference system
    Details are in the caption following the image
    Figure 8
    Open in figure viewerPowerPoint
    Measured and forecasted Hg by employing ANFIS methodology for cold and cloudy climate zone. ANFIS, adaptive neural-fuzzy inference system

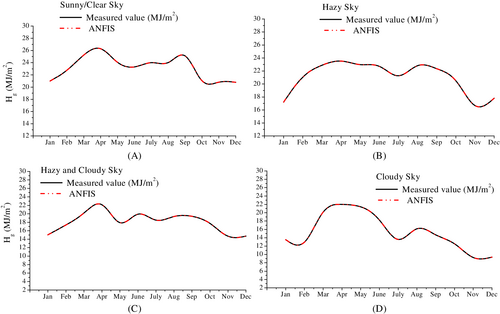
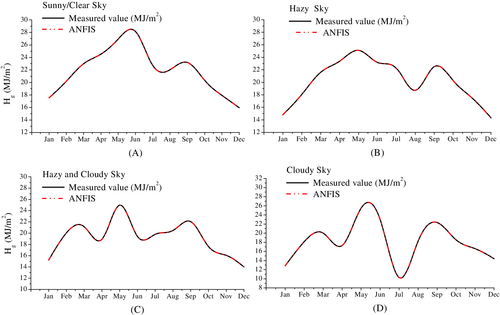
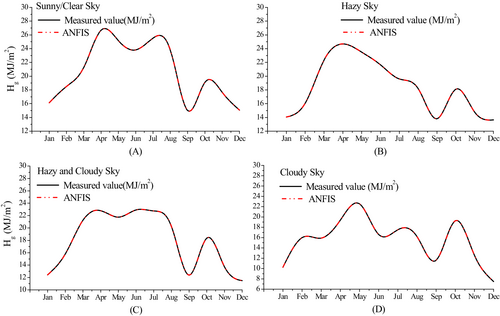
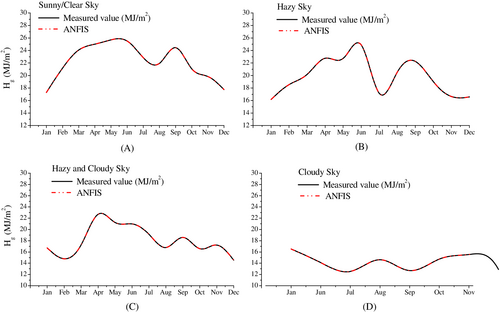
    From Figures 4-8, it has been observed that the forecasted data attained by employing ANFIS-based model for different weather condition closely follows the measured data. The model performance seems to be satisfied.

    Attributing to meteorological factor, the power output of the solar PV system is fluctuating and difficult to control. The output fluctuates along with the solar insolation intensity, which shows random behavior due to various environmental factors such as cloud cover, solar irradiance, dust on PV panels, topographical location, and seasonal variations affecting the power output in a smart grid system. Such problems may be overcome by forecasting renewable energy sources with intelligent models.

    In addition, the generation and load forecasting give an adequate solution to the problem, which depends on the power availability; the customers may decrease their demand. Keeping the above facts, ANFIS-based model has been employed to forecast solar energy for smart grid applications. In the present work, 250 Wp multicrystalline solar PV modules are used employing ANFIS-based model to forecast the behavior of power generation and are shown in Table 7 for the composite climate zone.

    Table 7. Forecasted power using ANFIS-based model for smart grid application under composite climatic zone
    Pmax (W)
    Months Vpmax (V) Ipmax (A) Solar irradiance (W/m2) Voc (V) Isc (A) Cell temperature (°C) Measured ANFIS MAPE (%) NMAE (%) nRMSE (%)
    January 60.48 1.05 341.98 69.53 1.12 20.80 64.15 64.12 0.0057 0.0027 0.0031
    February 59.95 1.49 450.78 69.61 1.58 28.19 89.61 89.57 0.0022 0.0017 0.0020
    March Data not available for these 2 months
    April
    May 56.93 1.38 557.92 66.45 1.46 44.53 79.08 79.06 0.0027 0.0020 0.0023
    June 57.57 1.20 528.54 66.20 1.28 42.32 68.28 70.19 0.0346 0.0262 0.0460
    July 57.03 1.02 532.32 66.33 1.09 39.15 59.03 59.03 0.0220 0.0156 0.0354
    August 57.07 1.03 411.69 66.78 1.12 38.15 59.52 59.52 0.0036 0.0022 0.0027
    September 57.36 1.11 418.73 66.98 1.20 35.56 64.35 64.28 0.0052 0.0024 0.0029
    October 57.78 1.52 464.71 68.10 1.63 37.75 88.08 88.09 0.0003 0.0002 0.0002
    November 58.90 1.15 346.12 68.61 1.24 29.33 68.21 68.21 0.0005 0.0003 0.0003
    December 60.09 1.26 359.34 69.84 1.35 23.94 76.30 76.30 0.0006 0.0004 0.0006
    Average 58.32 1.22 441.21 67.84 1.31 33.97 71.66 71.84 0.0077 0.0054 0.0096
    • Abbreviations: ANFIS, adaptive neural-fuzzy inference system; MAPE, mean absolute percentage error; NMAE, normalized mean absolute error; nRMSE, normalized root mean square error.

    From Table 7, it has been revealed that the average value of MAPE in a solar PV system has been observed to be 0.0077% by employing ANFIS methodology, which is comparatively accurate and found within the permissible error limit.

    Furthermore, it has been noted that for the winter season (January), the average MAPE is 0.0057%, for summer season (May), the average MAPE obtained is 0.0020%, and MAPE is comparatively large for the rainy season (July) of the value of 0.0220% due to uncertainty associated with the data. This method integrates the features of fuzzy logic and neural network resulting in increasing the system robustness and accuracy.

    The daily power generation in a solar PV system based on the performance characterization has been shown in Figure 9 wherein the generation of power for 3 consecutive days, that is, ninth, 10th, and 11th June, have been shown and the days considered to represent sunny days, so that the solar radiation remains almost the same.

    Details are in the caption following the image
    Figure 9
    Open in figure viewerPowerPoint
    Solar PV system power generation on a daily basis for 3 days. PV, photovoltaic

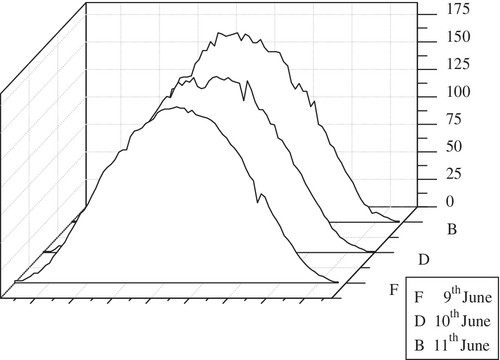
    Thus, it has been observed that a high correlation prevails for generated power on a daily basis. The power output is available during the entire day and causes fluctuation to the grid when integrating unsteady PV power into the grid. As many factors are involved, which affects the solar PV system power output, but the main factor is the variation in weather condition which makes it difficult to examine the performance characteristics with a single model.

    In this work, the input parameters include solar irradiance, cell temperature, and based on weather condition the solar PV power output has been obtained and arranged within 10 minute interval for estimating short-term PV power for smart grid applications by employing ANFIS-based models. Simulation has been carried out with ANFIS training details generated in MATLAB with two input parameters, that is, cell temperature and solar irradiance and PV power as the output parameter as shown in Figure 10. Statistical indicators have been used for performance evaluation of the models and are shown in Table 8.

    Details are in the caption following the image
    Figure 10
    Open in figure viewerPowerPoint
    The ANFIS architecture generated in MATLAB with two inputs for forecasting power of solar PV system. ANFIS, adaptive neural-fuzzy inference system; PV, photovoltaic
    Table 8. Short-term PV power forecast employing ANFIS-based model for clear sky (blue sky), and hazy and cloudy sky (partially) under composite climatic conditions
    Clear sky (blue sky) Hazy and cloudy sky (partially)
    Power (W) Power (W)
    Time (h) Cell temperature (°C) Solar irradiance (W/m2) Measured ANFIS MAPE (%) NMAE (%) nRMSE (%) Time (h) Cell temperature (°C) Solar irradiance (W/m2) Measured ANFIS MAPE (%) NMAE (%) nRMSE (%)
    6:50 31.03 140.93 20 23.88 0.19 0.02 15.08 7:30 27.78 126.72 21 21.97 0.05 0.00 0.94
    7:00 32.74 172.30 24 24.34 0.01 0.00 0.12 7:40 27.32 200.00 22 26.13 0.19 0.02 17.06
    7:10 33.82 203.49 28 25.74 0.08 0.01 5.10 7:50 30.58 213.53 34 36.12 0.06 0.01 4.49
    7:20 35.78 237.48 34 30.25 0.11 0.02 14.05 8:00 30.38 196.07 29 32.41 0.12 0.02 11.66
    7:30 36.38 273.82 39 39.70 0.02 0.00 0.49 8:10 32.13 155.48 21 24.05 0.15 0.01 9.27
    7:40 37.18 309.60 46 48.73 0.06 0.02 7.46 8:20 30.11 145.30 32 22.96 0.28 0.04 81.75
    7:50 38.67 344.42 52 52.28 0.01 0.00 0.08 8:30 30.71 189.78 43 45.36 0.05 0.01 5.57
    8:00 38.52 375.21 58 55.48 0.04 0.02 6.37 8:40 31.05 194.45 24 31.63 0.32 0.04 58.22
    8:10 40.17 416.11 65 62.59 0.04 0.01 5.81 8:50 31.60 198.55 48 45.23 0.06 0.01 7.67
    8:20 41.67 449.55 71 71.81 0.01 0.00 0.66 9:00 32.83 194.56 28 31.75 0.13 0.02 14.05
    8:30 41.37 473.28 76 76.98 0.01 0.01 0.97 9:10 32.52 171.08 25 26.34 0.05 0.01 1.80
    8:40 42.48 498.73 84 80.65 0.04 0.02 11.22 9:20 36.07 428.21 145 140.12 0.03 0.02 23.81
    8:50 44.24 526.30 90 84.07 0.07 0.04 35.11 9:30 39.29 556.78 137 135.26 0.01 0.01 3.03
    9:00 43.69 552.73 91 89.66 0.01 0.01 1.80 9:40 39.48 364.60 58 63.25 0.09 0.02 27.56
    9:10 43.29 572.15 95 95.71 0.01 0.00 0.50 9:50 36.55 291.87 50 55.56 0.11 0.03 30.91
    9:20 44.16 577.01 103 97.15 0.06 0.04 34.17 10:00 36.52 323.32 70 72.69 0.04 0.01 7.23
    9:30 42.08 608.90 111 110.15 0.01 0.01 0.72 10:10 40.46 647.12 56 59.36 0.06 0.02 11.29
    9:40 43.88 643.27 112 114.78 0.02 0.02 7.73 10:20 42.29 471.39 60 67.35 0.12 0.03 54.02
    9:50 44.97 660.41 118 116.86 0.01 0.01 1.30 10:30 40.12 422.82 69 74.25 0.08 0.02 27.56
    10:00 46.23 689.73 122 121.52 0.00 0.00 0.23 10:40 39.86 355.46 52 58.56 0.13 0.03 43.03
    10:10 47.69 721.67 134 130.12 0.03 0.02 15.03 10:50 37.21 335.57 190 187.56 0.01 0.01 5.95
    10:20 46.45 757.03 136 141.86 0.04 0.04 34.35 11:00 40.62 548.37 205 201.32 0.02 0.02 13.54
    10:30 46.66 776.57 140 146.16 0.04 0.04 37.95 11:10 43.14 614.47 35 38.45 0.10 0.02 11.90
    10:40 47.27 798.90 144 148.99 0.03 0.03 24.90 11:20 41.61 559.81 182 185.45 0.02 0.02 11.90
    10:50 49.59 804.94 148 149.45 0.01 0.01 2.09 11:30 47.08 685.34 165 160.25 0.03 0.02 22.56
    11:00 50.09 839.69 153 150.93 0.01 0.01 4.27 11:40 47.73 536.57 46 49.36 0.07 0.02 11.29
    11:10 50.22 852.43 152 151.16 0.01 0.01 0.70 11:50 39.88 190.67 24 32.13 0.34 0.04 66.06
    11:20 51.26 869.61 151 151.49 0.00 0.00 0.24 12:00 38.71 697.05 205 199.91 0.02 0.02 25.92
    11:30 52.55 871.66 155 151.89 0.02 0.02 9.65 12:10 48.17 691.84 44 48.25 0.10 0.02 18.06
    11:40 53.20 876.80 148 152.20 0.03 0.03 17.61 12:20 39.87 357.89 211 201.32 0.05 0.05 93.70
    11:50 54.57 881.92 157 152.62 0.03 0.03 19.17 12:30 49.96 999.30 95 97.56 0.03 0.01 6.55
    12:00 54.18 899.63 164 152.69 0.07 0.07 127.96 12:40 47.13 314.66 17 14.12 0.17 0.01 8.32
    12:10 52.84 908.85 158 152.26 0.04 0.03 32.89 12:50 33.73 159.05 42 27.91 0.34 0.07 198.40
    12:20 53.69 897.87 155 152.54 0.02 0.01 6.04 13:00 35.99 595.71 96 100.23 0.04 0.02 17.89
    12:30 53.28 887.53 158 152.33 0.04 0.03 32.14 13:10 45.39 494.68 116 117.25 0.01 0.01 1.56
    12:40 54.17 891.21 162 152.64 0.06 0.06 87.68 13:20 44.69 611.38 171 175.26 0.02 0.02 18.15
    12:50 53.98 887.54 149 152.56 0.02 0.02 12.66 13:30 48.66 771.60 47 48.56 0.03 0.01 2.43
    13:00 54.87 860.72 152 152.27 0.00 0.00 0.07 13:40 38.09 197.20 47 48.56 0.03 0.01 2.43
    13:10 54.84 878.20 150 152.61 0.02 0.02 6.82 13:50 32.41 269.89 129 130.89 0.01 0.01 3.57
    13:20 55.48 831.79 142 150.83 0.06 0.05 77.96 14:00 40.22 611.36 120 122.36 0.02 0.01 5.57
    13:30 54.47 820.42 130 149.67 0.15 0.12 386.98 14:10 44.97 622.18 131 131.64 0.00 0.00 0.41
    13:40 54.04 663.15 52 54.15 0.04 0.01 4.63 14:20 45.83 564.36 160 159.30 0.00 0.00 0.49
    13:50 49.97 544.29 53 80.33 0.52 0.17 747.13 14:30 50.30 816.62 140 142.35 0.02 0.01 5.52
    14:00 51.01 731.88 137 128.69 0.06 0.05 69.02 14:40 52.02 732.09 154 156.35 0.02 0.01 5.52
    14:10 52.71 735.79 128 117.28 0.08 0.07 114.83 14:50 51.68 601.10 69 70.85 0.03 0.01 3.42
    14:20 52.35 749.46 125 129.11 0.03 0.03 16.87 15:00 46.00 546.27 152 156.35 0.03 0.02 18.92
    14:30 52.34 753.09 137 131.53 0.04 0.03 29.91 15:10 49.51 730.86 132 136.78 0.04 0.02 22.85
    14:40 51.80 747.67 117 131.58 0.12 0.09 212.58 15:20 49.95 708.75 141 145.78 0.03 0.02 22.85
    14:50 51.56 711.90 116 114.97 0.01 0.01 1.07 15:30 49.20 559.45 53 52.82 0.00 0.00 0.03
    15:00 51.18 662.45 106 104.95 0.01 0.01 1.11 15:40 44.75 318.37 46 48.96 0.06 0.01 8.76
    15:10 51.41 638.30 107 96.93 0.09 0.06 101.36 15:50 42.11 492.21 61 65.89 0.08 0.02 23.91
    15:20 50.84 595.64 89 91.43 0.03 0.01 5.92 16:00 44.46 562.50 114 116.58 0.02 0.01 6.66
    15:30 50.35 577.80 99 89.09 0.10 0.06 98.29 16:10 45.29 498.01 77 79.36 0.03 0.01 5.57
    15:40 49.93 540.84 76 80.03 0.05 0.02 16.28 16:20 43.82 376.77 33 35.26 0.07 0.01 5.11
    15:50 49.64 485.17 69 68.35 0.01 0.00 0.42 16:30 36.07 141.85 18 20.45 0.14 0.01 6.00
    16:00 48.68 457.16 63 67.18 0.07 0.03 17.44 16:40 29.57 142.20 25 22.73 0.09 0.01 5.14
    16:10 47.84 425.11 66 60.73 0.08 0.03 27.75 16:50 32.19 264.58 68 70.58 0.04 0.01 6.66
    16:20 47.33 423.65 61 62.31 0.02 0.01 1.71 17:00 35.65 376.54 60 62.58 0.04 0.01 6.66
    16:30 46.93 365.12 53 51.48 0.03 0.01 2.31 17:10 38.40 362.04 35 38.69 0.11 0.02 13.62
    16:40 46.94 340.34 54 48.91 0.09 0.03 25.94 17:20 36.32 186.05 41 42.58 0.04 0.01 2.50
    16:50 46.08 322.37 46 48.30 0.05 0.01 5.31 17:30 35.49 263.20 37 39.58 0.07 0.01 6.66
    17:00 45.61 293.01 41 42.95 0.05 0.01 3.78 17:40 37.16 241.27 32 36.58 0.14 0.02 20.98
    17:10 45.02 258.41 34 33.69 0.01 0.00 0.10 17:50 36.45 197.13 27 32.74 0.21 0.03 32.94
    17:20 44.47 228.00 30 27.60 0.08 0.01 5.77 18:00 35.59 162.13 23 25.68 0.12 0.01 7.18
    17:30 44.00 209.78 26 25.58 0.02 0.00 0.18 18:10 34.88 170.54 22 30.57 0.39 0.04 73.46
    17:40 43.51 177.61 23 23.95 0.04 0.01 0.90 18:20 33.48 142.32 17 26.05 0.53 0.04 81.96
    Average 47.26 593.61 98.26 98.19 0.05 0.03 0.04 Average 39.53 407.10 77 78.85 0.09 0.02 0.02
    • Abbreviations: ANFIS, adaptive neural-fuzzy inference system; MAPE, mean absolute percentage error; NMAE, normalized mean absolute error; nRMSE, normalized root mean square error.

    From Table 8, it is evident that for clear sky condition (blue sky), the MAPE has been observed to be 0.05% when simulated between the forecasted and measured data; and for the hazy and cloudy sky (partially) the MAPE has been observed to be 0.09%, respectively.

    Similarly, for the hazy sky (fully) condition, the average MAPE has been observed to be 0.03% when simulated between the forecasted and measured data; and for the cloudy sky (fully) the MAPE has been observed to be 0.18% as shown in Table 9.

    Table 9. Short-term PV power forecast employing ANFIS-based model for a hazy sky (fully) under composite climatic conditions
    Hazy sky (fully) Cloudy sky (fully)
    Power (W) Power (W)
    Time (h) Cell temperature (°C) Solar irradiance (W/m2) Measured ANFIS MAPE (%) NMAE (%) NRMSE (%) Time (h) Cell temperature (°C) Solar irradiance (W/m2) Measured ANFIS MAPE (%) NMAE (%) NRMSE (%)
    9:50 10.41 120.74 19 22.30 0.17 0.02 10.87 8:40 14.86 168.07 19 25.00 0.32 0.09 36.00
    10:00 10.63 125.45 18 22.36 0.24 0.03 19.01 8:50 13.76 161.85 25 24.13 0.03 0.01 0.76
    10:10 10.21 126.52 22 22.27 0.01 0.00 0.07 9:00 14.97 182.38 21 24.99 0.19 0.06 15.89
    10:20 9.10 127.23 24 22.14 0.08 0.01 3.44 9:10 15.45 101.30 23 29.26 0.27 0.10 39.24
    10:30 5.45 125.81 24 22.08 0.08 0.01 3.70 9:20 15.35 135.45 15 24.57 0.64 0.15 91.63
    10:40 12.43 150.74 25 23.55 0.06 0.01 2.10 9:30 15.08 132.03 28 24.77 0.12 0.05 10.44
    10:50 8.37 171.66 25 22.95 0.08 0.01 4.19 9:40 15.75 101.30 60 54.25 0.10 0.09 33.06
    11:00 10.67 174.73 25 23.40 0.06 0.01 2.55 9:50 19.77 101.30 64 64.01 0.00 0.00 0.00
    11:10 11.50 208.48 33 34.07 0.03 0.01 1.14 10:00 19.73 181.75 27 27.16 0.01 0.00 0.03
    11:20 18.44 227.30 33 31.93 0.03 0.01 1.14 10:10 17.71 261.96 11 9.56 0.13 0.02 2.07
    11:30 17.34 247.76 39 41.64 0.07 0.02 6.95 10:20 16.14 187.71 16 22.69 0.42 0.10 44.71
    11:40 19.01 276.06 37 37.05 0.00 0.00 0.00 10:30 15.76 129.26 14 16.23 0.16 0.03 4.97
    11:50 16.92 406.26 57 55.45 0.03 0.01 2.40 10:40 15.14 101.30 21 22.89 0.09 0.03 3.58
    12:00 17.24 479.51 49 51.99 0.06 0.02 8.96 10:50 14.45 101.30 18 22.25 0.24 0.07 18.05
    12:10 17.48 498.50 69 66.41 0.04 0.02 6.70 11:00 14.77 101.30 24 22.28 0.07 0.03 2.97
    12:20 22.37 527.75 139 136.34 0.02 0.02 7.07 11:10 15.13 101.30 22 22.81 0.04 0.01 0.66
    12:30 25.23 527.66 135 142.69 0.06 0.05 59.15 11:20 15.32 120.11 23 24.85 0.08 0.03 3.42
    12:40 27.16 525.47 153 146.73 0.04 0.04 39.37 11:30 15.28 101.30 19 24.29 0.28 0.08 27.98
    12:50 31.56 525.18 150 147.44 0.02 0.02 6.54 11:40 14.93 127.09 22 24.52 0.11 0.04 6.37
    13:00 32.20 512.66 150 147.44 0.02 0.02 6.56 11:50 15.10 101.30 37 35.26 0.05 0.03 3.03
    13:10 30.07 500.73 159 147.39 0.07 0.07 134.88 12:00 16.76 101.30 26 29.56 0.14 0.06 12.67
    13:20 31.91 489.57 145 147.38 0.02 0.01 5.65 12:10 17.05 134.24 33 25.45 0.23 0.12 57.00
    13:30 35.14 494.87 143 147.41 0.03 0.03 19.41 12:20 17.61 123.50 30 27.67 0.08 0.04 5.45
    13:40 35.69 491.77 134 137.25 0.02 0.02 10.56 12:30 17.46 148.36 33 31.78 0.04 0.02 1.49
    13:50 32.66 427.95 143 141.34 0.01 0.01 2.75 12:40 17.42 142.59 17 22.95 0.35 0.09 35.42
    14:00 33.05 401.02 125 125.52 0.00 0.00 0.27 12:50 16.14 150.40 15 22.76 0.52 0.12 60.14
    14:10 34.07 400.24 127 124.92 0.02 0.01 4.33 13:00 15.43 145.55 33 24.21 0.27 0.14 77.35
    14:20 34.09 357.63 114 114.48 0.00 0.00 0.23 13:10 16.44 101.30 50 45.21 0.10 0.07 22.94
    14:30 31.96 331.88 114 113.55 0.00 0.00 0.21 13:20 16.17 101.30 23 23.58 0.03 0.01 0.34
    14:40 32.76 285.04 99 104.56 0.06 0.03 30.94 13:30 14.61 217.00 24 23.98 0.00 0.00 0.00
    14:50 29.54 261.53 95 89.16 0.06 0.04 34.07 13:40 14.99 155.18 44 36.78 0.16 0.11 52.13
    15:00 31.93 242.06 77 75.63 0.02 0.01 1.88 13:50 16.19 101.30 41 39.23 0.04 0.03 3.14
    15:10 31.82 230.01 69 69.24 0.00 0.00 0.06 14:00 16.00 151.67 29 22.76 0.22 0.10 38.94
    15:20 29.72 221.92 63 66.01 0.05 0.02 9.08 14:10 15.87 187.44 29 22.74 0.22 0.10 39.15
    15:30 27.89 188.42 58 60.77 0.05 0.02 7.70 14:20 15.65 176.43 18 23.09 0.28 0.08 25.95
    15:40 26.57 155.54 60 57.50 0.04 0.02 6.26 14:30 15.27 128.87 17 24.67 0.45 0.12 58.82
    Average 23.41 321.27 81.97 81.73 0.03 0.02 0.02 Average 15.93 137.94 27 27.56 0.18 0.06 0.08
    • Abbreviations: ANFIS, adaptive neural-fuzzy inference system; MAPE, mean absolute percentage error; NMAE, normalized mean absolute error; nRMSE, normalized root mean square error.

    From Tables 8, 9, it has been observed that the hazy sky model gives better performance to forecast short-term PV power in a smart grid system with MAPE of 0.03%, which is followed by clear sky, hazy and cloudy sky, and cloudy sky model with MAPE of 0.05%, 0.09%, and 0.18%, respectively. Furthermore, the comparative analysis of measured and forecasted power employing ANFIS-based model under four weather types is shown in Figure 11.

    Details are in the caption following the image
    Figure 11
    Open in figure viewerPowerPoint
    Graphical analysis of power output in a solar photovoltaic system for different weather condition under the composite climate zone

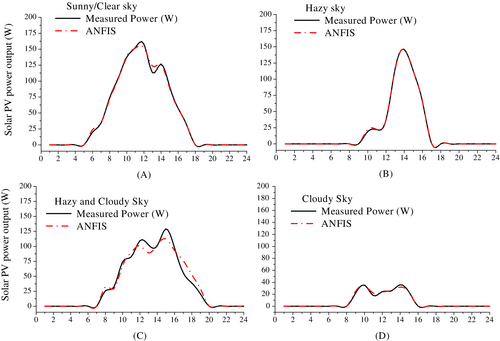
    It can be seen from Figure 11 that the power generation in a solar PV system has varied significantly with the varying weather condition. Such forecasts would be helpful for managing supply and demand in a smart grid environment and would help the technocrats, utility and designer for a smart energy management system where solar power forecasting has been important in this new paradigm.

    7 COMPARISON OF ANFIS-BASED MODEL WITH OTHER MODELS

    The proposed model has been compared with other available models in the literature to forecast global solar energy. Table 10 demonstrates the obtained statistical performance indices for SVM, MARS, GRNN, FFNN, LNN, fuzzy logic, and empirical models based on multiple regression analysis, respectively. Nevertheless, the SVM model performs better than the ANN model employing FFNN with MAPE of 2.9 × 10−5%. Furthermore, the variants of ANN model have been investigated, that is, FFNN, LNN, and GRNN and it has been observed that FFNN model performs better than the LNN and GRNN models. In addition, a comparison has been made between MARS and FFNN model, and it has been observed from the statistical analysis that the MARS model performs better than the FFNN model. In addition, the model has been developed using fuzzy logic-based approach and empirical models based on multiple regression analysis and it has been observed that the fuzzy logic-based model performs better than empirical models. From Table 10, it has been clearly shown that on comparing different models, however, the ANFIS-based model provides more accuracy in results as compared with other models with MAPE of 2.1 × 10−7%.

    Table 10. Comparison of ANFIS-based model with other models
    ANFIS SVM FFNN LNN GRNN MARS Fuzzy Regression
    Months Measured global solar energy Hg (MJ/m2) Forecasted Hg (MJ/m2) MAPE (%) Forecasted Hg (MJ/m2) MAPE (%) Forecasted Hg (MJ/m2) MAPE (%) Forecasted Hg (MJ/m2) MAPE (%) Forecasted Hg (MJ/m2) MAPE (%) Forecasted Hg (MJ/m2) MAPE (%) Forecasted Hg (MJ/m2) MAPE (%) Forecasted Hg (MJ/m2) MAPE (%)
    January 13.985 13.98 0.00000016 13.96 0.000036 13.969 0.0018 13.951 0.021 13.91 0.26 13.96 0.00015 13.85 0.79 14.02 1.21
    February 16.788 16.79 0.00000017 16.8 0.000021 16.903 0.0047 16.788 0 16.76 0.31 16.80 0.00042 16.62 0.82 16.79 0.96
    March 21.118 21.12 0.00000020 21.14 0.000010 21.131 0.0019 21.123 0.044 21.3 0.27 21.13 0.00017 21.12 0.19 21.11 1.53
    April 25.214 25.21 0.00000010 25.17 0.000025 25.166 0.0008 25.215 0.004 25.26 0.2 25.17 0.00021 25.16 0.13 25.25 0.89
    May 24.227 24.23 0.00000020 24.26 0.000046 24.251 0.0009 24.23 0.013 24.28 0.18 24.24 0.00032 23.58 1.65 24.22 0.31
    June 20.912 20.91 0.00000025 20.94 0.000026 20.931 0.0009 20.912 0 21.17 0.36 20.91 0.00016 21.23 1.70 20.93 2.58
    July 19.381 19.38 0.00000014 19.34 0.000045 19.339 0.0019 19.381 0.036 19.31 0.47 19.30 0.00051 19.53 1.25 19.38 3.23
    August 18.802 18.8 0.00000021 18.84 0.000021 18.837 0.0015 18.804 0.008 18.95 0.54 18.82 0.00062 18.98 0.69 18.85 3.51
    September 13.851 13.85 0.00000019 13.84 0.000015 13.854 0.0008 13.853 0.004 13.83 0.24 13.83 0.00071 13.89 0.85 13.90 1.37
    October 18.334 18.33 0.00000027 18.31 0.000021 18.339 0.0011 18.335 0.012 18.36 0.21 18.33 0.00022 18.72 1.12 18.36 0.39
    November 14.562 14.56 0.00000011 14.51 0.000032 14.568 0.0004 14.564 0.024 14.59 0.21 14.57 0.00023 14.48 1.01 14.58 0.76
    December 12.124 12.12 0.00000051 12.16 0.000055 12.151 0.0071 12.127 0.027 12.21 0.37 12.18 0.00035 12.30 1.56 12.12 3.27
    Average 18.275 18.27 0.00000021 18.2725 0.000029 18.287 0.0020 18.273 0.016 18.33 0.30 18.27 0.00034 18.29 0.98 18.29 1.67
    • Abbreviations: ANFIS, adaptive neural-fuzzy inference system; FFNN, feedforward neural network; GRNN, generalized regression neural network; LNN, linear neural network; MAPE, mean absolute percentage error; MARS, multivariate adaptive regression splines; SVM, support vector machine.

    8 CONCLUSION

    In this research, ANFIS-based model has been established for forecasting global solar energy with the aid of meteorological parameters for different weather condition such as clear sky (blue sky), hazy sky (partially), hazy and cloudy sky (fully), and cloudy sky (fully) and successfully applied for different climate zones across the entire country. The proposed model has been trained for forecasting global solar energy. The validation of the model was performed with the unknown test data, which the model has not seen before. It has been concluded from the overall analysis that by employing ANFIS-based model, the error has been reduced significantly for each of the climate zones across the entire country. Furthermore, out of the four models investigated, it has been observed that the sunny/clear sky model gives better performance for Jodhpur station representing a hot and dry climate zone. Similarly, the hazy sky model provides favorable results for Delhi station representing composite climatic conditions, hazy and cloudy sky model is favorable for Chennai station representing warm and humid climatic conditions and lastly, cloudy sky model achieves favorable results for Shillong station representing cold and cloudy climatic conditions. The accuracy has been found within the acceptable range used by design engineers, to confirm the validity of the proposed model. The advantage of the ANFIS-based model is that its convergence time has improved significantly, thus, ANFIS-based model provides more accuracy and have shown promising results in comparison to other models available in the literature. The number of sites used together with their geographical range allows us to conclude that the proposed model is generally valid for forecasting global solar energy in each climate zones across the entire country.

    Furthermore, the obtained results have been exploited to forecast short-term PV power in a smart grid system based on weather condition that employs 250 Wp multicrystalline solar PV modules operated at MPP conditions for composite climate zone. It has been concluded that the hazy sky model performs well for the composite climate zone as compared with other models. The comparative results demonstrate the predicting capability of ANFIS-based model and its compatibility for any region with varying climatic conditions. Possible application of the proposed model can be found in meteorology, renewable energy, and solar energy conversion devices. The prediction of solar energy makes it suitable for installation of a monitoring station for a remote place and furthermore, can be extended for sizing of a standalone PV system as a part of the future work.

    ACKNOWLEDGEMENTS

    The authors would like to thank Solar Energy Centre, Ministry of New and Renewable Energy (MNRE), New Delhi, India for providing data for current research work.

      CONFLICT OF INTEREST

      All the authors declare that they have no conflict of interest.

      AUTHOR CONTRIBUTIONS

      Gulnar Perveen, Methodology-Lead, Conceptualisation-Lead, Project administration-Lead, Validation-Lead, Writing-review & Editing-Lead, writing-original draft-lead; Mohammad Rizwan, lead conceptualization, methodology, project administration, software, supervision, validation, and editing and reviewed writing; Nidhi Goel, lead conceptualization, software, and writing original draft

      APPENDIX A

      Table A1. Statistical analysis of training and testing dataset for warm and humid climate zone (Latitude 13.082°N, Longitude 80.270°E)
      Dataset Parameter Max Min Mean Standard deviation
      Training Hg (MJ/m2) 21.92 12.80 17.64 2.33
      Sunshine hours (h) 10.90 3.00 8.94 1.87
      Air temperature (°C) 36.82 37.00 25.46 2.26
      Relative humidity (%) 81.33 60.54 71.32 5.69
      Wind speed (m/s) 12.17 5.42 8.22 1.59
      Dew-point (°C) 21.96 18.94 20.33 0.71
      Testing Hg (MJ/m2) 20.78 6.00 13.88 4.12
      Sunshine hours (h) 10.50 3.90 7.07 2.99
      Air temperature (°C) 34.97 23.66 26.09 2.27
      Relative humidity (%) 88.63 66.13 78.13 5.04
      Wind speed (m/s) 15.79 3.21 9.50 3.81
      Dew-point (°C) 23.42 19.09 21.17 1.07
      Table A2. Statistical analysis of training and testing dataset for hot and dry climate zone (Latitude 26.23°N, Longitude 73.020°E)
      Dataset Parameter Max Min Mean Standard deviation
      Training Hg (MJ/m2) 19.13 11.48 16.24 1.91
      Sunshine hours (h) 10.50 4.50 9.16 1.37
      Air temperature (°C) 22.12 14.76 18.09 1.60
      Relative humidity (%) 79.62 25.20 45.32 9.58
      Wind speed (m/s) 12.62 3.500 6.370 4.24
      Dew-point (°C) 6.30 −2.33 2.220 2.68
      Testing Hg (MJ/m2) 16.90 13.84 14.67 0.83
      Sunshine hours (h) 9.300 2.300 8.50 1.26
      Air temperature (°C) 21.28 14.87 18.63 1.62
      Relative humidity (%) 56.79 37.83 48.52 5.10
      Wind speed (m/s) 7.750 2.750 3.210 1.64
      Dew-point (°C) 11.82 −13.64 0.220 5.64
      Table A3. Statistical analysis of training and testing dataset for composite climate zone (Latitude 28.70°N, Longitude 77.10°E)
      Dataset Parameter Max Min Mean Standard deviation
      Training Hg (MJ/m2) 17.99 11.20 13.98 1.52
      Sunshine hours (h) 10.00 2.70 7.72 1.63
      Air temperature (°C) 17.93 10.76 14.12 1.83
      Relative humidity (%) 81.58 56.75 65.49 6.13
      Wind speed (m/s) 11.75 2.75 5.15 3.03
      Dew-point (°C) 8.90 −15.04 −4.60 5.99
      Testing Hg (MJ/m2) 15.32 7.48 12.12 2.12
      Sunshine hours (h) 8.50 3.80 5.26 2.70
      Air temperature (°C) 19.17 13.27 15.99 1.61
      Relative humidity (%) 87.58 45.41 65.68 8.69
      Wind speed (m/s) 11.58 2.66 5.93 2.85
      Dew-point (°C) 9.73 −5.01 0.03 3.64
      Table A4. Statistical analysis of training and testing dataset for moderate climate zone (Latitude 18.52°N, Longitude 73.85°E)
      Dataset Parameter Max Min Mean Standard deviation
      Training Hg (MJ/m2) 18.62 14.19 16.99 1.09
      Sunshine hours (h) 10.10 8.80 9.49 0.28
      Air temperature (°C) 21.93 17.98 19.78 0.93
      Relative humidity (%) 68.04 52.12 59.88 4.34
      Wind speed (m/s) 2.98 1.02 1.49 0.58
      Dew-point (°C) 17.56 5.79 11.58 3.35
      Testing Hg (MJ/m2) 18.93 10.78 17.10 1.95
      Sunshine hours (h) 9.90 4.30 8.74 1.68
      Air temperature (°C) 22.20 16.32 19.27 1.53
      Relative humidity (%) 75.41 55.37 63.01 4.82
      Wind speed (m/s) 3.87 1.02 2.43 0.81
      Dew-point (°C) 19.30 10.01 16.33 2.50
      Table A5. Statistical analysis of training and testing dataset for cold and cloudy climate zone (Latitude 25.57°N, Longitude 91.89°E)
      Dataset Parameter Max Min Mean Standard deviation
      Training Hg (MJ/m2) 19.75 3.62 14.43 3.51
      Sunshine hours (h) 9.10 5.20 7.060 2.38
      Air temperature (°C) 12.10 5.60 9.950 1.47
      Relative humidity (%) 97.50 60.50 75.58 8.54
      Wind speed (m/s) 11.00 2.00 3.630 2.66
      Dew-point (°C) 12.33 1.17 6.420 2.61
      Testing Hg (MJ/m2) 18.78 9.30 15.63 2.11
      Sunshine hours (h) 9.20 4.30 7.600 1.48
      Air temperature (°C) 15.50 10.30 11.88 1.11
      Relative humidity (%) 89.00 51.00 74.40 9.03
      Wind speed (m/s) 4.00 1.20 2.850 1.06
      Dew-point (°C) 14.36 5.14 10.04 2.24

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.